Математика группа 2-4 с 15.04 по 17.04

План урока

Урок №

Предмет :Математика

Дата проведения : 15.04.2020.

Группа № 2-4

Специальность: 35.01.13.Тракторист-машинист сельскохозяйственного производства.

Преподаватель :Хизриева Н.А.

Тема урока : Выполнение упражнений на нахождение производных .

Конспект урока

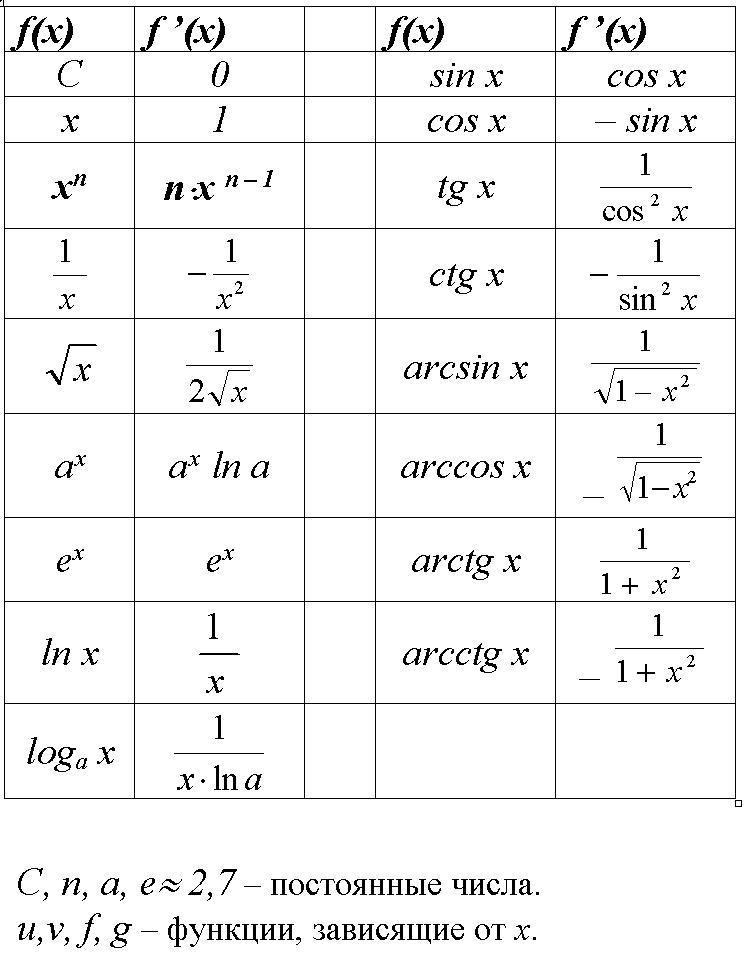
Производные - это такие функции, которые получаются из заданных функций путем вычисления предела разностного отношения. Разностным отношением называется отношение разности значения функции к разности значений переменной.

После закрепления знаний по таблице производной, приступаем к изучению теорем дифференцирования.

Теорема 1. Производная суммы любого числа функций равна сумме производных этих функций. Для трех функций, например, имеем:

Теорема 2. Производная произведения двух функций равна:

Теорема 3. Производная частного двух функций равна:

Приложение 1

Ранее мы рассматривали производные отдельных функций. Здесь мы рассмотрим правила дифференцирования, то есть правила дифференцирования суммы, разности, произведения и частного отдельных функций. Мы выведем соответствующие формулы, обоснуем их и решим типовые примеры.

Производная суммы

1.

Пример

1.  .

2. Найти значение производной функции   в точке  :

;   

Производная произведения

2.

Производная степенной функции

Производная степенной функции:

Рассмотрим частные случаи:

; 

Найдем эту производную по правилу произведения:

С другой стороны:

И так далее. Поэтому угадывается формула:

 – мы принимаем ее без доказательства.

Производная частного

3 .

Решение примеров

Пример

.

.

Домашнее задание: Итоговые тесты по теме «Производная функции»

1. Найдите производную функции y_(х) = x⁴+ 3x³ + 4.

1) 4x³ + 9x² + 4

2) 4x³ + 9x² + 4x

3) 4x² + 3x² + 4

4) 4x³ + 9x²

2. Производная функции F(x) = cos(4x) равна:

1) -4sin(4x)

2) 4cos(- 4x)

3) 4xsin(4x)

4) 4xcos(- 4x)

3. Вычислите значение производной функции в точке .

4. Производная функции y_(х) = x³+ 2x⁵ -6 равна:

1) 3x³ + 10x⁴ + 6

2) x³ + 10x² -6х

3) x² + 3x⁴

4) 3x³ + 10x⁴-6

5. Производная функции F(x) = sin(3x) равна:

1) 3cos(x)

2) 3xsin(3x)

3) cos(3x)

4) xcos(3x

Жду ваши ответы и вопросы на своей электронной почте
[email protected]

План урока

Урок №

Предмет :Математика

Дата проведения : 17.04.2020.

Группа № 2-4

Специальность: 35.01.13.Тракторист-машинист сельскохозяйственного производства.

Преподаватель :Хизриева Н.А.

Тема :Выполнение упражнений на нахождение наибольшего и наименьшего значения .

Конспект урока .

Нахождение наибольшего и наименьшего значений функции без производной

Дано: , . Нарисуем график функции (см. рис.1).

Рис. 1. График функции .

Известно, что эта функция возрастает на промежутке , значит, она возрастает и на отрезке . А значит, если найти значение функции в точках  и , то будут известны пределы изменения данной функции, ее самое большое и самое маленькое значение.

Когда аргумент возрастает от  до 8, функция возрастает от  до .

Ответ: ; .

4. Нахождение наибольшего и наименьшего значений функции с помощью производной

Дано: , . Найти наибольшее и наименьшее значение функции на данном отрезке.

Если в предыдущем случае можно было обойтись без производной – мы знали, как себя ведет функция, то в данном случае функция довольно сложная. Поэтому, ту методику, которую мы упомянули на предыдущей задаче, применим в полном объеме.

1. Найдем производную . Найдем критические точки  , отсюда ,  - критические точки. Из них выбираем те, которые принадлежат данному отрезку: . Сравним значение функции в точках

, , . Для этого найдем

;

;

.

Проиллюстрируем результат на рисунке (см. рис.3).

Рис. 3. Пределы изменения значений функции

Видим, что если аргумент меняется от 0 до 2, функция изменяется в пределах от -3 до 4. Функция меняется не монотонно: она либо возрастает, либо убывает.

Ответ: ; .

Алгоритм решения задачи на нахождение наибольшего и наименьшего значений функции

Итак, на трех примерах была продемонстрирована общая методика нахождения наибольшего и наименьшего значения функции на промежутке, в данном случае – на отрезке.

Алгоритм решения задачи на нахождение наибольшего и наименьшего значений функции:

1. Найти производную функции.

2. Найти критические точки функции и отобрать те точки, которые находятся на заданном отрезке.

3. Найти значения функции на концах отрезка и в отобранных точках.

4. Сравнить эти значения, и выбрать наибольшее и наименьшее.

6. Решение задачи

Рассмотрим еще один пример.

Найти наибольшее и наименьшее значение функции , .

Ранее был рассмотрен график этой функции (см. рис.4).

Рис. 4. График функции .

На промежутке  область значения этой функции . Точка  - точка максимума. При  - функция возрастает, при  – функция убывает. Из чертежа видно, что ,  - не существует.

7. Итог урока

Итак, на уроке рассмотрели задачу о наибольшем и наименьшем значении функции, когда заданным промежутком является отрезок; сформулировали алгоритм решения подобных задач.

Домашнее задание: Пример № 1

Найти наименьшее значение функции на отрезке .

Жду ваши ответы и вопросы на своей электронной почте
[email protected]