Математика. Комбинаторика. Перестановки. Примеры + решения.

Перестановки — это специальный случай размещений, когда выборка так же велика, как данное множество.

Размещения по n элементов из n называются перестановками из n элементов.

Вычисляя перестановки, определяется, сколькими различными способами можно переупорядочить элементы множества, не меняя их количество.

Количество перестановок обозначается как Pn, где n — количество элементов множества.

Перестановки вычисляются по формуле Pn=n!

Если дано множество из двух элементов a;b, из этого множества можно составить две упорядоченные выборки: a;b  и  b;a.

Из двух элементов (n=2) можно составить 2 перестановки, т.е. P2=2!=1⋅2

  Если дано 3 элемента a;b;c, размещения такие:

1. a;b;c    3. b;a;c     5. c;a;b  

2. a;c;b    4. b;c;a     6. c;b;a

Данные элементы можно переупорядочить 6 способами, т.е.  P3=3!=1⋅2⋅3=6

В заданиях на перестановки не важно назвать сами перестановки, а важно назвать их число.

Пример:

Сколькими различными способами можно составить список учеников из 6 человек?

P6=6!=6⋅5⋅4⋅3⋅2⋅1=720

Ответ: список учеников можно составить 720 различными способами. 

Пример:

В соревнованиях участвуют 6 команд: A; B; C; D; E и F. Сколько существует вариантов расположений команд с первого по шестое место, где команда A ни на первом, ни на последнем месте?

1. Вычисляются все возможные порядки построения команд. (Для команды A есть 6 различных позиций: 1-е место, 2-е место, 3-е место... 6-е место)

P6=6!=6⋅5⋅4⋅3⋅2⋅1=720

2. Вычисляются все возможные порядки, где команда A не на первом месте. (Значит, для команды A есть только 5 различных позиций: 2-е место, 3-е место... 6-е место)

P5=5!=5⋅4⋅3⋅2⋅1=120

3. Вычисляются все возможные порядки, где команда A не на последнем месте. (Значит, для команды A есть 5 различных позиций: 1-е место, 2-е место, 3-е место, 4-е место, 5-е место)

P5=5!=5⋅4⋅3⋅2⋅1=120

4. Вычисляется, сколько существует вариантов расположений команд с первого по шестое место, где команда Aни на первом, ни на последнем месте. Из количества всех возможных вариантов вычитаются вычисленные ограничения: 720−(120+120)=480 (способов).

Ответ: при данных условиях команды можно расставить 480 различными способами.

Перестановки в ряд

Перестановкой из  элементов (или -перестановкой) называется -элементное упорядоченное множество, составленное из элементов -элементного множества.

Иначе: Перестановкой из  элементов (или -перестановкой) называется размещение из элементов по  без повторений.

Число перестановок из  элементов без повторений обозначается  от французского словаperturbation.

Теорема: число способов расположить в ряд  различных объектов есть

Замечание: Рекуррентная формула: .

Перестановки симметричных объектов

 различных предметов можно расположить по кругу  способами, а если их можно еще и переворачивать, то  различными способами.

Перестановкой множества из  элементов называется расположение элементов в определенном порядке.

Так, все различные перестановки множества из трех элементов  — это

Очевидно, перестановки можно считать частным случаем размещений при >.

Число всех перестановок из  элементов обозначается  (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле

Пример. Сколькими способами можно расставить  ладей на шахматной доске так, чтобы они не били друг друга?

Решение. Искомое число расстановки  ладей

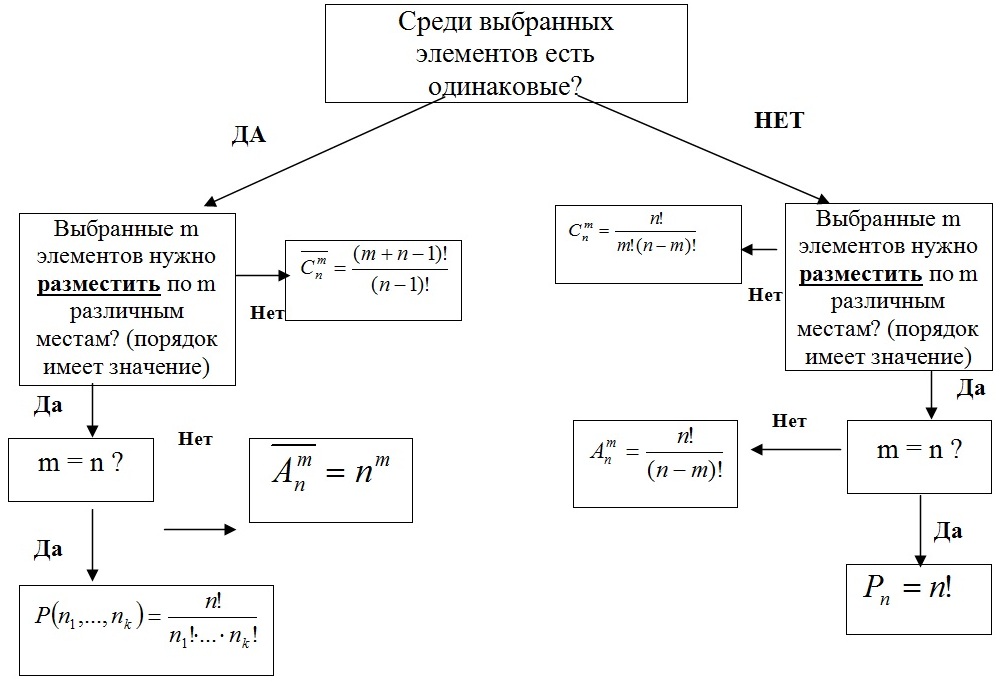
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ "КОМБИНАТОРИКА"