Математика. Комбинаторика. Сочетания. Примеры + решения.

Сочетаниями из  различных элементов по  элементов называются комбинации, которые составлены из данных  элементов по  элементов и отличаются хотя бы одним элементом (иначе говоря, -элементные подмножества данного множества из  элементов).

Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из  элементов по  элементов в каждом обозначается (от начальной буквы французского слова “combinasion”, что значит “сочетание”).

Числа 

Все сочетания из множества  по два — .

.

Свойства чисел {\sf C}_n^k

1. .

Действительно, каждому -элементному подмножеству данного -элементного множества соответствует одно и только одно -элементное подмножество того же множества.

2. .

Действительно, мы можем выбирать подмножества из  элементов следующим образом: фиксируем один элемент; число -элементных подмножеств, содержащих этот элемент, равно ; число -элементных подмножеств, не содержащих этот элемент, равно .

Треугольник Паскаля

В этом треугольнике крайние числа в каждой строке равны 1, а каждое не крайнее число равно сумме двух чисел предыдущей строки, стоящих над ним. Таким образом, этот треугольник позволяет вычислять числа .

.

Теорема.

Доказательство. Рассмотрим множество из  элементов и решим двумя способами следующую задачу: сколько можно составить последовательностей из  элементов данного множества, в каждой из которых никакой элемент не встречается дважды?

1 способ. Выбираем первый член последовательности, затем второй, третий и т.д. член

2 способ. Выберем сначала  элементов из данного множества, а затем расположим их в некотором порядке

Домножим числитель и знаменатель этой дроби на :

Пример. Сколькими способами можно в игре “Спортлото” выбрать 5 номеров из 36?

Искомое число способов

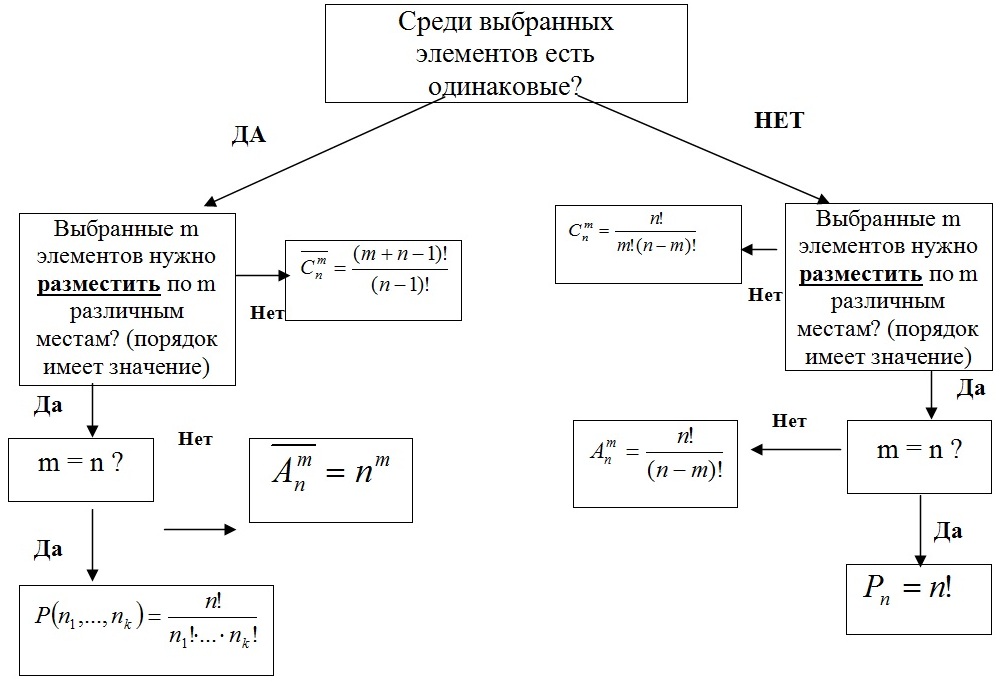
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ "КОМБИНАТОРИКА"