Материал к уроку

Многоугольники

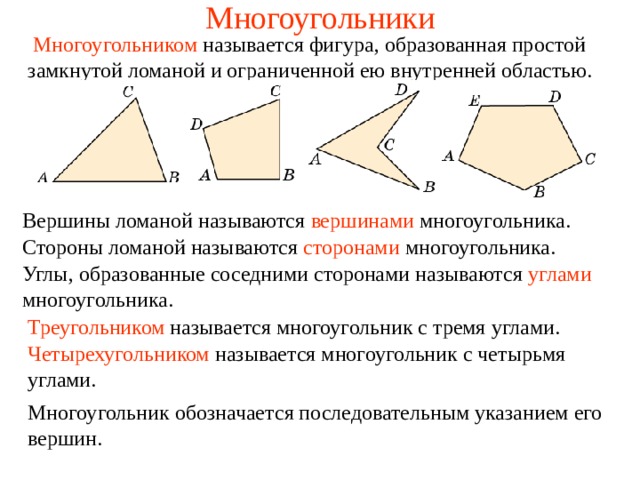
Многоугольником называется фигура, образованная простой замкнутой ломаной и ограниченной ею внутренней областью.

Вершины ломаной называются вершинами многоугольника.

Стороны ломаной называются сторонами многоугольника.

Углы, образованные соседними сторонами называются углами многоугольника.

В режиме слайдов ответы появляются после кликанья мышкой

Треугольником называется многоугольник с тремя углами.

Четырехугольником называется многоугольник с четырьмя углами.

Многоугольник обозначается последовательным указанием его вершин.

Правильные многоугольники

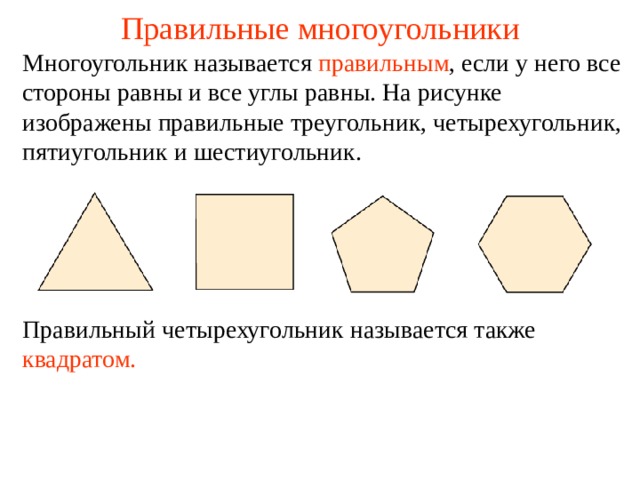
Многоугольник называется правильным , если у него все стороны равны и все углы равны. На рисунке изображены правильные треугольник, четырехугольник, пятиугольник и шестиугольник.

Правильный четырехугольник называется также квадратом.

Выпуклые многоугольники

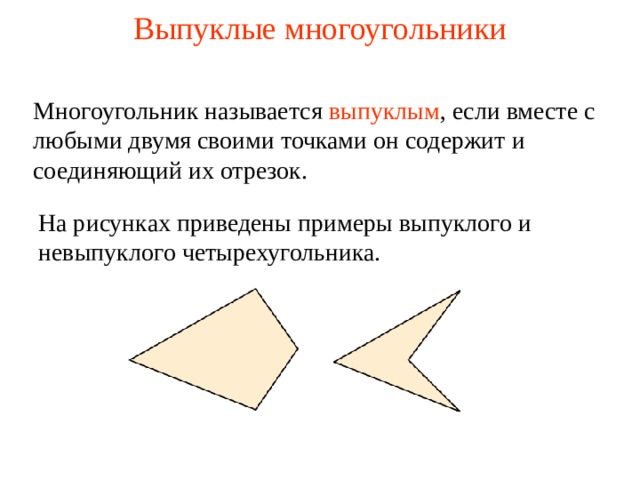
Многоугольник называется выпуклым , если вместе с любыми двумя своими точками он содержит и соединяющий их отрезок.

На рисунках приведены примеры выпуклого и невыпуклого четырехугольника.

Диагонали многоугольника

Д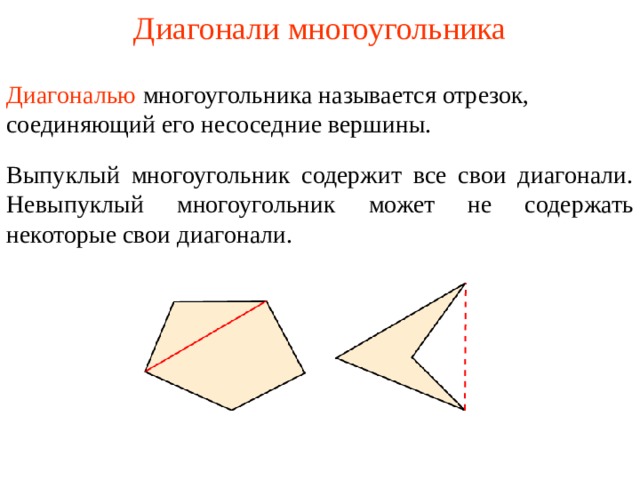 иагональю многоугольника называется отрезок, соединяющий его несоседние вершины.

Выпуклый многоугольник содержит все свои диагонали. Невыпуклый многоугольник может не содержать некоторые свои

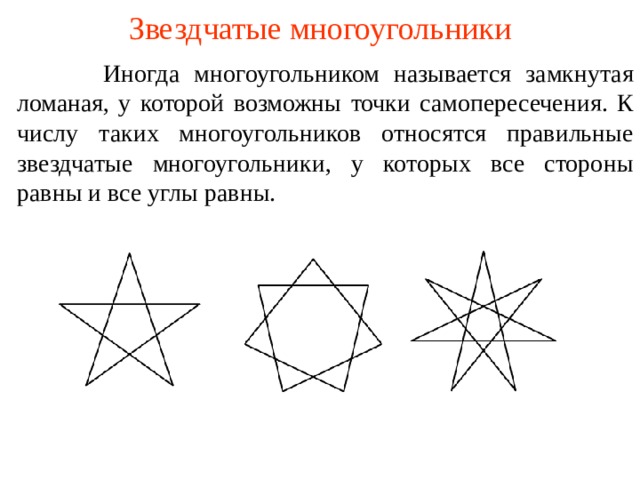
Звездчатые многоугольники

Иногда многоугольником называется замкнутая ломаная, у которой возможны точки самопересечения. К числу таких многоугольников относятся правильные звездчатые многоугольники, у которых все стороны равны и все углы равны.

Упражнение 1

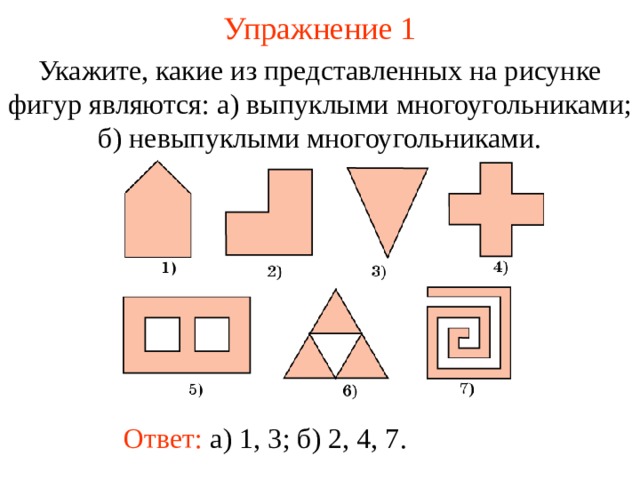
Укажите, какие из представленных на рисунке фигур являются : а) выпуклыми многоугольниками ; б) невыпуклыми многоугольниками.

Ответ: а) 1, 3; б) 2, 4, 7.

Упражнение 2

Какая имеется зависимость между числом вершин , числом углов и числом сторон многоугольника?

Ответ: Число вершин равно числу углов и равно числу сторон.

Упражнение 3

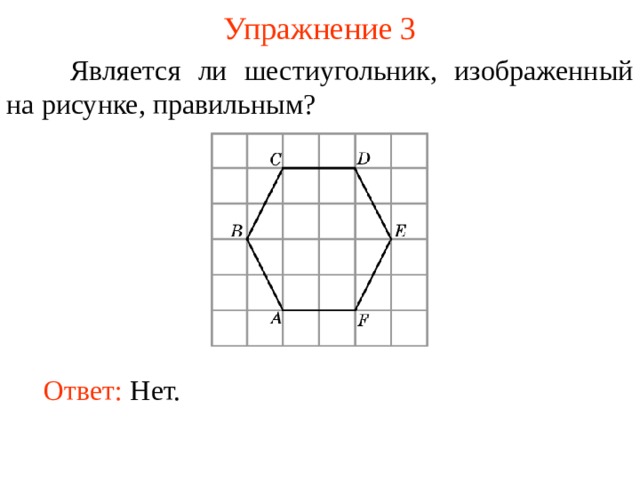
Является ли шестиугольник, изображенный на рисунке, правильным?

Ответ: Нет.

Упражнение 4

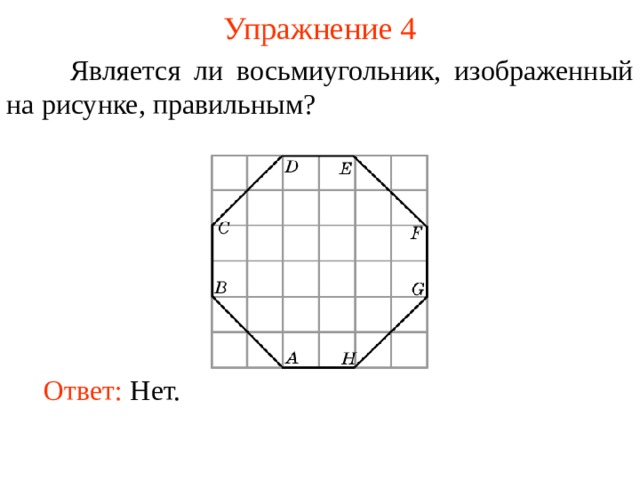
Является ли восьмиугольник, изображенный на рисунке, правильным?

Ответ: Нет.

Упражнение 5

Сколько диагоналей имеет:

а) треугольник? 0; б) четырехугольник? 2;

в) пятиугольник? 5;

г) шестиугольник? 9

Упражнение 6

Существует ли многоугольник, число диагоналей которого равно числу его сторон?

Ответ: Да, пятиугольник.

Упражнение 7

Выпуклый многоугольник имеет 14 диагоналей. Сколько у него сторон?

Ответ: 7.

Упражнение 8 Может ли многоугольник иметь 10 диагоналей ? Ответ: Нет

Упражнение 9. На сколько треугольников делится выпуклый: а) 4-угольник; б) 5-угольник; в) 6-угольник своими диагоналями, проведенными из одной вершины?

Ответ: а) 2; б) 3; в) 4 .

Упражнение 10

Изобразите два треугольника так, чтобы их общей частью (пересечением) был : а) треугольник; б) четырехугольник; в) пятиугольник; г) шестиугольник.

Ответ:

Упражнение 11

Может ли общей частью ( пересечением ) двух треугольников быть семиугольник?

Ответ: Нет.

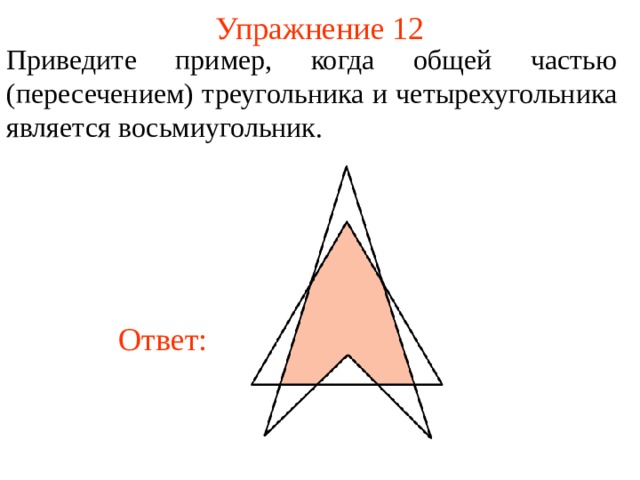
Упражнение 12

Приведите пример, когда общей частью (пересечением) треугольника и четырехугольника является восьмиугольник.

Ответ:

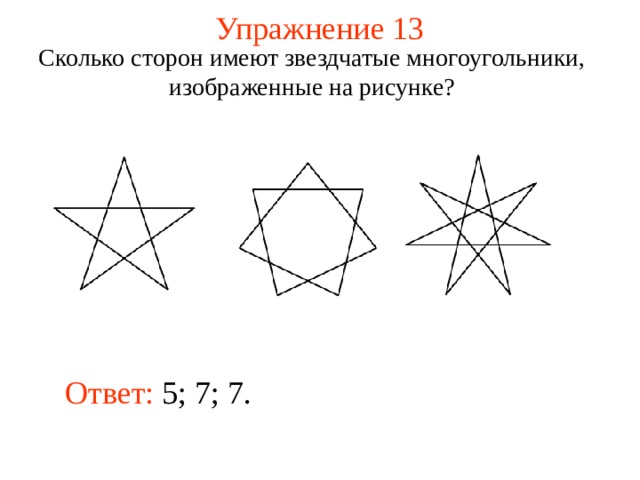
Упражнение 13

Сколько сторон имеют звездчатые многоугольники, изображенные на рисунке?

Ответ: 5; 7; 7.

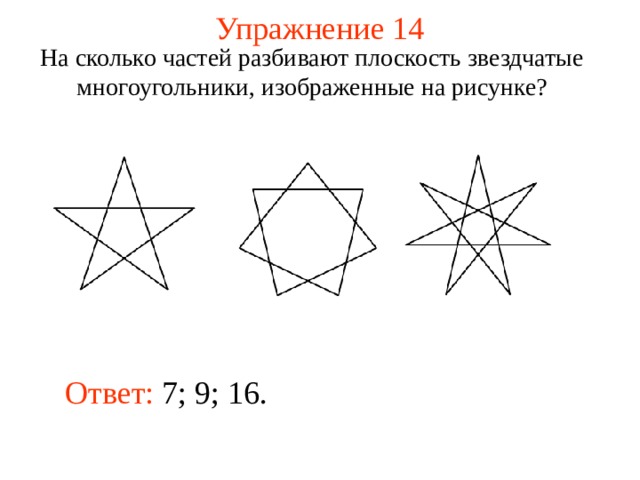
Упражнение 14

На сколько частей разбивают плоскость звездчатые многоугольники, изображенные на рисунке?

Ответ: 7; 9; 16.

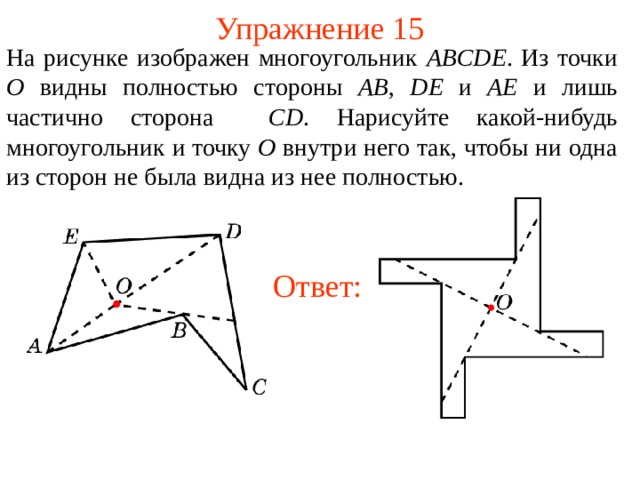
Упражнение 15

На рисунке изображен многоугольник ABCDE . Из точки O видны полностью стороны AB , DE и AE и лишь частично сторона CD . Нарисуйте какой-нибудь многоугольник и точку O внутри него так, чтобы ни одна из сторон не была видна из нее полностью.

Ответ: 20