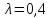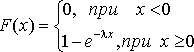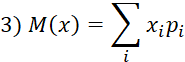Просмотр содержимого документа
«Материалы для проведения дифференцированного зачета по ЕН 03 Теория вероятностей и математическая статистика «Вероятности событий»»
Дифференцированный зачет по ЕН 03 Теория вероятностей и математическая статистика
«Вероятности событий»
Вариант 1.
При выполнении заданий № 1-3 соотнесите содержание столбца 2 с содержанием столбца 3.
| № | Задание | Варианты ответов |
| 1. | а) Наступление одного события исключает наступление других. б) Наступление какого-либо события не является более возможным, чем другие. | 1) Несовместные события.
2) Неопределяемые события. |
| 2. | а) Достоверное событие. б) Невозможное событие. | 1) Вероятность равна нулю. 2) Вероятность равна единице. |
| 3. | а) Формула Бернулли б) Математическое ожидание биноминального распределения в) Формула числа размещений с повторениями | 1) � �=np 2) �=np 2) 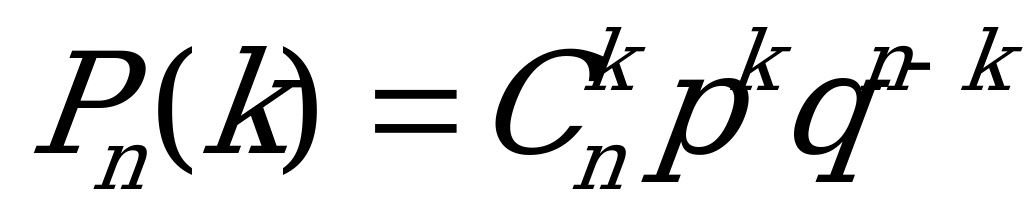 3) 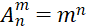 |
|
При выполнении заданий № 4-8 выберите букву, соответствующую правильному варианту ответа (с указанием решения) |
| 4. | 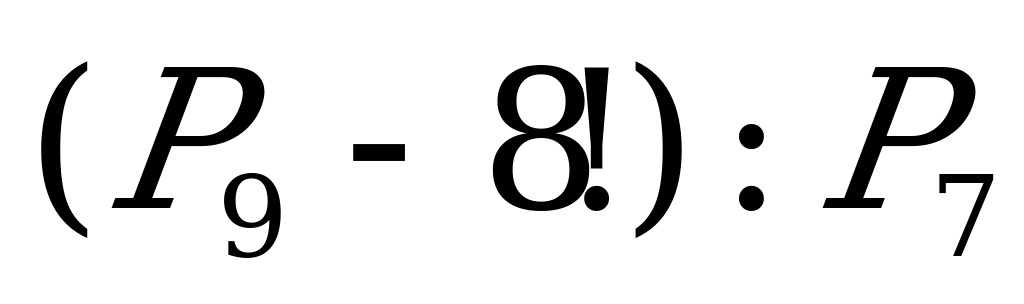
| а) 64; б) 32; в) 128; г) 256. |
| 5. | 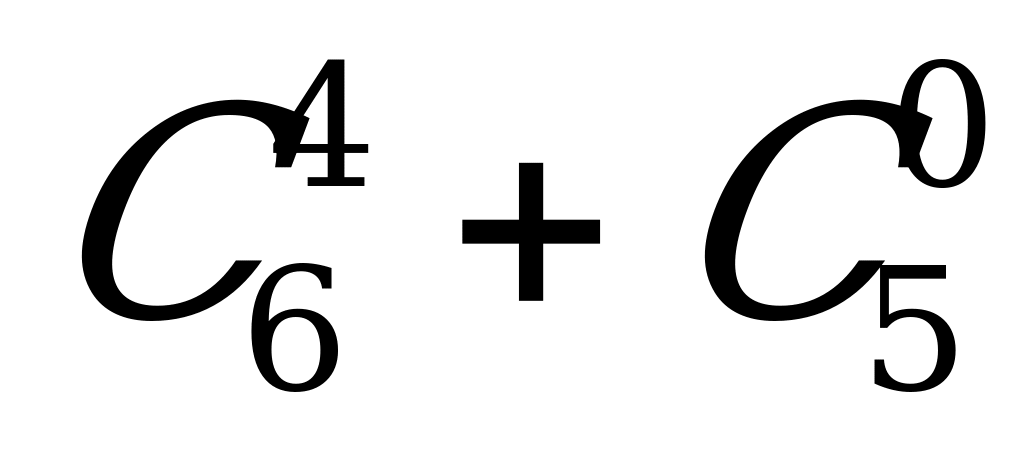
| а) 32; б) 16; в) 25; г) 1. |
| 6. | Вероятность встретить на улице однокурсника равна 0,002. Какова вероятность того , что среди 1200 случайных прохожих, можно встретить 3 однокурсников? | а) 0,031 б) 0,209 в) 0, 029 |
| 7. | Слово составлено из карточек, на каждой из которых написана одна буква. Карточки смешивают и вынимают без возврата по одной. Найти вероятность того, что получится слово «процессор». | а) 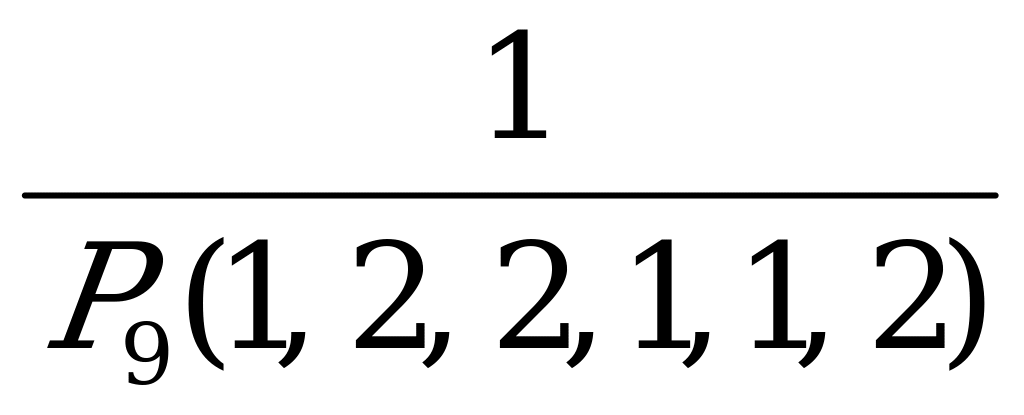 ; б) ; б) 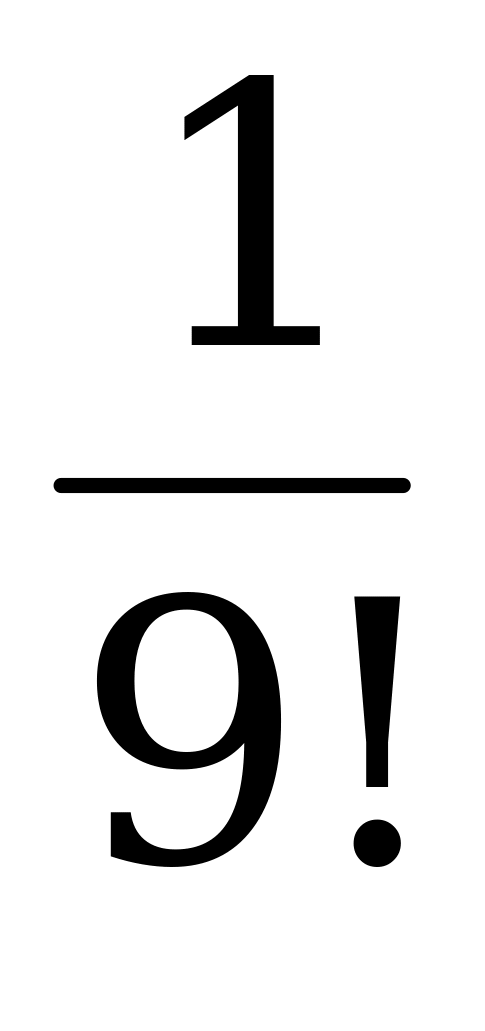 ; ; в) 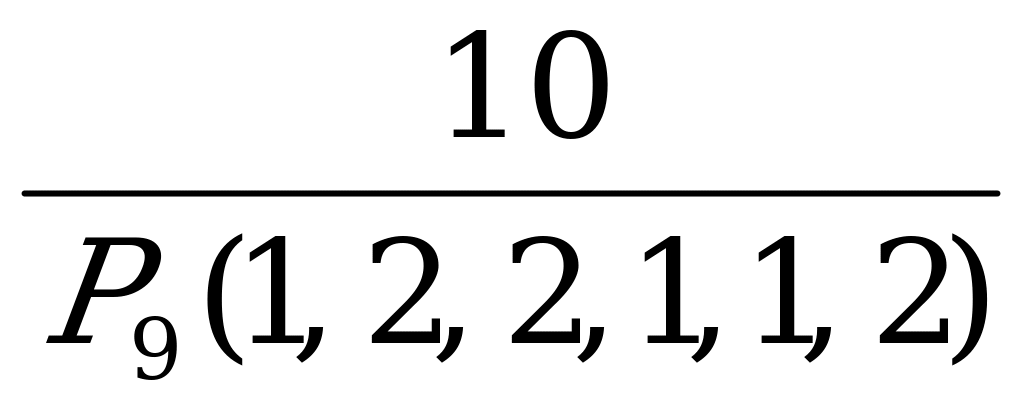 ; г) ; г) 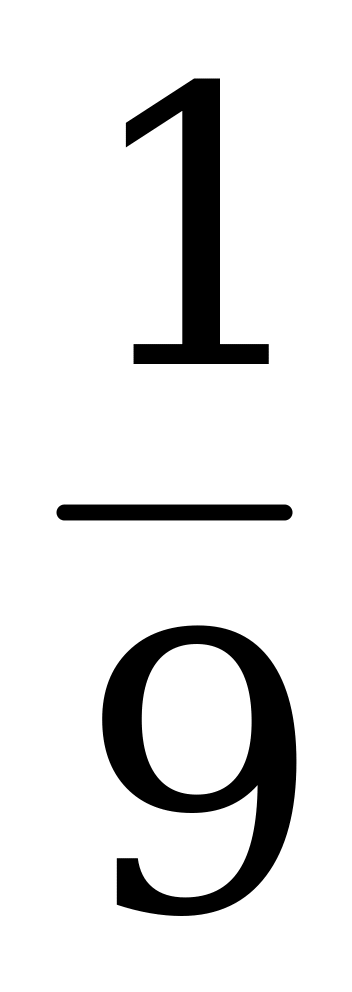 . . |
| 8. | Вероятность того, что из семи телевизоров, находящихся на ремонте, испытание выдержат ровно 5, если вероятность выдержки оценивается вероятностью 0,3. | а) 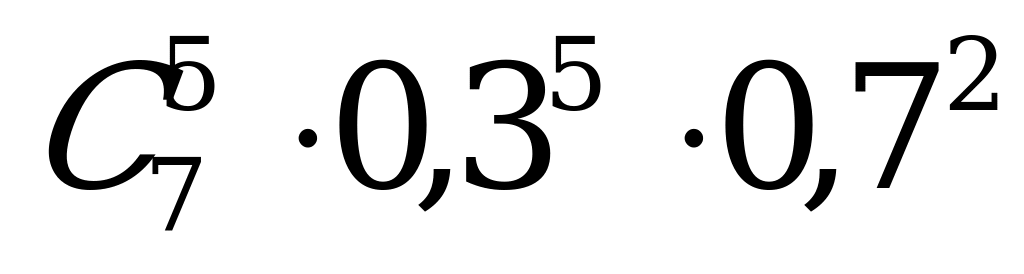 ; ; б) 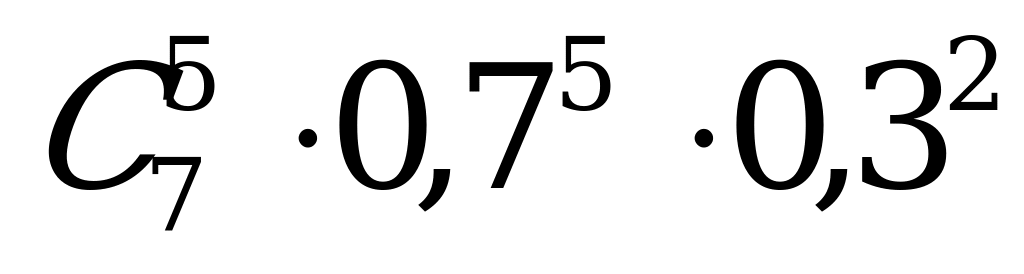 ; ; |
9. По формуле бинома Ньютона раскройте скобки и упростите выражение: (x+2)5.
10. Найти математическое ожидание дискретной случайной величины для ряда распределения
| х | 2 | 4 | 5 | 6 |
| р | 0,11 | 0,30 | 02 | 0,56 |
11. Устройство состоит из трёх взаимно независимых элементов. Вероятность отказа каждого элемента в одном испытании равна 0,1. Составить закон распределения случайной величины Х – число элементов, отказавших в одном испытании. Построить многоугольник распределений.
12. Вероятность безотказной работы элемента телевизора распределена по показательному закону 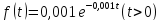 . Найти вероятность того, что телевизор проработает 1000 часов.
. Найти вероятность того, что телевизор проработает 1000 часов.
13. Найти М(Х), D(X), 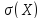 и плотность распределения показательного закона распределения случайной величины X заданной функцией распределения, если
и плотность распределения показательного закона распределения случайной величины X заданной функцией распределения, если
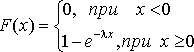
параметр 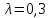
Дифференцированный зачет по ЕН 03 Теория вероятностей и математическая статистика
«Вероятности событий»
Вариант 2.
При выполнении заданий № 1-3 соотнесите содержание столбца 2 с содержанием столбца 3.
| № | Задание | Варианты ответов |
| 1. | а) Событие 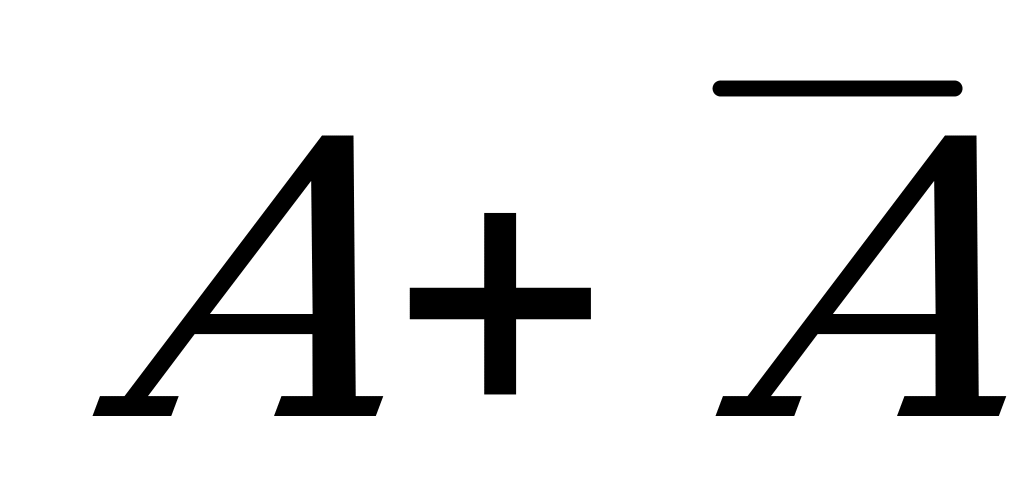 б) Событие 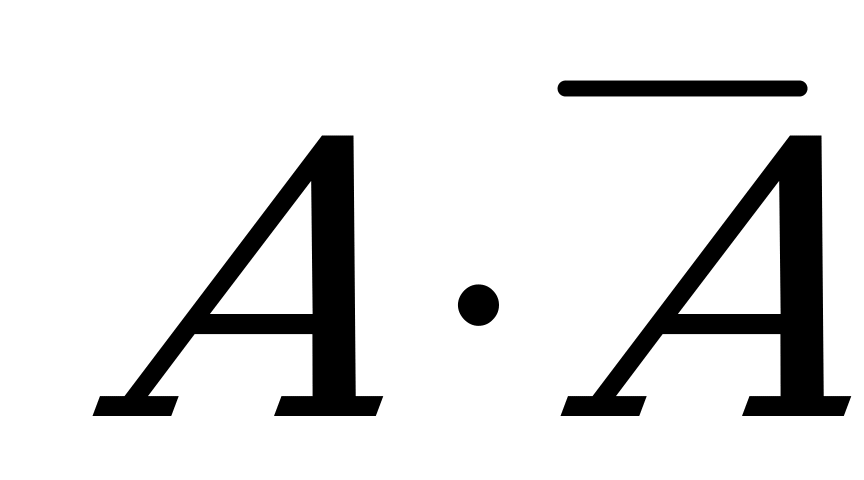 | 1) Достоверное событие. 2) Невозможное событие. |
| 2. | а) Если в результате эксперимента наступление одного из событий не исключает появления других, то события называются … б) Если в результате эксперимента появление одного события исключает появления других, то события называются … | 1) несовместными 2) совместными |
| 3. | а) Формула математического ожидания ДСВ б) Формула Бернулли в) Формула вероятности суммы несовместимых событий | 1) 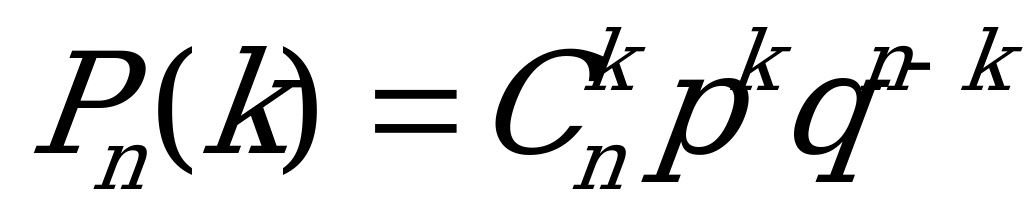 2) Р(А+В)=Р(А)+Р(В) 2) Р(А+В)=Р(А)+Р(В) 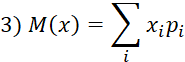
|
|
При выполнении заданий № 4-8 выберите букву, соответствующую правильному варианту ответа (с указанием решения) |
| 4. | 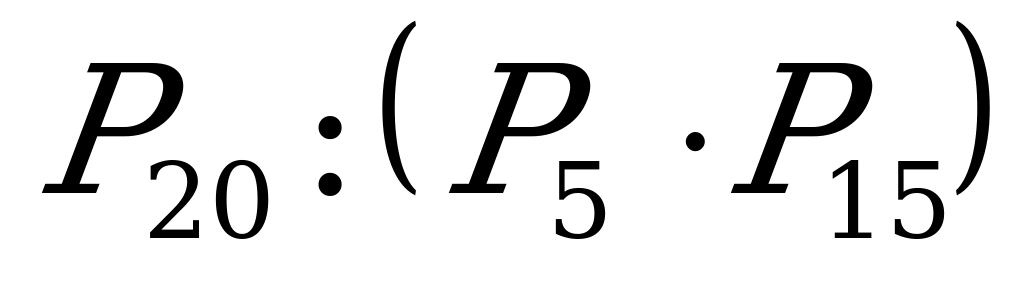
| а) 15504; б) 24120; в) 180; г) 60. |
| 5. | 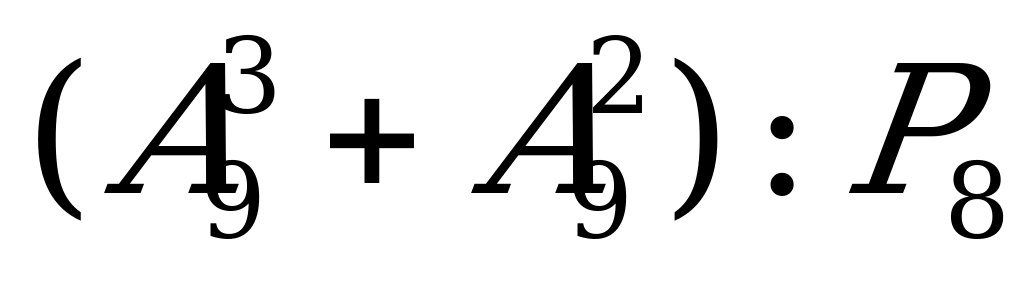
| а) 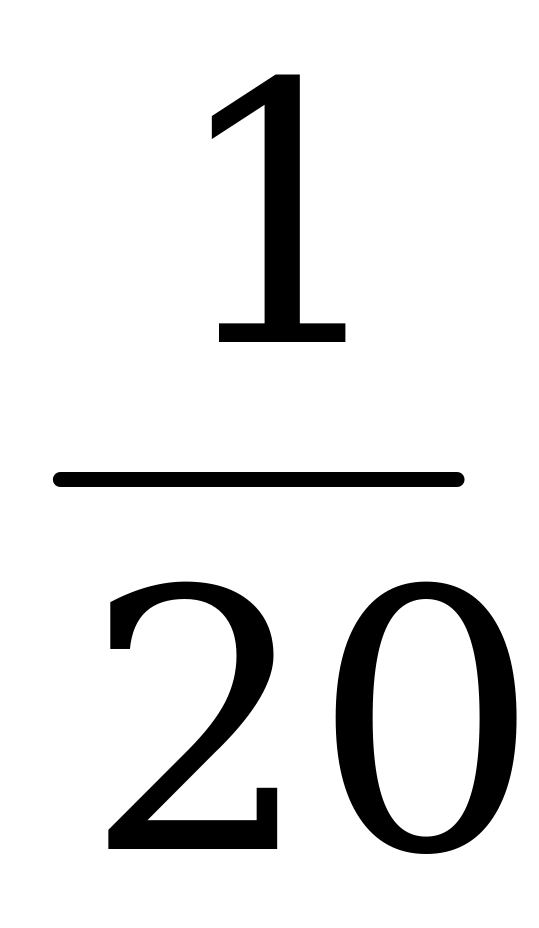 ; б) ; б) 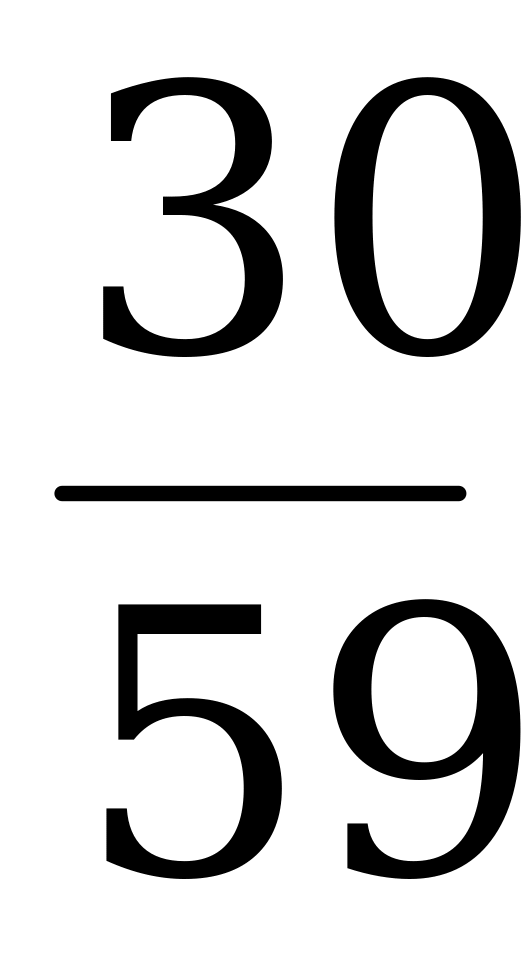 ; в) ; в) 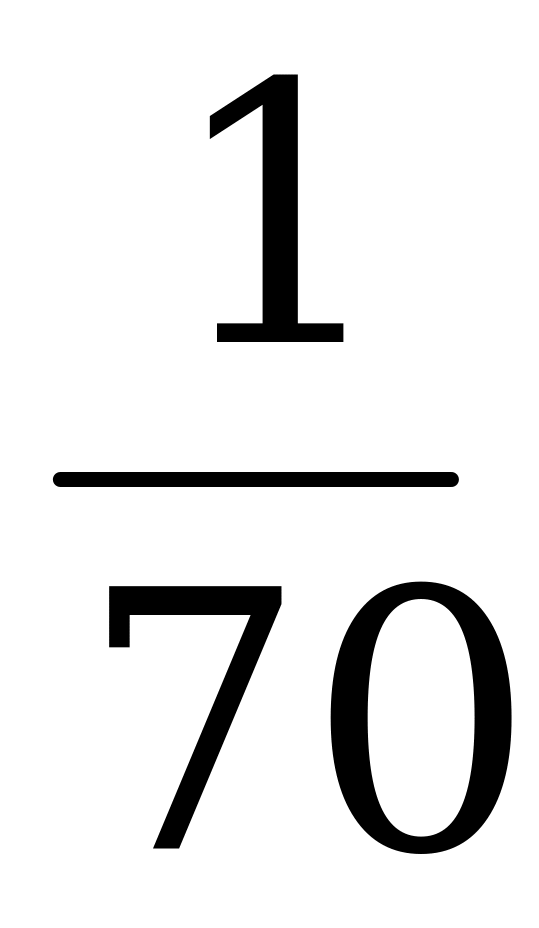 ; г) ; г) 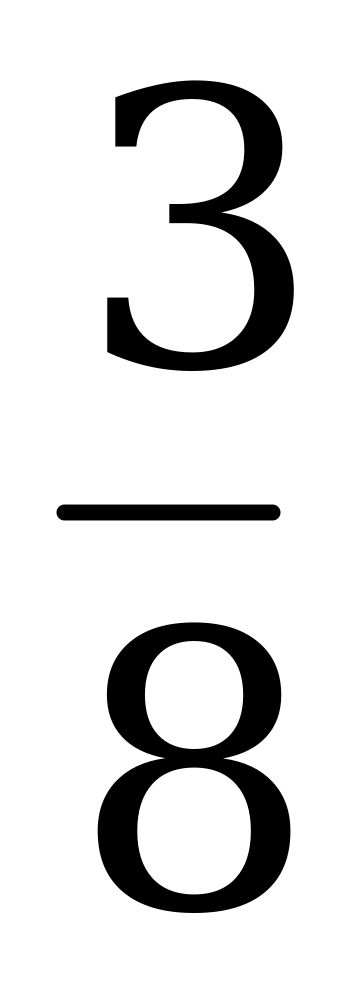 . . |
| 6. | Среди семян пшеницы 0,6 сорняков. Какова вероятность при случайном отборе 1000 семян обнаружить 6 семян сорняков? | а) 0, 08932 б) 0,08924 в) 0,0839 |
| 7. | Слово составлено из карточек, на каждой из которых написана одна буква. Карточки смешивают и вынимают без возврата по одной. Вероятность того, что получится слово «программист». | а) 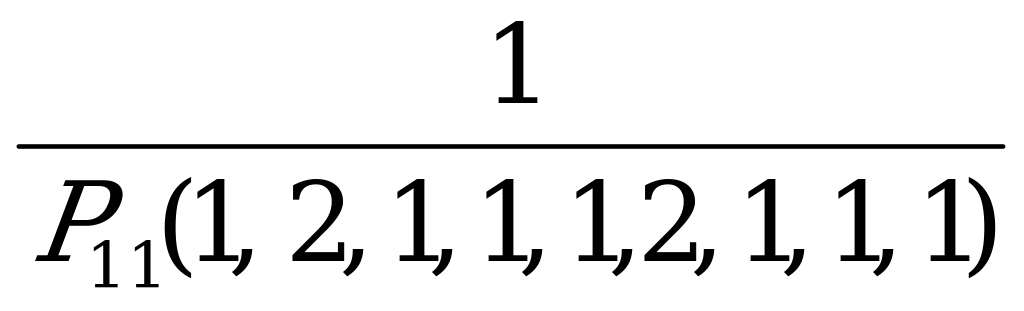 ; б) ; б) 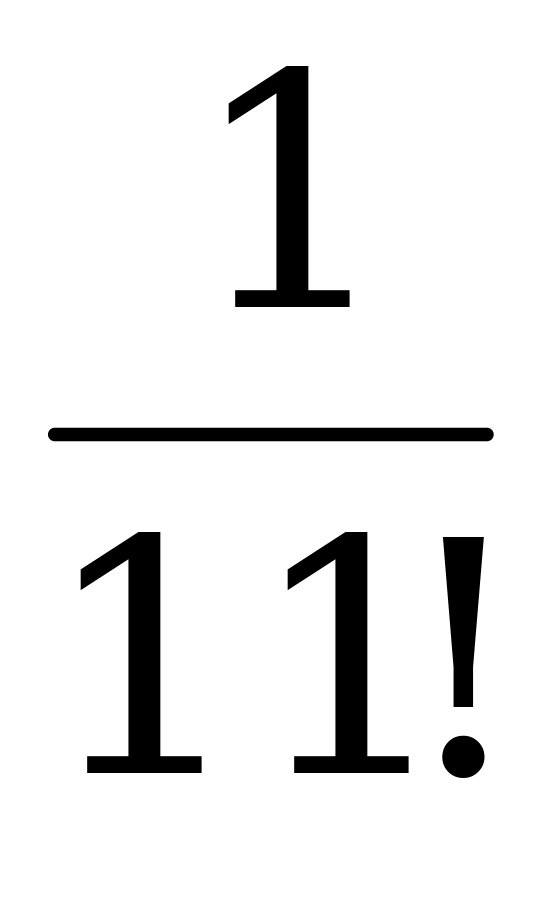 ; ; в) 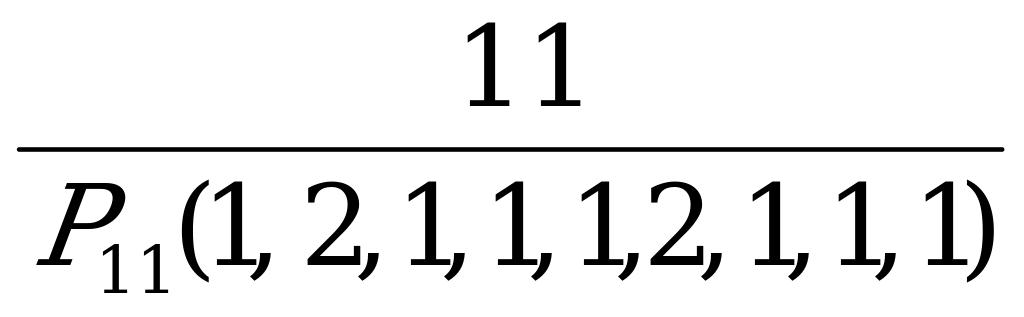 ; г) ; г) 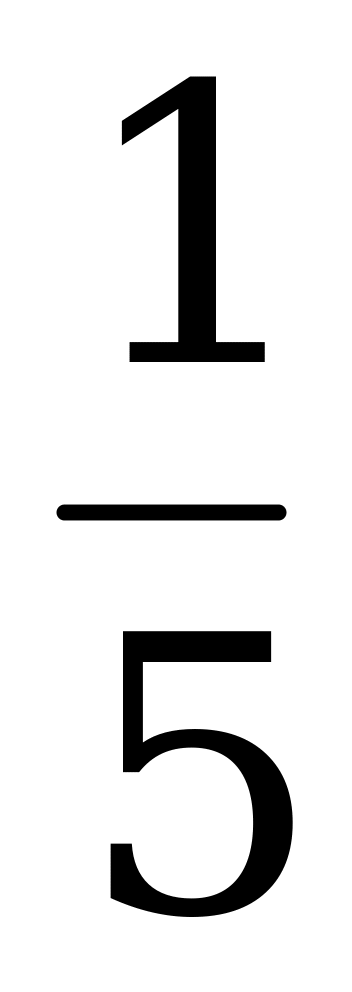 . . |
| 8. | Потребность необходимого размера оценивается вероятностью 0,2. Вероятность того, что из 5 первых посетителей салона обувь 41-го размера понадобится одному покупателю, равна … | а) 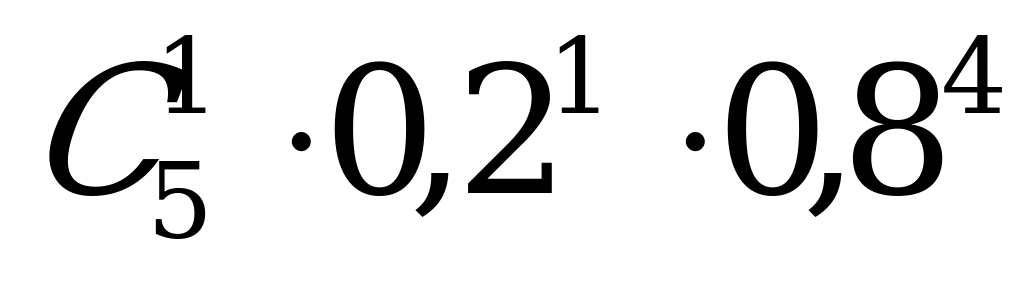 ; б) ; б) 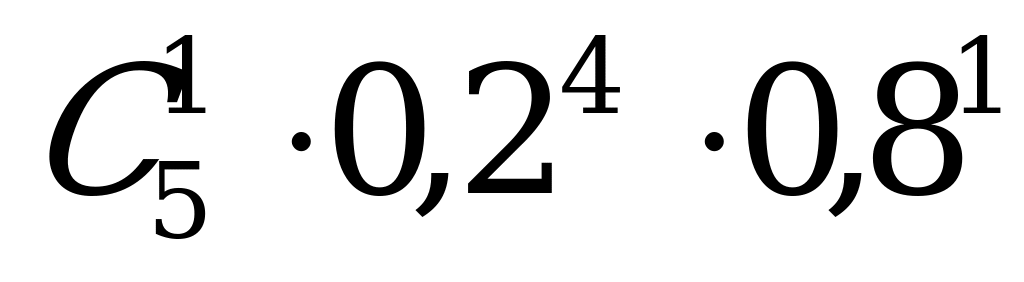 ; ; |
9. По формуле бинома Ньютона раскройте скобки и упростите выражение: (x+3)6.
10. Найти математическое ожидание дискретной случайной величины для ряда распределения
| х | 1 | 3 | 5 | 7 |
| р | 0,14 | 0,20 | 0,1 | 0,56 |
11. Стрелок производит несколько выстрелов в цель до первого попадания, имея всего 3 патрона. Вероятность попадания при одном выстреле равна 0,5. Найти закон распределения случайной величины и построить многоугольник распределения.
12. Вероятность безотказной работы элемента телевизора распределена по показательному закону 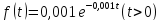 . Найти вероятность того, что телевизор проработает 1500часов.
. Найти вероятность того, что телевизор проработает 1500часов.
13. Найти М(Х), D(X), 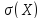 и плотность распределения показательного закона распределения случайной величины X заданной функцией распределения, если
и плотность распределения показательного закона распределения случайной величины X заданной функцией распределения, если
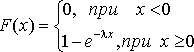
параметр