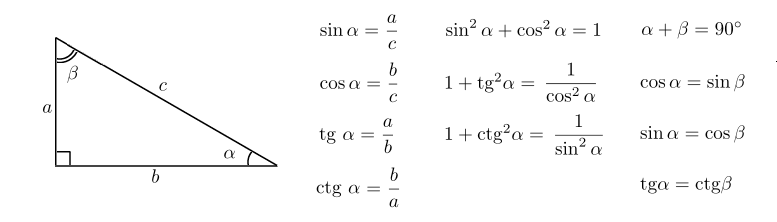Материал для дополнительного изучения темы «Треугольник»
Треуго́льник является геометрической фигурой , образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Часть плоскости, ограниченная сторонами, называется внутренностью треугольника: нередко треугольник рассматривается вместе со своей внутренностью (например, для определения понятия площади).
Стороны треугольника образуют в вершинах треугольника три угла, поэтому треугольник можно также определить как многоугольник, у которого имеется ровно три угла]. Треугольник является одной из важнейших геометрических фигур, повсеместно используемых в науке и технике, поэтому глубокое исследование его свойств проводилось начиная с глубокой древности.
Понятие треугольника допускает различные обобщения. Можно определить это понятие в неевклидовой геометрии (например, на сфере): на таких поверхностях треугольник определяется как три точки, соединённые геодезическими линиями. В n-мерной геометрии аналогом треугольника является n-й мерный симплекс.
Иногда рассматривают вырожденный треугольник, три вершины которого лежат на одной прямой. Если не оговорено иное, треугольник в данной статье предполагается невырожденным.
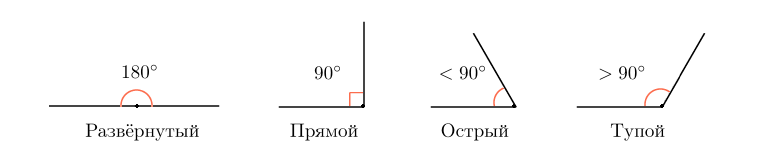
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин :-)
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается 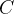 . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается
. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается 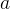 .
.
Угол  обозначается соответствующей греческой буквой
обозначается соответствующей греческой буквой  .
.
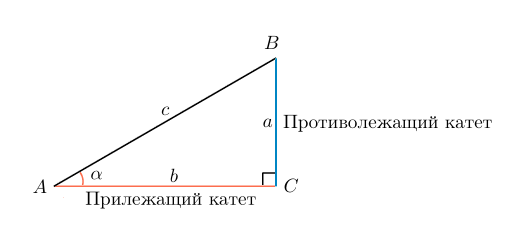
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет 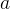 , лежащий напротив угла
, лежащий напротив угла  , называется противолежащим (по отношению к углу
, называется противолежащим (по отношению к углу  ). Другой катет
). Другой катет 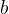 , который лежит на одной из сторон угла
, который лежит на одной из сторон угла  , называется прилежащим.
, называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
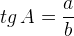
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
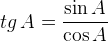
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
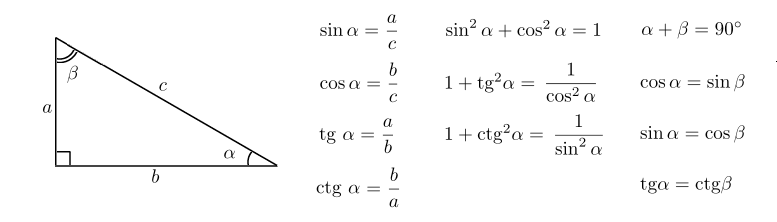
Давайте докажем некоторые из них.
Сумма углов любого треугольника равна 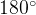 . Значит, сумма двух острых углов прямоугольного треугольника равнa
. Значит, сумма двух острых углов прямоугольного треугольника равнa  .
.
С одной стороны,  как отношение противолежащего катета к гипотенузе. С другой стороны,
как отношение противолежащего катета к гипотенузе. С другой стороны, 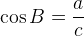 , поскольку для угла
, поскольку для угла  катет а будет прилежащим.Получаем, что
катет а будет прилежащим.Получаем, что  . Иными словами,
. Иными словами, 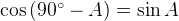 .
.
Возьмем теорему Пифагора: 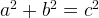 .Поделим обе части на
.Поделим обе части на  :
: Мы получили основное тригонометрическое тождество.
Мы получили основное тригонометрическое тождество.
Поделив обе части основного тригонометрического тождества на  , получим:
, получим: Это значит, что если нам дан тангенс острого угла
Это значит, что если нам дан тангенс острого угла  , то мы сразу можем найти его косинус.Аналогично,
, то мы сразу можем найти его косинус.Аналогично,

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна 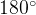 .
.
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: 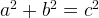 .
.
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от  до
до  .
.
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
1. В треугольнике  угол
угол 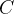 равен
равен  ,
,  . Найдите
. Найдите  .
.
Задача решается за четыре секунды.
Поскольку  ,
,  .
.
2. В треугольнике  угол
угол 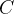 равен
равен  ,
,  ,
,  . Найдите
. Найдите  .
.
Имеем:
Отсюда
Найдем  по теореме Пифагора.
по теореме Пифагора.

Задача решена.
Часто в задачах встречаются треугольники с углами  и
и  или с углами
или с углами  и
и  . Основные соотношения для них запоминайте наизусть!
. Основные соотношения для них запоминайте наизусть!
Для треугольника с углами  и
и  катет, лежащий напротив угла в
катет, лежащий напротив угла в  , равен половине гипотенузы.
, равен половине гипотенузы.
Треугольник с углами  и
и  — равнобедренный. В нем гипотенуза в
— равнобедренный. В нем гипотенуза в  раз больше катета.
раз больше катета.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?
Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна 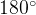 .
.
Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине  — это угол, смежный с углом
— это угол, смежный с углом  . Если угол
. Если угол  острый, то смежный с ним угол — тупой, и наоборот.
острый, то смежный с ним угол — тупой, и наоборот.
Обратите внимание, что:



Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.
Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
1. В треугольнике  угол
угол 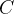 равен
равен  ,
,  . Найдите тангенс внешнего угла при вершине
. Найдите тангенс внешнего угла при вершине  .
.
Пусть  — внешний угол при вершине
— внешний угол при вершине  .
.

Зная  , найдем
, найдем  по формуле
по формуле

Получим: 
2. В треугольнике  угол
угол 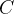 равен
равен  ,
,  . Найдите синус внешнего угла при вершине
. Найдите синус внешнего угла при вершине  .
.
Задача решается за четыре секунды. Поскольку сумма углов  и
и  равна
равна  ,
,  . Тогда и синус внешнего угла при вершине
. Тогда и синус внешнего угла при вершине  также равен
также равен  .
.
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
Перевод градусов в радианы и наоборот. Полный круг содержит  градусов, или
градусов, или  радиан.
радиан.
Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси  , а значение синуса — на оси
, а значение синуса — на оси  .
.
И синус, и косинус принимают значения от  до
до  .
.
Значение тангенса угла  тоже легко найти — поделив
тоже легко найти — поделив  на
на  . А чтобы найти котангенс — наоборот, косинус делим на синус.
. А чтобы найти котангенс — наоборот, косинус делим на синус.
Знаки синуса, косинуса, тангенса и котангенса.
Синус — функция нечётная, косинус — чётная.
Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен  .
.
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями  и
и  , в которой мы привыкли рисовать графики функций.
, в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси  против часовой стрелки.
против часовой стрелки.
Полный круг —  градусов.
градусов.
Точка с координатами  соответствует углу в
соответствует углу в  градусов. Точка с координатами
градусов. Точка с координатами  отвечает углу в
отвечает углу в 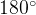 , точка с координатами
, точка с координатами  — углу в
— углу в  . Каждому углу от нуля до
. Каждому углу от нуля до  градусов соответствует точка на единичной окружности.
градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси  ) точки на единичной окружности, соответствущей данному углу
) точки на единичной окружности, соответствущей данному углу  .
.
Синусом угла называется ордината (то есть координата по оси  ) точки на единичной окружности, соответствущей данному углу
) точки на единичной окружности, соответствущей данному углу  .
.
Например:
 ;
;
 ;
;
 ;
;

Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса  , синус — ордината
, синус — ордината  . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от
. Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от  до
до  :
:
 ,
,
 .
.
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу  , смотрим, положительны или отрицательны ее координаты по
, смотрим, положительны или отрицательны ее координаты по  (это косинус угла
(это косинус угла  ) и по
) и по  (это синус угла
(это синус угла  ).
).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто:  градусов, то есть полный круг, соответствует
градусов, то есть полный круг, соответствует  радиан. На нашем рисунке подписаны и градусы, и радианы.
радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол  — это угол величиной в
— это угол величиной в  , который отложили от положительного направления оси
, который отложили от положительного направления оси  по часовой стрелке.
по часовой стрелке.
Легко заметить, что
 ,
,
 .
.
Углы могут быть и больше  градусов. Например, угол
градусов. Например, угол  — это два полных оборота по часовой стрелке и еще
— это два полных оборота по часовой стрелке и еще  . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по
. Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по  и по
и по  , значения синуса и косинуса повторяются через
, значения синуса и косинуса повторяются через  . То есть:
. То есть:
 ,
,
 ,
,
где  — целое число. То же самое можно записать в радианах:
— целое число. То же самое можно записать в радианах:
 ,
,
 .
.
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
 ,
,
 .
.
В результате получим следующую таблицу.
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| не существует | 
| 
| 
| 
|
| 
| не существует | 
| 
| 
| 
| 
| 
| 
| не существует |