Мебиус и его необычное открытие

Аннотация
Для многих людей математика является и трудной, и непонятной, и неинтересной. . Наш современник Сухомлинский считал», что чувство удивления –

могучий источник желания знать: от удивления к знаниям – один шаг». А математика замечательный предмет для удивления.
Цель данной работы: определить и опытно – экспериментальным путём проверить свойства ленты Мёбиуса.
Для определения необычных свойств листа Мёбиуса нами составлена методика, основанная на опытах, предложенных Кордемским Б.А. Результаты

проведённых опытов, позволили сделать вывод, что наше предположение подтвердилось: лента Мёбиуса обладает не толькосвойством односторонности,

но и такими, действительно, неожиданными свойствами, как непрерывность и связность.
«Математику уже затем учить следует, что она ум в порядок приводит».
Это знаменитое высказывание М.Л.Ломоносова известно всем.
На самом деле математика - орудие, с помощью которого человек познаёт и покоряет себе окружающий мир. Она нужна каждому и на ЕГЭ математику

сдают все. Однако результаты экзамена за последние два года показывают, что до 60% выпускников сдали его на «2» и «3». Это лишь один из показателей

того, что для многих людей математика является и трудной, и непонятной, и неинтересной. Отсутствие интереса к изучению математики создаёт

серьёзную исследовательскую проблему – как сделать данный предмет увлекательным для всех.
Ещё Блез Паскаль - великий французский физик и математик утверждал: «Предмет математики настолько серьёзен, что полезно не упускать случая,

сделать его немного занимательным».
Мы же сочли важным показать, что эта наука полна неожиданностей на примере открытия А.Ф. Мёбиуса, его знаменитого бумажного кольца с

сюрпризами. Мы предполагаем, что лист Мёбиуса, как топологическая фигура, обладает действительно неожиданными свойствами. 
Отсюда, объект исследования: лист Мёбиуса как модель односторонней поверхности. Предмет исследования: свойства односторонний поверхности на

примере ленты Мёбиуса
Цель работы: 
-определить и опытно – экспериментальным путём проверить удивительные свойства ленты Мёбиуса.
В соответствии с поставленной целью и выдвинутой гипотезой определились следующие задачи:
- раскрыть понятие топологии;
-изучить вклад А.Ф. Мёбиуса в развитие науки топологии;
- описать лист Мёбиуса и процесс его изготовления;
- показать использование листа Мёбиуса в искусстве;
- разработать методику определения удивительных свойств листа Мёбиуса;
- проверить опытно-экспериментальным путём эти свойства.
Метод исследования: практический эксперимент.
Теоретическая значимость нашей работы в том, что в последнее столетие большое влияние на ряд совершенно различных областей знания приобрела новая ветвь геометрии - топология. В наше время эта наука бурно развивается и находит применение в различных областях. Однако ей не уделяется должного

внимания в школьном курсе геометрии. 
^ Глава 1.А.Ф. Мёбиус и его поразительное открытие 
1.1. Мёбиус Август Фердинанд 
Таинственный и знаменитый лист Мёбиуса (иногда говорят лента Мёбиуса) открыл в1858г. немецкий геометр Август Фердинанд Мёбиус (1790-1868),

ученик «короля математиков» Гаусса. Мёбиус был первоначально астрономом, как Гаусс и многие другие из тех, кому математика обязана своим

развитием. В те времена изучение математики не встречало поддержки, а занятие астрономией давало достаточно денег, чтобы не думать о них, и

оставляло время для размышлений. А.Ф. Мёбиус - в течение более чем 15 лет наблюдатель, а потом директор Лейпцигской астрономической

обсерватории, был разносторонним ученым. Он сделал много интересных открытий, стал одним из крупнейших геометров Х1Х в.. В возрасте 68 лет

он сделал поразительное открытие - односторонние поверхности, одна из которых - лист Мёбиуса. Мёбиус является одним из основателей современной топологии.
^ 1.2.Что такое топология?
Лист Мёбиуса - один из объектов топологии. Топология-«геометрия положения». У этого листа есть удивительные свойства: он имеет один край, одну

сторону. Данные свойства не связаны с его положением в пространстве, с понятием расстояния, угла и, тем не менее, они имеют геометрический характер. Изучением этих свойств занимается топология. Свойства такого типа, несмотря на кажущуюся их непривычность, связаны с наиболее абстрактными математическими дисциплинами - алгеброй и теорией функций. В топологии изучаются свойства фигур и тел, которые не меняются при их непрерывных деформациях (как если бы они были сделаны из резины). С точки зрения топологии баранка и кружка – это одно и тоже. Сжимая и растягивая кусочек

резины, можно перейти от одного из этих тел ко второму. А вот баранка и шар – разные объекты, чтобы сделать отверстие, надо разорвать резину.
Понятие и теоремы топологии полезны во всех областях математики, в технике, в экономике, психологии.
Топология – одна из наук, в которых не решены многие проблемы. Быть может, кто-то внесёт свой вклад в её развитие.
1.3.^ Лист Мёбиуса в искусстве
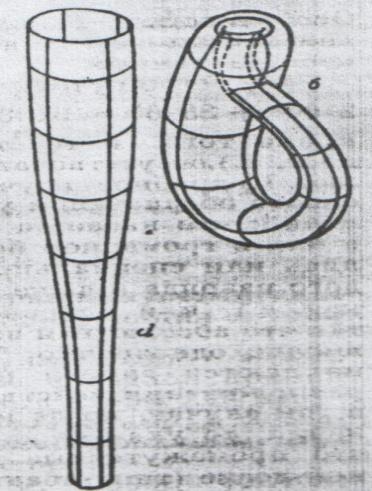
Лист Мёбиуса – это наиболее известная односторонняя поверхность. О нём упоминается в художественной литературе. Его не раз использовали

художники и скульпторы. Довольно много разнообразных рисунков с изображением листа Мёбиуса оставил известный график М.Эшер (1898-1971).

Серию вариантов листа Мёбиуса создал скульптор Макс Билл (родился в 1908). В течение почти 20 лет он неоднократно обращался к листу Мёбиуса,

стремясь выразить в скульптуре идею вечного движения и развёртывающейся в пространстве формы. Скульптура «Узел без конца» находится в музее современного искусства в Париже. [5] Немецкий математик Феликс Клейн в 1882г. построил ещё одну одностороннюю поверхность, но уже замкнутую,

которую в честь него назвали бутылкой Клейна (см. Приложение №2, рис.2, рис.3).
Глава 2. Сюрпризы листа Мёбиуса
2.1.Знаменитое бумажное кольцо
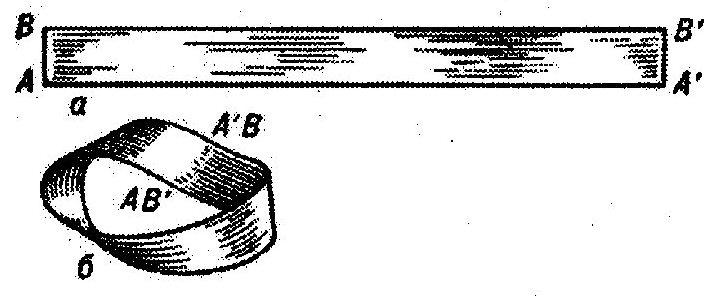
Оказывается, одностороннюю поверхность можно сконструировать. [8] Вот, например, цилиндр. Он представляет собой двустороннюю поверхность. Если двигаться по одной его поверхности то, не пересекая « границы », нельзя очутиться на другой его стороне, т. е. внутри цилиндра. Если склеить

прямоугольную полоску бумаги, как показано на рисунке 1, то получится односторонняя поверхность. (см. Приложение №1)
2.2 ^ Методика определения свойств листа Мёбиуса
Для определения необычных свойств листа Мёбиуса нами составлена методика, в основе которой лежат опыты, предложенные Кордемским Б.А. [4 ]:
1.Какой формы можно взять бумажную полоску, чтобы склеить ленту Мёбиуса?
а) бумагу нельзя мять;
б) бумагу не запрещается мять;
2. Что произойдёт с этим бумажным кольцом, если его разрезать 
на 1,2,3…одинаковых полосок?
3. Что получится, если перед склейкой:
а) ленту перекрутить дважды, а затем разрезать на две, три части?
б) ленту перекрутить трижды, а затем разрезать также на две или 
три части?
2.3. Эксперименты и полученные результаты
1) Результаты первого опыта
а) если бумагу нельзя мять, то лист Мёбиуса можно склеить только из прямоугольной полоски, где длина больше ширины.
б) если бумагу не запрещается мять, то ленту Мёбиуса можно склеить не только из квадрата, но и из прямоугольника любых размеров – склеиваемые

стороны могут быть во сколько угодно раз длиннее несклеиваемых.
Сделать это можно так. Сложим прямоугольный лист в гармошку, перегнув его чётное число раз. Затем из этой гармошки, как из толстой бумажной

полоски, склеим ленту Мёбиуса, вставляя, соответствующие части гармошки друг в друга. Лента Мёбиуса склеена, но лист бумаги оказался смятым.
2)Результаты второго опыта

- при разрезании ленты Мёбиуса на чётное число полосок получаются только большие сцепленные кольца, которых в два раза меньше, чем количество

разрезов (полосок).
-при разрезании ленты Мёбиуса на нечётное число полосок получаются одно маленькое и несколько больших колец, сцепленных с маленьким, которых

тоже в 2 раза меньше разности между количеством разрезов и маленьких колец. 
3)Результаты третьего опыта.

- если ленту перекрутить дважды и разрезать на четное или нечетное число полосок, то их количество совпадет с количеством получившихся

взаимосвязанных колец одинаковой величины, каждое из которых является лентой Мебиуса;
- если ленту перекрутить трижды, то результат получится такой же, т.е. количество разрезов, совпадает с количеством колец одинаковой величины,

каждое из которых является лентой Мебиуса, и вместе они образуют такую же поверхность;
Таким образом, лента Мёбиуса обладает не только свойством односторонности , но и такими неожиданными свойствами, как непрерывность и связность.
ЗАКЛЮЧЕНИЕ
«Мышление начинается с удивления»,- заметил 2500 лет назад Аристотель. Наш современник Сухомлинский считал», что чувство удивления – могучий

источник желания знать: от удивления к знаниям – один шаг». А математика замечательный предмет для удивления.
Именно это мы попытались показать в своей работе, описывая лист Мёбиуса и процесс его изготовления, раскрывая опытным путём свойства этого

поразительного открытия. Наше предположение подтвердилось: лента Мёбиуса обладает не только свойством односторонности, но и такими, действительно, неожиданными свойствами, как непрерывность и связность.
Знания о листе Мёбиуса имеют и практическое значение в жизни человека. Свойство односторонности ленты Мёбиуса используют в технике: если в

ременной передаче ремень сделать в виде листа Мёбиуса, то его поверхность будет изнашиваться вдвое медленнее, чем у обычного кольца. Это даёт

ощутимую экономию. Нами эти знания могут быть использованы на уроках технологии в швейных машинах.
Есть авторское свидетельство на магнитофон с лентой Мёбиуса: получают ленту, которая долговечней обычной также в 2 раза.
Представленная в работе односторонняя поверхность увековечена в памяти людей. У входа в Музей истории и техники в Вашингтоне медленно вращается

на пьедестале стальная лента – лист Мёбиуса. А в 1967г, когда в Бразилии состоялся международный математический конгресс, его устроители выпустили

марку с изображением листа или ленты Мёбиуса.
Список литературы:

1. Воронец А.М. Математические развлечения. М.: Учпедгиз, 1981.

2. Гарднер М. Математические досуги. М.: 1992.

3. Кордемский Б.А., Ахадов А.А. Удивительный мир чисел для учащихся. М.: Просвещение, 1996.

4. Кордемский Б.А. Топологические опыты своими руками./ «Квант» №3, 1974,стр73.

5. Коробенок Е.В., Столяр А.А. Сколько сторон у поверхности?: Беседы с учащимися VII-X классов. Минск: Народная асвета, 1995.

6. Леман И. Увлекательная математика. М.: Знание, 1985.

7. Лоповок Л.М. Математика на досуге: Книга для учащихся среднего школьного возраста (IV-VIII классы). М.: Просвещение, 1990.

8. Рупасов К.А. Математика на школьной сцене. Тамбов, 1999. 1.