Медианы, биссектрисы и высоты треугольников

ПЛАН-КОНСПЕКТ УРОКА

Тема урока: Равные треугольники. Медианы, биссектрисы и высоты треугольников

Учитель математики Васильева О.В.

Класс 7

Предмет геометрия

Тип урока Урок изучения нового материала.

Формируемые Предметные: ввести понятия: высота треугольника, медиана

результаты треугольника, биссектриса треугольника.

Личностные: формировать ответственное отношение к

получению новой информации, готовность к саморазвитию

и самообразованию на основе мотивации к обучению и познанию.

Метапредметные: формировать умения определять понятия,

создавать обобщения, устанавливать аналогии, классифицировать.

Планируемые Учащийся научится проводить высоты, медианы и биссектрисы

результаты треугольника, решать задачи, используя определения высоты,

медианы и биссектрисы треугольника.

Основные Треугольник, высота треугольника, медиана треугольника,

понятия биссектриса треугольника.

Оборудование урока:  презентация, доска, чертежные инструменты.

Ход урока

I. Организационный момент

II. Постановка целей и задач урока. Мотивация учебной деятельности учащихся.

III. Актуализация опорных знаний:

1. Проверка домашнего задания.

2. Геометрический марафон.

Задание учащимся: необходимо сопоставить фигуру, появляющуюся на экране, с её названием (слайд № 2)

На слайде №2 указать термины, которые будут использованы при изучении нового материала: перпендикулярные прямые, отрезок, биссектриса, треугольник, луч, прямой угол, прямая

• Взаимопроверка (слайд №3).

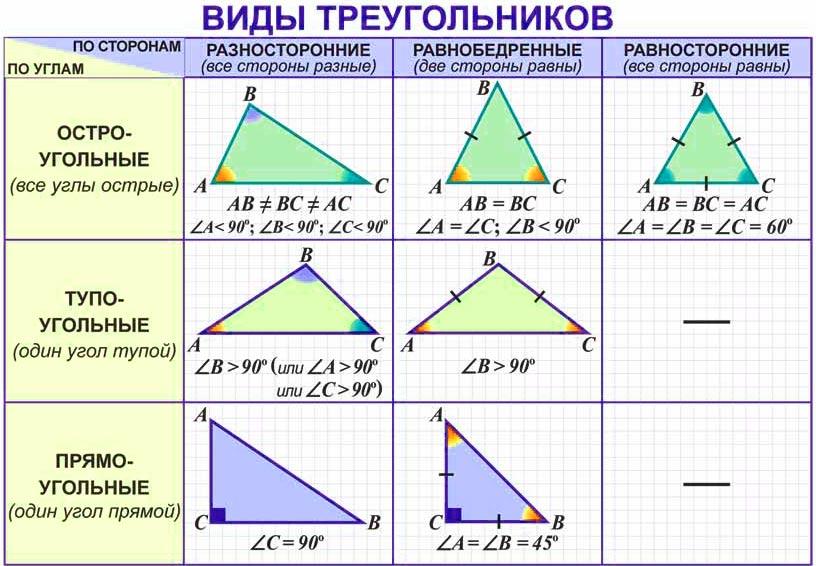
3. Повторение видов треугольников (слайд №4).

III. Изучение нового материала

Введение понятия перпендикуляра (слайд № 5).

Вспомнить, что означает запись: 

Учитель дает задание классу (одновременно идет иллюстрация слайда).

В тетрадях построить прямую а и точку А, не лежащую на этой прямой.

Построить прямую т, проходящую через точку А, и перпендикулярную прямой а.

Построить отрезок АН (т а = Н) – перпендикуляр.

Вместе с обучающимися сформулировать определение перпендикуляра. Вопрос к классу: «Сколько перпендикуляров можно провести из данной точки А к данной прямой а?»

2) Введение понятия медианы (слайд № 6).

Уточнить, чем является в треугольнике АВС точки М и В.

Вместе с обучающимися сформулировать определение медианы ВМ. Вопрос к классу: «Сколько медиан можно построить в треугольнике?».

Учащиеся комментируют построение медианы.

3) Введение понятия биссектрисы треугольника (слайд № 7).

Уточнить, что луч ВК – это биссектриса угла АВС и точка К лежит на стороне, противолежащей углу В треугольника АВС.

Вместе с обучающимися сформулировать определение ВК- биссектрисы треугольника. Вопрос к классу: «Сколько биссектрис можно построить в треугольнике?».

4) Введение понятия высоты треугольника (слайд №8).

а) Учитель показывает построение перпендикуляра из вершины В на прямую, содержащую сторону АС; говорит, что отрезок ВК называют высотой треугольника АВС - учащиеся дают определение высоты треугольника.

Затем открывает формулировку на слайде. Вопрос к классу: «Сколько высот можно построить в треугольнике?”.

Учащиеся выполняют построение высот к треугольникам разного вида:

б) построить высоты в тупоугольном треугольнике (слайд № 9).

в) построить высоты в прямоугольном треугольнике (слайд №10).

г) провести высоты из вершин остроугольного треугольника

IV. Первичное закрепление нового материала.

Построить высоту, медиану и биссектрису треугольника (слайд №11).

IV. Рефлексия определений (понятий) (слайд №12).

Замечательные точки есть у треугольника.
Точка первая – она
Чувством гордости полна:
Медианы в ней пересекаются,
Центром тяжести та точка называется.
Ортоцентр – вторая точка,
Архимед её открыл,
Все высоты в ней встречаются,
Удивив учёный мир.
Третья точка – тоже важная
Биссектрисы всех углов,
Бросив вызов свой отважный,
В ней “сошлись”, не тратя слов.
Эйлер точки все заметил, 
Свойства новые открыл, -
Так на радость школьникам
Возникла новая ветвь математики -
Геометрия треугольника.

V. Закрепление полученных знаний. 

Проверочная работа (слайд №13-14).

№105(учебник), №7, №11 (дидактические материалы).

Проверочная работа (слайд №12, №13).

1. Запишите номера треугольников, в которых проведены

а) высоты,

б) медианы,

в) биссектрисы:

1. Чем является линия AR , BL , CF на рисунках?

V. Итоги урока. Задание на дом.

§ 7, вопросы 8–12, № 134, 148, 150