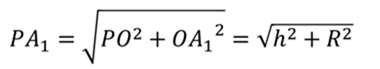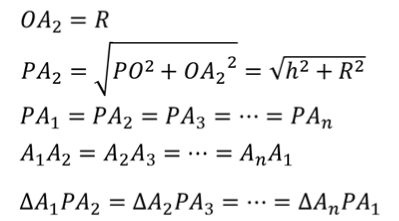| Государственное автономное профессиональное образовательное учреждение Чувашской Республики «Чебоксарский экономико-технологический колледж» Министерства образования Чувашской Республики
|
МЕТОДИЧЕСКАЯ РАЗРАБОТКА ОТКРЫТОГО УРОКА
По учебному предмету УПУУ.10. Математика
Специальность 29.02.04. «Конструирование, моделирование и технология швейных изделий»
Тема раздела программы:
«Геометрические тела и поверхности»
Тема лекции:
«Пирамида. Виды пирамид. Усеченная пирамида»
Чебоксары 2024
| РАССМОТРЕНО на заседании цикловой комиссии математических и естественно-научных дисциплин председатель цикловой комиссии ________________ Н.Н. Иванова «____»_________________2023 г. Протокол №______ ______________
| РЕКОМЕНДОВАНО Экспертной комиссией Чебоксарского экономико-технологического колледжа Минобразования Чувашии «____»______________________20_____г. Протокол №_________________________
|
Методическая разработка соответствует теме обучения. Материал может быть использован на уроках математики для студентов технологического отделения специальности 29.02.04. «Конструирование, моделирование и технология швейных изделий»
Автор: Чернова Т.В.
Рецензент: Иванова Н.Н.
Пояснительная записка
Методическая разработка предназначена для студентов первого курса технологического отделения по дисциплине «Математика». Данная методическая разработка поможет преподавателям преподнести тему «Пирамида. Виды пирамид. Усеченная пирамида» в интересной, легко усваиваемой форме.
Студенты познакомятся с новым видом многогранника. Узнают какие виды пирамид существуют. Полученные знания пригодятся ребятам в их будущей профессии и в повседневной жизни.
На уроке использованы индивидуальная и групповая формы работы, современные средства обучения – работа с яндекс-формой. Используются ИКТ технологии и технология критического мышления через чтение и письмо, используется приёма «Фишбоун»
ПЛАН УРОКА
по учебной дисциплине «Математика»
Специальность – «Конструирование, моделирование и технология швейных изделий»
Преподаватель – Чернова Татьяна Владимировна
Место проведения: учебный кабинет № 228
Тема раздела программы: Тема урока: «Пирамида. Виды пирамид. Усеченная пирамида
Цель занятия: обеспечить прочное и сознательное овладение обучающимися знаниями по данной теме и сформировать навыки по их применению для решения задач
Задачи:
1. Обучающие: познакомить с пирамидой, усеченной пирамидой, с элементами фигур; рассмотреть виды пирамид
2. Развивающие: развивать логическое мышление, пространственное воображение обучающихся, умение самостоятельно мыслить, делать выводы; развитие познавательного интереса к предмету
3. Воспитывающие: воспитывать самостоятельность, любознательность, сознательное отношение к изучению предмета
По результатам занятия студент должен:
- иметь понятие о пирамиде, усеченной пирамиде, виды пирамид
- строить пирамиду, усеченную пирамиду и находить элементы
Тип занятия: комбинированный урок
Технологии обучения: информационно – коммуникационная технология; здоровьесберегающие технологии
Методы обучения:
-объяснительно-иллюстративный;
-словесный метод (устный инструктаж, беседа, обсуждение, объяснение)
Материально-техническое обеспечение:
Учебно-наглядные: презентация, текст лекции, макеты фигур
ТСО: интерактивная панель Teach Touch
Основные термины и понятия: пирамида, грань, основание, ребро, вершина, диагональ, апофема, поверхность, усеченная пирамида
Ход урока
Организационный момент. «Добрый день, дорогие студенты!» (Преподаватель приветствует студентов, проверяет готовность группы к работе, остановка темы, цели, основных задач).
Мотивация. «На прошлом занятии мы с вами говорили о призме. Сегодня мы познакомимся еще с одним не менее интересным многогранником. Форму этой фигуры имеют замечательные, величественные и до сих пор загадочные объекты Египта. О какой фигуре идет речь? (Отвечают) Внешне вы без труда отличите ее от других фигур. (Преподаватель демонстрирует модели различных фигур) А сегодня мы дадим определение пирамиды, усеченной пирамиды, рассмотрим ее элементы и их свойства. Итак, записываем тему занятия: «Пирамиды»». Для выяснения этапов нашей работы вспомним основные моменты предыдущего занятия.
Актуализация опорных знаний:
Итак, мы повторили: определение, обозначение, элементы, построение, виды, свойства.
Перейдем к новой теме.
Изучение нового материала.
Пирамида
«Пирамида – слово произошло от названия формы хлебцев в Древней Греции – piros – рожь (пирог) или же от пламенеобразной формы пирамид pir – огонь.
Рассмотрим многоугольник A1A2…An и точку P, не лежащую в плоскости этого многоугольника. Соединим точку P отрезками с вершинами многоугольника. В итоге получим n треугольников: PA1A2, PA2A3, …, PAnA1. Многогранник, составленный из n-угольника A1A2…An и этих n треугольников, называется пирамидой.
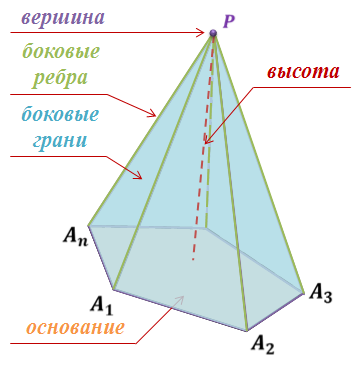
Многоугольник A1A2…An называется основанием пирамиды. Треугольники PA1A2, PA2A3, …, PAnA1 называются боковыми гранями пирамиды. Точка P – вершиной пирамиды, а отрезки PA1, PA2,…, PAn – ее боковыми ребрами.
Пирамиду с вершиной P и основанием A1A2…An называют n-угольной пирамидой и обозначают так: PA1A2…An.
Отрезок, соединяющий вершину пирамиды с плоскостью ее основания и перпендикулярный к этой плоскости, называется высотой пирамиды.
Объединение боковых граней называется боковой поверхностью пирамиды, а объединение всех граней называется полной поверхностью пирамиды. Тогда площадью боковой поверхности пирамиды называется сумма площадей ее боковых граней. А площадью полной поверхности пирамиды называется сумма площадей всех ее граней.
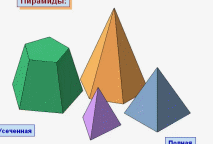
Виды пирамид
Пирамида в зависимости от того какой многоугольник лежит в основании имеет свое название. Если в основании лежит треугольник, то пирамида называется треугольной. Если четырехугольник – то четырехугольной пирамидой. А если n-угольник, то n-угольной пирамидой.
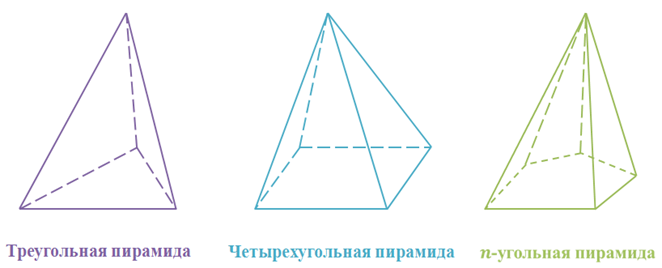
Элементы правильной пирамиды
Пирамида называется правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. Апофема: греч. apothemа от apo – от, из и thema – приложенное, поставленное».
Докажем одно из свойств правильной пирамиды. А именно докажем, что все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
Рассмотрим правильную пирамиду PA1A2…An. Сначала докажем, что все боковые ребра этой пирамиды равны. Проведем высоту пирамиды.
П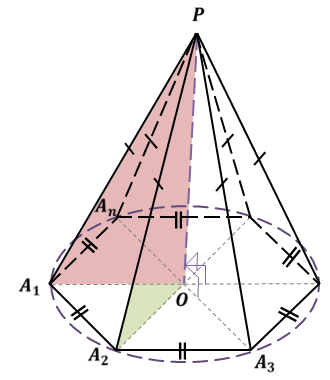 оскольку основанием правильной пирамиды является правильный многоугольник, значит, вокруг основания правильной пирамиды можно описать окружность. Тогда каждое боковое ребро пирамиды есть ничто иное, как гипотенуза прямоугольного треугольника, одним катетом которого служит высота PO пирамиды, а другим – радиус описанной около основания окружности. Например, если рассмотреть треугольник OPA1, то OP равно h, OA1 равно R.
оскольку основанием правильной пирамиды является правильный многоугольник, значит, вокруг основания правильной пирамиды можно описать окружность. Тогда каждое боковое ребро пирамиды есть ничто иное, как гипотенуза прямоугольного треугольника, одним катетом которого служит высота PO пирамиды, а другим – радиус описанной около основания окружности. Например, если рассмотреть треугольник OPA1, то OP равно h, OA1 равно R.
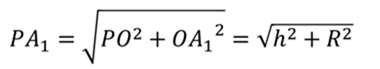
Таким образом, доказали, что боковые ребра правильной пирамиды равны. А значит, боковые грани правильной пирамиды – это равнобедренные треугольники. Поскольку в основании лежит правильный многоугольник, значит, основания боковых граней равны между собой. То есть боковые грани равны между собой по трем сторонам.
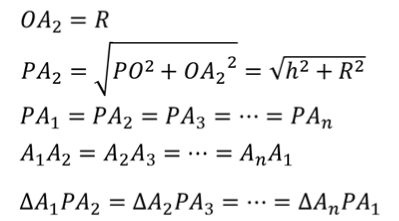
Что и требовалось доказать.
Теперь давайте сформулируем и докажем теорему о площади боковой поверхности правильной пирамиды.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Доказательство.
Запишем формулу для вычисления площади боковой поверхности правильной пирамиды.
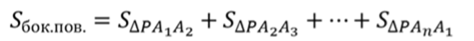
Мы уже доказали, что боковые грани правильной пирамиды – равные равнобедренные треугольники. Высоты этих треугольников равны апофеме пирамиды. Тогда площадь боковой грани находится по формуле 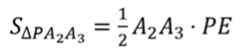 .
.
Подставим эти площади в формулу площади боковой поверхности. Вынесем половину апофемы за скобки, тогда в скобках получим периметр основания.
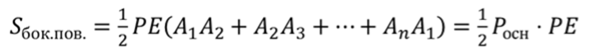
Что и требовалось доказать.
Усеченная пирамида
Возьмем произвольную пирамиду PA1A2...An и проведем секущую плоскость β, параллельную плоскости основания пирамиды α и пересекающую боковые ребра в точках В1,В2,...Вn . Плоскость β разбивает пирамиду на два многогранника. Многогранник, гранями которого являются n-угольники A1A2...An и В1В2...Вn (нижнее и верхнее основания соответственно), расположенные в параллельных плоскостях и n четырехугольников A1A2B2B1, A2A3B3B2, … A1AnBnB1 (боковые грани), называется усеченной пирамидой.
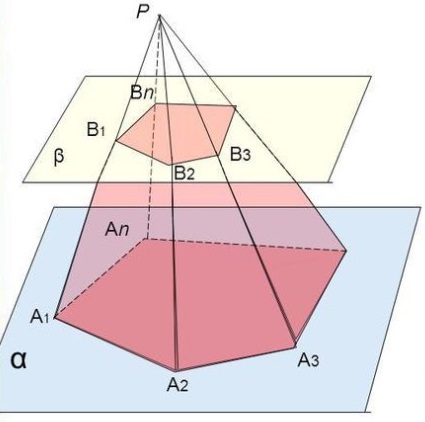
Отрезки A1B1, A2B2, … AnBn называют боковыми ребрами усеченной пирамиды.
Усеченную пирамиду с основаниями A1A2...An и В1В2...Вn обозначают следующим образом: A1A2...AnВ1В2...Вn.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания называется высотой усеченной пирамиды.
Первичное закрепление информации
Возьмите листы и пирамиды. 1 вариант – треугольную, 2 – четырехугольную. Исследуйте свою пирамиду и по результатам заполните таблицу (Приложение 2).
По результатам исследования, заполните пропуски в тексте возле таблицы.
А теперь проверим ответы, вписанные в текст.
Число вершин пирамиды на единицу больше числа вершин в ее основании.
Число боковых граней равно числу сторон основания.
У вас были разные пирамиды, а ответы – одинаковые. Какую гипотезу мы можем выдвинуть для любой пирамиды?
(Число вершин любой пирамиды на единицу больше числа вершин в ее основании, а число боковых граней равно числу сторон основания).
Закрепление изученного материала
Самостоятельная работа обучающихся (Приложение 3)
Перед вами на доске скелет рыбы. Задание: вы должны там, где голова, написать название сегодняшней темы «Пирамида. Виды пирамид. Усеченная пирамида». В скелете сверху перечислить виды пирамид, внизу – где встречаются эти пирамиды. В Хвосте записать какую фигуру можно получить из пирамиды и плоскости. На выполнение задания отводится 5 мин. По желанию один выполняет на доске.
Рефлексия.
Через яндекс-форму выполняют тест, для закрепления данной темы. Каждый из вас сможет проверить как усвоил урок, получит оценку.
Подведение итогов урока. Выставление оценок
Домашнее задание:
Повторить: определение; обозначение; элементы; построение; виды; свойства; формулы площади боковой и полной поверхности призмы.
Подготовить презентацию или мини-сочинение на тему «Пирамиды в нашей жизни и в моей будущей профессии»
Задание: построить пирамиду, основание которой прямоугольник, а вершина проецируется в центр описанной окружности.
Приложение 1
Фронтальный опрос по теме «Призмы»
1. Перед вами модели многогранников. Покажите многогранник, который мы изучали на предыдущих занятиях. Как он называется? (призма)
Сформулируйте определение призмы (картинки призм)
Как обозначается призма?
Какие элементы призмы вы знаете?
Какие виды призм вы знаете? (прямая и правильная, выберите их из представленных моделей).
2. Сформулируйте определение прямой призмы, правильной.
3. Верно ли утверждение:
Любая прямая призма является правильной;
Любая правильная призма является прямой.
4. Алгоритм построения призмы;
5. Из чего состоит поверхность призмы? Как можно вычислить площадь поверхности призмы? (формулы Sбок., Sполн.).
Приложение 2
Заполнить таблицу.
| № п/п | Вопросы. | Ответы. |
| 1. | Число вершин пирамиды |
|
| 2. | Число вершин основания пирамиды |
|
| 3. | Число ребер у пирамиды |
|
| 4. | Число боковых граней |
|
| 5. | Число сторон основания |
|
| № п/п | Вопросы. | Ответы. |
| I вариант | II вариант |
| 1. | Число вершин пирамиды | 4 | 5 |
| 2. | Число вершин основания пирамиды | 3 | 4 |
| 3. | Число ребер у пирамиды | 6 | 8 |
| 4. | Число боковых граней | 3 | 4 |
| 5. | Число сторон основания | 3 | 4 |
По данным таблицы заполните пропуски в тексте.
Число вершин пирамиды на _____ больше числа вершин в ее основании.
Число боковых граней _____ числу сторон основания.
Приложение 3
Перед вами на доске скелет рыбы. Задание: вы должны там, где голова, написать название сегодняшней темы «Пирамида. Виды пирамид. Усеченная пирамида». В скелете сверху перечислить виды пирамид, внизу – где встречаются эти пирамиды. В Хвосте записать какую фигуру можно получить из пирамиды и плоскости. На выполнение задания отводится 5 мин. По желанию один выполняет на доске.
Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы
Основные источники:
Гусев В.А.,Григорьев С.Г., Иволгина С.В. Математика для профессий и специальностей социально-экономического профиля. – Москва, 2019
Электронные УМК










 оскольку основанием правильной пирамиды является правильный многоугольник, значит, вокруг основания правильной пирамиды можно описать окружность. Тогда каждое боковое ребро пирамиды есть ничто иное, как гипотенуза прямоугольного треугольника, одним катетом которого служит высота PO пирамиды, а другим – радиус описанной около основания окружности. Например, если рассмотреть треугольник OPA1, то OP равно h, OA1 равно R.
оскольку основанием правильной пирамиды является правильный многоугольник, значит, вокруг основания правильной пирамиды можно описать окружность. Тогда каждое боковое ребро пирамиды есть ничто иное, как гипотенуза прямоугольного треугольника, одним катетом которого служит высота PO пирамиды, а другим – радиус описанной около основания окружности. Например, если рассмотреть треугольник OPA1, то OP равно h, OA1 равно R.