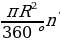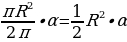I.ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Программа курса по выбору (факультатива) «Знай и повторяй математику» предназначена для эффективной подготовки учащихся 10 класса к Государственной Итоговой аттестации по математике. Программа составлена на основании многолетнего опыта работы с учащимися старшей школы по подготовке их к ГИА и вступительным испытаниям по математике, в т.ч. и с использованием тестовых технологий в учебном процессе.
Основной целью данной программы является формирование математического аппарата для решения задач по математики, смежных предметов, окружающей реальности и способствует расширению кругозора учащихся, знакомя их с индукцией и дедукцией, обобщением и конкретизацией, анализом и синтезом, классификацией и систематизацией, абстрагированием, аналогией. Активное использование задач на всех этапах учебного процесса развивает творческие способности школьников.
Ключевая идея Программы состоит в систематической дополнительной работе с учащимися по повторению, обобщению и систематизации их знаний по основным темам школьной математики.
Структура и содержание программы соответствует формату и программным требованиям вступительных испытаний и содержанию заданий Государственной Итоговой аттестации по математике. В Программе приведены основные опорные факты из разделов, входящих в программные требования школьной программы по математике и являющиеся их содержательными линиями: числа и выражения; уравнения и неравенства; функции; элементы комбинаторики, начала теории вероятностей и элементы статистики; геометрия (планиметрия и стереометрия).
Без базовой математической подготовки невозможно стать образованным человеком, так как математика является языком науки и техники, с её помощью моделируются и изучаются явления и процессы, происходящие в природе.
При организации процесса обучения в рамках данной программы предполагается применением следующих педагогических технологий обучения: традиционной классно-урочной, игровых технологий, элементов проблемного обучения, технологии уровневой дифференциации, здоровьесберегающих технологий, развивающего обучения, коллективной системы обучения, ИКТ.
II. ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ОСВОВЕНИЯ курса по выбору (факультатива) «Знай и повторяй математику»
Требования к предметным результатам освоения базового курса математики отражают:
сформированность представлений о математике как части мировой культуры и о месте математики в современной цивилизации, о способах описания на математическом языке явлений реального мира;
сформированность представлений о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;
владение стандартными приёмами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств;
сформированность представлений об основных понятиях, идеях и методах математического анализа;
владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах;
сформированность умения распознавать на чертежах, моделях и в реальном мире геометрические фигуры; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием;
В результате изучения математики учащийся будет знать/понимать:
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии
Занятия курса по выбору (факультатива) проводятся как правило, в виде спаренных уроков 1 раз в неделю. При недостаточном количестве или отсутствии часов школьного компонента возможна организация индивидуальной работы учащихся под руководством учителя в любом режиме. Повторение тем геометрии можно осуществлять параллельно с другими темами программы или в том порядке, какой имеется в программе. Возможна работа и по отдельным разделам программы.
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА ПО ПРОГРАММЕ курса по выбору (факультатива) «ЗНАЙ И ПОВТОРЯЙ МАТЕМАТИКУ» В 10 КЛАССЕ НА БАЗОВОМ УРОВНЕ (35 часов)
| Наименование разделов и тем | Количество часов | Формы контроля |
| Всего | Теория | Практика |
| Раздел 1. Числа и выражения Т-1. Делимость целых чисел и признаки делимости. Т-2. Проценты. Т-3. Действительные числа. Т-4. Алгебраические выражения. Т-5. Корень n-й степени. Т-6. Степени. Т-7. Прогрессии. | 8 1 1 1 1 1 1 2 | 4 0,5 0,5 0,5 0,5 0,5 0,5 1 | 4 0,5 0,5 0,5 0,5 0,5 0,5 1 |
Комбинированный тест №1
Комбинированный тест №6 Комбинированный тест №2 |
| Итого по разделу 1 | 8 | 4 | 4 |
|
| Раздел 2. Уравнения и неравенства Т-8. Рациональные уравнения. Т-9. Уравнения и неравенства с одной переменной. Т-10. Системы уравнений. Т-11. Решение уравнений и неравенств с модулями. | 8 2 2 2 2
| 4 0,5 0,5 0,5 0,5
| 6 1,5 1,5 1,5 1,5
|
Комбинированный тест №5
|
| Итого по разделу 2 | 8 | 2 | 6 |
|
| Раздел 3. Функции Т-12. Функция. Область определения и область значений. График функции. Т-13. Свойства функции. Т-14. Обзор основных видов функции. | 3 1 1 1
| 3 0,5 0,5 0,5
| 3 0,5 0,5 0,5
|
|
| Итого по разделу 3 | 3 | 1,5 | .5 |
|
| Раздел 4. Геометрия | 16 | 4 | 12 |
|
| Т-15. Углы. Параллельные и перпендикулярные прямые Т-16. Треугольники, их виды и свойства. Т-17. Подобие фигур. Т-18. Четырехугольники, их виды и свойства. Многоугольники. Т-19. Окружность и круг, хорды, дуги, касательные и секущие. Углы в окружности. Т-20. Вписанные и описанные многоугольники. Правильные многоугольники Т-21. Площади треугольников и четырехугольников. Т-22. Длина окружности и площадь круга. | 2 2 2 2 2
2
2 2
| 0,5 0,5 0,5 0,5 0,5
0,5
0,5 0,5
| 1,5 1,5 1,5 1,5 1,5
1,5
1,5 1,5
|
Комбинированный тест №10 |
| Итого по разделу | 16 | 4 | 12 |
|
| Всего | 35 | 11,5 | 23,5 |
|
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА ПО ПРОГРАММЕ курса по выбору (факультатива) «ЗНАЙ И ПОВТОРЯЙ МАТЕМАТИКУ» В 10 КЛАССЕ НА УГЛУБЛЁННОМ УРОВНЕ ( 70 часов)
| Наименование разделов и тем | Количество часов | Формы контроля |
| Всего | Теория | Практика |
| 1 | 2 | 3 | 4 | 5 |
| Раздел 1. Числа и выражения Т-1. Делимость целых чисел и признаки делимости. Т-2. Проценты. Т-3. Действительные числа. Т-4. Алгебраические выражения. Т-5. Корень n-й степени. Т-6. Степени. Т-7. Прогрессии. | 15 2
2 2 2 2 2 3 | 7 1
1 1 1 1 1 1 | 8 1
1 1 1 1 1 2 |
Комбинированный тест №1 Комбинированный тест №6 Комбинированный тест №2 |
| Итого по разделу 1 | 15 | 7 | 8 |
|
| Раздел 2. Уравнения и неравенства Т-8. Рациональные уравнения. Т-9. Уравнения и неравенства с одной переменной. Т-10. Системы уравнений. Т-11. Решение уравнений и неравенств с модулями. | 12 3 3
3 3
| 4 1 1
1 1
| 8 2 2
2 2
|
Комбинированный тест №5 |
| Итого по разделу 2 | 12 | 4 | 8 |
|
| Раздел 3. Функции Т-12. Функция. Область определения и область значений. График функции. Т-13. Свойства функции. Т-14. Обзор основных видов функции. | 8 3
3 2
| 3 1
1 1
| 5 2
2 1
|
|
| Итого по разделу 3 | 8 | 3 | 5 |
|
| Раздел 4. Геометрия | 35 | 8 | 27 |
|
| Т-15. Углы. Параллельные и перпендикулярные прямые Т-16. Треугольники, их виды и свойства. Т-17. Подобие фигур. Т-18. Четырехугольники, их виды и свойства. Многоугольники. Т-19. Окружность и круг, хорды, дуги, касательные и секущие. Углы в окружности. Т-20. Вписанные и описанные многоугольники. Правильные многоугольники Т-21. Площади треугольников и четырехугольников. Т-22. Длина окружности и площадь круга. |
4
4 5 4
5
4
5
4
|
1
1 1 1
1
1
1
1
|
3
3 4 3
4
3
4
3
|
Комбинированный тест №10
|
| Итого по разделу | 35 | 8 | 27 |
|
| Всего | 70 | 22 | 48 |
|
IV. СОДЕРЖАНИЕ ФАКУЛЬТАТИВНОГО КУРСА
Раздел 1. Числа и выражения
Т-1.Делимость целых чисел и признаки1) Определение делимости целого числа а на целое число в (в≠0)а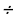 в=с, тогда в
в=с, тогда в с=а.2) Свойства делимости чисел.
с=а.2) Свойства делимости чисел.
Если а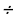 в и в
в и в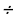 с, то а
с, то а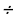 с Если а
с Если а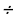 в и в
в и в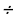 с, m и n – любые целые числа, то (m
с, m и n – любые целые числа, то (m а+n
а+n в)
в)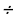 с. (при m
с. (при m 1и n=±1)
1и n=±1)
Если а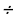 в и в
в и в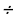 с, то (а
с, то (а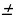 в)
в)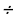 с
с
Если а в и k≠0, то а k в k
Если а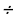 в и а
в и а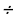 с, где в и с – взаимно простые числа, то а
с, где в и с – взаимно простые числа, то а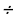 вс
вс
3) Признаки делимости:
На 2; На 5; На 10k; На 4; На 8; На 3 и 9.
Если последняя цифра числа делится на 2 (т.е. четные); любое четное число n можно представить в виде: n=2k (k є Z), а нечетные числа n=2k + 1 (k є Z)
Последняя цифра числа 0 или 5
Число оканчивается на k нулей
Число, выраженное двумя последними цифрами данного числа, делится на 4
Число, выраженное тремя последними цифрами данного числа, делится на 8 Сумма цифр числа делится на 3 или на 9 соответственно.
Т-2. Проценты1) Определение процента
Сотая часть целого (которое принимают за 1) 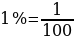
2) Основные задачи на проценты:
-Нахождение процентов от числа р%от числа а: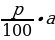 - Нахождение числа по данному значению его процентов
- Нахождение числа по данному значению его процентов
Если р% некоторого числа равно в, то это число равно в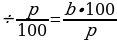
- Нахождение процентного отношения двух чисел
Число а составляет 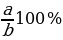 от числа в.
от числа в.
- увеличение на р% (уменьшение на р%)
Если число увеличить (уменьшить) на р%, то получим число ,
, 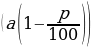
- Формулы сложных процентов
Если А начальный вклад, р – годовые проценты, то на конец n-го года вклад составляет 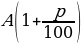 n
n
Т-3. Действительные числа.
1) Числовые множества:
- действительные числа R
Действительные числа, числа которые можно представить виде бесконечной десятичной дроби
- рациональные числа Q
Можно представить в виде несократимой дроби 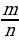 , где m– целое, n – натуральное число. Записываются в виде бесконечной периодической десятичной дроби.
, где m– целое, n – натуральное число. Записываются в виде бесконечной периодической десятичной дроби.
- иррациональные числа
Нельзя представить в виде несократимой дроби 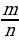 , где m– целое, n – натуральное число
, где m– целое, n – натуральное число
Записываются в виде бесконечной непериодической десятичной дроби (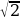 =1,4142135…
=1,4142135…
- целые числа Z
Включают натуральные числа, числа им противоположные и число 0.
-дробные числа
Числа, представляющие из себя целое число и части целой единицы (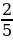 ) - обыкновенная дробь; 1,37 – десятичная дробь: 1,37=
) - обыкновенная дробь; 1,37 – десятичная дробь: 1,37=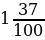 =
=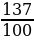 )
)
- натуральные числа N (целые положительные числа)
Натуральное число – основное неопределяемое понятие математики
- число 0
Число, которое при сложении с любым числом не изменяет его (а+0=а; 0+а=а), а при умножении на любое число дает в произведении 0 (0 а=0; а
а=0; а 0=0)
0=0)
2) Пропорции, прямая и обратная пропорциональность. Пропорциональное деление числа.
- определение пропорции
Пропорция – равенство двух отношений: а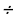 в=с
в=с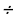 dили
dили 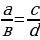 (а и d – крайние члены, в и с – средние члены)
(а и d – крайние члены, в и с – средние члены)
- свойства пропорции
Произведение крайних членов пропорции равно произведению средних ее членов
Если 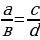 , то аd=вс.
, то аd=вс.
Если 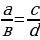 , то а=
, то а= 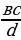 , с=
, с= 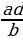 ,b=
,b= 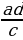 , d=
, d= 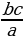
Если 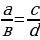 , то
, то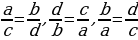
- Масштаб
Масштаб – отношение расстояния на карте к соответствующему расстоянию на местности.
Например, масштаб 1:100000 означает, что 1 см на карте соответствует 100000 см= 1000м=1км на местности.
- прямо пропорциональные величины
Две величины прямо пропорциональны, если с увеличением (уменьшением) значений одной из них в несколько раз значение второй увеличивается (уменьшается)во столько же раз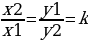 (k-коэффициент пропорциональности)
(k-коэффициент пропорциональности)
- обратно пропорциональные величины
Две величины обратно пропорциональны, если с увеличением (уменьшением) одной из них в несколько раз значение второй уменьшается (увеличивается) во столько же раз 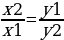
- деление числа на части, пропорциональные данным числам
Числа у1, у2, у3, пропорциональны числам х1, х2, х3, если 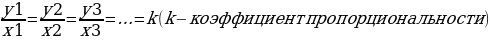
Разделить число на части, пропорциональные данным числам значит надо разделить его на сумму этих чисел и найденное частное умножить на каждое из них.
3) Модуль числа:
- определение
Модуль положительного числа – само это число.
Модуль отрицательного числа –число, ему противоположное.
Модуль 0 равно 0:

- геометрический смысл модуля:
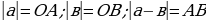
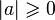 Модуль любого числа - число неотрицательное.
Модуль любого числа - число неотрицательное.
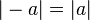 Модули противоположных чисел равны. а
Модули противоположных чисел равны. а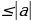 Любое число не превышает свой модуль.
Любое число не превышает свой модуль. 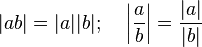 Модуль произведения равен произведению модулей
Модуль произведения равен произведению модулей
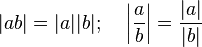 (в
(в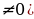 Модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю)
Модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю)
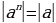 n, в частности Модуль степени числа равен той же степени модуля этого числа
n, в частности Модуль степени числа равен той же степени модуля этого числа
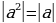 2,
2,
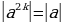 2k
2k
Т-4. Алгебраические выражения.
1)Основные законы алгебры а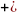 в=в
в=в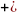 а; а
а; а в=в
в=в а; а
а; а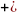 (в
(в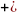 с)=(а
с)=(а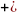 в)
в)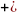 с; а
с; а (в
(в с)=(а
с)=(а в)
в) с; а
с; а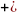 0=а; а
0=а; а 1=а; а
1=а; а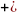 (-а)=0; а
(-а)=0; а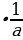 =1 (а
=1 (а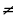 0); а(в
0); а(в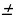 с)=ав±ас; (а
с)=ав±ас; (а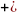 в)(с+d)=ac+ad+вc+вd.
в)(с+d)=ac+ad+вc+вd.
2) Правила раскрытия скобокa+(в+c)=a+ в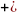 c; a-(b + c)=a-b-c; a+(b-c)=a+ b-c; a-(b-c)= a- b +c;
c; a-(b + c)=a-b-c; a+(b-c)=a+ b-c; a-(b-c)= a- b +c;
3) Умножение одночлена на многочлен x (a+b)= x
(a+b)= x a+x
a+x b
b
4) Умножение многочлена на многочлен (а + в)(x+y)=ax+ay+вx+by
5) формулы сокращенного умножения
(а + в)(а-в)=а2-в2; (а ± в)2=а2±2ав+ в2; (а + в)(а2-ав +в2)= а3+в3; (а-в)(а2+ав +в2)= а3-в3;
(а ± в)3=а3±3а2в+3ав2±в3; (а + в + с)2= а2+в2+с2+2ав+2ас+2вс.
6) разложение многочлена на множители:
- вынесение общего множителя за скобки; ха + хв = х(а + в)
-способ группировки: х а+х
а+х в+у
в+у а+у
а+у в=(х·а+х·в)+(у·а+у·в)=х(а+в)+у(а+в)= =(а+в)(х+у)
в=(х·а+х·в)+(у·а+у·в)=х(а+в)+у(а+в)= =(а+в)(х+у)
- применение формул сокращенного умножения
а2-в2=(а+в)(а-в); а2±2ав+в2=(а±в)2; а3±3а2в+3ав2±в3=(а±в)3 а2+в2+с2+2ав+2ас+2вс= (а+в+с)2.
- применение других формул
ах2+вх+с=а(х-х1) (х-х2), где х1и х2 корни уравнения ах2+вх+с=0
аn-1=(a-1)(an-1+ an-2+…+a+1) а2m+1=(a+1)(a2m- a2m-1- a2m-2-…-a-1)
xn –an=(x-a)(xn-1+ axn-2+a2xn-3+…+an-2x+an-1)
7) Выделение квадрата двучлена
ах2+вх+с=а(х+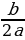 )2+
)2+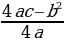
Т-5. Корень n-й степени и его свойства
1) Квадратный корень
Квадратным корнем из числа а называют такое число в, квадрат которого равен а. Если а=в2, то в= 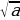
2) Корень n-й степени
Корнем n-й степени из числа а называют такое число в, n-я степень которого равна а
Если а=вn,n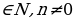 , то в=
, то в= 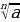
3) Арифметический корень
Арифметический корень – неотрицательное значение корня
Тождества (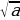 )2=а и
)2=а и  )n=a.
)n=a.
4) Область допустимых значений (ОДЗ)
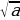 существует только при а≥0;
существует только при а≥0; 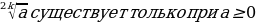 (k
(k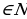 );
); 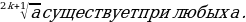
5) Свойства корня n-й степени
| Основные формулы для корней n-й степени (для 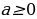 и и 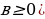 | Можно ли пользоваться формулой для любых а и в из ОДЗ левой части формулы |
| Корни нечетной степени | Корни четной степени |
| 1.  )n=a )n=a | Да | Только для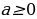 |
| 2. 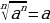 | Да | 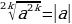
|
| 3. корень из корня 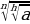 = =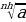 | Да | Да |
| 4. а) корень из произведения 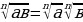
| Да
| 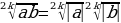
|
| б) произведение корней 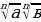 = =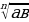
| Да
| Да
|
| 5. а) корень из частого 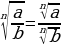
| Да
| 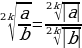
|
| б) частное корней 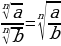
| Да
| Да
|
| 6. основное свойство корня 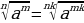 и наоборот и наоборот
| Да, если все корни нечетной степени | Да, если переход четный – четный. Если переход нечетный - четный, то 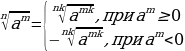
|
| 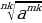 = = 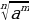
|
| 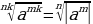
|
| 7. вынесение множителя за знак корня 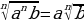
| Да | 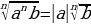
|
| 8. Внесение множителя под знак корня 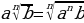
| Да | 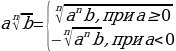 , где b≥0 , где b≥0
|
Т-6. Степени
1) Степень с натуральным и целым показателем
| 6. Степени 1) Степень с натуральным и целым показателем
|
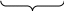 а1=а; аn=а а1=а; аn=а a a a a … … a, a a, a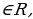 n n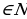 , (n≥2) , (n≥2)
nраз а0=1(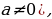 a-n= a-n=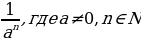 |
| 2) Степень с дробным показателем | 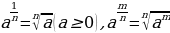
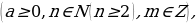
|
| 3) Свойства степеней | aman=am+n; am:an=am-n; (am)n=amn; (ab)n= an bn 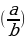 n= n=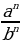
| - степень положительного числа – число положительное; - четная степень отрицательного числа – число положительное; - нечетная степень отрицательного числа – число отрицательное. |
Т-7. Прогрессии
1) Определения:
а) арифметической прогрессии
Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом (это число – разность d арифметической прогрессии)
б) геометрической прогрессии
Числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему, умноженному на одно и то же число, отличное от нуля (это число – знаменатель qгеометрической прогрессии).
2) Обозначения
а) в арифметической прогрессии
a1, a2,a3, …, an-1, an, an+1- арифметическая прогрессия
d= a2 - a1 = a3- a2 = an - an-1–разность прогрессии
б) в геометрической прогрессии
b1, b2, b3, …, bn-1, bn, bn+1–арифметическая прогрессия
q= 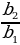 =
= 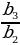 = … =
= … = 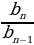 –знаменатель прогрессии
–знаменатель прогрессии
3) Характеристическое свойство
а) арифметической прогрессии
an= 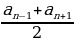 – любой член арифметической прогрессии – равен среднему арифметическому предыдущего и последующего членов.
– любой член арифметической прогрессии – равен среднему арифметическому предыдущего и последующего членов.
б) геометрической прогрессии
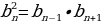 – квадрат любого члена геометрической прогрессии равен произведению предыдущего и последующего членов.
– квадрат любого члена геометрической прогрессии равен произведению предыдущего и последующего членов.
4) формулыn-го члена
а) арифметической прогрессии
an=an-1+d(по определению) an= a1+d(n-1).
б) геометрической прогрессии
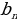 =
=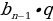 (по определению)
(по определению)
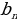 =
=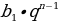
5) формулы суммы n первых членов
а) арифметической прогрессии 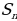 =
= 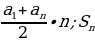 =
= 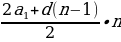 .
.
б) геометрической прогрессии 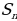 =
= 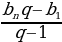 =
=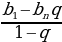 ;
; 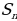 =
= 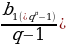 =
=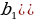
6) бесконечно убывающая геометрическая прогрессия
а) определение
Бесконечная геометрическая прогрессия, у которой знаменатель 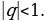
б) сумма членов
 Cумма членов бесконечной геометрической прогрессии – это предел, к которому стремится сумма ее первых n членов, когда n
Cумма членов бесконечной геометрической прогрессии – это предел, к которому стремится сумма ее первых n членов, когда n 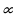 :
:
S=lim Sn , формула для ее вычисления S = 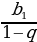
 n
n 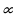
Раздел 2. Уравнения и неравенства
Т-8 Рациональные уравнения
1) Определение уравнений
Уравнение–это равенство, содержащее неизвестное, обозначенное переменной.
Корень уравнения (решение уравнения) – это значение переменной, при которой уравнение обращается в верное числовое равенство.
Решить уравнение- значит найти все его корни или доказать, что их нет.
2) Линейные уравнения:
а) определение
Общий вид: ах=b, где а и b- некоторые числа, х-неизвестное число.
б) решение
1) а ≠0 – единственный корень х=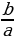
2) a=0 0x=b 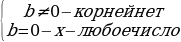
3) Квадратные уравнения:
а) определение
Уравнение вида ах2+bx +c=0, где х - неизвестная переменная, а,b и с некоторые числа, причем а≠0
Если b=0 или с =0 – уравнение неполное: ах2=0,
ах2+bx=0, ах2+c=0
б) формулы корней полных квадратных уравнений
ах2+bx +c=0 (а ≠0) 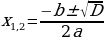 , где D =
, где D = 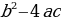 . (D – дискриминант)
. (D – дискриминант)
При D 0 – два корня; D
0 – два корня; D 0 – один корень; D
0 – один корень; D 0 – не имеет корней.
0 – не имеет корней.
в) приведенные квадратные уравнения
Если первый коэффициент равен 1:
х2+px +q=0. 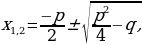 где D1=
где D1=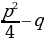 – дискриминант
– дискриминант
г) теорема Виета для приведенных квадратных уравнений
х2+px +q=0, х1 и х2 – его корни, тогда х1 х2 = q, х1+ х2 = - p.
х2 = q, х1+ х2 = - p.
д) уравнения, которые сводятся к квадратным
Если в уравнении переменная входит в одном и том же виде, то удобно соответствующее выражение с переменной обозначить новой переменной. Пример: биквадратное уравнение ах4+bx2 +c=0 (а ≠0).
4) Дробно-рациональные уравнения
Схема решения:
1) Перенести все члены уравнения в левую часть;
2) выполнить все действия с алгебраическими дробями, т.е. получить уравнение, левая часть которой дробь, а правая – нуль;
3) использовать свойство равенства дроби нулю (дробь равна нулю, если ее числитель равен нулю, а знаменатель – не равен нулю) и приравнять числитель полученной дроби нулю;
4) решить получившееся уравнение;
5) проверить, все ли найденные решения удовлетворяют условие равенства дроби нулю (если получим в знаменателе нуль, то найденное число не является корнем данного уравнения).
Или другая схема решения (с помощью ОДЗ)
1) Определить ОДЗ данного уравнения;
2) Найти общий знаменатель всех дробей, которые входят в запись уравнения;
3) Умножить обе части уравнения на общий знаменатель (полученное уравнение равносильно заданному на ОДЗ)
4) Решить получившееся целое уравнение;
5) Отобрать из всех найденных решений те, которые входят в ОДЗ.
Т -9 Уравнения и неравенства с одной переменной
1) Определение неравенства с переменной
Неравенства с одной переменной – это два выражения с переменной, соединённых знаком: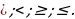
Решением неравенства называют значения переменной, при которых неравенство превращается в верное числовое неравенство.
Решить неравенство – значит найти все его решения или доказать, что их нет.
2) Числовые промежутки3) Область допустимых значений (ОДЗ)
ОДЗ уравнения (или неравенства) – это общая область определения всех функций, которые имеются во всех частях уравнения (неравенства)
4) Уравнения - следствия
- Если каждый корень первого уравнения является корнем другого уравнения, то второе уравнение называется следствием первого.
- Если из правильного первого равенства вытекает правильность каждого
следующего, то получается уравнение- следствие.
При этом возможно появление посторонних корней. Поэтому при использовании уравнений – следствий обязательна проверка полученных корней в начальном уравнении.
5) Равносильные уравнения и неравенства:
а) Определение
Два уравнения (два неравенства) равносильны на некотором множестве, если на этом множестве они имеют одни и те же решения.
б) Теоремы о равносильности уравнений ( неравенств)
1.Если из одной части уравнения (неравенства) перенести в другую часть слагаемые с противоположным знаком, то получим уравнение(неравенство), равносильное данному на любом множестве.
2.Еслиобе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну й ту же функцию, которая определена и не равна нулю на ОДЗ данного уравнения), то получим уравнение, равносильное данному на ОДЗ этого уравнения.
3. Если обе части неравенства умножить или разделить на одно и то же положительное число, (или на одну й ту же функцию, которая определена и положительна на ОДЗ данного неравенства), не меняя знака неравенства, то получим неравенство, равносильное данному на ОДЗ этого неравенства.
4.Если обе части неравенства умножить или разделить на одно и то же отрицательное число, (или на одну й ту же функцию, которая определена и отрицательна на ОДЗ данного неравенства) и при этом поменять знак неравенства на противоположный, то получим неравенство, равносильное данному на ОДЗ данного неравенства.
6) Схема поиска плана решения уравнений:
1. С помощью уравнений- следствий:
-преобразования, которые гарантируют сохранение правильности равенства;
- проверка корней подстановкой в начальное уравнение.
2. С помощью равносильных преобразований:
- учесть ОДЗ данного уравнения.
- сохранять на ОДЗ правильное равенство при прямых и обратных преобразованиях.
3. Применение свойств функций.
7) Схема поиска плана решения неравенств
1. С помощью равносильных преобразований:
- преобразования, которые гарантируют сохранение правильности неравенства.
- проверка корней подстановкой в начальное неравенство.
2. С помощью метода интервалов (f(x)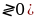 :
:
- найти ОДЗ
- найти нули функции: f(x)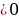 .
.
- обозначить нули на ОДЗ и найти знак функции f(x) на каждом промежутке, на которые разбивается ОДЗ.
- записать ответ, учитывая знак данного неравенства.
Т-10. Системы уравнений
1) Понятие системы и её решений
-Если надо найти общие решения двух (и более) уравнений с одной или несколькими переменными, то говорят, что надо решить систему уравнений ( запись этих уравнений объединяют фигурною скобкой).
- Решением системы называют такое значение переменной или такой упорядоченный набор значений переменных (если их несколько), которые удовлетворяют все уравнения системы.
- Решить систему уравнений – значит найти все её решения или доказать, что их нет, ( если система не имеет решений, то её называют несовместимой)
2) Равносильность систем уравнений
- Две системы уравнений равносильны на некотором множестве, если на этом множестве они имеют одинаковые решения.
(ОДЗ системы называют общую область определения всех выражений, входящих в её запись.
Все равносильные преобразования систем выполняются на ОДЗ заданной системы).
- Если изменить порядок записи уравнений заданной системы, то получим систему, равносильную заданной. - Если одно из уравнений системы заменить на равносильное ему уравнение, то получим систему, равносильную данной 3) Основные способы решения систем уравнений:
- способ подстановки;
- способ сложения; - графический способ решения систем уравнений с двумя переменными.
Т -11 Решение уравнений и неравенств с модулями
| 1.Основные способы | - по определению модуля: 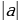 = =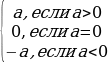 - по геометрическому смыслу модуля: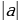 – расстояние на числовой прямой от точки О до точки – расстояние на числовой прямой от точки О до точки 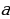 1.f(x) = 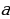 2.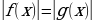 3.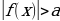 4.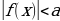 - по общей схеме: 1.Найти ОДЗ 2.Найти нули всех подмодульных функций 3.Обозначить нули на ОДЗ и разбить ОДЗ на промежутки 4.Найти решение на каждом промежутке и проверить, входит ли это решение в данный промежуток. |
| 2. Применение геометрического смысла модуля | 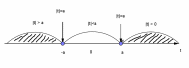 1. 1.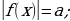 f(x) = f(x) = 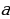 , или f(x) = , или f(x) = 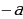 . .
2.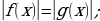 f(x) f(x)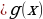 или f(x) или f(x)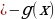 . . 3.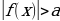 ;f(x) ;f(x) 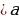 или f(x) или f(x) 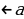 4.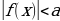 ; ;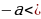 f(x) f(x)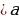 или или 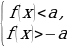 |
| 3) Специальный способ решения неравенств вида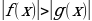 | 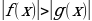 равносильно равносильно 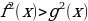 или (f(x) - или (f(x) - 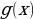 ) (f(x) + ) (f(x) +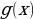 ) )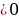 . .
|
| 4.Неравенства, имеющие несколько модулей (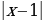 + + 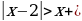 4 4 | 1.Найти ОДЗ; 2. Найти нули всех подмодульных функций; 3.Разбить ОДЗ на промежутки нулями подмодульных функций; 4.Найти решения на каждом промежутке и объединить их. |
Раздел 3. Функции
Т-12. Функция. Область определения и область значений. График функции.
1) Понятие функции
Функция – зависимость, при которой каждому значению переменной х (х – аргумент, независимая переменная) из некоторого множества D соответствует единственное значение переменной у (у – функция от х).
Множество D – область определения функции (для функций, заданных формулой, где ничего не сказано об области её определения, D – множество всех значений переменной, при которых заданная формула имеет смысл).
Область значений функции (множество Е) – это множество тех значений, которые может принимать сама функция при всех значениях аргумента из области определения.
2) График функции
График функции – множество всех точек координатной плоскости, абсциссы которых равны значению аргумента, а ординаты - соответствующим значениям функции.
3) Нахождение области определения функции
| Вид функции
| Ограничения, которые учитываются при нахождении области определения функции |
y =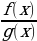 | 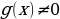 | Знаменатель дроби отличен от нуля |
| 2.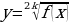 ; ; k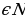 | f (x)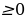 | Под знаком чётной степени может быть лишь неотрицательное число |
| 3.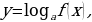 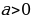
| f(x)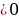 | Под знаком логарифма может быть только положительное число |
| 4.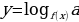 , , 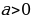
| 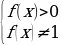
| Основание логарифма - положительно выражение, не равное единице. |
| 5.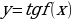 | f(x) =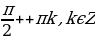 | Под знаком тангенса может быть выражение, отличное от 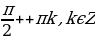 |
| 6. 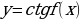 | f(x)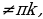 k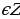 | Под знаком котангенса может быть выражение, отличное от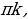 k k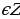 |
| 7.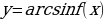 | 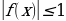 , -1 , -1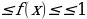
| Под знаком арксинуса и арккосинуса может быть выражение, модуль которого не превышает единицу |
| 8.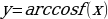 |
| 9.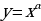 |
|
|
| а)α–натуральное число б) α–целое отрицательное число или нуль в)α – положительное нецелое число г)α– отрицательное нецелое число |
| x– любое число
x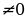
x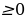
x 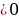
|
Т-13. Свойства функций
1) Возрастающие и убывающие функции
Функцияf(x) возрастающая, если для 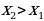 и
и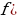 )
)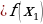 для всех
для всех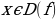 .
.
Функцияf(x) убывающая, если для 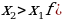 )
)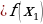 для всех
для всех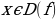 .
.
2) Чётные и нечётные функции
Функцияf(x)- чётная, если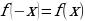 для всех
для всех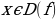 .
.
График чётной функции симметричен относительно оси Oy.
Функцияf(x) – нечетная, еслиf(-x) = -f(x)для всех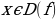 .
.
График нечётной функции симметричен относительно начала координат/
3) Периодичность функции
Функция f(x) периодическая с периодом 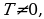 если для любогоx (
если для любогоx (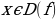 ) числа (x + T)и (x -T)также принадлежат
) числа (x + T)и (x -T)также принадлежат 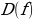 и выполняется равенство:
и выполняется равенство: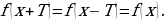
ЕслиT – период функции,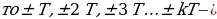 также периоды этой функции(k
также периоды этой функции(k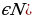 и T- наименьший её положительный период.
и T- наименьший её положительный период.
Функции 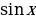 иcosx имеют период T = 2
иcosx имеют период T = 2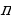
Функции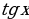 и
и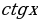 имеют период T =
имеют период T = 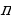
Если функцияy = f(x) периодическая с периодомT, то функцияy = Af(kx + b) также периодическая с периодом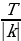 , где A, k, и b некоторые числа и k
, где A, k, и b некоторые числа и k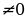 Т-14 Обзор основных видов функции
Т-14 Обзор основных видов функции
1) Линейная функцияy = kx +b
2) Степенная функцияy =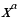
Построение графиков функций и их свойства 3) Преобразование графика функцииy = f(x)
1) y = -f(x) - симметрия графика относительно оси Ох
2) y = f(-x) - симметрия графика относительно оси Оу
3) y = f(x-a) – параллельный перенос графика вдоль оси Ох
4) y =f(x) + c –параллельный перенос графика вдоль оси Оуна с единиц
5) y =kf(x) (k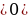 –растяжение или сжатие графика вдоль оси Оу (при k
–растяжение или сжатие графика вдоль оси Оу (при k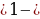 растяжение, при 0
растяжение, при 0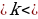 1 -сжатие)
1 -сжатие)
6) y = f(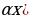 (
( 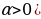 –растяжение или сжатие графика вдоль оси Ох ( при
–растяжение или сжатие графика вдоль оси Ох ( при 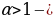 сжатие ,при
сжатие ,при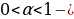 растяжение)
растяжение)
7) y = 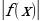 –выше оси Ох (и на самой оси) график остается без изменений; ниже оси Ох- симметрично отображается относительно оси Ох.
–выше оси Ох (и на самой оси) график остается без изменений; ниже оси Ох- симметрично отображается относительно оси Ох.
8) y = f ) – правее оси Оу (и на самой оси) график остается без изменений; та же самая часть графика отображается симметрично относительно оси Оу.
) – правее оси Оу (и на самой оси) график остается без изменений; та же самая часть графика отображается симметрично относительно оси Оу.
Раздел 4. Геометрия
Т-15. Углы. Параллельные и перпендикулярные прямые
1) Понятие угла
Угол как фигура, образованная двумя лучами с общим началом(вершиной угла)
Плоский угол – часть плоскости, ограниченной двумя лучами с общим началом.
2) Виды углов
Прямой угол, острый угол, тупой угол, развернутый угол, больший развернутого угла
3) Биссектриса угла
Биссектриса угла – это луч, имеющий начало в вершине угла, лежащей в его внутренней области и делящий угол на два равных угла
4) Смежные и вертикальные углы
| Смежные и вертикальные углы 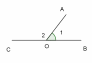
(рис. 1) 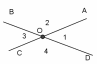
(рис. 2) | 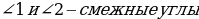
∠1 + ∠2 = 180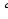 (рис. 1) (рис. 1) ∠1 и ∠3, ∠2 и ∠4 - вертикальные углы . ∠1 = ∠3 , ∠2 =∠4 (рис. 2) |
| Углы при пересечении двух прямых секущей 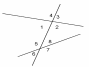
| ∠1 и ∠5, ∠2 и ∠8 – внутренние односторонние углы, ∠1 и ∠8 , ∠2 и ∠5 – внутренние накрест лежащие углы , ∠4 и∠5; ∠3 и ∠8 ;∠1 и ∠6 ; ∠2 и ∠7 – соответственные углы. |
6) Параллельные прямые
1. Две прямые параллельны, если они лежат в одной плоскости и не пересекаются: a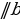
2. Через точку вне данной прямой можно провести одну прямую, параллельную данной.
3. Признаки параллельности прямых:
1) Если внутренние накрест лежащие или соответственные углы равны, то a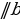
2) Если сумма внутренних односторонних углов равна 180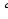 , то a
, то a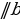
3) Если a⊥ с и b⊥c, то a ‖ b
4) Если a ‖ b, b ‖ c, то a ‖ c.
4.Свойства параллельных прямых и секущей
Если a ‖ b, а с- секущая, то
1) внутренние накрест лежащие углы равны;
2) соответственные углы равны;
3) сумма внутренних односторонних углов равна 180
4) если a ‖ b и c⊥a, то c⊥b
7) Перпендикулярные прямые
1. Две прямые перпендикулярные, если они пересекаются под прямым углом: a⊥b, ∠AOB= 90
2. Через данную точку можно провести единственную прямую, перпендикулярную данной прямой.
3. Перпендикуляр к прямой – отрезок ОА, проведенный из точки О к прямой а под прямым углом (А – основание перпендикуляра, ОА – кратчайшее расстояние от точки О до прямой а.
Т-16. Треугольники, их виды и свойства.
| 1)Равенство треугольников | Две фигуры равны, если они движением переходят одна в другую. ∆ABC=∆A1B1C1,тогда АВ=A1B1BC=B1C1AC=A1C1, ∠A =∠A , ∠B =∠B1, ∠C=∠C1 |
| 2) Признаки равенства треугольников | 1.По двум сторонам и углу между ними 2.По стороне и двум прилежащим углам 3.По трём сторонам |
| 3) Признаки равенства прямоугольных треугольников | 1.По двум катетам 2.По катету и острому углу 3.По гипотенузе и острому углу 4.По гипотенузе и катету |
| 4) Свойства сторон и углов треугольника 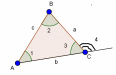
| В ∆ ABC (AB = с, BC= a , AC = b , ∠A =∠1 , ∠B =∠2, ∠C=∠3, ∠4 - внешний при вершине C) 1.∠A +∠B +∠C = 180 2.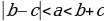 -неравенство треугольника -неравенство треугольника 3.∠4 = ∠1+ ∠2 – свойство внешнего угла |
| 5) Равнобедренный треугольник | В равнобедренном треугольнике ∆ABC (AB=BC, AC- основание, BD- медиана к основанию AC) Свойства: 1.∠A = ∠C (углы при основании равны) 2.Медиана BD является также высотой и биссектрисой. Признаки: 1.Если∠A = ∠C, то AB= BC 2.Треугольник ABC равнобедренный с основанием AC, если BD - медиана и высота или - высота и биссектриса или - медиана и биссектриса. |
| 6) Равнобедренный прямоугольный треугольник 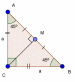
| ∠C = 90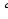 , AC=CB=a, ∠A=∠B=45 , AC=CB=a, ∠A=∠B=45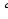 ,AB=a√2, CM⊥ABCM=AM=MB ,AB=a√2, CM⊥ABCM=AM=MB |
| 7) Высота, медиана, биссектриса и средняя линия треугольника 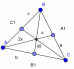
(рис. 1). 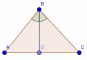
(рис. 2) | 1. Медиана треугольника(рис. 1): 1)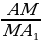 = =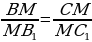 = =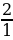 ; ;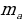 = =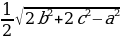 2)В прямоугольном треугольнике с гипотенузой с и медианой 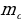 к ней к ней 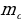 = =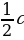 2.Биссектриса BD треугольника ABC(рис. 2): 1)∠ABD=∠CBD=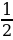 ∠B; ∠B; 2)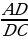 = =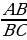 - пропорциональное свойство биссектрисы угла треугольника; - пропорциональное свойство биссектрисы угла треугольника; 3) О – точка пересечения биссектрис – центр вписанной окружности. |
|
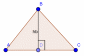
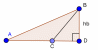

|
3. Высота треугольника: 1) BD – высота, BD⊥AC. 2)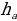 : :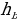 : :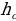 = =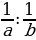 : :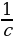 – высоты обратно пропорциональные сторонам. – высоты обратно пропорциональные сторонам. 4.Средняя линия треугольника M -середина AB, N- середина BC; MN - средняя линия. |
| Соотношения между сторонами и углами треугольника 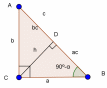
(рис. 1) 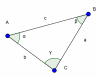
(рис. 2) | 1. Прямоугольный треугольник(рис. 1) 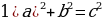 –Теорема Пифагора –Теорема Пифагора
2)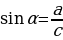 ; a= c ; a= c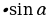 ; ; 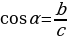 ; ; b = c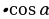 ; ;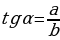 ; a= b ; a= b 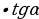 . . 3)∆ACD ∆ABC , ∆ABC , 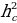 = =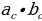 ∆CBD ∆ABC, и ∆ABC, и 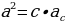 ∆ACD ∆CBD ∆CBD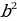 = c = c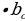 . . 2.Произвольный треугольник (a,b,c - стороны, R- радиус описанной окружности)(рис. 2) 1)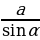 = = 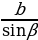 = = 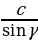 = = 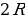 –теорема синусов –теорема синусов 2)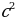 = = 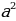 + + 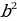 – 2ab – 2ab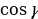 - теорема косинусов - теорема косинусов 3) Следствия: - если 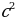 = = 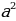 + + 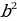 , то , то 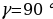 - если 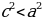 + + 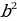 , то , то 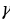 – острый угол – острый угол -если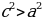 + +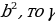 – тупой угол – тупой угол
- в треугольнике против большей стороны лежит больший угол и наоборот. |
Т-17. Подобие фигур.
1.Подобие треугольников
1) ∆ ABC ∆ A1B1C1 , тогда∠A =∠A1 , ∠B =∠B1, ∠C=∠C1 и
∆ A1B1C1 , тогда∠A =∠A1 , ∠B =∠B1, ∠C=∠C1 и 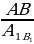 =
=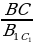 =
=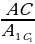 =
=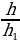 =
=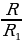 =k (k-коэффициент подобия)
=k (k-коэффициент подобия)
2)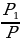 =
= 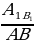 = k;
= k;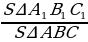 =
=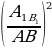 =
=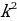
2.Признаки подобия треугольников
1) По двум равным углам:
∆ ABC ∆ A1B1C1, если ∠A =∠A1 , ∠B =∠B1
∆ A1B1C1, если ∠A =∠A1 , ∠B =∠B1
2) По двум пропорциональным сторонам и углу между ними:
∆ ABC ∆ A1B1C1, если
∆ A1B1C1, если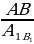 =
=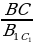 и тогда∠B =∠B1
и тогда∠B =∠B1
3) По трём пропорциональным сторонам
∆ ABC ∆ A1B1C1, если
∆ A1B1C1, если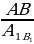 =
=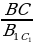 =
=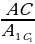
4) Прямая, пересекающая две стороны треугольника и параллельная третьей его стороне , отсекает треугольник, подобный данному.
Т-18. Четырехугольники, их виды и свойства. Многоугольники.
1) Определение параллелограмма
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны
2) Свойства параллелограмма
1) равенство противоположных сторон и углов;
2) диагональ делит параллелограмм на два равных треугольника;
3) диагонали точкой пересечения делятся пополам;
4) ABCD– параллелограмма, ACи BD- его диагонали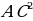 + B
+ B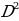 = 2
= 2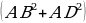
3) Признаки параллелограмма
ЧетырёхугольникABCD – параллелограмм, если
1) две стороны попарно равны и параллельны;
2) противоположные стороны попарно равны;
3) диагонали пересекаются и точкой пересечения делятся пополам.
4) Виды параллелограммов и их дополнительные свойства
1.Прямоугольник:
- диагонали прямоугольника равны.
2. Ромб:
-диагонали ромба перпендикулярны и являются биссектрисами его углов.
3. Квадрат:
- имеет свойства любого из параллелограммов.
5) Трапеция
1.Определение трапеции, её элементы. Виды трапеции
2. Равнобокая трапеция и её свойства
1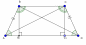 ) ∠A =∠D;∠B =∠C. 2)AC=BD. 3)A
) ∠A =∠D;∠B =∠C. 2)AC=BD. 3)A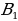 =
=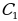 D =
D =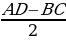 . 3.В прямоугольной трапеции высота равна боковой стороне, которая перпендикулярна основаниям.
. 3.В прямоугольной трапеции высота равна боковой стороне, которая перпендикулярна основаниям.
4. Средняя линия трапеции MN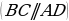 :
:
- MN ‖ AD; MN‖ BC.
- MN = 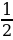 (BC + AD).
(BC + AD).
6) Многоугольники
1.Определение выпуклого многоугольника, его диагонали.
2.Углы многоугольника. Внешний угол при данной вершине.
3.Свойства:
- сумма всех внутренних углов вычисляется по формуле 180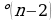 ( n- число углов многоугольника);
( n- число углов многоугольника);
- сумма всех внешних углов, взятых по одному при вершине, равна 360
Т-19. Окружность и круг, хорды, дуги, касательные и секущие. Углы в окружности.
1) Определение окружности, хорды, дуги.
2) Свойства дуги хорд 1.Равные дуги стягивают равные хорды и наоборот
| 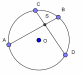
(рис. 1) 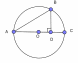
(рис. 2) | 2.Параллеьные хорды отсекают на окружности равные дуги. 3.Диаметр, перпендикулярный к хорде, делит её и стягиваемую дугу пополам и наоборот. 4.S – точка пересечения хорд AB и CD,тогда AS SB =CS SB =CS SD (рис. 1) SD (рис. 1) AB – хорда , AC – диаметр и BD⊥AC. Тогда -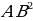 = AC = AC  AD AD - B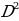 =AD =AD  DC(рис. 2). DC(рис. 2). |
| 3) Свойства касательных и секущих | 1.Определение секущей и касательной |
|
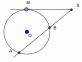
(рис. 1) 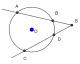 (рис. 2) (рис. 2)
| 2.Равенство двух касательных, проведенных из одной точки. 3.SM- касательная,SA- секущая:S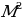 =SA =SA SB (рис. 1) SB (рис. 1) 4. SAи SC – секущие:SA SB =SC SB =SC SD (рис. 2) SD (рис. 2) |
| 4) Углы в окружности |
|
|
| 1.Определение центральных и вписанных углов, их измерение |
|
| 2.Свойства вписанных углов - опирающихся на одну и ту же дугу (эти углы равны) - опирающихся на диаметр (эти углы – прямые) |
| 
| 3. Угол между касательной и секущей MA- касательная , MB - секущая:∠AMB= 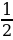 ⌣ ⌣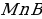 |
| 
| 4. Угол между двумя хордами ∠M =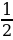 (⌣AC + ⌣BD) (⌣AC + ⌣BD) |
Т-20. Вписанные и описанные многоугольники. Правильные многоугольники
| 1) Определение | 1. Вписанные многоугольники 2. Описанные многоугольники |
| 2) Окружность, описанная около треугольника. | 1.Центр окружности О – точка пересечения серединных перпендикуляров к сторонам треугольника. 2.OA = OB = OC = R – радиус окружности, описанной около ∆ ABC (О – центр этой окружности). 3. R =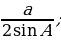 R = R = 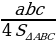 (a,b,c– стороны ∆ ABC, S – его площадь , R – радиус описанной окружности) (a,b,c– стороны ∆ ABC, S – его площадь , R – радиус описанной окружности) |
|
| 4.Положение центра окружности, описанной около - остроугольного и тупоугольного треугольников; - прямоугольного треугольника (центр- середина гипотенузы c и R = 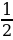 c c |
| 3) Окружность, вписанная в треугольник | 1.Центр О окружности, вписанной в∆ ABC - точка пересечения биссектрис внутренних углов этого треугольника. 2.OD⊥AB;OD = r – радиус вписанной окружности. 3.r =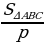 ; где p = ; где p = 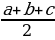 (a,b,c– стороны ∆ ABC, S – его площадь, r– радиус вписанной окружности) (a,b,c– стороны ∆ ABC, S – его площадь, r– радиус вписанной окружности) 4.В прямоугольном треугольнике с катетамиa и b и гипотенузой c:r = 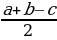 . . 5.Радиус окружности, вписанной в равнобедренный треугольник. |
| 4) Правильные многоугольники | 1.Определение правильного многоугольника. Его центр. 2. Формулы стороны 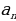 правильного n- угольника через R и r(радиусы описанной и вписанной окружностей) правильного n- угольника через R и r(радиусы описанной и вписанной окружностей) 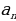 =2 =2 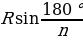 ; ;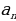 = 2r = 2r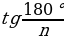 . . 3.Формулы вычисления 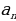 через R и r , если n =3,4,6. через R и r , если n =3,4,6. 4.Формулы площадей некоторых правильных многоугольников. 1) Правильный треугольник:S =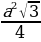 S = 3 S = 3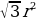 S =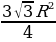 . . 2) Квадрат: S = 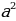 ; S = 4 ; S = 4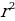 ; S = 2 ; S = 2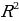 . . 3) Правильный 6 – угольникS=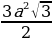 ;S = 2 ;S = 2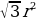 ;S = ;S = 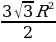 . .
|
Т-21. Площади треугольников и четырехугольников.
| 1)Площадь треугольника 
| 1.Площадь произвольного треугольника S =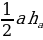 ; S = ; S = 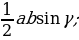 S = S =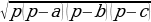 гдеp = гдеp = 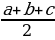 - Формула Герона; ( - Формула Герона; (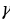 - угол между сторонами а и - угол между сторонами а и 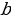 ) ) S =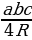 , где R–радиус описанной окружности S =rp , где r – радиус вписанной окружности , где R–радиус описанной окружности S =rp , где r – радиус вписанной окружности |
| 
| 2.Площадь прямоугольного треугольника S= 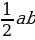 ; S = ; S =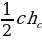 ;S = ;S = 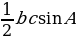 . . |
|
| 3.Площадь равностороннего треугольника S =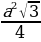 ( (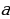 - его сторона ) - его сторона ) |
| 2) Площади четырёхугольников | 1.Произвольный выпуклыйS = 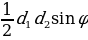 , , 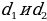 -его диагонали, -его диагонали,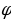 – угол между диагоналями. – угол между диагоналями. 2.Прямоугольник:S = a b; S = b; S = 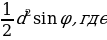 aи b - aи b - 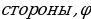 - угол между диагоналями, d - диагональ - угол между диагоналями, d - диагональ 3.Квадрат: S= 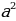 ; S = ; S =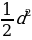 . . 4. Параллелограмм: S = 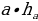 ; S = ; S = 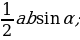 S = S = 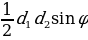 ( ( 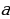 и b - и b - 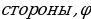 - угол между диагоналями, - угол между диагоналями,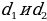 -его диагонали , -его диагонали ,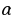 – угол между сторонами., – угол между сторонами., 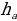 – высота к стороне а – высота к стороне а 5. Ромб: S = a h ;S = h ;S = 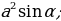 S = S = 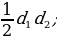 ( a – сторона , ( a – сторона , 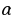 -угол ромба , -угол ромба , 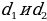 - его диагонали , h- высота). - его диагонали , h- высота). 6.Трапеция: S = 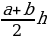 или S = m или S = m h(aи b –основания, m - средняя линия,m = h(aи b –основания, m - средняя линия,m =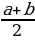 , h- высота) , h- высота) S = 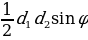 , , 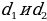 - диагонали , - диагонали , 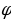 – угол между диагоналями. – угол между диагоналями.
|
Т-22. Длина окружности и площадь круга
| 1) Длина окружности и дуги | 1.ДлинаокружностиC = 2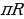 ( R- радиус), ( R- радиус), и длина дуги в 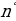 ℓ ℓ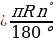 или 𝓵 = или 𝓵 =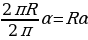 ( (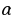 -центральный угол , соответствующий этой дуге, в радианах) -центральный угол , соответствующий этой дуге, в радианах) |
| 2) Площадь круга и его частей 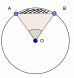
| 1.Площадь круга радиуса R: S =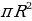 . . 2.Площадь кругового сектора - в 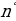 : S = : S = 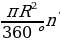 - в 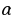 радиан: S = радиан: S = 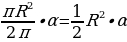 3.Площадь кругового сегмента: Sсегм=Sсект 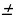 S∆AOB S∆AOB |







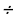 в=с, тогда в
в=с, тогда в с=а.2) Свойства делимости чисел.
с=а.2) Свойства делимости чисел. 1и n=±1)
1и n=±1)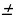 в)
в)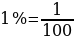
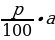 - Нахождение числа по данному значению его процентов
- Нахождение числа по данному значению его процентов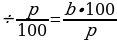
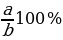 от числа в.
от числа в.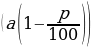
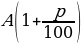 n
n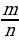 , где m– целое, n – натуральное число. Записываются в виде бесконечной периодической десятичной дроби.
, где m– целое, n – натуральное число. Записываются в виде бесконечной периодической десятичной дроби.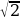 =1,4142135…
=1,4142135…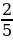 ) - обыкновенная дробь; 1,37 – десятичная дробь: 1,37=
) - обыкновенная дробь; 1,37 – десятичная дробь: 1,37=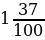 =
=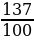 )
) 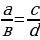 (а и d – крайние члены, в и с – средние члены)
(а и d – крайние члены, в и с – средние члены)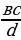 , с=
, с= 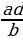 ,b=
,b= 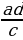 , d=
, d= 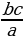
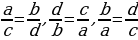
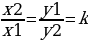 (k-коэффициент пропорциональности)
(k-коэффициент пропорциональности)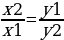
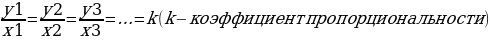

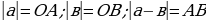
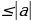 Любое число не превышает свой модуль.
Любое число не превышает свой модуль. 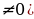 Модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю)
Модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю)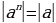 n, в частности Модуль степени числа равен той же степени модуля этого числа
n, в частности Модуль степени числа равен той же степени модуля этого числа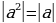 2,
2,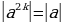 2k
2k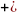 в=в
в=в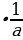 =1 (а
=1 (а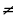 0); а(в
0); а(в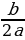 )2+
)2+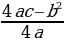
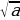
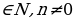 , то в=
, то в= 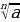
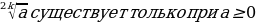 (k
(k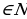 );
); 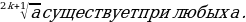
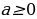 и
и 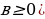
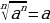
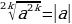
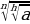 =
=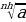
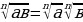
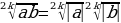
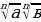 =
=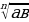
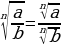
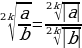
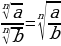
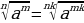 и наоборот
и наоборот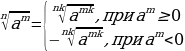
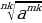 =
= 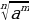
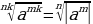
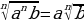
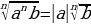
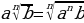
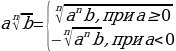 , где b≥0
, где b≥0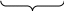 а1=а; аn=а
а1=а; аn=а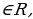 n
n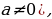 a-n=
a-n=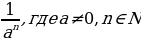
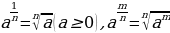
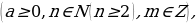
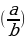 n=
n=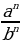
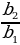 =
= 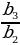 = … =
= … = 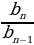 –знаменатель прогрессии
–знаменатель прогрессии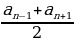 – любой член арифметической прогрессии – равен среднему арифметическому предыдущего и последующего членов.
– любой член арифметической прогрессии – равен среднему арифметическому предыдущего и последующего членов.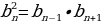 – квадрат любого члена геометрической прогрессии равен произведению предыдущего и последующего членов.
– квадрат любого члена геометрической прогрессии равен произведению предыдущего и последующего членов.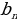 =
=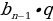 (по определению)
(по определению)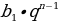
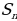 =
= 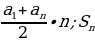 =
= 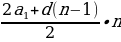 .
.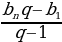 =
=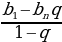 ;
; 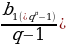 =
=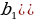
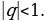
 Cумма членов бесконечной геометрической прогрессии – это предел, к которому стремится сумма ее первых n членов, когда n
Cумма членов бесконечной геометрической прогрессии – это предел, к которому стремится сумма ее первых n членов, когда n 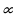 :
: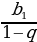
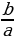
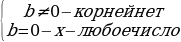
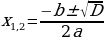 , где D =
, где D = 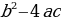 . (D – дискриминант)
. (D – дискриминант)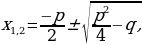 где D1=
где D1=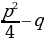 – дискриминант
– дискриминант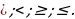
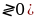 :
: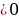 .
.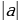 =
=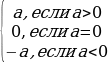
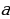
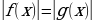
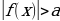
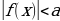
 1.
1.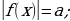 f(x) =
f(x) = 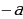 .
.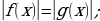 f(x)
f(x)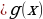 или f(x)
или f(x)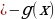 .
.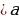 или f(x)
или f(x) 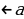
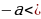 f(x)
f(x)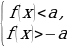
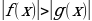
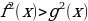 или (f(x) -
или (f(x) - 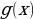 ) (f(x) +
) (f(x) +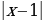 +
+ 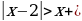 4
4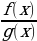
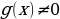
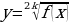 ;
;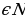
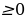
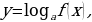
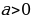
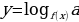 ,
,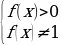
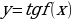
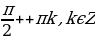
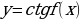
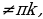
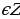
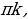 k
k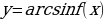
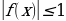 , -1
, -1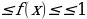
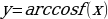
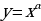
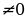
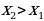 и
и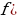 )
)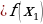 для всех
для всех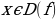 .
.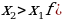 )
)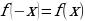 для всех
для всех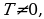 если для любогоx (
если для любогоx (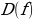 и выполняется равенство:
и выполняется равенство: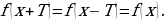
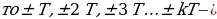 также периоды этой функции(k
также периоды этой функции(k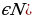 и T- наименьший её положительный период.
и T- наименьший её положительный период.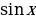 иcosx имеют период T = 2
иcosx имеют период T = 2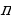
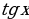 и
и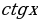 имеют период T =
имеют период T = 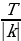 , где A, k, и b некоторые числа и k
, где A, k, и b некоторые числа и k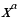
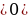 –растяжение или сжатие графика вдоль оси Оу (при k
–растяжение или сжатие графика вдоль оси Оу (при k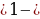 растяжение, при 0
растяжение, при 0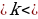 1 -сжатие)
1 -сжатие)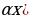 (
( 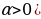 –растяжение или сжатие графика вдоль оси Ох ( при
–растяжение или сжатие графика вдоль оси Ох ( при 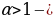 сжатие ,при
сжатие ,при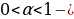 растяжение)
растяжение)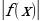 –выше оси Ох (и на самой оси) график остается без изменений; ниже оси Ох- симметрично отображается относительно оси Ох.
–выше оси Ох (и на самой оси) график остается без изменений; ниже оси Ох- симметрично отображается относительно оси Ох.

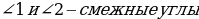
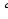 (рис. 1)
(рис. 1)
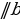

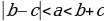 -неравенство треугольника
-неравенство треугольника


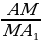 =
=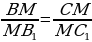 =
=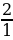 ;
;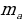 =
=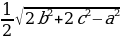
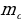 к ней
к ней 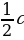
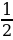 ∠B;
∠B;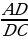 =
=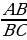 - пропорциональное свойство биссектрисы угла треугольника;
- пропорциональное свойство биссектрисы угла треугольника;


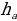 :
: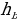 :
: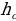 =
=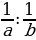 :
: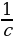 – высоты обратно пропорциональные сторонам.
– высоты обратно пропорциональные сторонам.

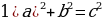 –Теорема Пифагора
–Теорема Пифагора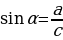 ; a= c
; a= c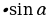 ;
; 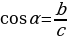 ;
;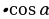 ;
;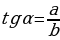 ; a= b
; a= b 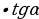 .
. ∆ABC ,
∆ABC , 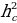 =
=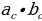
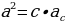
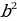 = c
= c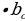 .
.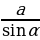 =
= 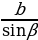 =
= 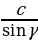 =
= 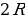 –теорема синусов
–теорема синусов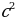 =
= 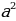 +
+ 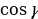 - теорема косинусов
- теорема косинусов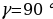
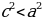 +
+ 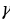 – острый угол
– острый угол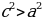 +
+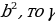 – тупой угол
– тупой угол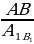 =
=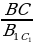 =
=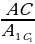 =
=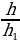 =
=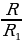 =k (k-коэффициент подобия)
=k (k-коэффициент подобия)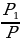 =
= 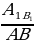 = k;
= k;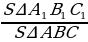 =
=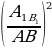 =
=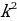
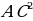 + B
+ B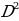 = 2
= 2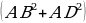
 ) ∠A =∠D;∠B =∠C. 2)AC=BD. 3)A
) ∠A =∠D;∠B =∠C. 2)AC=BD. 3)A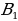 =
=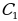 D =
D =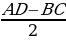 . 3.В прямоугольной трапеции высота равна боковой стороне, которая перпендикулярна основаниям.
. 3.В прямоугольной трапеции высота равна боковой стороне, которая перпендикулярна основаниям.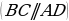 :
: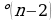 ( n- число углов многоугольника);
( n- число углов многоугольника);

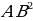 = AC
= AC 
 (рис. 2)
(рис. 2)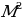 =SA
=SA
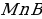

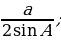 R =
R = 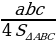 (a,b,c– стороны ∆ ABC, S – его площадь , R – радиус описанной окружности)
(a,b,c– стороны ∆ ABC, S – его площадь , R – радиус описанной окружности)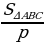 ; где p =
; где p = 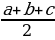 (a,b,c– стороны ∆ ABC, S – его площадь, r– радиус вписанной окружности)
(a,b,c– стороны ∆ ABC, S – его площадь, r– радиус вписанной окружности)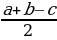 .
.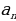 правильного n- угольника через R и r(радиусы описанной и вписанной окружностей)
правильного n- угольника через R и r(радиусы описанной и вписанной окружностей) 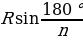 ;
;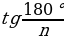 .
.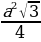 S = 3
S = 3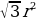
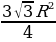 .
.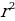 ; S = 2
; S = 2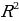 .
.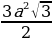 ;S = 2
;S = 2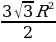 .
.
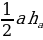 ; S =
; S = 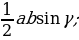 S =
S =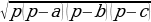 гдеp =
гдеp = 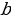 )
)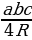 , где R–радиус описанной окружности S =rp , где r – радиус вписанной окружности
, где R–радиус описанной окружности S =rp , где r – радиус вписанной окружности
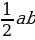 ; S =
; S =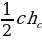 ;S =
;S = 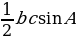 .
.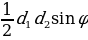 ,
, 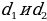 -его диагонали,
-его диагонали,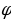 – угол между диагоналями.
– угол между диагоналями.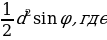 aи b -
aи b - 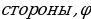 - угол между диагоналями, d - диагональ
- угол между диагоналями, d - диагональ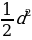 .
.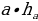 ; S =
; S = 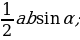 S =
S = 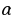 – угол между сторонами.,
– угол между сторонами., 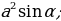 S =
S = 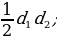 ( a – сторона ,
( a – сторона , 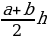 или S = m
или S = m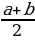 , h- высота)
, h- высота)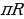 ( R- радиус),
( R- радиус),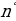 ℓ
ℓ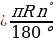 или 𝓵 =
или 𝓵 =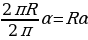 (
(
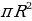 .
.