Методическая разработка урока алгебры в 9 классе.
Плохой учитель преподносит истину, хороший учит её добывать.
А. Дистервег
Учитель: Орлова Светлана Геннадьевна, учитель математики ГБОУ школа №471 Выборгского района Санкт- Петербурга.
Тема урока: «Построение графиков функций сдвигами вдоль осей координат»
Тип урока: урок усвоения новых знаний.
Цель: показать учащимся приём построения параболы с помощью сдвигов графика функции вдоль осей координат.
Задачи:
Обучающие: сформировать умение строить параболу y=a(x-m)2+n сдвигом вдоль осей координат и показать применение приобретённых навыков при построении графиков функций y=x-m +n , y=x-m
+n , y=x-m +n , y=kx-m
+n , y=kx-m  + n.
+ n.
Развивающие: развитие познавательных умений, аналитического и сравнительного мышления, математической грамотности, способности обобщать и делать выводы.
Воспитывающие: воспитание интереса к предмету, аккуратности, ответственности, требовательности к себе и другим.
Планируемые результаты:
Предметные: уметь по формуле определять характер сдвига графика функции и строить его.
Личностные: уметь отстаивать свою точку зрения и работать в коллективе.
Метапредметные: уметь планировать и оценивать процесс и результат своей деятельности, обрабатывать информацию.
Педагогические технологии: элементы проблемного и опережающего обучения.
Оборудование: интерактивная доска, компьютер, раздаточные материалы.
Содержание учебного материала.
1.Свойства и график функции y=ax2, зависимость направления ветвей параболы, её «растяжения» и «сжатия» вдоль оси ординат от коэффициента a.
2.Функции y=x , y=x
, y=x , y= kx
, y= kx  , их графики.
, их графики.
3.Построение графика функции y=f(x-m)+n, если y=f(x) – «исходная» функция.
Структура урока.
1. Организационная часть.
2. Актуализация знаний:
- проверка домашнего задания
- устная работа по готовым чертежам
- подготовка к изучению нового материала (создание проблемной ситуации)
3. Объяснение нового материала (первичное усвоение новых знаний).
4. Закрепление
- первичная проверка понимания
- применение знаний и умений в новой ситуации.
5. Подведение итогов урока.
6. Домашнее задание.
7. Рефлексия урока.
Технологическая карта урока алгебры в 9 классе по теме: «Построение графиков функций сдвигами вдоль осей координат»
|
Этапы урока
|
Задачи этапа
|
Деятельность учителя
|
Деятельность учащихся
|
УУД
|
|
1.Организационная часть
1 минута
|
Создание рабочего настроения в начале урока
|
Здоровается с учениками,
проверяет их подготовку к уроку, отмечает отсутствующих, записывает на доске дату.
|
Готовятся к работе на уроке, приветствуют учителя
|
Регулятивные:
организация учебной деятельности.
|
|
2.Актуализация знаний
10 минут
|
Проверить выполнение домашнего задания, повторить и обобщить изученный на прошлых уроках материал и создать условия для восприятия и усвоения новой темы (мотивация учебной деятельности).
|
Вызывает к боковой доске двух человек для проверки домашнего задания. Пока они готовятся, работает с классом
(приложение№2). Проверка домашнего задания осуществляется с помощью интерактивной доски
(приложение №1). Итак, где же находится вершина любой параболы вида y=ax2? Как зависит направление её ветвей от знака коэффициента а? От чего зависит «толщина» параболы?
y = ax2- простейшее, но не единственное уравнение параболы. Как построить графики более сложных квадратичных функций, вам предстоит узнать самим.
Лучший способ изучить
что-либо – это открыть самому.
Д.Пойа
Делимся на три команды (по рядам), выбираем капитанов, которые выходят к доске. Задание для команд написано на трёх досках, соревнование начинается!
|
Два ученика на боковой доске решают домашнее задание (приложение№1), после чего получают индивидуальное задание на карточках (приложение№3).
Вершина параболы y=ax2 находится в начале координат. Если а<0,ветви вниз, если а>0, ветви вверх. Чем а больше, тем парабола «уже», чем а больше, тем парабола «уже», чем а меньше, тем она «толще». меньше, тем она «толще».
По одному человеку от каждого ряда выходят к доске, строят графики функций цветными мелками, используя таблицу.
|
Познавательные:
приведение знаний в систему.
Коммуникативные:
умение прислушиваться к мнению окружающих.
Регулятивные:
оценивание результатов своей деятельности.
Личностные:
оценивание уровня усвоения материала.
|
|
3.Объяснение нового материала
15 минут
|
Создание благоприятной обстановки для выхода из проблемной ситуации,
восприятия и осмысления нового материала,
самостоятельного
прихода к правильному выводу.
|
В одной системе координат построить графики функций
1 команда:
а)y= - x2 б)y= - x2-2 в)y=-(x-2)2
2 команда:
а)y= x2 б)y= x2-3 в)y=(x-3)2
3 команда:
а)y= 2x2 б)y= 2x2+3 в)y=2(x+3)2
Задание выполнено! (приложение №4). Найдите закономерность расположения графиков относительно осей координат. Капитаны советуются со своими командами. Будем условно называть график а) «исходным».
Вот и тема нашего урока звучит так: «Построение графиков функций сдвигами вдоль осей координат».
Оказывается, эти правила верны для всех функций, а не только для параболы. Попробуйте их сформулировать, если y=f(x)-исходная функция.
Как вы думаете, можно ли обойтись без каких-то лишних построений. В самом деле, попробуем сдвинуть не сам исходный график, а систему координат. Построим таким образом параболу y=(x-3)2+2.Куда сдвиг? Значит, в точке (3;2)-начало дополнительной системы координат, которую мы и проводим пунктиром. От «нового» нуля и будем вести отсчёт, а таблица будет для исходной функции y=x2.Учитель строит график функции на доске.
|
Остальные ученики делают это в тетрадях, оказывая помощь друг другу.
График б) получен сдвигом исходного графика а) вверх-вниз, а график в) влево-вправо.
Записывают тему урока в тетрадь.
Формулируют и записывают в тетрадь правило:
y=f(x+3)-сдвиг на 3 влево
y=f(x-3)-сдвиг на 3 вправо
y=f(x)+3-сдвиг на 3 вверх
y=f(x)-3-сдвиг на 3 вниз
Наверное, но ученики не понимают, о чём речь.
На 3 вправо и на 2 вверх.
В тетрадях строят график функции новым способом.
|
Познавательные:
анализ условий поставленной задачи и поиск её рационального решения.
Личностные:
формирование устойчивого интереса к изучаемому материалу.
Коммуникативные:
умение прислушиваться к чужому мнению и работать в коллективе.
|
|
4.Закрепление:
-первичная проверка понимания
-применение знаний и умений в новой ситуации
15 минут
|
Способствовать осознанному и прочному усвоению темы,
корректировать пробелы в знаниях у слабых учащихся.
Проверить правильность усвоения темы и распространение полученных знаний на новые объекты.
|
Работа с презентацией
(приложение № 4).
Математику нельзя изучать, наблюдая как это делает сосед!
А.Нивен
Работа по вариантам.
Построить графики функций:
1 вариант:
y=x-5 +3 +3
2 вариант:
y = 4x+2  -1 -1
Если останется время, все вместе:
y=x-4  -2. -2.
|
Отвечают на вопросы из презентации, работают на интерактивной доске.
Строят графики функций новым способом.
|
Коммуникативные:
общение и взаимодействие с партнёрами по совместной деятельности, умение грамотно выражать свои мысли.
Регулятивные:
справедливая и адекватная оценка собственной деятельности.
|
|
5.Подведение итогов урока
1 минута
|
Осознание каждым учащимся: чему, как и зачем он научился сегодня на уроке и с какими знаниями и умениями он должен прийти на следующий урок.
|
Вы познакомились с новым способом построения графиков. В чём он состоит? Есть ли у вас вопрос, на который вы не получили сегодня ответ?
Оценки за урок.
|
Графики функций можно строить сдвигами вдоль осей координат.
|
Регулятивные:
умение оценить качество и уровень усвоения
|
|
6. Домашнее задание
2 минуты
|
Комментарии по домашнему заданию с целью его успешного выполнения.
|
П.6, №110(а, в),111 - построить графики изученным сегодня способом;
на повторение темы «Сокращение дробей» №104(а);
задание для любознательных: построить график функции y= x . .
|
Записывают домашнее задание в дневники и задают по нему вопросы.
|
|
|
7. Рефлексия.
1 минута
|
Заставить детей задуматься в конце урока о своём настроении,
эмоциональном состоянии и результатах взаимодействия с другими участниками образовательного процесса.
|
Выходя из кабинета, оцените по пятибалльной шкале своё настроение в конце урока и поставьте оценку на доске. Урок закончен, всем спасибо!
|
Собирают свои вещи, ставят оценки на доске.
|
Коммуникативные:
умение грамотно и честно выражать свои мысли.
Регулятивные:
умение оценить достигнутый результат.
Личностные:
чувство гордости за хорошо проделанную работу.
|
Литература.
1.Макарычев Ю. Н. Алгебра: 9 кл. / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и др. – М., Просвещение, 2012.
2.Миндюк Н. Г. Алгебра. Рабочие программы. Предметная линия учебников Ю. Н. Макарычева и других. 7 - 9 классы: пособие для учителей общеобразов. учреждений / Н. Г. Миндюк. – М.: Просвещение, 2011.
3. Асмолов А. Г. Формирование универсальных учебных действий в основной школе. Система знаний /, О. А. Карабанова. М.: Просвещение, 2010
4.Ким Н.А. Нестандартные уроки алгебры. Сост. Ким Н.А. – Волгоград: ИТД «Корифей», 2006.
Информационные средства (интернет-ресурсы):
ФЦИОР: http://school-collection.edu.ru/catalog/teacher/
«Математический конструктор»: http://school-collection.edu.ru/catalog/rubr/903077b7-0221-4823-b549-b236326d48d4/?interface=teacher&class[]=51&subject[]=17
Методическая разработка урока алгебры в 9 классе.
Плохой учитель преподносит истину, хороший учит её добывать.
А. Дистервег
Учитель: Орлова Светлана Геннадьевна, учитель математики ГБОУ школа №471 Выборгского района Санкт- Петербурга.
Тема урока: «Построение графиков функций сдвигами вдоль осей координат»
Тип урока: урок усвоения новых знаний.
Цель: показать учащимся приём построения параболы с помощью сдвигов графика функции вдоль осей координат.
Задачи:
Обучающие: сформировать умение строить параболу y=a(x-m)2+n сдвигом вдоль осей координат и показать применение приобретённых навыков при построении графиков функций y=x-m +n , y=x-m
+n , y=x-m +n , y=kx-m
+n , y=kx-m  + n.
+ n.
Развивающие: развитие познавательных умений, аналитического и сравнительного мышления, математической грамотности, способности обобщать и делать выводы.
Воспитывающие: воспитание интереса к предмету, аккуратности, ответственности, требовательности к себе и другим.
Планируемые результаты:
Предметные: уметь по формуле определять характер сдвига графика функции и строить его.
Личностные: уметь отстаивать свою точку зрения и работать в коллективе.
Метапредметные: уметь планировать и оценивать процесс и результат своей деятельности, обрабатывать информацию.
Педагогические технологии: элементы проблемного и опережающего обучения.
Оборудование: интерактивная доска, компьютер, раздаточные материалы.
Содержание учебного материала.
1.Свойства и график функции y=ax2, зависимость направления ветвей параболы, её «растяжения» и «сжатия» вдоль оси ординат от коэффициента a.
2.Функции y=x , y=x
, y=x , y= kx
, y= kx  , их графики.
, их графики.
3.Построение графика функции y=f(x-m)+n, если y=f(x) – «исходная» функция.
Структура урока.
1. Организационная часть.
2. Актуализация знаний:
- проверка домашнего задания
- устная работа по готовым чертежам
- подготовка к изучению нового материала (создание проблемной ситуации)
3. Объяснение нового материала (первичное усвоение новых знаний).
4. Закрепление
- первичная проверка понимания
- применение знаний и умений в новой ситуации.
5. Подведение итогов урока.
6. Домашнее задание.
7. Рефлексия урока.
Технологическая карта урока алгебры в 9 классе по теме: «Построение графиков функций сдвигами вдоль осей координат»
|
Этапы урока
|
Задачи этапа
|
Деятельность учителя
|
Деятельность учащихся
|
УУД
|
|
1.Организационная часть
1 минута
|
Создание рабочего настроения в начале урока
|
Здоровается с учениками,
проверяет их подготовку к уроку, отмечает отсутствующих, записывает на доске дату.
|
Готовятся к работе на уроке, приветствуют учителя
|
Регулятивные:
организация учебной деятельности.
|
|
2.Актуализация знаний
10 минут
|
Проверить выполнение домашнего задания, повторить и обобщить изученный на прошлых уроках материал и создать условия для восприятия и усвоения новой темы (мотивация учебной деятельности).
|
Вызывает к боковой доске двух человек для проверки домашнего задания. Пока они готовятся, работает с классом
(приложение№2). Проверка домашнего задания осуществляется с помощью интерактивной доски
(приложение №1). Итак, где же находится вершина любой параболы вида y=ax2? Как зависит направление её ветвей от знака коэффициента а? От чего зависит «толщина» параболы?
y = ax2- простейшее, но не единственное уравнение параболы. Как построить графики более сложных квадратичных функций, вам предстоит узнать самим.
Лучший способ изучить
что-либо – это открыть самому.
Д.Пойа
Делимся на три команды (по рядам), выбираем капитанов, которые выходят к доске. Задание для команд написано на трёх досках, соревнование начинается!
|
Два ученика на боковой доске решают домашнее задание (приложение№1), после чего получают индивидуальное задание на карточках (приложение№3).
Вершина параболы y=ax2 находится в начале координат. Если а<0,ветви вниз, если а>0, ветви вверх. Чем а больше, тем парабола «уже», чем а больше, тем парабола «уже», чем а меньше, тем она «толще». меньше, тем она «толще».
По одному человеку от каждого ряда выходят к доске, строят графики функций цветными мелками, используя таблицу.
|
Познавательные:
приведение знаний в систему.
Коммуникативные:
умение прислушиваться к мнению окружающих.
Регулятивные:
оценивание результатов своей деятельности.
Личностные:
оценивание уровня усвоения материала.
|
|
3.Объяснение нового материала
15 минут
|
Создание благоприятной обстановки для выхода из проблемной ситуации,
восприятия и осмысления нового материала,
самостоятельного
прихода к правильному выводу.
|
В одной системе координат построить графики функций
1 команда:
а)y= - x2 б)y= - x2-2 в)y=-(x-2)2
2 команда:
а)y= x2 б)y= x2-3 в)y=(x-3)2
3 команда:
а)y= 2x2 б)y= 2x2+3 в)y=2(x+3)2
Задание выполнено! (приложение №4). Найдите закономерность расположения графиков относительно осей координат. Капитаны советуются со своими командами. Будем условно называть график а) «исходным».
Вот и тема нашего урока звучит так: «Построение графиков функций сдвигами вдоль осей координат».
Оказывается, эти правила верны для всех функций, а не только для параболы. Попробуйте их сформулировать, если y=f(x)-исходная функция.
Как вы думаете, можно ли обойтись без каких-то лишних построений. В самом деле, попробуем сдвинуть не сам исходный график, а систему координат. Построим таким образом параболу y=(x-3)2+2.Куда сдвиг? Значит, в точке (3;2)-начало дополнительной системы координат, которую мы и проводим пунктиром. От «нового» нуля и будем вести отсчёт, а таблица будет для исходной функции y=x2.Учитель строит график функции на доске.
|
Остальные ученики делают это в тетрадях, оказывая помощь друг другу.
График б) получен сдвигом исходного графика а) вверх-вниз, а график в) влево-вправо.
Записывают тему урока в тетрадь.
Формулируют и записывают в тетрадь правило:
y=f(x+3)-сдвиг на 3 влево
y=f(x-3)-сдвиг на 3 вправо
y=f(x)+3-сдвиг на 3 вверх
y=f(x)-3-сдвиг на 3 вниз
Наверное, но ученики не понимают, о чём речь.
На 3 вправо и на 2 вверх.
В тетрадях строят график функции новым способом.
|
Познавательные:
анализ условий поставленной задачи и поиск её рационального решения.
Личностные:
формирование устойчивого интереса к изучаемому материалу.
Коммуникативные:
умение прислушиваться к чужому мнению и работать в коллективе.
|
|
4.Закрепление:
-первичная проверка понимания
-применение знаний и умений в новой ситуации
15 минут
|
Способствовать осознанному и прочному усвоению темы,
корректировать пробелы в знаниях у слабых учащихся.
Проверить правильность усвоения темы и распространение полученных знаний на новые объекты.
|
Работа с презентацией
(приложение № 4).
Математику нельзя изучать, наблюдая как это делает сосед!
А.Нивен
Работа по вариантам.
Построить графики функций:
1 вариант:
y=x-5 +3 +3
2 вариант:
y = 4x+2  -1 -1
Если останется время, все вместе:
y=x-4  -2. -2.
|
Отвечают на вопросы из презентации, работают на интерактивной доске.
Строят графики функций новым способом.
|
Коммуникативные:
общение и взаимодействие с партнёрами по совместной деятельности, умение грамотно выражать свои мысли.
Регулятивные:
справедливая и адекватная оценка собственной деятельности.
|
|
5.Подведение итогов урока
1 минута
|
Осознание каждым учащимся: чему, как и зачем он научился сегодня на уроке и с какими знаниями и умениями он должен прийти на следующий урок.
|
Вы познакомились с новым способом построения графиков. В чём он состоит? Есть ли у вас вопрос, на который вы не получили сегодня ответ?
Оценки за урок.
|
Графики функций можно строить сдвигами вдоль осей координат.
|
Регулятивные:
умение оценить качество и уровень усвоения
|
|
6. Домашнее задание
2 минуты
|
Комментарии по домашнему заданию с целью его успешного выполнения.
|
П.6, №110(а, в),111 - построить графики изученным сегодня способом;
на повторение темы «Сокращение дробей» №104(а);
задание для любознательных: построить график функции y= x . .
|
Записывают домашнее задание в дневники и задают по нему вопросы.
|
|
|
7. Рефлексия.
1 минута
|
Заставить детей задуматься в конце урока о своём настроении,
эмоциональном состоянии и результатах взаимодействия с другими участниками образовательного процесса.
|
Выходя из кабинета, оцените по пятибалльной шкале своё настроение в конце урока и поставьте оценку на доске. Урок закончен, всем спасибо!
|
Собирают свои вещи, ставят оценки на доске.
|
Коммуникативные:
умение грамотно и честно выражать свои мысли.
Регулятивные:
умение оценить достигнутый результат.
Личностные:
чувство гордости за хорошо проделанную работу.
|
Литература.
1.Макарычев Ю. Н. Алгебра: 9 кл. / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и др. – М., Просвещение, 2012.
2.Миндюк Н. Г. Алгебра. Рабочие программы. Предметная линия учебников Ю. Н. Макарычева и других. 7 - 9 классы: пособие для учителей общеобразов. учреждений / Н. Г. Миндюк. – М.: Просвещение, 2011.
3. Асмолов А. Г. Формирование универсальных учебных действий в основной школе. Система знаний /, О. А. Карабанова. М.: Просвещение, 2010
4.Ким Н.А. Нестандартные уроки алгебры. Сост. Ким Н.А. – Волгоград: ИТД «Корифей», 2006.
Информационные средства (интернет-ресурсы):
ФЦИОР: http://school-collection.edu.ru/catalog/teacher/
«Математический конструктор»: http://school-collection.edu.ru/catalog/rubr/903077b7-0221-4823-b549-b236326d48d4/?interface=teacher&class[]=51&subject[]=17
Методическая разработка урока алгебры в 9 классе.
Плохой учитель преподносит истину, хороший учит её добывать.
А. Дистервег
Учитель: Орлова Светлана Геннадьевна, учитель математики ГБОУ школа №471 Выборгского района Санкт- Петербурга.
Тема урока: «Построение графиков функций сдвигами вдоль осей координат»
Тип урока: урок усвоения новых знаний.
Цель: показать учащимся приём построения параболы с помощью сдвигов графика функции вдоль осей координат.
Задачи:
Обучающие: сформировать умение строить параболу y=a(x-m)2+n сдвигом вдоль осей координат и показать применение приобретённых навыков при построении графиков функций y=x-m +n , y=x-m
+n , y=x-m +n , y=kx-m
+n , y=kx-m  + n.
+ n.
Развивающие: развитие познавательных умений, аналитического и сравнительного мышления, математической грамотности, способности обобщать и делать выводы.
Воспитывающие: воспитание интереса к предмету, аккуратности, ответственности, требовательности к себе и другим.
Планируемые результаты:
Предметные: уметь по формуле определять характер сдвига графика функции и строить его.
Личностные: уметь отстаивать свою точку зрения и работать в коллективе.
Метапредметные: уметь планировать и оценивать процесс и результат своей деятельности, обрабатывать информацию.
Педагогические технологии: элементы проблемного и опережающего обучения.
Оборудование: интерактивная доска, компьютер, раздаточные материалы.
Содержание учебного материала.
1.Свойства и график функции y=ax2, зависимость направления ветвей параболы, её «растяжения» и «сжатия» вдоль оси ординат от коэффициента a.
2.Функции y=x , y=x
, y=x , y= kx
, y= kx  , их графики.
, их графики.
3.Построение графика функции y=f(x-m)+n, если y=f(x) – «исходная» функция.
Структура урока.
1. Организационная часть.
2. Актуализация знаний:
- проверка домашнего задания
- устная работа по готовым чертежам
- подготовка к изучению нового материала (создание проблемной ситуации)
3. Объяснение нового материала (первичное усвоение новых знаний).
4. Закрепление
- первичная проверка понимания
- применение знаний и умений в новой ситуации.
5. Подведение итогов урока.
6. Домашнее задание.
7. Рефлексия урока.
Технологическая карта






 +n , y=x-m
+n , y=x-m +n , y=kx-m
+n , y=kx-m  + n.
+ n. , y=x
, y=x , y= kx
, y= kx  , их графики.
, их графики. больше, тем парабола «уже», чем а
больше, тем парабола «уже», чем а +3
+3  -1
-1 -2.
-2. .
.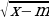 +n , y=
+n , y=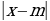 +n , y=
+n , y=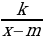 + n.
+ n.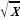 , y=
, y=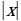 , y=
, y=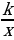 , их графики.
, их графики.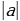 больше, тем парабола «уже», чем
больше, тем парабола «уже», чем 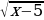 +3
+3 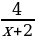 -1
-1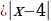 -2.
-2.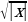 .
.


















