Методическая разработка урока геометрии в 7 классе на тему "Третий признак равенства треугольников"

Урок № ____ Дата: _._.___ Класс: 7 Предмет: геометрия

Тема урока: «Третий признак равенства треугольников»

Цели урока

Образовательные: изучить третий признак равенства треугольников

Развивающие: способствовать развитию умений ставить перед собой цели и добиваться их решения; развивать интеллектуальную сферу: внимание, память, речь, мышление; развивать эмоциональную сферу: уверенность в себе; развивать мотивационную сферу: стремление добиться успехов; развивать коммуникативную сферу: навыки работы в парах и группах.

Воспитательные: способствовать развитию у обучающегося заботливого отношения к своему здоровью; воспитывать целостное восприятие мира; формировать познавательный интерес к предмету.

Планируемые результаты урока:

Предметные: свободное применение третьего признака равенства треугольников

Личностные: осознавать значимость знаний, формировать адекватную самооценку, уметь видеть и признавать свои ошибки, развитие готовности к решению творческих задач, умения находить адекватные способы поведения и взаимодействия с партнёрами во время учебной деятельности, способности оценивать проблемные ситуации и оперативно принимать ответственные решения в различных продуктивных видах деятельности.

Метапредметные:

Регулятивные УУД: сформировать умения самостоятельно формулировать учебную проблему, определять цель учебной деятельности, выдвигать версии решения проблемы, работать по алгоритму с правилами по формированию общих приемов учебной деятельности по усвоению химических понятий.

Коммуникативные УУД: сформировать умение организовывать учебное сотрудничество с учителем и сверстниками; умение самостоятельно организовывать свою работу по закреплению материала; умение владеть устной речью.

 Познавательные УУД: сформировать умение ориентироваться в своей системе знаний, находить и использовать нужную информацию, строить логическое рассуждение, включающее установление причинно-следственных связей, анализировать и обобщать изученную информацию, сравнивать, делать выводы, применение новых знаний в жизненной ситуации.

Тип урока: Комбинированный урок

Оборудование: тетради, учебник, дид. материалы, чертежные принадлежности

Ход урока

1.Организационный момент.

2. Мотивация учебной деятельности учащихся.

Мы хорошо поработали над предыдущей темой! А сегодня мы узнаем третий признак равенства треугольников.

3. Целеполагание

Итак, дети, какая цель нашего урока?

4. Актуализация накопленного опыта и опорных знаний учащихся, проверка домашнего задания.

Опрос устно:

- Что такое медиана, биссектриса и высота треугольника?

- Какими свойствами они обладают?

- Определение равнобедренного треугольника; его боковые стороны и основание.

- Определение равностороннего треугольника.

- Свойства равнобедренного треугольника.

- 2 ПРТ. Если сторона и прилежащие к ней углы одного треугольника соответственно равны, стороне и прилежащим к ней углам другого треугольника то такие треугольники равны.

Решение задач устно

2. Решение задач по готовым чертежам с целью повторения первого признака равенства треугольников:

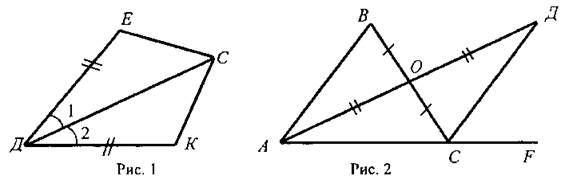
1) На рисунке 1 ДЕ = ДК, ∠1 = ∠2. Найдите ЕС, ∠ДCK и ∠ДKC, если КС = 1,8 дм; ∠ДCE = 45°, ∠ДEC = 115°.

2) На рисунке 2 ОВ = ОС, АО = ДО; ∠ACB = 42°, ∠ДCF = 68°.

Найдите ∠ABC.

5. Восприятие и усвоение учащимися нового учебного материала.

Формулировка третьего признака равенства треугольников и его доказательство.

Можно дать формулировку третьего признака в таком виде: Два треугольника будут равными, если для каждой стороны одного треугольника найдется равная сторона в другом треугольнике.

Доказательство третьего признака равенства треугольников отличается от доказательств первого и второго признаков тем, что здесь не проводится наложение одного треугольника на другой. В процессе изучения теоремы о третьем признаке весьма полезна работа с рисунком 70, б и в учебника, по которому можно показать, что в случае, когда луч С₁С совпадает с одной из сторон угла А₁С₁В₁ или проходит вне этого угла, доказательство проводится аналогично случаю, когда луч С₁С проходит внутри угла А₁С₁В₁ или проходит вне этого угла, доказательство проводится аналогично случаю, когда луч С₁С проходит внутри угла А₁С₁В₁ (рис. 70, а). Можно также, после того как доказательство теоремы изложено учителем по рис. 70, а, предложить одному из учащихся доказать третий признак равенства треугольников для случая, изображенного на рисунке 70, в.

2. Треугольник – жесткая фигура (рис. 71 и 72).

Первичное применение приобретенных знаний

1. Устно решить задачи по готовым чертежам (см. рис. 1–6).

Найдите пары равных треугольников и докажите их равенство (цель устной работы – учить учащихся читать чертеж по изображениям на нем равных элементов):

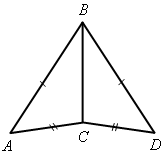
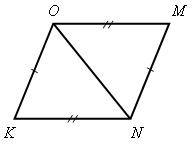
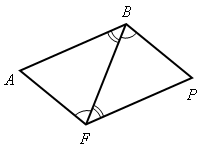
Рис. 1 Рис. 2 Рис. 3

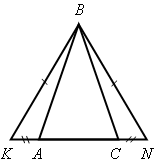
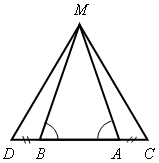
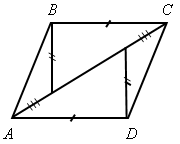
Рис. 4 Рис. 5 Рис. 6

2. Устно решить задачу № 135.

6. Применение учащимися знаний и действий в стандартных условиях с целью усвоения навыков (тренировочные упражнения).

Решить задачу № 138 на доске и в тетрадях (по рис. 75):

Дано: АВ = СD и ВD = АС.

Доказать: а)  САD = АDВ; б)  ВАС = СDВ.

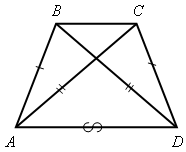
Доказательство

1) Рассмотрим треугольник АВD и треугольник DСА (можно отрезок ВС сначала стереть на доске, тогда учащиеся легко доказывают равенство этих треугольников):

АВ = СD (по условию)

ВD = АС (по условию)

АD – общая сторона (знак  )

АВD = DСА (третий
признак по трем сторонам).

Отсюда имеем, что в равных треугольниках против равных сторон лежат равные углы, значит,  САD = АDВ.

2) Рассмотрим треугольник ВАС и треугольник СDВ (восстанавливаем на доске отрезок ВС и стираем отрезок АD).

ВС – общая сторона этих треугольников. Аналогично доказывается равенство ВАС = СDВ по третьему признаку. Тогда ВАС = СDВ.

Физминутка.

Дополнительные задачи

Рассмотрим некоторые задачи, чтобы закрепить пройденный материал.

Пример 1: Известно, что 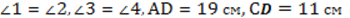 . Найти стороны АВ и ВС.

Решение: Выполним пояснительный рисунок к задаче.

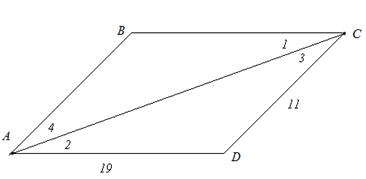
Рис. 7. Чертеж к примеру 1

Поскольку 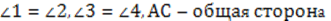 , то треугольники АВС и ADC равны по второму признаку. Из равенства треугольников следует, что  .

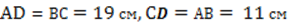Ответ: 11 см, 19 см.

Пример 2: В изображенных треугольниках 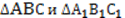 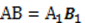  , 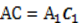 , и медианы ВМ и ВМ₁ тоже равны. Доказать равенство треугольников:  .

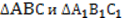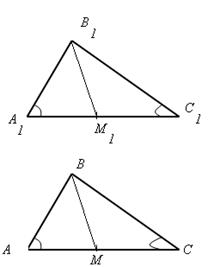
Рис. 8

Доказательство:                                                    

Вследствие того, что М и М₁ – середины равных отрезков, то А₁М₁ = АМ. 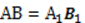 , ВМ = ВМ₁  (по условию). Следовательно,  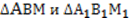 по третьему признаку. Из равенства треугольников следует равенство углов  .

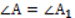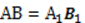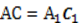,   (по условию),  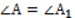 (по доказанному). Следовательно,  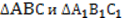 по первому признаку.

6. Подведение итогов урока (рефлексия) и сообщение домашнего задания

П. 15 № 139