| Этапы урока, время | Задачи этапа | Деятельность учителя | Деятельность учащихся | УУД |
| 1. Организационный момент (1 мин.) | Создание благоприятного климата на уроке. | Приветствует учащихся, организует их внимание, а также проверяет готовность к работе на уроке. | Приветствуют учителя, а также проверяют наличие учебного материала, который пригодится для работы на уроке. | Личностные: психологическая готовность учащихся к уроку.
|
|
2. Актуализация знаний (3 мин.) | Участие в устной работе, понимание необходимости совершенствования знаний по этой теме. | Учитель задаёт вопросы: - Что называют тригонометрическими функциями? - Как находить их производную? - Как находить наибольшее и наименьшее значение таких функций?
| Обучающиеся отвечают на вопросы учителя, включаются в работу на уроке. | Регулятивные: целеполагание (как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что еще неизвестно) Познавательные: Личностные: смыслообразование (учащийся должен задаваться вопросом о том, «какое значение, смысл имеет для меня учение», и уметь находить ответ на него) |
|
3. Этап создания проблемной ситуации. Целеполагание (5 мин.) | Помочь обучающимся самим сформулировать тему и цель урока. | Так как седьмое задание из ЕГЭ включает в себя задачи на нахождение первообразной функции, то можете ли вы уже сейчас сформулировать тему нашего сегодняшнего урока? | Обучающиеся внимательно слушают учителя и записывают в тетрадях число и тему урока «Исследование тригонометрических функций». | Познавательные: развитие у учащихся умение анализировать информацию, устанавливать причинно-следственные связи, проводить умозаключение и делать выводы; осознанное и произвольное построение речевого высказывания в устной и письменной форме; |
| 4.Этап «открытия» нового знания. (10 мин.) | Научить детей самостоятельно находить и применять новые способы действия. Ученик должен попытаться реализовать эти знания, применить их на практике, испытать новое действие. Также, происходит формирование умения находить физический смысл производной.
| Учитель предлагает рассмотреть некоторые задания по данной теме. (Задание №1)
| Учащиеся записывают формулу, а также разбирают задачи, представленную учителем на доске. | Регулятивные: планирование — определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий; Познавательные: Выделение необходимой информации, планирование своей деятельности, прогнозирование результата. поиск необходимой информации и её понимание; самостоятельное создание способов решения проблем творческого и поискового характера Коммуникативные: планируют сотрудничество с одноклассниками и учителем; инициативное сотрудничество в поиске и сборе информации. |
| 5.Этап применения нового знания. Первичное закрепление знаний. (22 мин.) | Выявление качества и уровня усвоения знаний и способов действий. | Учитель предлагает решить следующие задания из ЕГЭ, относящиеся к заданию 12 (Задание №2). | На каждую задачу к доске выходит обучающийся, а остальные помогают. Если возникают вопросы, учитель пытается помочь разобраться с ними. (Задание №3) | Познавательные: умение анализировать способы выполнения задания; выбор эффективных способов решения задач в зависимости от конкретных условий; построение речевых высказываний в устной и письменной формах. Коммуникативные: |
| 6. Итог урока. Рефлексия (3 мин.) | Оценивание проделанной работы. | Всё ли вам было понятно по теме урока? Были ли трудности в решении заданий? | Обучающиеся отвечают на вопросы, оценивают степень достижения цели. Делают выводы. | Регулятивные: оценка своей деятельности. Личностные: способов и условий действия, контроль и оценка процесса и результатов деятельности. Коммуникативные: |
| 7. Домашнее задание (1 мин.) | Формирование понимания учащимися содержания, цели, а также способов выполнения домашнего задания. | Предлагает ученикам открыть дневники и записать домашнее задание. Домашним заданием является каждому на выбор решить по одному заданию из ЕГЭ (двенадцатое задание). | Обучающиеся записывают домашнее задание в дневник. | Познавательные: рефлексия способов и условий действия; самоконтроль и самооценка процесса и результатов деятельности.
|
1. «Найдите наибольшее значение функции y=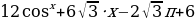 на отрезке [0;
на отрезке [0;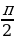 ].
].
Решение.
2. «Найдите наименьшее значение функции 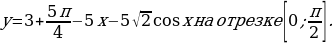
Решение.
1. «Найдите наименьшее значение функции 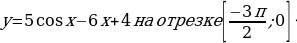 »
»
2. «Найдите наибольшее значение функции 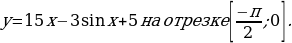 »
»
1. «Решение. Найдем производную заданной функции: 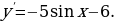 Уравнение
Уравнение 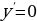 не имеет решений, производная отрицательна при всех значениях переменной, поэтому заданная функция является убывающей. Следовательно, наименьшим значением функции на заданном отрезке является
не имеет решений, производная отрицательна при всех значениях переменной, поэтому заданная функция является убывающей. Следовательно, наименьшим значением функции на заданном отрезке является
2. «Решение. Найдем производную заданной функции: 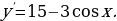 Уравнение
Уравнение 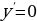 не имеет решений, производная положительна при всех значениях переменной, поэтому заданная функция является возрастающей. Следовательно, наибольшим значением функции на заданном отрезке является
не имеет решений, производная положительна при всех значениях переменной, поэтому заданная функция является возрастающей. Следовательно, наибольшим значением функции на заданном отрезке является






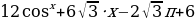 на отрезке [0;
на отрезке [0;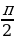 ].
].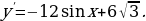
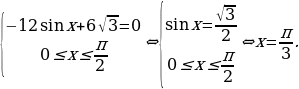
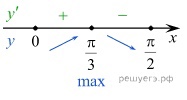
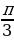 заданная функция имеет максимум, являющейся ее наибольшим значением на заданном отрезке.
заданная функция имеет максимум, являющейся ее наибольшим значением на заданном отрезке.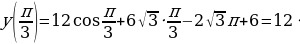
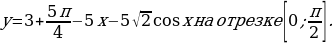
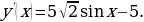
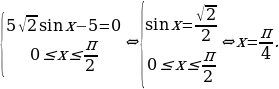
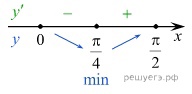
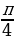 заданная функция имеет минимум, являющейся ее наименьшим значением на заданном отрезке.
заданная функция имеет минимум, являющейся ее наименьшим значением на заданном отрезке.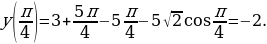
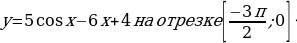 »
»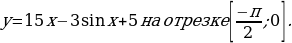 »
» 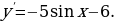 Уравнение
Уравнение 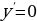 не имеет решений, производная отрицательна при всех значениях переменной, поэтому заданная функция является убывающей. Следовательно, наименьшим значением функции на заданном отрезке является
не имеет решений, производная отрицательна при всех значениях переменной, поэтому заданная функция является убывающей. Следовательно, наименьшим значением функции на заданном отрезке является 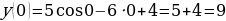 .
.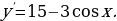 Уравнение
Уравнение 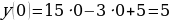 .
.









