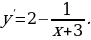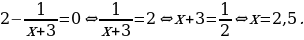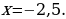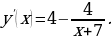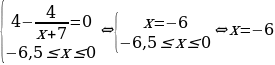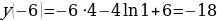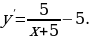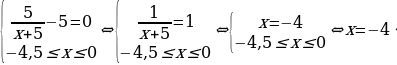Просмотр содержимого документа
«Методическая разработка урока по теме «Исследование показательных и логарифмических функций»»
Технологическая урока по теме «Исследование показательных и логарифмических функций»
Предмет: Алгебра 11 класс
Тема урока: Исследование показательных и логарифмических функций.
Цель урока: создать условия и организовать деятельность учащихся, которая направлена на освоение системой математических знаний и умений по теме «Исследование показательных и логарифмических функций», которые необходимы для использования в практической деятельности учащихся.
Задачи урока:
закрепить знания о понятиях производной показательной и логарифмической функции;
развить познавательный интерес учащихся, а также развивать математическую речь, умение наблюдать, сравнивать, делать выводы.
Тип урока: систематизация знаний.
Время: 45 мин.
Учебник: С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. Алгебра 11 класс, 2009 г.
| Этапы урока, время | Задачи этапа | Деятельность учителя | Деятельность учащихся | УУД |
| 1. Организационный момент (1 мин.) | Создание благоприятного климата на уроке. | Приветствует учащихся, организует их внимание, а также проверяет готовность к работе на уроке. | Приветствуют учителя, а также проверяют наличие учебного материала, который пригодится для работы на уроке. | Личностные: психологическая готовность учащихся к уроку.
|
|
2. Актуализация знаний (3 мин.) | Участие в устной работе, понимание необходимости совершенствования знаний по этой теме. | Учитель задаёт вопросы: - Что называется показательной и логарифмической функцией? - Как их находить? - Как находить максимум, минимум, наибольшее и наименьшее значение таких функций?
| Обучающиеся отвечают на вопросы учителя, включаются в работу на уроке. | Регулятивные: целеполагание (как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что еще неизвестно) Познавательные: Личностные: смыслообразование (учащийся должен задаваться вопросом о том, «какое значение, смысл имеет для меня учение», и уметь находить ответ на него) |
|
3. Этап создания проблемной ситуации. Целеполагание (5 мин.) | Помочь обучающимся самим сформулировать тему и цель урока. | Так как седьмое задание из ЕГЭ включает в себя задачи на нахождение первообразной функции, то можете ли вы уже сейчас сформулировать тему нашего сегодняшнего урока? | Обучающиеся внимательно слушают учителя и записывают в тетрадях число и тему урока «Исследование показательных и логарифмических функций». | Познавательные: развитие у учащихся умение анализировать информацию, устанавливать причинно-следственные связи, проводить умозаключение и делать выводы; осознанное и произвольное построение речевого высказывания в устной и письменной форме; |
| 4.Этап «открытия» нового знания. (10 мин.) | Научить детей самостоятельно находить и применять новые способы действия. Ученик должен попытаться реализовать эти знания, применить их на практике, испытать новое действие. Также, происходит формирование умения находить физический смысл производной.
| Учитель предлагает рассмотреть некоторые задания по данной теме. (Задание №1)
| Учащиеся записывают формулу, а также разбирают задачи, представленную учителем на доске. | Регулятивные: планирование — определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий; Познавательные: Выделение необходимой информации, планирование своей деятельности, прогнозирование результата. поиск необходимой информации и её понимание; самостоятельное создание способов решения проблем творческого и поискового характера Коммуникативные: планируют сотрудничество с одноклассниками и учителем; инициативное сотрудничество в поиске и сборе информации. |
| 5.Этап применения нового знания. Первичное закрепление знаний. (22 мин.) | Выявление качества и уровня усвоения знаний и способов действий. | Учитель предлагает решить следующие задания из ЕГЭ, относящиеся к заданию 12 (Задание №2). | На каждую задачу к доске выходит обучающийся, а остальные помогают. Если возникают вопросы, учитель пытается помочь разобраться с ними. (Задание №3) | Познавательные: умение анализировать способы выполнения задания; выбор эффективных способов решения задач в зависимости от конкретных условий; построение речевых высказываний в устной и письменной формах. Коммуникативные: |
| 6. Итог урока. Рефлексия (3 мин.) | Оценивание проделанной работы. | Всё ли вам было понятно по теме урока? Были ли трудности в решении заданий? | Обучающиеся отвечают на вопросы, оценивают степень достижения цели. Делают выводы. | Регулятивные: оценка своей деятельности. Личностные: способов и условий действия, контроль и оценка процесса и результатов деятельности. Коммуникативные: |
| 7. Домашнее задание (1 мин.) | Формирование понимания учащимися содержания, цели, а также способов выполнения домашнего задания. | Предлагает ученикам открыть дневники и записать домашнее задание. Домашним заданием является каждому на выбор решить по одному заданию из ЕГЭ (двенадцатое задание). | Обучающиеся записывают домашнее задание в дневник. | Познавательные: рефлексия способов и условий действия; самоконтроль и самооценка процесса и результатов деятельности.
|
Задание №1
1. «Найдите наименьшее значение функции y=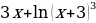 на отрезке [-2,5;0].
на отрезке [-2,5;0].
Решение.
Найдём производную заданной функции: 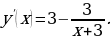
Найдем нули производной на заданном отрезке:
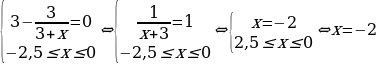 .
.
Определим знаки производной функции и изобразим на рисунке поведение функции:
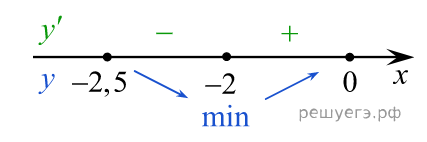
В точке х=-2 заданная функция имеет минимум, являющейся ее наименьшим значением на заданном отрезке.
Найдем это наименьшее значение: 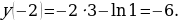
Ответ: -6.»[7]
2. «Найдем точку максимума функции 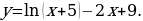
Решение.
Функция определена и дифференцируема на 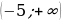 . Найдем производную заданной функции:
. Найдем производную заданной функции: 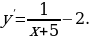
Найдем нули производной:
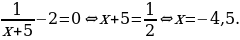
Определим знаки производной функции и изобразим на рисунке поведение функции:
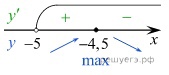
Искомая точка максимума 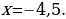
Ответ: -4,5.» [7]
Задание №2
1. «Найдите точку минимума функции 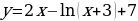 .» [7]
.» [7]
2. «Найдите наименьшее значение функции 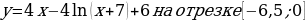 »
»
3. «Найдите наибольшее значение функции 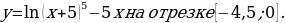 »
»
Задание №3
1. «Решение. Найдем производную заданной функции: 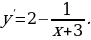
Найдем нули производной: 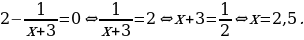
Определим знаки производной функции и изобразим на рисунке поведение функции:
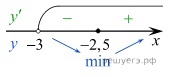
Искомая точка минимума 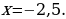
Ответ: -2,5.»
2. «Решение. Найдем производную заданной функции: 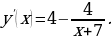
Найдем нули производной на заданном отрезке: 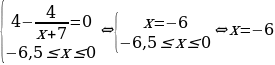
Определим знаки производной функции и изобразим на рисунке поведение функции:
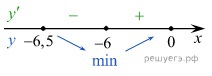
В точке х=-6 заданная функция имеет минимум, являющейся ее наименьшим значением на заданном отрезке.
Найдем это наименьшее значение: 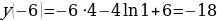
Ответ: -18.» [7]
3. «Решение. Найдем производную заданной функции: 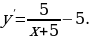
Найдем нули производной на заданном отрезке: 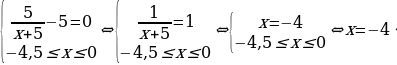
Определим знаки производной функции и изобразим на рисунке поведение функции:
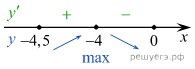
В точке х=-4 заданная функция имеет максимум, являющейся ее наибольшим значением на заданном отрезке.
Найдем это наибольшее значение: 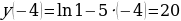
Ответ: 20.






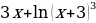 на отрезке [-2,5;0].
на отрезке [-2,5;0].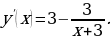
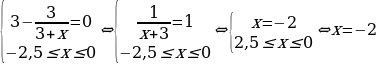 .
.
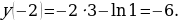
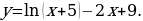
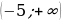 . Найдем производную заданной функции:
. Найдем производную заданной функции: 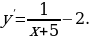
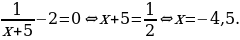

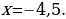
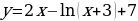 .» [7]
.» [7]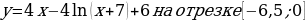 »
» 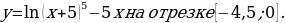 »
»