ПРЕДЕЛ ФУНКЦИИ. ПОНЯТИЕ О НЕПРЕРЫВНОСТИ ФУНКЦИИ.
(Раздел «Начала математического анализа»)
ДЕЯТЕЛЬНОСТНАЯ КАРТА УЧЕБНОГО ЗАНЯТИЯ
Профессии: 15.01.20 Слесарь по контрольно-измерительным приборам и автоматике, 09.01.03 Мастер по обработке цифровой информации, 23.01.03 Автомеханик, 09.01.01 Наладчик аппаратного и программного обеспечения
Учебные группы: КИП-11, М-11, А-11, Н-11
Учебная дисциплина: ООПу.04 Математика
Тема учебного занятия: Предел функции. Понятие о непрерывности функции.
Тип урока: урок «открытия» новых знаний
Вид урока: лекция-беседа
Средства обучения:
технические: мультимедийный проектор, персональный компьютер;
информационно-коммуникационные: электронная презентация.
Цели урока:
методическая: использование объяснительно-иллюстративного метода обучения с целью формирования математического мышления студентов;
образовательная: создание условий для овладения знаниями о пределах функции, понятие о непрерывности функции.;
развивающая: развитие умений планировать, анализировать, выдвигать гипотезы по решению заданий, применять полученные знания для выполнения упражнений;
воспитательная: воспитание интереса к изучению математики, математической культуры студентов.
Прогнозируемые результаты:
1) предметные:
сформированность знаний о вычислениях пределов функции;
владение умением решать задачи на пределы функции;
2) метапредметные:
умение ставить перед собой цель, видеть ожидаемый результат работы;
умение рационально распределять рабочее время;
умение объективно оценивать свои возможности, анализировать свои результаты, корректировать свои действия;
владение навыками познавательной рефлексии;
умение осуществлять поиск и отбор необходимой информации;
умение сопоставлять и анализировать, выделять в тексте базовые и вспомогательные концепты, опорные понятия, тезисы, структурировать их взаимосвязь;
умение структурировать полученную информацию;
умение анализировать и обобщать информацию;
умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности;
умение выражать свои мысли с достаточной полнотой и точностью.
Образовательные технологии: традиционное обучение.
Формы организации обучения: фронтальная, индивидуальная.
Методы обучения и контроля:
вербальные: беседа;
практические: метод сравнения, метод анализа и структурирования.
методы контроля и самоконтроля: устный контроль, самоконтроль.
Нормативный документ
Федеральный государственный образовательный стандарт среднего общего образования (утв. приказом Министерства образования и науки Российской Федерации (Минобрнауки России) от 17 мая 2012 г. № 413 г.). – М.: Министерство образования и науки РФ, – 2012.
Образовательные ресурсы:
Основная литература
Башмаков М. И. Математика: учебник для студ. учреждений сред. проф. образования. − М.: Издательский центр «Академия», 2018. – 256 с.
Башмаков М. И. Математика. Сборник задач профильной направленности: учеб. пособие для студ. учреждений сред. проф. образования. − М.: Издательский центр «Академия», 2014. – 416 с.
Дополнительная литература
Алимов Ш.А., Колягин Ю.М. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. Учебник. − М.: Просвещение, 2014. – 464 с.
Атанасян Л.С. Геометрия. 10 − 11 классы: учебник для общеобразовательных учреждений: базовый и профильный уровни / Атанасян Л.С., Бутузов В.Ф. и др. – М.: Просвещение, 2013. – 255 с.
Богомолов Н.В. Практические занятия по математике: Учеб. пособие для техникумов / Н.В. Богомолов. – М.: Высш. шк., 2013. – 495 с.
Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика (Книга 1): Учебное пособие. – М.: Издательство «Новая волна», 2013. – 656 с.
Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика (Книга 2): Учебное пособие. – М.: Издательство «Новая волна», 2013. – 592 с.
Никольский С.М. Алгебра и начала анализа: учебник для 10 класса общеобразоват. учреждений: базовый и профильный уровни / С.М. Никольский, М.К. Потапов. – М.: Просвещение, 2013. – 430 с.
Никольский С.М. Алгебра и начала анализа: учебник для 11 класса общеобразоват. учреждений: базовый и профильный уровни / С.М. Никольский, М.К. Потапов. – М.: Просвещение, 2013. – 464 с.
Интернет-ресурсы:
Федеральный центр информационно-образовательных ресурсов [Электронный ресурс] URL: www. fcior. edu. ru
Единая коллекции цифровых образовательных ресурсов [Электронный ресурс] URL: www. school-collection. edu. ru
Научно-методические ресурсы:
Инновационные педагогические технологии: учебное пособие/ Михелькевич В.Н., Нестеренко В.М., Кравцова П.Г. – Самар. гос. тех. ун-т Самара, 2001. – 89 с.
Кульневич С.В., Лакоценина Т.П. Современный урок. Часть 1: Научно-практич. пособие для учителей, методистов, руководителей учебных заведений, студентов пед. заведений, слушателей ИПК. – Ростов н/Д: Учитель, 2005. – 288 с.
Кульневич С.В., Лакоценина Т.П. Современный урок. Часть 3: Научно-практич. пособие для учителей, методистов, руководителей учебных заведений, студентов пед. заведений, слушателей ИПК. – Ростов н/Д: Учитель, 2007. – 288 с.
Махмутов М.И. Проблемное обучение: Основные вопросы теории. – М.: Педагогика, 1975. – 368 с.
Основные термины и понятия: предел функции, непрерывность функции.
ПЛАН УЧЕБНОГО ЗАНЯТИЯ
Содержание учебного материала:
1) Сформированность знаний о вычислениях пределов функции.
2) Закрепление теоретического материала по теме с помощью решения упражнений.
Этап мотивации (самоопределения) к учебной деятельности (2 мин)
Преподаватель приветствует студентов, создает деловую обстановку, настраивает на продуктивную мыслительную деятельность.
Этап актуализации опорных знаний. Целеполагание (15 мин)
Преподаватель задает вопросы студентам:
Какие вы знаете пределы функции?
Приведите пример предела функции.
Студенты отвечают на эти вопросы, вспоминая знания, полученные на предыдущем занятии.
Формулирование темы и целей учебного занятия.
Работа над новой темой («открытие» нового знания) (48 мин)
Алгоритм работы над «открытием» нового знания:
Формулирование преподавателем определений предела функции, понятия о непрерывности функции.
Предел функции на бесконечности
Рассмотрим несколько видов записи предела функции на бесконечности
1. Дана функция 𝑦=𝑓(𝑥), в области определения которой содержится луч [𝑎;+∞), и пусть прямая 𝑦=𝑏 является горизонтальной асимптотой графика функции 𝑦=𝑓(𝑥).
В этом случае используется запись: 𝑙𝑖𝑚𝑥→+∞𝑓(𝑥)=𝑏
(читают: предел функции 𝑦=𝑓(𝑥) при стремлении 𝑥 к плюс бесконечности равен 𝑏).
2. Если дана функция 𝑦=𝑓(𝑥), в области определения которой содержится луч (−∞;𝑎], и прямая 𝑦=𝑏является горизонтальной асимптотой графика функции 𝑦=𝑓(𝑥), то в этом случае используется запись: 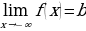
(читают: предел функции 𝑦=𝑓(𝑥) при стремлении 𝑥 к минус бесконечности равен 𝑏).
3. Если одновременно выполняются соотношения:
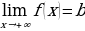 и
и 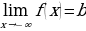 — то можно объединить их одной записью:
— то можно объединить их одной записью: 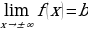 .
.
Но обычно используют более экономную запись: 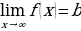
(читают: предел функции 𝑦=𝑓(𝑥) при стремлении 𝑥 к бесконечности равен 𝑏).
В этом случае прямая 𝑦=𝑏 является горизонтальной асимптотой графика функции 𝑦=𝑓(𝑥) как бы с двух сторон.
Вычисление предела функции на бесконечности осуществляется по тем же правилам, что и вычисление предела последовательности. Приведём их (с соответствующими изменениями).
1. Для любого натурального показателя 𝑚 и любого коэффициента 𝑘 справедливо соотношение:
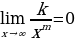 .
.
2. Если 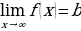 ,
, 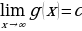 , то
, то
а) предел суммы равен сумме пределов:
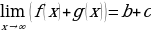 ;
;
б) предел произведения равен произведению пределов:
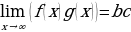 ;
;
в) предел частного равен частному пределов (разумеется, при условии, что 𝑐≠0):
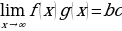 ;
;
г) постоянный множитель можно вынести за знак предела:
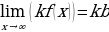 .
.
Предел функции в точке
Рассмотрим функцию, график которой изображён на рисунке:
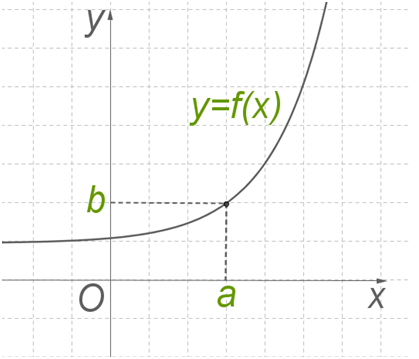
Для заданного случая предел функции 𝑦=𝑓(𝑥) при стремлении 𝑥 к 𝑎 равен 𝑏. Записывают: 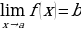 .
.
Содержательный смысл приведённой выше записи заключается в следующем:
если значения аргумента выбираются всё ближе и ближе к значению 𝑥=𝑎, то значения функции всё меньше и меньше отличаются от предельного значения 𝑏.
Можно сказать и так:
в достаточно малой окрестности точки 𝑎 справедливо приближенное равенство 𝑓(𝑥)≈𝑏 (причём это приближенное равенство тем точнее, чем меньшая окрестность выбирается).
При этом, подчеркнём, сама точка 𝑥=𝑎 исключается из рассмотрения.
Функцию 𝑦=𝑓(𝑥) называют непрерывной в точке 𝑥=𝑎, если выполняется соотношение:
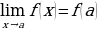 .
.
Иными словами, функцию 𝑦=𝑓(𝑥) называют непрерывной в точке 𝑥=𝑎, если предел функции 𝑦=𝑓(𝑥) при стремлении 𝑥 к 𝑎 равен значению функции в точке 𝑥=𝑎.
Функцию 𝑦=𝑓(𝑥) называют непрерывной на промежутке 𝑋, если она непрерывна в каждой точке промежутка.
Eсли выражение 𝑓(𝑥) составлено из рациональных, иррациональных, тригонометрических и обратных тригонометрических выражений, то функция 𝑦=𝑓(𝑥) непрерывна в любой точке, в которой определено выражение 𝑓(𝑥).
Приращение аргумента. Приращение функции
Изучая поведение функции 𝑦=𝑓(𝑥) около конкретной точки 𝑥0, важно знать, как меняется значение функции при изменении значения аргумента. Для этого используют понятия приращений аргумента и функции.
Пусть функция 𝑦=𝑓(𝑥) определена в точках 𝑥0 и 𝑥1. Разность 𝑥1−𝑥0 называют приращением аргумента (при переходе от точки 𝑥0 к точке 𝑥1), а разность 𝑓(𝑥1)−𝑓(𝑥0) называют приращением функции.
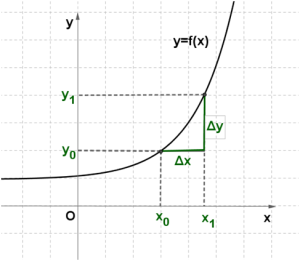
Приращение аргумента обозначают Δ𝑥 (читают: дельта икс; Δ — прописная буква греческого алфавита «дельта»; соответствующая строчная буква пишется так: δ). Приращение функции обозначают Δ𝑦 или Δ𝑓.
Итак, 𝑥1−𝑥0=Δ𝑥, значит, 𝑥1=𝑥0+Δ𝑥.
𝑓(𝑥1)−𝑓(𝑥0)=Δ𝑦, значит, Δ𝑦=𝑓(𝑥0+Δ𝑥)−𝑓(𝑥0).
Нельзя истолковывать термин «приращение» как «прирост».
Функция 𝑦=𝑓(𝑥) непрерывна в точке 𝑥=𝑎, если в этой точке выполняется следующее условие: если Δ𝑥→0, то Δ𝑦→0.
Использование правила Лопиталя
Правило Лопиталя для неопределённостей вида 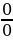 .
.
Допустим, что функции 𝑓(𝑥) и 𝑔(𝑥) определены и имеют производные в некоторой окрестности точки a (за исключением, может быть, самой точки a), к тому же 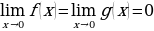 и 𝑔′(𝑥)≠0.
и 𝑔′(𝑥)≠0.
Значит, если существует предел (конечный или бесконечный) отношения производных 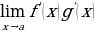 , то существует и предел деления функций:
, то существует и предел деления функций:
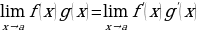 .
.
Такая же теорема справедлива для неопределённости вида  .
.
Пример:
1.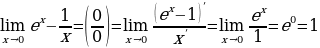 ;
;
2. 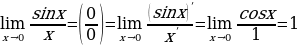 .
.
Включение нового знания в систему имеющихся знаний (20 мин)
Неопределённость 0 × ∞
Неопределённости 0⋅∞ и ∞−∞
можно свести к неопределённостям 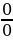 или
или  .
.
Если нужно вычислить предел 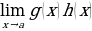 , где 𝑔(𝑥) стремится к нулю, а ℎ(𝑥) стремится к бесконечности, это произведение можно изменить так, чтобы получить одну из двух необходимых неопределённостей:
, где 𝑔(𝑥) стремится к нулю, а ℎ(𝑥) стремится к бесконечности, это произведение можно изменить так, чтобы получить одну из двух необходимых неопределённостей:
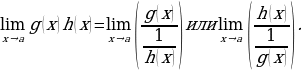
Пример:
1.
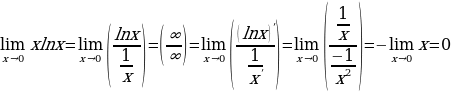 ;
;
2.
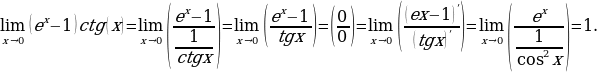
Неопределённость ∞ - ∞
Если нужно вычислить предел 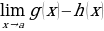 , где функции 𝑔(𝑥) и ℎ(𝑥) стремятся к бесконечности (т. е. существует неопределённость ∞−∞), эту разность можно преобразовать в неопределённость 00 следующим образом (если невозможно вычислить предел более простым способом):
, где функции 𝑔(𝑥) и ℎ(𝑥) стремятся к бесконечности (т. е. существует неопределённость ∞−∞), эту разность можно преобразовать в неопределённость 00 следующим образом (если невозможно вычислить предел более простым способом):
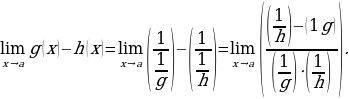
Пример:
1.
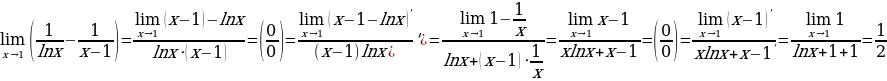 .
.
2.
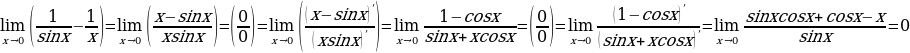 .
.
Неопределённости со степенями
Допустим, что нужно вычислить предел 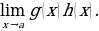
В таком случае возможны эти 3 варианта:
1. обе функции — 𝑔(𝑥) и ℎ(𝑥) — стремятся к нулю — неопределённость 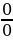 ;
;
2. функция 𝑔(𝑥) стремится к бесконечности, а функция ℎ(𝑥) стремится к нулю — неопределённость ∞0;
3. функция 𝑔(𝑥) стремится к одному, а функция ℎ(𝑥) стремится к бесконечности — неопределённость 1∞.
В этих случаях нужно использовать преобразование 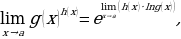 вычислить предел, находящийся в показателе степени (справляясь с неопределённостью 0⋅∞), и тогда возводить в степень.
вычислить предел, находящийся в показателе степени (справляясь с неопределённостью 0⋅∞), и тогда возводить в степень.
Пример:
неопределённость 00:
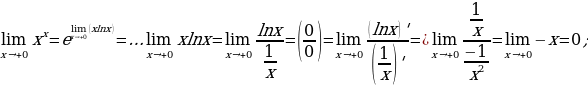
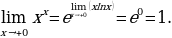
Неопределённость 1∞:
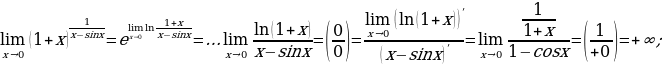
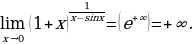
Неопределённость ∞0:
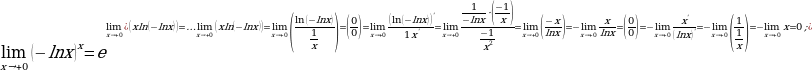
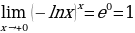 .
.
Рефлексия. Подведение итогов учебного занятия (5 мин)
Беседа со студентами по содержанию занятия. Вопросы для беседы:
Какая была тема сегодняшнего занятия?
Что нового вы узнали?
Какая была цель занятия?
Что получилось у вас сегодня?
Что не получилось?
Достигли ли мы поставленной цели?
Инструктирование о выполнении домашнего задания
Лекция







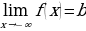
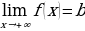 и
и 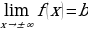 .
.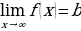
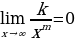 .
.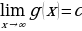 , то
, то 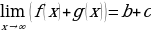 ;
;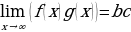 ;
;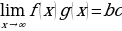 ;
;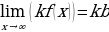 .
.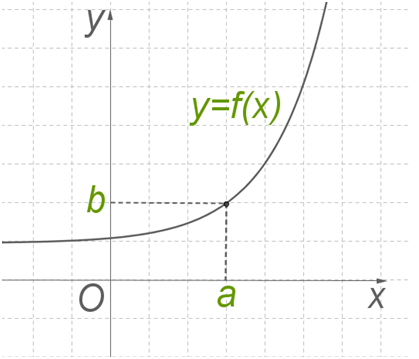
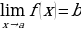 .
.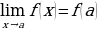 .
.
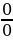 .
.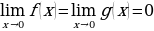 и 𝑔′(𝑥)≠0.
и 𝑔′(𝑥)≠0. 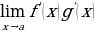 , то существует и предел деления функций:
, то существует и предел деления функций: 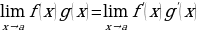 .
. .
.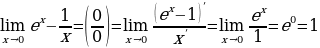 ;
;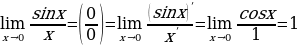 .
.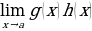 , где 𝑔(𝑥) стремится к нулю, а ℎ(𝑥) стремится к бесконечности, это произведение можно изменить так, чтобы получить одну из двух необходимых неопределённостей:
, где 𝑔(𝑥) стремится к нулю, а ℎ(𝑥) стремится к бесконечности, это произведение можно изменить так, чтобы получить одну из двух необходимых неопределённостей: 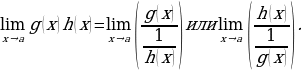
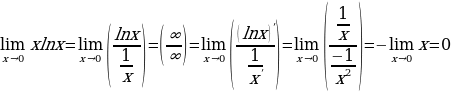 ;
;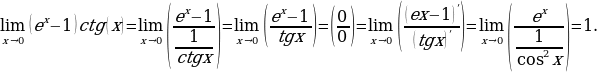
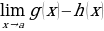 , где функции 𝑔(𝑥) и ℎ(𝑥) стремятся к бесконечности (т. е. существует неопределённость ∞−∞), эту разность можно преобразовать в неопределённость 00 следующим образом (если невозможно вычислить предел более простым способом):
, где функции 𝑔(𝑥) и ℎ(𝑥) стремятся к бесконечности (т. е. существует неопределённость ∞−∞), эту разность можно преобразовать в неопределённость 00 следующим образом (если невозможно вычислить предел более простым способом):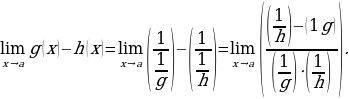
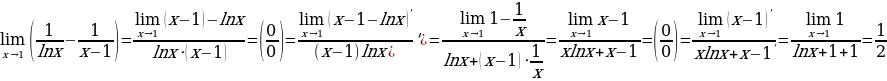 .
.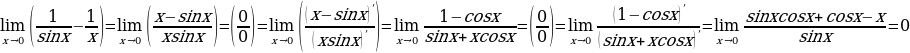 .
.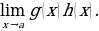
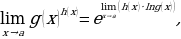 вычислить предел, находящийся в показателе степени (справляясь с неопределённостью 0⋅∞), и тогда возводить в степень.
вычислить предел, находящийся в показателе степени (справляясь с неопределённостью 0⋅∞), и тогда возводить в степень.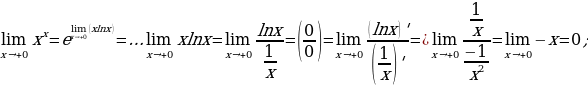
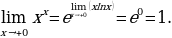
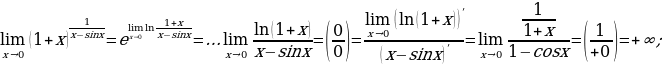
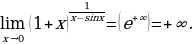
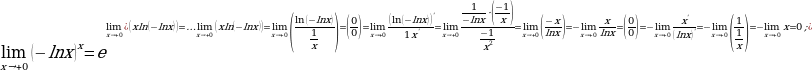
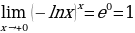 .
.









