ОБЛАСТНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ ПРОФЕССИОНАЛЬНОЕ УЧРЕЖДЕНИЕ «РЯЗАНСКИЙ МНОГОПРОФИЛЬНЫЙ КОЛЛЕДЖ»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
ВНЕКЛАССНОГО МЕРОПРИЯТИЯ
ПО МАТЕМАТИКЕ
ИГРА-ПУТЕШЕСТВИЕ
СТРАНА «МАТЕМАТИКА».
Составлена:
преподавателем математики
Моргуновой С.В.
Игра-путешествие Страна «Математика»
игровая познавательная программа для обучающихся 1 курса
Цель игры:
- показать красоту математики, ее роль в нашей жизни;
- развивать познавательную активность, творческие способности, смекалку и сообразительность у обучающихся;
- вырабатывать интерес к предмету;
- развивать умение использовать и применять ресурсы Интернета для получения необходимой информации.
Оборудование: план путешествия, плакаты, таблицы, ребусы, интерактивный комплекс.
Подготовительная работа: поиск информации и подготовка сообщений по темам «Математика в профессии повара, кондитера», «Из истории математики», «Что такое логика и для чего она нужна», «Математические шутки», «Мебиус. Лист Мебиуса».
Ход игры.
В игре участвуют 2 команды групп по пять человек в каждой. Победит та команда, которая получит наибольшее количество баллов.
Вступительное слово преподавателя: Дорогие ребята, я надеюсь, что наше знакомство со страной «Математика» будет приятным для вас и для меня, и что наша игра пройдет интересно, с большой пользой для всех присутствующих. Очень хочу, чтобы те, кто еще равнодушен к царице всех наук, с нашего урока ушел с глубоким убеждением: математика – интересный и нужный предмет.
Нашу игру – путешествие мы проведем по плану, который перед вами.(слайд 1)

Для того, чтобы победить, Вы должны быть волевыми, настойчивыми, целеустремленными, поэтому эпиграфом нашей игры будут слова: «Усердие все превозмогает». (слайд 2)

Я вижу, все готовы к началу путешествия. Итак, добро пожаловать в страну «Математика».
Ведущий: Первым этапом путешествия у нас будет «Край применения математических знаний».(слайд 3)

1 этап: Край применения математических знаний.
Иногда обучающиеся задают вопрос: «Зачем нам эта математика?»
С математикой мы сталкиваемся везде: в магазине, в бухгалтерии, на транспорте, в парикмахерской. Каждый может попасть, например, в ситуацию, в которой оказались герои следующих задач.
Задача 1. Восьмилитровый бидон заполнен доверху молоком. Как разделить жидкость поровну, если у вас имеется два пустых бидона вместимостью 5л и 3л.
Ответ:
1. Налить из восьмилитрового бидона в трехлитровый 3 литра молока, в большом бидоне останется 5 литров.
2. Перелить три литра в пятилитровый бидон.
3. Снова налить из восьмилитрового бидона в трехлитровый 3 литра, в большом бидоне останется 2 литра молока.
4. Долить в пятилитровый бидон из трехлитрового недостающие 2 литра, при этом в трехлитровом бидоне останется 1 литр молока.
5. Вылить обратно из пятилитрового бидона в восьмилитровый 5 литров молоко, при этом в большом бидоне станет 7 литров.
6. Перелить из трехлитрового бидона оставшийся 1 литр в пятилитровый бидон.
7. Налить из восьмилитрового бидона в трехлитровый 3 литра молока и перелить эти 3 литра в пятилитровый бидон. При этом в восьми литровом останется 4 литра молока и в пятилитровом бидоне станет 4 литра молока).
Задание 2. Как из трех спичек сделать одиннадцать?
Ответ: ХI
Предлагаю командам решить эти задачи. Каждое верно решенное задание оценивается в 1 балл. Команды работают, а мы в это время посмотрим презентацию о важности математики в профессии «Повар, кондитер». (с сообщением - презентацией №1 «Математика в профессии повара, кондитера» выступает преподаватель слайды 4-28). После выступления команды передают свои ответы жюри, которое подведет итоги конкурса.
Ведущий: Из всех затруднительных положений помогут нам выйти знания математики.
Занимаясь математикой, вы учитесь думать, критически осмысливать и оценивать происходящее, отстаивать свои мысли и идеи, развиваете свое логическое мышление. (слайд 29)

«Логика есть искусство, которое упорядочивает и связывает мысли. Люди ошибаются именно потому, что им недостает логики», - так говорил немецкий математик Готфрид Лейбниц. Теперь, я думаю, вам понятна роль такого предмета, как математика.
Слово предоставляется жюри, которое подведет итоги первого этапа.
Ведущий: Мы переходим ко второму этапу нашего путешествия – историческому. (слайд 30)

2 этап: Исторический район.
Продолжая мысль о важности математики, я хочу заглянуть назад, то есть обратиться к истории. Если бы не математика, мы бы ничего не узнали о древнем математике Диофанте, жившем в III веке до нашей эры. История сохранила мало фактов из его биографии. Все, что известно о нем, почерпнуто из надписи на его гробнице – надписи, составленной в форме математической задачи. Вот эта надпись (показ задачи о Диофанте на прокторе) (слайд 31):

| Путник! Здесь прах погребен Диофанта. И числа поведать могут, о чудо, сколь долог был век его жизни.
|
х |
| Часть шестую его представляло прекрасное детство. | 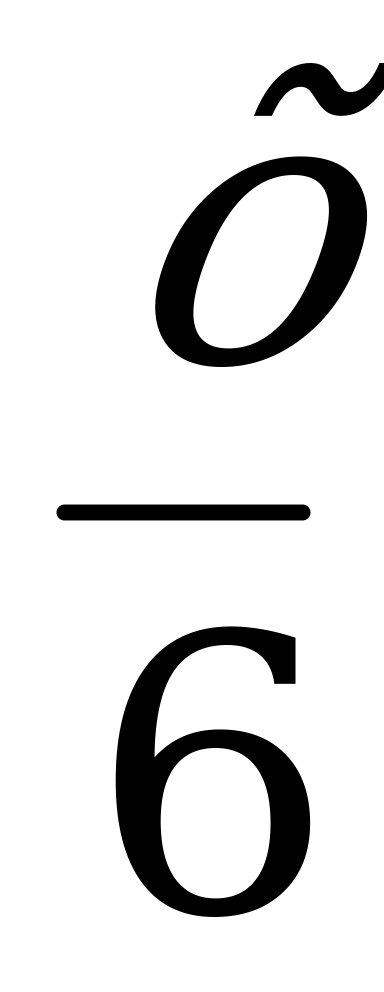 |
| Двенадцатая часть протекла еще жизни – и покрылся пухом тогда подбородок. |
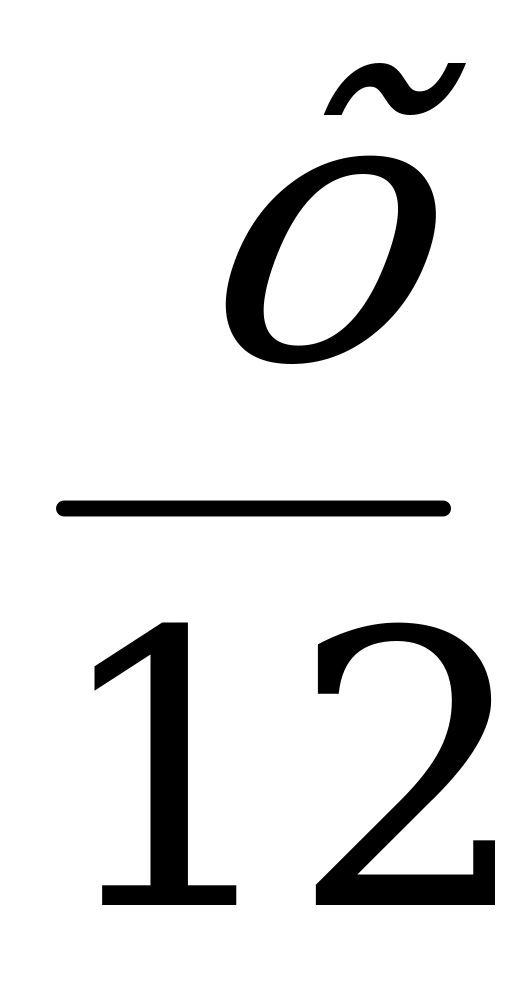 |
| Седьмую в бездетном браке провел Диофант. | 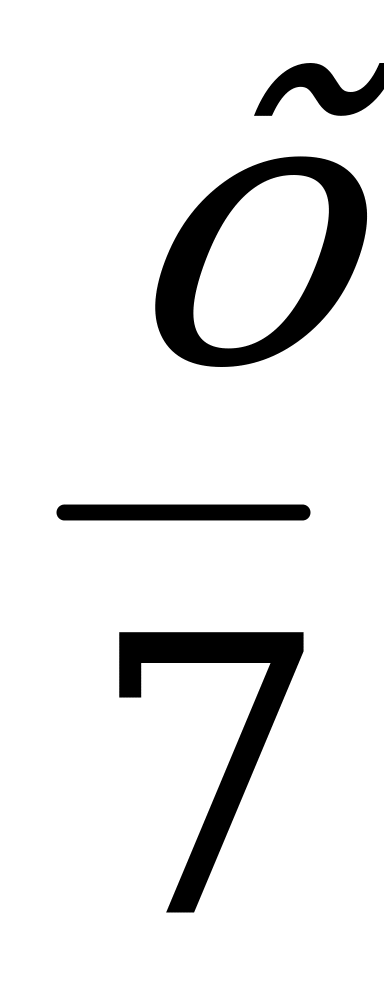 |
| Прошло пятилетие, он был осчастливлен рождением первенца-сына. |
5 |
| Коему рок половину лишь жизни прекрасной дал на земле по сравненью с отцом. |
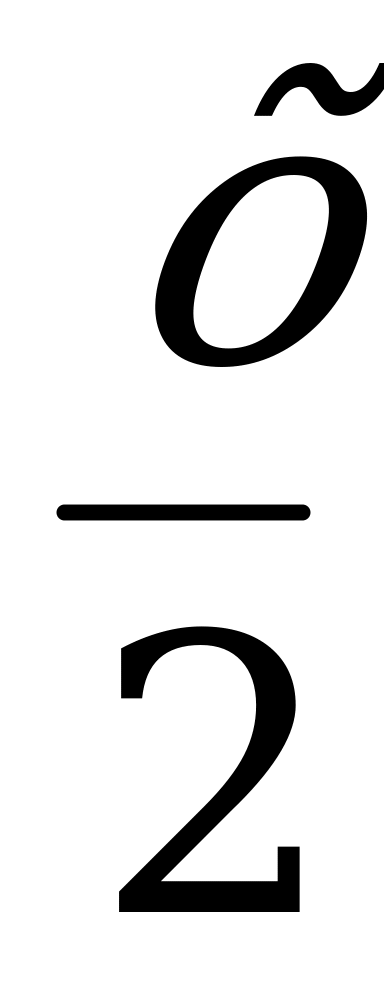 |
| И в печали глубокой старец земного удела конец воспринял, переживши года четыре с тех пор, как сына лишился. |
х=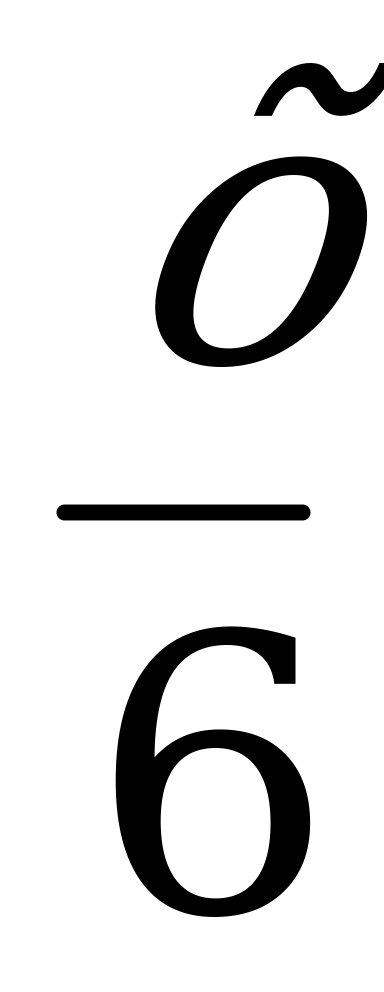 + +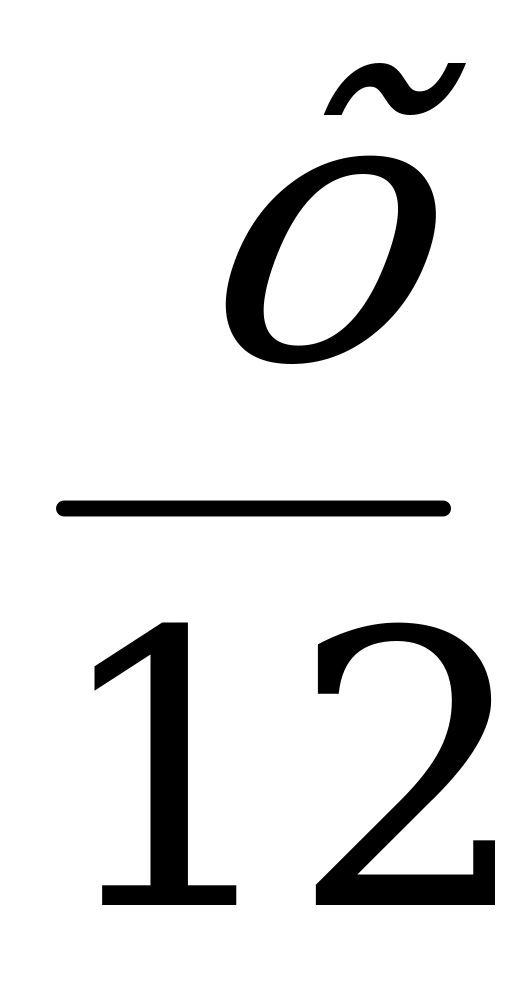 + +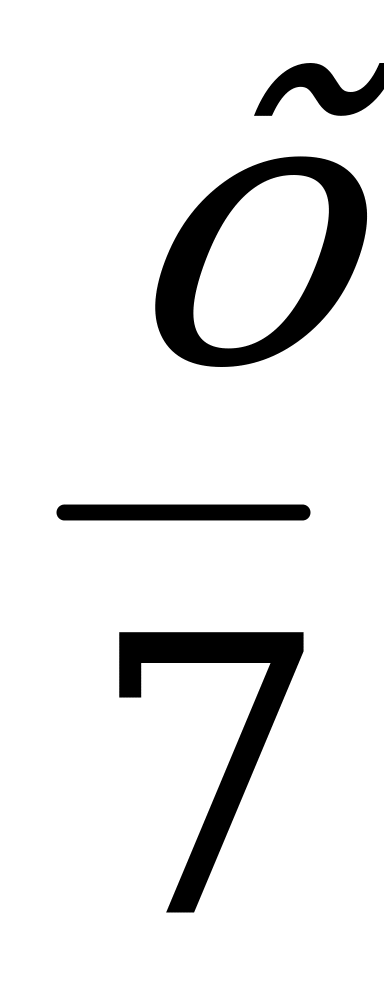 +5+ +5+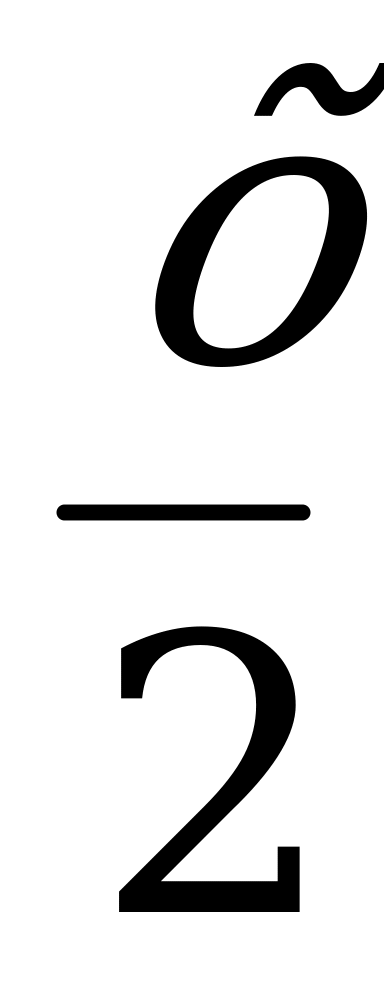 +4 +4 |
| Скажи, сколько лет жизни достигнув, смерть воспринял Диофант? |
|
(Ответ: 84 года)
Ведущий: Командам предлагается решить эту задачу. 2 балла получает команда, решившая задачу первой, 1 балл получит команда, решившая задачу второй. При этом неверное решение не оценивается. А в это время выступит обучающийся с сообщением №2
Выступающий 1,2. «Математика Древнего мира».
Что дала математика людям? Зачем ее изучать? Когда она родилась и, что явилось причиной ее возникновения?
Человеку нужно знать, что он из себя представляет. Чтобы что-то делать, нужно вспомнить, как это делается, т.е. необходима память. Память основа разумной жизни, а отсутствие ее ведет к бесконечному движению по кругу.
История - коллективная память человечества, история математики предохраняет человечество от движения по кругу.
Память человечества не сохранила, не донесла до нас имя изобретателя колеса или гончарного круга. Назвать же имя гения, впервые задавшего вопрос «сколько?», тем более невозможно.
В каменном веке, когда люди собирали плоды, ловили рыбу и охотились на животных, потребность в счете возникла так же естественно, как и потребность в добывании огня. Об этом свидетельствуют находки археологов на стоянках первобытных людей. Например, в Моравии, на месте одной из таких стоянок найдена волчья кость с 55 глубокими зарубками. Позже в других местах ученые находили столь же древние каменные предметы с точками и черточками, сгруппированные по три и по пять. Такая система записи чисел называется единичной. Единичная система записи чисел не забыта и в наши дни. Как узнать на каком курсе учится курсант военного училища? Сосчитайте сколько полосок нашито на рукаве его мундира. О количестве самолетов противника, сбитых в воздушных боях, говорит число звездочек, нарисованных на фюзеляже самолета.
Поштучно считать предметы удобно тогда, когда их не очень много. Пересчитывать же таким образом большие совокупности долго и утомительно, поэтому возникла идея объединить единицы в группы. Появился счет пятерками, десятками и двадцатками – по количеству пальцев рук и ног «счетовода».
Основными источниками, по которым мы можем судить о математике Древнего Египта, являются два папируса, дошедшие до нашего времени.
Во-первых, это папирус Райда, названный так по имени своего первого владельца. Он был найден в 1858 году, расшифрован и издан в 1870 году. Рукопись содержала 84 задачи с решениями.
Во-вторых, так называемый Московский папирус – его в декабре 1888 года приобрел в Луксоре русский египтолог Владимир Степанович Голенищев. Этот свиток включает в себя 25 задач.
Все правила счета египтян основывались на умении складывать и вычитать, удваивать числа и дополнять дроби до единицы. Умножение и деление сводили к сложению при помощи особой операции – многократного удвоения или раздвоения чисел. Высшей ступенью математики Древнего Египта является решение уравнений.
Поразительно, но при довольно примитивной и громоздкой арифметике египтяне добились значительных успехов в геометрии. Они умели вычислять площади треугольника, трапеции, прямоугольника. Нашли очень хорошее приближение числа  , которое было равно 3, 1605. Умели вычислять объем усеченной пирамиды с квадратным основанием.
, которое было равно 3, 1605. Умели вычислять объем усеченной пирамиды с квадратным основанием.
Таким образом, математика Древнего Египта представляет собой совокупность определенных знаний. Это были правила для решения конкретных задач, имевших практическое значение. И лишь постепенно задачи начали обобщаться и приобретать более абстрактные черты.
В Древнем Вавилоне получила развитие позиционная система чисел. Числам приписывались разные величины в зависимости от того, какую позицию они занимают в записи числа.
Писали вавилоняне на глиняных табличках, назывались они клинописными, так как на них рисовались клинья. Таблички обжигались и становились неразрушимыми.
Широкое применение таблиц – характерная особенность вавилонской математики. Они составили таблицы умножения, таблицы квадратов натуральных чисел, кубов, квадратных корней. Большинство задач древних вавилонян сводилось к решению квадратных уравнений. Это поразительное открытие позволило отнести рождение алгебры не к 5 веку до нашей эры, а к 18 веку до нашей эры, т.е. на 13 веков назад.
Вавилоняне решали задачи на арифметическую и геометрическую прогрессии. Впервые у них встречаются задачи на проценты и правило для приближенного вычисления квадратных корней.
Успехи в геометрии были скромнее. Одно из самых значительных открытий – это открытие теоремы, которую впоследствии стали называть теоремой Пифагора.
Пожалуй, дату появления математики как науки можно определить достаточно точно 6 век до нашей эры. На протяжении 20-30 веков народы Древнего Востока сделали немало открытий в арифметике, геометрии и астрономии, но единой математической науки они не создали. Грекам же это удалось за одно столетие.
В Греции жили и творили самые знаменитые ученые древности: Фалес, Пифагор, Евклид, Зенон, Архимед и т.д.
Греки превратили геометрию в науку: доказали теоремы о равенстве углов при основании равнобедренного треугольника, установили один из признаков равенства треугольников, теорему Фалеса. Открыли учение о четных и нечетных числах, доказали теорему Пифагора, знали формулу арифметической прогрессии, изучали пропорции и средние значения, ввели понятие бесконечности. Полагают, что именно Пифагор ввел аксиоматический метод, а Евклид ввел планиметрию прямоугольных фигур, основы геометрической алгебры, свойства круга, его касательных и хорд, ввел правила построения правильных n- угольников, теорию отношений величин, учение о подобии, теорию целых и рациональных чисел, учение о правильных многогранников.
О математике Древнего мира можно говорить долго. Математика, так же как и поэзия , живопись, музыка, театр и вообще – искусство, была вызвана к жизни духовными потребностями человека, его стремлением к познанию и красоте.
(Во время выступления ведущий собирает решения команд, которое оценит жюри, после выступления докладчика жюри объявляет итоги этапа).
Ведущий: А теперь на нашем пути «Математическое кафе», где я вам предлагаю пообедать и немного отдохнуть, но отдых у нас будет активным.
(слайд 32)

3 этап: Математическое кафе «Эврика».
Итак, познакомимся с меню.(слайд 33)

МЕНЮ
САЛАТЫ
Винегрет из анаграммы.
Салат «Ромашка» из загадок с числительными.
ПЕРВЫЕ БЛЮДА
Борщ с математическими обгонялками.
Суп из математических смекалок.
ВТОРЫЕ БЛЮДА
Кроссворд «И в шутку и в серьез».
Ребус с геометрическим содержанием.
СЛАДКИЕ БЛЮДА И НАПИТКИ
Компот из натуральных чисел.
Мороженное из логических задач.
Пирожное с математическим буриме.
Приступим к праздничному обеду. Как всегда, сначала легкая закуска – салаты. 1-ое блюдо «Винегрет из анаграмм».
Задание 1. Решите анаграмму. Переставьте буквы так, чтобы получился математический термин.
РИГФАК, АВИНУРЕНЕ, КОЧТА, ВАРТАДК.
(график, уравнение, точка, квадрат).
Команда, выполнившая задание первой, получает 2 балла, второй – 1 балл. (Пока команды выполняют задание, игра со зрителями в презентации слайд 34,35).


Ведущий: Второе блюдо нашего меню салат «Ромашка» из загадок с числительными.(слайд 36-меню)
Задание 2.(Оценивается верный ответ – 1 балл)
Отгадайте по четыре загадки с числительными.
Отвечает1-ая команда:
Сто один брат и все в один ряд. Вместе связаны стоят. Что это?
Ответ: Изгородь, забор.
Два брата купаются, а третий насмехается.
Ответ: Два ведра и коромысло.
Двенадцать братьев друг за другом бродят, друг друга не обходят.
Ответ: двенадцать месяцев.
Есть семь братьев: годами равные, именами разные.
Ответ: Дни недели.
Отвечает 2-ая команда:
Лежит брус на всю Русь. На том брусу 12 гнезд. И во всяком гнезде по четыре птицы.
Ответ: Год.
Только одно дерево без ветра шумит. Какое?
Ответ: Осина.
Шесть ног, а бежит не быстрее, чем на четырех.
Ответ: Всадник на коне.
Два раза родится, а один умирает.
Ответ: Птица
Задание 3. А теперь, пока не остыл борщ, займемся «математическими обгонялками» (балл получает та команда, которая первой ответит на вопрос).
Назовите автора главной теоремы геометрии. (Пифагор)
Что больше: произведение или сумма всех чисел от-5 до5? (они равны)
Какой знак надо поставить между двумя двойками, чтобы получить число больше двух, но меньше трех? (запятую)
Разделите полсотни на половину. (сто)
Что тяжелее: один килограмм ваты или один килограмм железа? (они равны)
Цифровой знак, обозначающий отсутствие величины. (ноль)
Геометрическая фигура, не имеющая ни начала, ни конца (круг)
Задание 4 . А теперь попробуем «Суп из математических смекалок» (1 балл за каждую правильно решенную задачу, каждой команде по три одинаковых задачи (на 3 минуты)). Как вы уже поняли, задания, которые получают команды не простые, а требующие развитой логики. А что такое логика? Об этом узнаем из следующего сообщения №3:
Выступающий 3,4. «Что такое логика и для чего она нужна?».
Математика является наукой, в которой все утверждения доказываются с помощью умозаключений, а именно путем использования законов человеческого мышления. Изучением таких законов занимается наука логика.
Можно ли применять математическую логику в повседневной жизни? Вы идете в магазин. Покупаете сколько-то килограммов капусты. Умножая вес капусты на цену килограмма, вы определяете, сколько денег надо отдать продавцу. Подбираете нужные купюры, складывая в уме их достоинство. Затем, вычитая, рассчитываете в уме сдачу. Действия привычные и обычные для всех. Вы применяете математику и ее конкретный раздел – арифметику, а строите свои умозаключения с помощью логики.
Мы живем в таком мире, когда получаем очень много информации из непроверенных источников. Из рекламы, из никем не проверяемых книг, из средств массовой информации, от малознакомых людей. Если мы не хотим быть обманутыми, стоит научиться распознавать ложь. В мире появилось новое, быстро растущее пространство: Internet. Нужно в полной мере использовать открывающиеся возможности, но и оградить себя от неточной или неверной информации, которой в Internet предостаточно. Математическая логика помогает разобраться в море информации, путем рассуждений и сопоставлений определенных фактов.
Ученье – свет, а неученье – тьма. Знание – сила. Это поговорки, известные каждому с детства. И действительно, чем значительнее знание человека, тем больше его могущество. Однако получить истинное знание без помощи специальных приемов практически невозможно. Существует мнение, что правильно мыслить можно, не пользуясь законами логики и даже не зная о них, на основе житейского опыта и здравого смысла. Однако это не так. Например, решить математическую задачу можно, дойдя, как говорится, «своим умом», однако другая такая задача уже не покорится, потому что основана на правилах, не известных решающему. Или он легко может совершить ошибку, которая приведет в результате к совершенно неправильному ответу. Так обстоит дело и в случае с мышлением. Только изучение логики и постоянная тренировка логических способностей позволяют человеку мыслить правильно, четко и без ошибок. А ошибка, даже самая малая, может стоить отдельному человеку и даже человечеству очень дорого. Например, фашизм как политическое явление, приведшее к самой опустошительной войне современного мира, был основан на идеологии, содержащей заведомо допущенную неправильность. Однако не нашлось человека, который смог бы вовремя опровергнуть идеи фашизма, разоблачить их.
Это лишь один из примеров, который ясно дает понять, насколько актуальна логика в жизни человека, не только занимающегося наукой или политикой, но и простого гражданина.
Так зачем нужна логика, какую роль она играет в нашей жизни? Логика помогает нам правильно строить свои мысли и верно их выражать, убеждать других людей и лучше понимать собеседника, объяснять и отстаивать свою точку зрения, избегать ошибок в рассуждениях, чтобы не попасть впросак, не быть обманутым, не подвергнуться нежелательным последствиям неосторожно сказанного слова.
Задание для команд.
Спутники, имеющие одну орбиту, делают оборот вокруг Земли один за 1 ч 40 мин, а другой за 100 мин. Как это объяснить? (Один и тот же период времени).
В харчевню пришли 11 человек и потребовали подать им по рыбине. К сожалению, у хозяина оказалось три небольших рыбины. Тем не менее, хозяин не желал упустить случая, поживиться: имея в своем распоряжении три рыбы, он обещал гостям подать на стол одиннадцать. Гости заинтересовались этим и даже согласились уплатить деньги вперед. Как хозяин харчевни исполнил свое обещание? (Уложил рыбу на тарелке так: ХI).
На улице в 11 часов вечера идет дождь. Можно ли утверждать, что через 72 ч будет солнечная погода? Ответ объясните.(Нет, так как будет ночь).
Ведущий: Прошу команды передать свои решения жюри. А пока подводятся итоги, командам предлагается разгадать шуточный кроссворд. Правильное решение оценивается в 1 балл.
Задание 5. Решите кроссворд «И в шутку и в серьез».
ПО ГОРИЗОНТАЛИ:
Название нашего кафе.
ПО ВЕРТИКАЛИ:
Самая нелюбимая оценка ученика.
Независимая переменная функции.
«Вымирающая» разновидность учеников.
Проверка учеников на выживание.
Утверждение, которое не доказывается.
Ответы: По горизонтали: 1. Эврика.
По вертикали: 2. Два. 3. Аргумент. 4. Отличник. 5. Контрольная.
6.Аксиома.
Ведущий: Пока команды заняты кроссвордом, мы тоже не будем сидеть, сложа руки, поэтому я объявляю игру со зрителями.
Игра со зрителями.
Ответьте на вопросы.
Утром на четырех, днем на двух, а вечером на трех. Кто это?
Ответ: ребенок, взрослый человек, старик.
2. Решите уравнение : 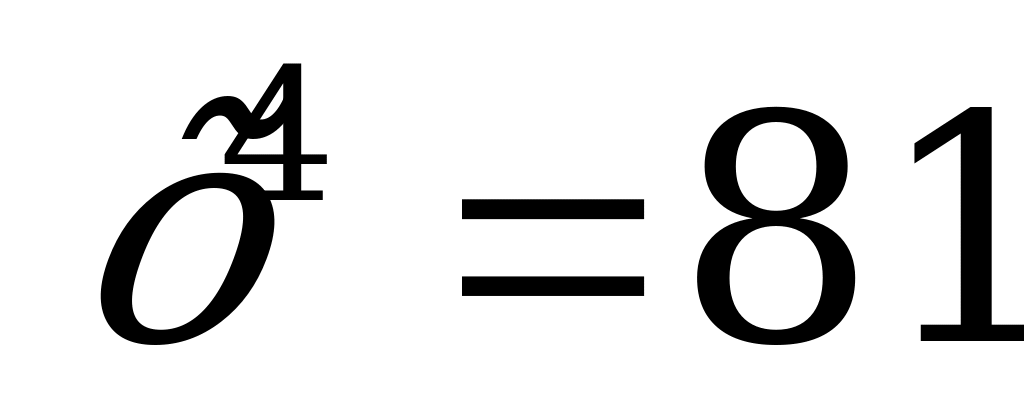
Ответ: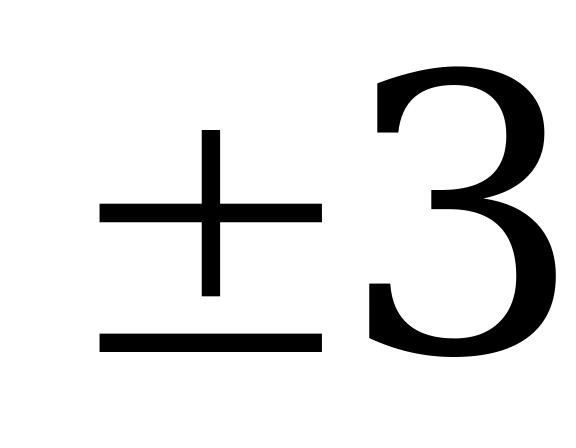
3.Два бочонка днем полны, а ночью пусты.
Ответ: сапоги.
Четверо братьев не сходятся и не расходятся, не отстают и не догоняют
друг друга.
Ответ: колеса
Острый угол параллелограмма 66 градусов. Чему равен тупой угол
параллелограмма?
Ответ: 114 градусов.
Какая из тригонометрических функций – четная?
Ответ: косинус.
Назовите число, разделяющее положительные и отрицательные числа.
Ответ: ноль.
Название какого города в Крыму состоит из двух мужских имен и натурального числа?
Ответ: Севастополь.
Какая геометрическая фигура изображена на самой известной картине Казимира Малевича?
Ответ: квадрат.
Среднее арифметическое женщины и рыбы.
Ответ: русалка.
Ведущий: Чтобы перейти к десерту, нам необходимо разгадать «ребусы с математическим содержанием».
Задание 6. На решение ребуса дается 1 мин. Каждая команда получает свой ребус. Правильно решенный ребус оценивается на 1 балл. (Ребусы прилагаются).
Ведущий: Шутить любят все. Вот и математики не лишены чувства юмора.
Расскажет об этом наш следующий докладчик с сообщением №5
Выступающий 5. «Из жизни замечательных людей».
Выступающий №1. Однажды с Великим русским ученым М.В.Ломоносовым произошел следующий случай:
На его камзоле протерлись локти. Повстречавший его придворный щеголь ехидно заметил по этому поводу:
- Ученость выглядывает оттуда…
- Нисколько, сударь, - немедленно ответил он, - глупость заглядывает туда!
Альберту Эйнштейну очень нравились фильмы с участием Чарли Чаплина, он питал большую симпатию к герою актера. Как-то раз Чаплин получил от Эйнштейна письмо, в котором тот писал: «Ваш фильм «Золотая лихорадка» понятен всем в мире, и Вы непременно станете великим человеком. Эйнштейн».
На это Чаплин ответил так: «Я Вами восхищаюсь еще больше. Вашу теорию относительности никто в мире не понимает, а Вы все-таки стали великим человеком. Чаплин».
Эйнштейна попросили в двух словах объяснить теорию относительности.
Он говорит:
- Все очень просто. Смотрите: один волос на голове - это мало, не правда ли?
- конечно...
- Вот ... а в тарелке супа - много.
Ведущий: И, наконец, десерт «Компот из натуральных чисел». Команды получают очередные задания.
Задание 7. Всем командам одинаковые задания с натуральными числами
 (3 мин).
(3 мин).
1
 . Найдите разность:
. Найдите разность:
8888 - 8 - 8 = ?


Ответ: 440
2. К однозначному натуральному числу припишите такую же цифру. Во сколько раз увеличится число?
Ответ: 11
3. Тремя двойками, не употребляя знаков действий, напишите возможно большее число.
Ответ: 
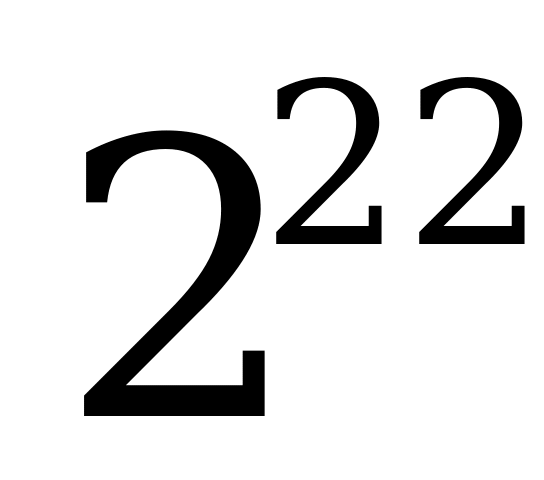
Ведущий: И наконец, основная «изюминка» меню – «мороженное из логических задач». На решение отводится 2 мин. А пока участники решают задачи, продолжим слушать некоторые зарисовки из жизни замечательных людей.
Высту3пающий 6. «Из жизни замечательных людей».
Немецкий математик Петер Густов Дирихле, был очень немногословен.
В тот знаменательный день, когда у него родился сын, он отправил своему тестю телеграмму, пожалуй, самую короткую за всю историю телеграфа: +1.
Эрнст Цермело (1871-1953), немецкий математик, один из основателей теории множеств, был приват-доцентом, то есть внештатным преподавателем с почасовой оплатой, в Геттингенском университете, когда деканом математического факультета был другой выдающийся ученый — Феликс Клейн (1849-1925). Декан держал творческие устремления своих сотрудников в железной узде. Однажды на лекции по математической логике Цермело смутил студентов такой логической задачкой:
- Все математики Геттингена принадлежат к двум классам. Одни делают то, что не нравится им, но нравится Клейну. Другие делают то, что нравится им, но не нравится Клейну. К какому классу относится в таком случае сам герр Клейн?
Никто не мог ответить. Тогда Цермело воскликнул:
- Но это же очень просто! Сам Феликс Клейн — не математик!
Французский математик Боссюэ отличался большой приверженностью к вычислениям. Однажды он тяжело заболел. Друзья опасались за его состояние. Они столпились у его постели, но больной настолько ослабел, что не отвечал на вопросы.
-Да он уже не дышит, - сказал кто-то.
-Подождите, - перебил другой, знавший ученого больше. – Я его спрошу. Боссюэ, квадрат двенадцати?
-144, - послышался шепот математика .
Он вычислял, значит, был жив.
Знаменитый немецкий математик Гильберт очень скромный и едкий на высказывания ученый, так шутил о своем сыне, лишенном математического дарования:
-Математические способности сын унаследовал от матери, все остальное – от меня.
Давида Гильберта спросили об одном из его бывших учеников.
-Ах, этот-то? – вспомнил Гильберт. – Он стал поэтом. Для математики у него было слишком мало воображения.
Задание 8. Решите логические задачи.
1-ой команде: Три брата – Ваня, Саша, Коля – учились в разных классах. Ваня был не старше Коли, а Саша не старше Вани. Назовите имя старшего из братьев, среднего и младшего.
Ответ: Коля, Ваня, Саша.
2 – ой команде: Трое девушек – Валя, Галя, Катя – пришли на праздничный обед в платьях разного цвета: одна в сером, другая в белом, третья в черном. Катя была не в черном платье, Валя не в черном и не в сером. Угадайте, в каком платье была каждая из девушек.
Ответ: Катя в сером, Валя в белом, Галя в черном.
Ведущий: Уважаемые участники, передайте решения жюри для окончательного подведения итогов. Наш отдых закончен, и представьте себе: мы находимся на Поле математических чудес.
4 этап: Поле математических чудес. (слайд 37)

Ведущий: Лист Мебиуса. Кто слышал об этом чуде? (Выслушать ответы).
Лист Мебиуса был открыт в 1858 году Лейпцигским профессором Августом Мебиусом, учеником знаменитого Гаусса. (слайд38) Получить его очень просто: склеиваем из бумажной полоски кольцо, только перед склеиванием повернем один конец полоски на 180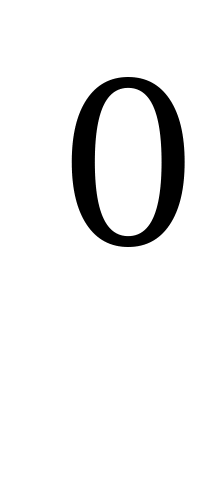 . Что же неожиданного увидел Мебиус у этого кольца? А то, что у листа Мебиуса одна сторона. Сейчас я вам это докажу (можно пригласить кого – то из ребят). Фломастером , не отрывая его от листа, можно провести линию с обеих сторон полосы, начиная с любого места. Что произойдет, если я сейчас разрежу по этой линии лист Мебиуса? Он превратится в одно кольцо, перекрученное, которое будет уже двусторонним. Свойство односторонности Мебиуса используют в технике: если в ременной передаче ремень сделать в виде листа Мебиуса, то его поверхность будет изнашиваться вдвое медленнее, чем у обычного кольца. Это дает ощутимую экономию.
. Что же неожиданного увидел Мебиус у этого кольца? А то, что у листа Мебиуса одна сторона. Сейчас я вам это докажу (можно пригласить кого – то из ребят). Фломастером , не отрывая его от листа, можно провести линию с обеих сторон полосы, начиная с любого места. Что произойдет, если я сейчас разрежу по этой линии лист Мебиуса? Он превратится в одно кольцо, перекрученное, которое будет уже двусторонним. Свойство односторонности Мебиуса используют в технике: если в ременной передаче ремень сделать в виде листа Мебиуса, то его поверхность будет изнашиваться вдвое медленнее, чем у обычного кольца. Это дает ощутимую экономию.
5 этап: Математическая таможня (слайд 39)

Ведущий: Наше жюри подвело итоги.
Объявляются итоги игры, жюри проводит награждение команд.
Ведущий: В заключении игры я хочу пожелать вам новых открытий и надеюсь, что «Страна математика» в будущем еще не раз порадует новыми интересными фактами. (слайд 40)


















 (3 мин).
(3 мин).
 . Найдите разность:
. Найдите разность: 












