Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа №4»
Лужского муниципального района
Ленинградской области РФ
Методическая тема:
«Решение нестандартных задач по математике».
Форма проведения- конференция
Срок реализации-5 лет

Выполнила
Смирнова Надежда Михайловна- учитель математики,
высшая квалификационная категория
Руководитель: Старший преподаватель кафедры математики
Голубева Светлана Александровна
Луга.
2016г
Содержание
1.Введение…………………………………………………………………………..3
2.Цели, задачи и формы работы…………………………………………………...3-4
3.Какая задача называется нестандартной? ……………………………………...4
4.Виды нестандартных задач………………………………………………………4-5
5. Методы решения нестандартных задач………………………………………...5
6. Как развивать способность к нестандартному мышлению?..............................5-6
7.Этапы решения нестандартных задач………………………………………........6-7
8. Формирование логического мышления при решении нестандартных задач…7
9. Формы занятий по обучению решения нестандартных задач………………….7
10.Примеры решения нестандартных задач…………..………………………….7-18
10. Заключение………………………………………………………………………18
11. Список литературы…………………………………………………………….18-19
Рано или поздно всякая правильная математическая идея
находит применение в том или ином деле. А. Н. Крылов.
Введение.
Математическое образование в системе основного общего образования занимает одно из ведущих мест, что определяется практической значимостью математики, ее возможностями в развитии и формировании мышления человека, ее вкладом в создание представлений о научных методах познания действительности. Важную роль играет формирование у учащихся правильных представлений о природе математики, характере отражения ею явлений реального мира, роли математических методов в преобразующей деятельности человека.
Актуальной задачей сегодняшней школы является обеспечение каждому учащемуся своей образовательной траектории на основе осознания своих возможностей и имеющегося выбора содержания и форм образовательной деятельности, позволяющей, с одной стороны, обеспечить базовую математическую подготовку, а с другой – углубленного изучения предмета и подготовка учащихся к продолжению образования в профильных вузах.
Решению нестандартных задач в школьной программе не уделяется должного внимания, большинство учащихся не владеют приемами их решения. Причиной этого является отсутствие системы заданий по данной теме в школьных учебниках. Они не входят в базовый курс математики основной школы, но решать их с учащимися очень важно потому, что они учат находить новые, оригинальные способы решения, обеспечивают прочность и глубину знаний учащихся по математике. С помощью нестандартных задач проверяется техника владения формулами элементарной математики, методами решения уравнений и неравенств, умение выстраивать логическую цепочку рассуждений, уровень логического мышления учащихся и их математической культуры.
Цели:
создание условий для развития творческого математического мышления обучающихся через решение нестандартных задач
подготовка учащихся к творческой деятельности (умение переносить знания и способы действий в незнакомые ситуации и видеть новые функции объекта)
Задачи:
создать условия для углубления предметных и межпредметных знаний через разнообразную учебную деятельность;
сформировать умение решать исследовательские задачи;
сформировать готовность к творческой деятельности;
сформировать умения проводить несложные доказательные рассуждения, действовать в соответствии с предложенным алгоритмом;
сформировать умения планировать свою деятельность при решении нестандартных математических задач, видеть различные стратегии решения задачи и осознанно выбирать способ решения;
развивать логическое и критическое мышление, культуру речи, способность к умственному эксперименту;
развивать приёмы самоконтроля при решении учебных задач;
развивать коммуникативные компетенции, самостоятельно организовывать учебное взаимодействие в группе (определять общие цели, распределять роли, договариваться друг с другом и т.д.).
сформировать готовность к участию в олимпиадах, семинарах, конкурсах и конференциях по математике различных уровней и получения высоких результатов.
Формы работы:
проектная и исследовательская деятельность;
инновационные технологии;
самостоятельная работа;
внеурочная деятельность
Какая задача называется нестандартной?
Определение нестандартной задачи приведено в книге «Как научиться решать задачи» авторов Л.М. Фридмана, Е.Н. Турецкого. Нестандартные задачи – это такие задачи, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения. Их часто путают с задачами повышенной сложности, однако это не так. Условия задач повышенной сложности таковы, что позволяют ученикам легко выделить тот математический аппарат, который нужен для решения задачи по математике. Все этапы решения задачи повышенной сложности учащиеся решают, опираясь на знания программы школьного курса математики. Учитель контролирует процесс закрепления знаний, предусмотренных программой обучения.
Нестандартную задачу так решать нельзя, она предполагает наличие исследовательского характера. Однако если решение задачи по математике для одного учащегося является нестандартным, поскольку он незнаком с методами решения задач данного вида, то для другого – решение задачи происходит стандартным образом, так как он уже решал такие задачи и не одну. Одна и та же задача по математике в 5 классе нестандартна, а в 6 классе она является обычной, и даже не повышенной сложности. Если учащиеся не знают, как решать задачу, на какой теоретический материал им опираться, то в этом случае задачу по математике можно назвать нестандартной на данный период времени.
Таким образом, нестандартная задача – это задача, алгоритм решения которой учащимся неизвестен, то есть учащиеся не знают заранее ни способа ее решения, ни того, на какой учебный материал опирается решение. Очень часто ученикам предлагается единственный способ решения нестандартных задач, требующий большой практики по его овладению. Такой подход к обучению решения задач убивает интерес, тормозит умственное развитие учащихся.
Виды нестандартных задач.
Многообразие нестандартных задач охватывает весь курс школьной математики.
Задачи, примыкающие к школьному курсу математики, но повышенной трудности - типа задач математических олимпиад. Предназначаются в основном для школьников с определившимся интересом к математике. Тематически эти задачи обычно связаны с определённым разделом школьной программы. Они углубляют учебный материал, дополняют и обобщают отдельные положения школьного курса, расширяют математический кругозор, развивают навыки в решении трудных задач.
Задачи типа математических развлечений. Прямого отношения к школьной программе не имеют и, как правило, не предполагают большой математической подготовки. Они бывают простыми, но есть задачи с очень трудным решением и такие задачи, решение которых до сих пор не получено. «Нестандартные задачи, поданные в увлекательной форме, вносят эмоциональный момент в умственные занятия. Не связанные с необходимостью всякий раз применять для их решения заученные правила и приёмы, они требуют мобилизации всех накопленных знаний, приучают к поискам своеобразных, не шаблонных способов решения, обогащают искусство решения красивыми примерами, заставляют восхищаться силой разума»
Виды задач: задачи на переправы; задачи на переливание; задачи на разрезание; задачи на графы; логические квадраты; числовые ряды; задачи на чётность; задачи на раскраски; задачи на решетках; на правду и ложь; задачи на взвешивание; принцип Дирихле; задачи, решаемые с «конца»; задачи на выигрышные ситуации; комбинаторные задачи; многовариантные задачи и т.д.
Нестандартные задачи требуют от учащихся высокой и устойчивой концентрации внимания и прекрасно подходят для развития и тренировки зрительной памяти. Математику любят в основном те ученики, которые умеют решать задачи. Научив их решать задачи, учитель окажет влияние на их интерес к предмету, на развитие мышления и речи. Нестандартные задачи не должны иметь уже готовых, заученных детьми алгоритмов. Они должны быть доступны по содержанию всем учащимся, быть интересными по содержанию. Для их решения учащимся должно хватать знаний, усвоенных ими по программе.
Методы решения нестандартных задач.
Как же помочь учащимся научиться решать нестандартные задачи? Каковы же методы обучения решению задач по математике, которые на данный момент ее решения можно назвать нестандартными?
Методы: арифметический; алгебраический; графический; практический; метод предположения; метод перебора.
Универсального рецепта, к сожалению, никто не придумал, учитывая уникальность данных задач. Очень часто учителя, «натаскивают» на решение с помощью шаблонных упражнений. Происходит это следующим образом: учитель показывает способ решения, а затем ученики повторяют это при решении задач многократно. Такой способ убивается интерес учащихся к математике. Владение приемами их решения можно считать критерием знаний основных разделов школьной математики, уровня математического и логического мышления.
Как же развивать способность к нестандартному мышлению?
Выдающиеся математики и педагоги С.А. Яновская, Л.М. Фридман, Э.Н. Балаян нашли ряд общих указаний и рекомендаций, которыми можно руководствоваться при решении нестандартных задач. Нужно направить учеников думать не как привычно, а «выйти за рамки», подойти к проблеме с другой стороны. Можно разбить задачу на множество мелких задач и решить каждую маленькую задачу разными способами. Для придумывания решений мелких задач можно использовать мозговой штурм, или предложить учащимся составить рисунок к задаче, сочинить стихотворение по условию задачи. Мозг будет думать над решением задачи, но в другой плоскости, то есть попробовать другой подход. Можно решать задачу «задом наперед», избавиться от стереотипов. Или же заменять формулировку вопроса, используя проблемные жизненные ситуации, используя метод подбора вспомогательных задач. Обычно в таких случаях думающий ученик пытается самостоятельно, без помощи учителя находить вспомогательные задачи, упрощая и видоизменяя условия исходной задачи. Полезно решить одну задачу разными способами. Если при решении не работает ни один из перечисленных методов, тогда нужно изобрести свой особый метод и доказать, что он применим в данных условиях.
Научить решать задачи можно только в том случае, если у учащихся будет желание их решать, то есть если задачи будут содержательными и интересными. Поэтому проблема первостепенной важности, стоящая перед учителем, - вызвать у учащихся интерес к решению той или иной задаче. Необходимо тщательно отбирать интересные задачи и делать их привлекательными для учащихся, анализируя проведенное решение. Математике нельзя научиться, глядя, как это делает сосед.
Методические принципы обучения учащихся умению решать нестандартные задачи подробно описаны в книгах Д. Пойа «Как решать задачу», «Математическое открытие», «Математика и правдоподобные рассуждения», Л. М. Фридмана, Е. Н. Турецкого «Как научится решать задачу», Ю. М. Колягина, В. А. Оганесяна «Учись решать задачи». Эти книги адресованы учащимся, желающим научиться решать задачи, так же могут быть использованы учителями при обучении школьников умениям решать нестандартные задачи.
Этапы решения нестандартных задач.
При формировании умения решать нестандартные задачи учитель должен руководствоваться следующими правилами: научить своих учеников догадываться, доказывать и с помощью наводящих указаний, не навязывать своего мнения насильно. Помогая ученику, учитель должен оказать ему внутреннюю помощь, т.е. ограничиться такими подсказками, которые могли бы рождаться в сознании самого ученика, и избегать внешней помощи, т.е. давать куски решения, которые не связаны с сознанием ученика. (Д.Пойа)
На ранних этапах обучения учащимся полезно давать памятки, включающие все шаги решения, а также использовать серию однотипных задач. Усложнять задачи постепенно, используя ранее решенные задачи (метод подсказок). Такой прием систематизирует знания и опыт по решению нестандартных задач. Решая одну задачу разными способами, учащиеся приобретают жизненный опыт и прочные знания по данному типу задач.
1.Анализ текста задачи:
Усвоение содержания; составление схемы, рисунка, чертежа, таблицы; выписать данные и искомые величины и соотношения между ними; проверить их достаточность и непротиворечивость; перевести условие задачи на математический язык, предполагаемый для решения задачи; переформулировать условие задачи, заменив данное в ней описание ситуации другими объектами, сохраняющими все отношения, связи и количественные характеристики, т.е. преобразовать текс задачи в форму, сокращающуюся поиск решения.
2.Поиск решения (выдвижение идеи, разбор задачи, составление плана)
Попытаться свести ее к ранее решенным задачам; отбросить не существенную, излишнюю информацию; заменить описание некоторых понятий соответствующими терминами, изменить текст задачи в форму, удобную для поиска решения; расчленить задачу на серию вспомогательных задач, последовательное решение которых составит решение данной задачи.
3.Осуществление плана решения.
Выбор способа оформления задачи, гарантирующего фиксацию рассуждений в форме, достаточной для полного решения; провести коррекцию правильности решения путем сравнения с условием.
4. Проверка ответа.
Прикинуть правильность результата сопоставлением с условием и здравым смыслом; установить соответствие между данными и искомыми величинами; составить и решить обратную задачу.
Формирование логического мышления при решении нестандартных задач.
Нестандартные задачи способствуют развитию логического мышления в еще большей степени и являются мощным средством активизации познавательной деятельности, т. е. вызывают у детей огромный интерес и желание работать.
Решая нестандартные задачи, учащиеся применяют не только готовые алгоритмы, но и самостоятельно находят новые способы решения, развивают сообразительность, препятствуют выработке вредных штампов при решении задач, учатся переносить знания в новую ситуацию. Они приобретают умения владения разнообразными приемами умственной деятельности, создают благоприятные условия для повышения прочности и глубины знаний и обеспечивают сознательное усвоение математических понятий.
Формы занятий по обучению решения нестандартных задач
Основной формой обучения решению нестандартных задач является урок. Форма урока может меняться в зависимости от типов решаемых задач. Повысить эффективность урока, можно через использование компьютерного программного обеспечения. Его можно использовать в качестве домашнего задания для самоподготовки учащихся, для подготовки и защиты исследовательского проекта, для внеклассной работы по предмету, для отбора материала по темам, практиковать «выход» в Интернет. Во внеурочной деятельности: математические кружки, бои и конкурсы, турниры, факультативы, устные и письменные олимпиады, элективные курсы, семинары и групповые занятия подготовки к ОГЭ и ЕГЭ. Включение в образовательный процесс нестандартных математических задач практического содержания обеспечивает формирование познавательного интереса обучающихся и приобретение жизненного опыта, при подготовке к конкурсам, олимпиадам и итоговой аттестации. Внеурочная работа – это творческий процесс, при котором учащиеся проявляют свои способности, раскрывают свои интересы и увлечения.
Примеры решения нестандартных задач.
Задача «Переправа»
В задачах на переправы необходимо кого- то переправить, чаще на лодке на другой берег. Задачи данного типа решаются по алгоритму, то есть по понятному и точному предписанию действий исполнителю, с целью получения результата.
Виды задач: Переправы без условий: переправляющиеся находятся на одном берегу или переправляющиеся находятся на разных берегах. Переправы с условиями: условие вместимости или затрудненные переправы (наличие острова)
Задача. Волк, коза и капуста. На берегу реки стоит крестьянин с лодкой, а рядом с ним находятся волк, коза и капуста. Крестьянин должен переправиться сам и перевезти волка, козу и капусту на другой берег. Однако в лодку кроме крестьянина помещается либо только волк, либо только коза, либо только капуста. Оставлять же волка с козой или козу с капустой без присмотра нельзя – волк может съесть козу, а коза – капусту. Как должен вести себя крестьянин?
Решение. Крестьянин может следовать одному из двух алгоритмов:
| Алгоритм 1 | Алгоритм 2 |
| крестьянин и коза | крестьянин и коза |
| крестьянин | крестьянин |
| крестьянин и волк | крестьянин и капуста |
| крестьянин и коза | крестьянин и коза |
| крестьянин и капуста | крестьянин и волк |
| крестьянин | крестьянин |
| крестьянин и коза | крестьянин и коза |
Задачи на переливания
Задачи на переливание – это задачи, в которых с помощью сосудов известных ёмкостей требуется отмерить некоторое количество жидкости.
Задача. Дядя Федор собрался ехать к родителям в гости и попросил у кота Матроскина 4 л молока. А у Матроскина только 2 пустых бидона: трехлитровый и пятилитровый. И восьмилитровое ведро, наполненное молоком. Как Матроскину отлить 4 литра молока с помощью имеющихся сосудов?
Ход рассуждений: 1) Переливаем из восьмилитрового ведра 5 литров молока в пятилитровое.
2) Переливаем из пятилитрового бидона 3 литра в трёхлитровый бидон.
3)Переливаем их теперь в восьмилитровое ведро. Трёхлитровое ведро пусто, в восьмилитровом 6 литров молока, а в пятилитровом - 2 литра молока.
4)Переливаем 2 литра молока из пятилитрового бидона в трёхлитровый.
5) наливаем 5 литров из восьмилитрового ведра в пятилитровый бидон. Теперь в восьмилитровом 1 литр молока, в пятилитровом - 5, а в трёхлитровом – 2 литра молока.
6)Доливаем дополна трёхлитровый бидон из пятилитрового и переливаем эти 3 литра в восьмилитровое ведро. В восьмилитровом ведре стало 4 литра, так же, как и в пятилитровом бидоне.
| Ходы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 8 л | 8 | 3 | 3 | 6 | 6 | 1 | 1 | 4 |
| 3 л | - | - | 3 | - | 2 | 2 | 3 | - |
| 5 л | - | 5 | 2 | 2 | - | 5 | 4 | 4 |
Задача решена.
Задачи на разрезание
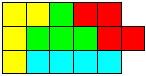
Задача. Разрезать фигуру на 4 фигуры разных по форме и равных по площади.
Ход рассуждения: нарисуйте сначала отдельно все виды фигур равной площади
16:4 =4(клетки) и повторите метод перебора вариантов.
| 1 | 4 | 7 | 10 | 13 |
|
| 2 | 5 | 8 | 11 | 14 | 16 |
| 3 | 6 | 9 | 12 | 15 |
|
Задачи на графы.
Граф – геометрическая фигура, состоящая из точек (вершины графа) и линий, их соединяющих (рёбра графа).
Задача. На пришкольном участке растут 8 деревьев: тополь, дуб, клён, берёза, рябина, лиственница, сосна и яблоня. Рябина выше лиственницы, яблоня выше клёна, дуб ниже берёзы, но выше сосны, сосна выше рябины, берёза ниже тополя, а лиственница выше яблони. Расположите деревья от самого низкого к самому высокому.
Решение. Вершины графа - деревья, обозначенные первой буквой названия дерева. В данной задаче два отношения: - «быть ниже» и – «быть выше». Рассмотрим отношение – «быть ниже» и проведем стрелки от более низкого дерева к более высокому. Если в задаче сказано, что рябина выше лиственницы, то проводим стрелку от лиственницы к рябине и т.д. Получаем граф, на котором видно, что самое низкое дерево – клён, выше яблоня, потом лиственница, рябина, сосна, дуб, берёза и тополь.

Ответ: клён, яблоня, лиственница, рябина, сосна, дуб, берёза, тополь.
Логические квадраты.
Отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата, который был разработан еще средневековыми логиками. Вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так суждения вида А и вида I, а также суждения вида Е и О находятся в отношении подчинения. Суждения вида А и Е находятся в отношении противоположности, а суждения вида I и О – частичного совпадения. Общие суждения (А, Е) являются подчиняющими, а частные (I, O) – подчинёнными. Для суждений, находящихся в отношении подчинения, имеет значение следующее условие истинности: если истинно А, то истинно и I; если истинно Е, то также истинно и О, но не наоборот. Действительно, если истинно, что «Все студенты сдают зачет по логике» (А), то же самое верно и относительно некоторых из них (I) «Некоторые студенты сдают зачет по логике», но не наоборот. Из того, что «Некоторые дни недели являются нерабочими» (I), вовсе не следует, что «Все дни недели являются нерабочими» (А). Если истинно суждение «Ни один месяц не содержит тридцать второго числа» (Е), то истинным будет также подчиненное ему частно отрицательное суждение «В некоторых месяцах нет тридцать второго числа» (О). Обратное суждение не верно. Из истинности частного отрицательного суждения «Некоторые плоды не являются съедобными» (0) не следует, что и «Ни один из плодов не употребляется в пищу» (Е). В отношении противоречия находятся суждения Е и I, и А и О. Согласно законам логики, два противоречивых суждения не могут быть одновременно ни истинными, ни ложными. Значит, в двузначной логике они будут принимать разные логические значения: I если А – истинно, то О – ложно О если А – ложно, то О – истинно, если О – истинно, то А – ложно, если О – ложно, то А – истинно, если E – истинно, то I – ложно, если E – ложно, то I – истинно, если I – истинно, то E – ложно, если I – ложно, то E – истинно. Установив вид одного из противоречивых суждений и его логическое значение, можно без труда установить также логическое значение противоречивого ему суждения. Например, зная, что суждение «Ни один дельфин не живет на суше» (Е) является истинным, заключают, что противоречивое ему суждение «Некоторые дельфины способны жить на суше» (I) - ложно.

Отношением контрарности связаны только общие суждения А и Е. Как мы уже знаем, контрарность означает противоположность, крайние позиции и не охватывает весь класс предметов. Здесь возможно «и третье», «и четвертое». Значит, контрарные суждения не обязательно должны принимать разные логические значения. Верхняя О грань квадрата связывает такие виды суждений (А, Е), которые могут быть одновременно ложными, но не могут быть одновременно истинными. Например, оба суждения: «Все люди любят музыку Шнитке» и «Ни один человек не любит музыку Шнитке» очевидно ложны. Истинное суждение при этом будет выражать последний тип отношения- субконтрарность.
Отношение субконтрарности может возникать только между частными суждениями I и O. Это отношение выражено нижней гранью квадрата. Помня о том, что суждения I и O подчинены суждениям А и Е, и беря во внимание отношение противоположности между суждениями А и Е, заключаем, что поскольку суждение А и О, Е и I связаны законом не противоречия, то в случае контрарных отношений О между А и Е отношения подчинения I→A и O→E «отменяются». В том случае, когда «верхние» суждения А и Е оказываются оба ложными (как в нашем примере), то истинными оказываются противоречащие им «нижние» суждения I и О. Поскольку суждения А и Е могут оказаться одновременно ложными, но не могут быть одновременно истинными, то суждения I и О, наоборот, могут быть одно- временно истинными, но не могут быть одновременно ложными (это и означает субконтрарность). Значит, в нашем примере истинными будут суждения: «Некоторые люди любят музыку Шнитке» (I), «Некоторые люди не любят музыку Шнитке» (О). Установление логических отношений между суждениями «по логическому квадрату позволяет производить ряд практических операций с суждениями. Например, зная истинное значение одного из суждений A, E, I, O, при помощи логического квадрата можно установить истинное значение трех остальных суждений. Данная логическая операция в формальном виде предстает в виде решения «задачи по логическому квадрату».
Задача. необходимо установить, каково логическое значение суждений E, I, O, если А – суждение истинное. Итак, А – истина, Е - ? I - ? O - ?
Решение. Выясняем значение другого общего суждения Е. Оно связано с А логическим отношением контрарности и также истинным быть не может (по определению контрарности). Значит, Е – ложно. Устанавливаем значения суждений I и О, связанных с общими суждениями А и Е отношением противоречия. Поскольку при таком отношении суждения принимают разные логические значения, устанавливаем: если А истинно, то О – ложно; если Е ложно, то I – истинно. Таким образом, решив задачу, устанавливаем, что: Если А - истина, то Е – ложь, I – истина, O – ложь
Задачи на числовые ряды.
Задача. Продолжите ряд чисел: а) 1; 3; 4; 7; 11; 16; ?
Ход рассуждений: поиск закономерностей, попытка определения закономерности в расстановке чисел: а) на сколько, во сколько больше или меньше; б) при сравнении: последовательных чисел или через число, или через два числа и т.д.; в) разработка аналогичных числовых рядов; г) решение теста.
Тест
Цель: диагностика уровня развития логического мышления. Инструкция к тесту. Предъявляются письменно ряды чисел. Необходимо проанализировать каждый ряд и установить закономерность его построения. Ученик должен определить два числа, которые бы продолжили ряд. Время решения заданий фиксируется.
2; 5; 7; 9; ….
15; 18; 21;…..
1, 2, 4, 8, 16, 32…
4; 5; 9; 14; 25;…..
1; 4; 9; 16; 25; 36….
Задачи на чётность.
Свойства четности (нечетности) часто используются при решении математических задач. Число называется четным, если оно кратно 2. Любое чётное число n можно представить в виде n=2k, где k – целое число, а любое нечётное число, в виде n=2k+1 или виде n=2k-1. Ноль является целым числом. Сумма двух чётных чисел - чётное число. Сумма двух нечётных чисел - чётное число. Сумма чётного и нечётного чисел - нечётное число. Произведение двух нечётных чисел - нечётное число. Произведение двух чётных чисел - чётное число. Произведение чётного и нечётного чисел - чётное число.
Задача. По кругу в произвольном порядке записано 4 единицы и 5 нулей. Над этими числами выполняется следующая операция: между одинаковыми цифрами пишут ноль, а между различными – единицу, после чего предыдущие цифры вытирают. Затем такая же операция выполняется над полученными цифрами и так далее. Докажите, что после нескольких таких операций невозможно получить 9 нулей.
Решение. Допустим, что после k таких операций получено 9 нулей. Тогда после (k–1)-й операции все цифры должны были быть единицами, а потому после (k–2)-й операции произвольные две соседние цифры, записанные по кругу, должны были быть различными. Тогда нулей должно быть столько же, сколько и единиц, откуда получаем, что общее количество цифр – чётное число, что противоречит условию. Предположение ложно, значит, 9 нулей описанным способом получить невозможно.
Задача. Спонсор решил устроить телефонизацию деревни Горбунки. Он хочет 7 имеющихся телефонов соединить между собой попарно так, чтобы каждый был соединен ровно с тремя другими. Можно ли это сделать?
Решение. При решении этой задачи используется такое соображение - если мы рассматриваем объекты типа веревки - провода, дороги, рукопожатия, знакомства и т. д. - то при любом количестве объектов число концов должно быть четным. Предположим, что мы соединили 7 телефонов между собой попарно так, чтобы каждый был соединен ровно с тремя другими. Посчитаем количество концов проводов, соединяющих эти телефоны. Понятно, что их число должно быть четным. От каждого из 7 телефонов отходит 3 конца, всего 7•3 = 21 конец, число нечетное, значит нельзя 7 телефонов соединить между собой попарно так, чтобы каждый был соединен ровно с тремя другими.
Задача. Максим Олегович написал на доске 2016 целых чисел. Петя заметил, что сумма любых 2015 чисел четна. Четна или нечетна сумма всех чисел?
Решение. Рассмотрим набор любых 2015 чисел, так как их сумма четна, то среди них есть хотя бы одно четное число. Действительно, если бы все из этих 2015 чисел были нечетными, то и сумма всех этих 2015 чисел была бы нечетной, что противоречит условию. Итак, мы нашли четное число. Теперь рассмотрим сумму всех чисел без этого четного числа. Она тоже будет четной (по условию), так как помимо этого числа на доске ровно 2015 чисел. Посчитать сумму всех 2016 чисел – это тоже самое что к найденному нами четному числу прибавить сумму остальных 2015 чисел, а так как четное + четное = четное получаем, что сумма всех чисел четна. Ответ: Четна
Задачи на раскраски.
На олимпиадах различного уровня учащимся предлагают задачи, в которых заданы условия для изменения исходного объекта и спрашивается, можно ли в данных условиях получить другое состояние этого объекта? Например, обойти шахматным слоном доску и вернуться на определенную клетку. В случае положительного ответа достаточно указать одно из решений, а если решения нет, то убедиться в этом, перебором вариантов, часто нелегко. В таких случаях красивое и лаконичное решение можно получить, используя метод раскрасок.
Задача. Шахматная доска размером 6×6 покрыта 18 костями домино размером 1×2 (каждая кость покрывает две клетки). Докажите, что при любом таком покрытии можно разрезать доску на две части по горизонтальной или вертикальной линии, не повредив ни одной кости домино.
Решение. Предположим, что можно уложить кости домино на доску так, что каждая из горизонтальных и вертикальных прямых, разделяющих доску на клетки, пересекает хотя бы одну кость домино. Всего имеется 10 таких прямых. Каждая из этих прямых разбивает доску на 2 части, состоящие из чётного числа клеток. В любой из этих частей содержится какое-то количество неразрезанных костей домино. Эти кости занимают чётное число клеток. Оставшиеся клетки заняты половинками разрезанных костей, а так как их чётное число, то и число разрезанных костей тоже чётно.
Итак, каждая из 10 прямых разрезает не меньше двух костей, а так как каждую кость пересекает только одна прямая, то число разрезанных костей не меньше 20. Однако общее количество костей, покрывающих доску, – 18. Противоречие. Доказательство окончено.
Задачи на решетках.
Задача. Все вершины выпуклого многогранника находятся в узлах решётки, причём других узлов решётки внутри, на гранях и на рёбрах нет. Докажите, что число вершин многогранника не превосходит восьми.
Решение. Каждая из трёх координат узла решётки может быть либо чётной, либо нечётной; всего получается 23 = 8 различных вариантов. Поэтому если у многогранника есть девять вершин, расположенных в узлах решётки, то две из них имеют координаты одной чётности. Середина отрезка, соединяющего эти вершины, является узлом решётки, и лежит внутри многогранника, если этот отрезок – его диагональ; принадлежит грани, если отрезок – диагональ грани; лежит на ребре, если отрезок – ребро многогранника.
Задачи на правду и ложь
Задача. На необитаемом острове растут три дерева: ёлка, берёза и сосна. Под одним из них пираты зарыли клад, а на деревья повесили таблички: на ёлку - «Клад зарыт под березой», на сосну - «Клад зарыт не здесь», на березу - «Клад зарыт под сосной». Две надписи правдивые, одна - ложная. Под каким деревом клад?
Решение. 1 способ. В парах берёза-ёлка и сосна-берёза таблички противоречат друг другу. При этом мы знаем, что из трёх надписей только одна - ложная. Тогда, аналогично тому, как мы это делали в предыдущей задаче, мы делаем вывод, что ложной является табличка под берёзой. Соответственно, остальные две таблички правдивые, из них конкретное указание на место расположения клада даёт табличка на ёлке - "Клад зарыт под берёзой".
Решение. 2 способ. Составим таблицу. Заполняя строку «елка» мы предполагаем, что клад зарыт под ней и записываем, правдивы ли надписи в свете этого предположения. Заполняя строку, сосна предполагаем, что клад здесь, и т. д. Строка, в которой две надписи будут правдивые, а одна ложная указывает на присутствия там клада - так как по условию задачи только одна табличка из трёх врёт.
|
| «Клад зарыт под березой» | «Клад зарыт не здесь» | «Клад зарыт под сосной» |
| елка | ложь | правда | ложь |
| сосна | ложь | ложь | правда |
| береза | правда | правда | ложь |
Ответ: клад под березой.
Задачи на взвешивание
Ключевая идея решения таких задач – правильная трисекция, т. е. последовательное деление множества вариантов на три равные части. После первой трисекции должно остаться не более трех подозрительных монет, после второй – не более одной ПМ, которой и является ФМ.
Задача. Из девяти монет одна фальшивая: она легче остальных. Как за два взвешивания на чашечных весах без гирь определить, какая именно монета фальшивая?
Решение. Разбиваем монеты на 3 кучки по 3 монеты. Первое взвешивание: положим по 3 монеты на каждую чашку весов. Возможны два варианта. Равновесие. Тогда на весах только настоящие монеты, а фальшивая среди тех монет, которые не взвешивались. Одна из кучек легче. Значит в ней фальшивая монета. Второе взвешивание: теперь требуется найти фальшивую среди трёх монет (по методу первого взвешивания).
Задача. Имеется 80 монет, одна из которых фальшивая. За какое наименьшее число взвешиваний на весах без гирь можно найти фальшивую монету?
Решение. Проводим первое взвешивание: кладем на чаши по (80-2):3=26 монет. В случае равновесия- ФМ среди оставшихся 28; взвешивая настоящие 26 монет с 26 «подозрительными», мы определим, легче ФМ или тяжелее настоящей (в случае равновесия, она в оставшихся двух и далее надо еще 2 взвешивания). Если при первом взвешивании весы не оказались в равновесии, то фальшивая - в какой–то из чаш на весах. Сравниваем первую группу монет с настоящими из третьей и делаем вывод. Потом делим ту группу монет, где есть фальшивая на 9, 9, 8, взвешиваем, далее взвешиваем по 3 монеты, а затем - по одной.
Ответ: за 5 взвешиваний.
Принцип Дирихле
При решении различных математических задач применяется специальный метод, получивший название по имени немецкого математика: принцип Дирихле. (Петер Густав Лежен Дирихле 13.02.1805 - 05.05.1859). «Принцип ящиков») — утверждение, устанавливающее связь между объектами «кроликами» и контейнерами «клетками» при выполнении определённых условий. В некоторых языках утверждение известно как «принцип голубей и ящиков», когда объектами являются голуби, а контейнерами — ящики.
Существует несколько разных формулировок принципа Дирихле. Самая понятная и простая подразумевает, что нельзя посадить 8 кроликов в 3 клетки так, чтобы в каждой было не больше 2. Более научная и сложная формулировка, объясняющая принцип Дирихле, гласит: если в k ячеек находится k+1 зайцев, то, по крайней мере, в 1 ячейке будет располагаться больше одного зайца. А если в k ячеек находится k-1 зайцев, то по крайней мере в 1 ячейке будет располагаться меньше одного зайца. Доказательство этого утверждения совсем простое, так сказать, от противного. Если предположить, что в каждой ячейке располагается зайцев меньше, чем k-1/k, тогда в k ячеек зайцев меньше, чем k*k-1/k = k-1, а это противоречит первоначальным условиям. В действительности такой простой и понятный принцип значительно облегчает решение задач по математике и доказательства многих трудоемких теорем. Просто необходимо учитывать, что зайцев и ячейки можно легко заменить на математические предметы и объекты (цифры, точки, отрезки, фигуры и т. д.). Решение через утверждение Дирихле не всегда простое и понятное. Иногда очень трудно определить, какую величину считать животным, а какую – клеткой, и каким образом факт наличия двух животных в одной клетке поможет решению задачи. Да и если удастся в этом разобраться, все равно нельзя определить, в какой именно клетке будет находиться объект. То есть можно просто доказать существование такой ячейки, но нельзя конкретизировать ее.
Задача. Прямая k проходит через плоскость треугольника ABC, однако не пересекает ни одну его вершину. Необходимо доказать, что она не может пересекать три его стороны. Решение. Представим, как прямая k разбивает треугольник на две плоскости, назовем их s1 и s2. Будем считать, что s1 и s2 открытые, то есть не содержащие прямую k. Применяем принцип Дирихле. Задачи с решениями могут продемонстрировать, что под кроликами и ячейками в современных условиях подразумеваются разнообразные объекты. Так, вместо зайцев мы подставим вершины треугольника, а вместо ячеек – полуплоскости. Поскольку проведенная прямая k не пересекает ни одну из вершин, то каждая из них находится в той или иной плоскости. Но поскольку вершины в треугольнике три, а плоскости у нас всего две (s1 и s2), то одна из них будет содержать две вершины. Предположим, что это вершины A и B, и находятся они в полуплоскости s2 (то есть лежат по одну сторону от k). В таком случае отрезок АВ не пересекает прямую k. То есть в треугольнике есть сторона, которую прямая k не пересекает.
Задача. В классе 15 учеников. Докажите, что найдутся как минимум 2 ученика, отмечающих дни рождения в один месяц.
Решение. Пусть 15 учеников будут «зайцы». Тогда «клетками» будут месяцы года, их 12.Так как 15 12, то, по принципу Дирихле, найдется, как минимум, одна клетка, в которой будет сидеть, по крайней мере, 2 «зайца». То есть, найдется месяц, в котором будут отмечать дни рождения не менее 2 учеников класса.
Задачи, решаемые с «конца».
Выделение данных задач в отдельную группу связано со способом рассуждения при решении, которое выполняется с «конца» задачи. В математической литературе он назван методом инверсии. Суть его состоит в следующем: если надо найти число, которое после ряда операций приводит к известному числу, то необходимо с известным числом произвести в обратном порядке все обратные операции. Решать с конца можно задачи на лабиринты. В них содержатся несколько возможных путей, отходящих от начальной точки, и среди них только один верный путь, который приведет в конец лабиринта к заветной цели. Ускорить решение такой задачи можно, если пойти в обратном направлении. Способ решения с «конца» очень удобен, если от конечной цели ведет меньше путей, чем из исходного положения. Особенно на ЕГЭ, при решении задачи на вероятность, учащиеся сэкономят время на решение более сложных задач.
Задача. Первого мая в пруду расцвела лилия. На следующий день расцвели уже две лилии. Ещё на следующий день – четыре. И так далее. Каждый день количество лилий в пруду удваивалось, пока 31 мая пруд не оказался заполнен лилиями целиком. Какого числа пруд был заполнен лилиями только наполовину?
Решение. Решить задачу можно «в лоб»: посчитать количество лилий, которые расцвели на пруду 31 числа, а потом посмотреть, когда же расцвела половина от этого числа. Однако числа получатся огромными – ведь уже на 11 день на пруду зацветёт аж 1024 лилии. Попробуем пойти другим путём, а именно – рассмотрим ситуацию с конца. Если 31 числа пруд был заполнен лилиями целиком, то на сколько он был заполнен лилиями 30 мая? Мы знаем, что 31 мая лилий распустилось в два раза больше, чем 30, и стало равно целому пруду. Но сколько нужно удвоить, чтобы получить целое? Половину. Значит, 30 мая пруд зацвёл наполовину. Тем самым мы нашли ответ. Стоит отметить, что мы ничего не считали! И нам было абсолютно неважно, сколько именно лилий расцвело на пруду! Ответ.30 мая.
Комментарий: Условие можно понять так, что лилии расцветают и так и остаются цвести. Новые лилии добавляются к уже имеющимся. То есть может показаться, что, например, на второй день на пруду цвели 3 лилии, а не две. Но это не так. Лилии, как все цветы, на ночь закрывают свои бутоны, и, естественно, если прийти на пруд достаточно рано, то он будет пуст – цветов не будет. Поэтому, согласно условию задачи, на второй день на пруду цвели 2 лилии, а не 3. Часто ребёнок, не задумываясь, выпаливает ответ, который кажется самым естественным в этой задаче – 15 или 16 мая. Рассуждая, что половину озера закроют лилии за половину месяца. Задачи этого занятия заставят ребёнка задуматься о том, что очевидный ответ не всегда является правильным.
Задачи на выигрышные ситуации
Метод решения игровых задач - симметричная стратегия. Суть его в том, что нужно делать каждый раз ход, симметричный ходу противника или дополняющий его до чего-либо. Доказательство правильности стратегии состоит в том, что после каждого хода позиция симметрична: раз так, то если противник сумел сделать свой ход, то и мы сможем сделать ход, симметричный ему.
Задача. Имеется три кучки камней: в первой - 10, во второй - 15, в третьей - 20. За ход можно разбить любую кучку на две меньшие. Проигрывает тот, кто не может сделать ход. Кто выиграет?
Решение. Количество возможных ходов для раскладывания кучек: 45 – 3 = 42. Поэтому, как бы ни ходил первый игрок, при его ходе всегда будет четное число кучек. При ходе же второго игрока количество кучек будет всегда нечетно. Значит, победит первый игрок, так как по окончании игры всегда остается ровно 45 кучек по одному камню в каждой.
Комбинаторные задачи
Комбинаторика-раздел математики, рассматривающий задачи, связанные с подсчётом числа всевозможных комбинаций из элементов данного конечного множества при сделанных исходных предположениях.
Задача. В шахматном турнире принимали участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего партий было сыграно в этом турнире?
Решение. Способ 1. В одной игре участвуют 2 человека, следовательно, нужно вычислить, сколькими способами можно отобрать 2-х человек из 15, причем порядок в таких парах не важен. Воспользуемся формулой для нахождения числа сочетаний (выборок, отличающихся только составом) из n различных элементов по m элементов
C m из n = n!/( m!*( n- m)! , где n!= 1⋅ 2 ⋅3⋅...⋅ n , при n=15, m=2.
C 2 из 15 = 15!/( 2!*( 15- 2)! В процессе решения исключили 13! Из 15!, т.е. сократили произведение 15! = 1⋅ 2 ⋅3⋅...⋅15 на 13! = 1⋅ 2 ⋅ 3⋅...⋅13, остались после сокращения множители 14 и 15).
Способ 2. Первый игрок сыграл 14 партий (с2-м, 3-м, 4-м, и так до 15-го), 2- ой игрок сыграл 13 партий (3-м, 4-м, и т.д. до 15-го, исключаем то, что с первым партия уже была), 3-ий игрок − 12 партий, 4-ый − 11 партий, 5 – 10 партий, 6 – 9 партий, 7 – 8 партий, 8 – 7 партий, 9 – 6 10 – 5 11 – 4 12 – 3 13 – 2 14 – 1, а 15-ый уже играл со всеми. Итого: 14+13+12+11+10+9+8+7+6+5+4+3 +2+1=105 партий. Ответ: 105 партий.
Многовариантные задачи по планиметрии.
Основные причины возникновения нескольких случаев при решении геометрических задач заключаются в выполнении чертежа, проведении решения или написании ответа. В условии задачи есть «некая недосказанность».
Не указано, где именно расположена точка на прямой: на стороне фигуры или на ее продолжении;
Не указано, считать отношение, данное в условии, от одного конца отрезка, или же от другого;
Не указано, происходит внешнее касание окружностей, или же внутреннее;
Не указано, пересекаются прямые(лучи) внутри фигуры, или же вне ее;
Не указано, в какую именно из областей вписана окружность;
Не указано, как именно расположена прямая, образующая с данной прямой данный угол;
Не указано, лежит ли основание высоты треугольника на его стороне или на ее продолжении (острый угол или тупой);
Возможны два треугольника с заданным синусом угла (угол тупой или острый);
Не указано, расположены центры двух пересекающихся окружностей - по одну сторону от общей хорды, или же по разные;
10)Не указано, проведена внешняя или внутренняя общая касательная.
Сложности могут возникнуть: при обнаружении всех случаев расположения фигур или всех возможных конфигураций фигуры, а также при составлении и решении уравнений. При изменении уравнения в соответствии с новой конфигурацией. Необходимо помнить, что в решении должны быть использованы все условия и рассмотрены все случаи. Нужно убедится, что среди них нет случаев, не удовлетворяющих условию задачи, и других решений не существует.
Задача. Вычислите площадь треугольника, если две его стороны равны 25 и 17, а высота, проведенная к третьей стороне, равна 15.
Комментарий. Неоднозначность формулировки состоит в том, что в условии не указано, лежит или нет основание высоты, проведенной к третьей стороне, на ней. Возможно два варианта чертежа. Ответ: 210 или 90.
Задача. Площадь трапеции ABCD равна 90, а одно из оснований трапеции вдвое больше другого. Диагонали пересекаются в точке O; отрезки, соединяющие середину P основания AD с вершинами B и C, пересекаются с диагоналями трапеции в точках M и N соответственно. Найти площадь четырехугольника OMPN.
Решение. Возможны два случая, удовлетворяющие условию задачи и получающиеся в результате обозначения вершин. Пусть BC = a — верхнее основание трапеции, тогда нижнее основание AD = 2BC = 2a (рис. 7.29) и h — высота трапеции. Площадь трапеции
SABCD=(a+2a)*h/2=3ah/2=90.
Отсюда ah = 60.
Так как четырехугольники ABCP и BCDP — параллелограммы, то точки M и N являются точками пересечения их диагоналей. Тогда BN и CM — медианы треугольника BCP. Следовательно, SOMPN=1/3SBCP=1/3*1/2ah=1/6*60=10
2. Пусть AD = a — верхнее основание, тогда BC = 2AD = 2a (рис. 7.30).
Так как треугольники COB и AOD подобны с коэффициентом подобия, равным 2, то высота треугольника AOD составляет 1/3 высоты трапеции ABCD и SAOD=1/2*a*1/3*h= 10.
Соответственно, треугольники CMB и PAM подобны с коэффициентом подобия, равным 4. Тогда SPAM=1/2*1/2*a*1/5*h=1/20*ah=3.
Аналогично получаем, что SDNP = 3. Тогда SOMPN = SAOD– SPAM – SPAM = 10 – 3 – 3 = 4.
Ответ: 10 или 4.
Заключение
Рассмотрены лишь некоторые подходы к обучению учащихся решению нестандартных задач. От того, насколько удастся создать для каждого обучающегося на уроках математики и во внеурочное время условия, соответствующие его умственным возможностям, будет зависеть не только его успеваемость, но и развитие личности в целом. Как показала практика, нестандартные задачи весьма полезны не только для уроков, но и для внеклассных занятий, для олимпиадных заданий, так как при этом открывается возможность по-настоящему дифференцировать результаты каждого участника. Такие задачи могут с успехом использоваться и в качестве индивидуальных заданий для тех учеников, которые легко и быстро справляются с основной частью самостоятельной работы на уроке, или для желающих в качестве дополнительных заданий. В результате учащиеся получают интеллектуальное развитие и подготовку к активной практической деятельности.
Список литературы
Абдрашитов Б.М., ,Абдрашитов Т.М., Шлихунов В.Н., Учитесь мыслить нестандартно //Москва// Просвещение// 1996г
Антипов И.Н., и др. Избранные вопросы математики. 9 кл. Факультативный курс .- //М.// Просвещение, 1979г
Балаян Э.Н. 1001 олимпиадная и занимательная задачи по математике // Ростов на Дону //Феникс, 2008г.
Винокурова Н.К. Развитие творческих способностей учащихся // М.: Образовательный центр «Педагогический поиск», -1999г.
Воронцова Л.Я. Развитие логического мышления на уроках математики // Образование в современной школе. -//2007г
Гаврилова И. Логические задачи // Математика.// -2009г
Галкин Е.В. Нестандартные задачи по математике. // М., Просвещение, 1996г
Голубев В.И. Решение сложных и нестандартных задач по математике. //М. //2007г
Иванов О.А. 100 олимпиадных задач по математике//С-Пб// Гос университет// 1994
Игнатьев Е. И. Математическая смекалка. – М.: Омега, 1994
Левитас Г.Г. Нестандартные задачи по математике в 7-11 классах. // М. ИЛЕКСА, 2012г.
Лоповок Л.М. 1000 проблемных задач для старшеклассников // М//, Просвещение, 1995г
Кашуба Р. Как решать задачу, когда не знаешь, как: пособие для учащихся общеобразовательных учреждений //.М// Просвещение, 2012г. (Решаем нестандартные задачи).
Фарков А.В. Математические олимпиады: метод. Пособие/А.В. М.: Гуманитар.изд. Центр. ВЛАДОС, 2004. (Библиотека учителя математики)
Список электронно-образовательных ресурсов
http://www.comp-science.narod.ru –олимпиадные задачиX
http://www.zaba.ru – математические олимпиады X
http://www.imo-official.org – международные математические олимпиадыX
http://www.problems.ru для учителей и учеников для подготовки к олимпиадам.X
Материально – техническая база
Мультимедийный проектор;
Компьютер;
Экран для демонстрации слайдов и презентаций;
15





















