Методические подходы к использованию различных способов решения арифметических задач в развитии логического мышления младших школьников
На практике часто наблюдается, что вопрос о решении арифметической задачи различными способами возникает только тогда, когда задание дано в учебнике: решите задачу различными способами. Однако, поскольку такие задания обычно сопровождают задачи, решения которых связаны со свойствами арифметических действий, то у обучающихся формируется некоторое представление о возможности решения задачи различными способами и связывают это только со свойствами арифметических действий. Кажется, что работа, связанная с решением задач различными способами по-разному не ограничивается и не должна ограничиваться этим. Кроме того, работа над задачей должна специальным образом организовываться, чтобы обучающимся было легко осознать возможность ее решения различными способами.
Конечно, некоторые обучающиеся могут самостоятельно предложить различные способы решения к задаче из-за их индивидуальных особенностей мышления, но большинство учеников должны выполнять целенаправленную работу в этом отношении, используя различные приемы обучения.
В школьном курсе по математике есть понятия, о которых еще рано говорить в начальной школе, но ученики все еще должны быть готовы к их сознательному восприятию. Одним из таких понятий является функция. Возможность разработки первой функциональной концепции уже появляется в обучении решению арифметических задач.
К тому времени, когда обучающиеся изучают основные арифметические действия и знакомятся с кратным сравнением чисел, математика представляет задачи с прямыми и обратными пропорциями величин, где необходимо установить связь и найти связь между данными и искомыми отношениями. Эти задачи традиционно решаются с помощью так называемого способа приведения к единице, суть которого заключается в том, чтобы сначала найти, например, цену, количество материала (на продукт) и т. д., а затем искомой в задаче величины.
Среди задач, связанных с пропорциональной зависимостью, есть задачи, в которых числовые данные находятся в некотором отношении, что предлагает другой способ решения, который интересен с точки зрения функциональной пропедевтики.
Решение задач прямой пропорциональности вторым способом будет продолжать работать в будущем, то есть формировать функциональные представления среди школьников только в том случае, если учитель выполняет
При работе над задачами, связанных с пропорциональной зависимостью величин, школьники должны ориентироваться на одно решение двумя способами, конечно, если возможно второе решение. При организации работы по нахождению второго способа решения задачи можно использовать следующие приемы: построить схему для представления взаимосвязи между величинами, изменить данные в условии задачи; опора на уже решенную задачу; анализ задачи, не решаемой путем приведением к единице.
Пример приемов на задачах.
Задача 1. За 12 пачек молока надо заплатить 84 р. Сколько денег надо заплатить за 6 таких же пачек молока?
Очевидно, что решение этой задачи будет наиболее рациональным, если воспользоваться тем, что 6 пачек молока в 2 раза меньше, чем 12 пачек. Здесь удобно показать эту зависимость на схеме (Рис. 1.). Для этого учитель может построить отрезок, обозначающий 12 пачек молока, а отрезок, обозначающий 6 пачек молока, он может предложить начертить обучающимся. При построении второго отрезка школьники заметят, что он должен быть в 2 раза меньше первого.
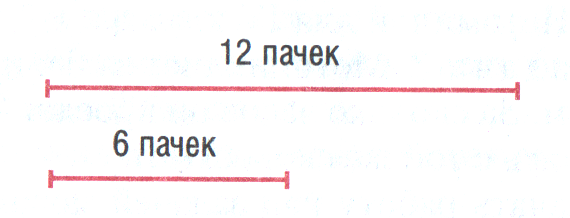
Рис. 1. Графическая схема к задаче 1
После проделанной работы ученикам не составит труда прийти к выводу, что если количество пачек молока в 2 раза меньше, то и стоить они будут в 2 раза меньше. Опираясь на построенную схему, решение задачи можно записать в одно действие: 84 : 2 = 42 (р.).
Работа по формированию функциональных представлений у обучающихся продолжается в 4 классе. Здесь появляются задачи на движение и производительность, которые дают обширный материал для функциональной пропедевтики. Пример:
Задача 2. Мотоциклист за 6 ч проехал 480 км. За сколько часов он проедет 240 км, двигаясь с той же скоростью?
Начать работу над задачей можно с записи условия в таблице.
Таблица 1
Условие задачи 2
| Скорость | Время | Расстояние |
| одинаковая | 6 ч | 480 км |
| одинаковая | ? | 240 км |
Найдутся ученики, которые предложат решить задачу уже известным им способом, так называемым приведением к единице, т.е. сначала найти скорость мотоциклиста, а потом решить обратную задачу, т.е. найти, за сколько часов он проехал 240 км.
Решение запишется следующим образом:
1) 480 : 6 = 80 (км) – проехал мотоциклист за 1 ч;
2) 240 : 80 = 3 (ч) – за столько часов мотоциклист проедет 240 км.
Полученный результат можно внести в таблицу и продолжить работу над задачей.
Таблица 2
Полученный результат к задаче 2
| Скорость | Время | Расстояние |
| одинаковая | 6 ч | 480 км |
| одинаковая | 3 ч | 240 км |
Анализируя числовые данные, четвероклассники самостоятельно смогут прийти к выводу: во сколько раз меньшее расстояние пройдено мотоциклистом, во столько раз меньше времени ему потребуется, чтобы его преодолеть, т.е. между этими величинами существует прямо пропорциональная зависимость.
Возможность решения задачи на прямо пропорциональную зависимость различными способами (способом приведения к единице и способом отношений) возникла в связи с подбором числовых данных. Чтобы обучающиеся осознали это, используется прием сравнения.
Данный прием целесообразно использовать и при решении задач, которые связаны со свойствами арифметических действий. Например, прежде чем приступить к решению задачи 1: «У Лены было 6 тетрадей в клетку и 4 тетради в линейку. 2 тетради она отдала сестре. Сколько тетрадей осталось у Лены?», можно рассмотреть такую задачу: «У Лены было 6 тетрадей в клетку и 4 тетради в линейку. 2 тетради в линейку она отдала сестре. Сколько тетрадей осталось у Лены?». Постановка вопросов в определенной логической последовательности при разборе задачи оказывает немалое влияние на выбор способа решения задачи. Так, если задается вопрос: какие тетради отдала Лены сестре? И ученик отвечает: «В линейку», то ход рассуждений приведет ученика к следующему решению: 6 + (4 – 2) = 8 (т.). Если при разборе задачи используется краткая запись:
Было – 6 т. и 4 т.
Отдала – 2 т.
Осталось - ?
То анализ данной краткой записи приведет ученика к решению: (6 + 4)–2 = 8 (т.)
Анализ ситуации задачи исключает возможность ее решения еще одним способом, так как Лена отдала сестре тетради в линейку, поэтому способ решения: (6 – 2) + 4 = 8 (т.) не соответствует ситуации, данной в задаче. Сравнение этой задачи с задачей 1, которую можно решить тремя способами, поможет ученику не только сознать возможность решения одной и другой задачи различными способами, но и будет способствовать формированию у него умения внимательно вчитываться в текст задачи и анализировать ситуацию, которая в ней рассматривается.
Осознание реальной ситуации, данной в задаче, и использование ее для поиска различных способов решения задачи имеет большое практическое значение. Примеры на различных задачах:
Задача 3: «Из лагеря учащиеся возвращались в двух автобусах, в одном было 38 учащихся, столько же в другом, всего возвращалось 43 мальчика. Сколько девочек возвращалось из лагеря?»
При работе с данной задачей учитель обращает внимание на слово «столько же» и выясняет, сколько учащихся ехало во втором автобусе. После этого большинство учащихся легко справляются с решением задачи, предлагая такой способ решения: (38 + 38) – 43 = 33 (д.). Вопроса о возможности решения этой задачи другим способом обычно не возникает ни у ученика, ни у учителя. Но достаточно при анализе задачи задать вопрос «Могут ли все 43 мальчика поместиться в одном автобусе?» (Нет, в одном автобусе могут поместиться только 38 мальчиков, остальные поедут в другом автобусе.), как сразу же возникают предложения о другом способе решения задачи: 1) 43 – 38 = 5 (м.), 2) 38 – 5 = 33 (д.). Решение данной задачи двумя способами интересно в том плане, что при записи решения этой задачи выражением: (38 + 38) – 43 = 33 (д.), его значение можно найти только одним способом. К другому способу приводит только анализ той ситуации, которая дана в задаче. На это целесообразно обратить внимание учащихся.
В зависимости от целей урока и подготовленности учащихся можно использовать и другие приемы обучения решению арифметических задач различными способами, например, использовать такой прием, как продолжение начатого решения. Используя групповую форму работы, дается задание закончить решение и написать пояснение к каждому действию.
Задача 4:
1-й способ 2-й способ 3-й способ
1) 60 · 4 = 240 (км) 1) 180 : 60 = 3 (ч) 1) 180 : 60 = 3 (ч)
2) 180 + 240 = 2) 3 + 4 = 7 (ч) 2) …
3) … 3) … 3) 7 + 3 = 10 (ч)
4) … 4) …
Можно использовать также прием отыскивания решения задачи по предложенному плану. Например: 1) найти время движения на первом участке пути; 2) найти время, которое потребуется для прохождения второго участка пути; 3) найти время, которое потребуется на весь путь; 4) найти расстояние между городами.
Большое значение для осознания возможности решения задач различными способами имеет и такой прием, как наглядная интерпретация задачи.
Задача 5: «Длина огорода прямоугольной формы 72 м, ширина в 2 раза меньше. ¾ площади занято овощами, остальная площадь картофелем. Сколько квадратных метров занято картофелем?»
Решая данную задачу без схематического чертежа, обучающиеся обычно предлагают 1-й способ решения:
1) 72 : 2 = 36 (м) – ширина огорода.
2) 72 · 36 = 2592 (кв.м) – площадь огорода.
3) 2592 : 4 · 3 = 1944 (кв.м) – занято овощами.
4) 2592 – 1944 = 648 (кв.м) – занято картофелем.
Использование же схематического чертежа помогает найти и другие способы решения.
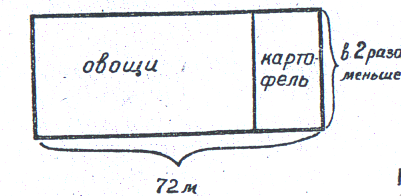
Рис. 2. Графическая схема к задаче 5
На чертеже хорошо видно, что площадь, занятая картофелем, занимает ¼ всего огорода (обучающиеся могут даже не записывать действие, так как это хорошо видно на рисунке). Проведение же устных рассуждений им вполне доступно и является хорошим упражнением для усвоения понятий доли и дроби.
Проведенные рассуждения позволяют решить задачу другими способами:
2-й способ
1) 72 : 2 = 36 (м) – ширина огорода
2) 72 · 36 = 2592 (кв.м) – площадь огорода.
3) 2592 : 4 = 648 (кв.м) – площадь, занятая картофелем.
3-й способ
1) 72 : 4 = 18 (м) – длина участка, занятая картофелем.
2) 72 : 2 = 36 (м) – ширина участка, занятая картофелем.
3) 18 · 36 = 648 (кв.м) – площадь, занятая картофелем.
4-й способ
1) 72 : 4 · 3 = 54 (м) – длина участка, занятая овощами.
2) 72 – 54 = 18 (м) – длина участка, занятая картофелем.
3) 72 : 2 = 36 (м) – ширина участка, занятая картофелем.
4) 18 · 36 = 648 (кв.м) – площадь, занятая картофелем.
Работа над осознанием возможности различных подходов к решению задач и выбор наиболее рационального из них имеет большое значение для развития логического мышления учащихся и формирования у них умения решать задачи различными способами.


















