
Областное государственное бюджетное
профессиональное образовательное учреждение
«Томский политехнический техникум»
Методические рекомендации
для самостоятельной работы студентов
по теме «Определение реакций связи»
по учебной дисциплине
«Техническая механика»
Автор:
Шабалин Вадим Сергеевич
Томск
2022
| Р ассмотрено на заседании ЦМК ассмотрено на заседании ЦМК Общепрофессиональных дисциплин Протокол № ______ «_____» ________ 20___ г. Председатель ЦМК _______________О.П. Седюкевич | Одобрено и рекомендовано к использованию методическим советом техникума «_____»_______________20___г. Зам. директора по УМР ______________Н.А.Калугина |
Шабалин, В.С. Методические рекомендации для самостоятельной работы студентов по теме «Определение реакций связи» по учебной дисциплине «Техническая механика» / В.С. Шабалин. – Томск: ТПТ, 2022. – 12 с.
Рецензент: Головнева А.В., преподаватель высшей квалификационной категории, ОГБПОУ «Томский коммунально-строительный техникум».
Рецензент: Метелькова Е.А., старший методист высшей квалификационной категории, ОГБПОУ «Томский политехнический техникум».
Аннотация: Методические рекомендации предназначены для актуализации ранее полученных знаний из базового курса геометрии: некоторых понятий, свойств объектов, теорем геометрических фигур для студентов как очной так и заочной формы обучения.
Содержание
Пояснительная записка 4
Справочный материал для решения задач 5
Определение реакций связи плоской системы сходящихся сил 7
Определение реакций связи заделки консольная балка 11
Список источников информации 13
Пояснительная записка
Методические рекомендации предназначены для студентов следующих специальностей:
- 13.02.07 Электроснабжение (по отраслям);
- 13.02.08 Электроизоляционная, кабельная и конденсаторная техника»;
- 13.02.11 Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям);
- 15.02.12 Монтаж, техническое обслуживание и ремонт промышленного оборудования (по отраслям)
- 21.02.01 Разработка и эксплуатация нефтяных и газовых месторождений;
- 21.02.02 Бурение нефтяных и газовых скважин.
Практические занятия выполняются студентами в процессе теоретического обучения после изучения соответствующих тем программы с целью практического закрепления знаний.
Рабочей программой по учебной дисциплине Техническая механика предусмотрено проведение практических занятий для закрепления теоретических знаний, обучения студентов решению практических задач и развития навыков самостоятельной работы.
Методические рекомендации для самостоятельно работы студентов разработаны в соответствии с рабочей программой Техническая механика как для очной так и заочной формы обучения.
Методическое пособие предназначено для проведения практических занятий по программе Техническая механика, а также самостоятельного решения задач. Здесь рассматривается ряд вопросов, содержащихся в Федеральном государственном образовательном стандарте по этому курсу.
Цель методических рекомендаций – оказание помощи в подготовке студентов к занятиям, для самостоятельного решения задач и освоения данных тем по программе Техническая механика являющихся обязательным компонентом сопровождения образовательных программ.
Учебно-методические материалы содержат требования к решению практических задач на данную тему.
В данных методических рекомендациях содержится справочный материал о нахождении проекции векторов на ось, об определении углов у простейших геометрических фигур, определения знака скалярной величины проекции вектора, нахождения значения тригонометрической функции в прямоугольном треугольнике.
Справочный материал для решения задач
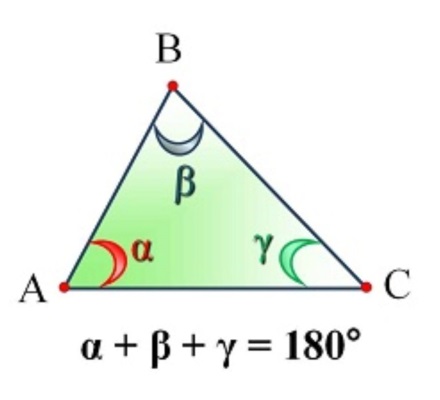
Рисунок 1 – Теорема о сумме углов треугольника
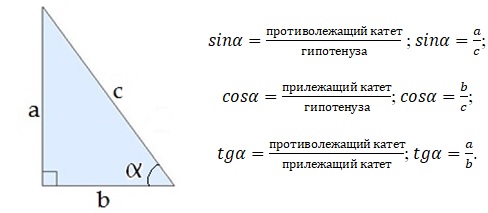
Рисунок 2 – Формулы нахождения значения тригонометрических функций в прямоугольном треугольнике

Рисунок 3 – Определение проекции векторов на ось
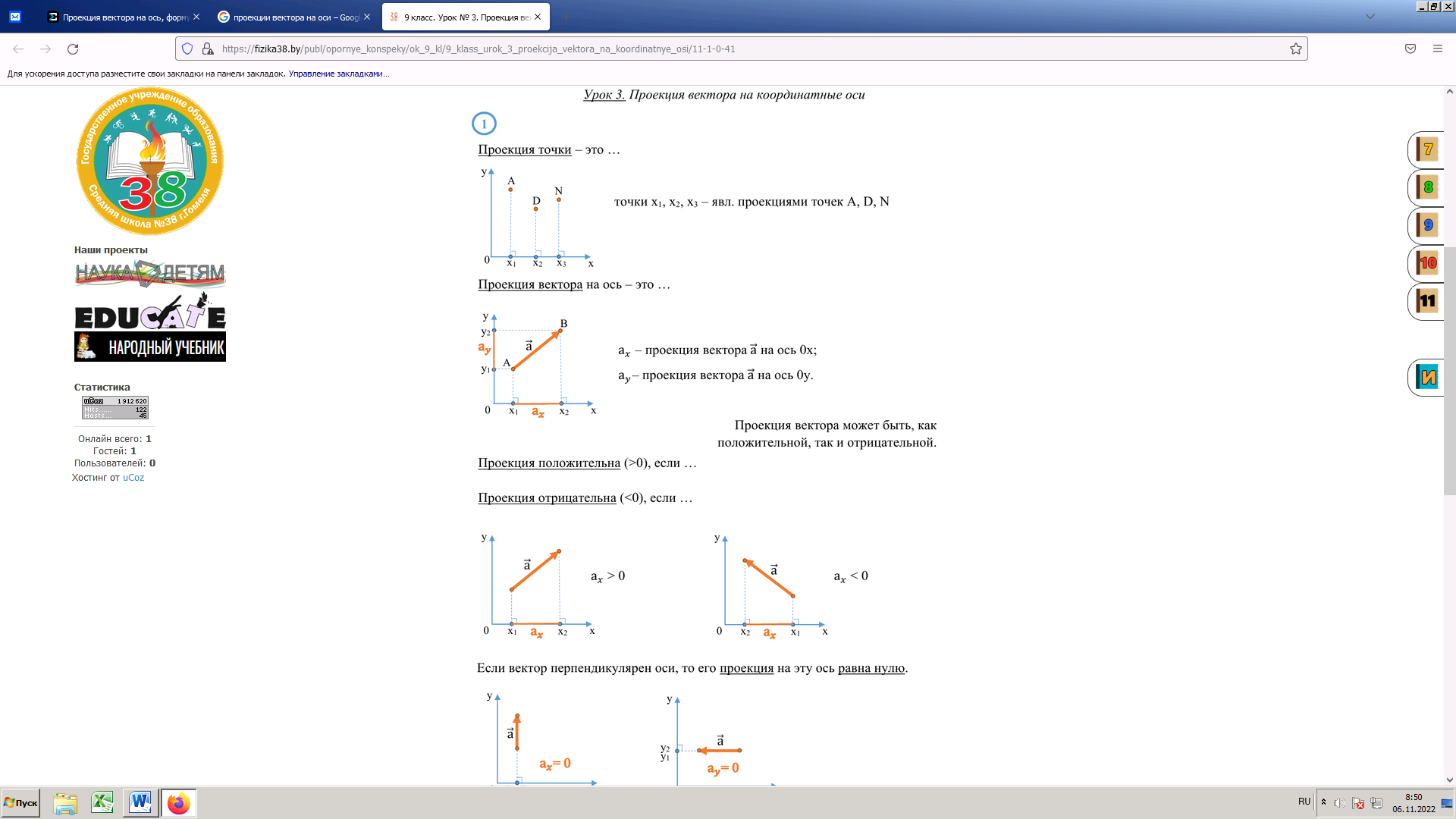
Рисунок 4 – Определения знака проекции вектора
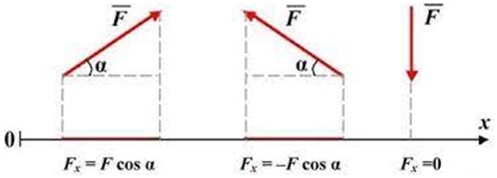
Рисунок 5 – Формулы для определения величины проекции вектора
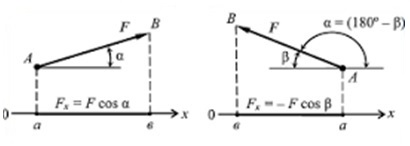
Рисунок 6 – Определение угла при проекции вектора на ось
Определение реакций связи плоской системы сходящихся сил
Теоретический материал
Связь – это тело, препятствующее перемещению другого тела под действием силы.
Реакция связи – сила, возникающая внутри самой связи. Реакция всегда противоположна тому направлению, по которому связь препятствует движению тела. Все тела могут быть свободными и несвободными. Свободное тело не имеет связи. Любое несвободное тело можно представить свободным, если действующие на него связи заменить реакциями.
Виды связей:
а) Гладкая поверхность (рис. 7) или плоскость (рис. 8), то есть поверхность, не имеющая трения. Реакция этой связи всегда направлена перпендикулярно точке соприкосновения. NA – реакция связи.
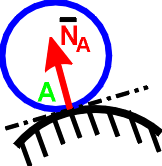
Рисунок 7 – Гладкая поверхность
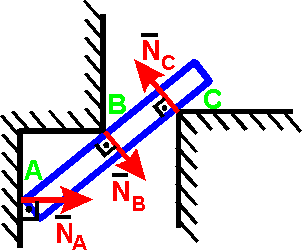
Рисунок 8 – Пример другой гладкой поверхности
б) Гибкая нить (провода, канаты, цепи, ремни). Реакция Т направлена вдоль нити к точке подвеса (рис. 9).
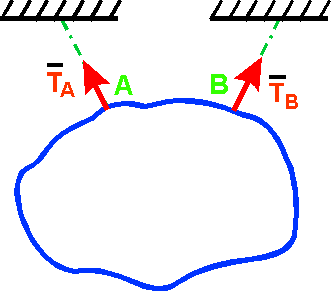
Рисунок 9 – Расчетная схема гибкой нити
в) Невесомый стержень с шарнирами
Реакция N невесомого стержня направлена вдоль стержня. Обычно реакция N изображается от тела по стержню, в предположении, что в равновесии стержень растянут (рис.10).
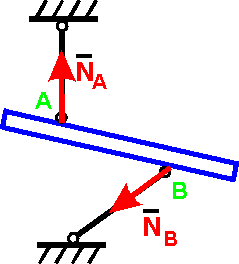
Рисунок 10 – Расчетная схема невесомого стержня
.
г) Неподвижный цилиндрический шарнир или подшипник
Реакция RA цилиндрического шарнира может иметь любое направление в плоскости, перпендикулярной оси вращения, т. е. в плоскости Аху.
Обычно ее раскладывают на две составляющие ХА и YA по двум взаимноперпендикулярным направлениям (рис. 11).
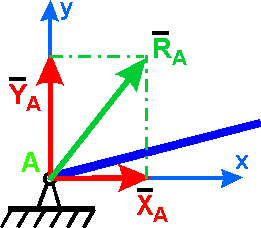
Рисунок 11 – Расчетная схема неподвижного цилиндрического шарнира или подшипника
д) Шарнирно-подвижная опора (опора на катках)
Реакция R проходит через ось шарнира и направлена перпендикулярно к опорной плоскости (рис. 12)
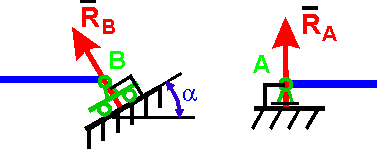
Рисунок 12 – Расчетная схема шарнирно-подвижной опоры (опоры на катках)
е) Жесткая заделка
Нахождение реакции жесткой заделки сводится к определению составляющих ХА и YA препятствующих линейному перемещению балки в плоскости действия сил, и алгебраической величине момента mA, препятствующего вращению балки под действием приложенных к ней сил (рис. 13).
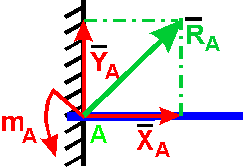
Рисунок 13 – Расчетная схема жесткой заделки
Методика решения задач плоской системы сходящихся сил:
Число неизвестных в данных задачах не превышает двух.
Рассматриваем точку, находящуюся в равновесии.
Определяем наличие активных сил.
Освобождаемся от связей и заменяем их реакциями.
Выбираем оси координат и располагаем в этих осях имеющиеся активные и реактивные силы.
Решаем уравнения равновесия относительно неизвестных.
Выполняем проверку.
Пример. Груз, силой тяжести F1=10Н удерживается в равновесии с помощью связей –гладких поверхностей (рис. 14). Определить реакции связи аналитически и графически.
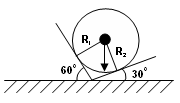
Рисунок 14 – Расчетная схема определения груза лежащего на гладкой поверхности
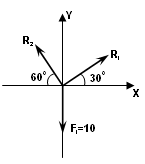
Рисунок 15 – Иллюстрация задачи
Решение.
I. Аналитическое решение
Освобождаемся от связей, заменяя их реакциями. Получаем систему трех сходящихся в точке О сил.
Составляем систему уравнений, сумму проекций всех сил на ось х и y и решаем уравнения.
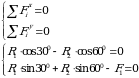
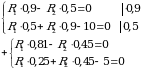
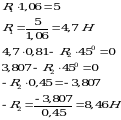
Проверка: 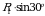 +
+ 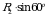
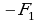 = 4,7 · 0,5 + 8,46 · 0,9 – 10 = 0
= 4,7 · 0,5 + 8,46 · 0,9 – 10 = 0
Ответ: R1=4,7 H; R2=8,46 H
II. Графическое решение.
Выбираем масштаб 1:20 и из точки О откладываем вектор силы тяжести F1.
Полученная система сил находится в равновесии, поэтому силовой многоугольник должен быть замкнут, R1+R2+F1=0. Поэтому, из конца и начала вектора F проводим прямые параллельные векторам R1 и R2 до их пересечения (рис. 16).
Определяем реакции связей R1 и R2 , умножая полученные в результате графического построения отрезки на масштаб.
Проверка: Заключается в сравнении значений векторов R1 и R2, найденных аналитическим и графическим способами. l = (R1а - R1б)/ R1а; l = (R2а - R2б)/ R2а.
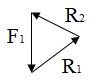
Рисунок 16 – Иллюстрация графического решения
Определение реакций связи заделки консольная балка
Теоретический материал
| 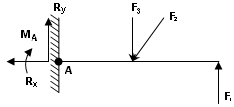
| F1, F2, F3 – активные силы МА – реактивный момент RX – горизонтальная составляющая реакции RY – вертикальная составляющая реакции
|
Рисунок 13 - Консольная балка с жестким защемлением
Пример. Для консольной балки (рис.2), нагруженной равномерно распределенной нагрузкой интенсивностью q, силой F , определить реакции заделки консольной балки.
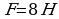
Рисунок 2.
Рисунок 14 - Консольная балка нагруженная равномерно распределенной нагрузкой
Решение
1. Освобождаемся от связей и заменяем их реакциями
2. Выбираем оси координат и определяем точки вращения
3. Составляем уравнения моментов равновесия всех сил относительно жесткой заделки (точка А). При составлении уравнения моментов равновесия всех сил необходимо помнить, что согласно определению момент считается положительным.
Так как у реакций Ry и Rx плечо будет равно 0, то и реакция будет равна 0.
Q=4·2=8 H
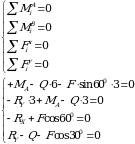
Из 1-го уравнения находим МА
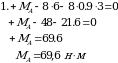
Из 2 –го уравнения находим RY
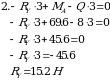
Из 3-го уравнения находим RX
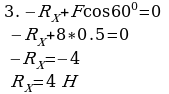
Все неизвестные найдены, делаем проверку
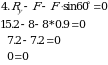 - проверочное уравнение
- проверочное уравнение
Список источников информации
1. Бабичева И.В. Техническая механика [Электронный ресурс] : учеб. пособие / И. В. Бабичева. – М. : Русайнс, 2021. – 101 с. – (Среднее профессиональное образование). – Режим доступа : https://book.ru/book/937045
2. Сербин, Е.П., Техническая механика : учебник / Е.П. Сербин. — Москва : КноРус, 2020. — 399 с. — ISBN 978-5-406-01476-9. — URL:https://book.ru/book/936144 (дата обращения: 25.10.2022). — Текст : электронный.
3. Опарин И. С. Основы технической механики : учебник / И.С. Опарин. - 2-е изд., испр. - Москва : Академия, 2012. - 142 с. : ил., цв. ил. ; 22 см. - (Начальное профессиональное образование . Общетехнические дисциплины). - (Соответствует ФГОС). - Библиогр.: с.141.

2







 ассмотрено на заседании ЦМК
ассмотрено на заседании ЦМК










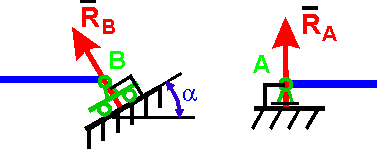



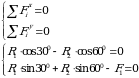
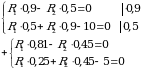
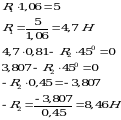
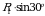 +
+ 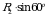
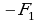 = 4,7 · 0,5 + 8,46 · 0,9 – 10 = 0
= 4,7 · 0,5 + 8,46 · 0,9 – 10 = 0

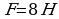
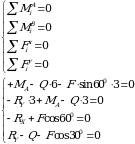
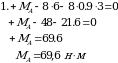
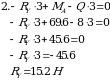
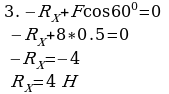
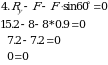 - проверочное уравнение
- проверочное уравнение










