комитет образования и науки Волгоградской области
государственное бюджетное профессиональное образовательное учреждение
«Волжский политехнический техникум»
Методические рекомендации
практического занятия
по учебной дисциплине
Математика
на тему: «Матрицы. Действия над матрицами. Определители матриц»
Курс: 1
Отделение: заочное
Специальность: 23.02.03 Техническое обслуживание и ремонт автомобильного транспорта
Автор: Берсенева Ирина Николаевна, преподаватель первой квалификационной категории
2018
Пояснительная записка.
Методические рекомендации к практическому занятию по учебной дисциплине Математика на тему «Матрицы. Действия над матрицами. Определители матриц» предназначено для студентов 1 курса заочного отделения специальности 23.02.03 Техническое обслуживание и ремонт автомобильного транспорта. Позволяют студентам осуществить самостоятельный контроль по изученной теме, а преподавателю облегчить работу при проверке.
Выполнение практического занятия направлено на обобщение, систематизацию, углубление теоретических знаний учебной дисциплины; формирование умений применять полученные знания в практической деятельности; на развитие аналитических, проектировочных, конструктивных умений; выработку самостоятельности, ответственности и творческой инициативы.
Содержит в себе краткие теоретические основы по данной теме, разбор некоторых примеров, 10 вариантов для самостоятельной работы студентов (Таблица 1, 2, 3).
Для выполнения работы, студент обязан знать:
- определение матрицы;
- основные понятия матрицы;
- действия над матрицами;
- понятие определителя;
- правила нахождения определителей второго и третьего порядка;
Уметь:
- применять полученные знания на сложение, вычитание и произведение матриц;
- верно производить арифметические расчеты;
- применять правила нахождения определителей при выполнении заданий.
Варианты заданий представлены в таблице, где номер варианта соответствует порядковому номеру студента по журналу. При верном выполнении:
6 заданий – 5 (отлично);
5 заданий – 4 (хорошо);
4,3 задания – 3 (удовлетворительно);
менее трех заданий – 2 (неудовлетворительно);
Теоретический материал.
Матрицей называется прямоугольная таблица чисел. А= 
А- матрица,  - элемент матрицы, m- номер строки, n- номер столбца, в которой расположен данный элемент. Числа m,n называют размерностями матрицы.
- элемент матрицы, m- номер строки, n- номер столбца, в которой расположен данный элемент. Числа m,n называют размерностями матрицы.
Матрица называется квадратной, если m=n. Число n называют порядком квадратной матрицы.
Матрицы одинаковой размерности называются равными, если у них соответственно равны элементы, стоящие на одинаковых местах.
Матрица называется нулевой, если все ее элементы равны нулю.
Квадратная матрица называется единичной, если элементы, стоящие на ее главной диагонали, равны 1, а остальные равны нулю.
Суммой (разностью) матриц А и В одинаковой размерности m×n называется матрица С той же размерности, каждый элемент которой равен сумме (разности) элементов матрицы А и В, стоящих на тех же местах.
Пример: А= , В=
, В= . Найти А+В, А-В.
. Найти А+В, А-В.
Решение: А+В=
А-В=
Произведением матрицы на число называется матрица той же размерности что и искомая, все элементы которой равны элементам исходной матрицы, умноженными на данное число.
Пример: А= . Найти 5*А
. Найти 5*А
Решение 5А=
Произведением матрицы  , имеющей m строк и k столбцов, на матрицу
, имеющей m строк и k столбцов, на матрицу  , имеющую k строк и n столбцов, называется матрица
, имеющую k строк и n столбцов, называется матрица  , имеющая k строк и n столбцов, у которой элемент
, имеющая k строк и n столбцов, у которой элемент  равен сумме произведений элементов i-ой строки матрицы А и j-го столбца матрицы В.
равен сумме произведений элементов i-ой строки матрицы А и j-го столбца матрицы В.
Пример:

Квадратной матрице А порядка n можно сопоставить число, называемое определителем, следующим образом:
n=1, А= ;
; 
n=2, A=
n=3, A=
При вычислении определителя третьего порядка удобно пользоваться правилом треугольников (или правилом Саррюса), которое символически можно записать так:
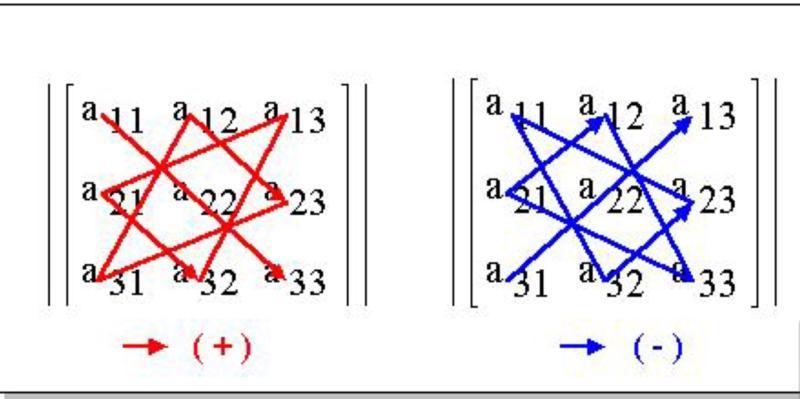
Свойства определителей.
Определитель не изменится, если его строки заменить столбцами, и наоборот.
При перестановке двух параллельных рядов определитель меняет знак.
Определитель, имеющий два одинаковых ряда, равен нулю.
Общий множитель элементов какого – либо ряда определителя можно вынести за знак определителя.
Минором некоторого элемента  определителя n-го порядка называется определитель n-1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается
определителя n-го порядка называется определитель n-1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается  .
.
Так, если  , то
, то 
Алгебраическим дополнением элемента  определителя называется его минор, взятый со знаком «плюс», если сумма i+j- четное число, и со знаком «минус», если эта сумма нечетная. Обозначается
определителя называется его минор, взятый со знаком «плюс», если сумма i+j- четное число, и со знаком «минус», если эта сумма нечетная. Обозначается 
Пример: Вычислить определитель матрицы
 =3*
=3* +1*=
+1*=
3*(7*3*4+(-1)*0*2+5*7*1-(-1)*3*1-7*7*2-5*0*4)+(5*3*4+(-1)*7*2+5*7*8-(-1)*3*8-5*7*4-5*7*2)-(5*0*2+7*1*5+7*3*8-5*0*8-3*1*5-7*7*2)=122
Квадратная матрица А называется невырожденной, если определитель ее не равен нулю, в противном случае матрица называется вырожденной.
Матрица  называется обратной матрице А, если выполнено условие: А*
называется обратной матрице А, если выполнено условие: А* =
= *А=Е, Е – единичная матрица того же порядка, что и матрица А.
*А=Е, Е – единичная матрица того же порядка, что и матрица А.
Пример: Найти матрицу С
3С=
3С=
С=
Варианты заданий:
Найти значение матричного выражения:
| Вариант 1 | |
| Вариант 2 | Найти 3А-ВС |
| Вариант 3 | Найти АВ+3СD |
| Вариант 4 | Найти АВ-5С |
| Вариант 5 | Найти АВ+3С |
| Вариант 6 | Найти  |
| Вариант 7 | Найти АВ-5С |
| Вариант 8 | Найти АВ+2С |
| Вариант 9 | Найти А-3В² |
| Вариант 10 | Найти 4А-ВС |
Таблица 1
Вычислить определители
Таблица 2
Найти матрицу С:
| Вариант 1 | |
| Вариант 2 | |
| Вариант 3 | |
| Вариант 4 | |
| Вариант 5 | |
| Вариант 6 | |
| Вариант 7 | |
| Вариант 8 | |
| Вариант 9 | |
| Вариант 10 | |






 - элемент матрицы, m- номер строки, n- номер столбца, в которой расположен данный элемент. Числа m,n называют размерностями матрицы.
- элемент матрицы, m- номер строки, n- номер столбца, в которой расположен данный элемент. Числа m,n называют размерностями матрицы. , В=
, В= . Найти А+В, А-В.
. Найти А+В, А-В.

 . Найти 5*А
. Найти 5*А
 , имеющей m строк и k столбцов, на матрицу
, имеющей m строк и k столбцов, на матрицу  , имеющую k строк и n столбцов, называется матрица
, имеющую k строк и n столбцов, называется матрица  , имеющая k строк и n столбцов, у которой элемент
, имеющая k строк и n столбцов, у которой элемент  равен сумме произведений элементов i-ой строки матрицы А и j-го столбца матрицы В.
равен сумме произведений элементов i-ой строки матрицы А и j-го столбца матрицы В.
 ;
; 



 определителя n-го порядка называется определитель n-1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается
определителя n-го порядка называется определитель n-1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается  .
. , то
, то 

 =3*
=3*









