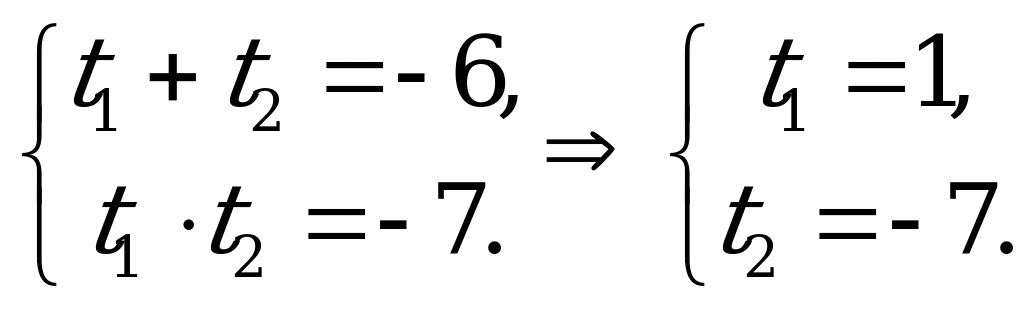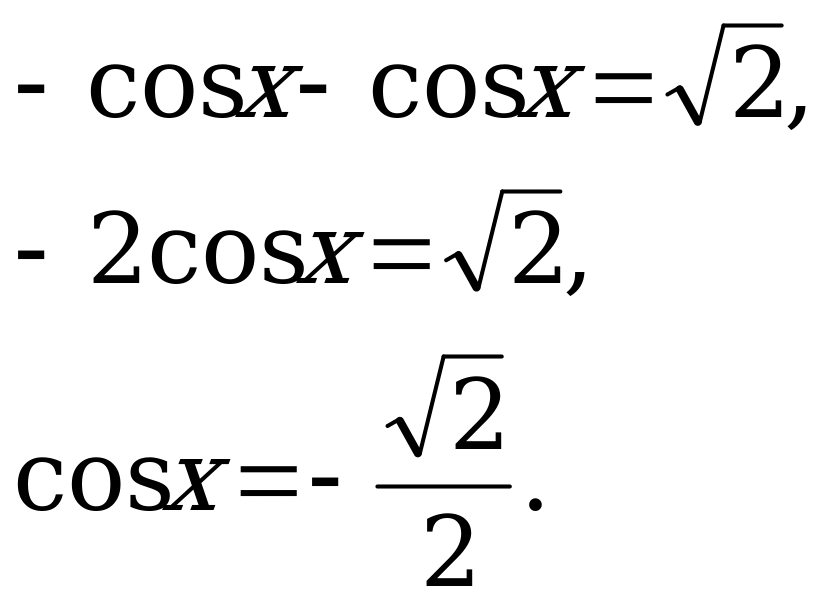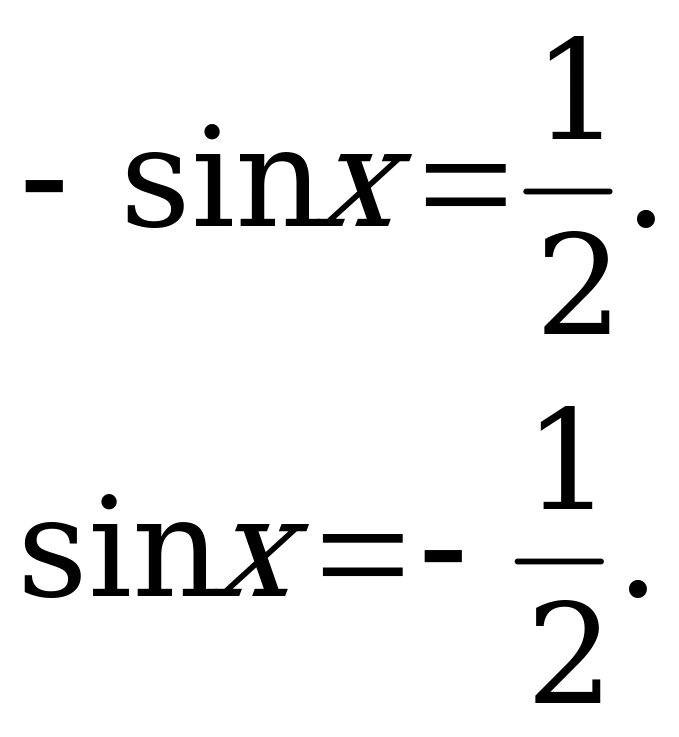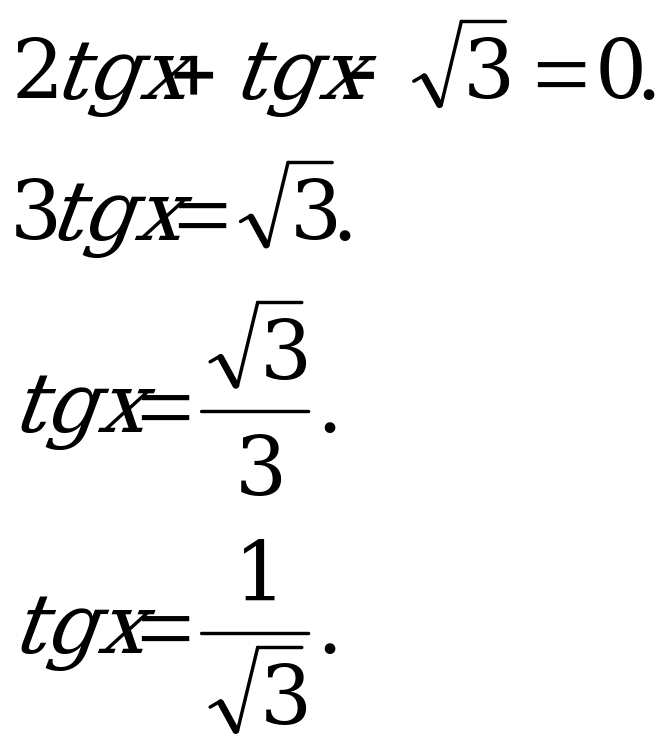ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«СТРОГАНОВСКИЙ КОЛЛЕДЖ»
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО УЧЕБНОЙ ДИСЦИПЛИНЕ
ОУД.04 МАТЕМАТИКА
общеобразовательного цикла
программы подготовки специалистов среднего звена
по специальности
35.02.07 Механизация сельского хозяйства
Раздел 6. «основы тригонометрии»
Очер, 2019
| ОДОБРЕНА Методической комиссией Математических и общих естественнонаучных дисциплин Председатель __________________ О.В. Зверева _______________________________ | УТВЕРЖДАЮ Заместитель директора ________ Т. Л. Кузьмина ______________________ |
Пояснительная записка
Данное пособие предназначено для студентов, испытывающих затруднения в изучении раздела 6. «Основы тригонометрии». Так же пособие может быть использовано студентами при подготовке к итоговой аттестации по учебной дисциплине ОУД.04 МАТЕМАТИКА.
В пособие представлены основные темы раздела «Основы тригонометрии», изучаемые в колледже.
Методическое пособие состоит из пяти параграфов:
тригонометрические функции числового аргумента;
тригонометрические функции и их графики;
обратные тригонометрические функции;
тригонометрические уравнения;
применение основных тригонометрических формул для решения уравнений.
Все параграфы содержат:
справочный материал;
упражнения с решениями;
задания для самостоятельной работы;
список рекомендуемой литературы.
§ 1 Тригонометрические функции числового аргумента.
1.1. Градусная и радианная меры угла.
Справочный материал.
Градус – единица измерения углов равная 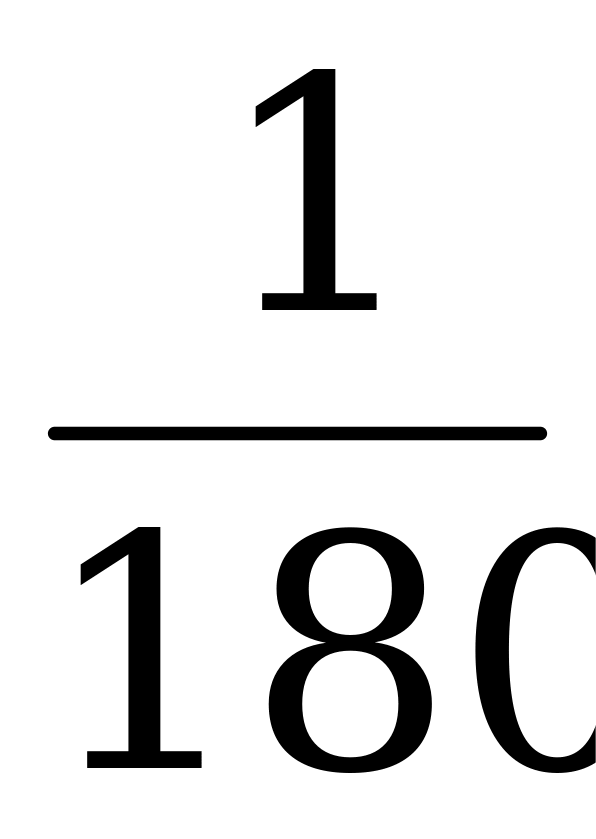 развернутого угла.
развернутого угла.
Радиан – единица измерения углов, равная величине центрального угла, которому соответствует длина дуги, равная длине радиуса окружности.
Единичная окружность – окружность с радиусом равным единице и центром в начале координат.
Р
 адианная и градусная меры связанны зависимостью 1800 = π радиан; угол в n0 равен
адианная и градусная меры связанны зависимостью 1800 = π радиан; угол в n0 равен 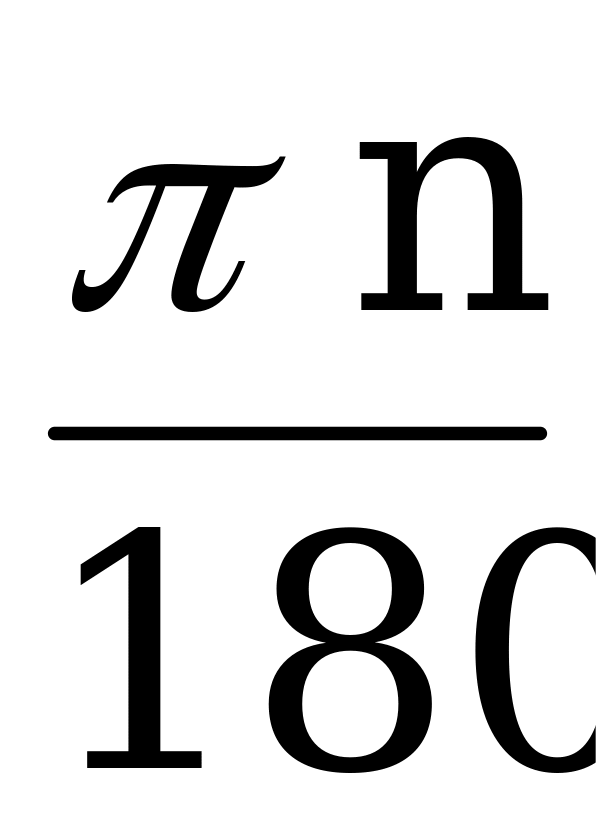 радиан.
радиан.
Упражнения с решениями.
Пример 1. Выразите в радианах величину угла  , если
, если 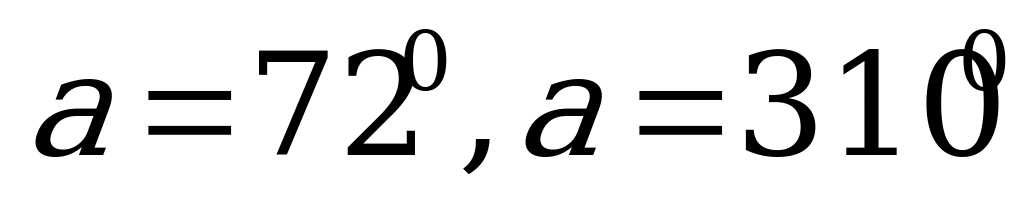 .
.
Решение. Так как n0 = 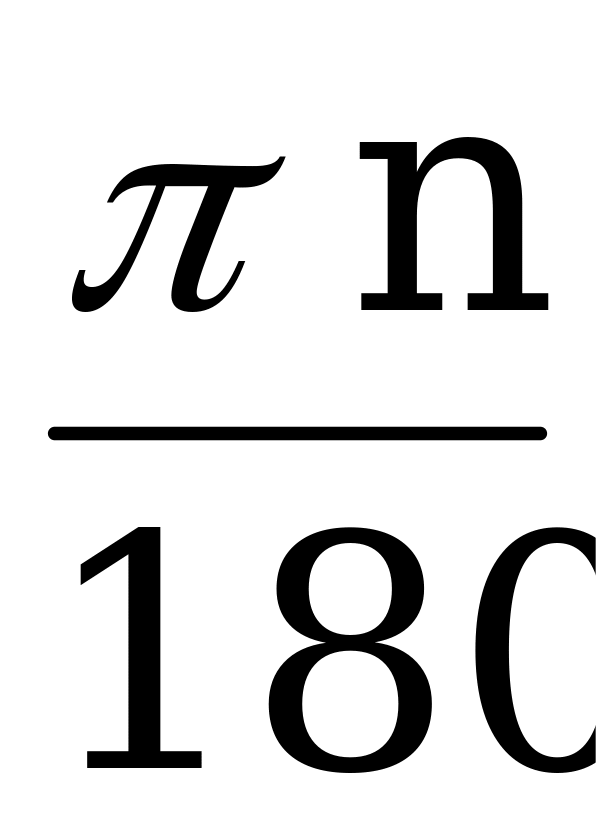 радиан, то
радиан, то
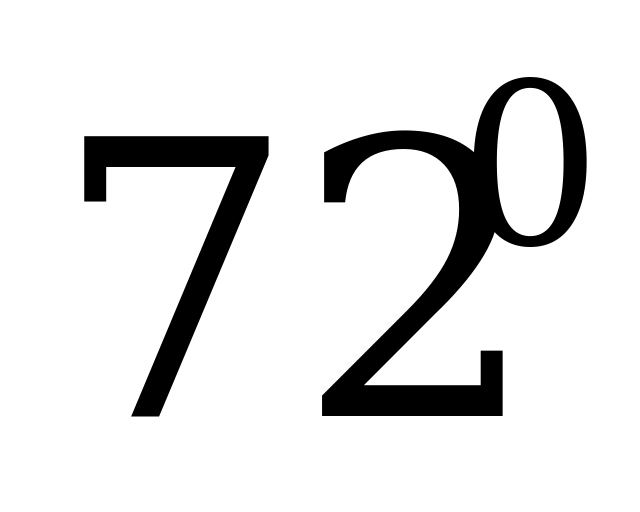 =
= 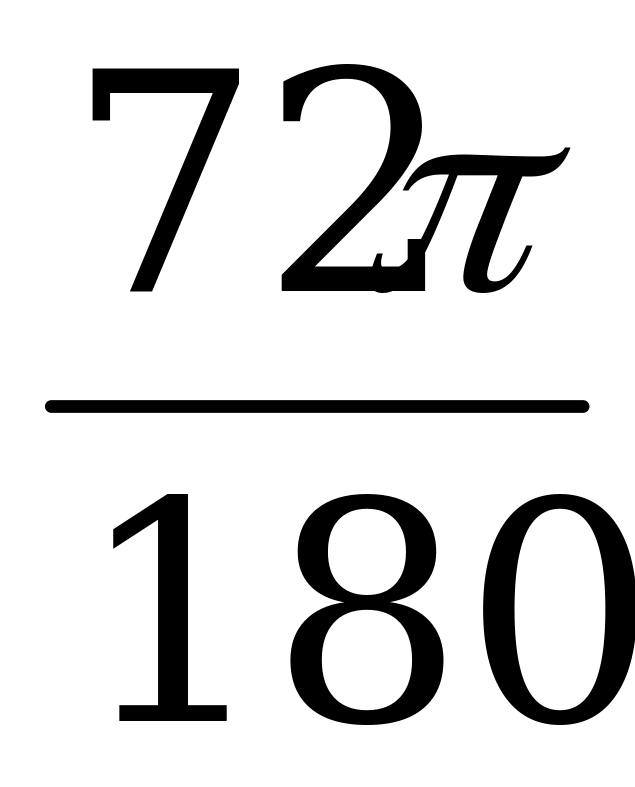 =
= 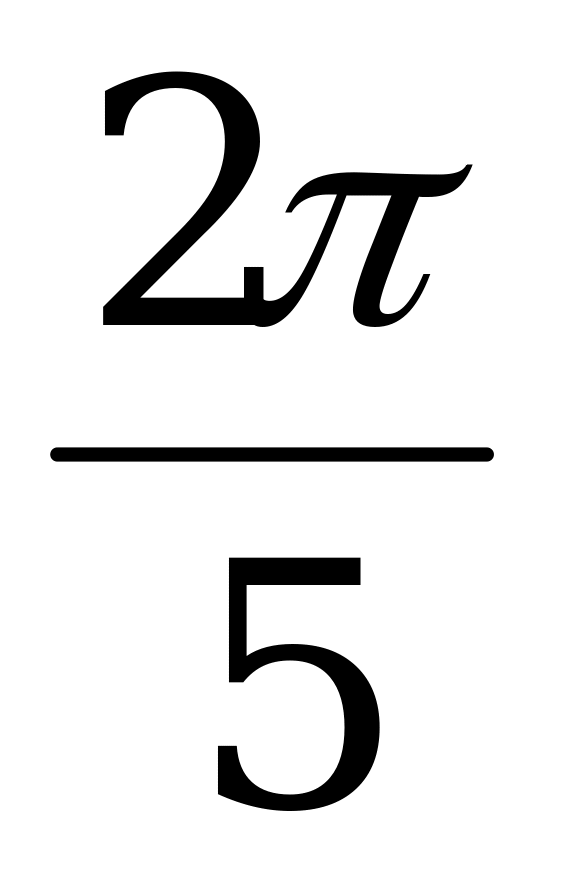 радиан,
радиан,
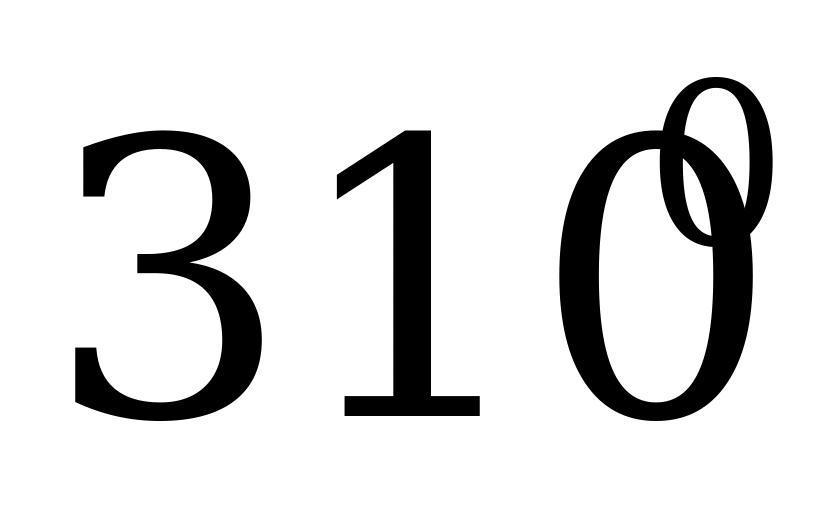 =
= 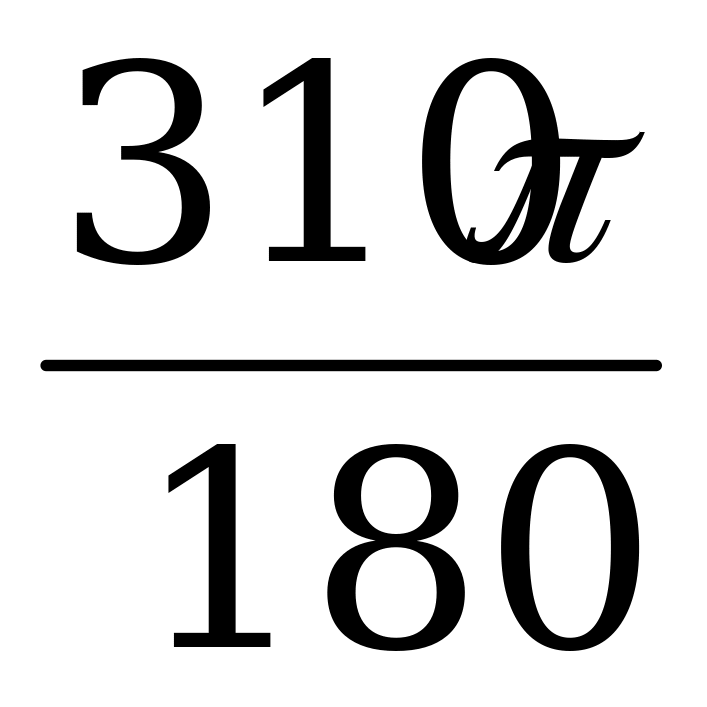 =
= 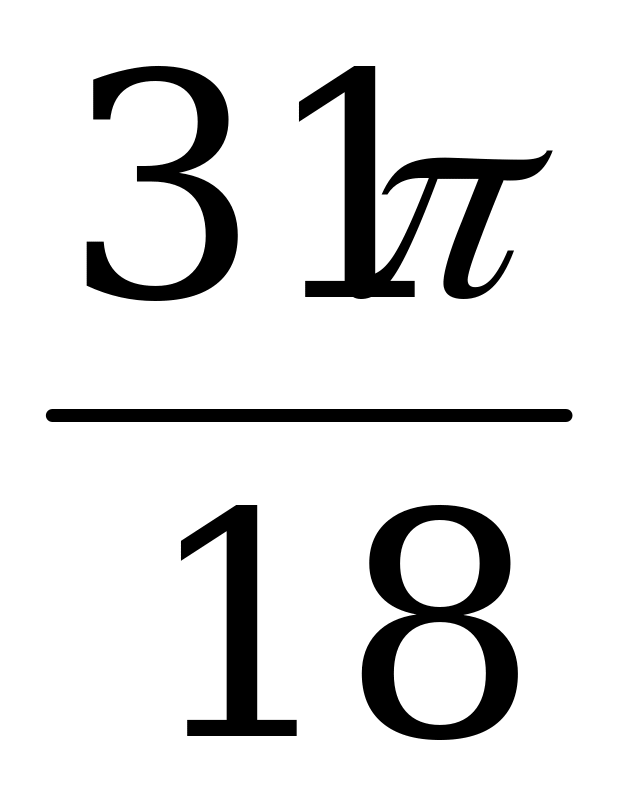 радиан.
радиан.
Пример 2.Выразите в градусной мере величину угла  , если
, если  =
= 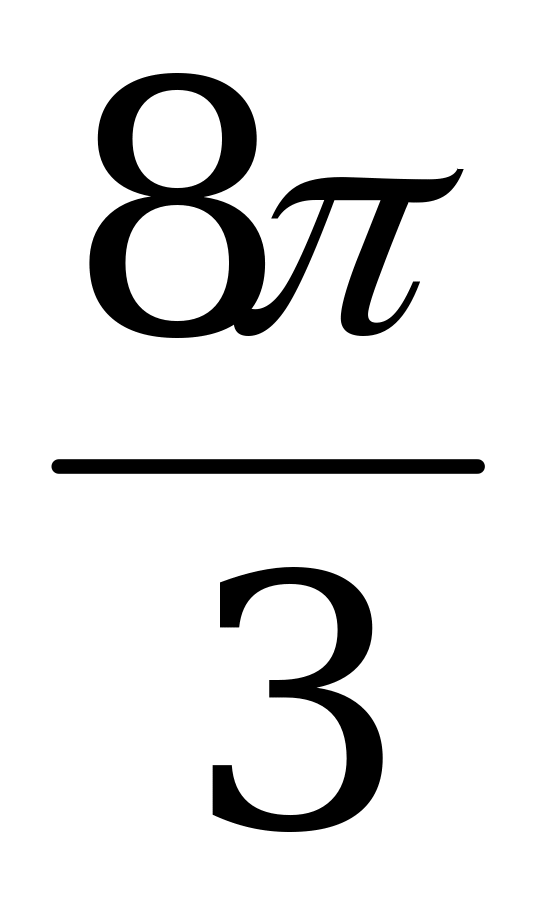 ,
,  =
= 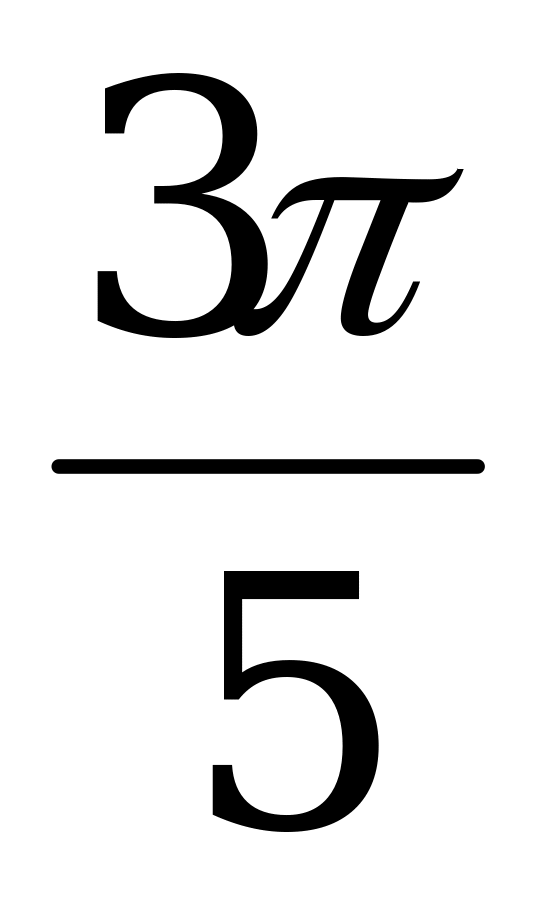 .
.
Решение: Так как 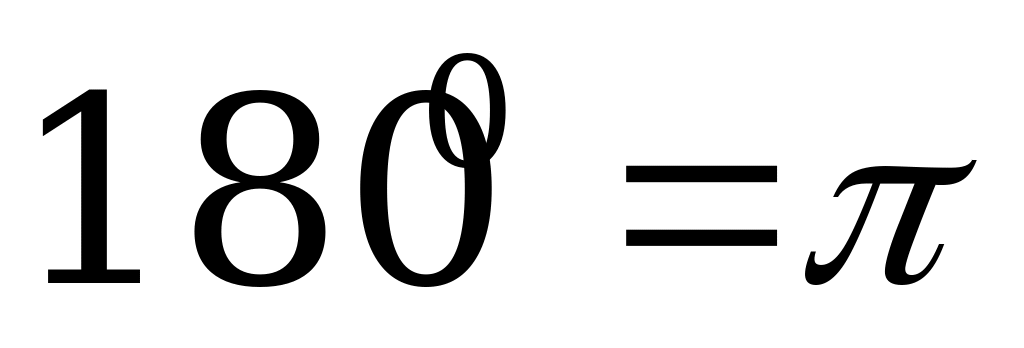 радиан, то
радиан, то
 ;
;
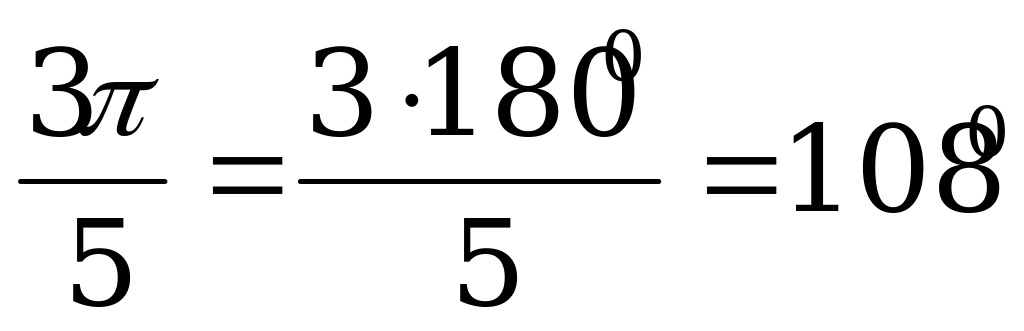 .
.
1.2. Синус, косинус, тангенс и котангенс числового аргумента.
Справочный материал.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
sin α = 
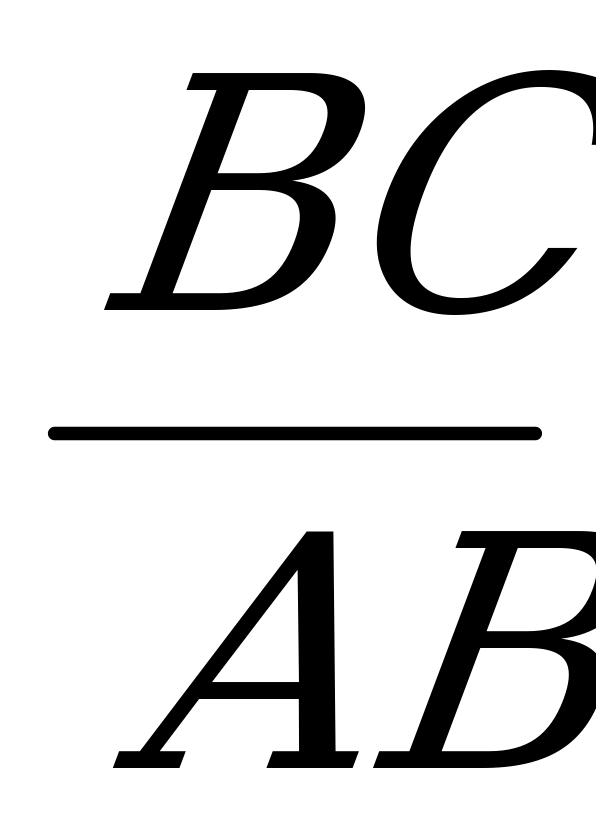 (рис 1.)
(рис 1.)
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
cos α = 
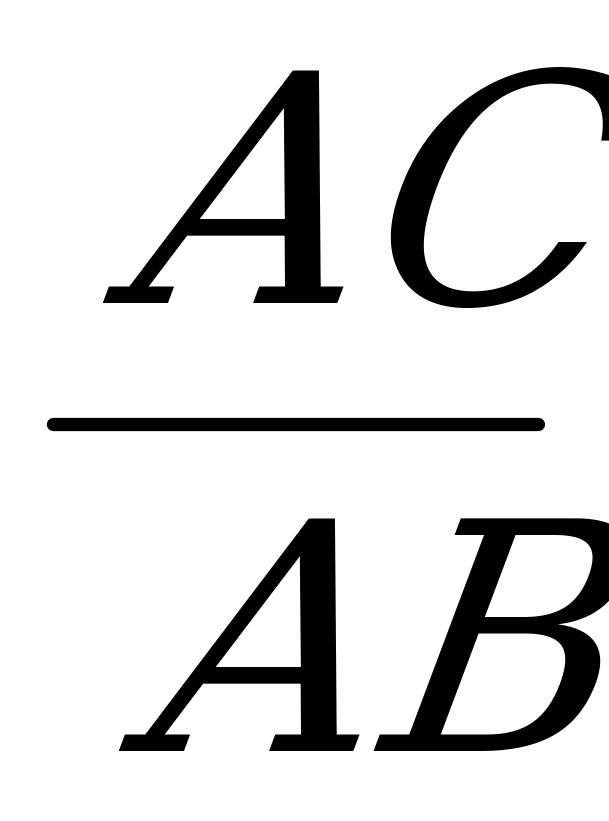 (рис 1.)
(рис 1.)
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
tg α = 
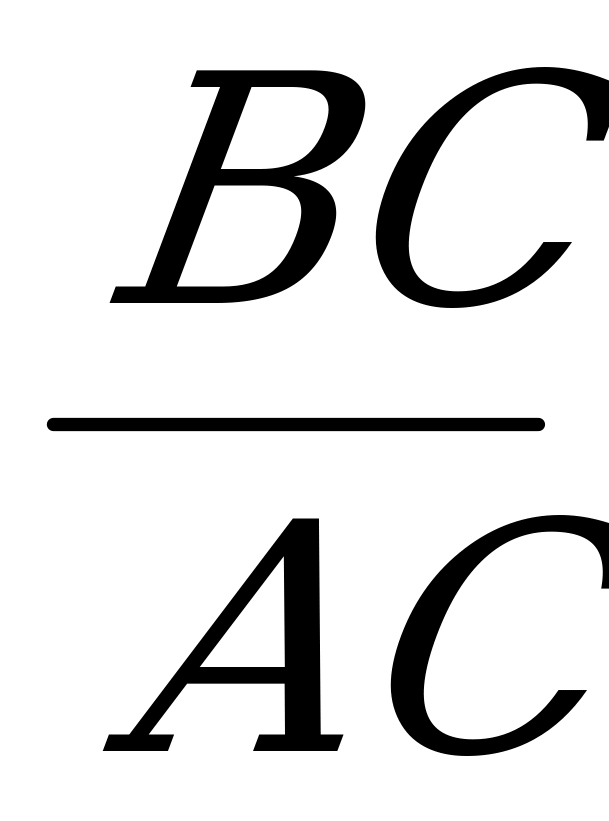 (рис 1.)
(рис 1.)
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
ctg α = 
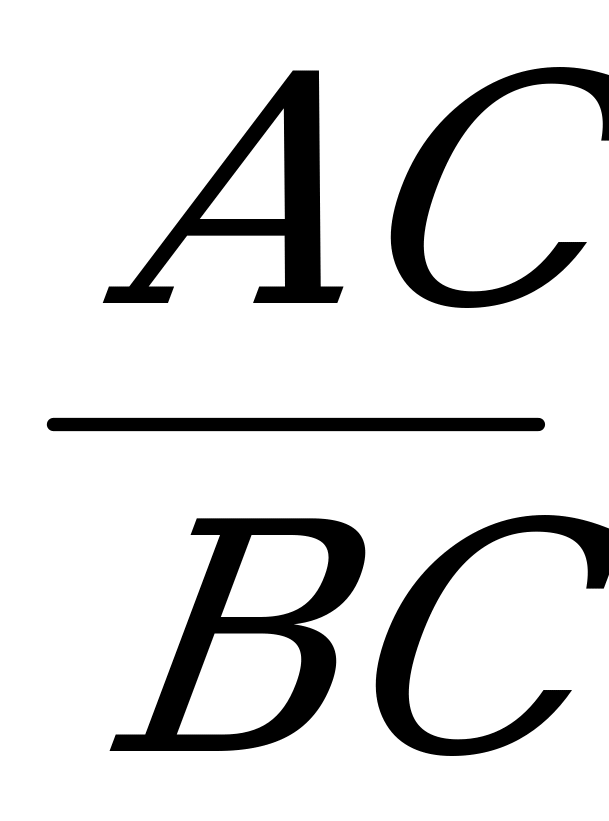 (рис 1.)
(рис 1.)
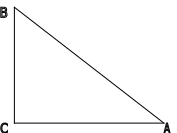
(рис 1.)
1.3 Основные формулы тригонометрии.
Справочный материал.
Основные тригонометрические тождества.
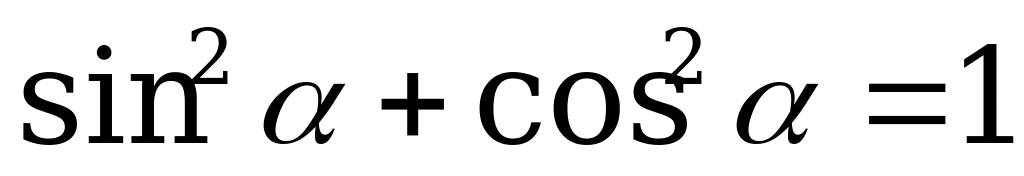 ; (1)
; (1)
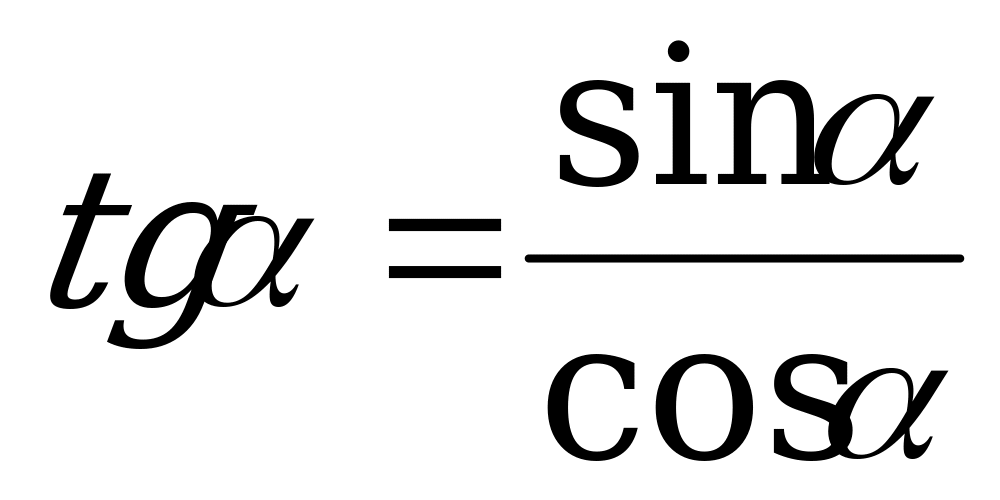 ; (2)
; (2)
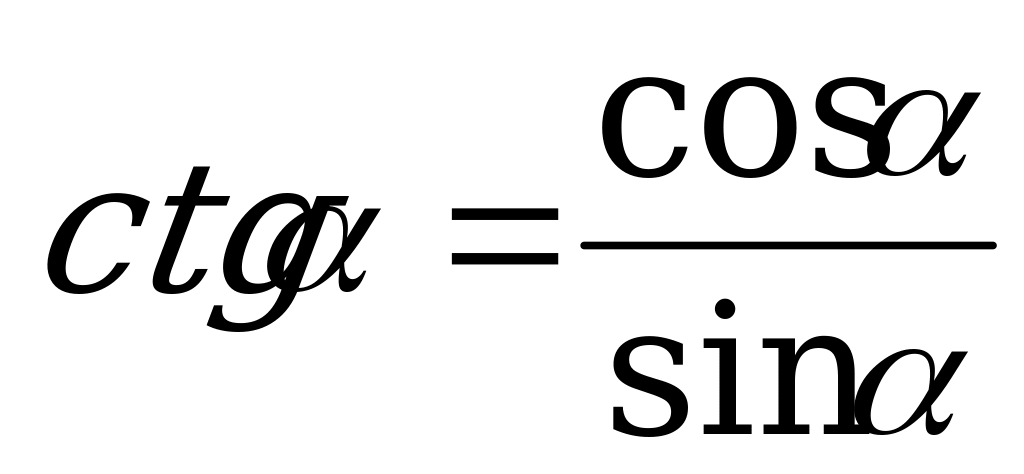 ; (3)
; (3)
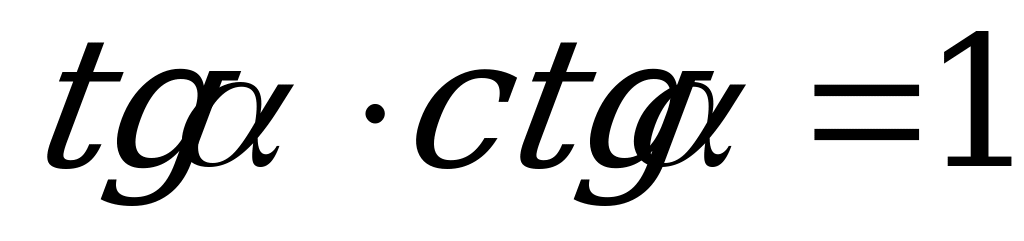 ; (4)
; (4)
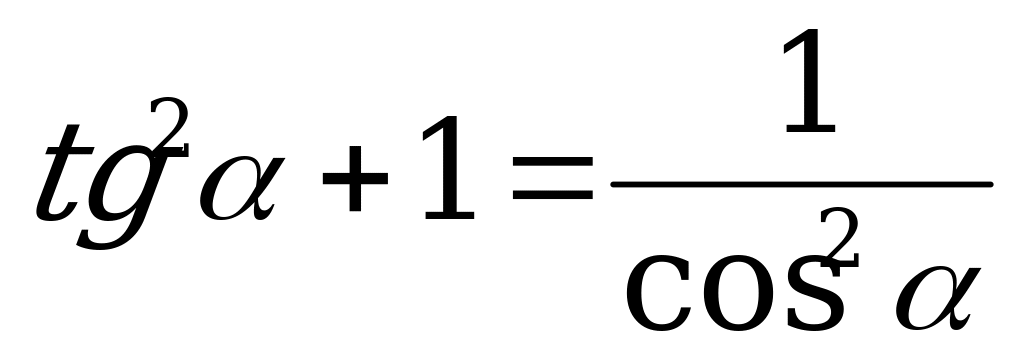 ; (5)
; (5)
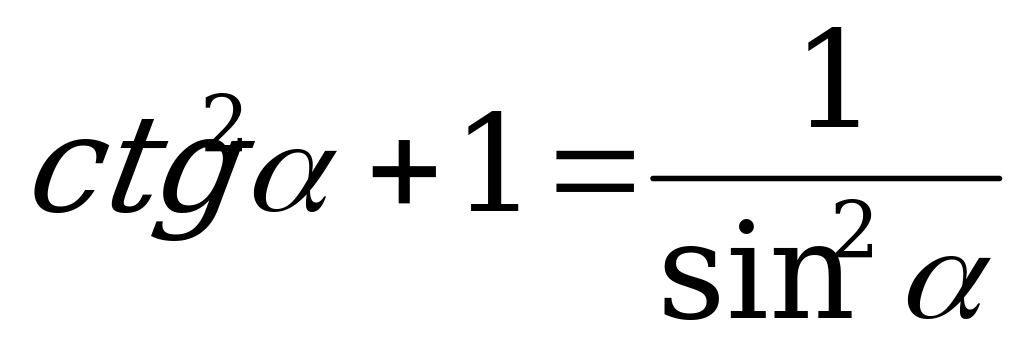 ; (6)
; (6)
Знаки тригонометрических функций в различных четвертях
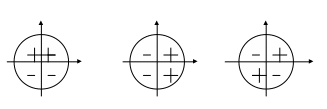
Знаки синуса. Знаки косинуса. Знаки тангенса и
котангенса.
(рис 2.).
Упражнения с решениями.
Пример 1. Вычислите cos α, tg α и ctg α, если sin α = - 0,6, 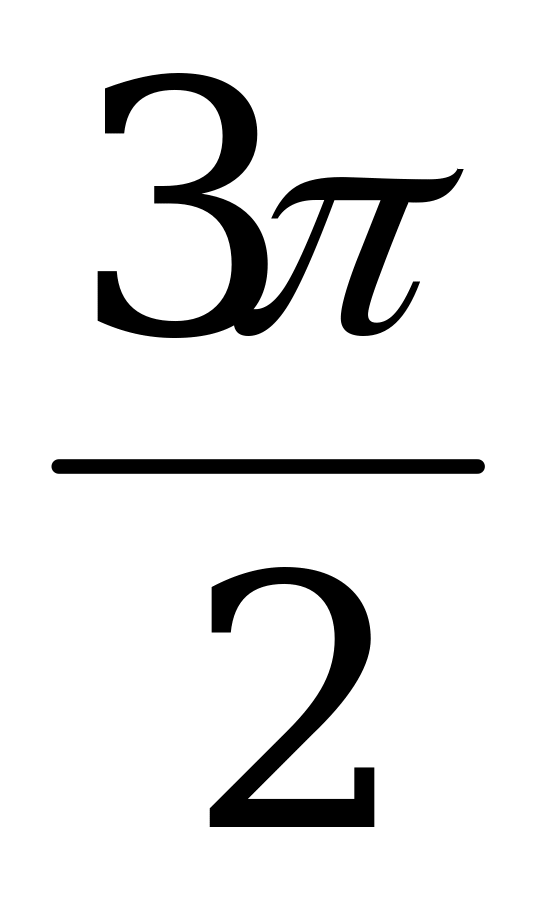
Решение: По формуле (1)
cos2 α = 1-sin2 α = 1- (-0,6)2= 1-0,36 = 0,64.
Так как 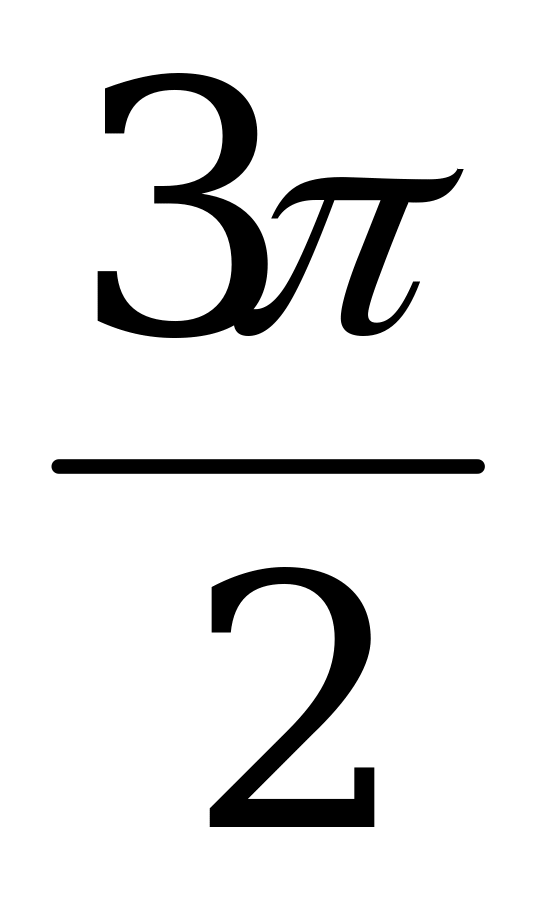 cos α 0, следовательно
cos α 0, следовательно
cos α = 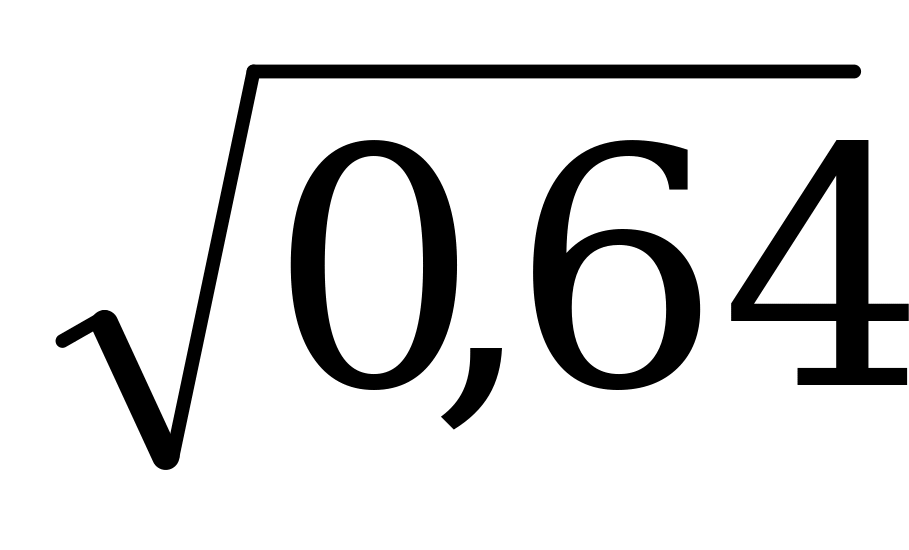 = 0,8.
= 0,8.
По формуле (2)
 =
= 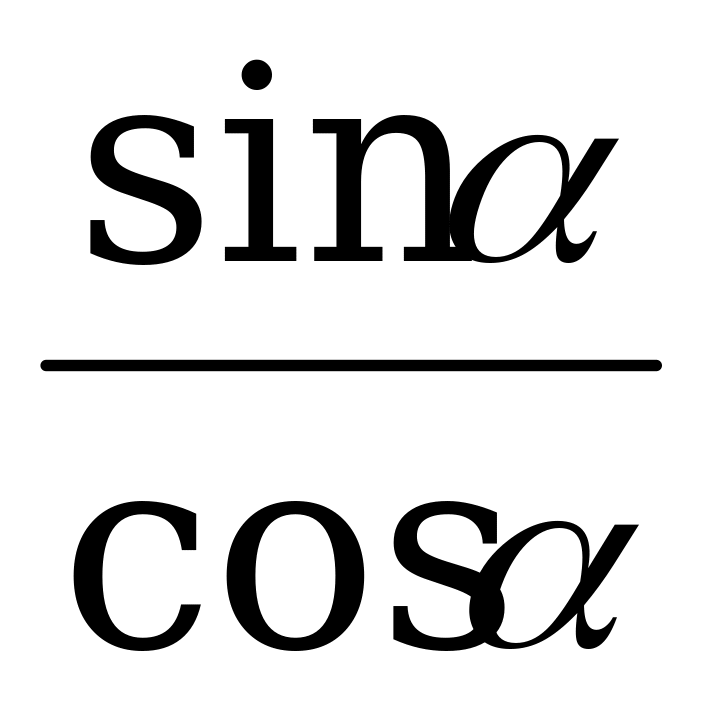 = -
= -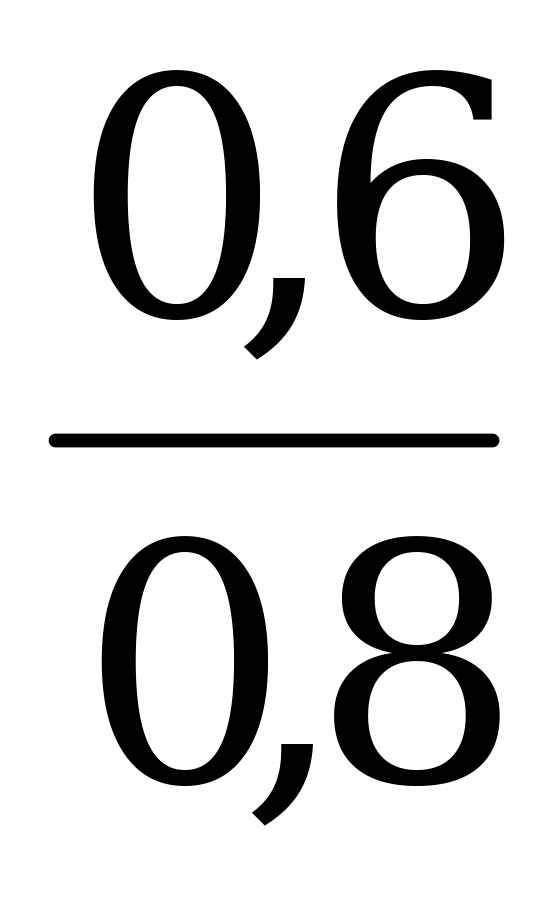 = -
= -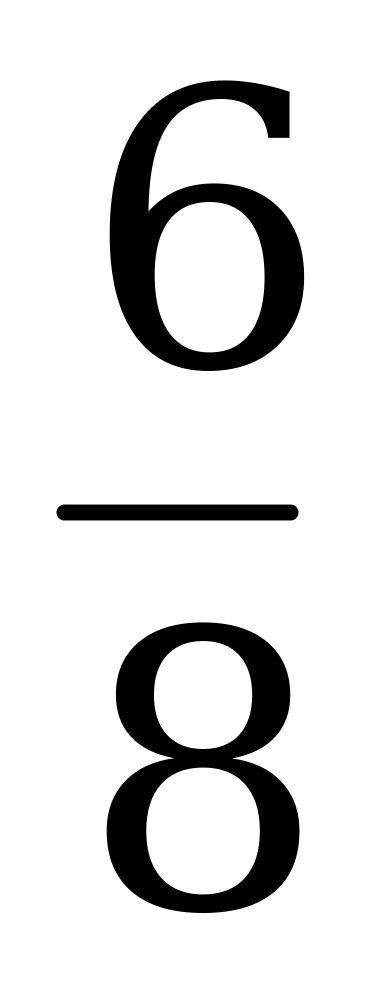 = -
= - 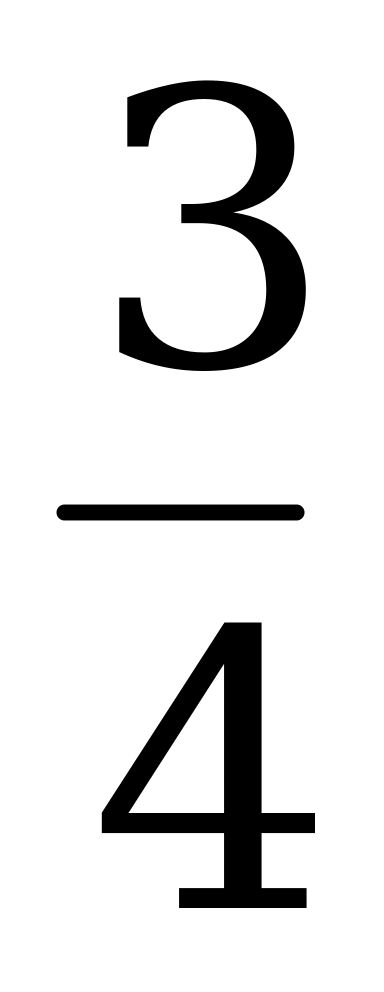 .
.
По формуле (4)
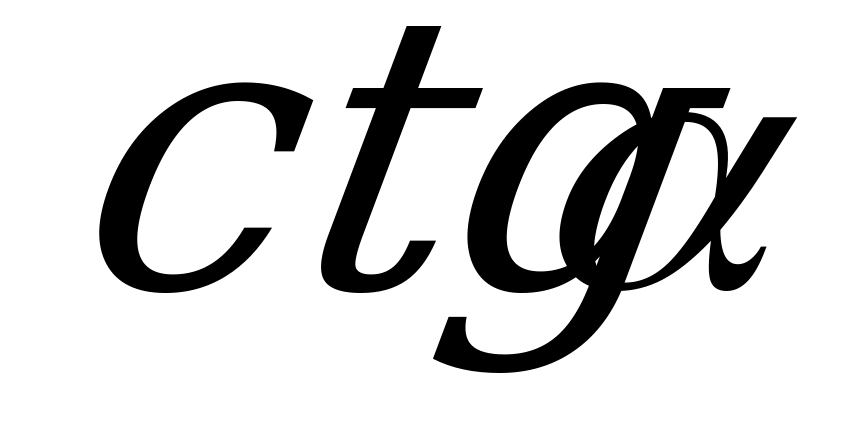 =
= 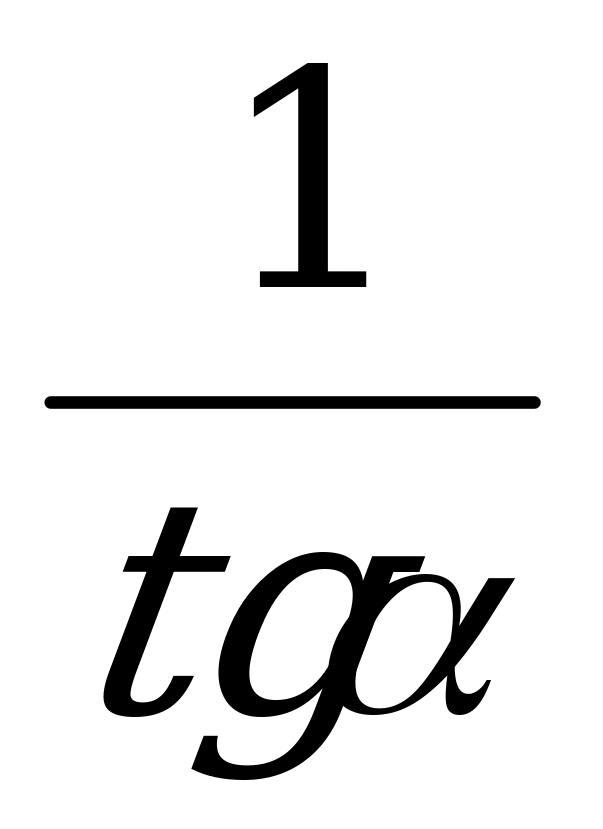 =
= 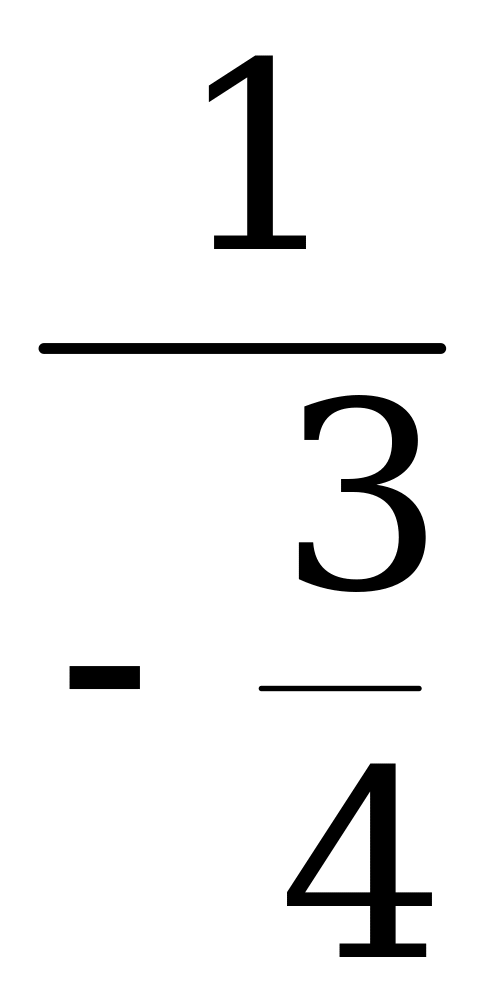 = -
= - 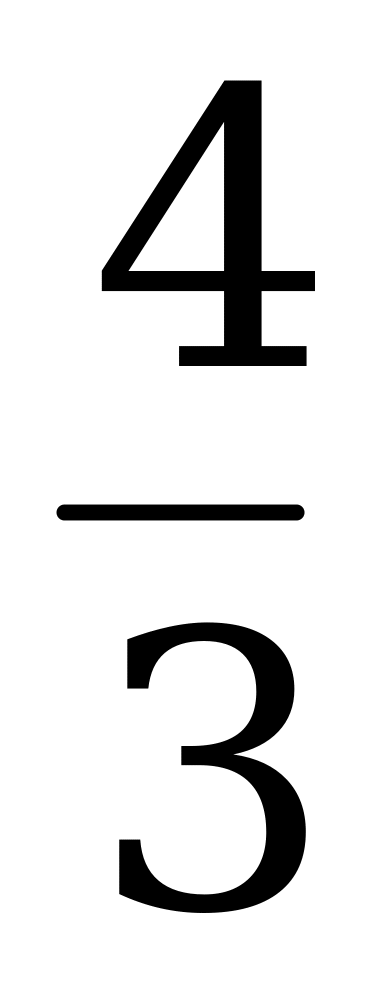 .
.
Ответ: cos α = 0,8; tg α = - 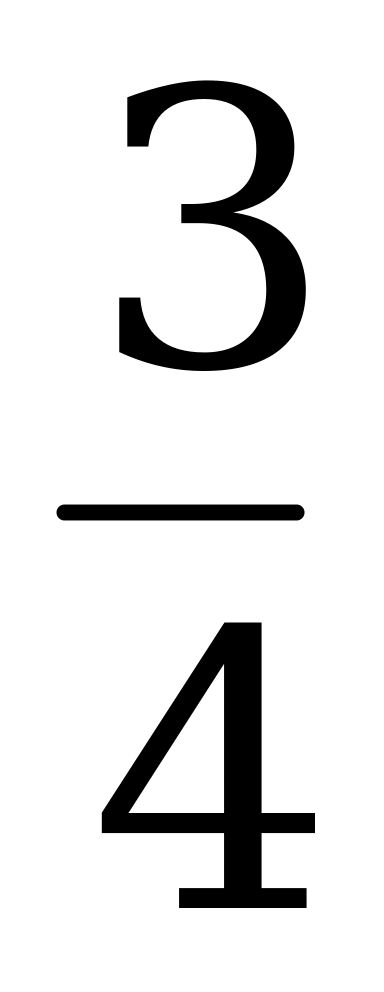 ; ctg α = -
; ctg α = - 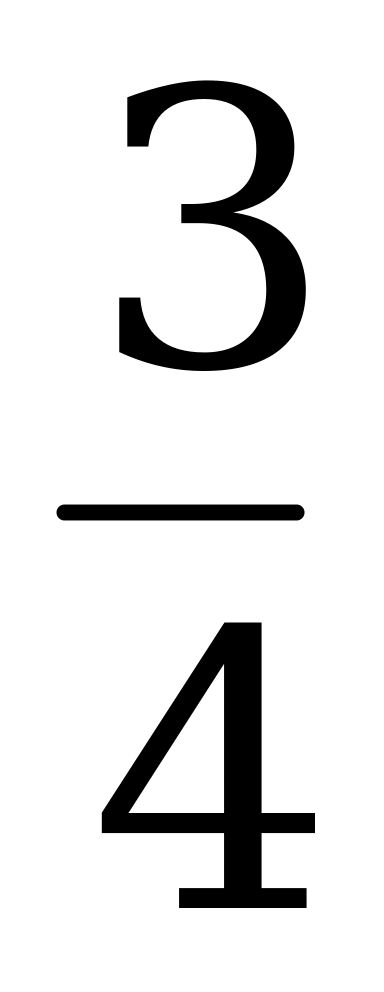 .
.
Пример 2. Вычислите sin α, cos α и ctg α, если tg α = 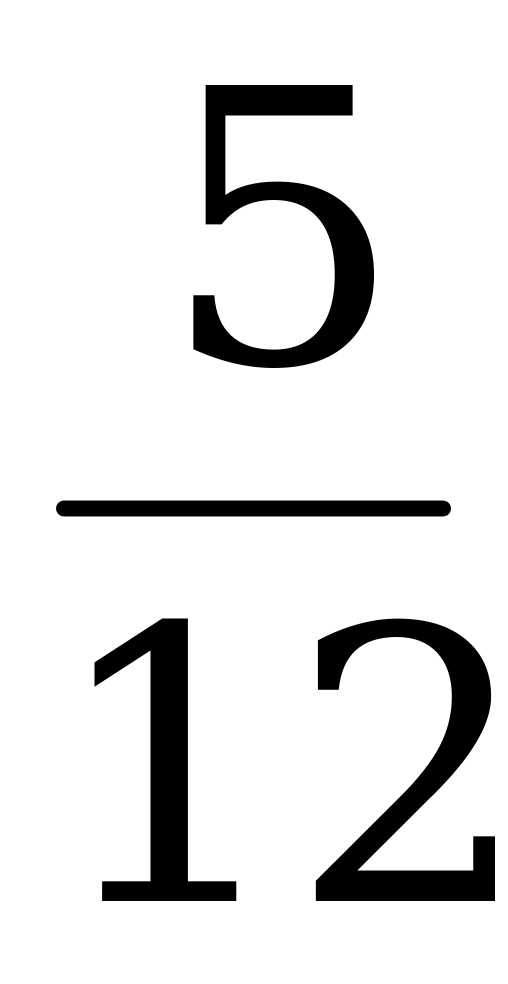 , π
, π 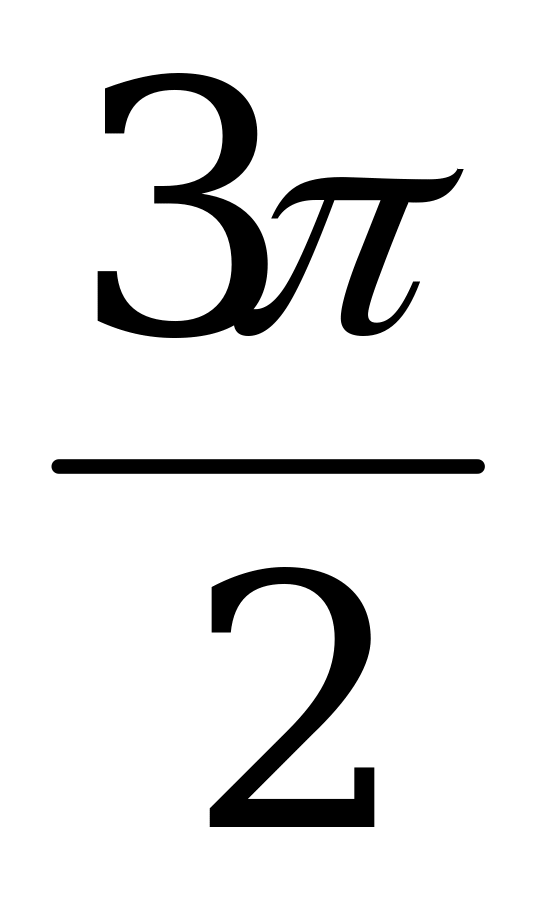
Решение: По формуле (4)
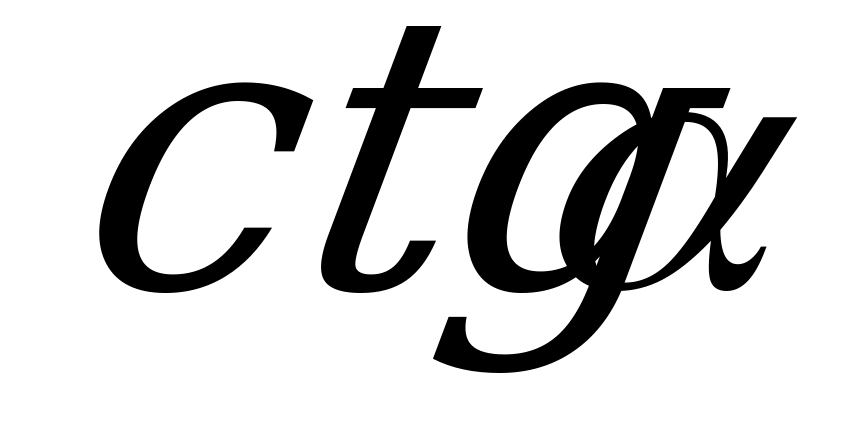 =
= 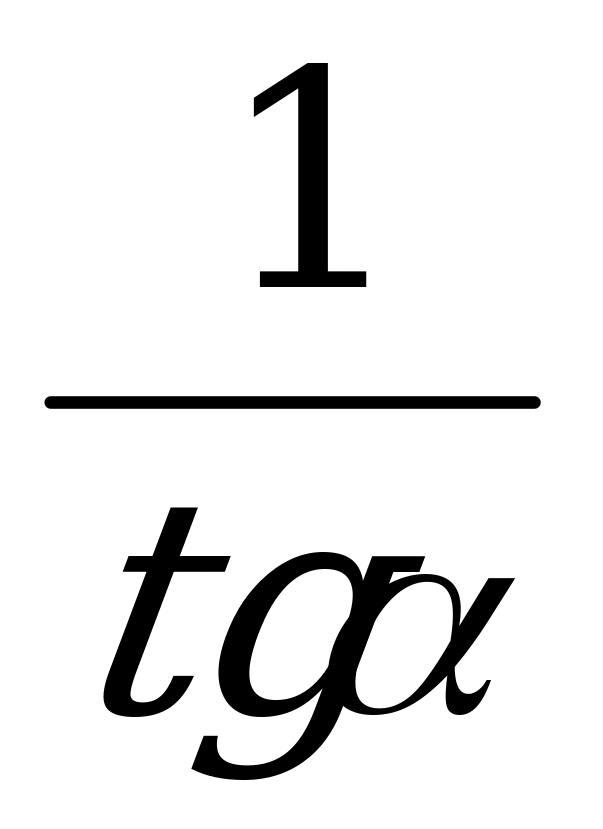 =
=  =
= 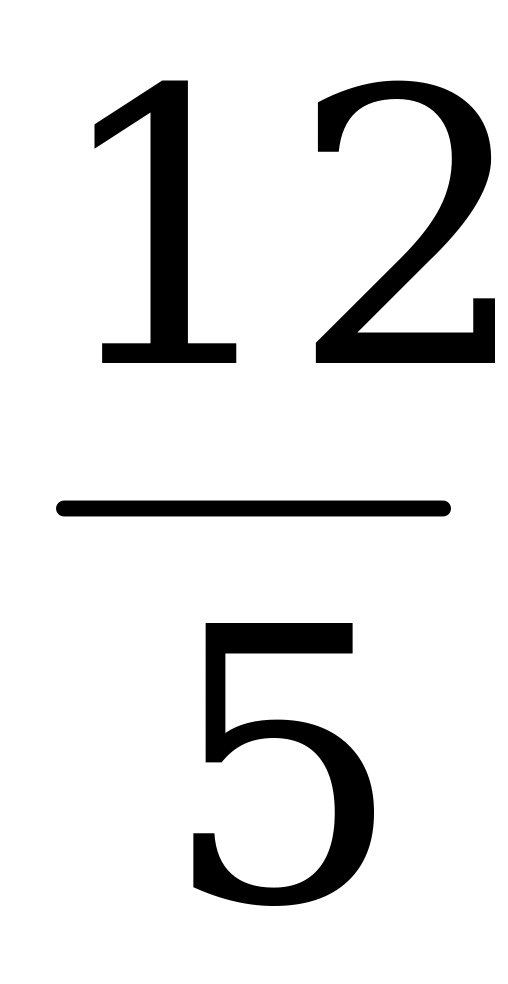
По формуле (5)

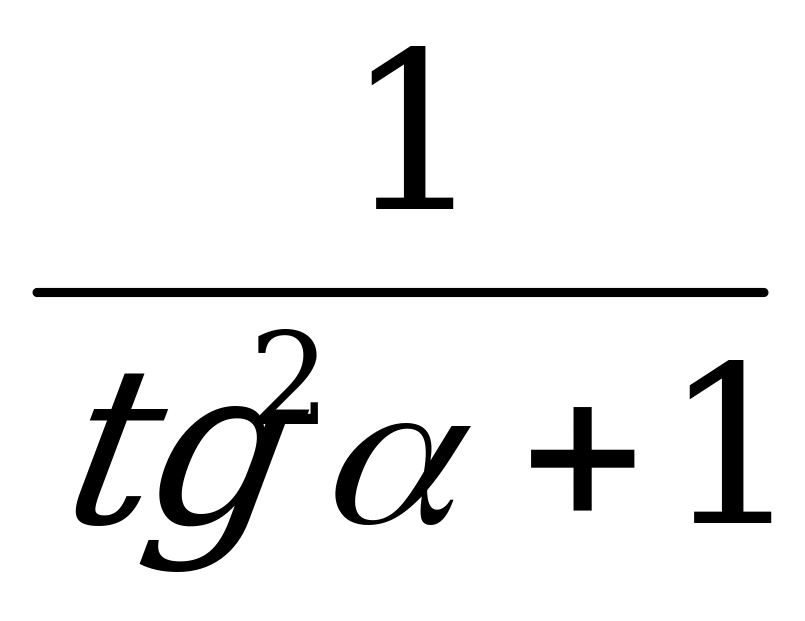 =
= 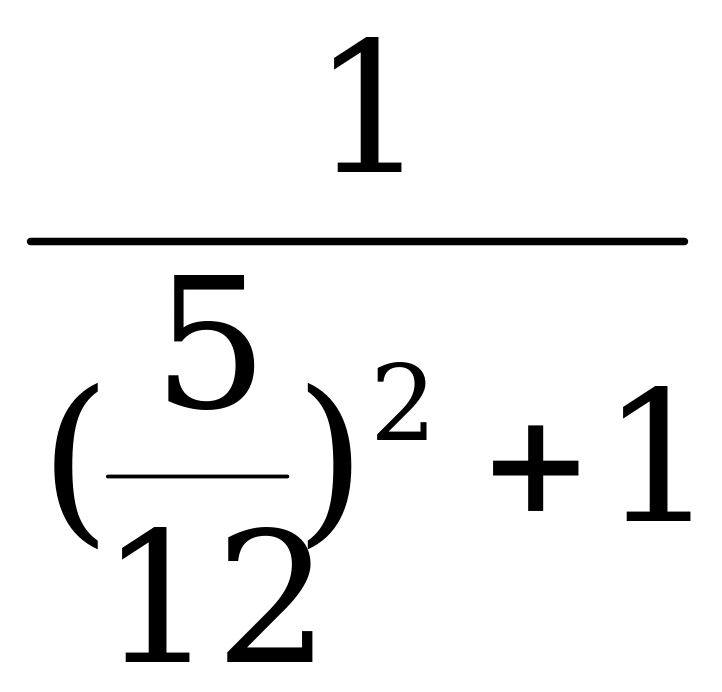 =
= 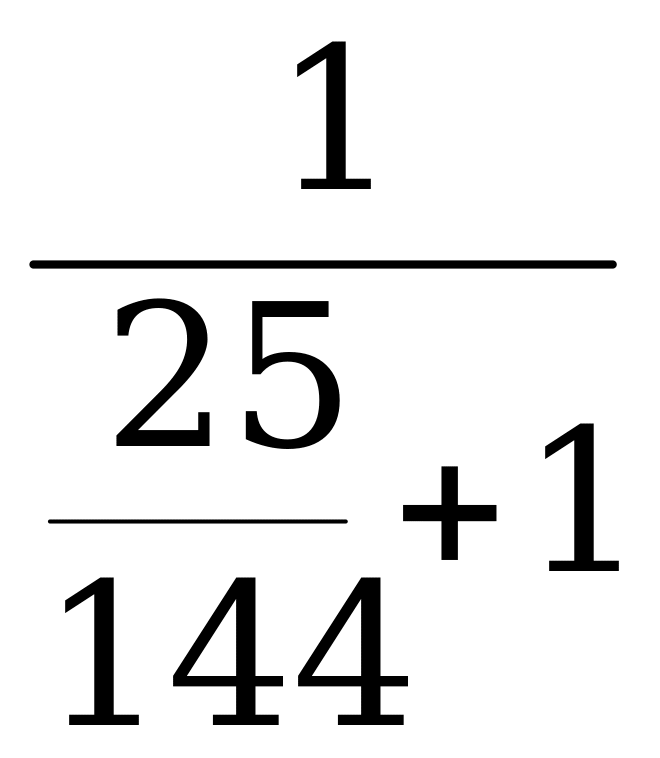 =
= 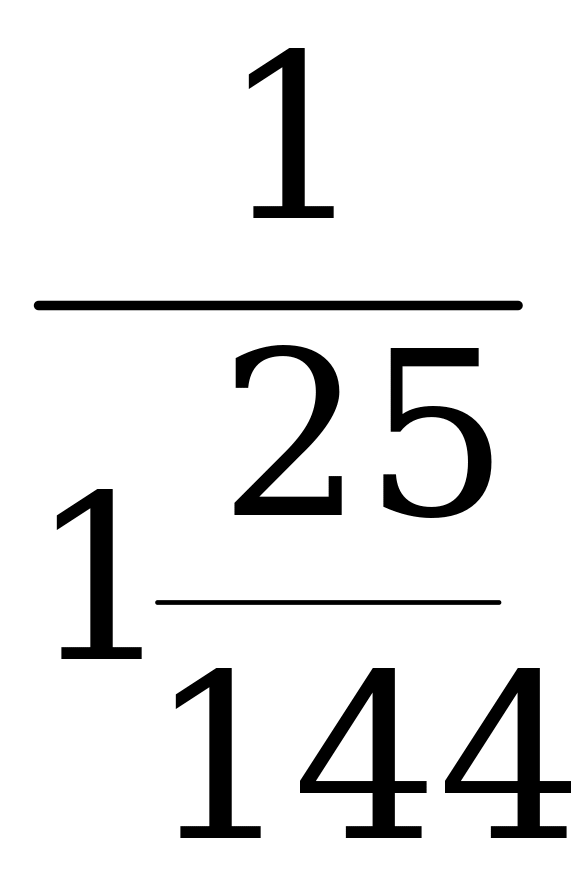 =
= 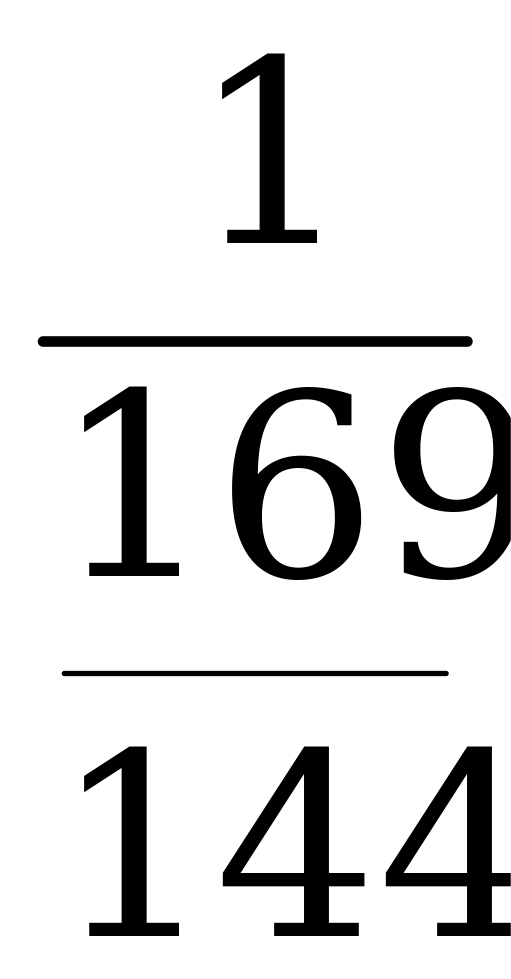 =
= 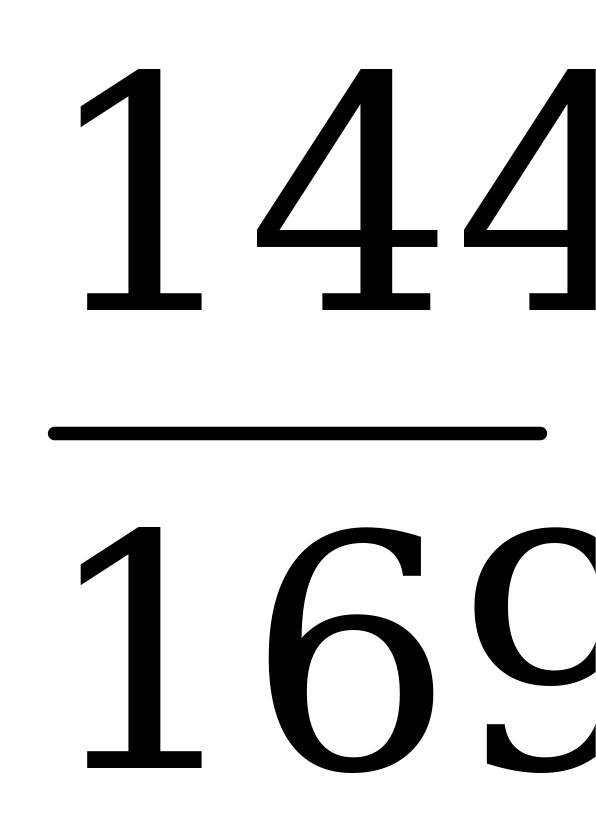 .
.
Так как π 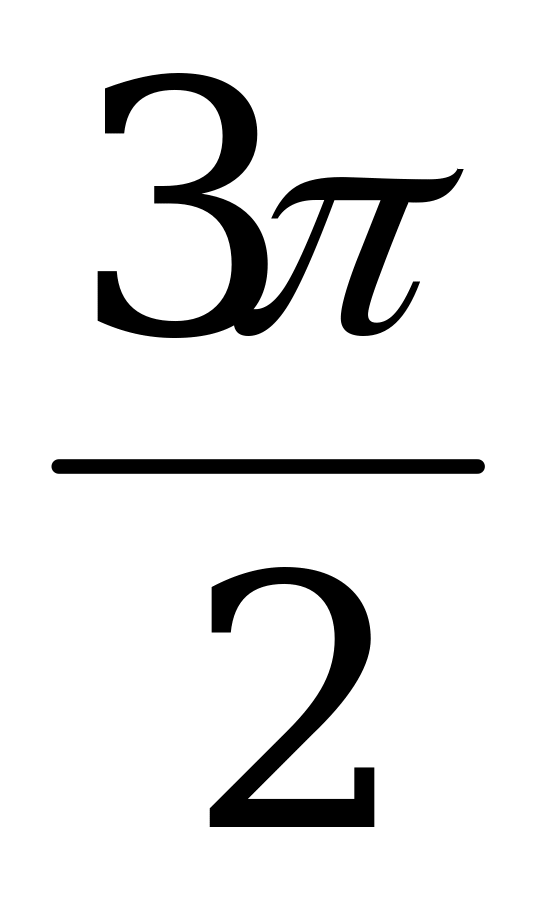 , то cos α
, то cos α
cos α = - 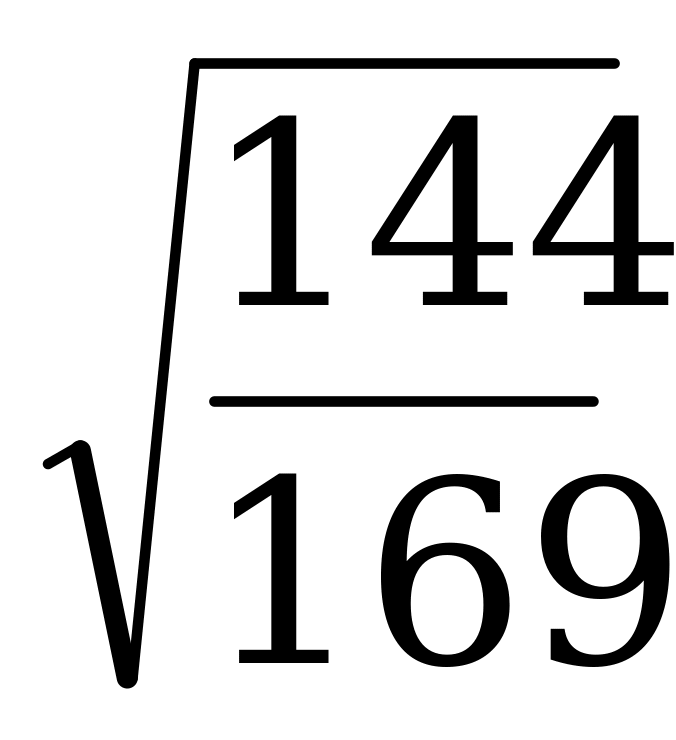 = -
= - 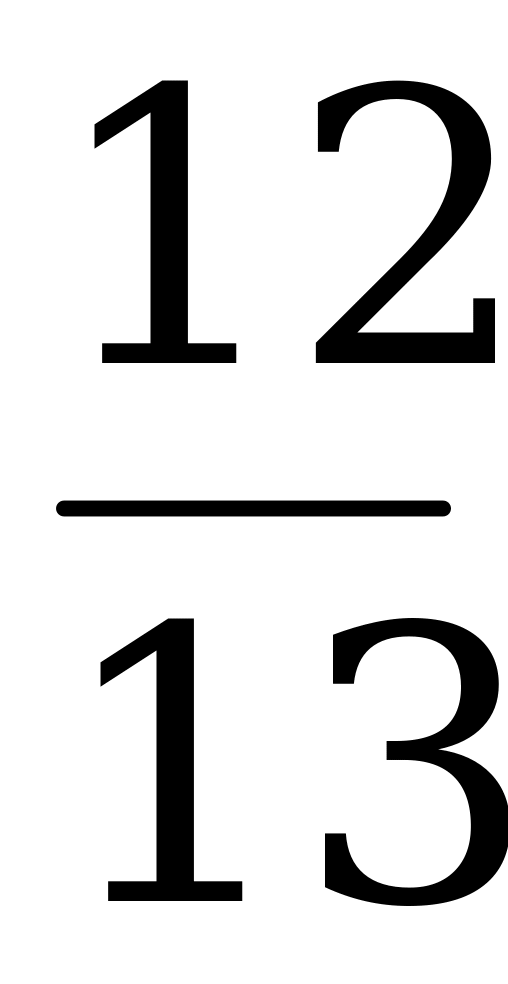
По формуле (2)
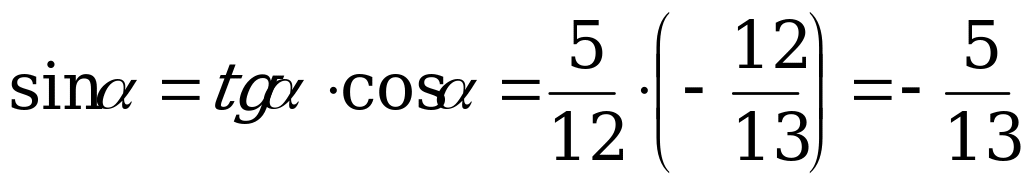 .
.
Ответ: sin α = - 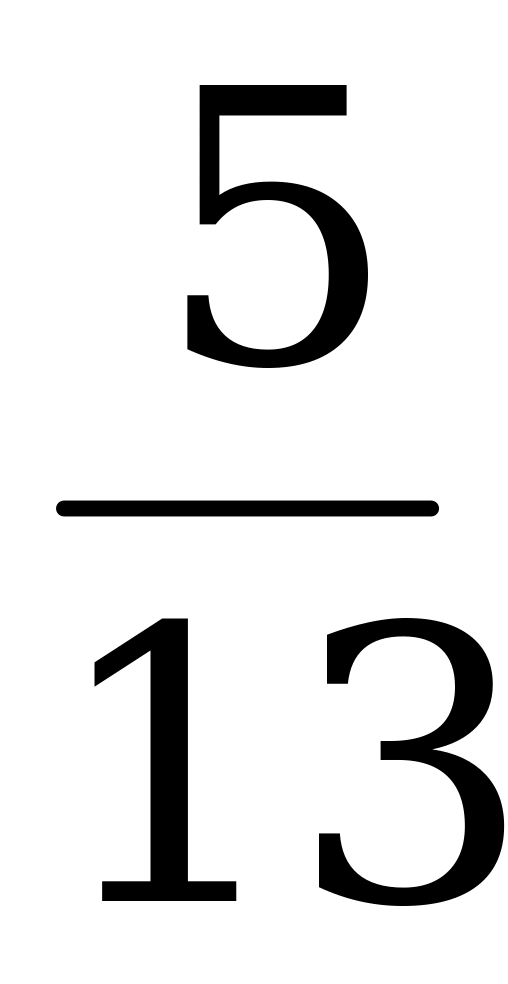 , cos α = -
, cos α = - 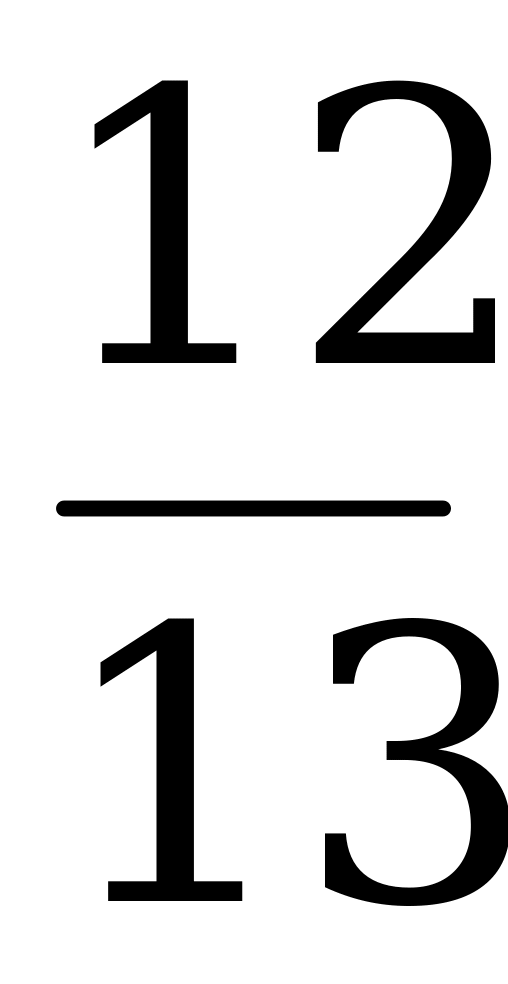 , ctg α =
, ctg α = 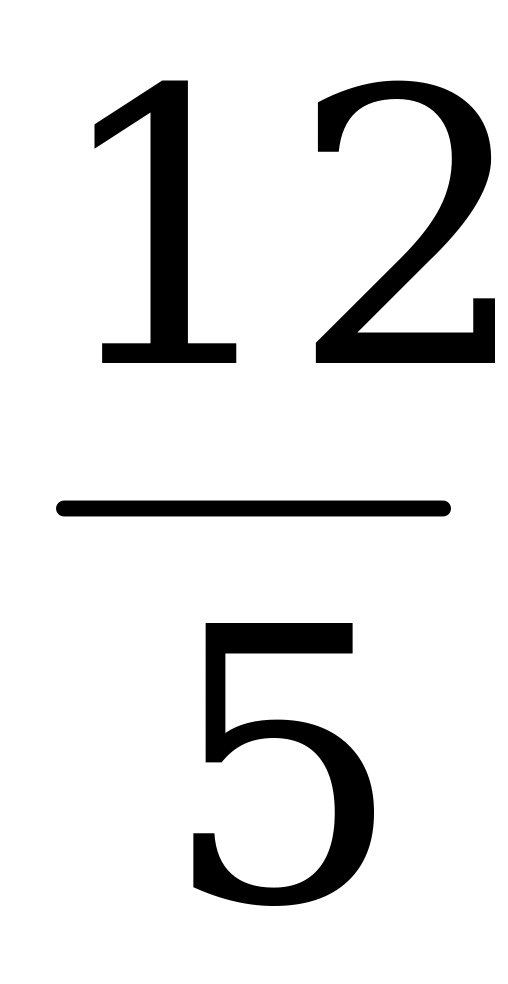 .
.
Пример 3. Докажите тождество
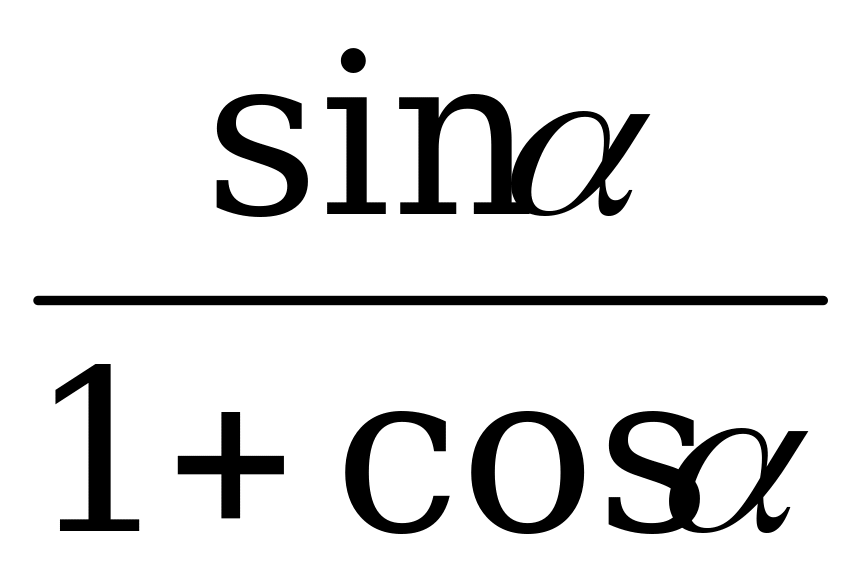 +
+ 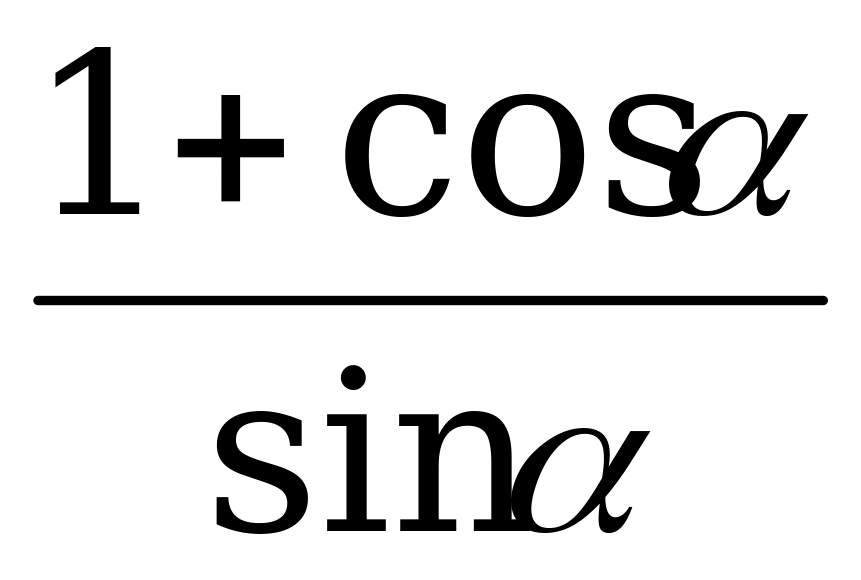 =
= 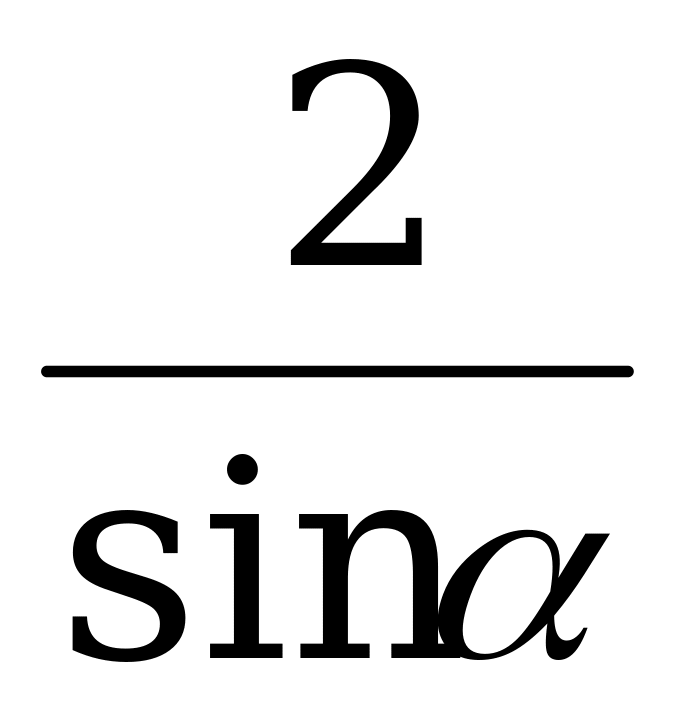 .
.
Доказательство. Правую часть равенства приведём к общему знаменателю:
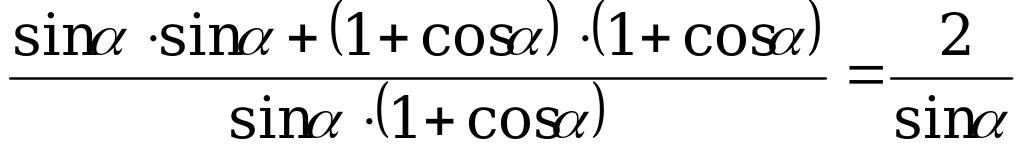 .
.
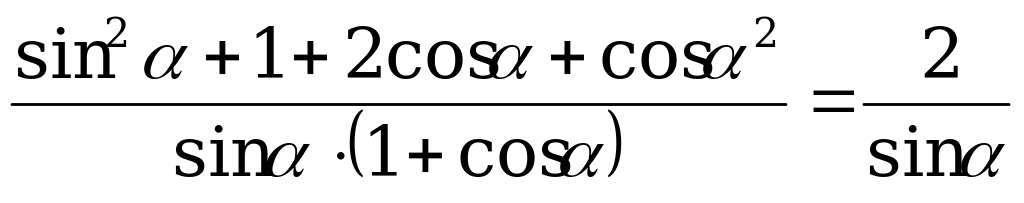 .
.
Так как 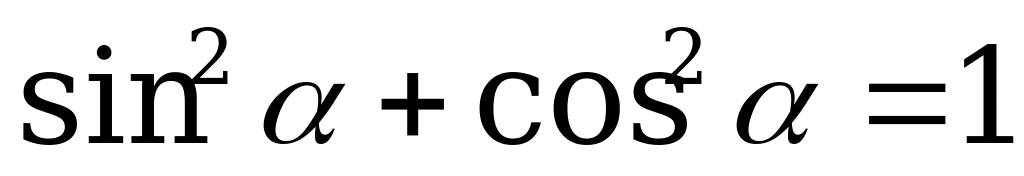 , то
, то
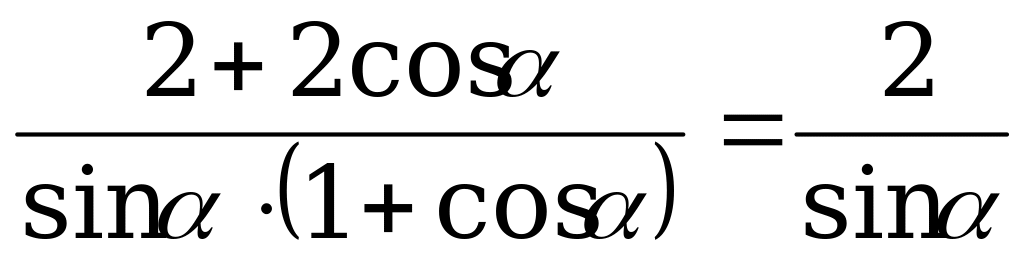 .
.
Вынесем в числители общий множитель за скобки
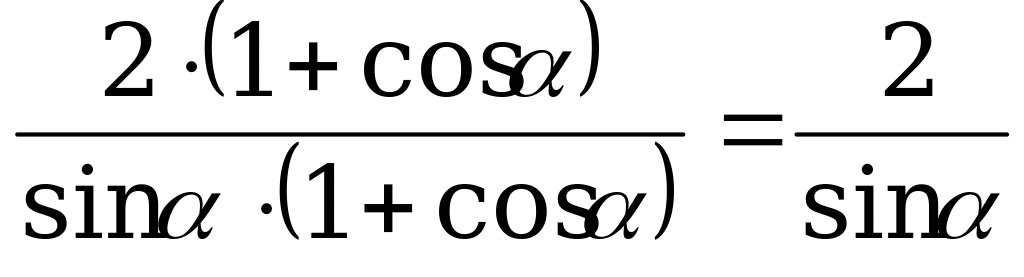 .
.
Сократим дробь в правой части равенства:
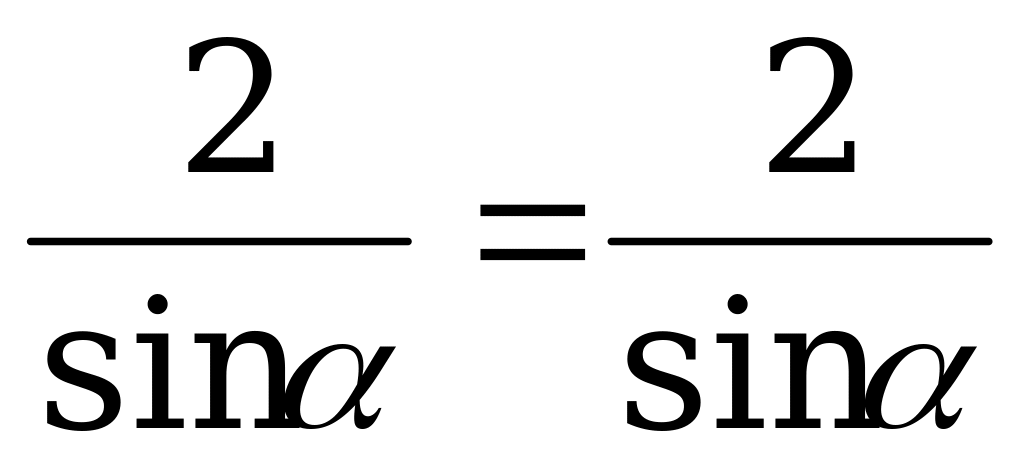 .
.
Что и требовалось доказать.
Самостоятельная работа № 1
Вариант 1.
1) Выразите в радианах величину угла α, если:
а) α = 360; б) α = 2700.
2) Выразите в градусной мере величину угла α, если:
а) α = 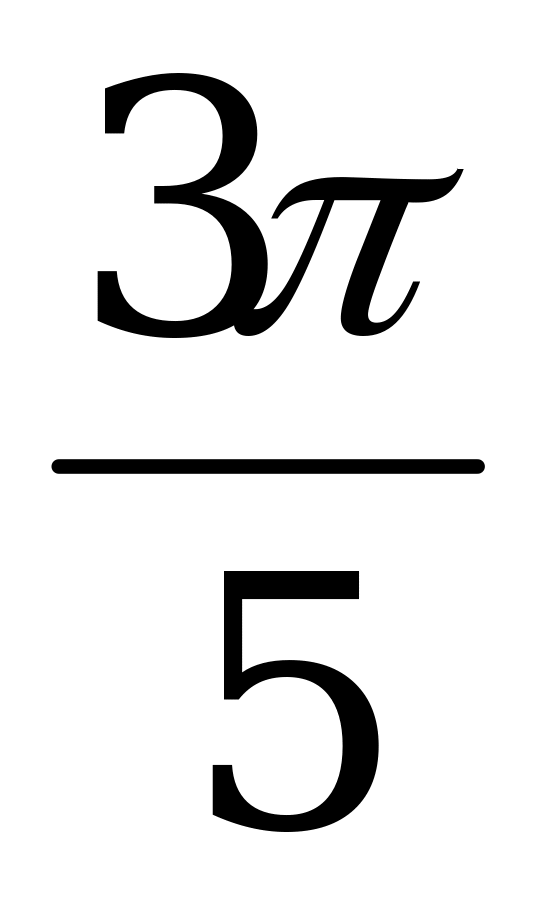 ; б) α =
; б) α = 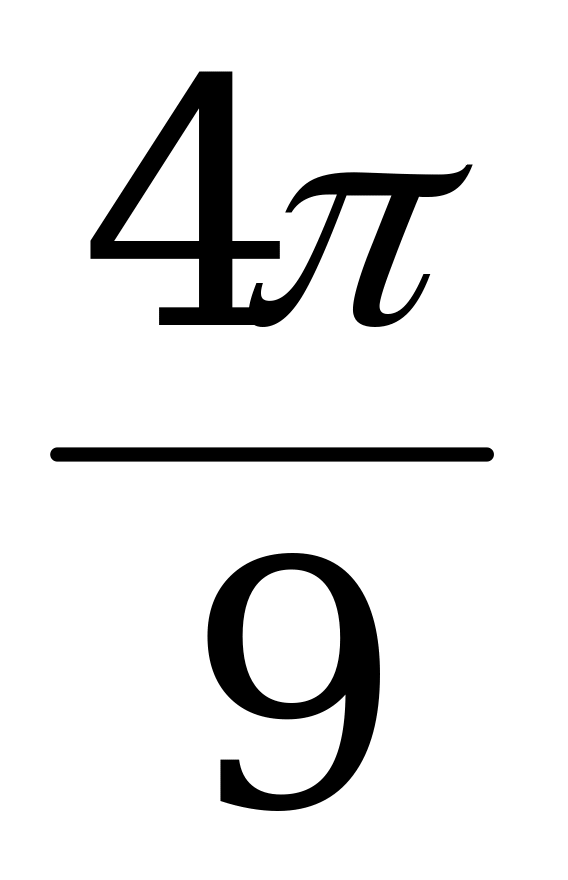 .
.
3) Вычислите sin α, tg α и ctg, если cos α = 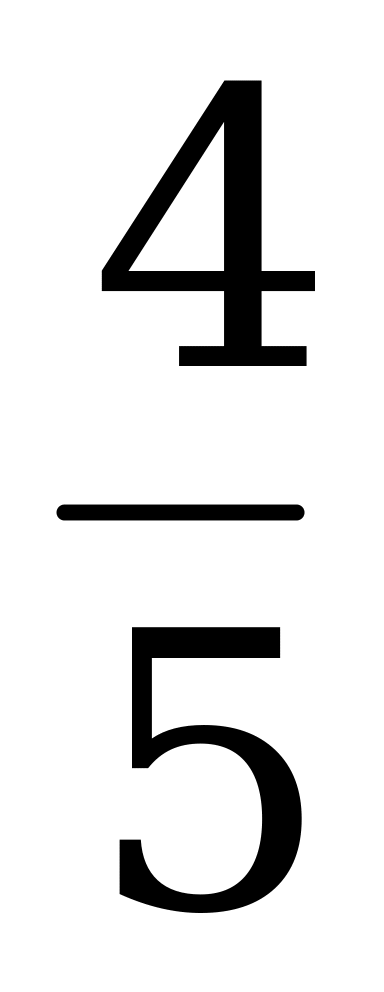 , 3π
, 3π
4) Вычислите sin α, cos α и tg α, если ctg α = - 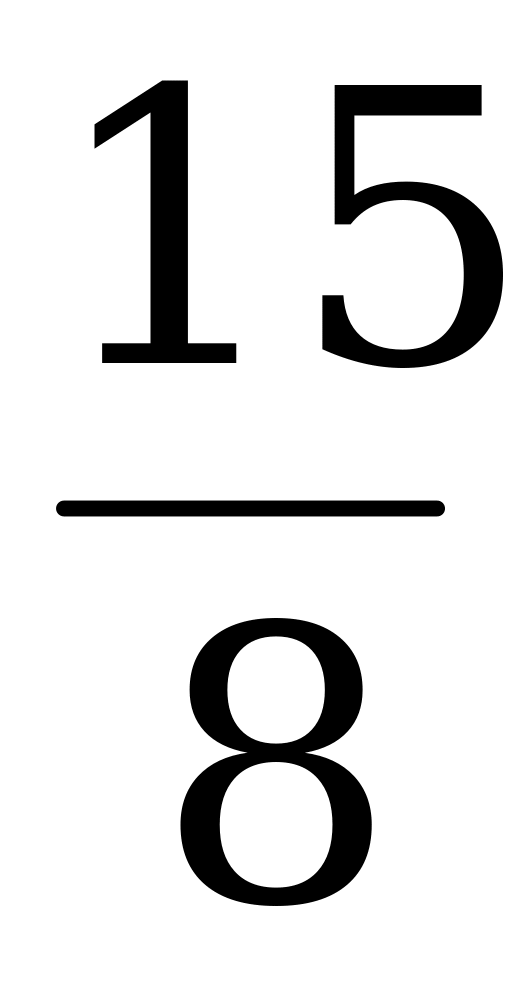 ,
, 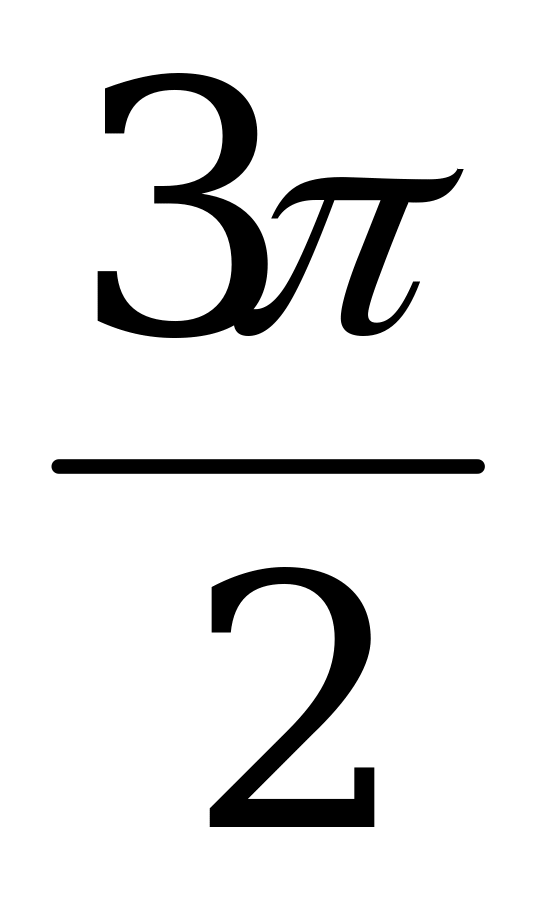 π.
π.
5) Докажите тождество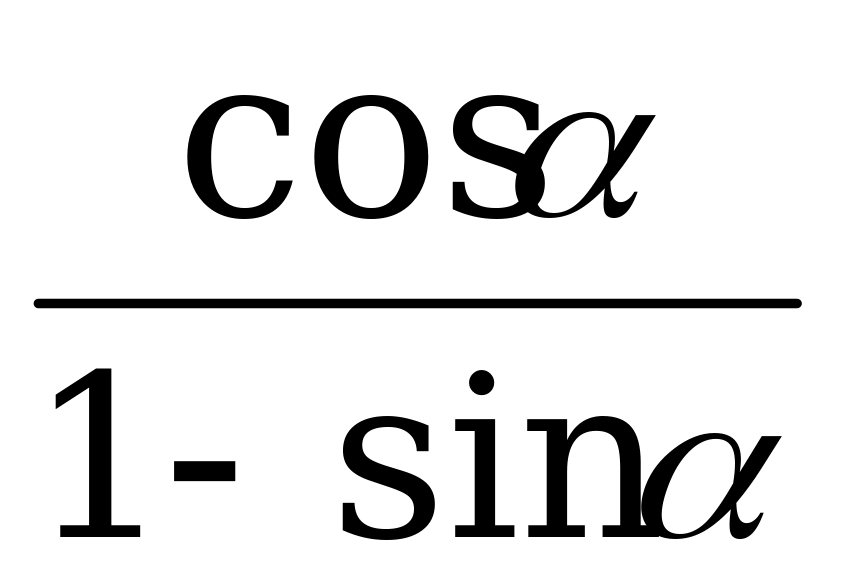 =
=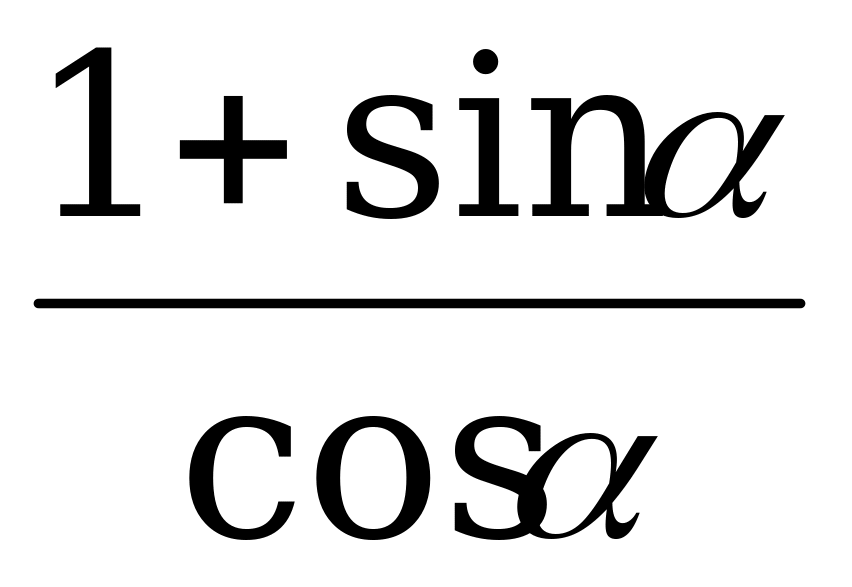 .
.
Вариант № 2.
1) Выразите в радианах величину угла α, если:
а) α = 500; б) α = 2400
2) Выразите в градусной мере величину угла α, если:
а) α = 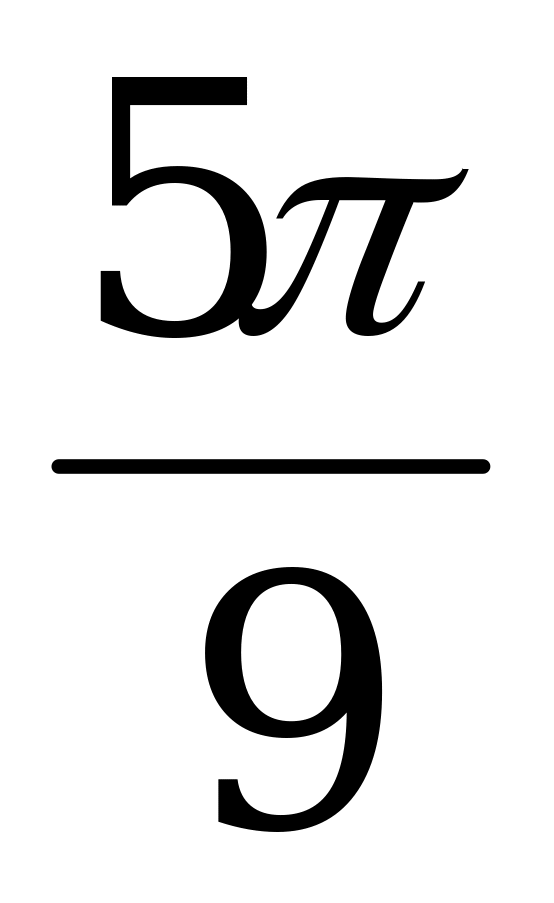 ; б) α =
; б) α = 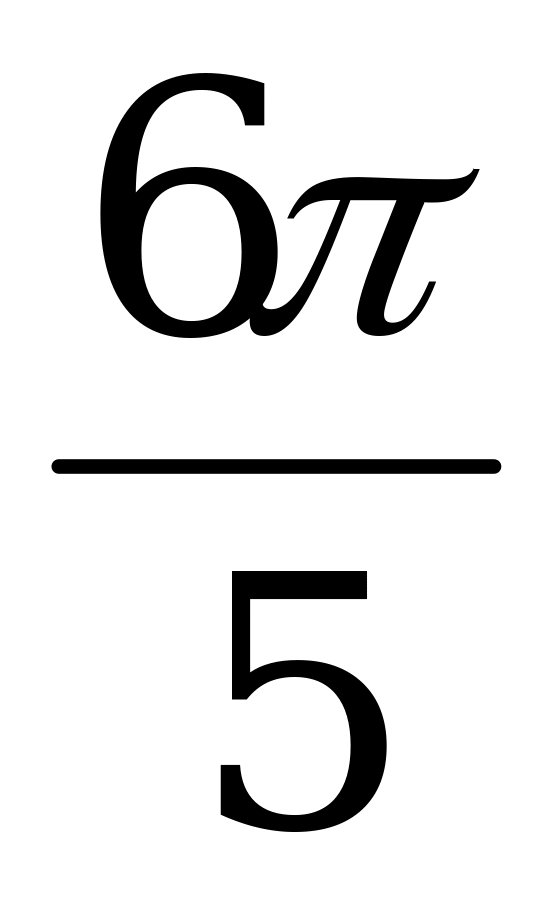 .
.
3) Вычислите sin α, tg α и ctg, если cos α = - 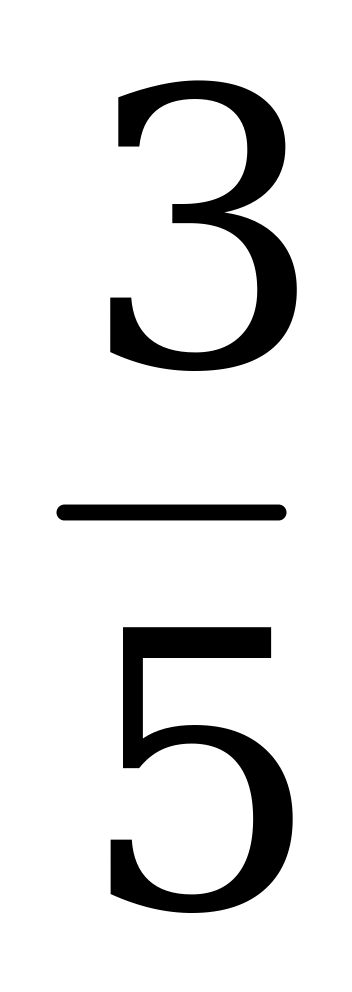 , π .
, π .
4) Вычислите sin α, cos α и tg α, если ctg α = - 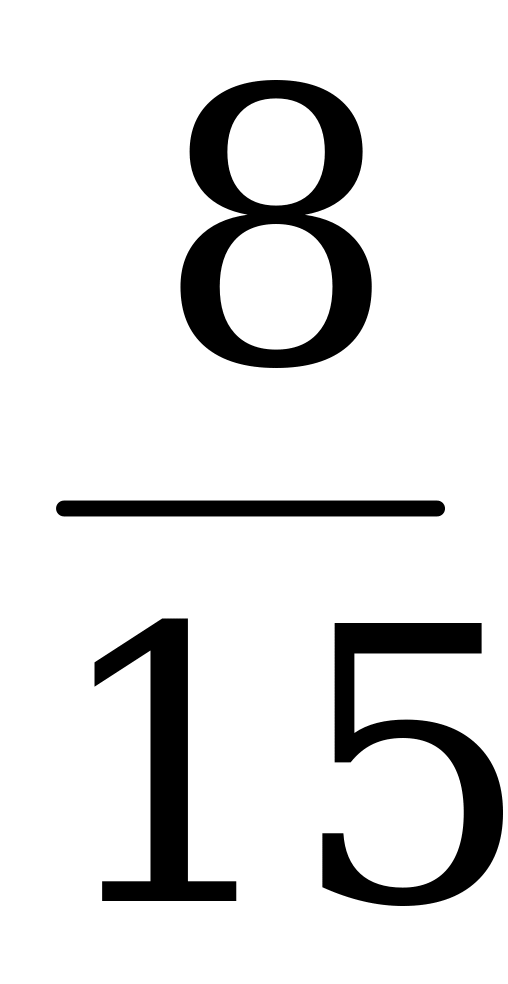 ,
, 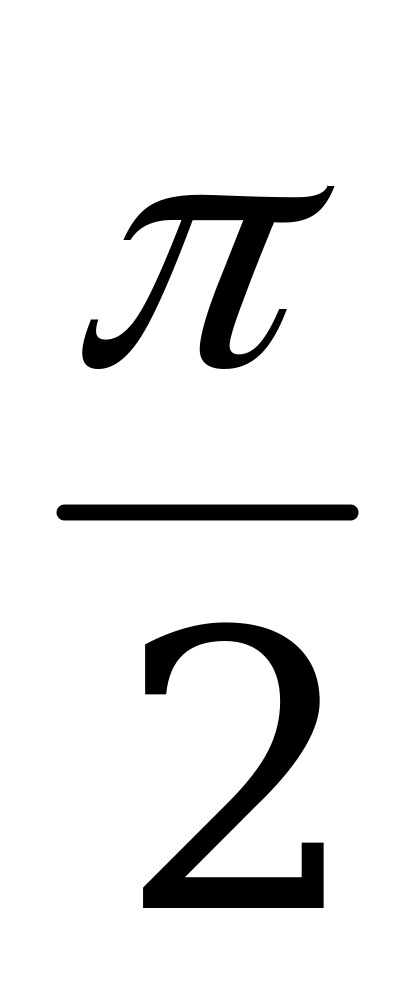 π.
π.
5) Докажите тождество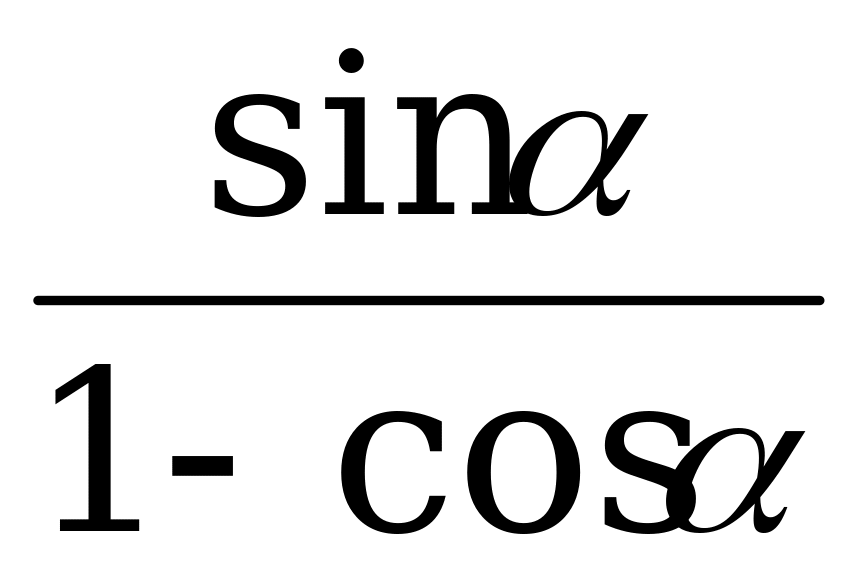 =
=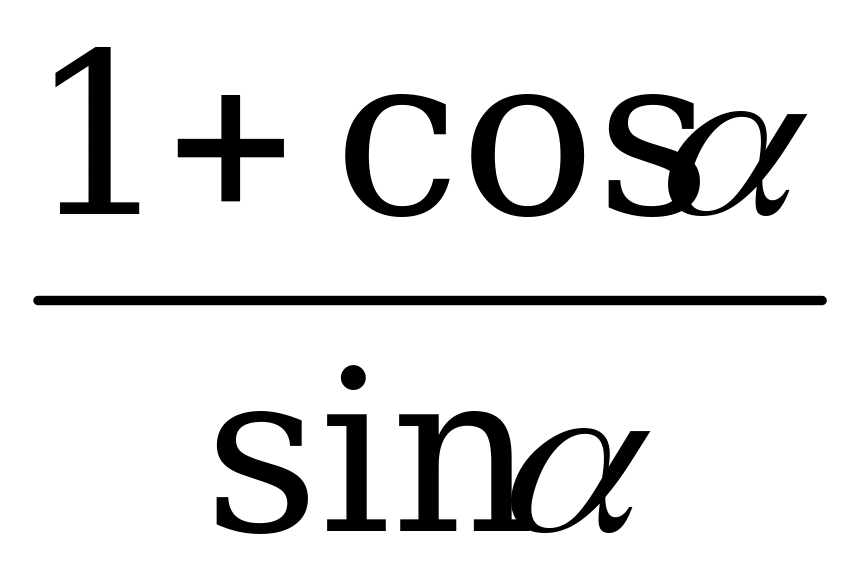 .
.
Значения тригонометрических функций
Справочный материал
|  
| 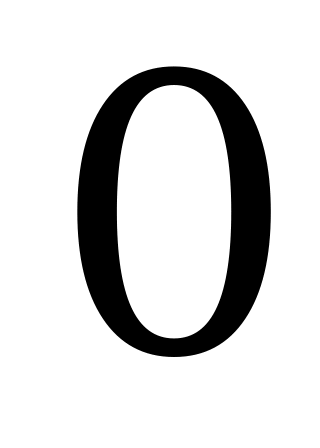
| 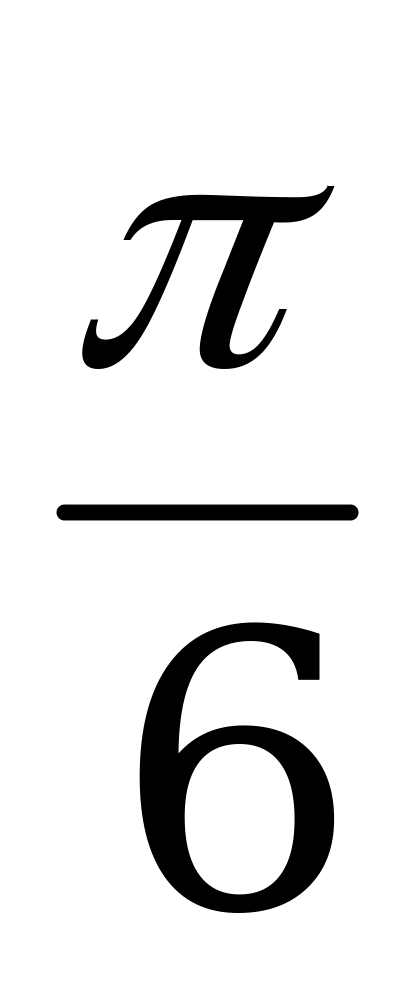
| 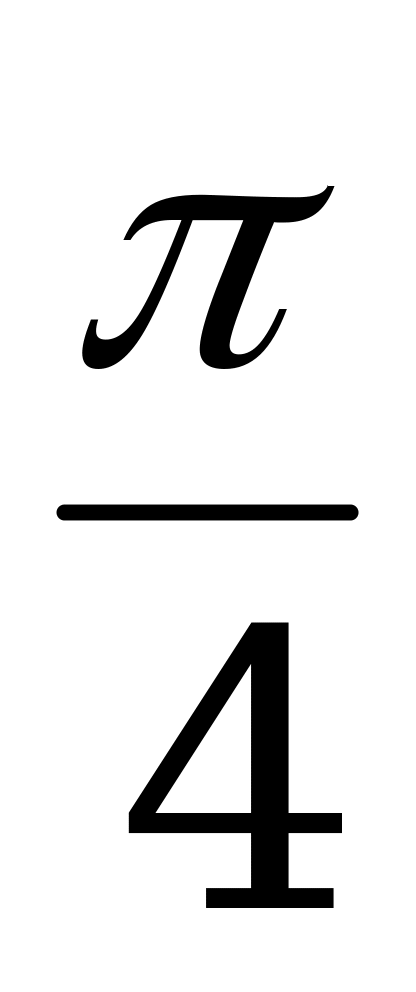
| 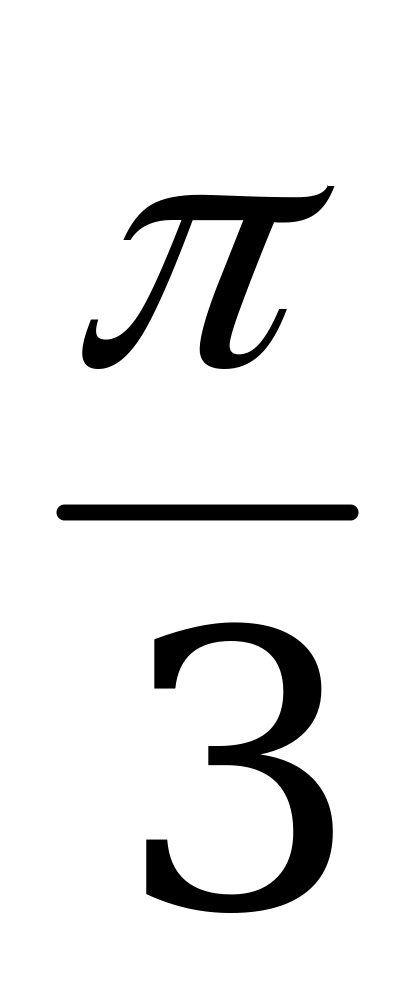
| 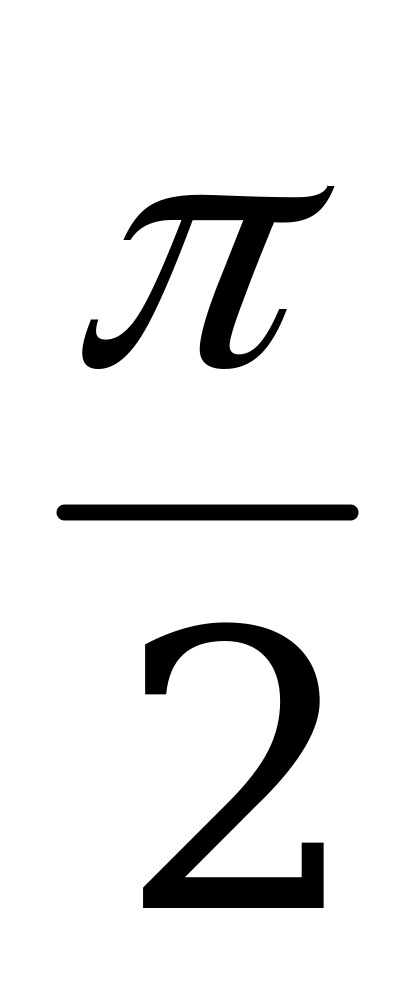
| 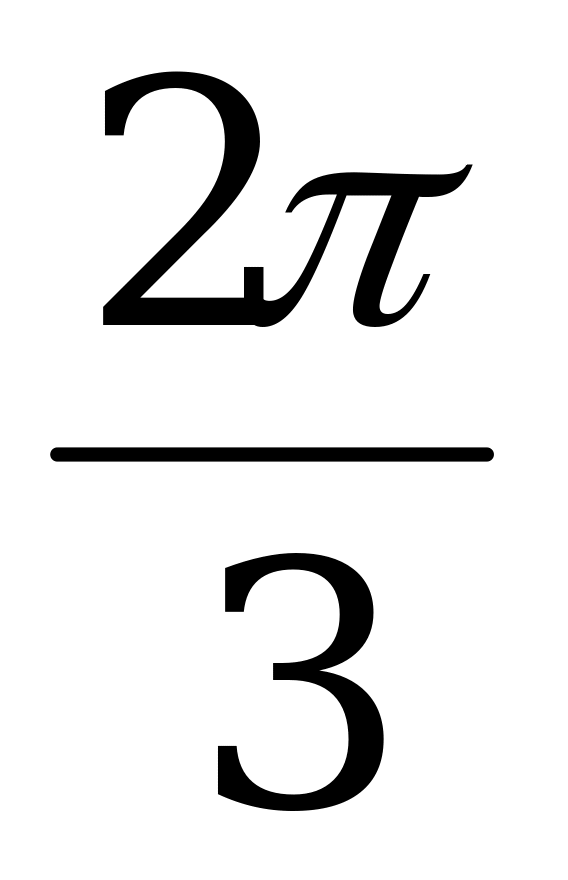
| 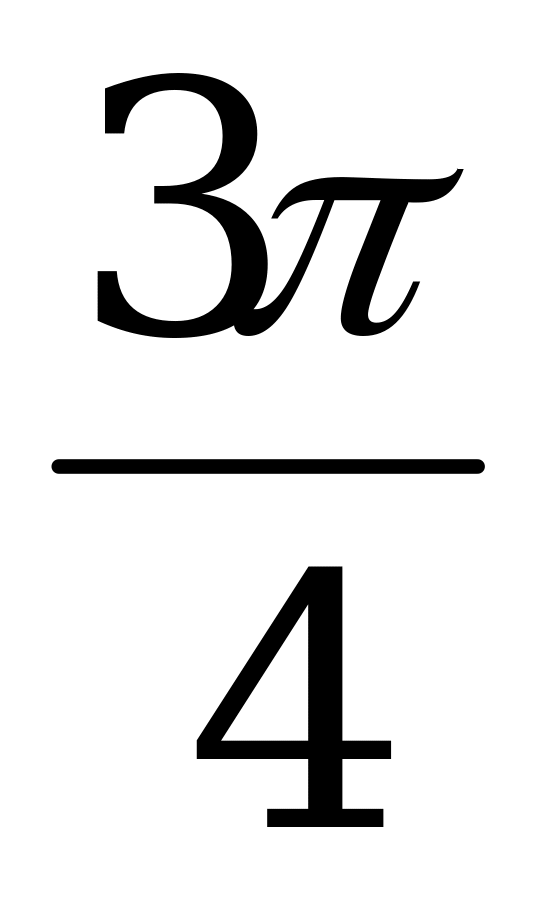
| 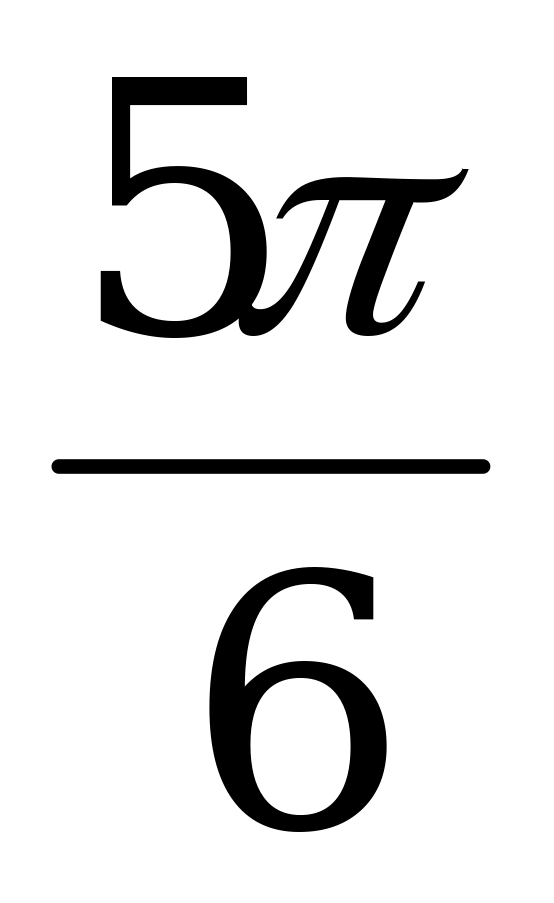
| 
| 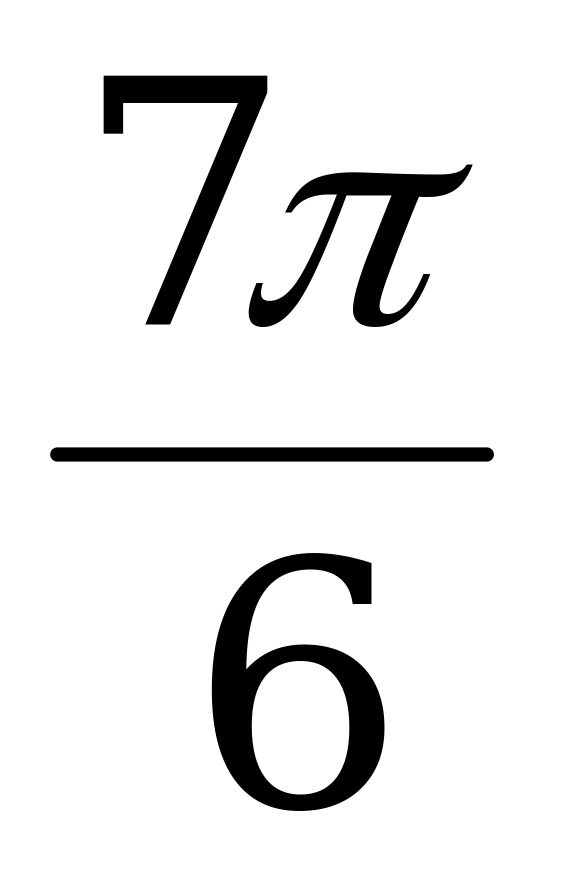
| 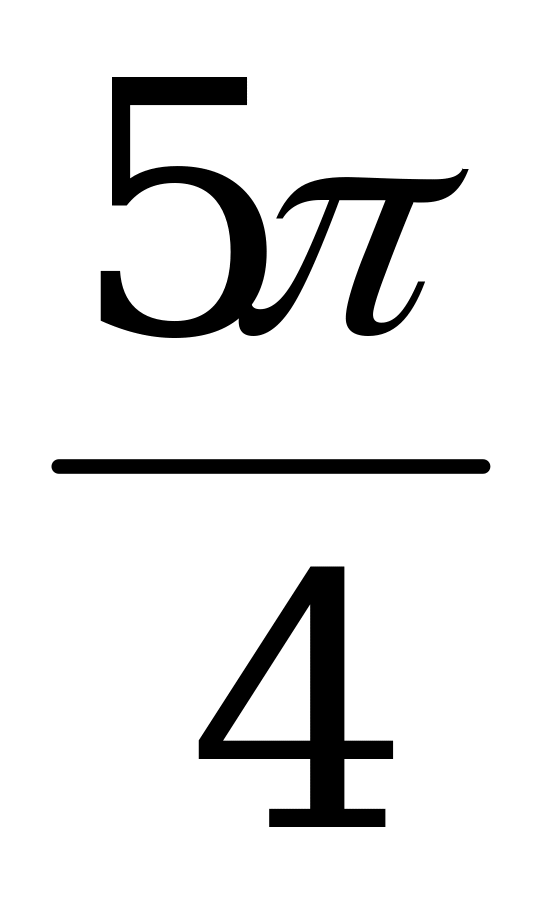
| 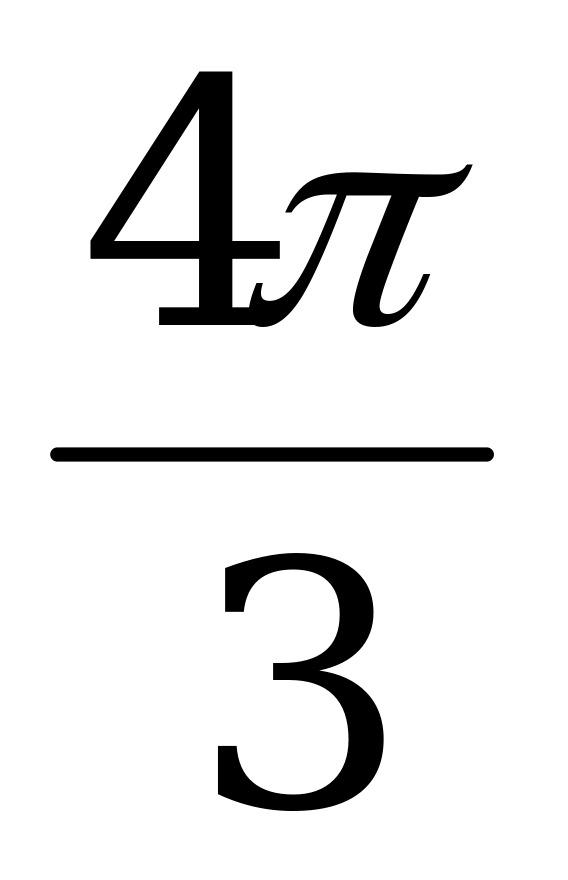
| 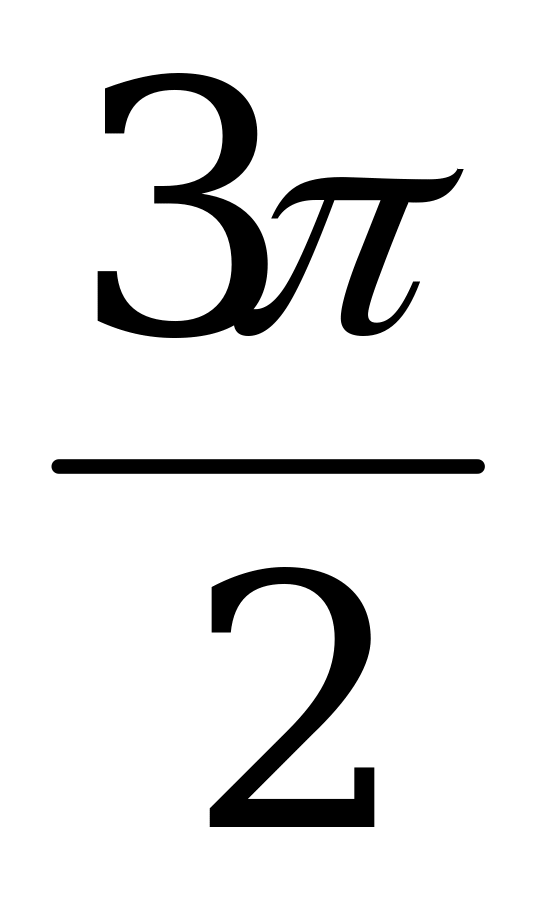
| 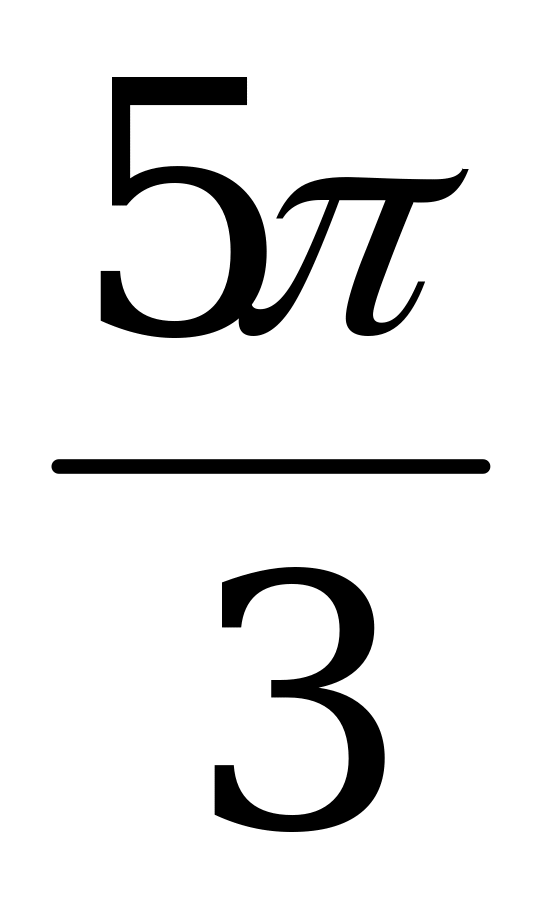
| 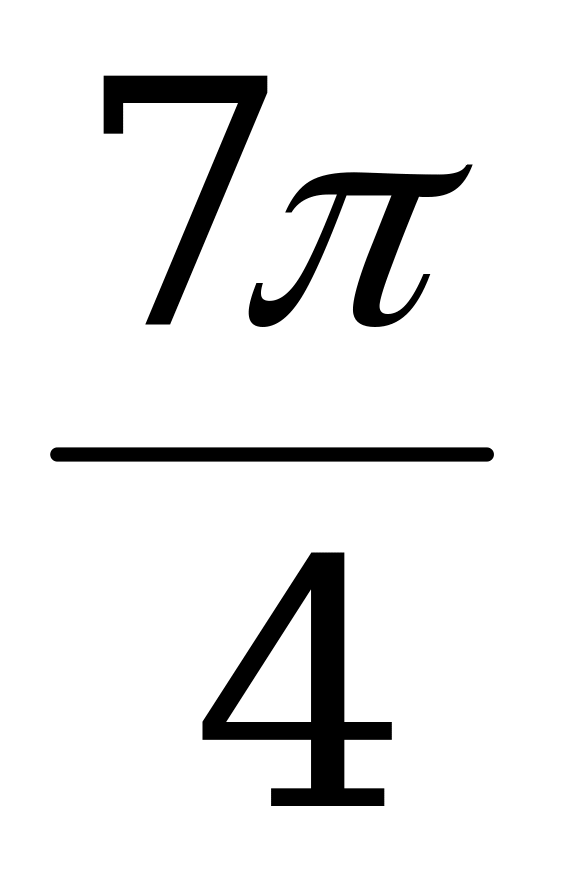
| 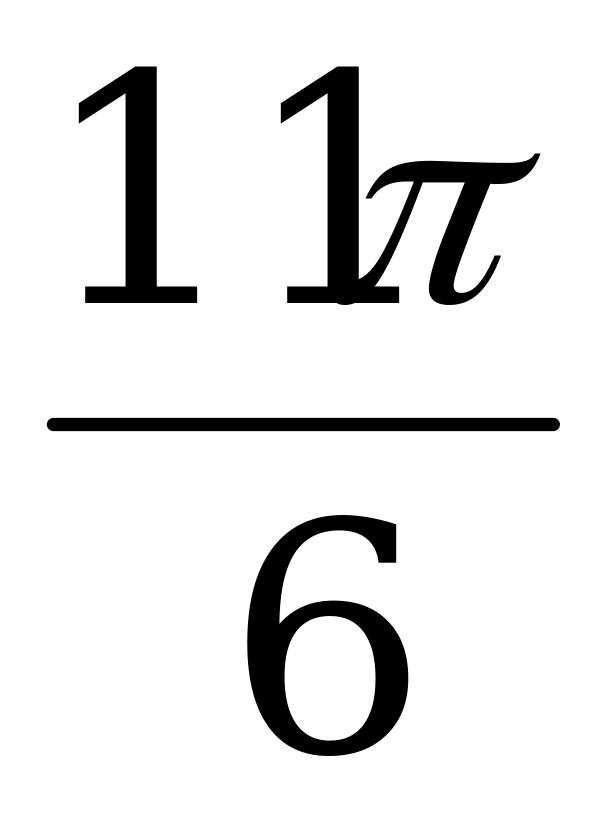
| 
|
| 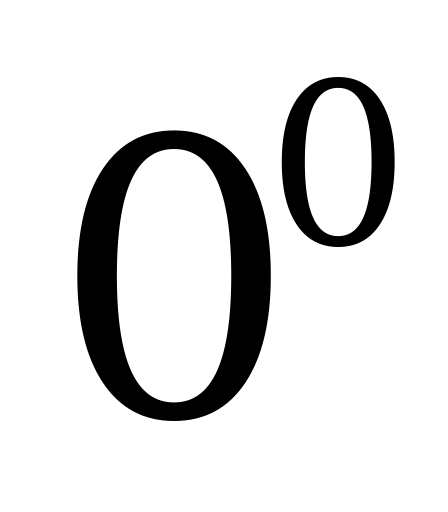
| 
| 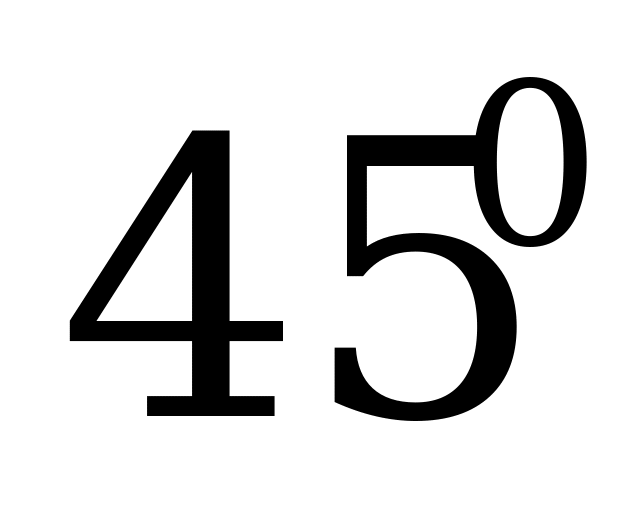
| 
| 
| 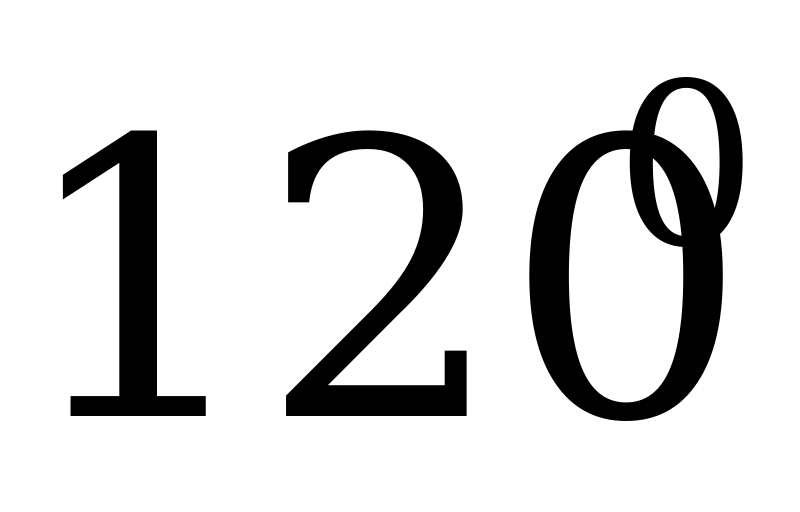
| 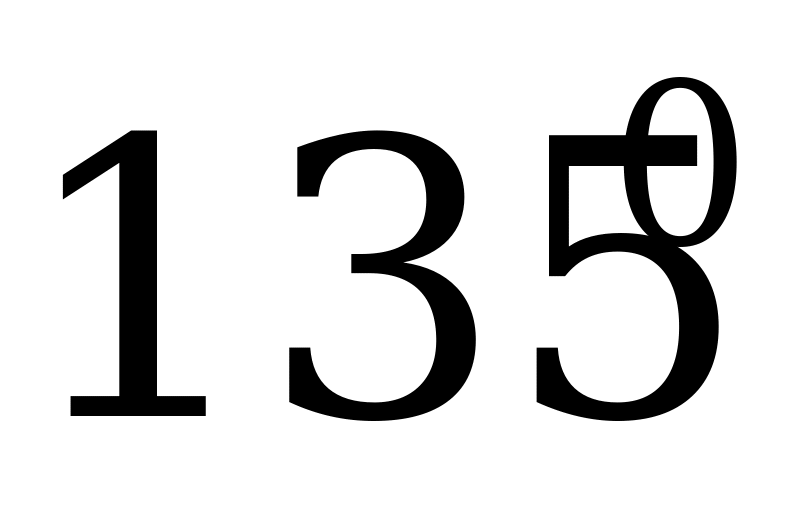
| 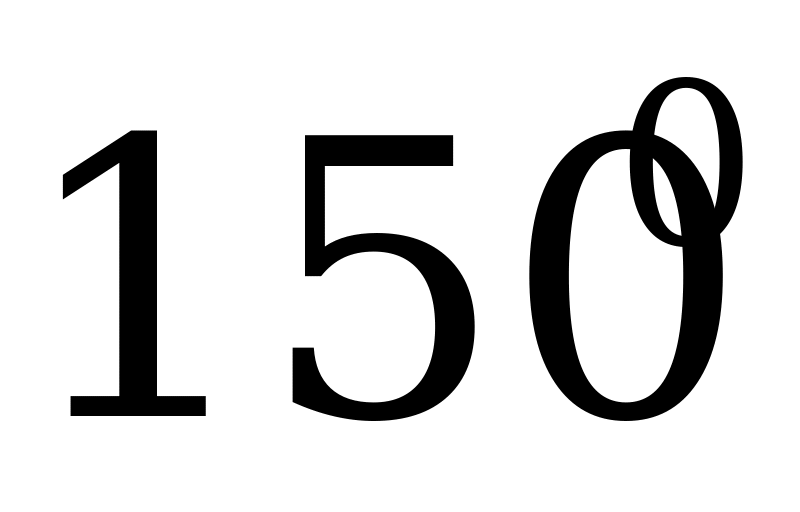
| 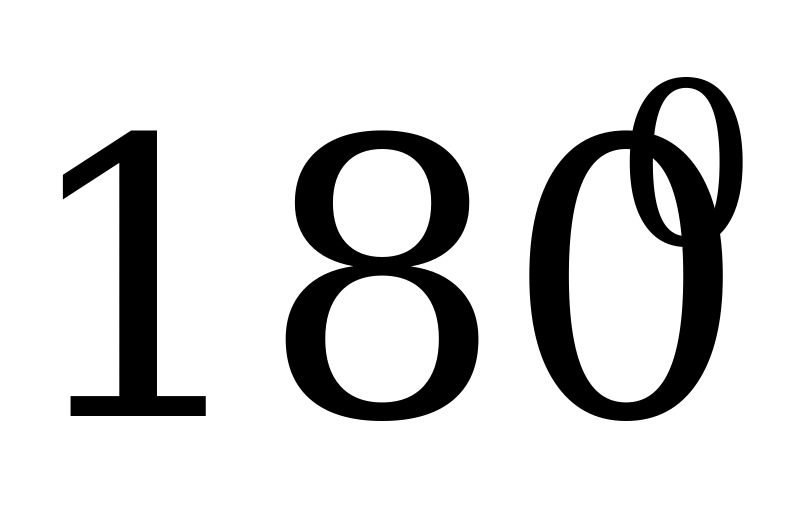
| 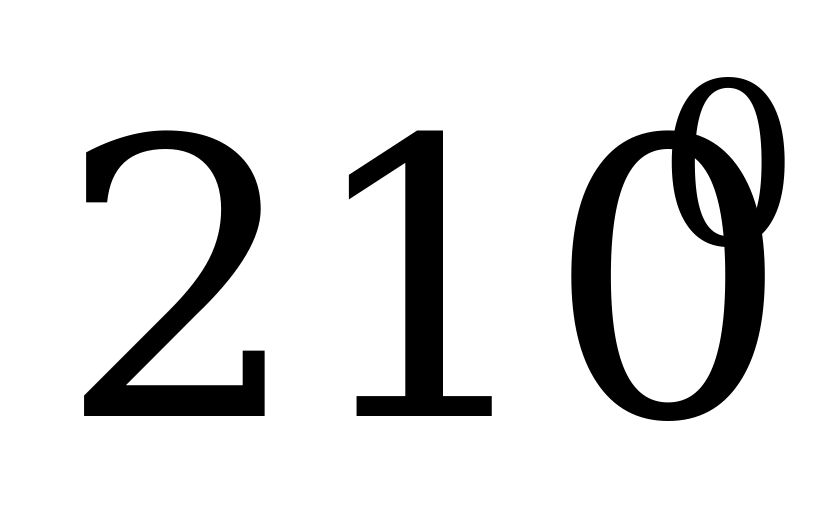
| 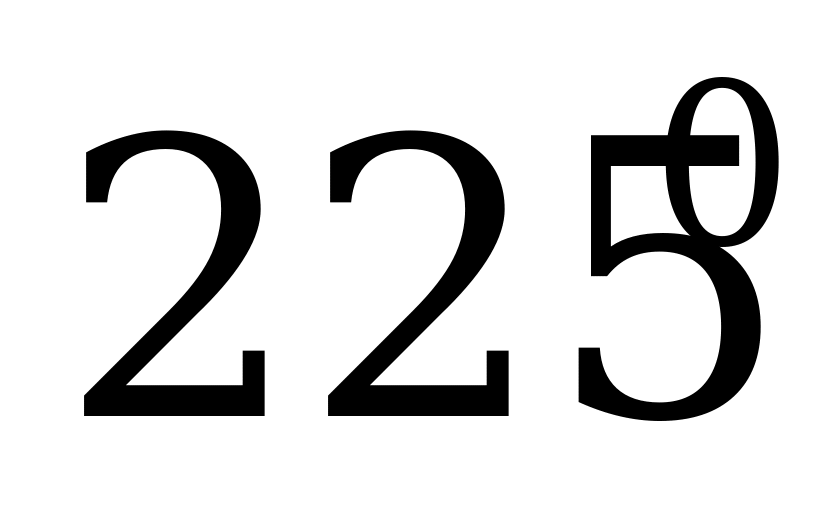
| 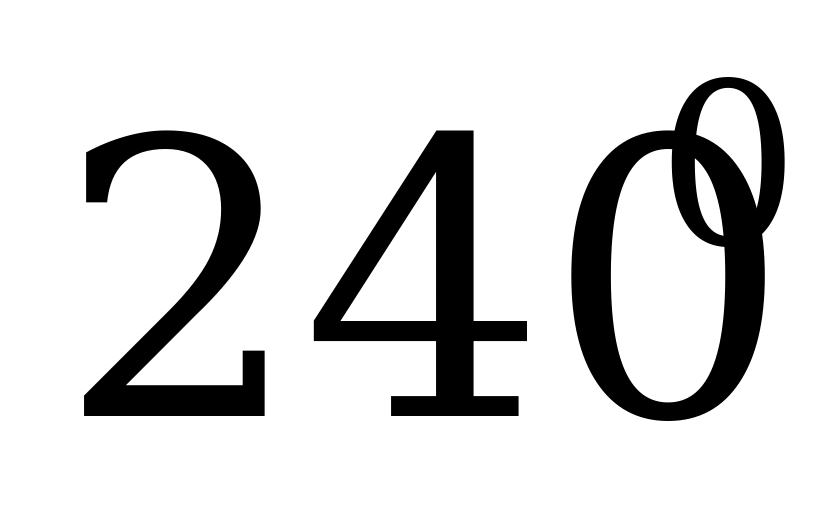
| 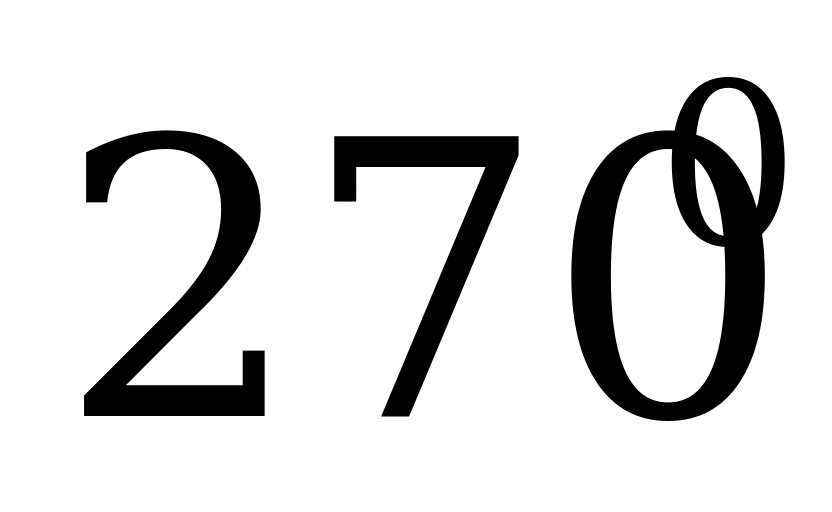
| 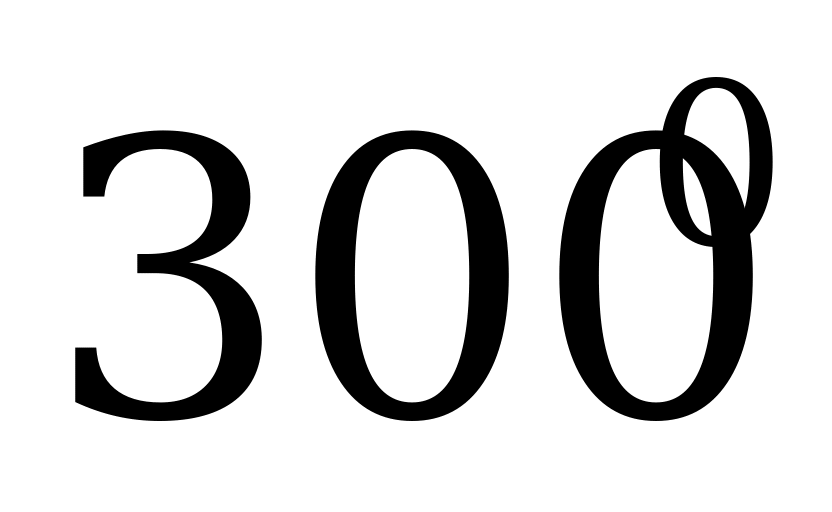
| 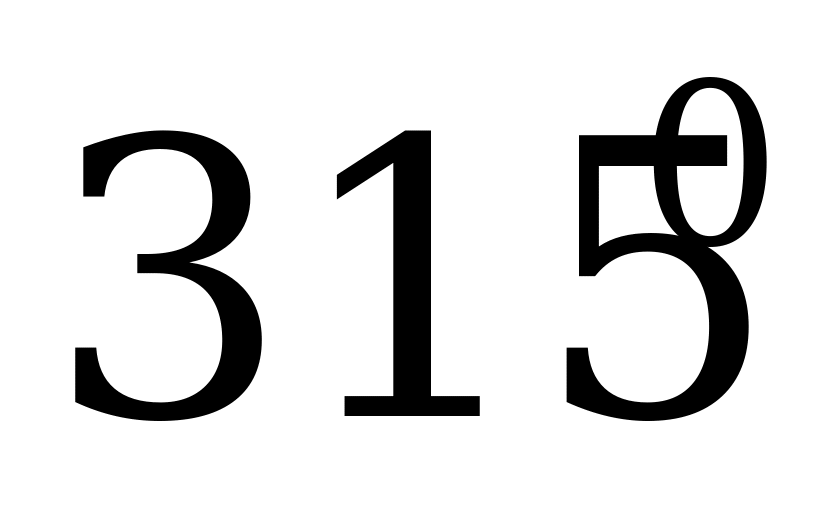
| 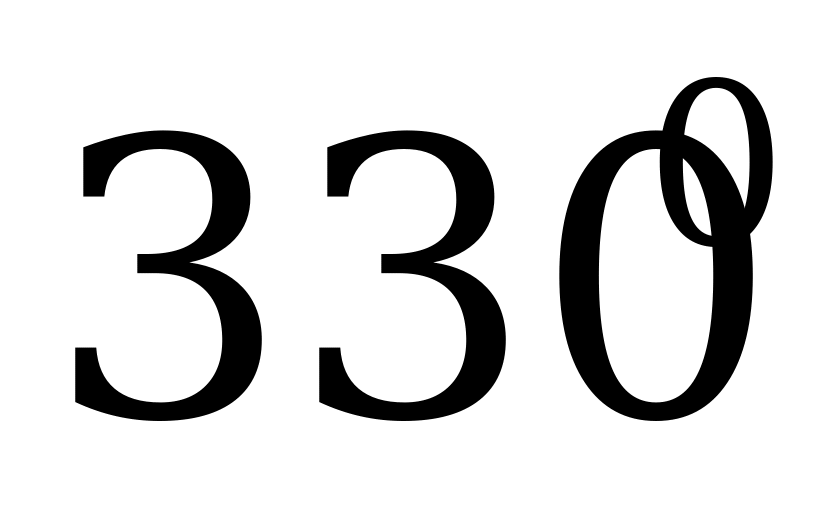
| 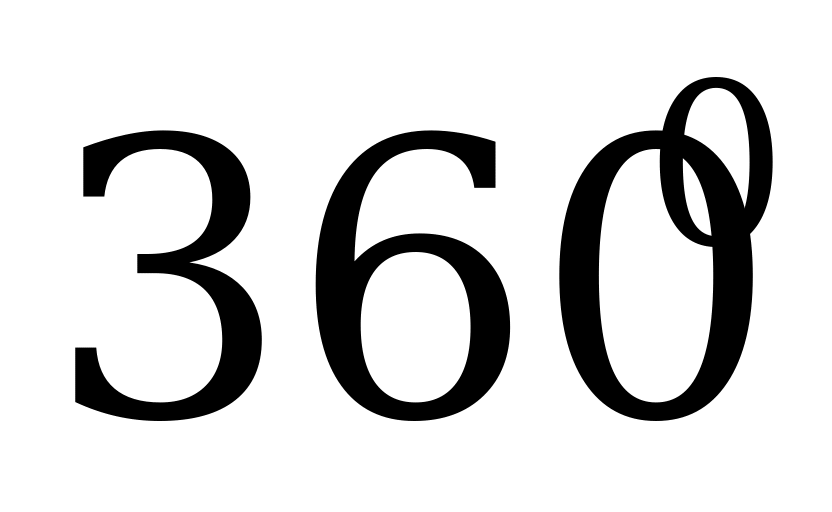
|
| 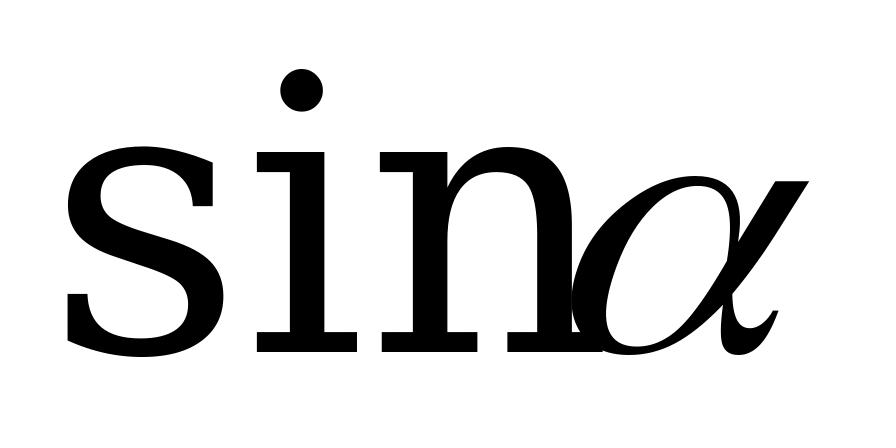
| 0 | 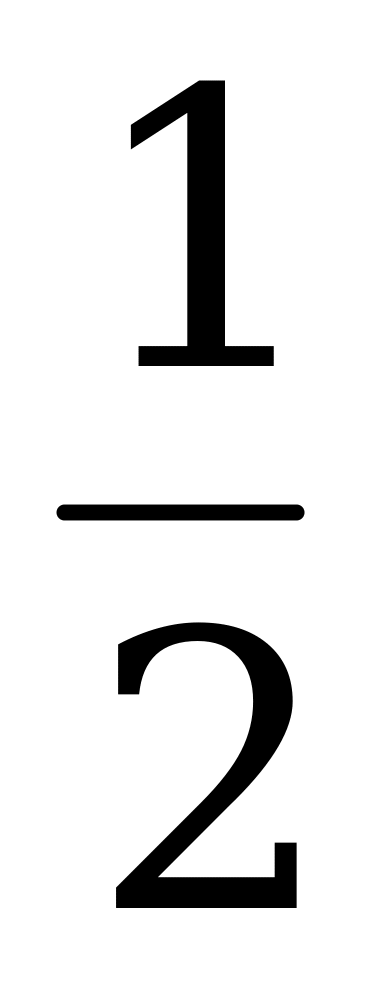
| 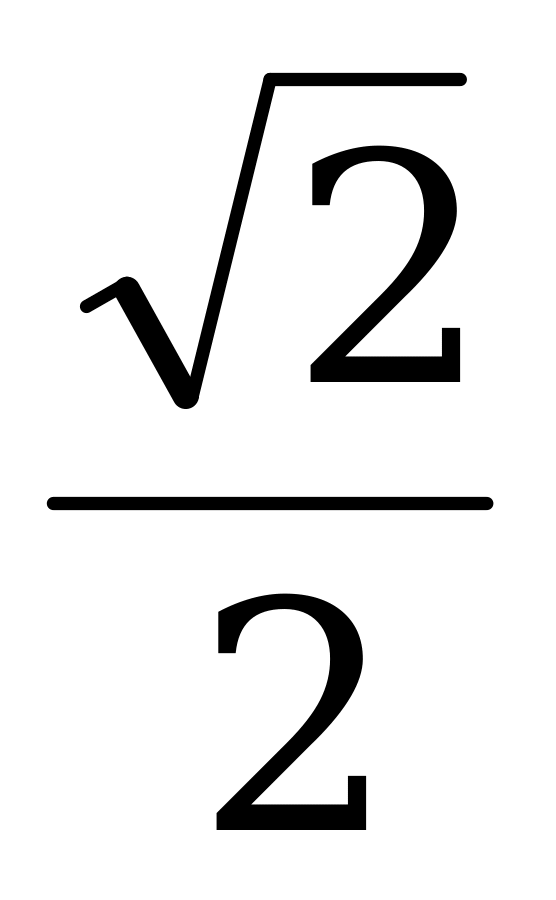
| 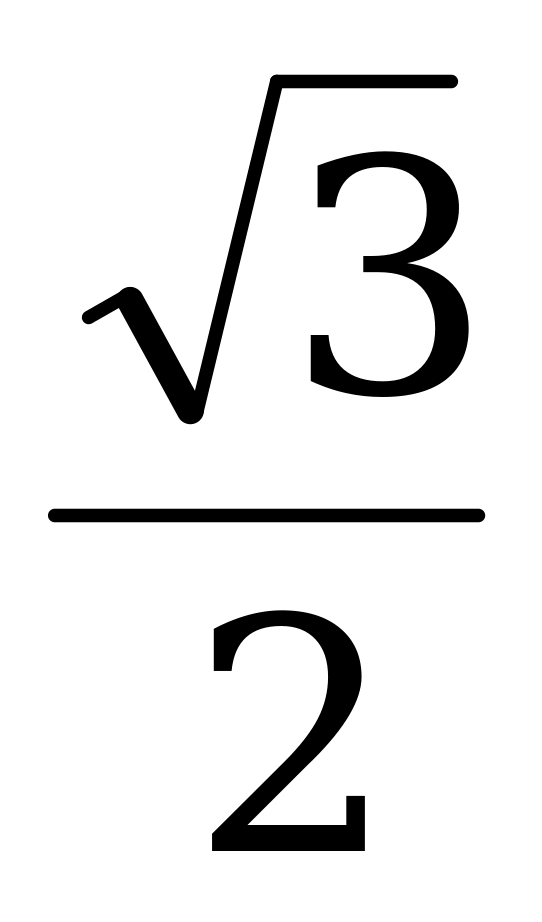
| 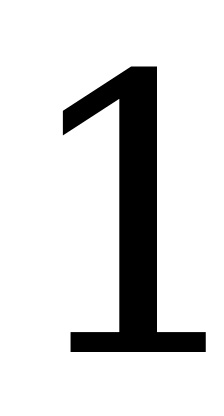
| 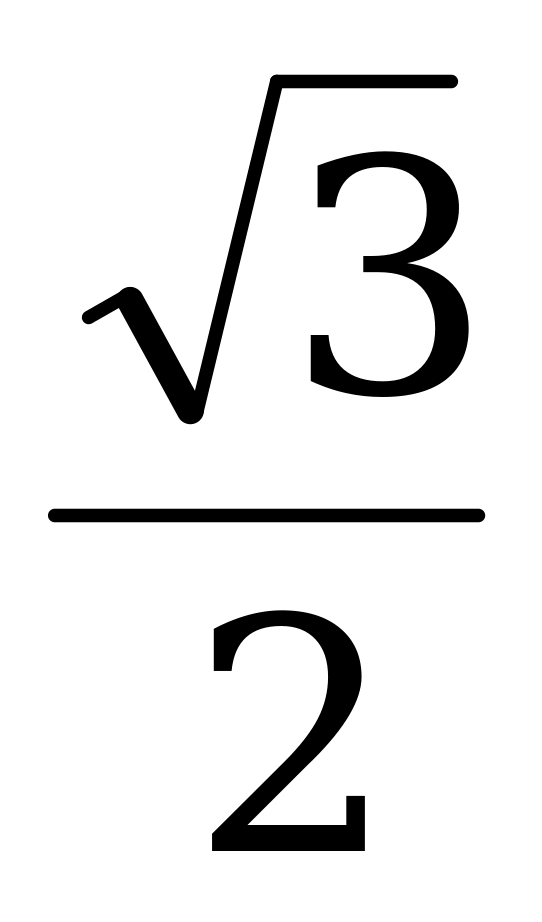
| 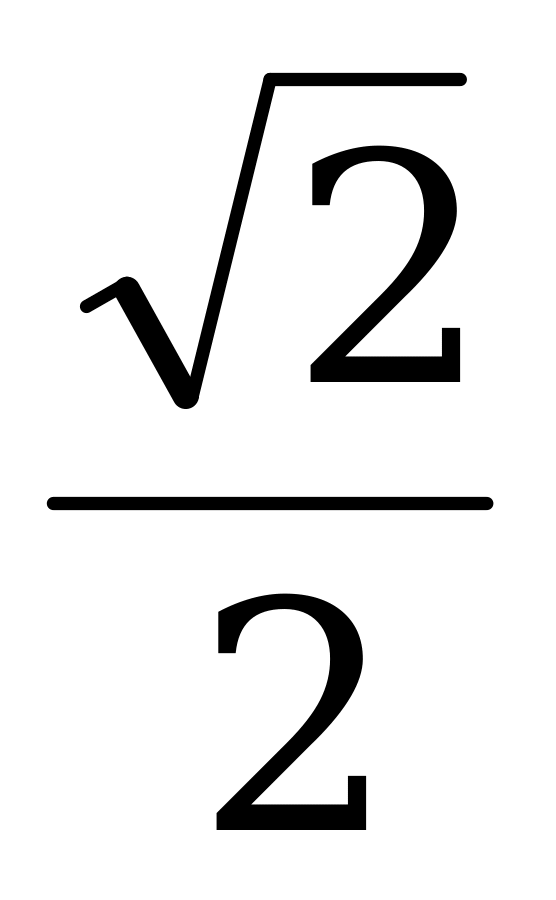
| 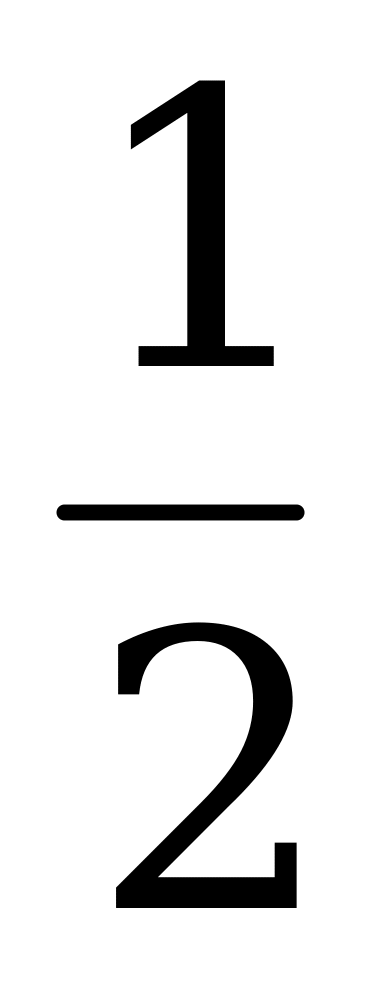
| 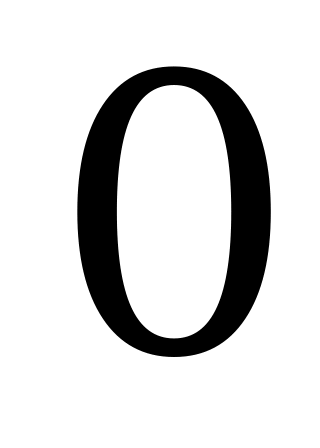
| 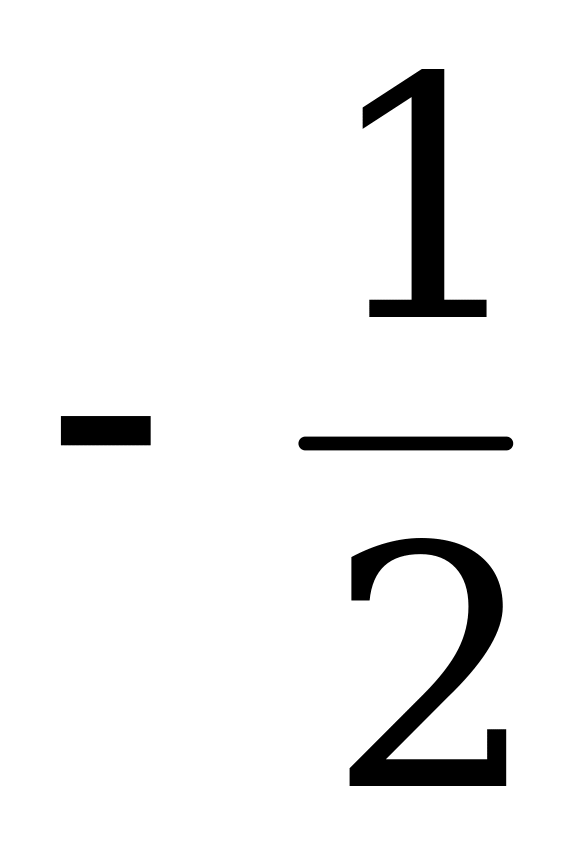
| 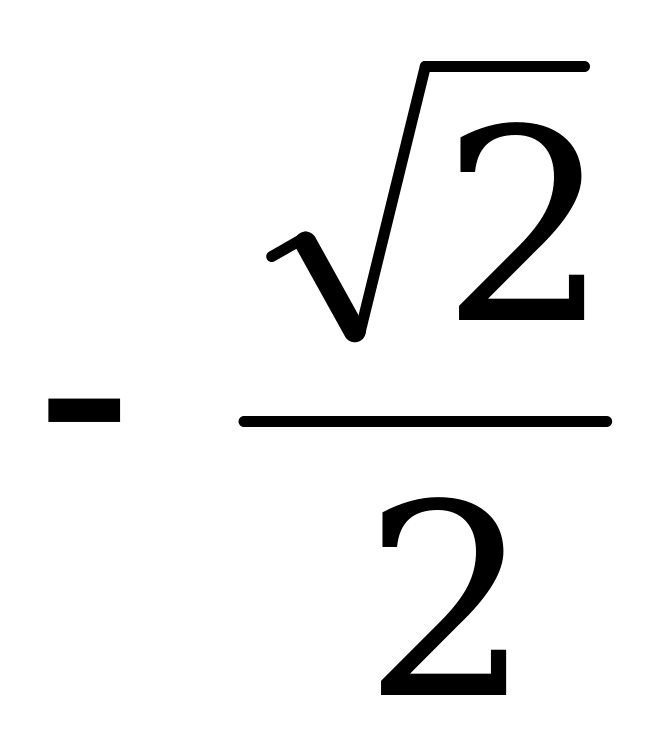
| 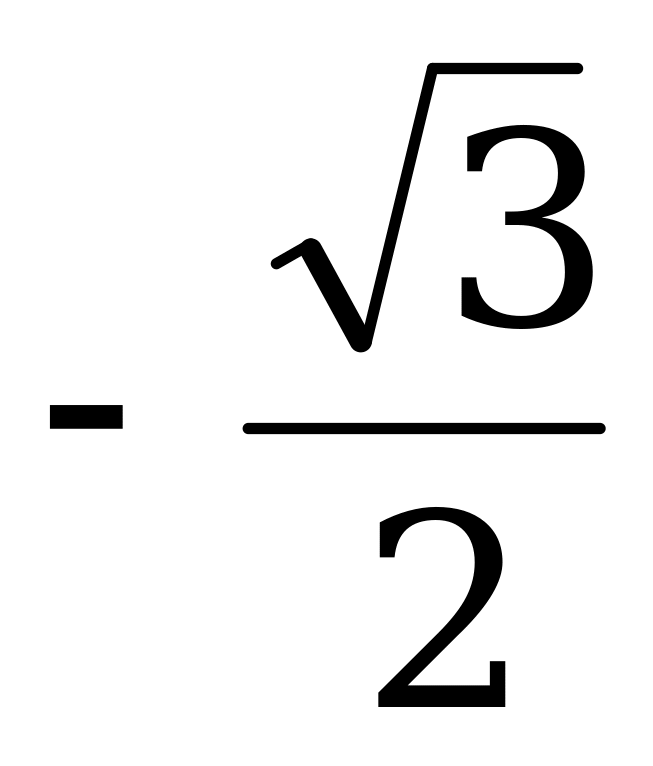
| 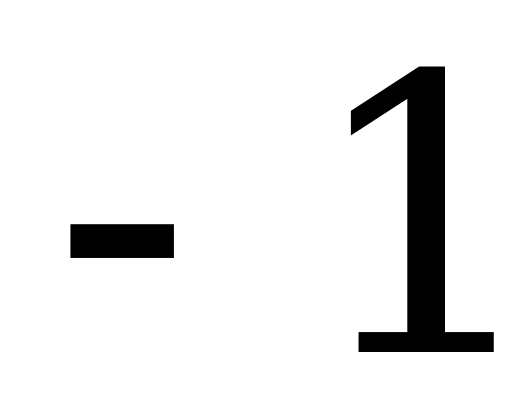
| 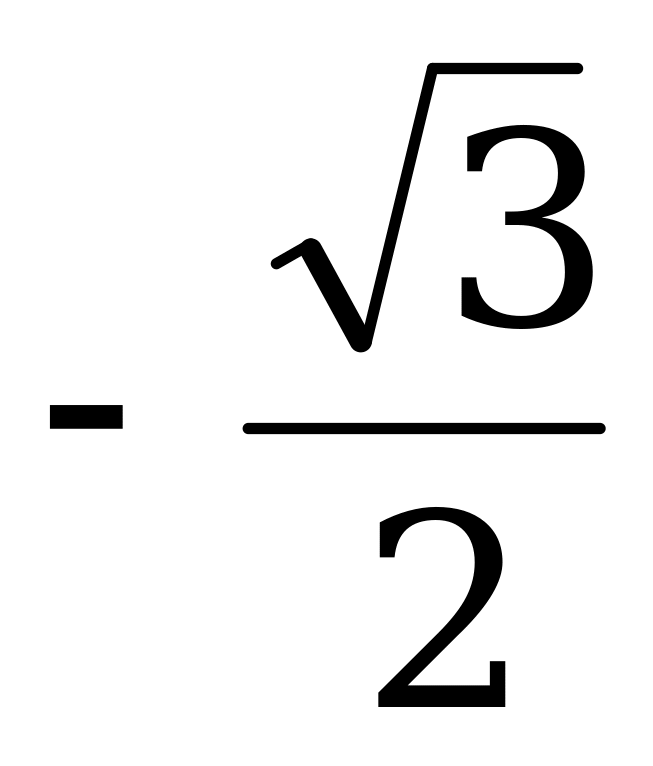
| 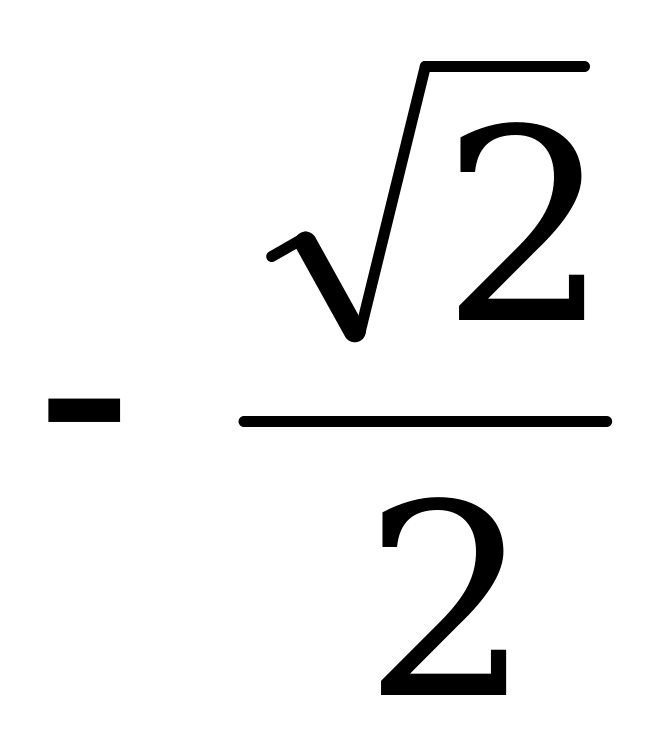
| 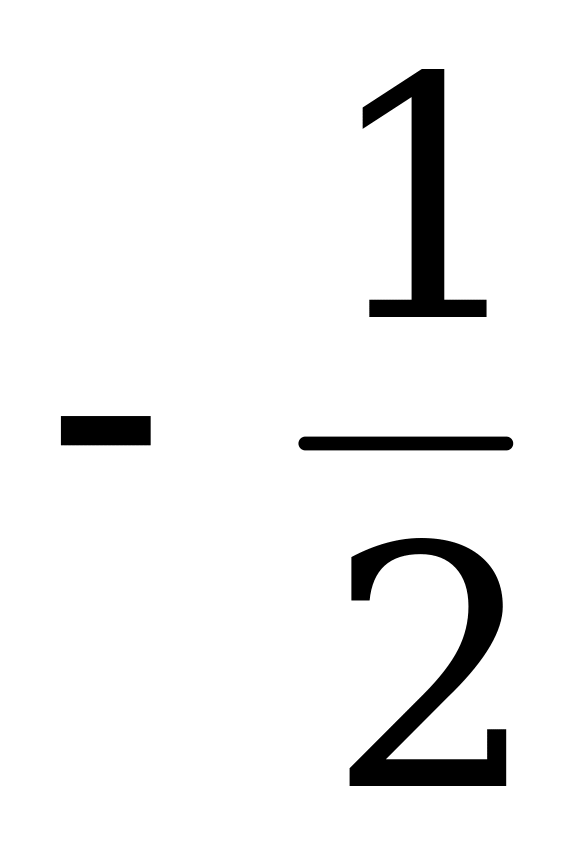
| 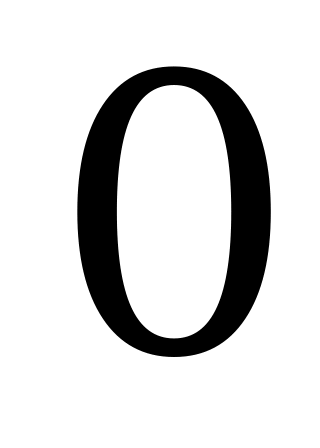
|
| 
| 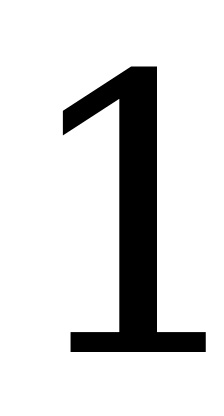
| 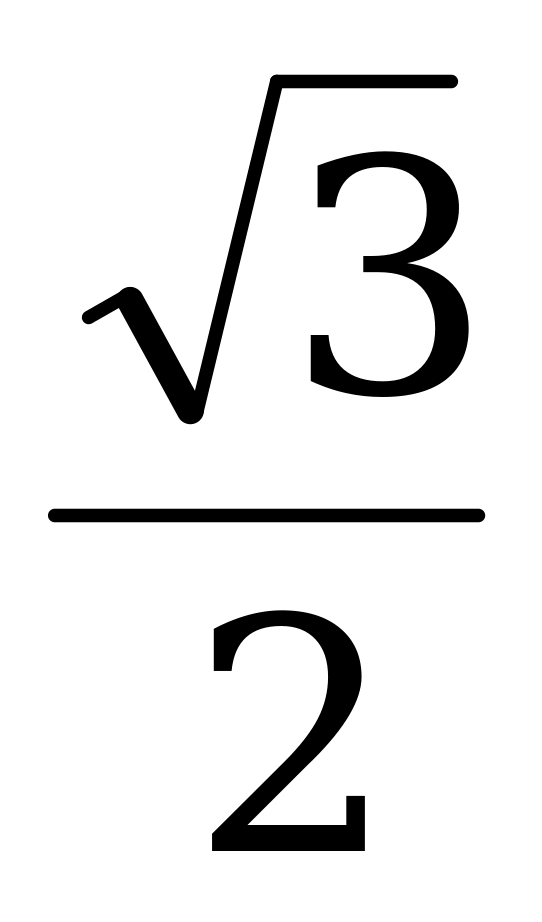
| 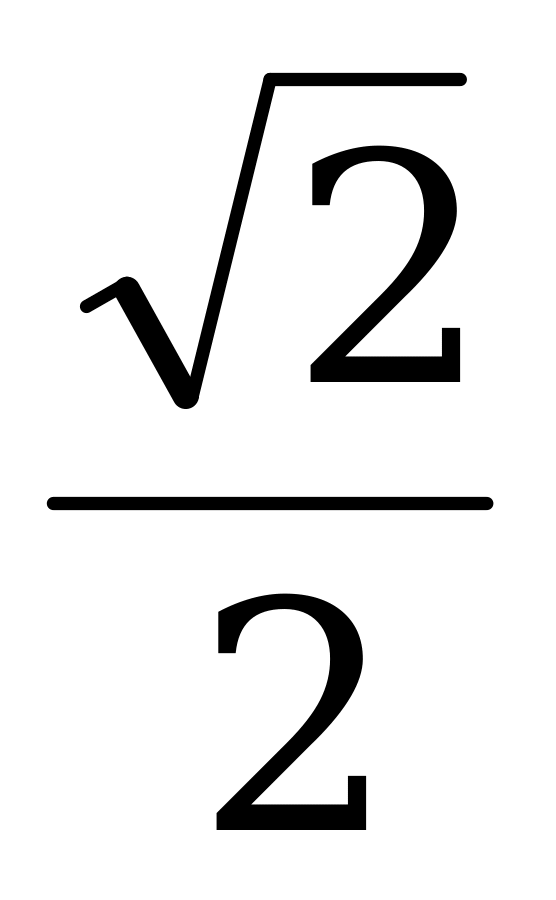
| 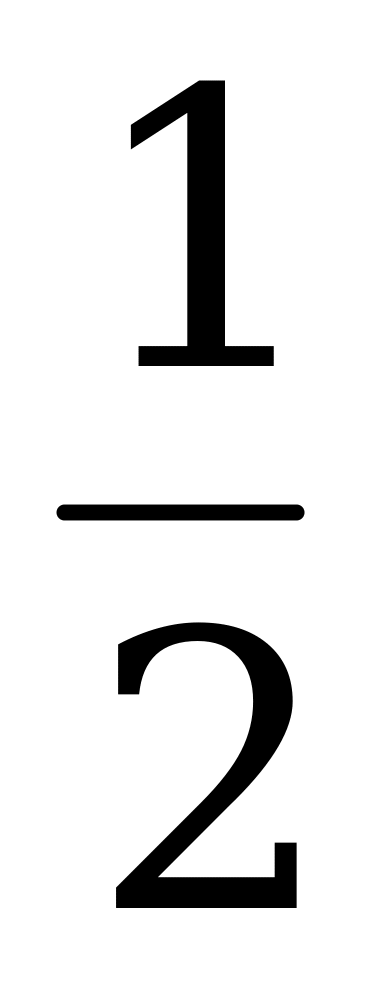
| 0 | 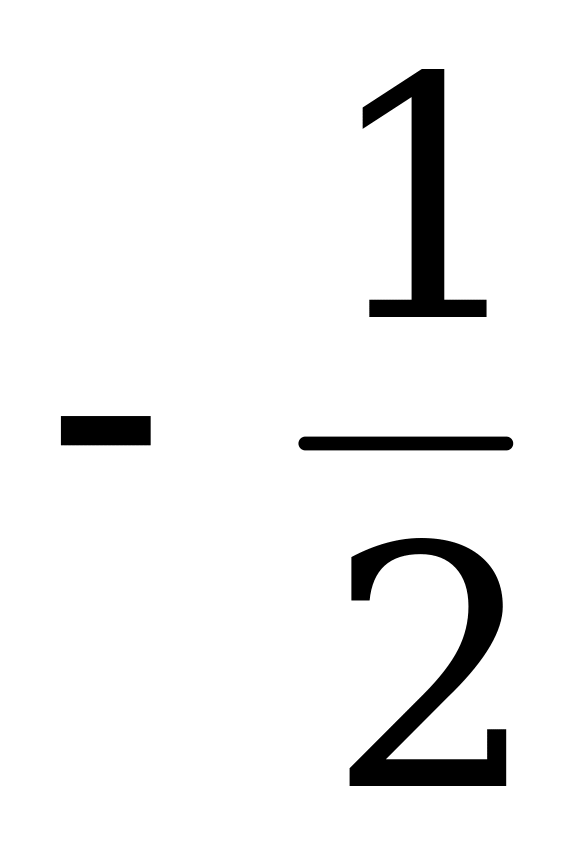
| 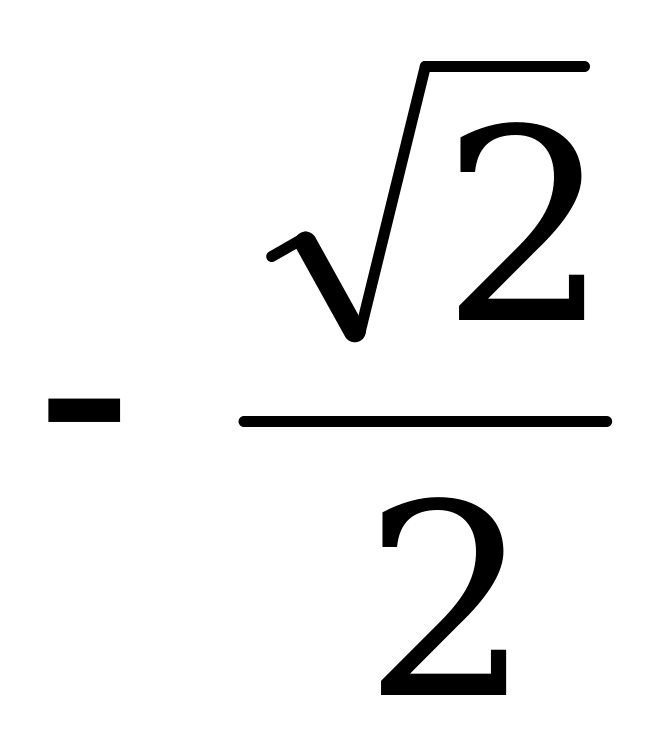
| 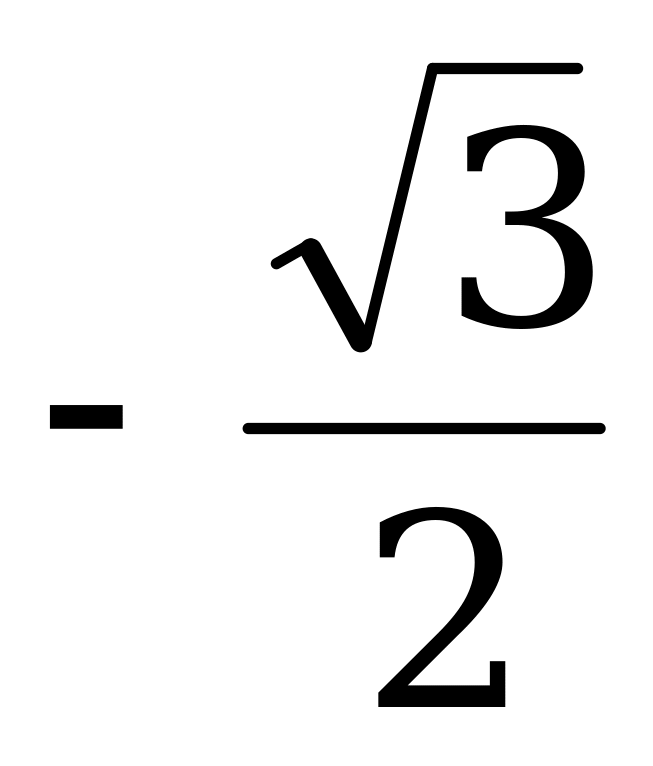
| -1 | 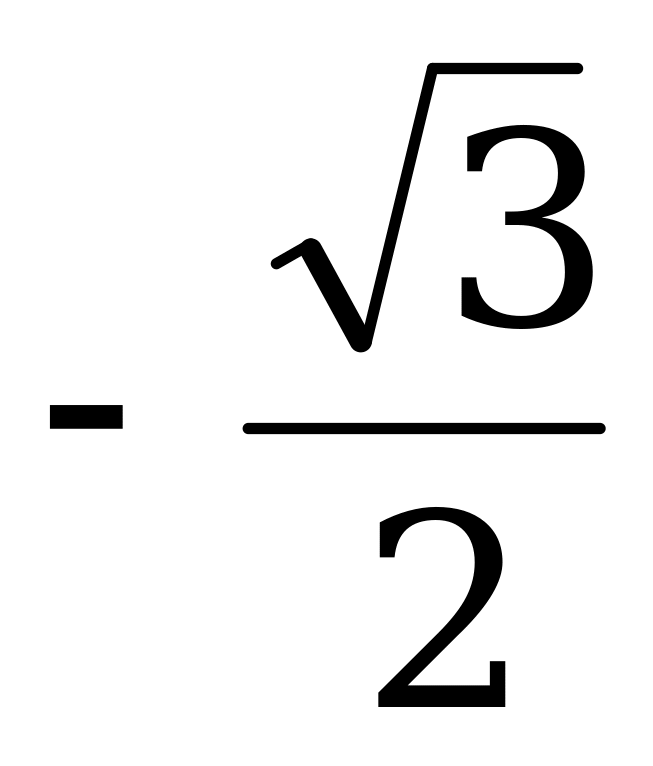
| 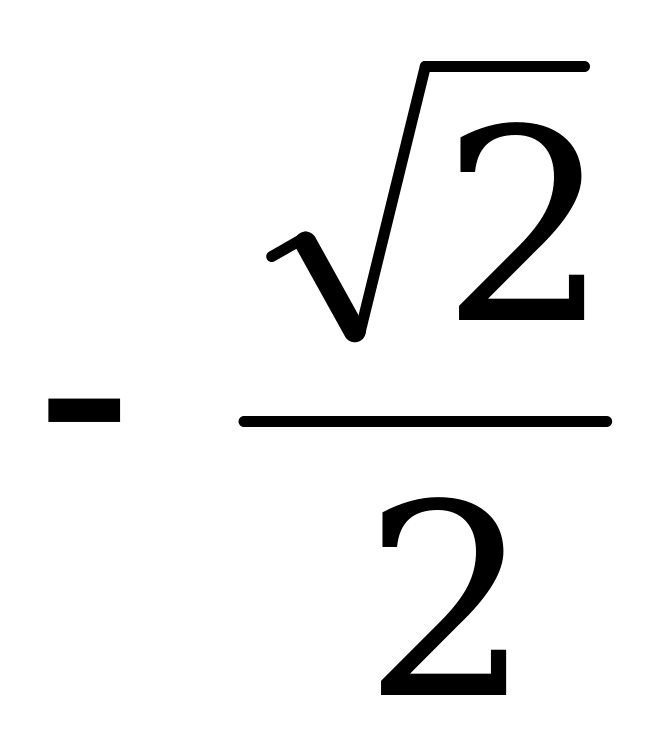
| 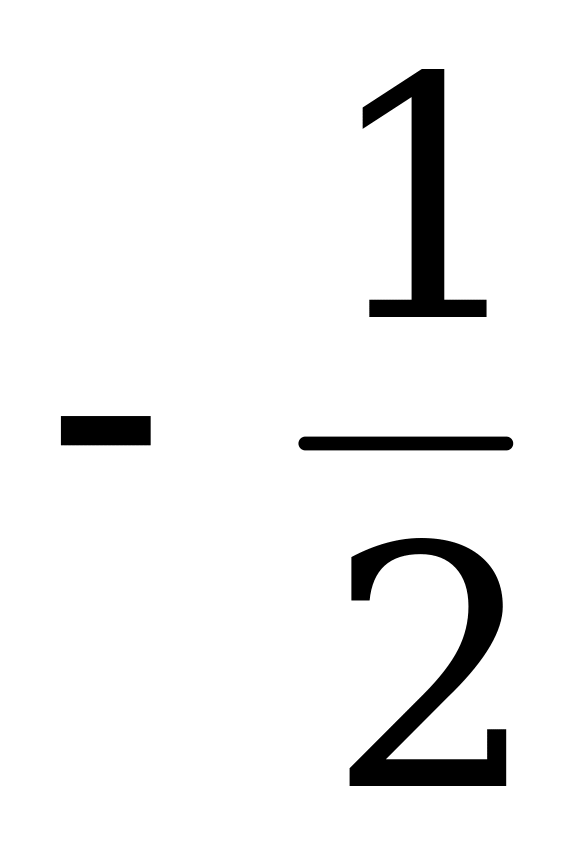
| 0 | 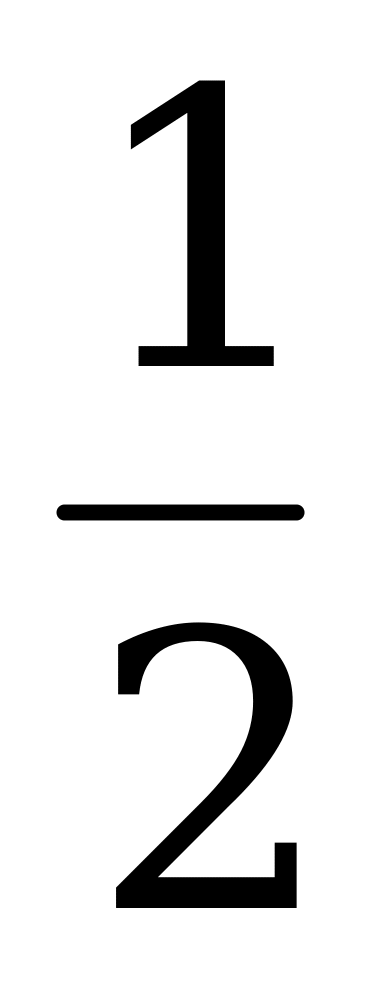
| 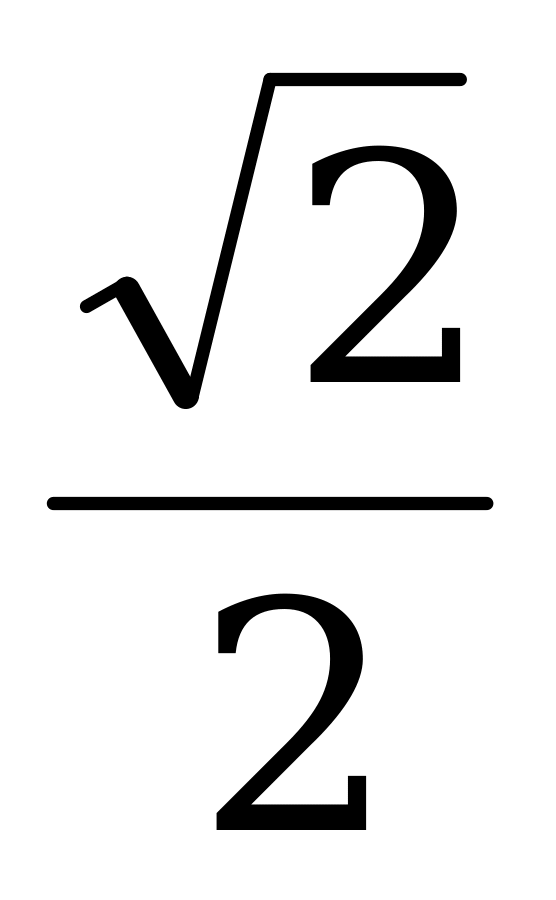
| 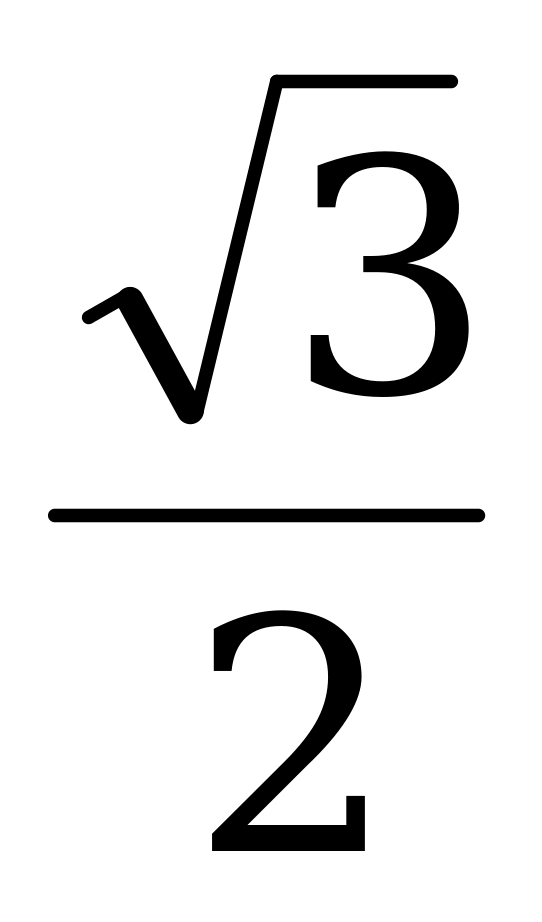
| 1 |
| 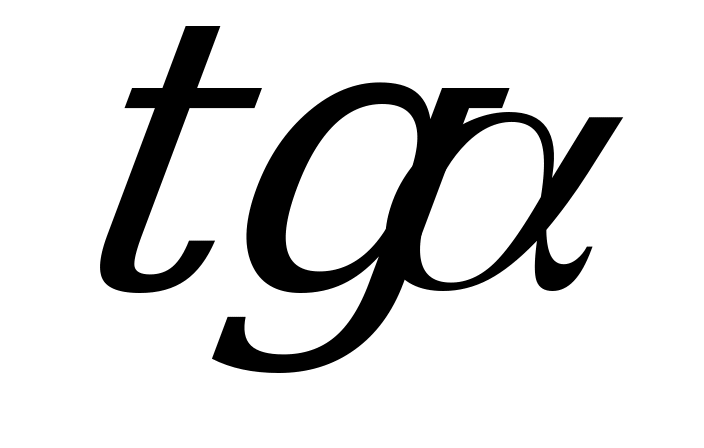
| 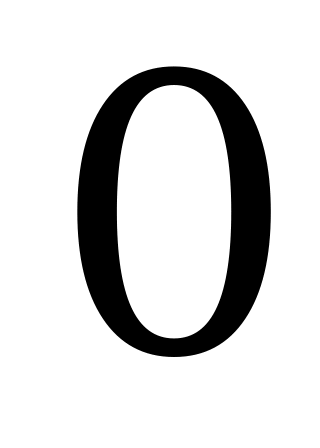
| 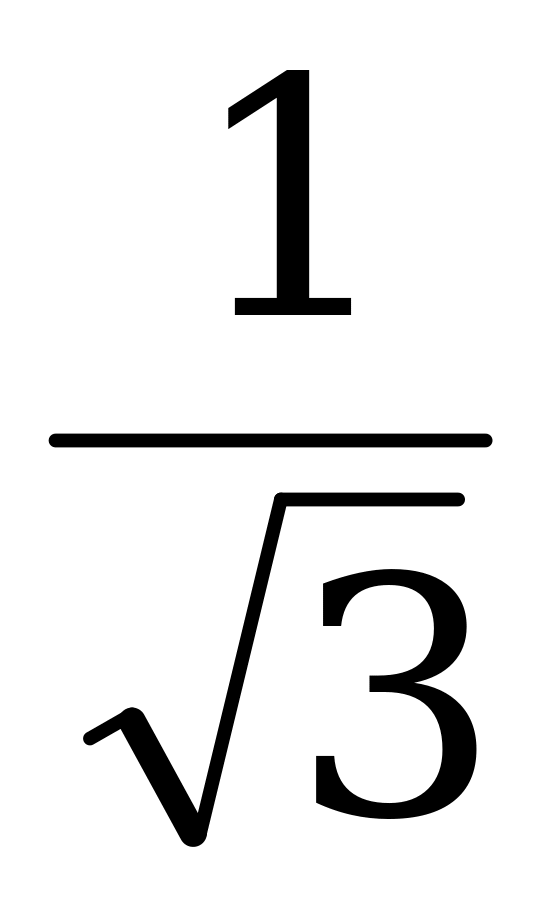
| 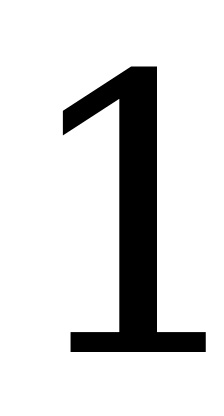
| 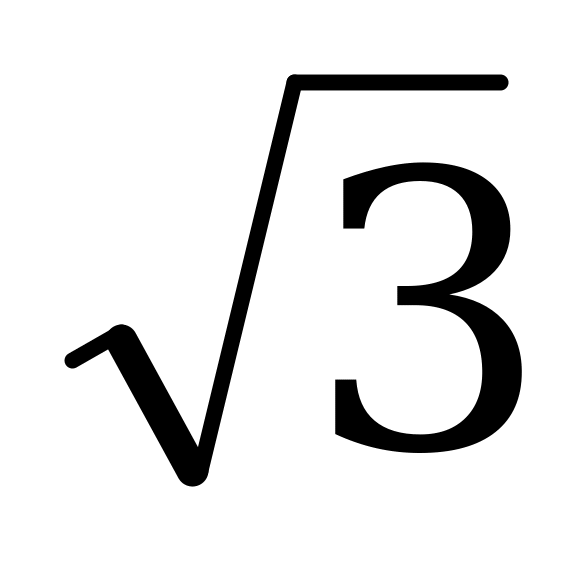
| - | 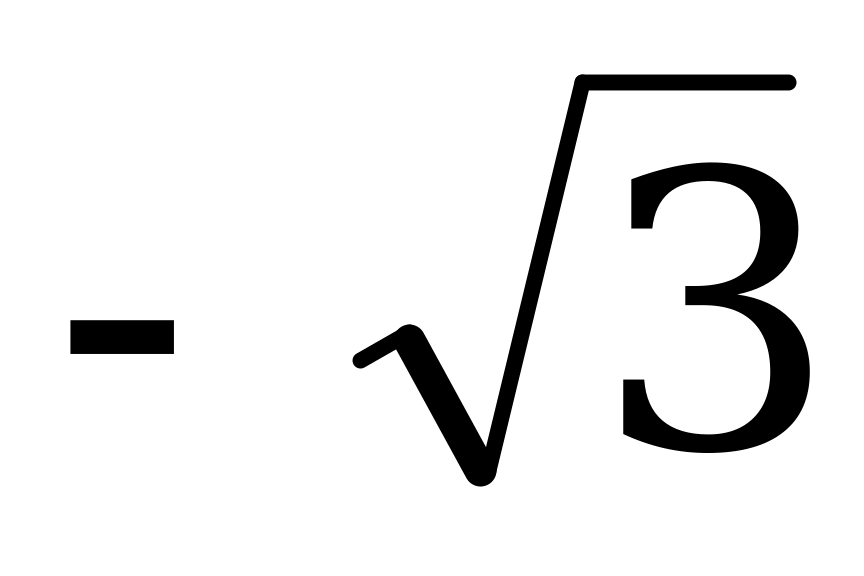
| -1 | 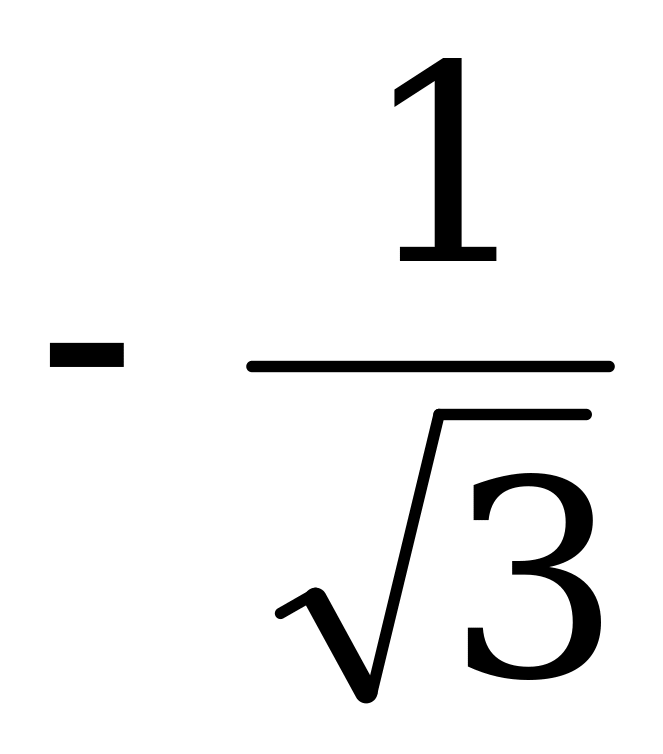
| 0 | 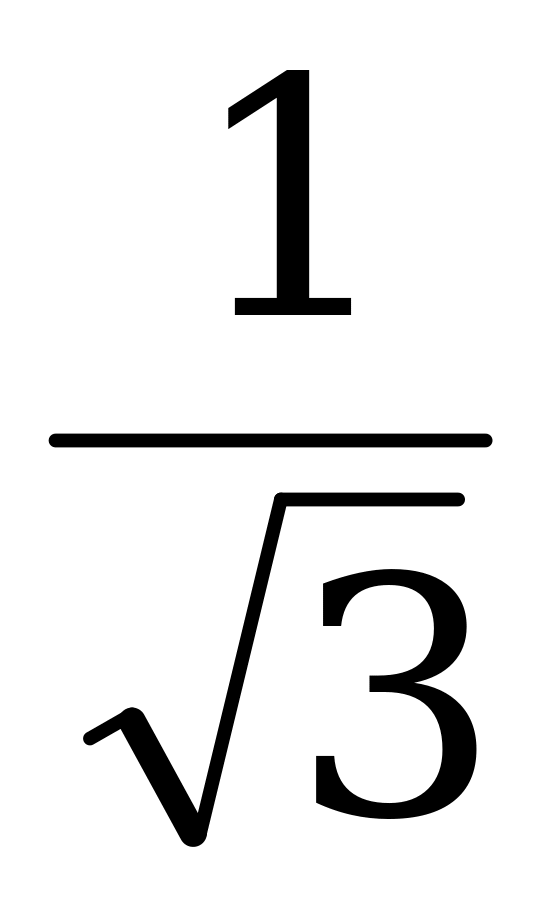
| 1 | 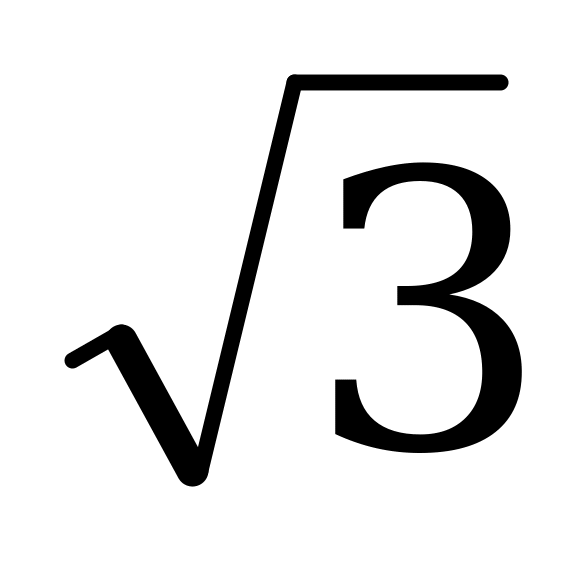
| - | 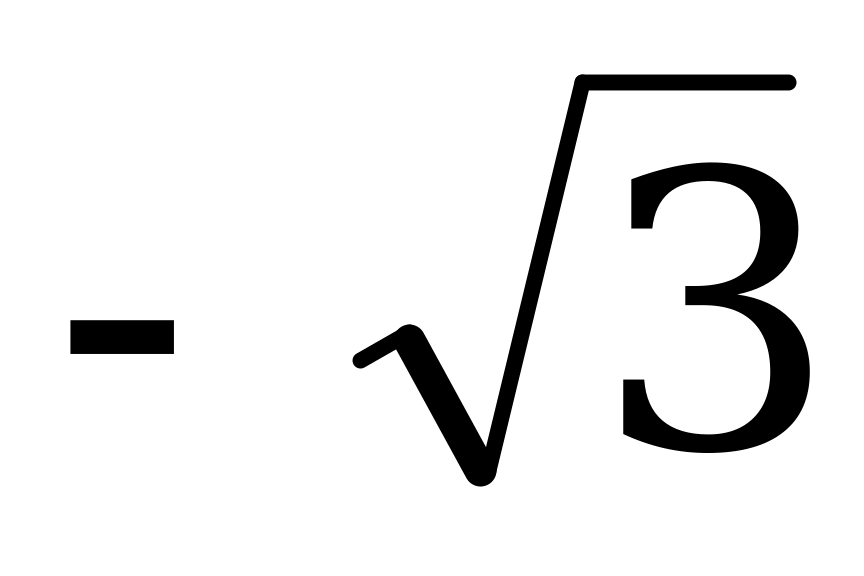
| -1 | 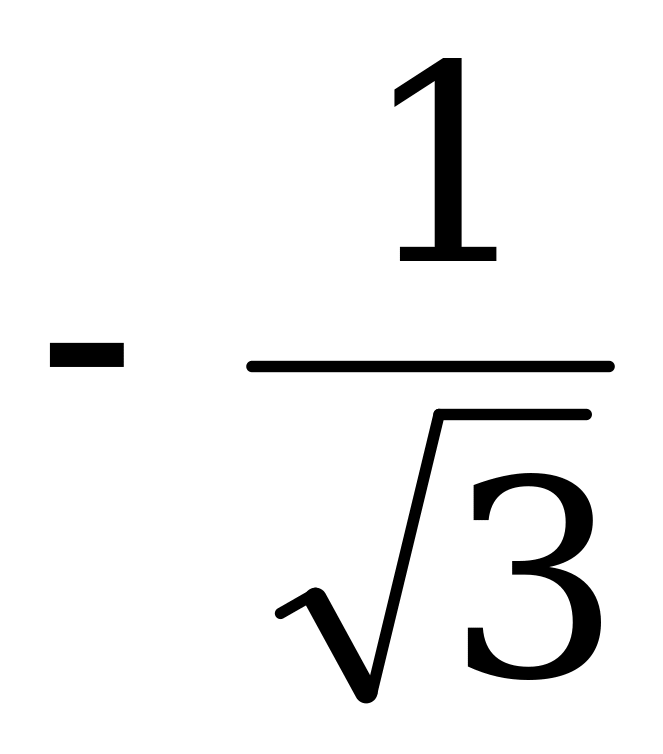
| 0 |
| 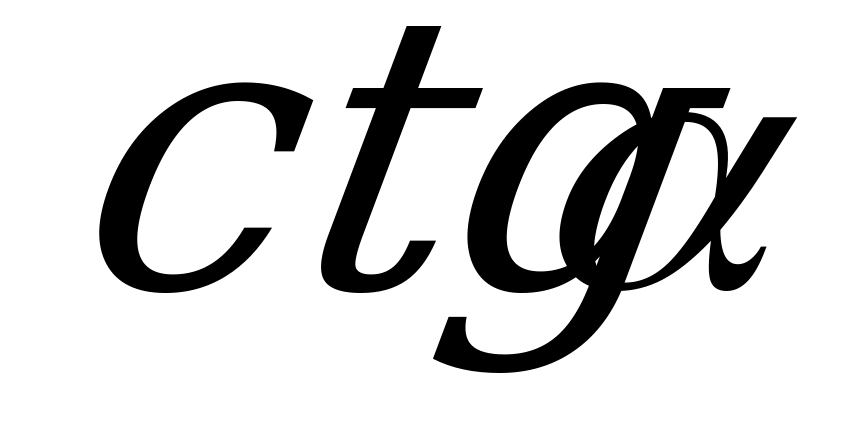
| - | 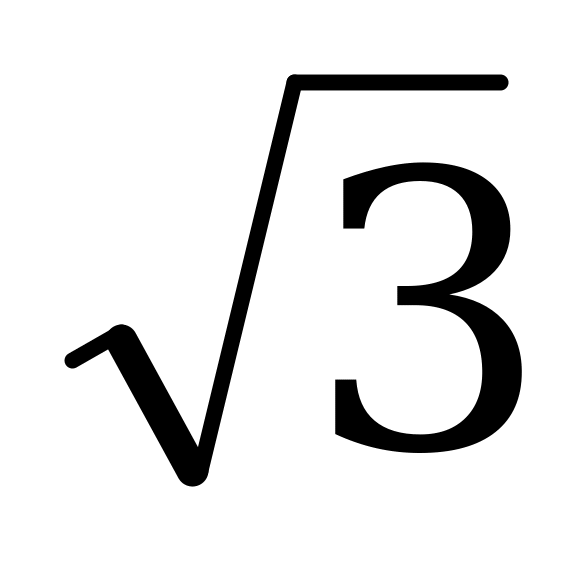
| 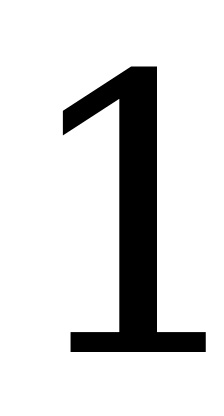
| 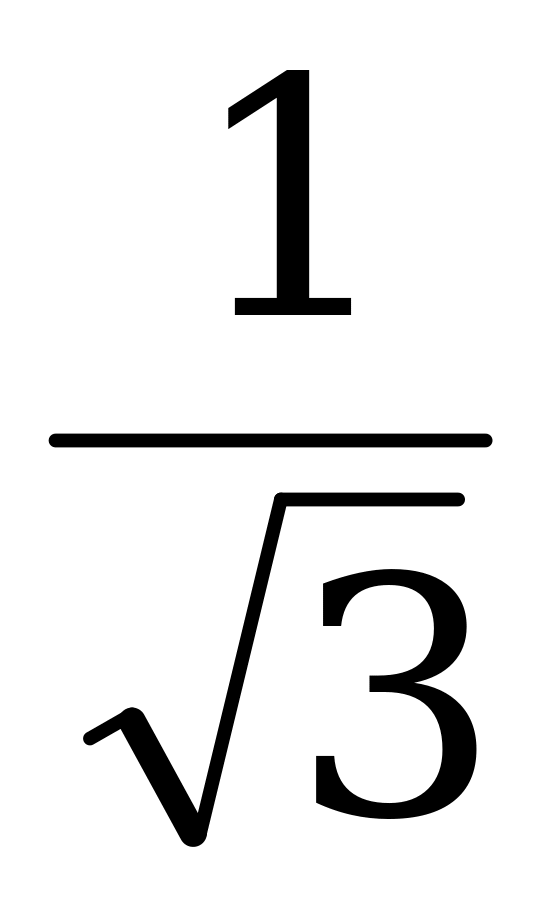
| 0 | 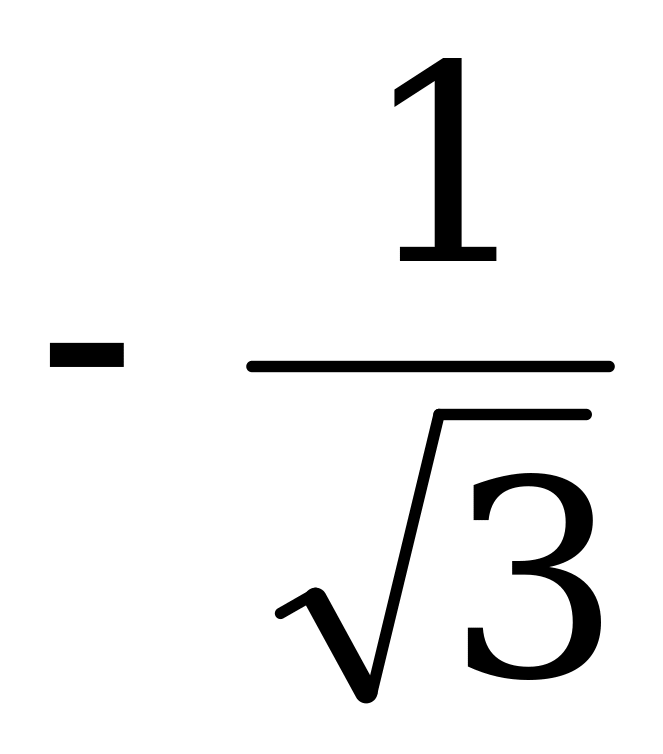
| -1 | 
| - | 
| 1 | 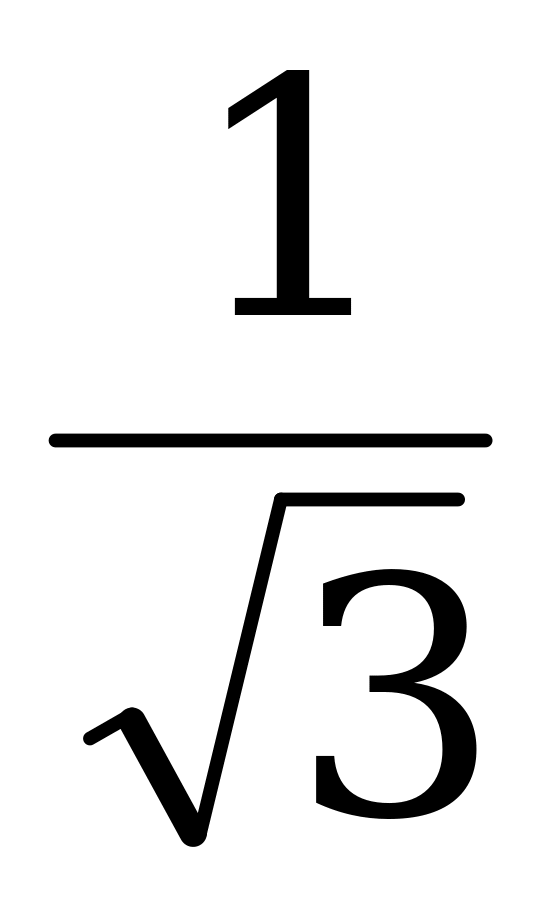
| 0 | 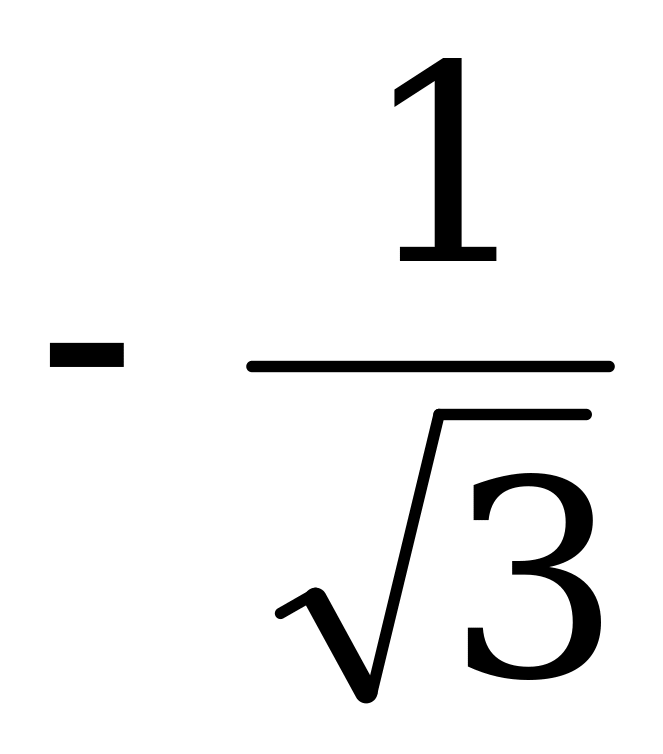
| -1 | 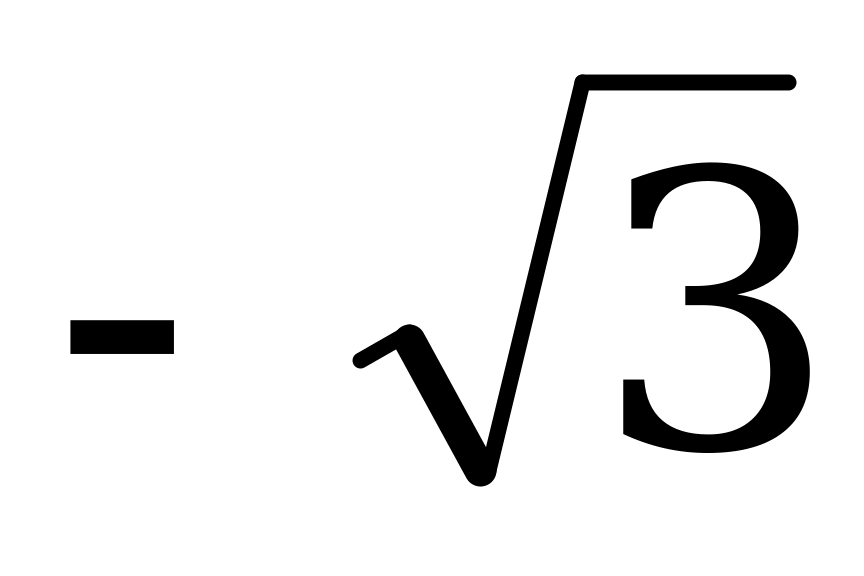
| - |
Формулы сложения
Справочный материал.
cos (α - β) = cos αcos β + sin αsin β; (1)
cos (α + β) = cos αcos β - sin αsin β; (2)
sin (α - β) = sin αcos β - cos αsin β; (3)
sin (α + β) = sin αcos β + cos αsin β; (4)
tg (α + β) = 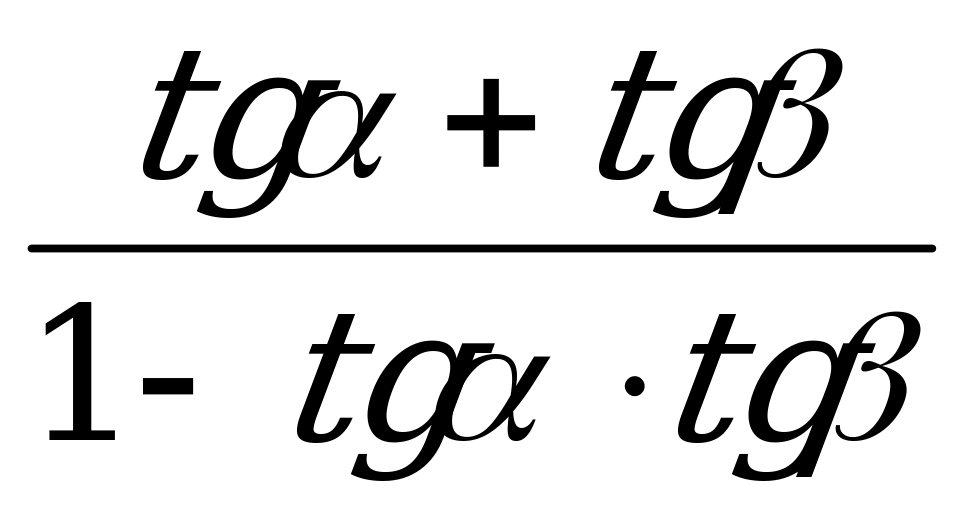 ; (5)
; (5)
tg (α - β) = 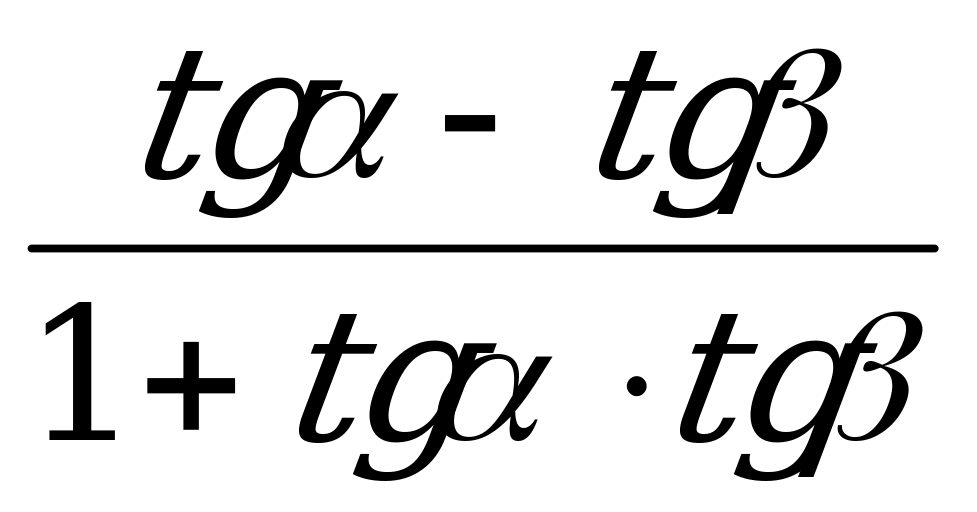 ; (6)
; (6)
Упражнения с решениями.
Пример 1. Вычислите:
а) А = cos 430cos 470 – sin 430sin 470;
б) B = sin 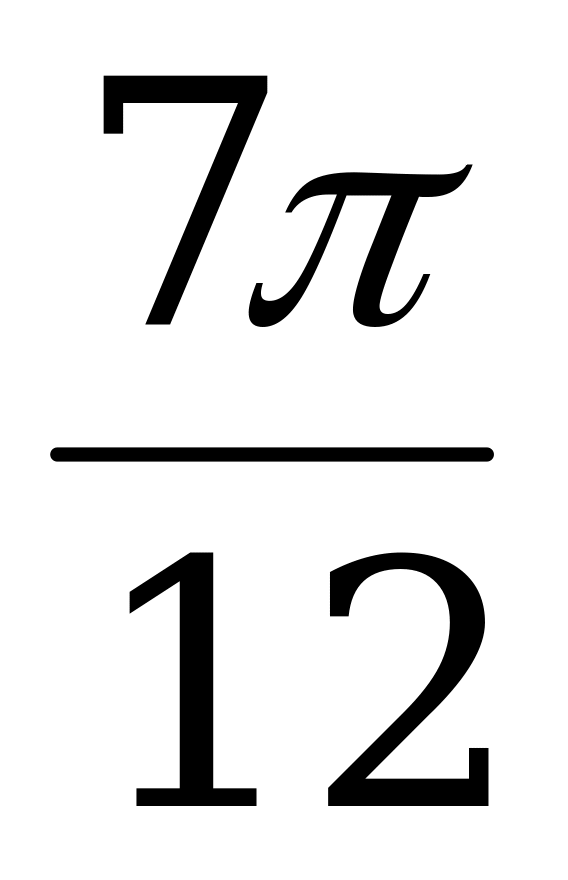 cos
cos 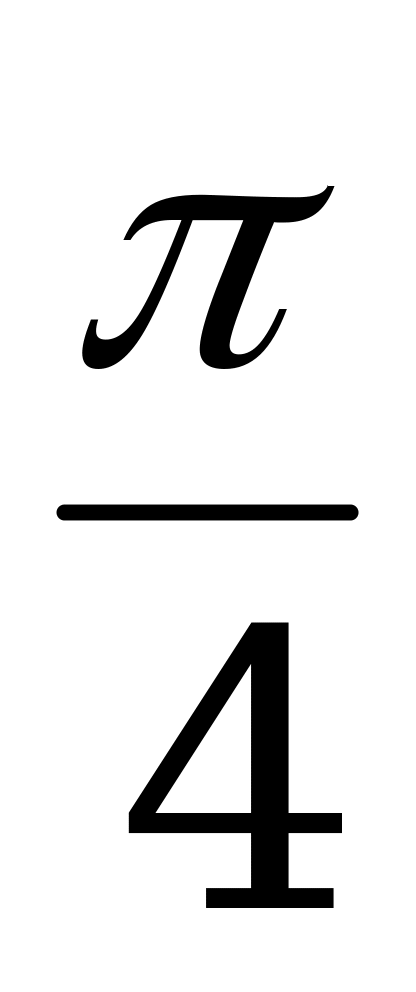 + cos
+ cos 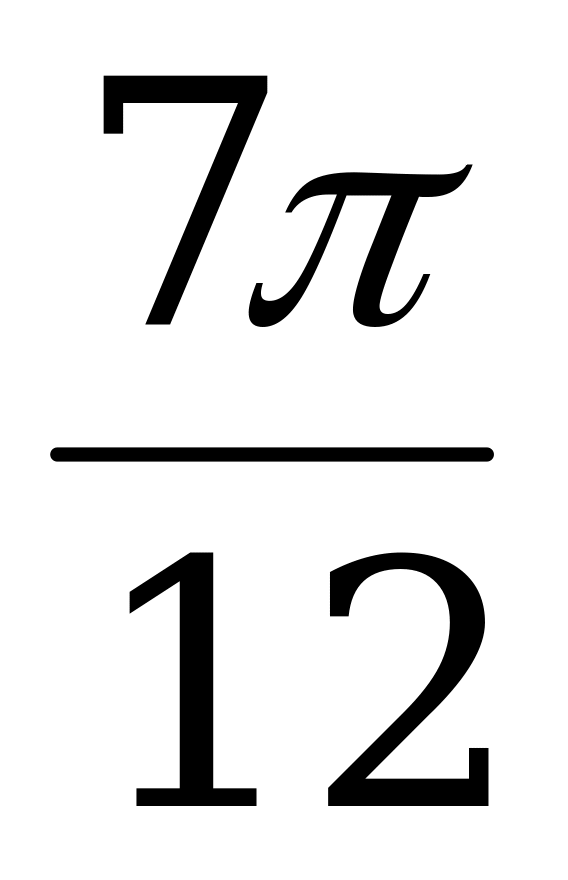 sin
sin 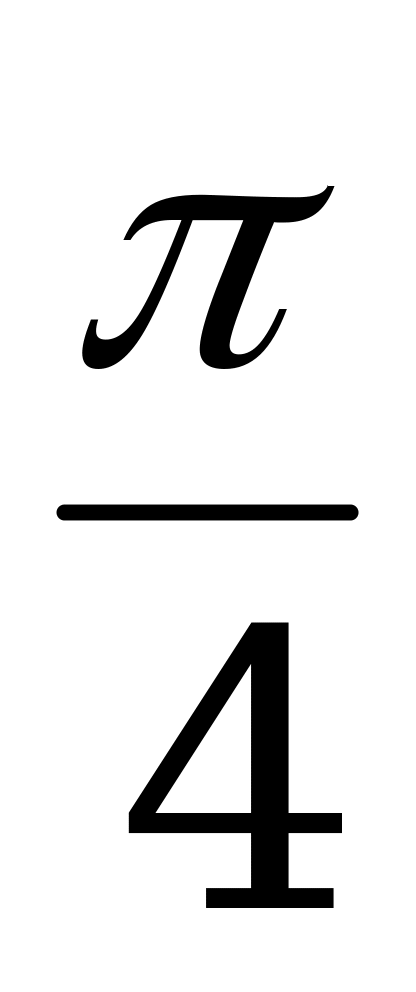 ;
;
в) C = 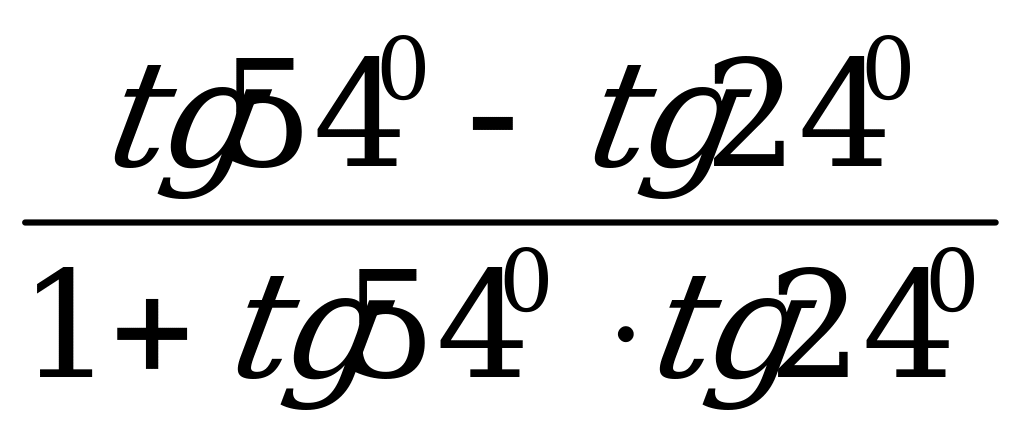 .
.
Решение:
а) По формуле (2)
А = cos (430 + 470) = cos 900 = 0.
б) По формуле (4)
В = sin (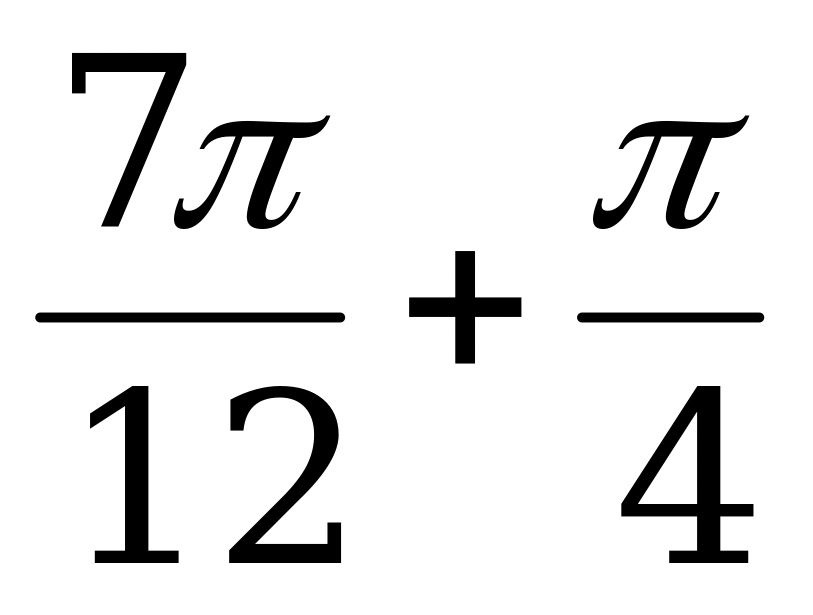 ) = sin (
) = sin (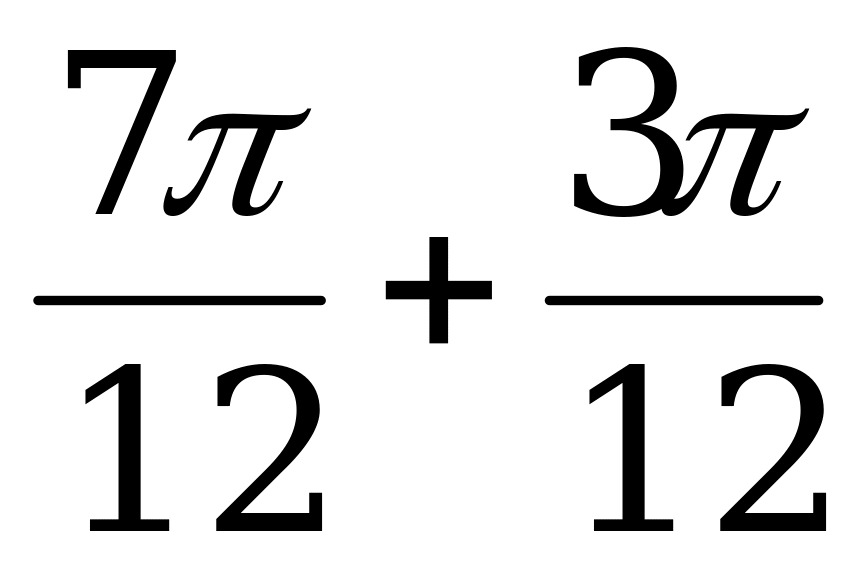 ) = sin
) = sin 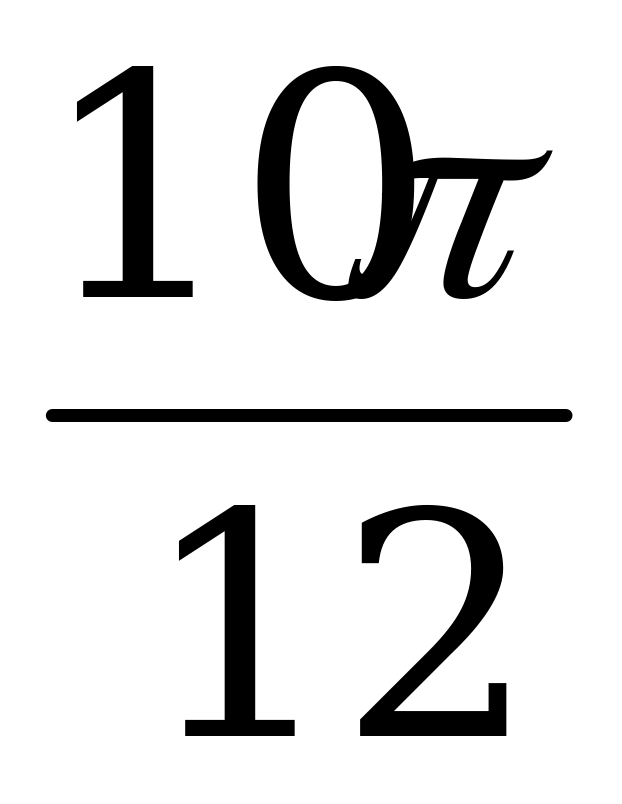 = sin
= sin 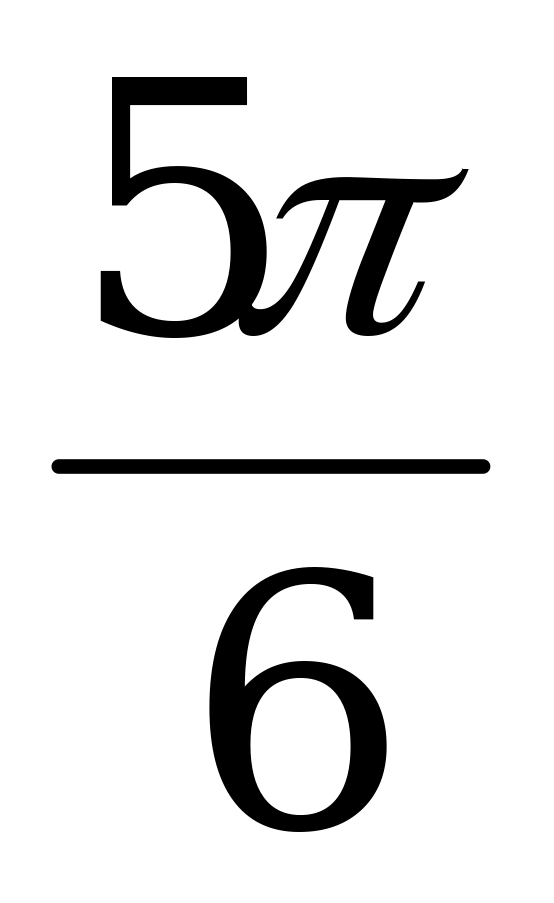 =
= 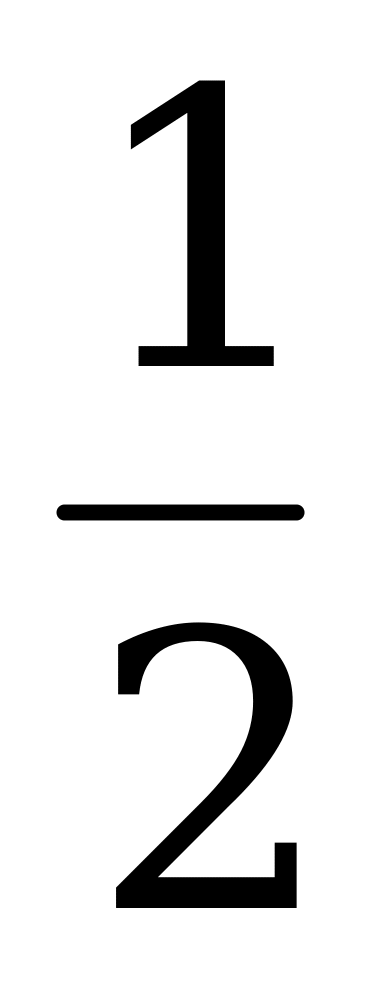 .
.
в) По формуле (6)
С = tg (540 - 240) = tg 300 = 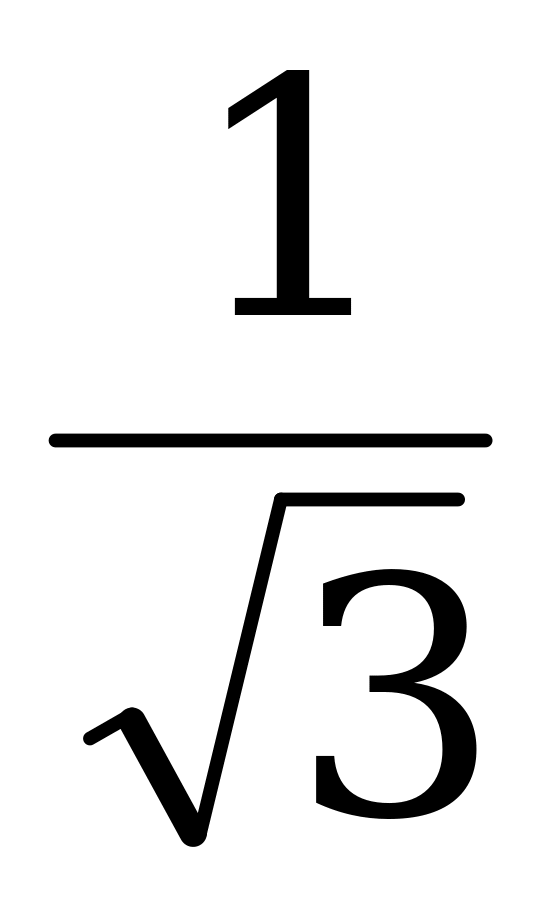 .
.
Пример 2. Вычислите:
Д = 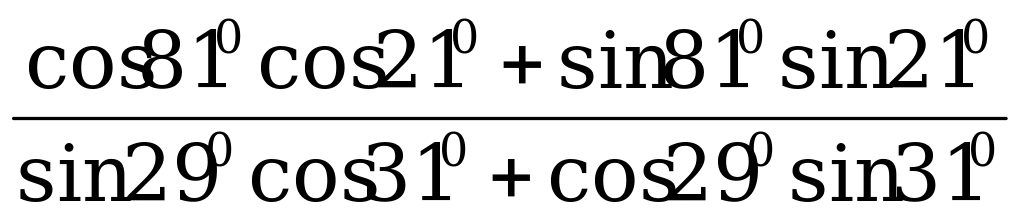 .
.
Решение:
По формулам (1) и (4)
Д = 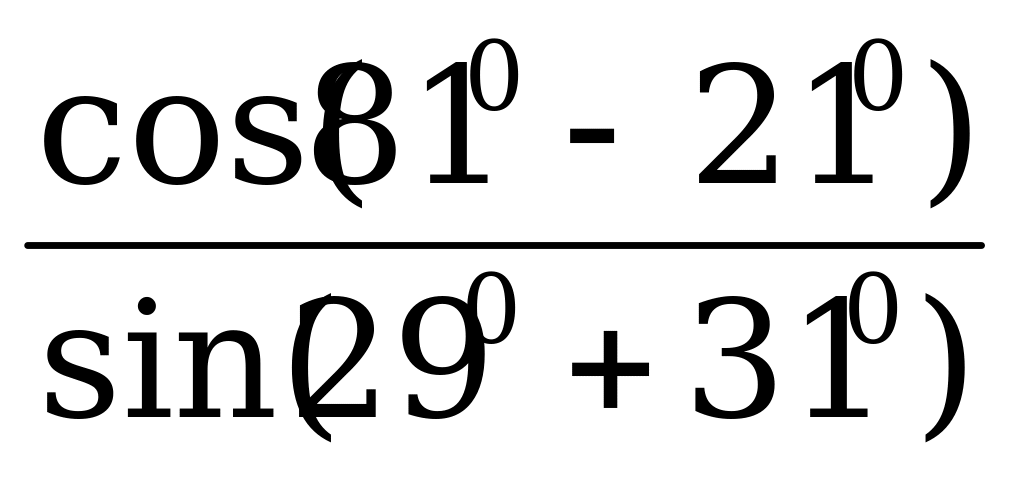 =
= 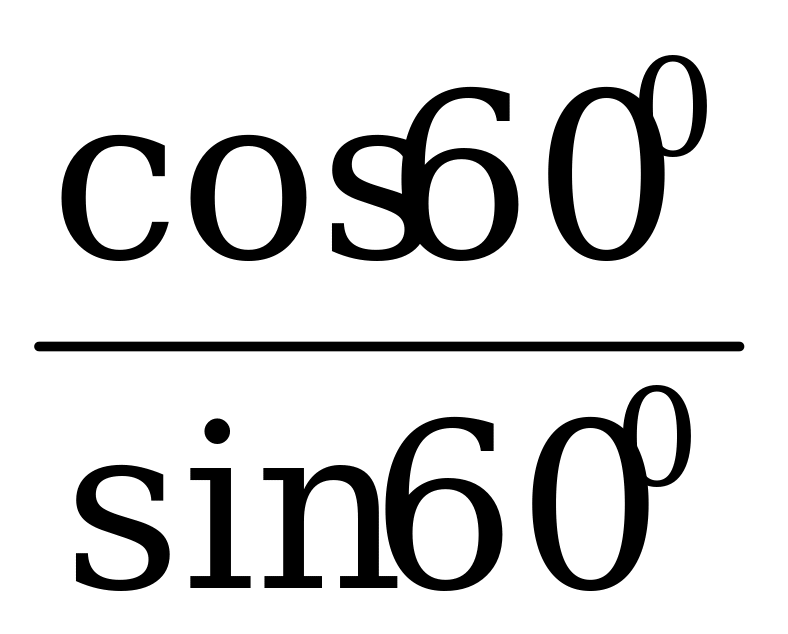 = ctg 600 =
= ctg 600 = 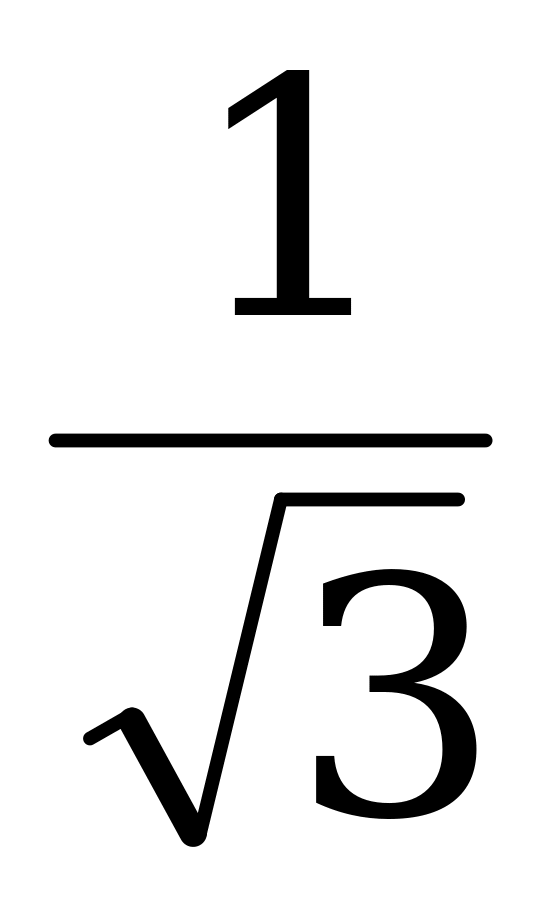 .
.
Пример 3. Докажите тождество 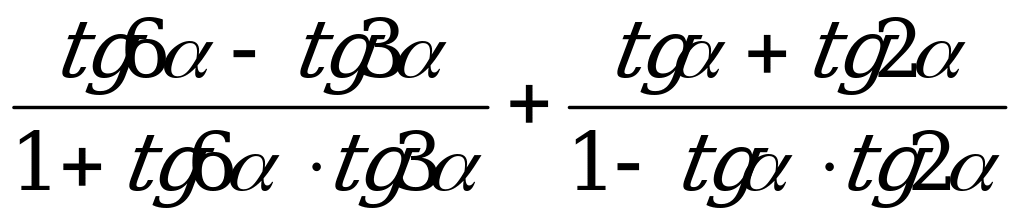 = 2 tg 3α для тех α, для которых определены обе его части.
= 2 tg 3α для тех α, для которых определены обе его части.
Доказательство:
Преобразуем равенство по формулам (5) и (6):
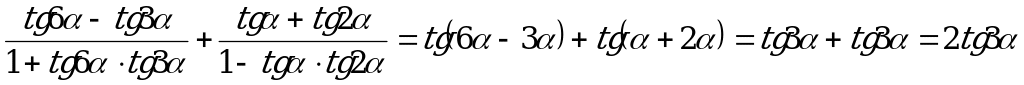 .
.
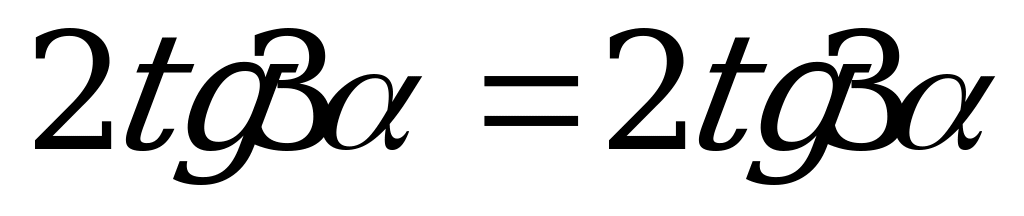 ,
,
что и требовалось доказать.
Пример 4. Вычислите tg (α + β) и tg (α - β), если tg α = 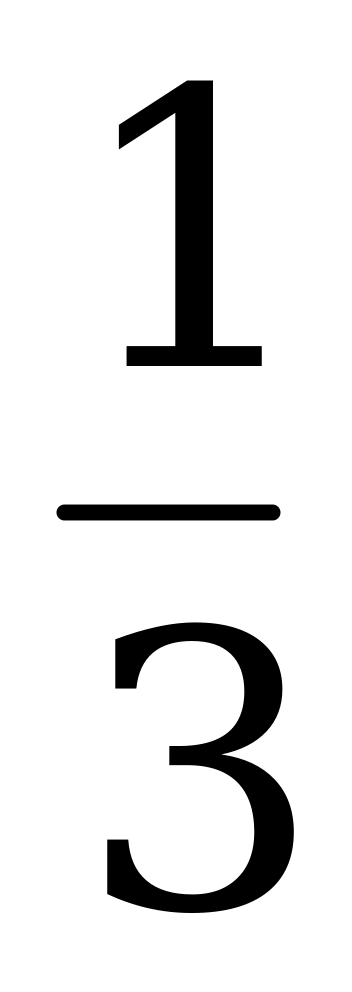 , tg β =
, tg β = 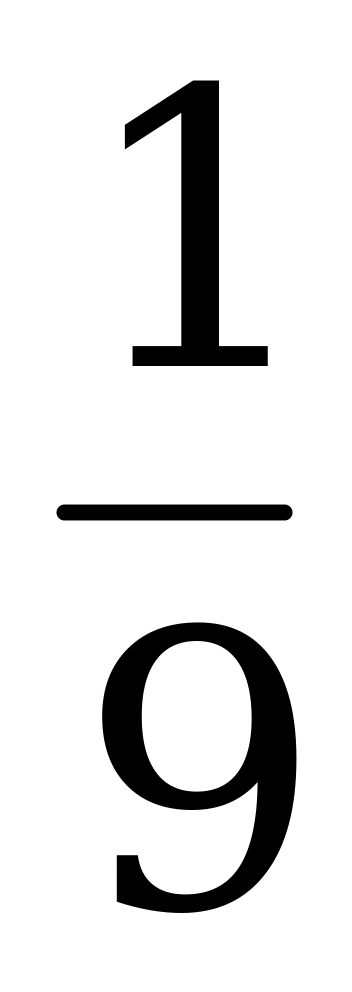 .
.
Решение:
По формулам (5) и (6)
tg (α + β) = 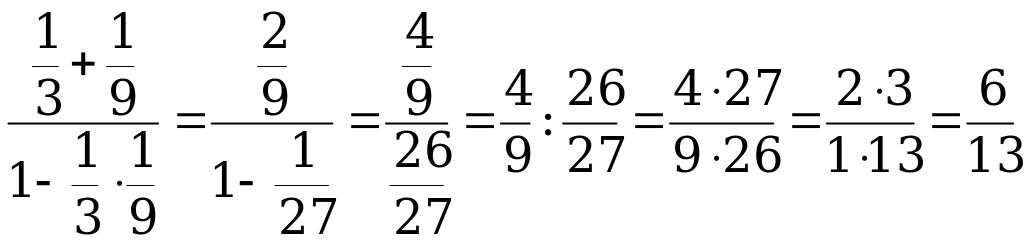 .
.
tg (α - β) = 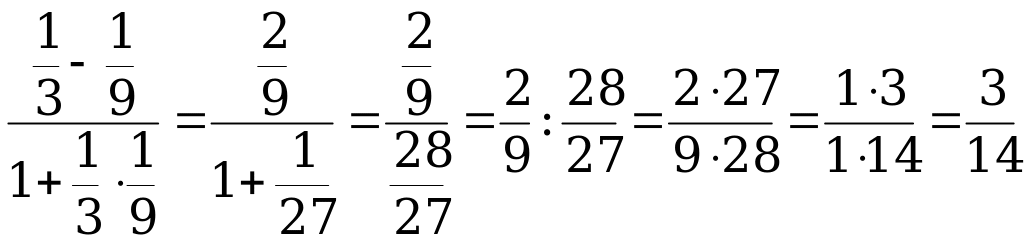 .
.
Пример 5. Упростите выражение
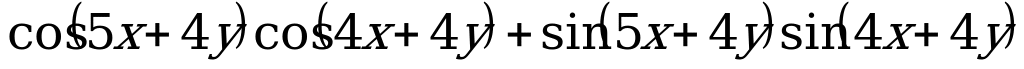 .
.
Решение:
По формуле (1)
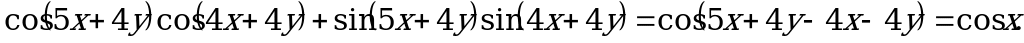
Самостоятельная работа № 2
Вариант № 1
1) Вычислите:
а) 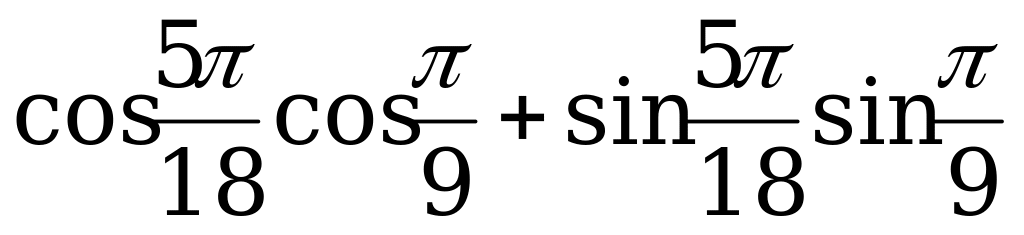 ;б)
;б) 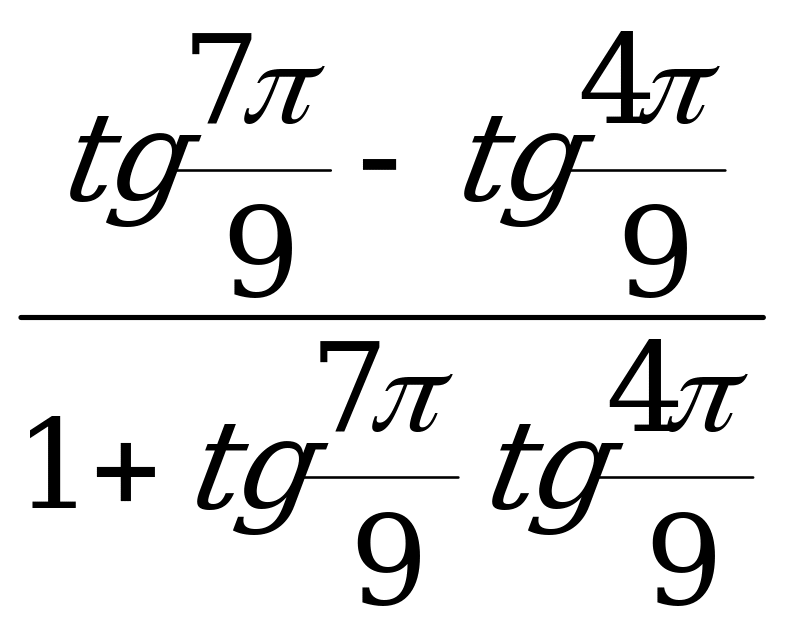 .
.
2) Вычислите: 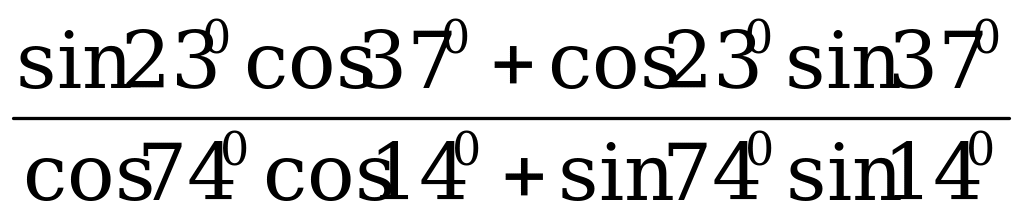 .
.
3) Докажите тождество:
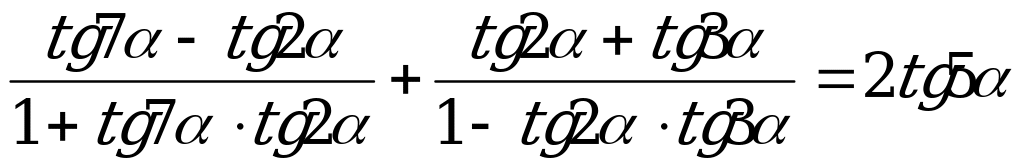 .
.
4) Вычислите tg (α + β) и tg (α - β), если tg α = 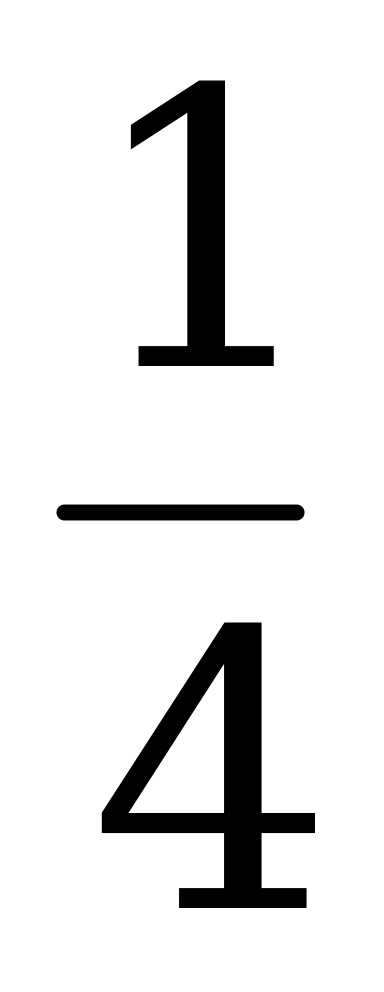 , tg β =
, tg β = 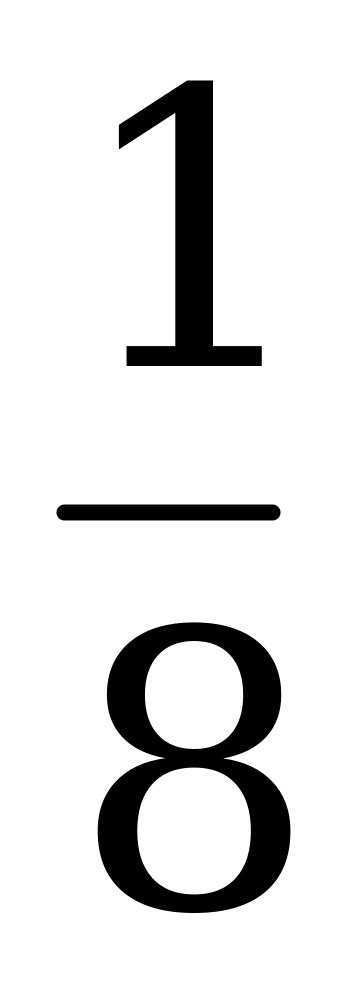 .
.
5) Упростите выражение:
sin (4x + 3y)cos (3x + 3y) – cos (4x + 3y)sin (3x + 3y).
Вариант № 2
1) Вычислите:
а) 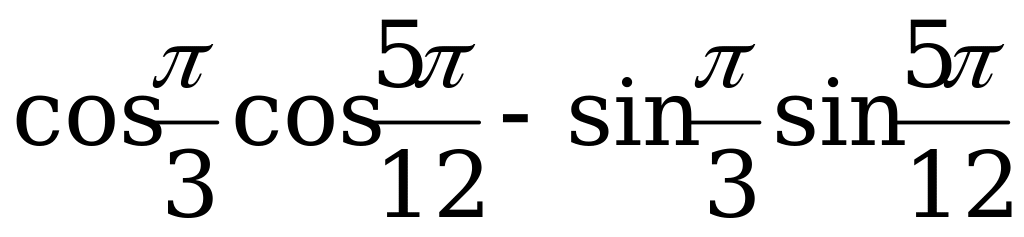 ; б)
; б) 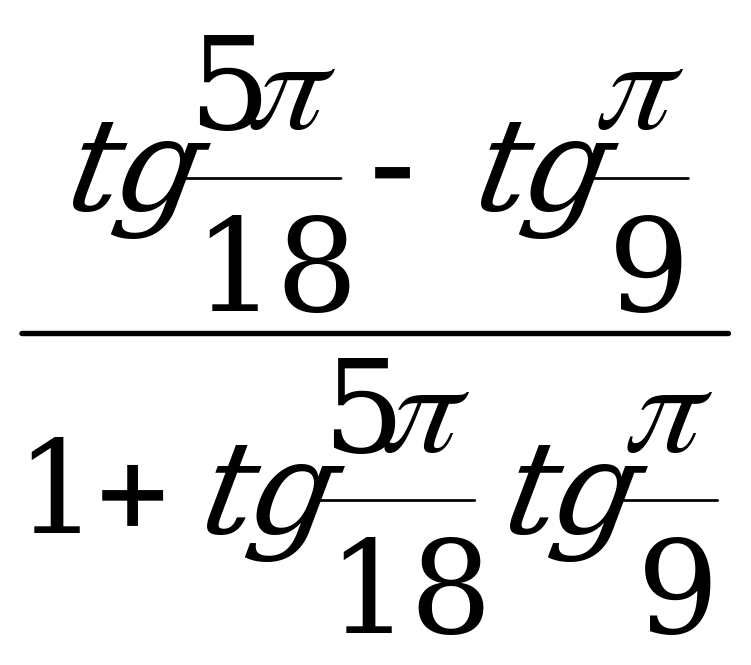 .
.
2) Вычислите: 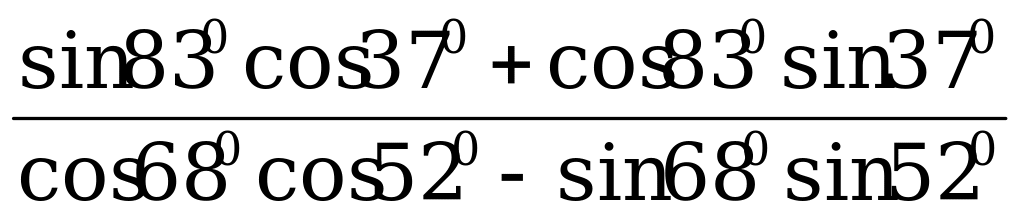 .
.
3) Докажите тождество:
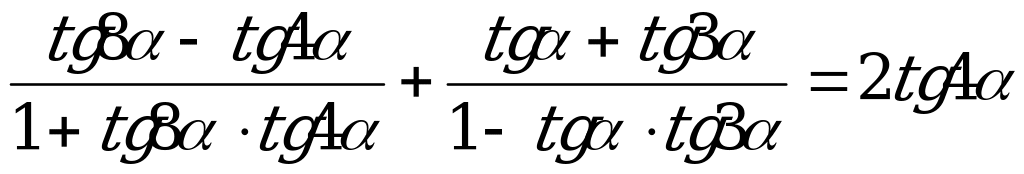 .
.
4) Вычислите tg (α + β) и tg (α - β), если tg α = 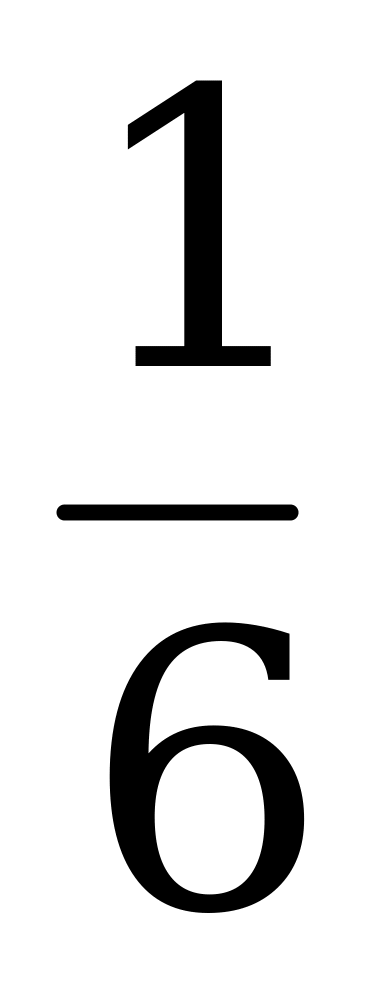 , tg β =
, tg β = 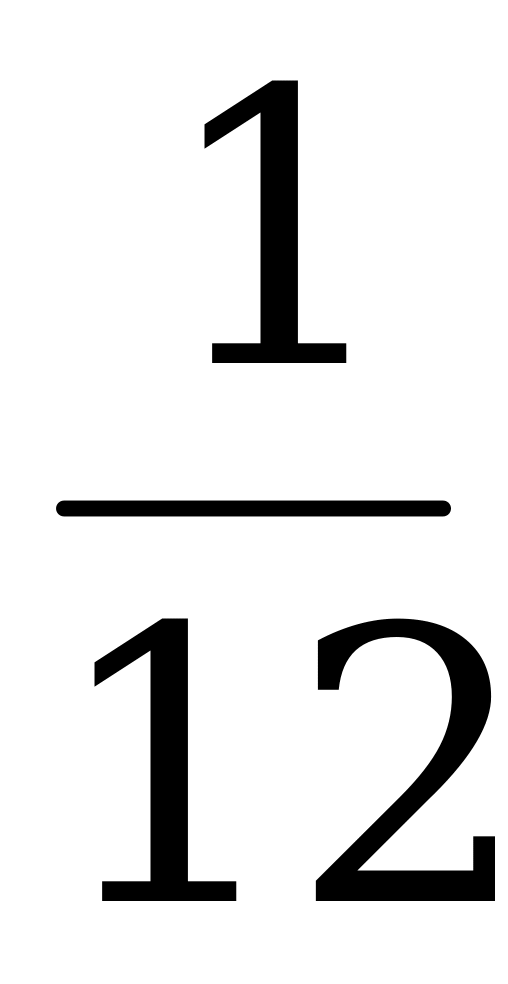 .
.
5) Упростите выражение:
sin (3x + 4y)cos (2x - 4y) + cos (3x +4y)sin (2x - 4y)
Формулы приведения.
Справочный материал.
С помощью формул приведения осуществляется преобразование выражений вида: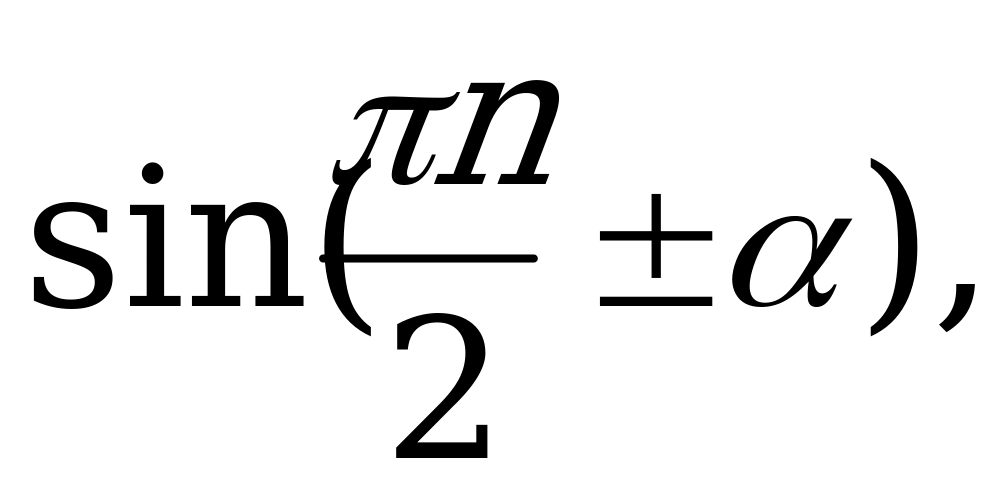
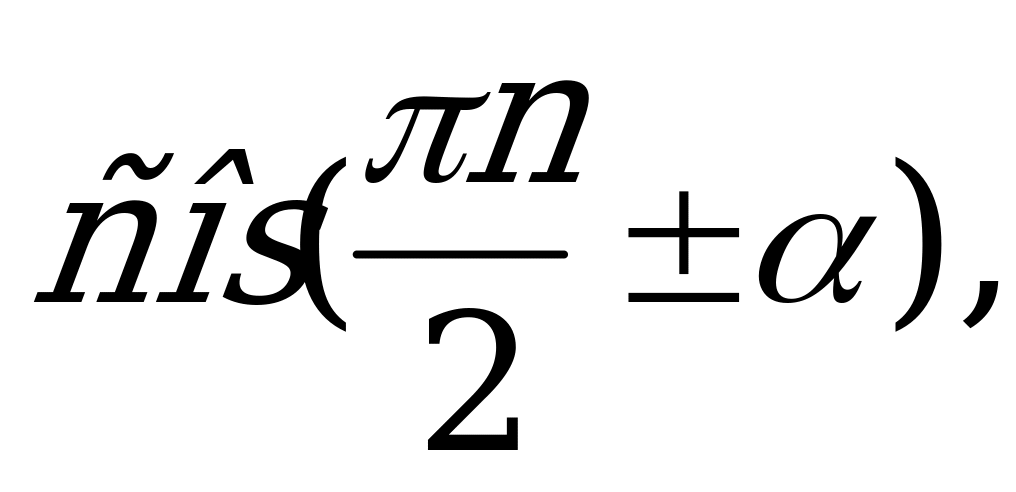
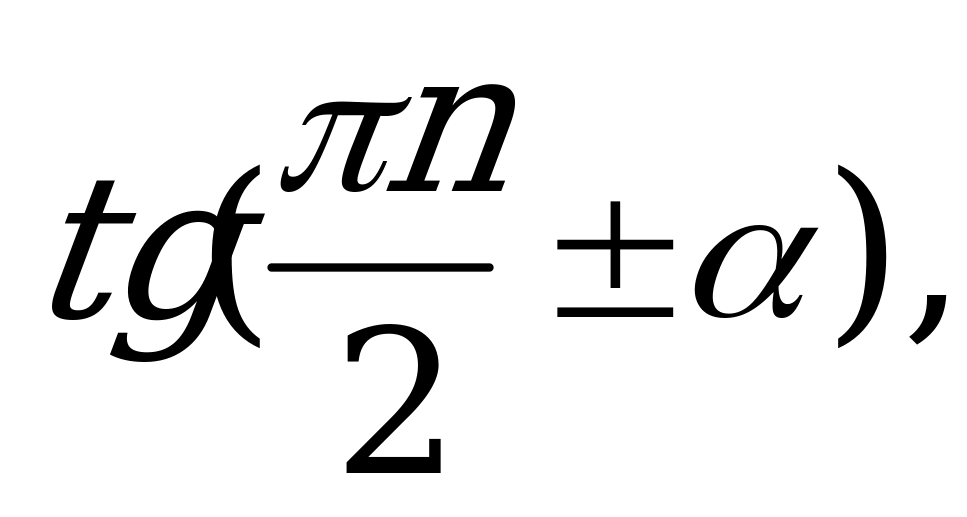
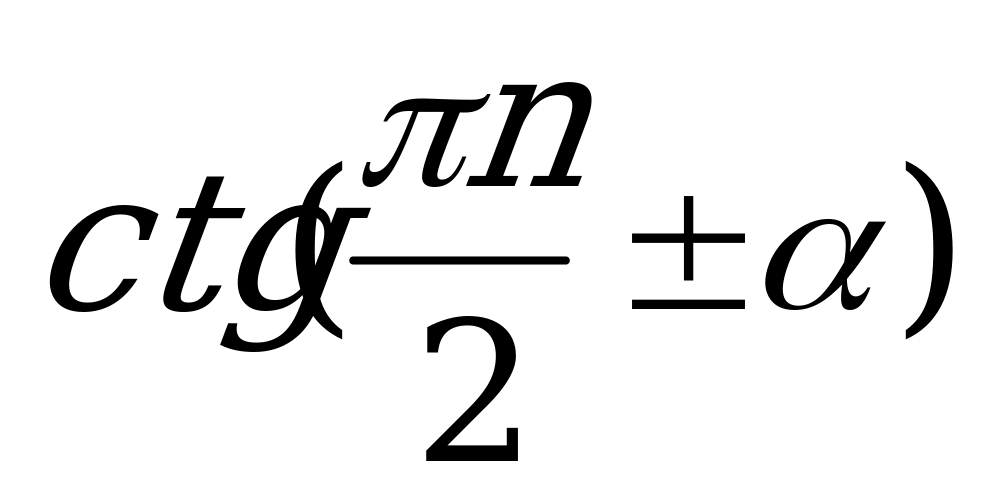 , n
, n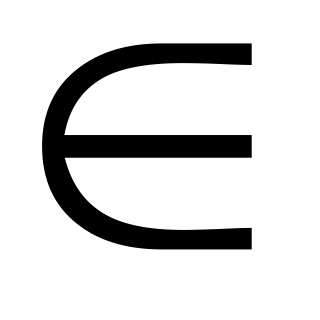 Z.
Z.
Правило для записи формул приведения:
перед приведённой функцией ставится тот знак, который имеет исходная функция, если  (рис.4);
(рис.4);
функция меняется на «кофункцию», если n нечётно, функция не меняется, если n чётно. (Кофункциями синуса, косинуса, тангенса и котангенса называются соответственно косинус, синус, котангенс и тангенс.).
Формулы приведения тригонометрических функций аргументов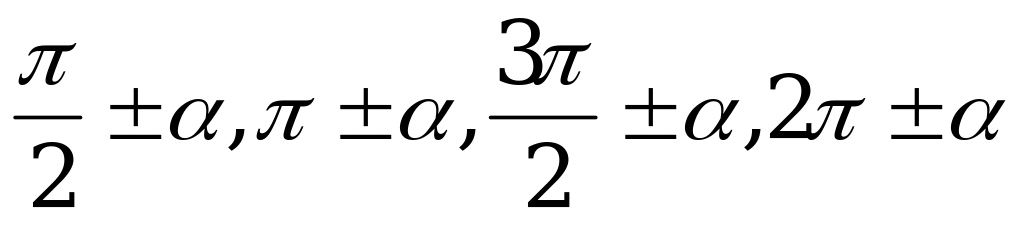 .
.
Упражнения с решениями.
Пример 1. Упростите выражение
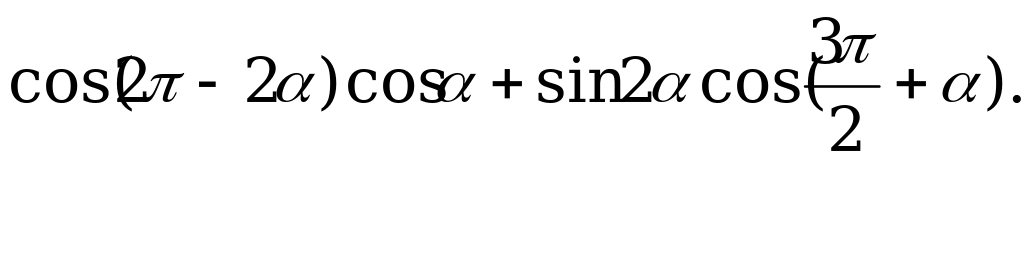

Решение. Так как по формулам приведения 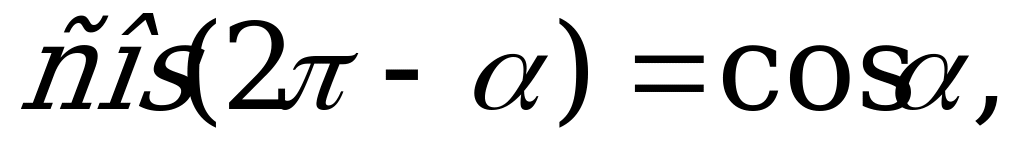 и
и 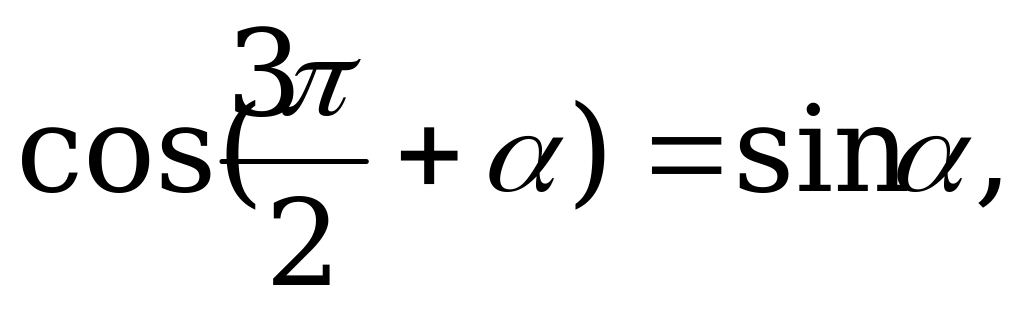 то
то
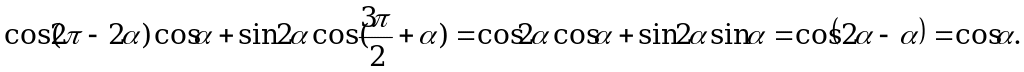
Пример 2. Вычислите 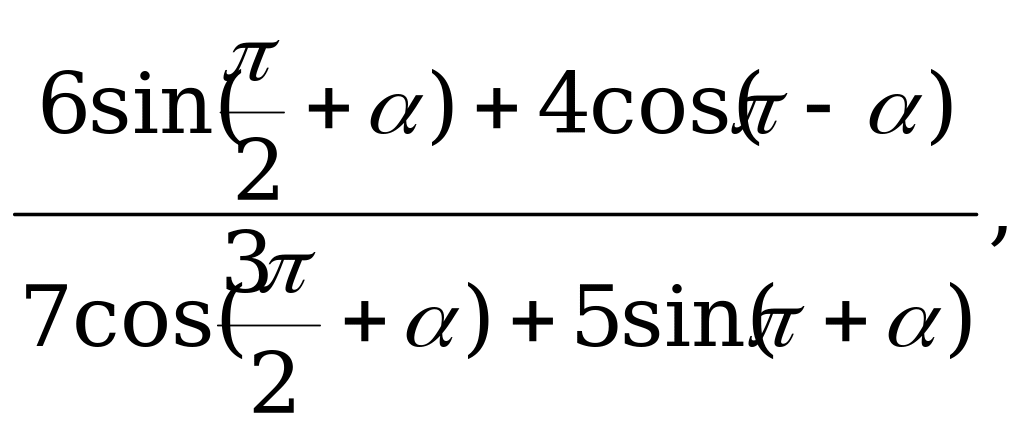 если
если 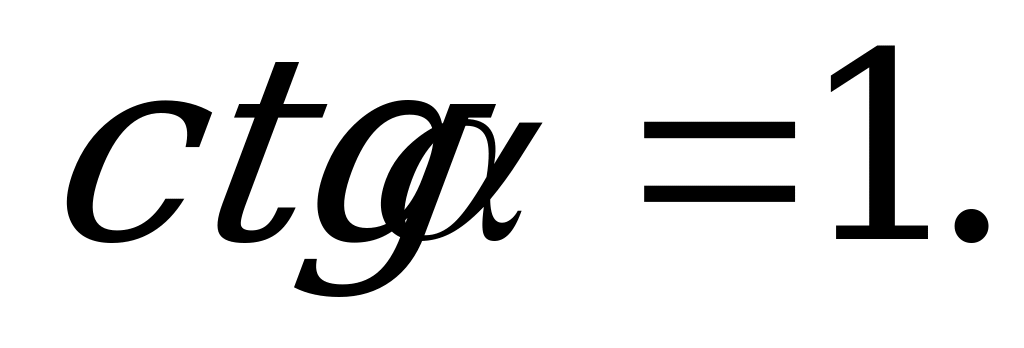
Решение. Используя формулы приведения, преобразуем числитель и знаменатель:
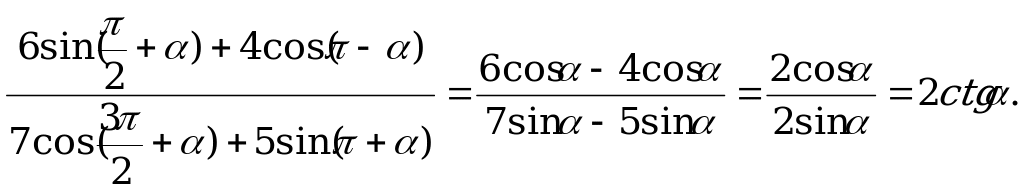


Если 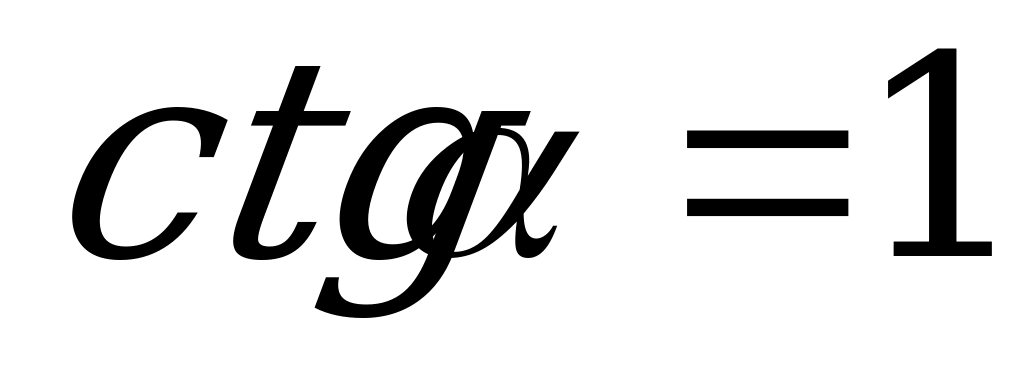 , то
, то 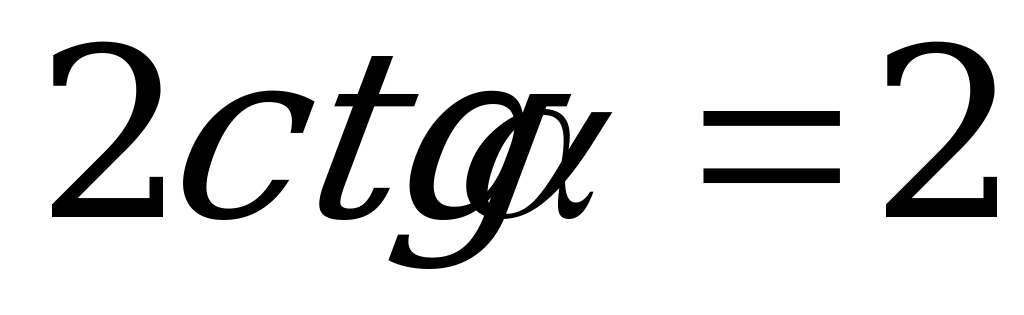 .
.
Ответ: 2.
Пример 3. Вычислите
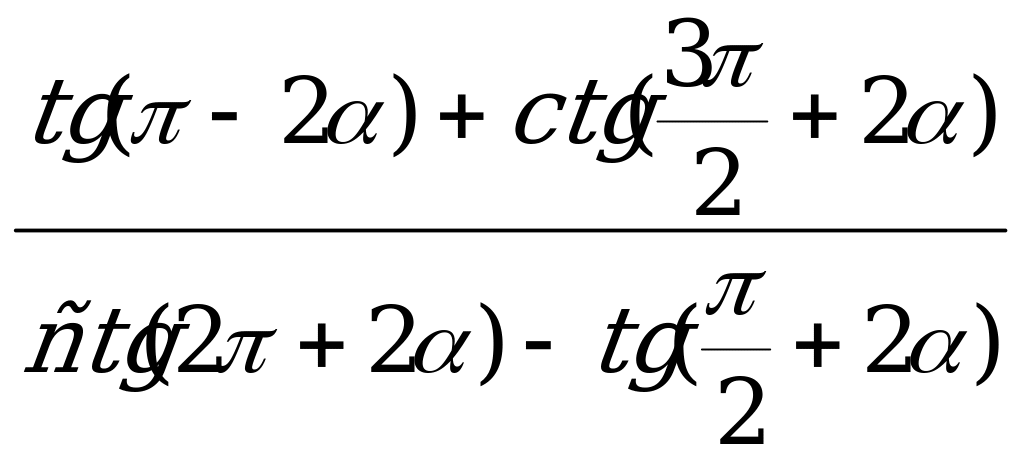 ,если
,если 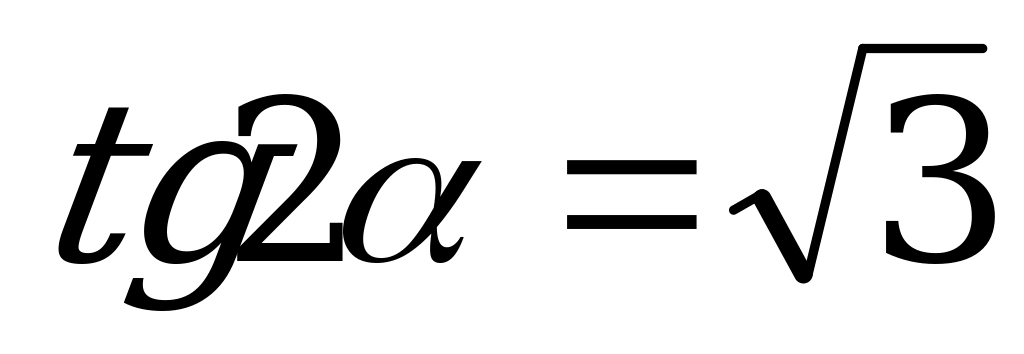 .
.
Решение. По формулам приведения
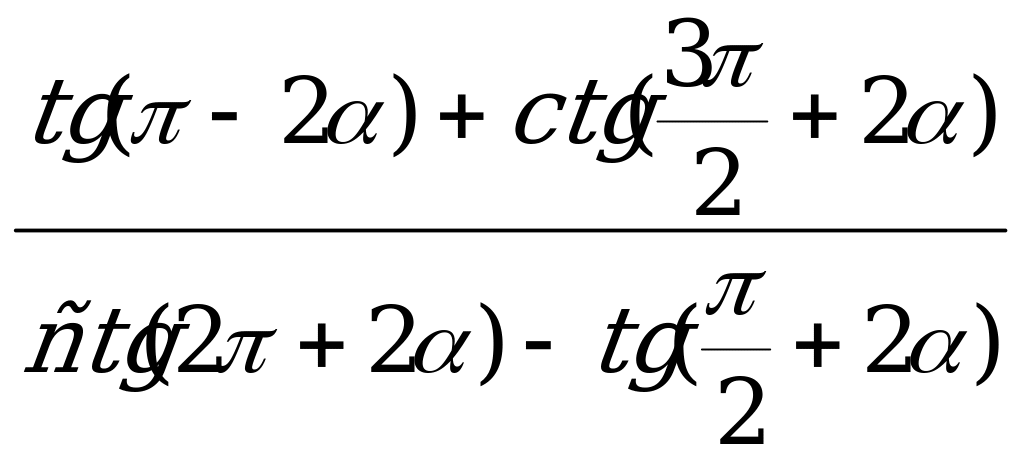 =
=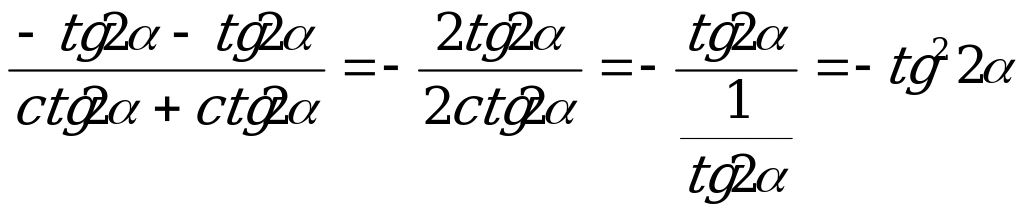 .
.
Если 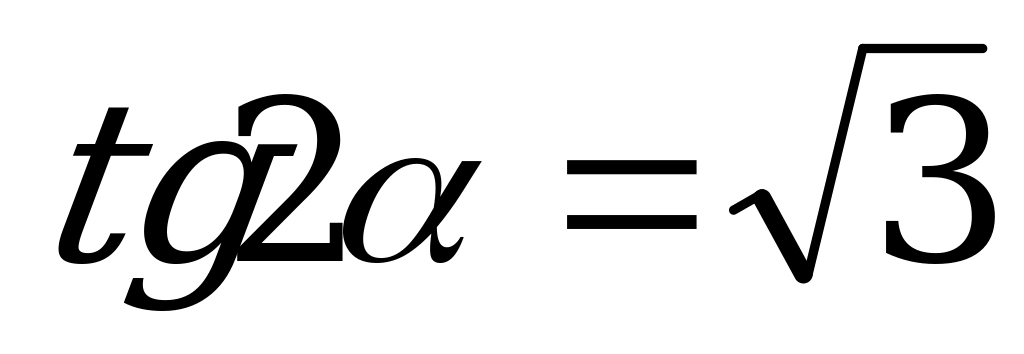 , то
, то 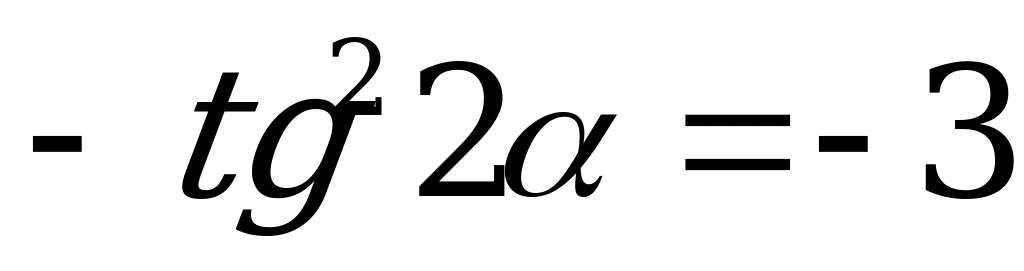 .
.
Ответ:-3.
Самостоятельная работа № 3.
Вариант № 1.
Упростите выражение 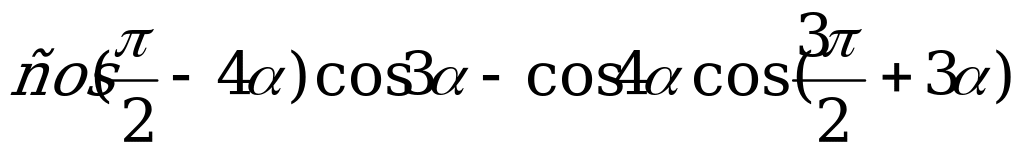 .
.
Вычислите 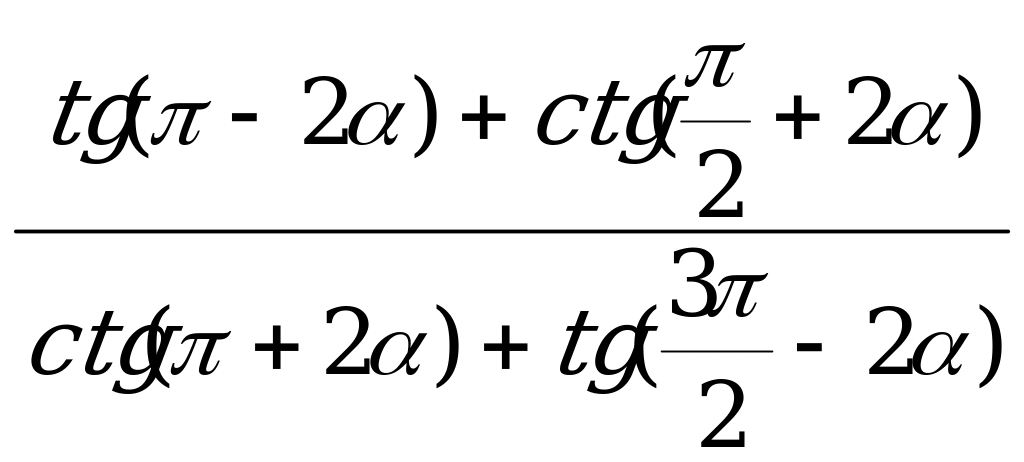 , если
, если 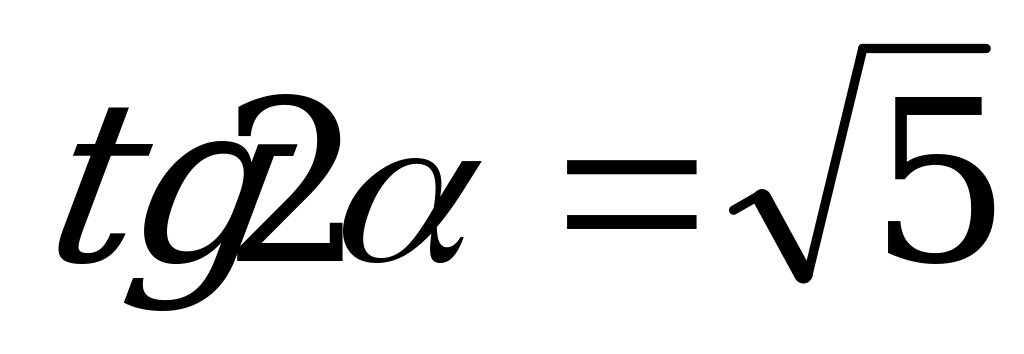 .
.
Докажите тождество 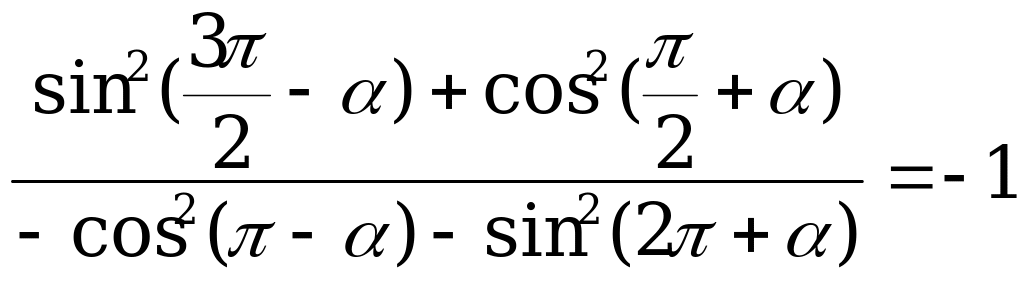 .
.
Вычислите 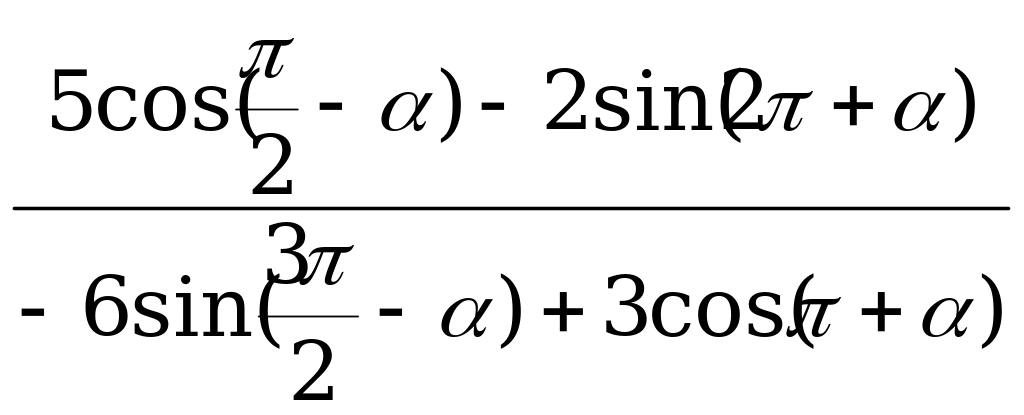 , если
, если 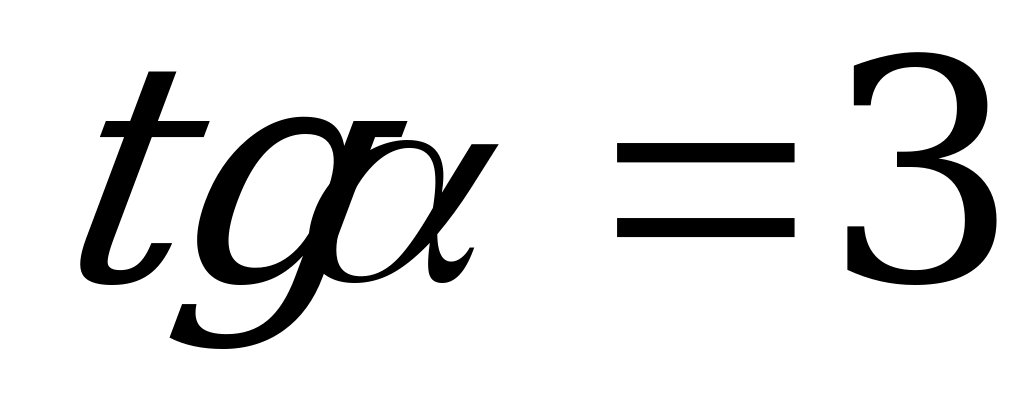 .
.
Вариант № 2.
1. Упростите выражение 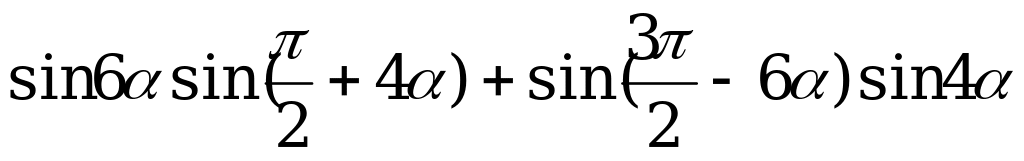 .
.
2. Вычислите 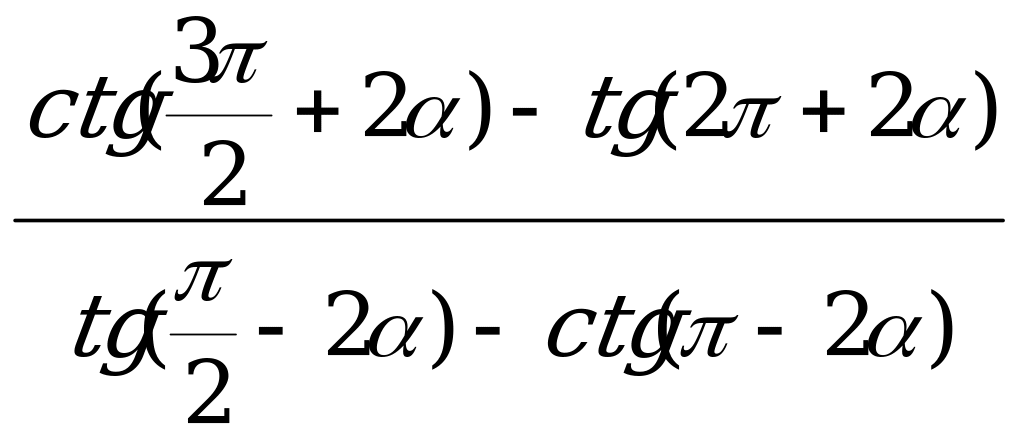
 , если
, если 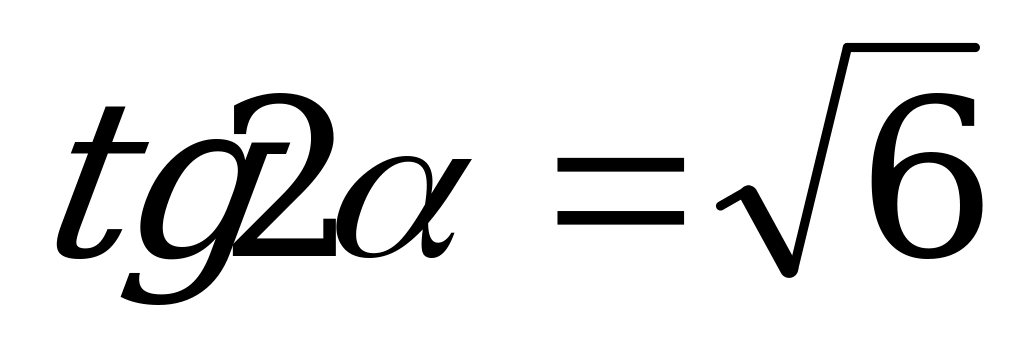 .
.
3. Докажите тождество 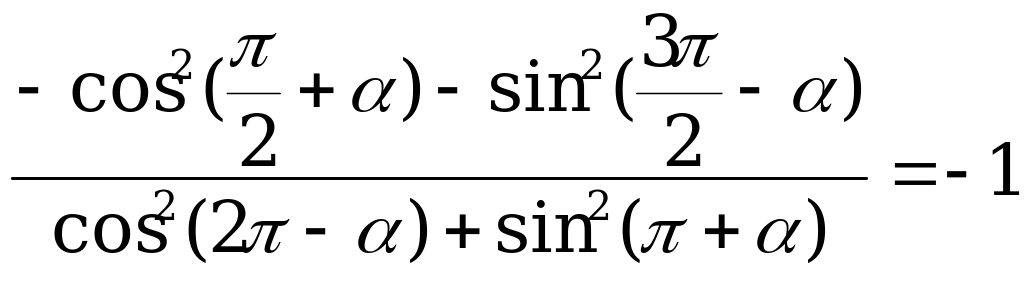 .
.
4. Вычислите 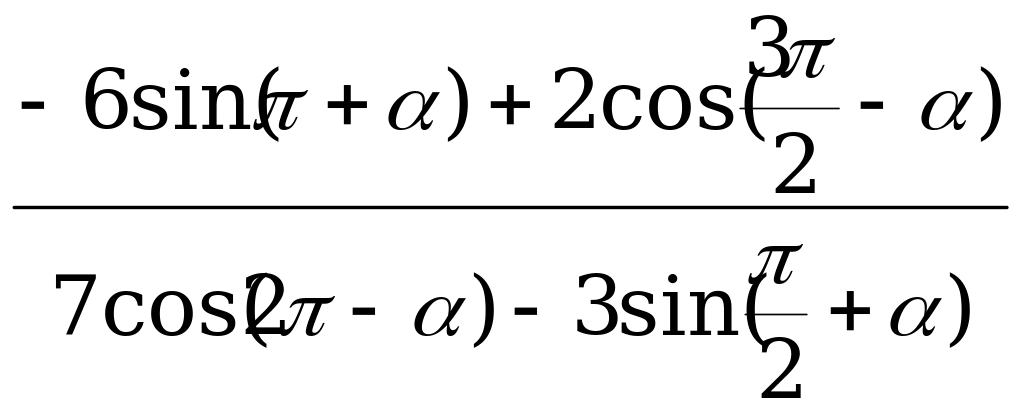 , если
, если 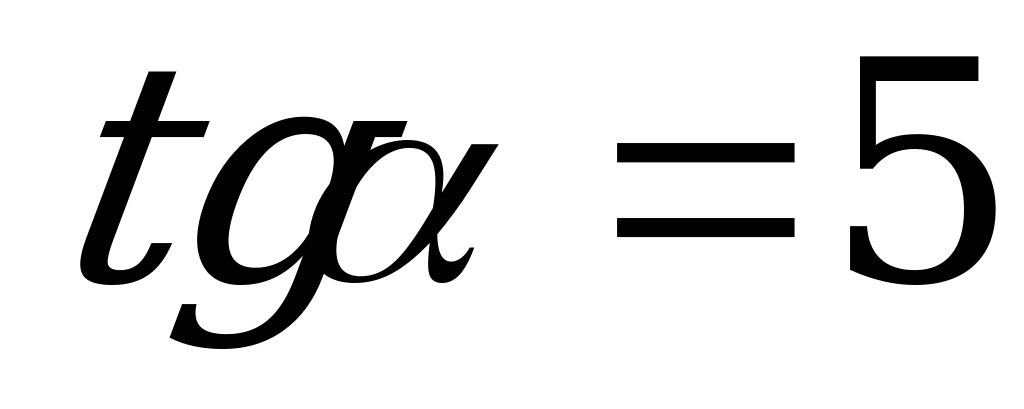 .
.
Формулы суммы и разности синусов и косинусов.
Справочный материал.
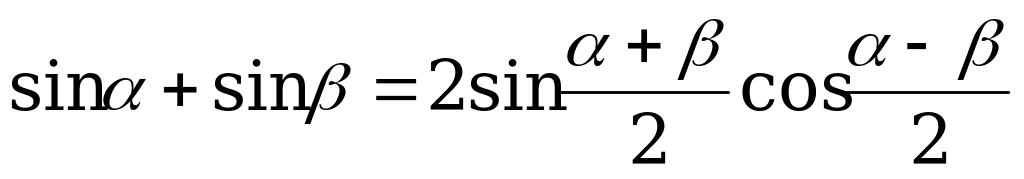 ; (1).
; (1).
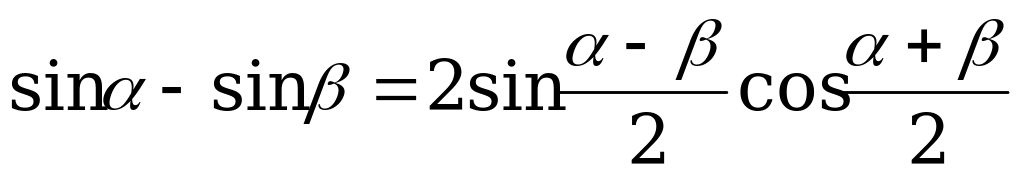 ; (2).
; (2).
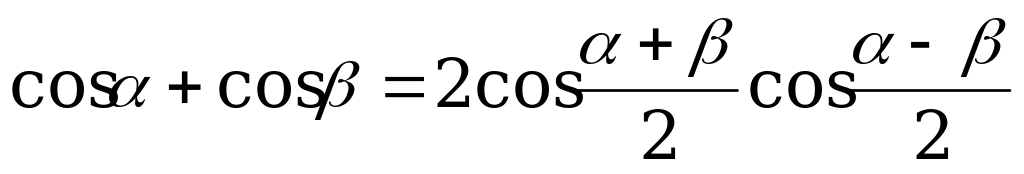 ; (3).
; (3).
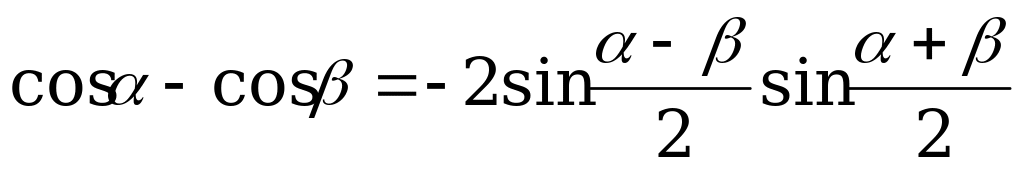 ; (4).
; (4).
Упражнения с решениями.
Пример 1. Вычислите 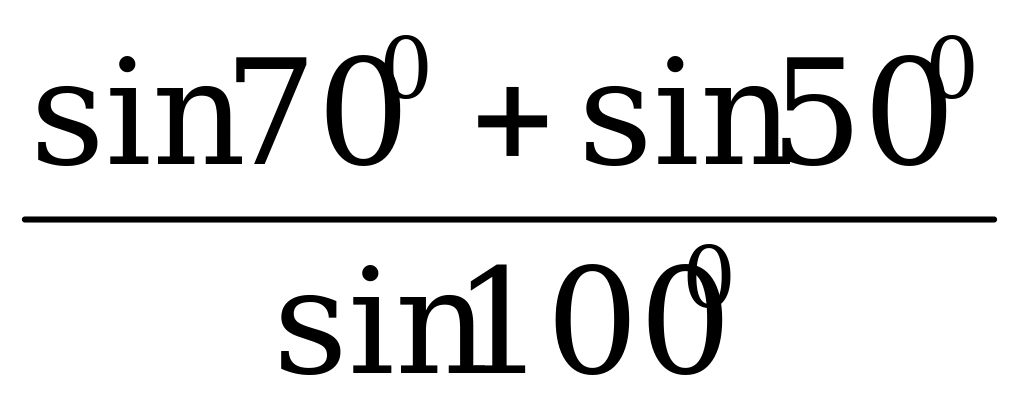 .
.
Решение. Преобразуем числитель по формуле (1), а знаменатель по формулам приведения:
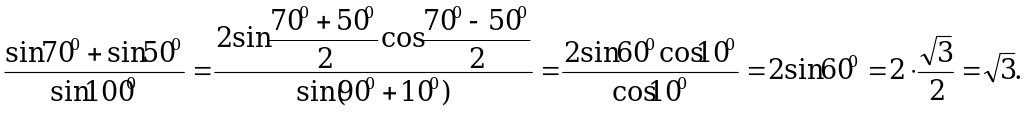 Пример 2. Вычислите
Пример 2. Вычислите 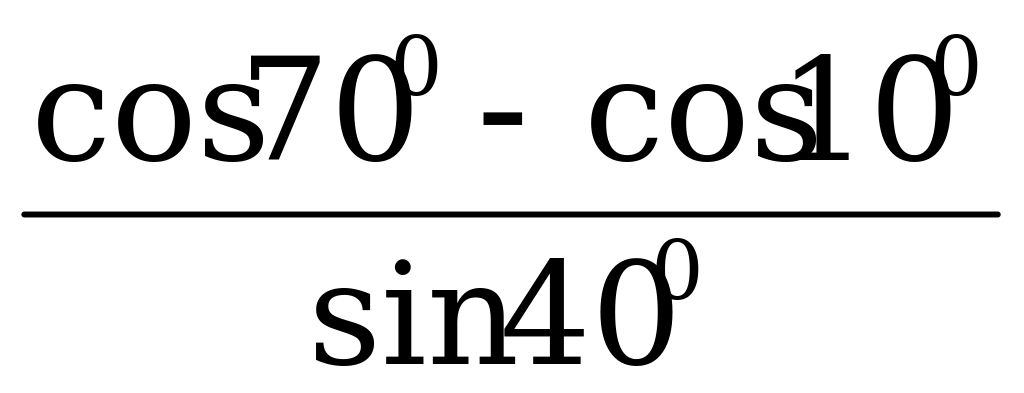 .
.
Решение. Преобразуем числитель по формуле (4), а знаменатель оставим прежним:
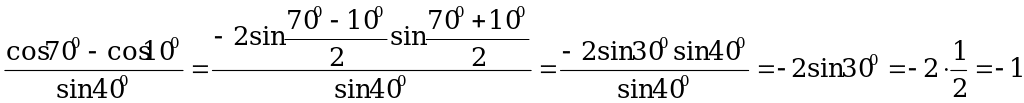
Формулы двойного угла.
Справочный материал.
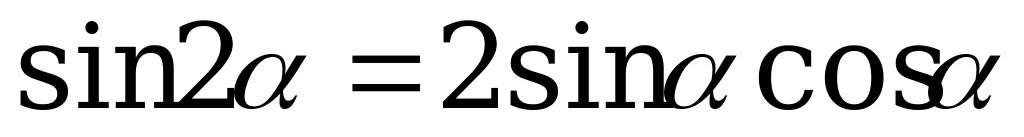 ; (1).
; (1).
 ; (2).
; (2).
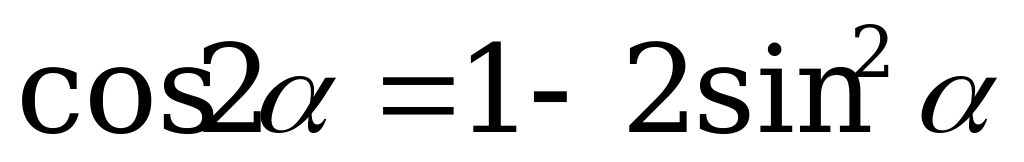 ; (3).
; (3).
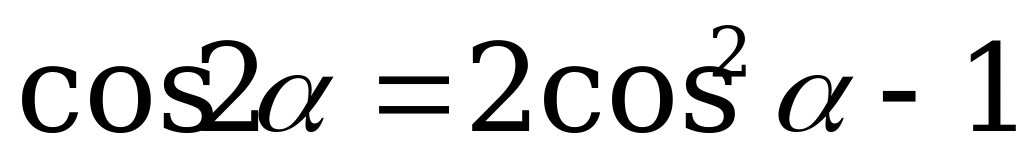 ; (4).
; (4).
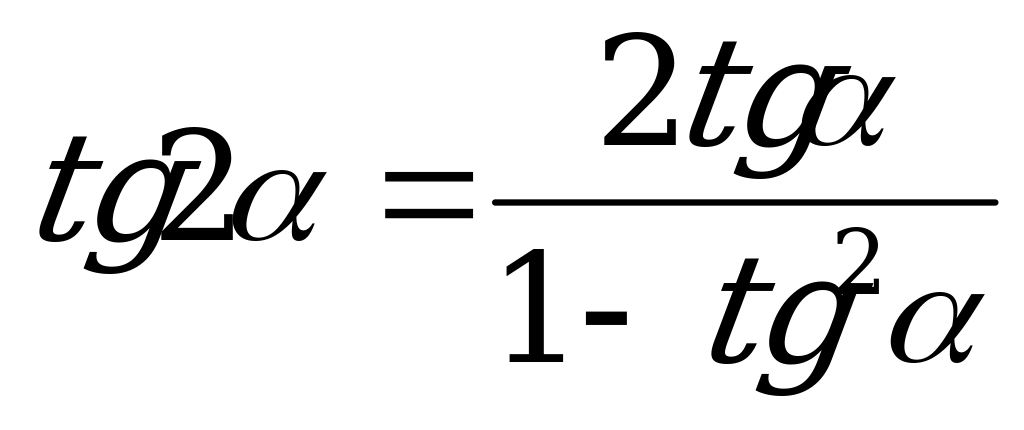
 ; (5).
; (5).
Упражнения с решениями.
Пример 1. Вычислите 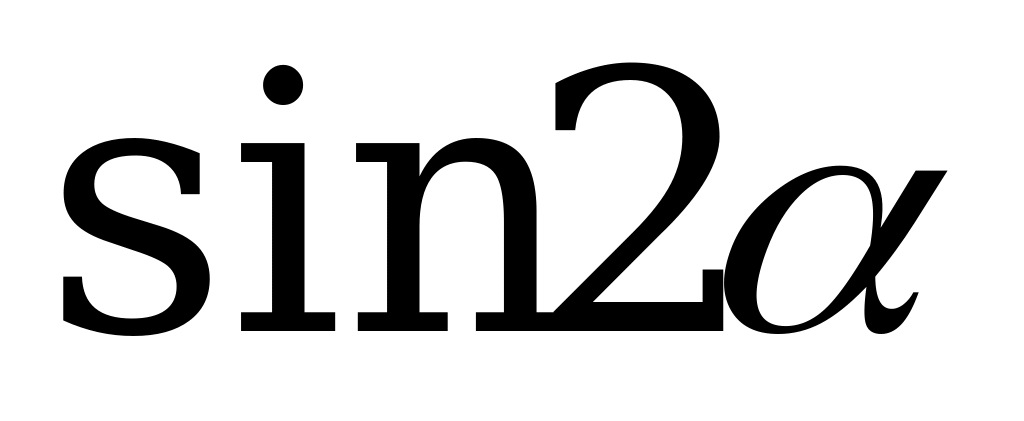 и
и 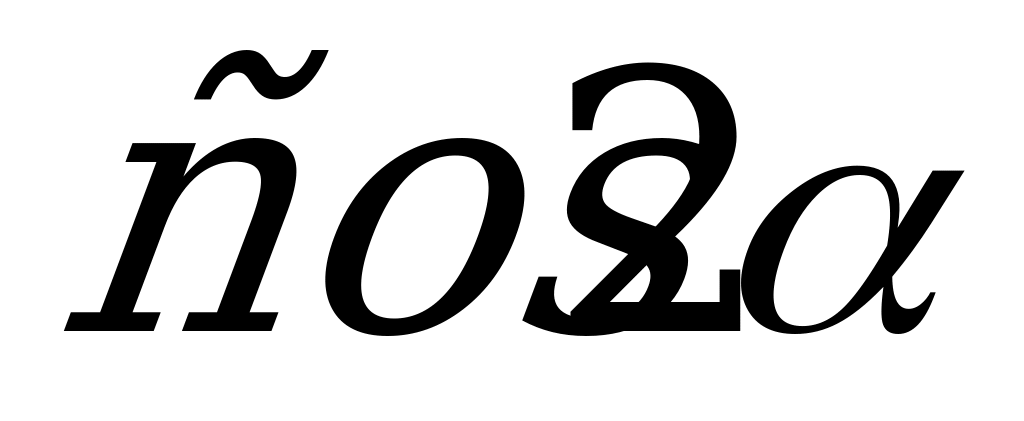 , если
, если 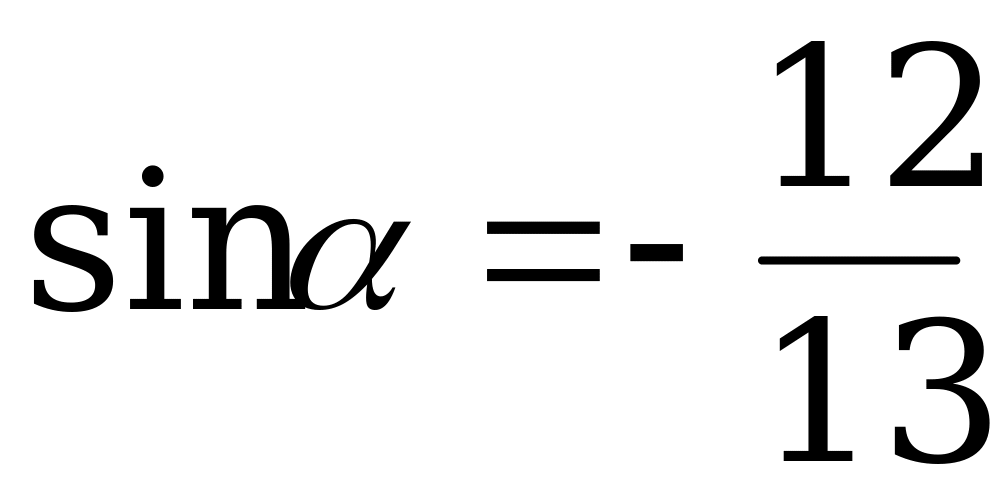 и
и 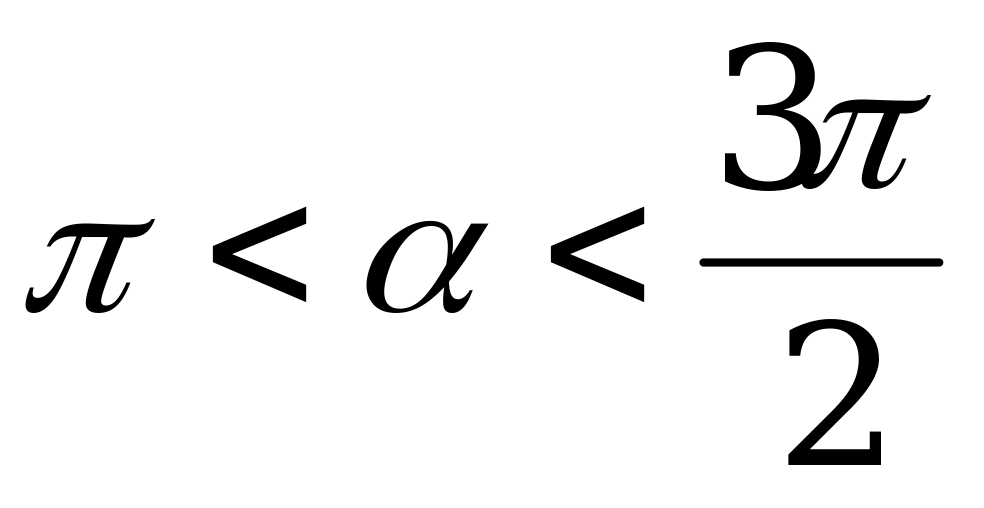 .
.
Решение. Используя основное тригонометрическое тождество 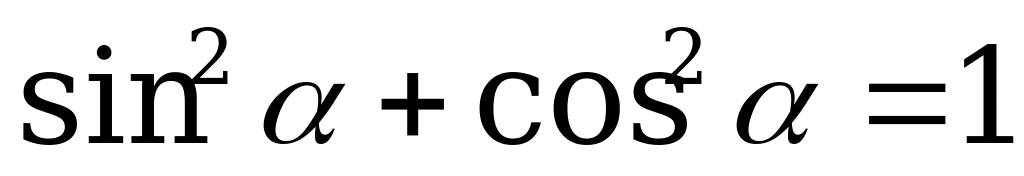 , найдём
, найдём  .
.
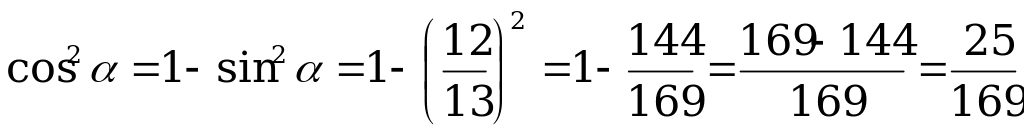 .
.
Так как 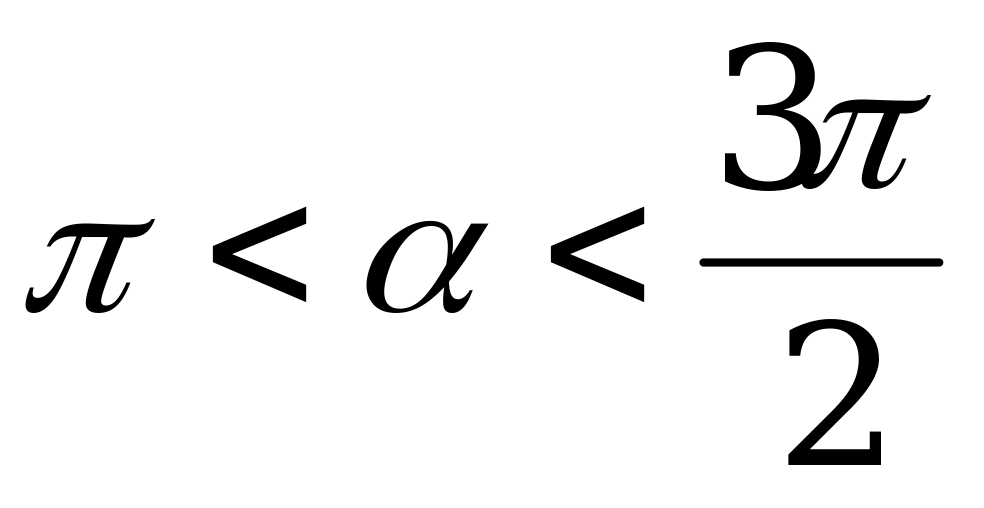 , то
, то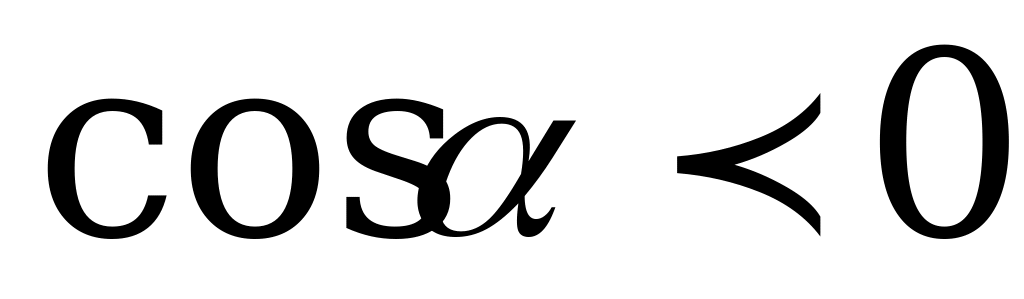 , следовательно
, следовательно 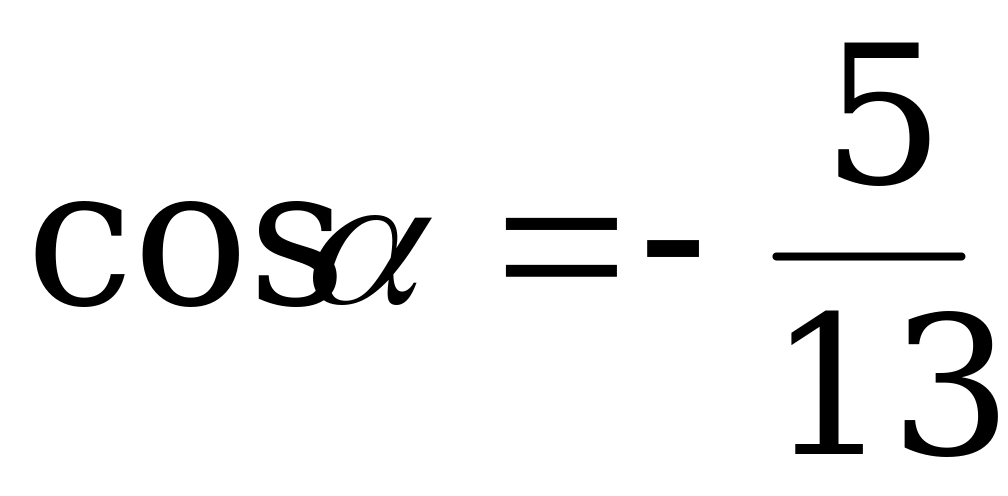 .
.
По формулам (1) и (2) имеем:
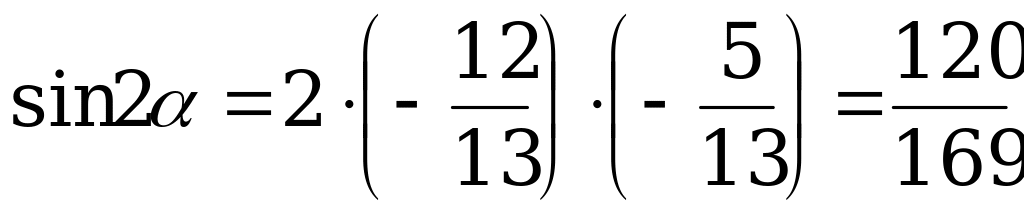 ;
;
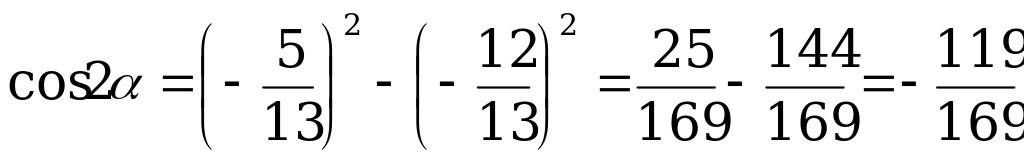 .
.
Ответ: 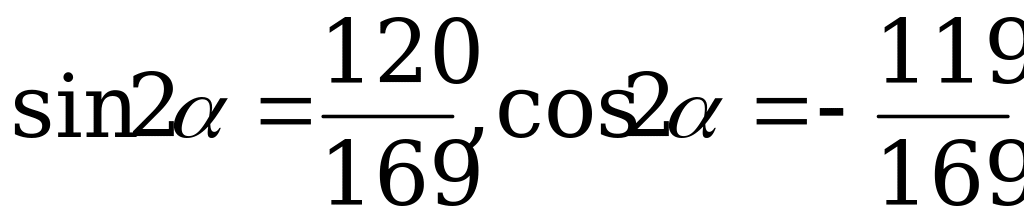 .
.
Пример 2. Вычислите  , если
, если 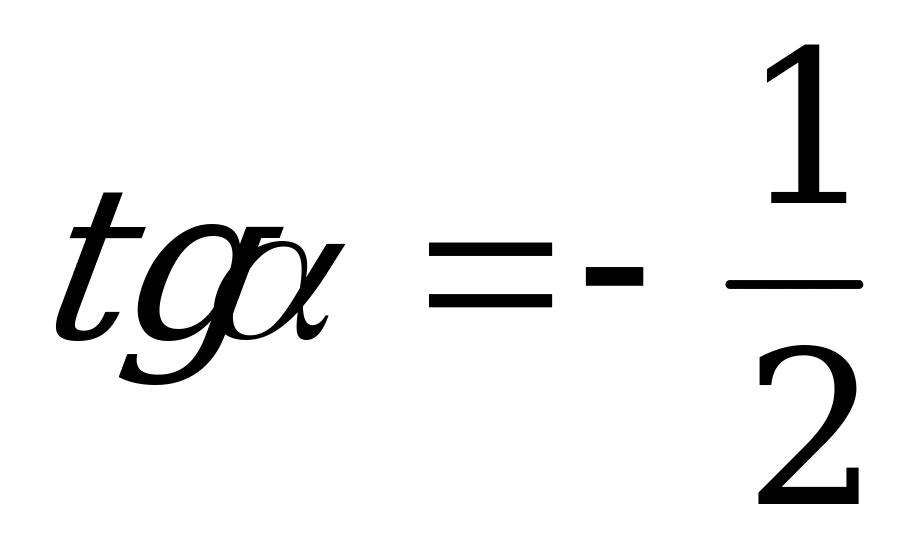 .
.
Решение. По формуле (5):
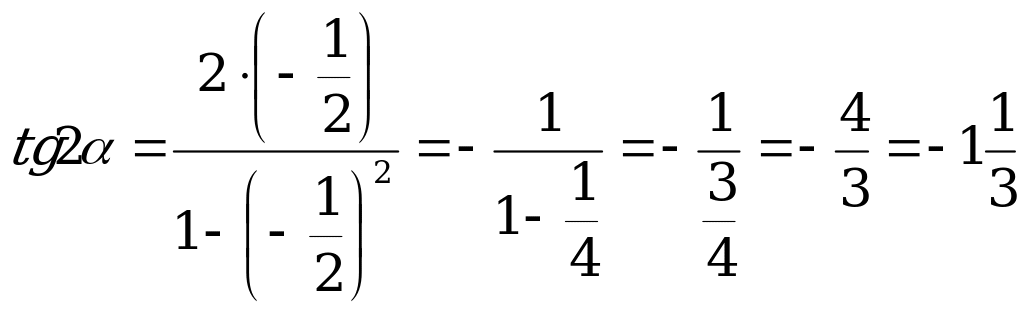 .
.
Формулы половинного аргумента.
Справочный материал.
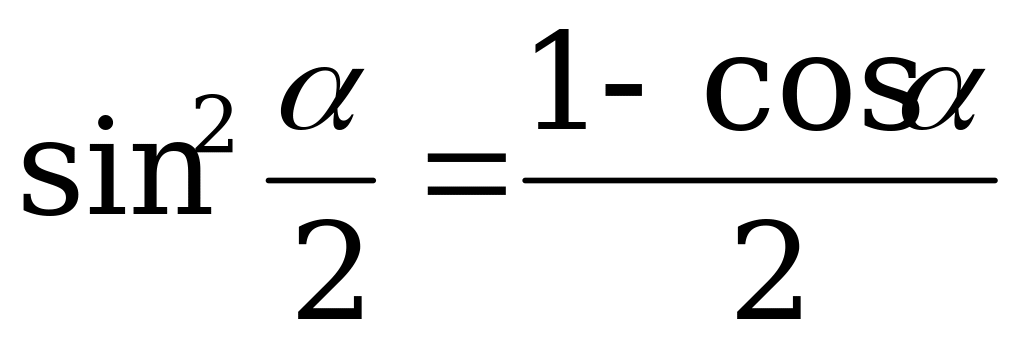 ; (1).
; (1).
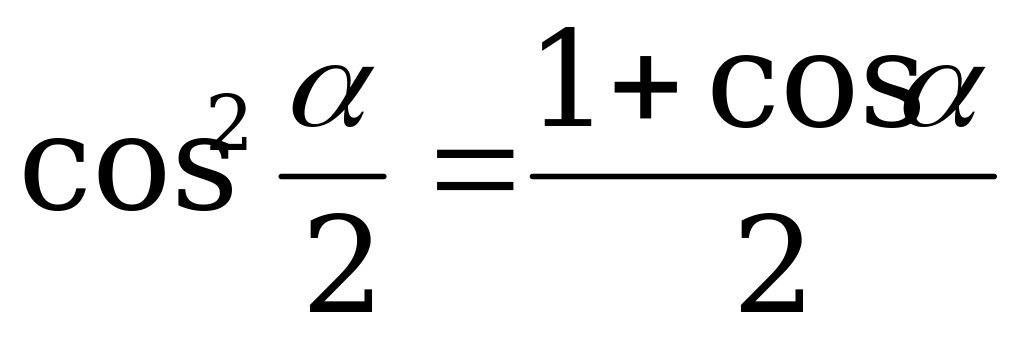 ; (2).
; (2).
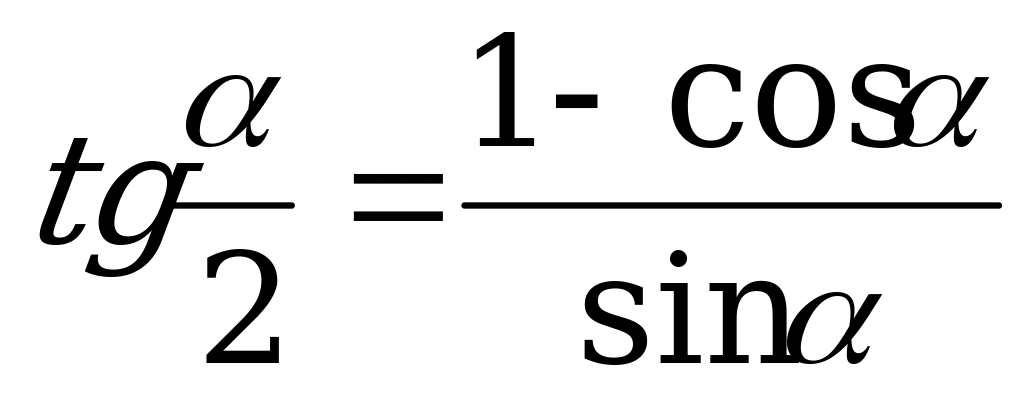 ; (3).
; (3).
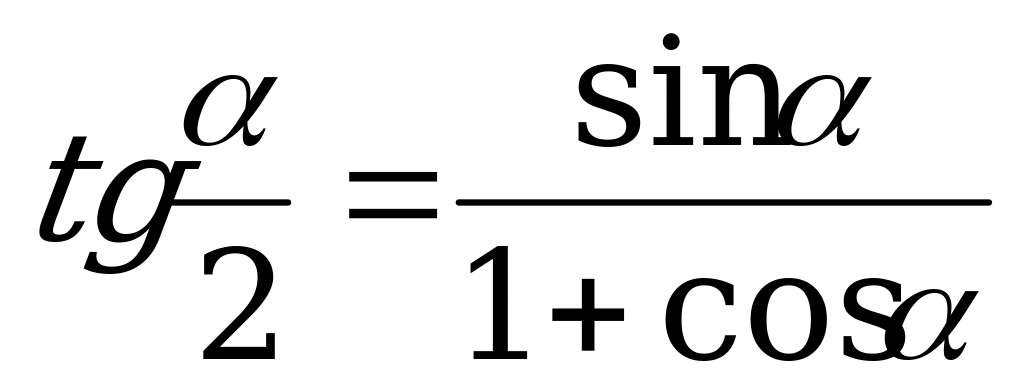 ; (4).
; (4).
Упражнения с решениями.
Пример 1. Вычислите 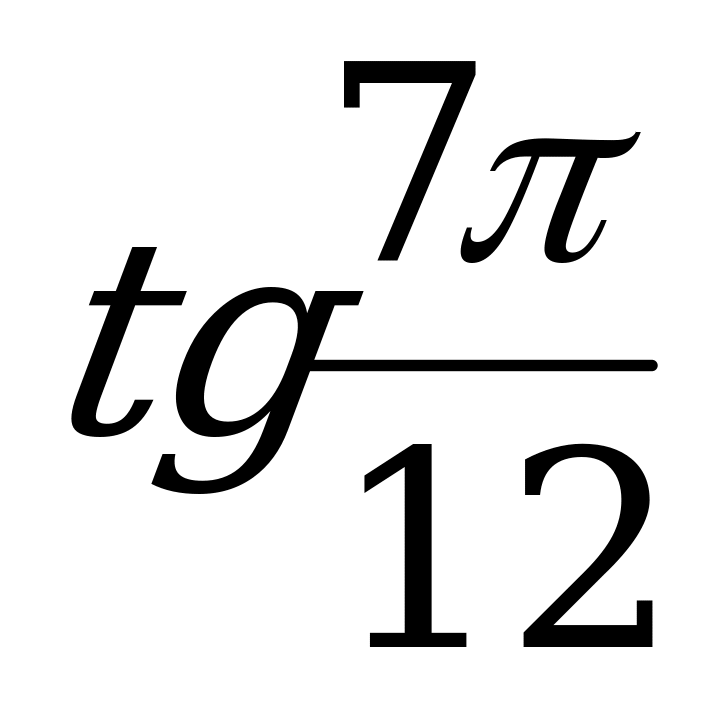 .
.
Решение. По формуле (4) имеем:
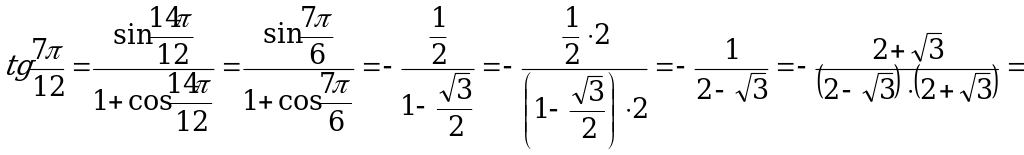
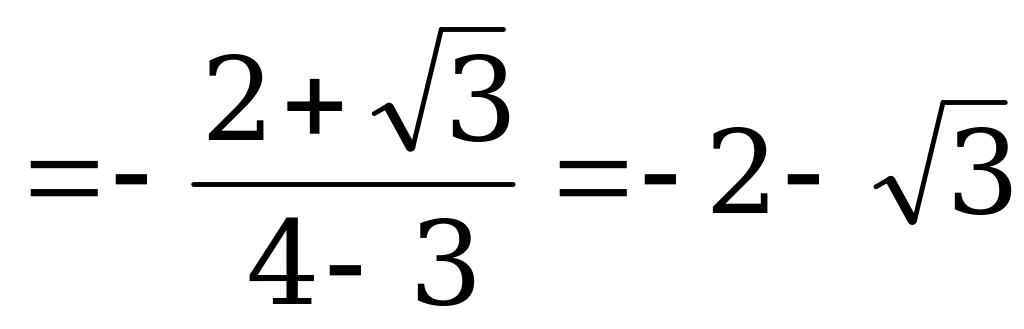 .
.
Пример 2. Найдите 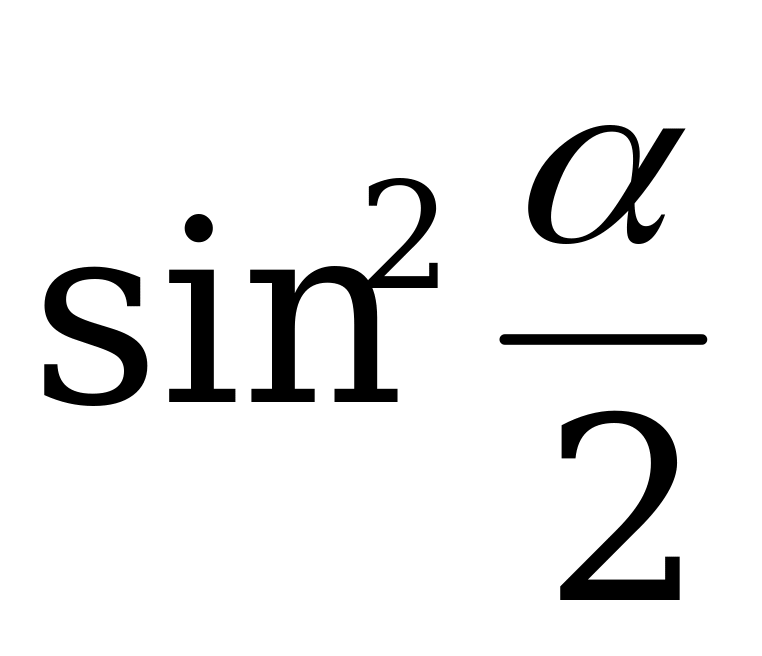 и
и 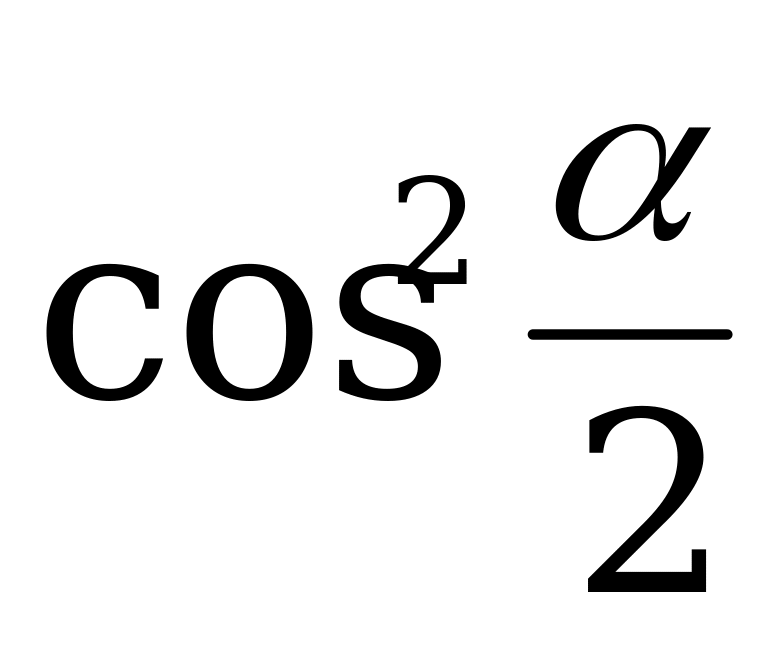 , если
, если 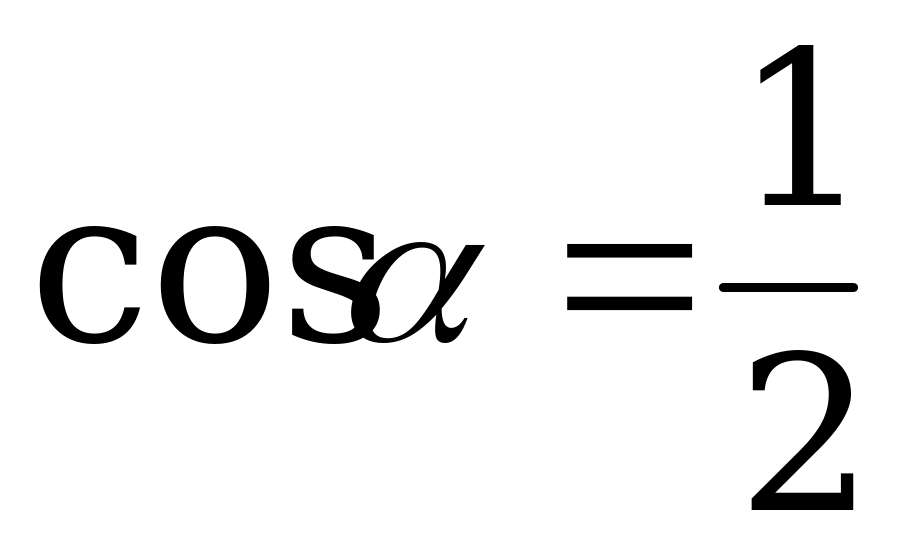 .
.
Решение. По формуле (1) имеем: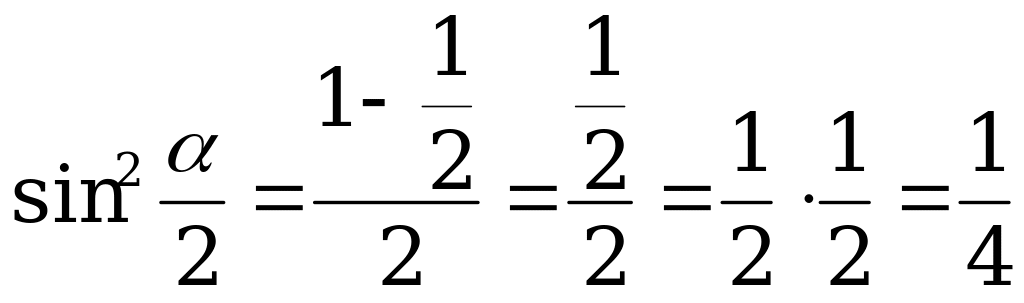 .
.
По формуле (2):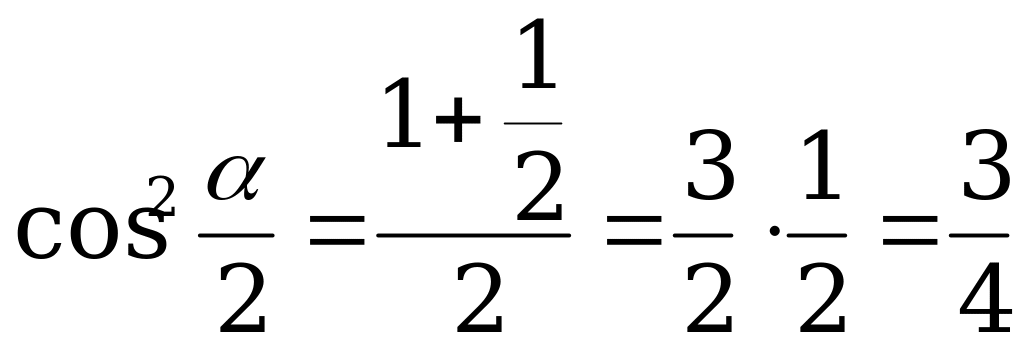 .
.
Ответ: 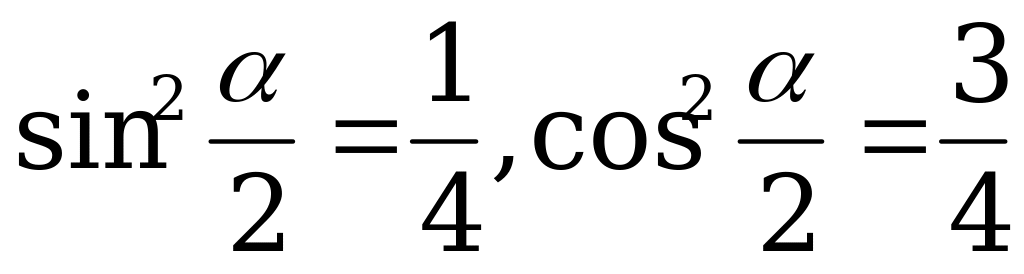 .
.
Самостоятельная работа № 4.
Вариант №1.
Вычислите 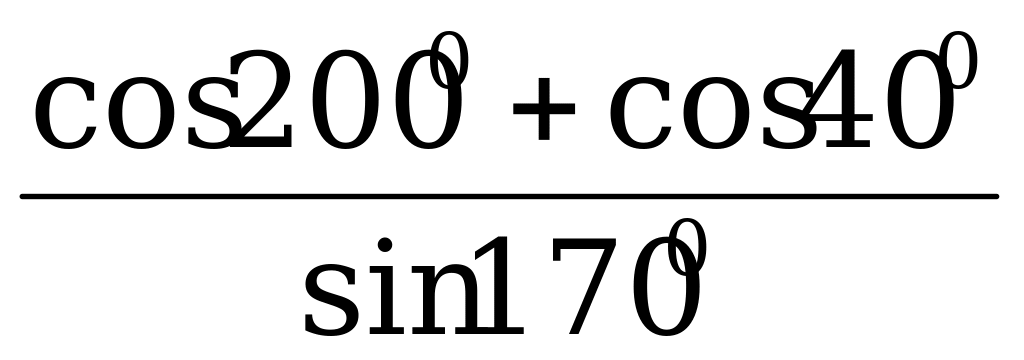 .
.
Вычислите 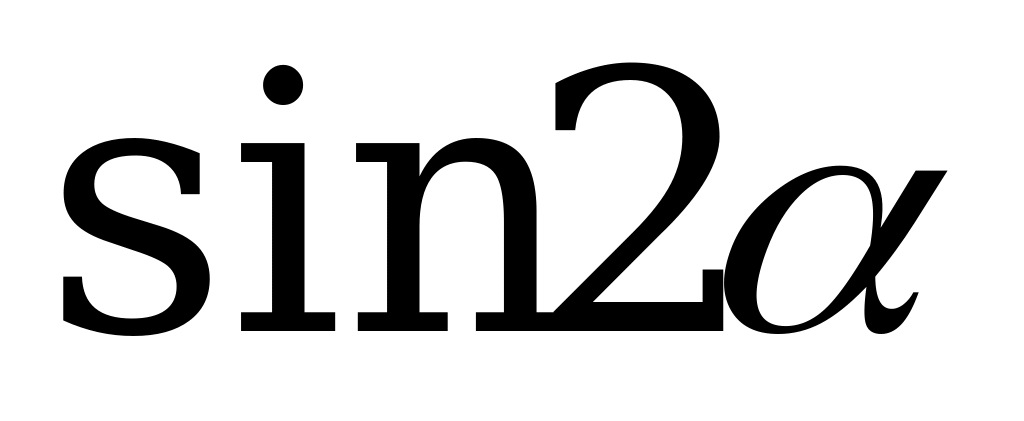 и
и , если
, если 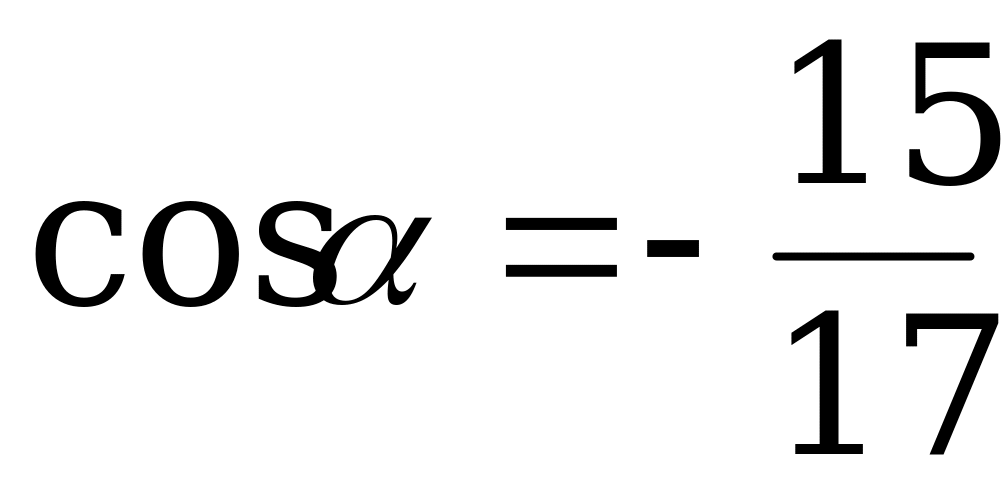 и
и 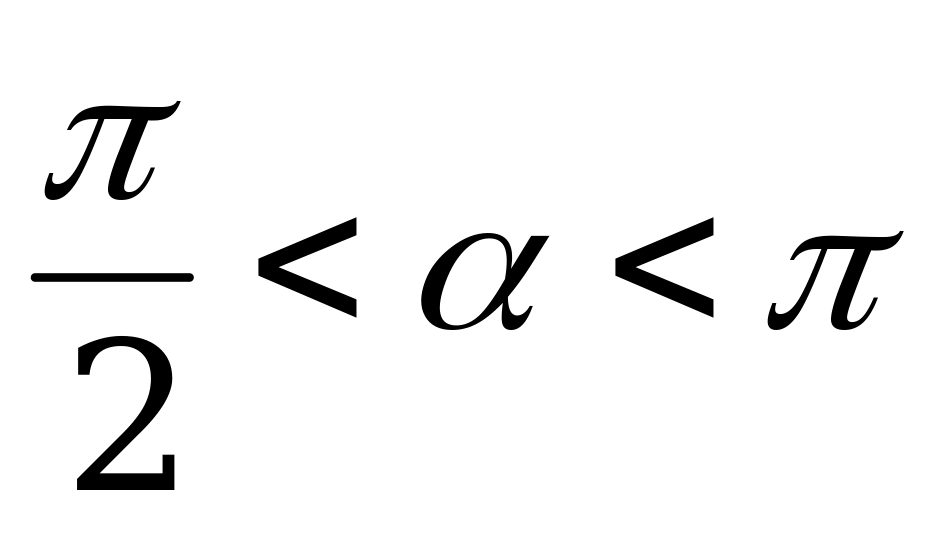 .
.
Вычислите  , если
, если 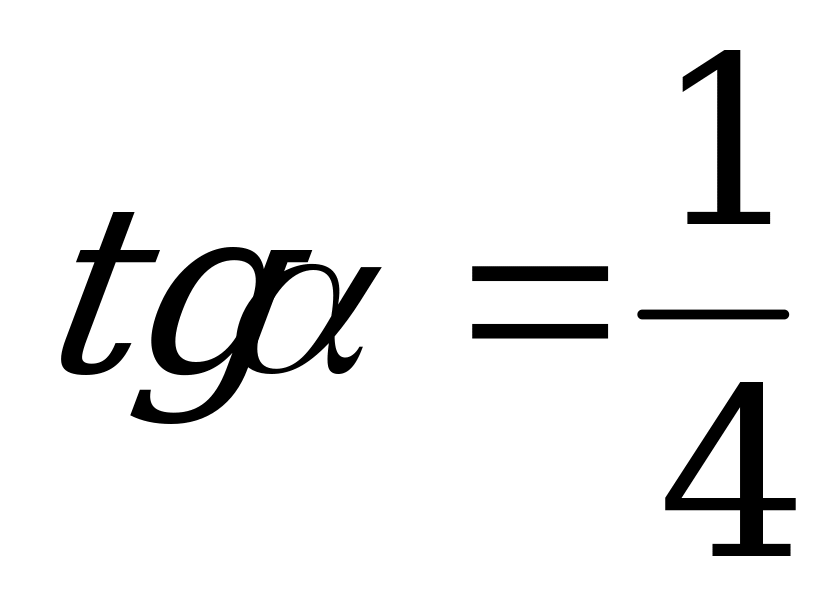 .
.
Вычислите 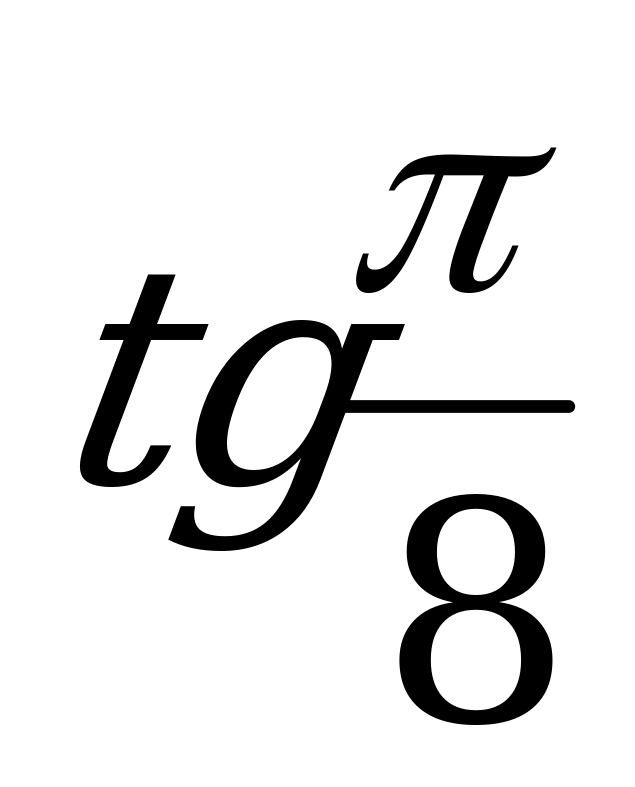 .
.
Вычислите 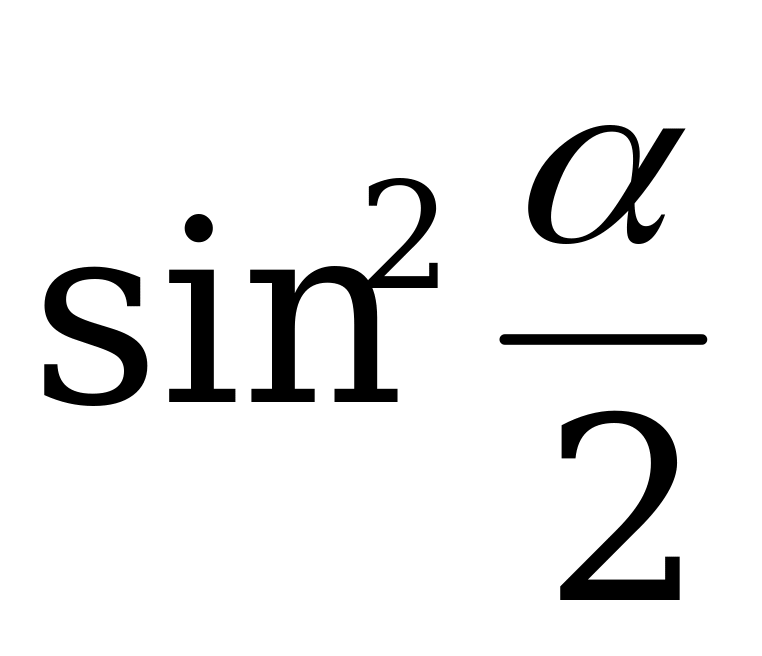 и
и 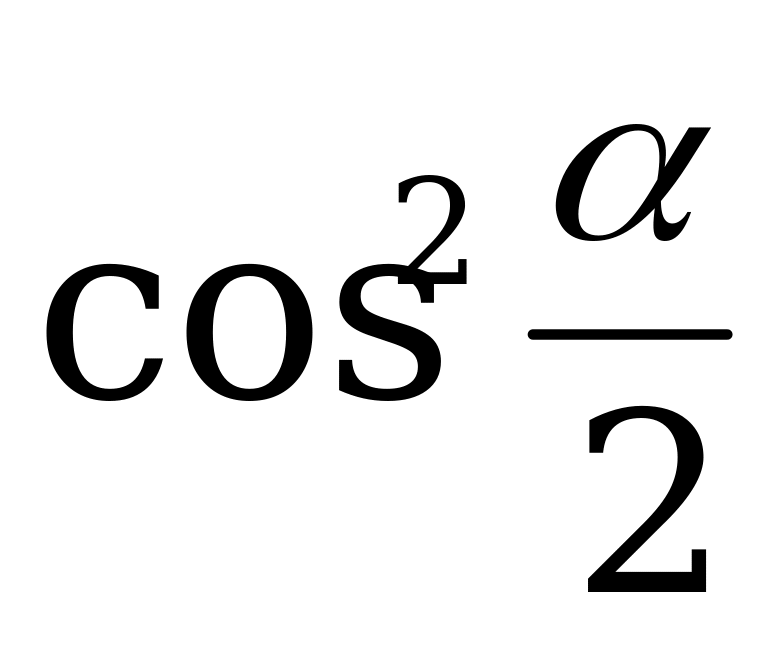 , если
, если 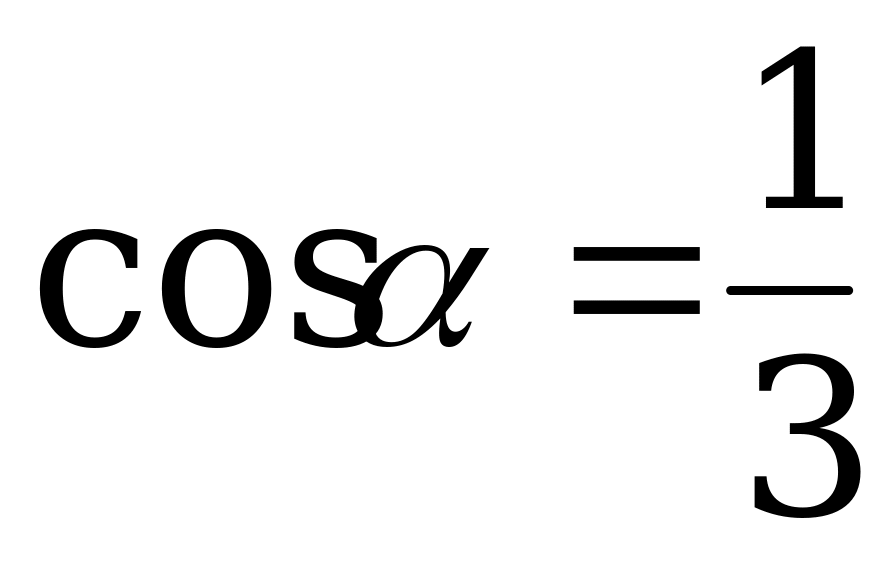 .
.
Вариант №2.
Вычислите 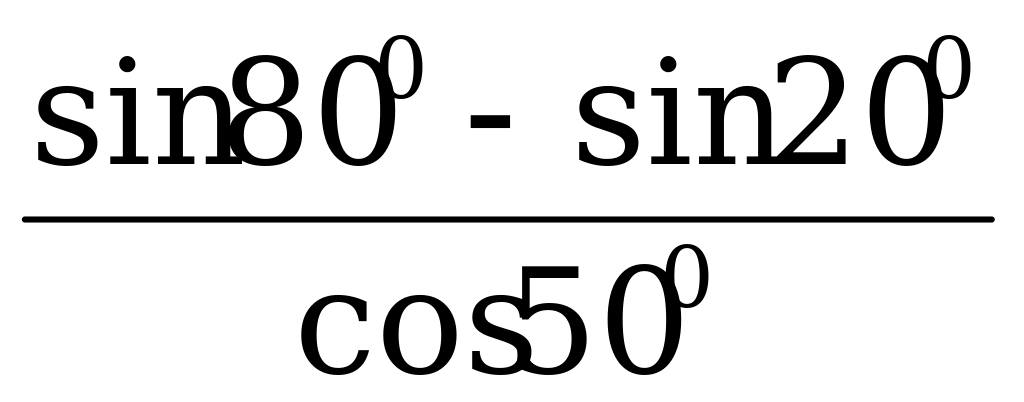 .
.
Вычислите 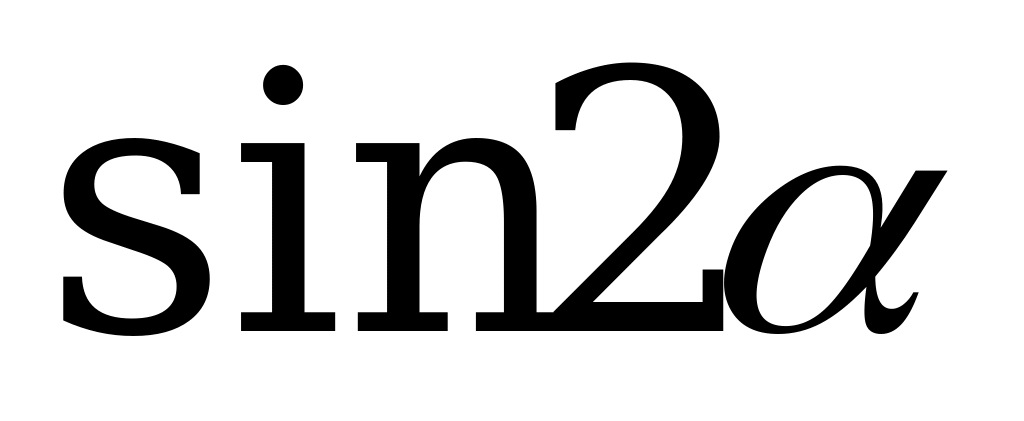 и
и  , если
, если 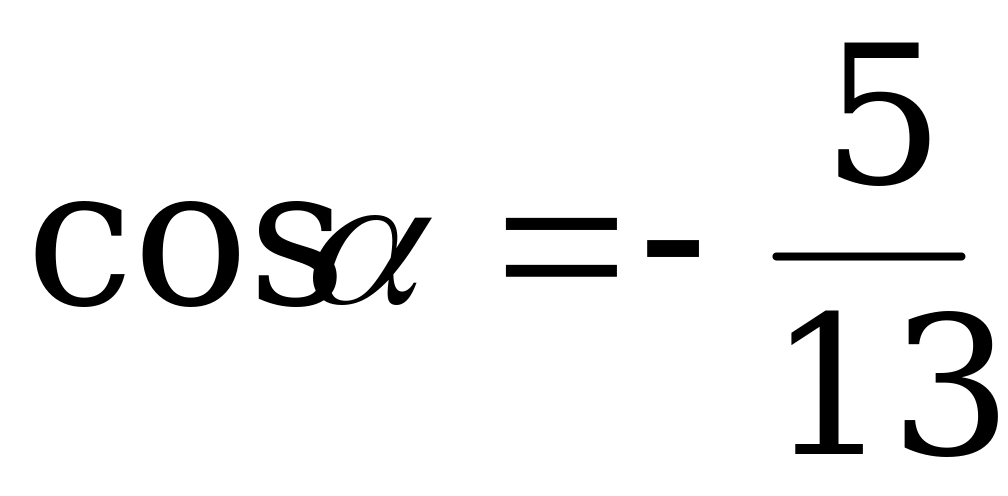 и
и 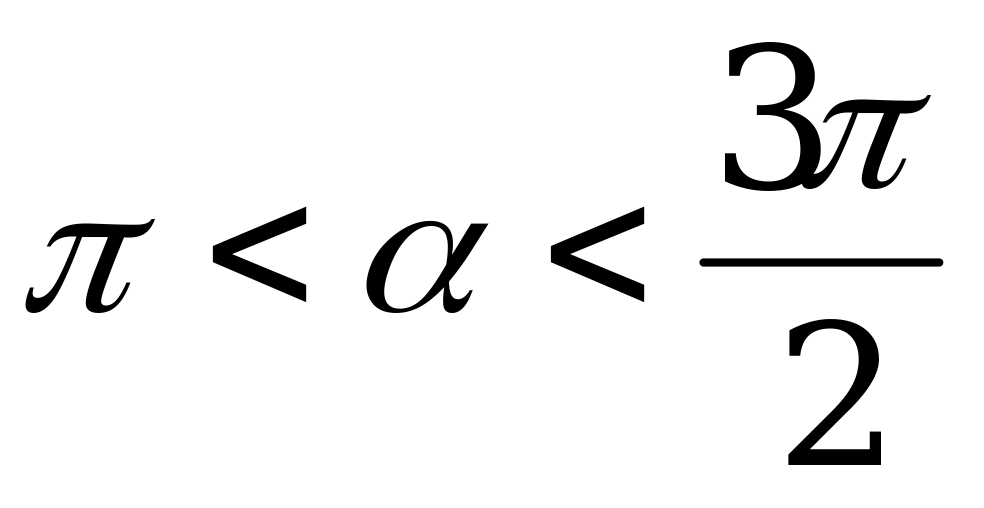 .
.
Вычислите  , если
, если 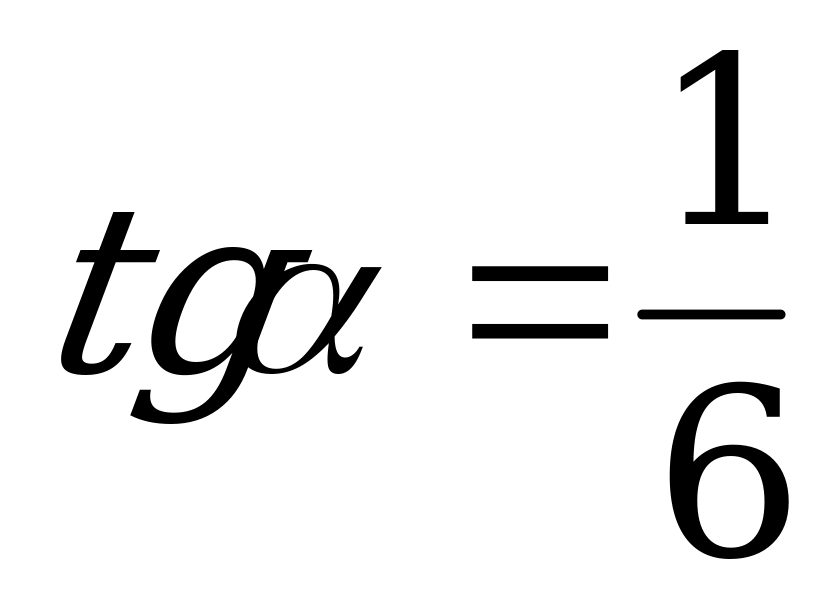 .
.
Вычислите 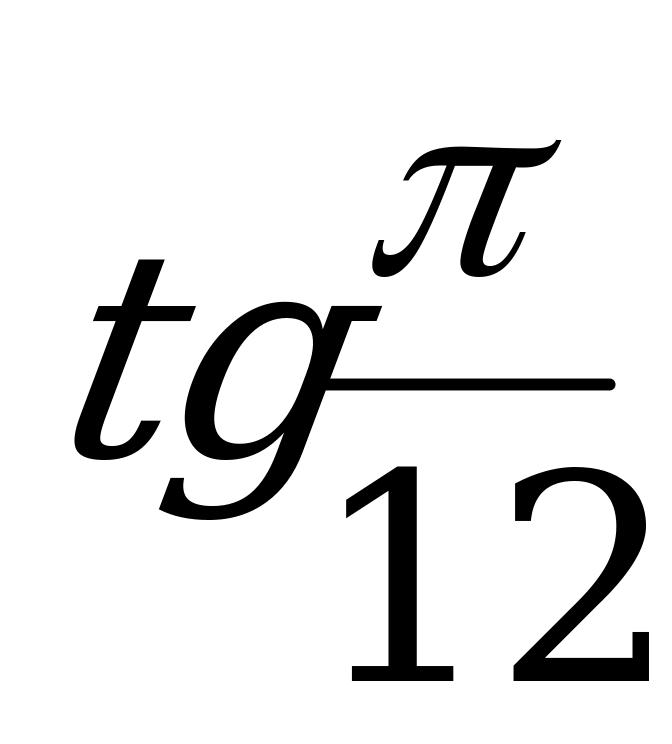 .
.
Вычислите 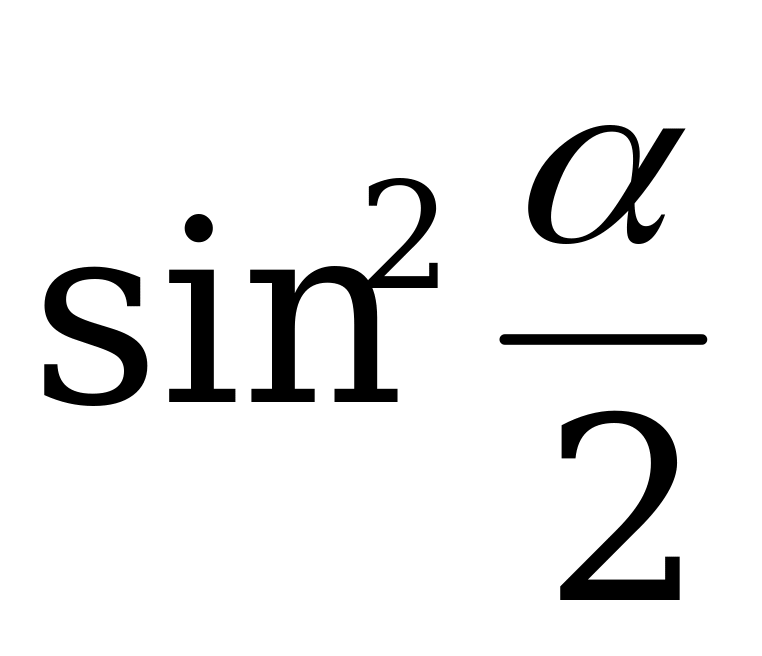 и
и 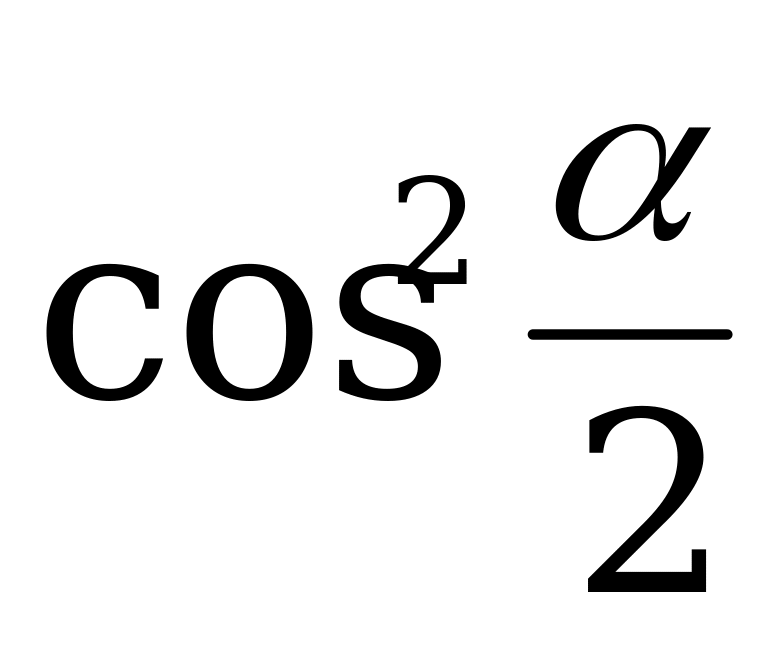 , если
, если 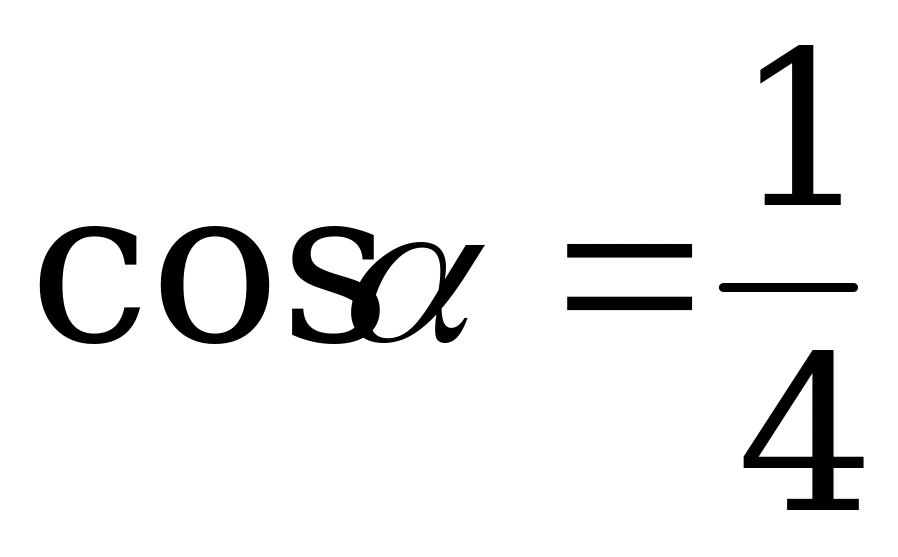 .
.
Формулы преобразования произведения синусов и косинусов в сумму.
Справочный материал.
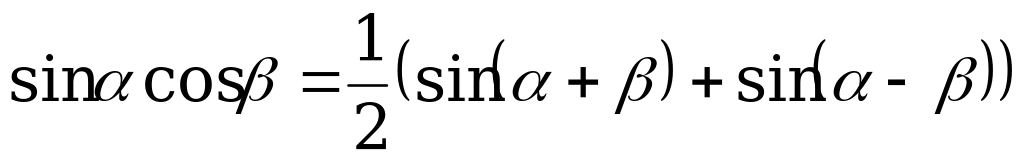 ; (1)
; (1)
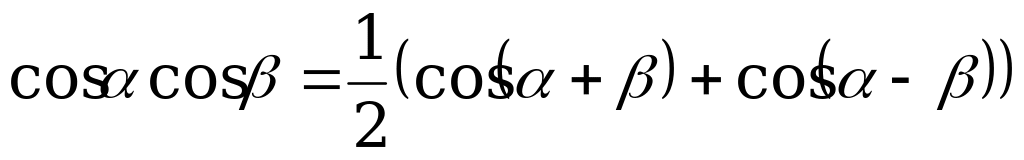 ; (2)
; (2)
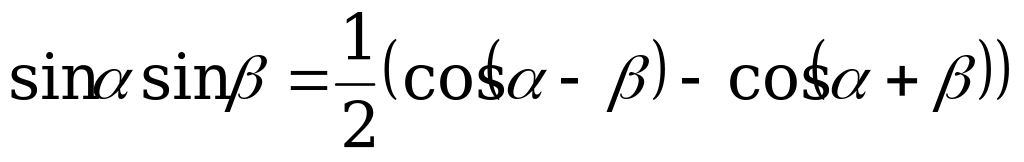 . (3)
. (3)
Упражнения с решениями.
Пример 1. Запишите в виде суммы или разности:
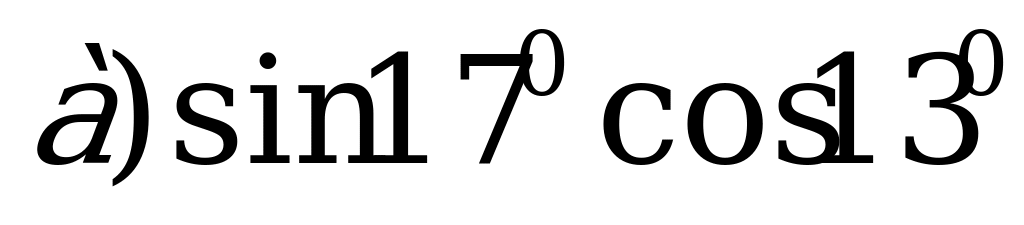 ;
;
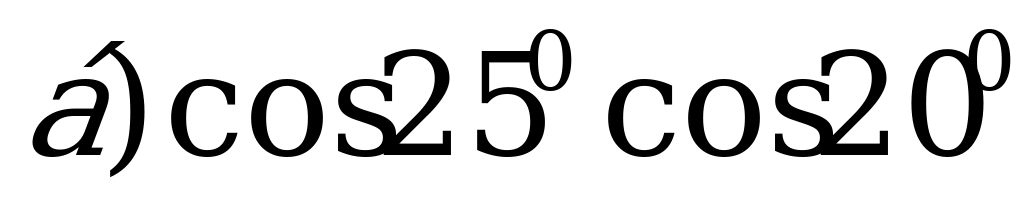 ;
;
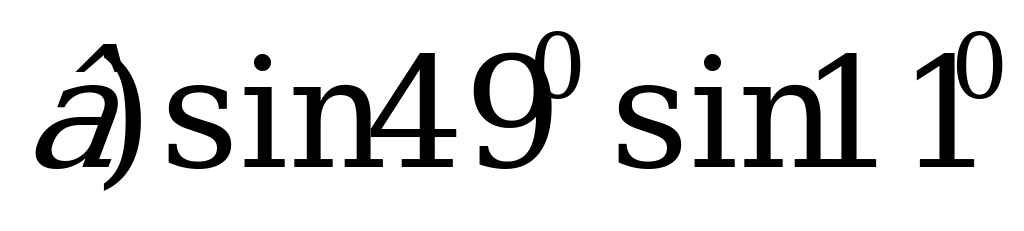 .
.
Решение. а) По формуле (1):
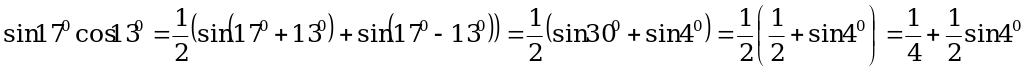 б) По формуле (2):
б) По формуле (2):
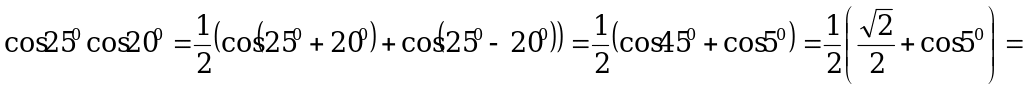
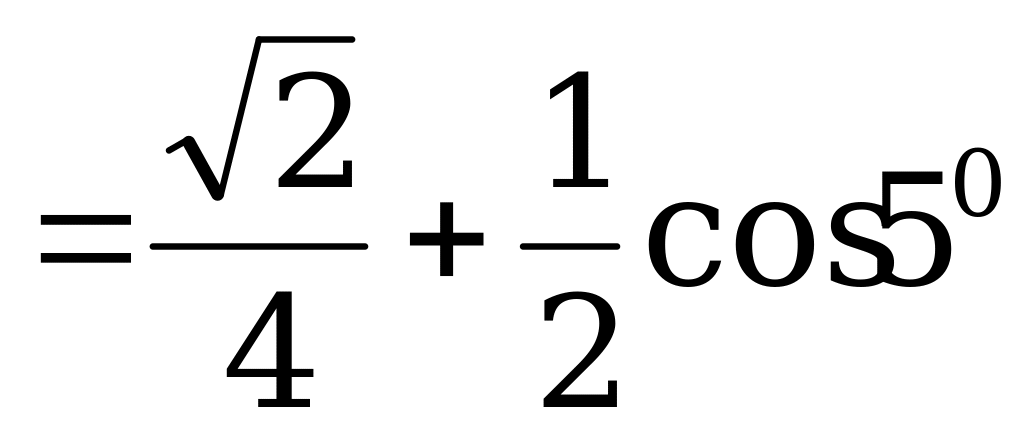 .
.
в) По формуле (3):
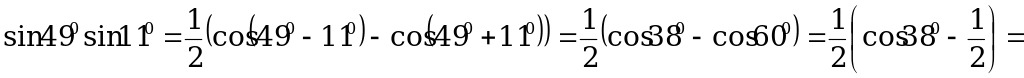
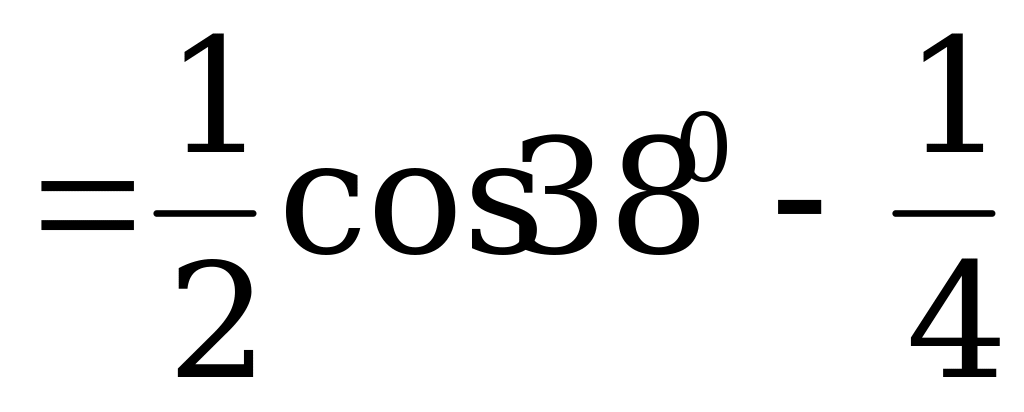 .
.
Пример 2. Вычислите:
а) 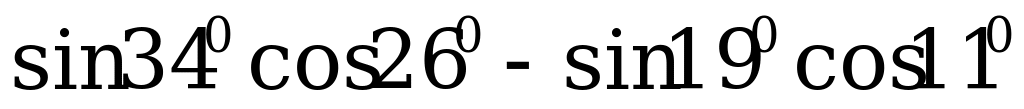 ;
;
б) 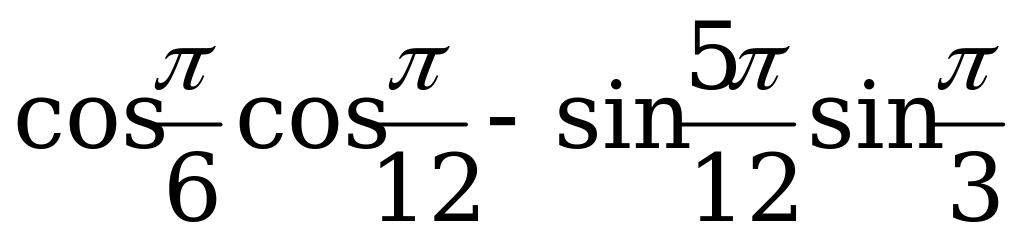 .
.
Решение.
а) По формуле (1):
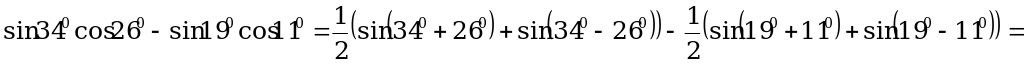
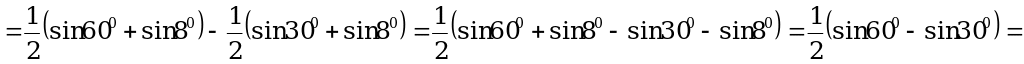
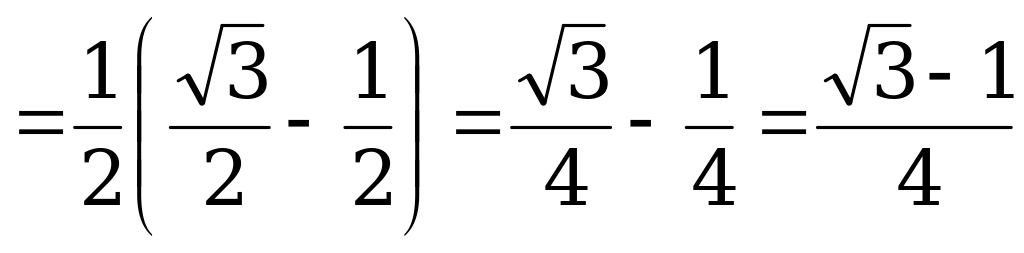 .
.
б) По формулам (2) и (3):
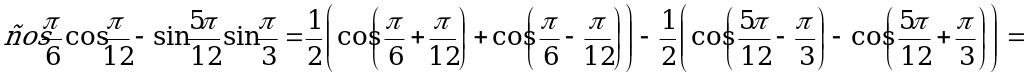
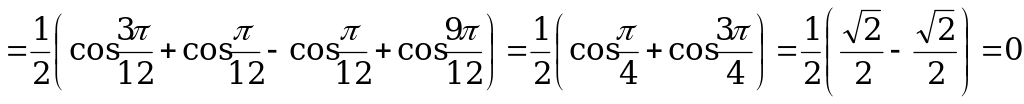 .
.
Самостоятельная работа №5.
Вариант №1.
1. Запишите в виде суммы или разности:
а) 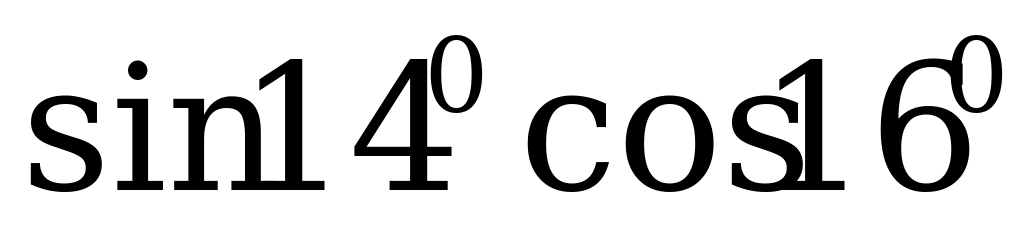 ; б)
; б) 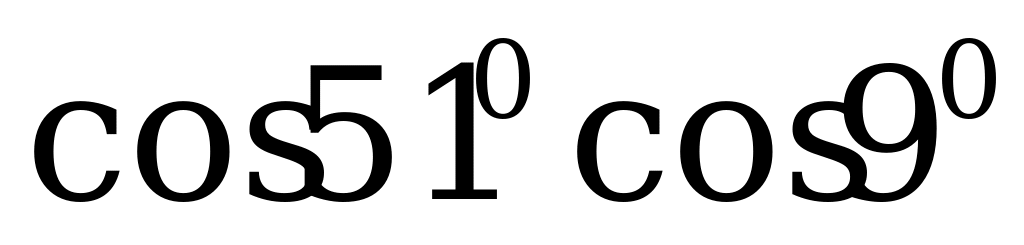 ; в)
; в) 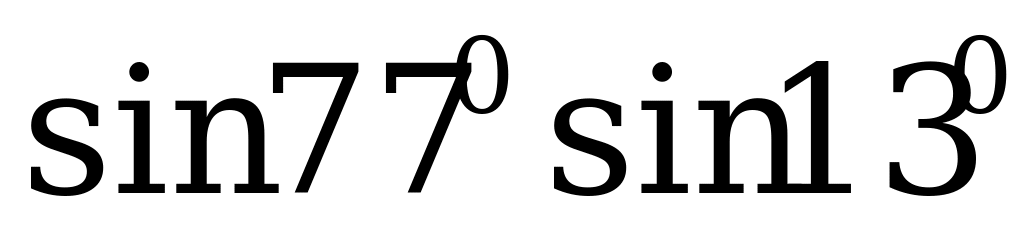 .
.
2. Вычислите:
а) 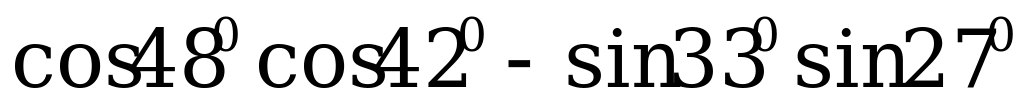 ; б)
; б) 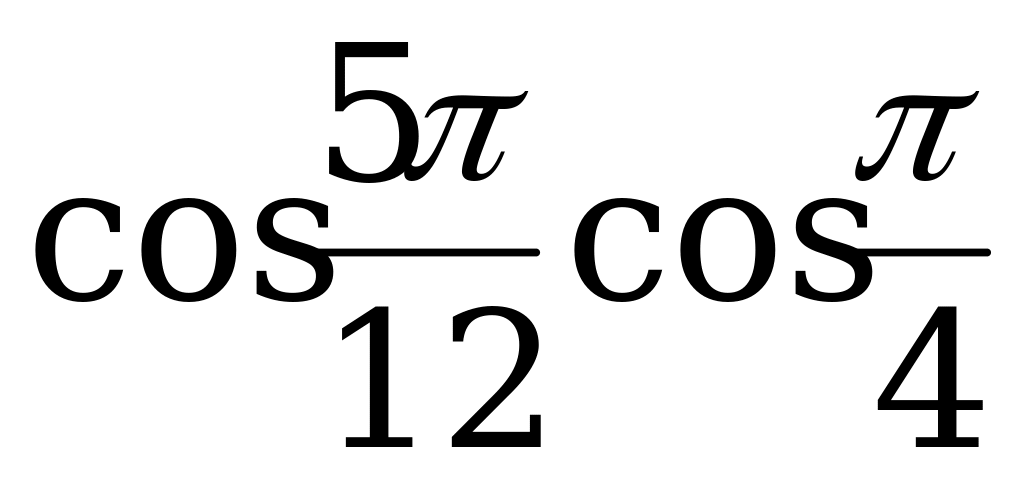 .
.
Вариант №2.
1. Запишите в виде суммы или разности:
а) 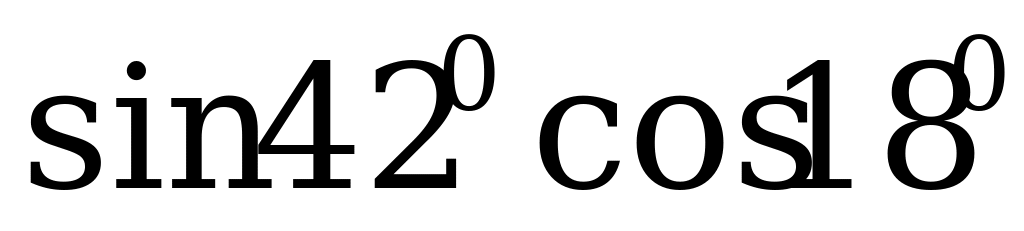 ; б)
; б) 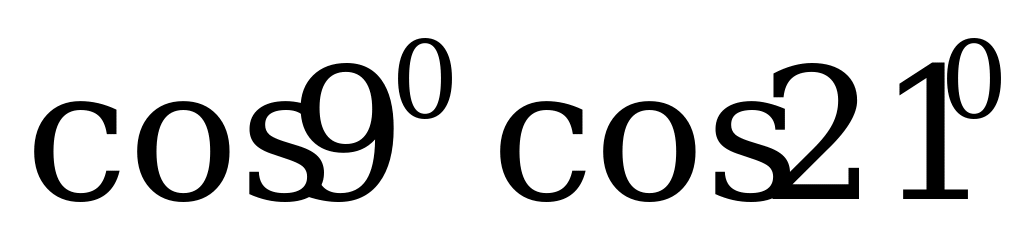 ; в)
; в) 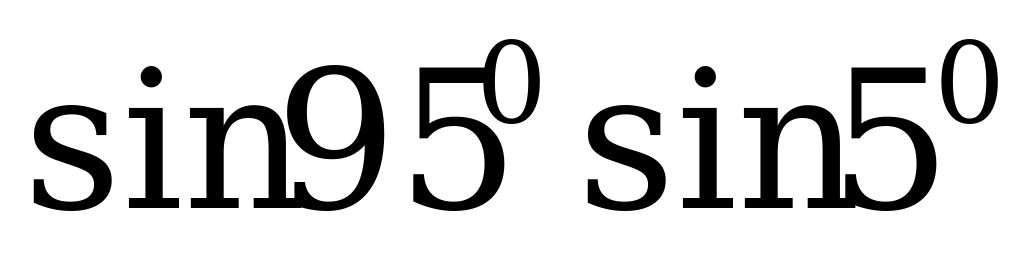 .
.
2. Вычислите:
а) 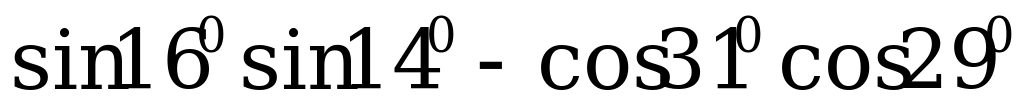 ; б)
; б) 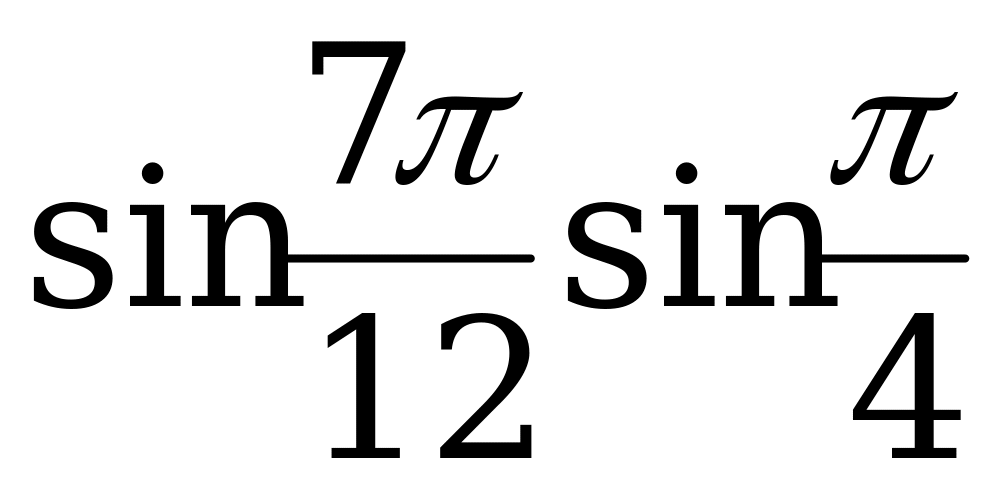 .
.
§ 2 Тригонометрические функции и их графики.
2.1. Функция. Область определения и область значений функции.
Справочный материал.
Функцией называется зависимость переменной y от переменной x ,при которой каждому x ставится в соответствие единственное значение y.
При этом x называется независимой переменной (аргументом), а y – зависимой переменной (функцией).
Обозначается функция:y=f(x).
Областью определения функции D(f) называется множество всех значений переменной x, при которых данная функция имеет смысл.
Областью значений функции Е(f) называется множество, состоящее из всех чисел f(x), таких, что x принадлежит области определения функции f.
Графиком функции f называют множество всех точек 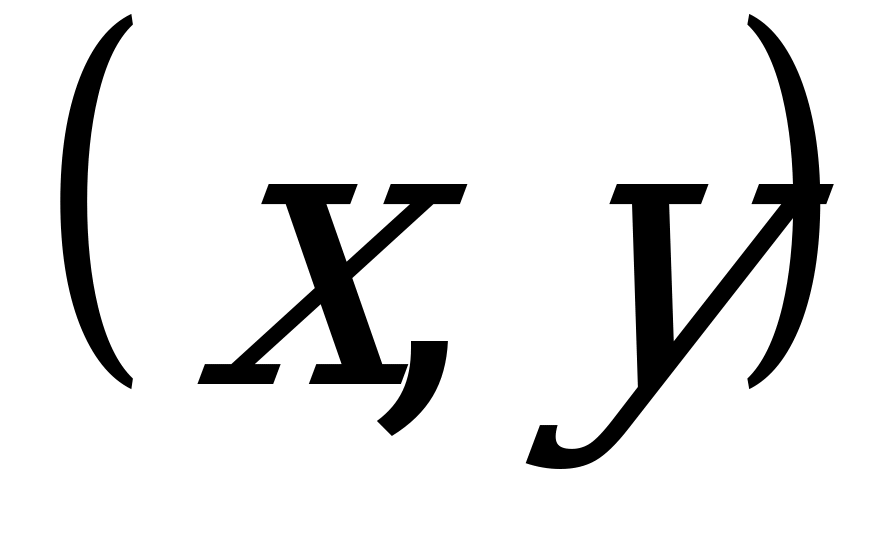 координатной плоскости, где
координатной плоскости, где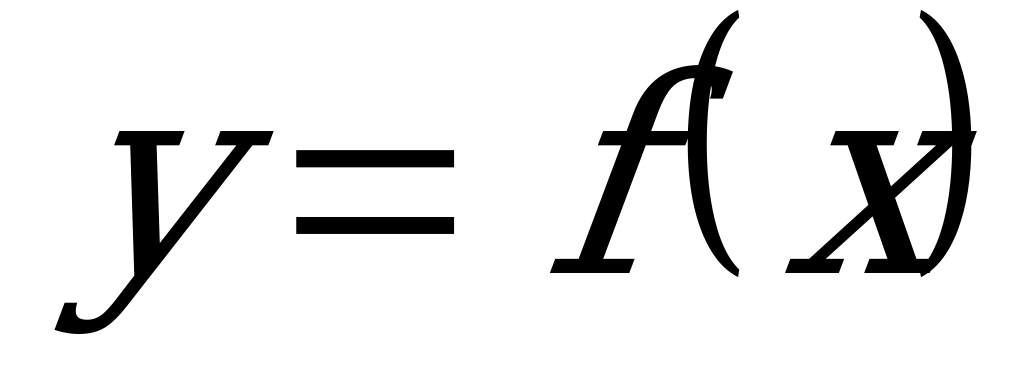 , а x «пробегает» всю область определения функции f.
, а x «пробегает» всю область определения функции f.
Функцию f называют чётной, если для любого x из области определения функции выполняется равенство: f(-х)= f(х).
Функцию f называют нечётной, если для любого x из области определения функции выполняется равенство: f(-х)= - f(х).
2.2. Функция синус.
Числовая функция, заданная формулой 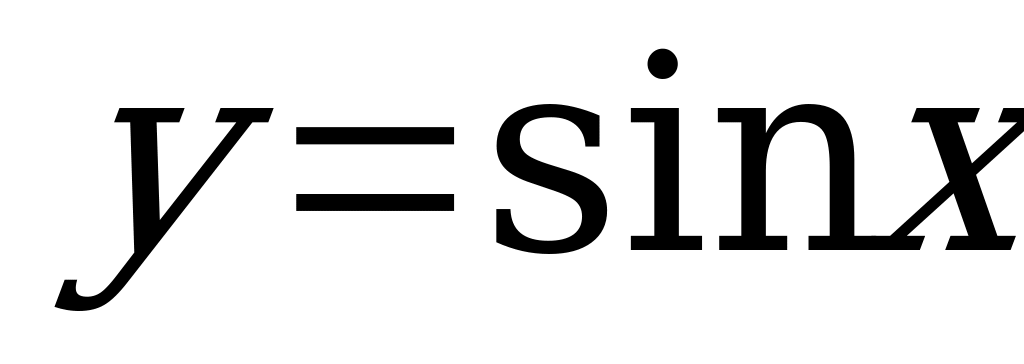 , называется функцией синус.
, называется функцией синус.
Область определения функции синус – множество всех действительных чисел, т.е. D(sin)=R.
Областью значений функции синус является отрезок [-1;1], т.е. 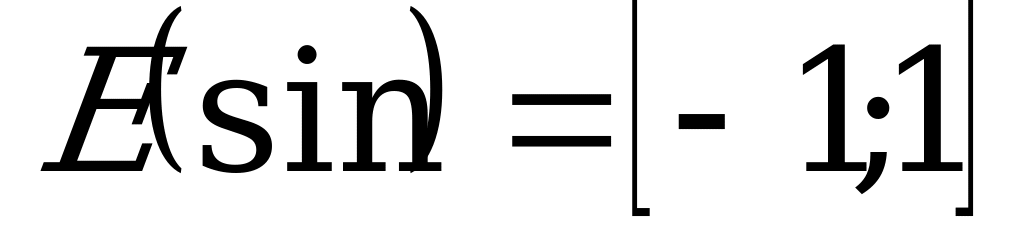 .
.
Синус – нечётная функция, т.е. для любого числа x выполняется равенство sin(-x) = - sin x
Синус периодическая функция с пределом Т=2π, т.е. для любого x выполняется равенство sin(x+2πn) = sin x, где n – произвольное целое число.
График синуса называется синусоидой (рис.1).

y












2

1


x
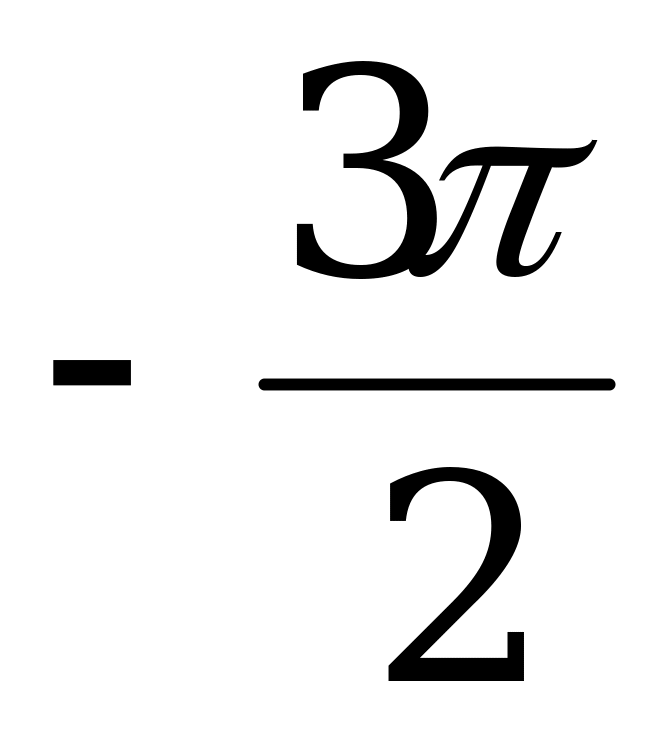



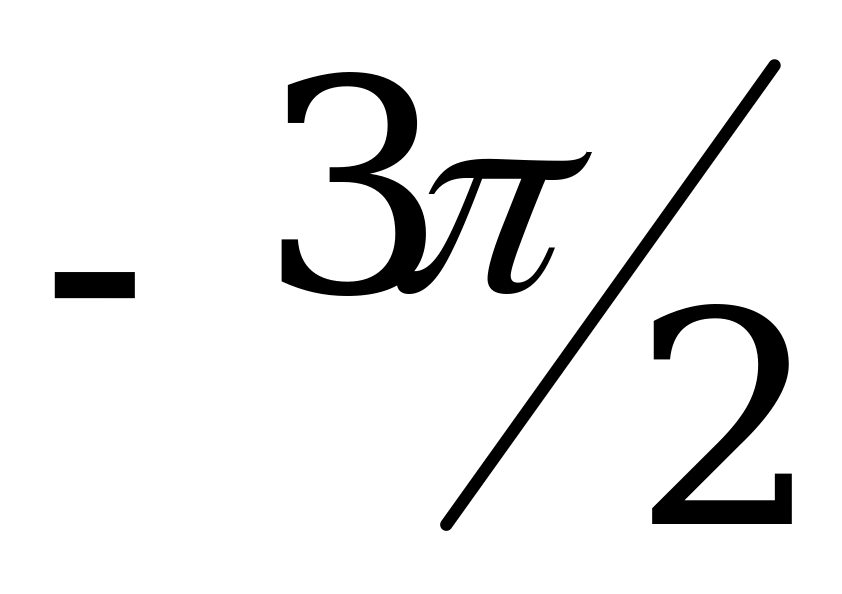

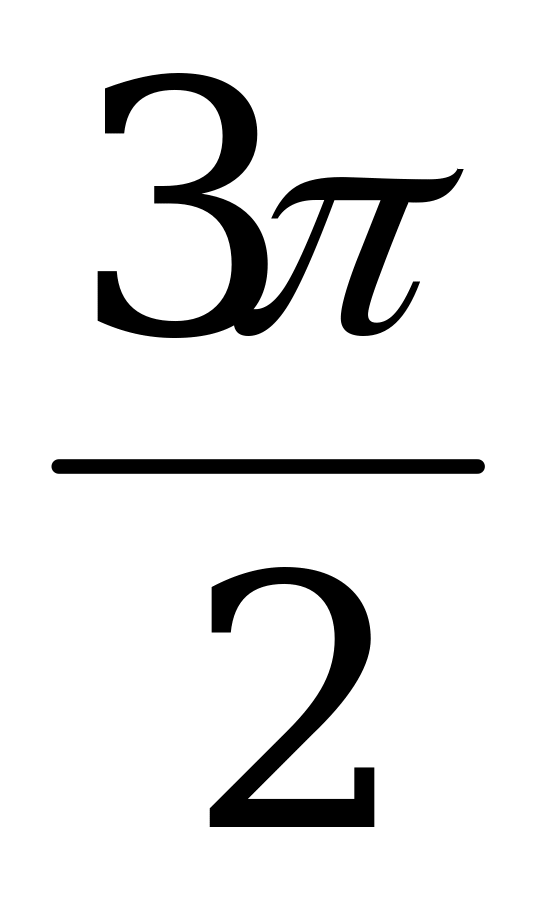
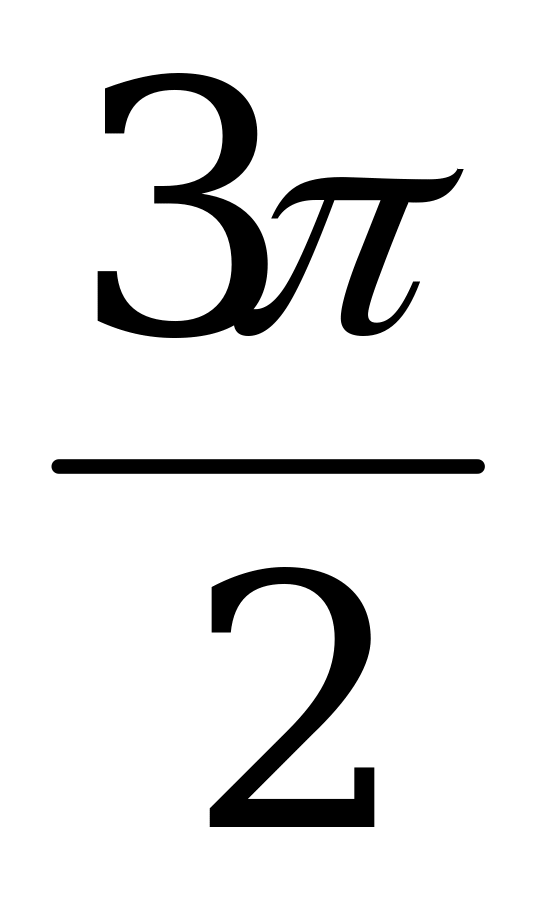
0

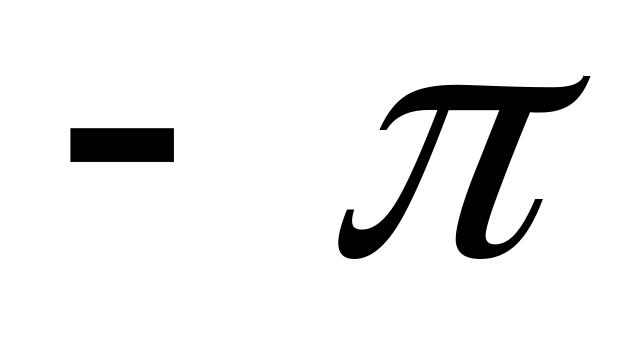
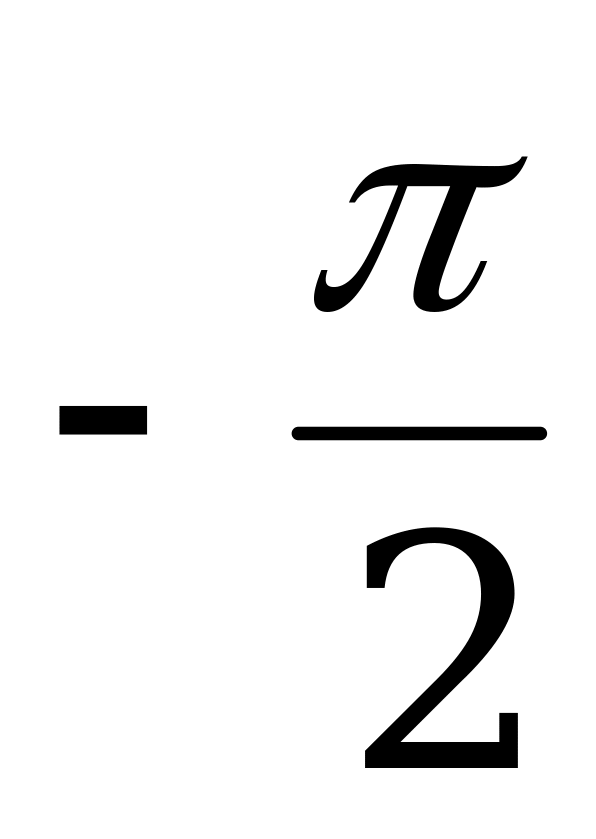
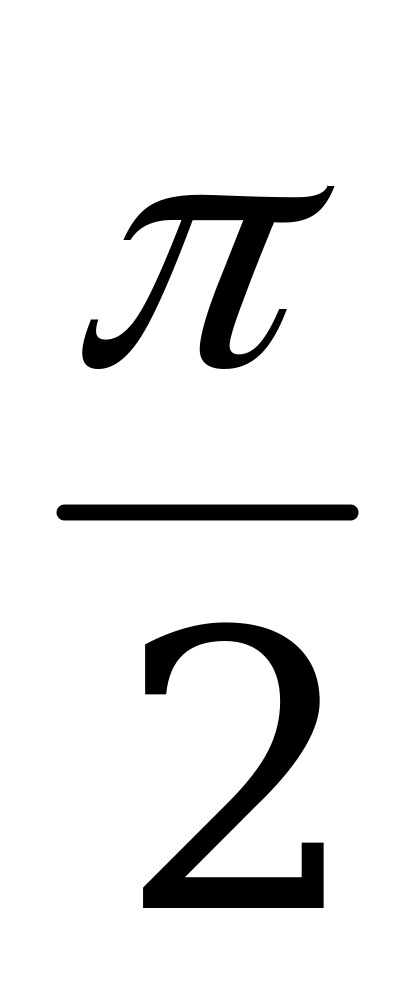

-1

-2


2.3. Функция косинус.
Числовая функция, заданная формулой 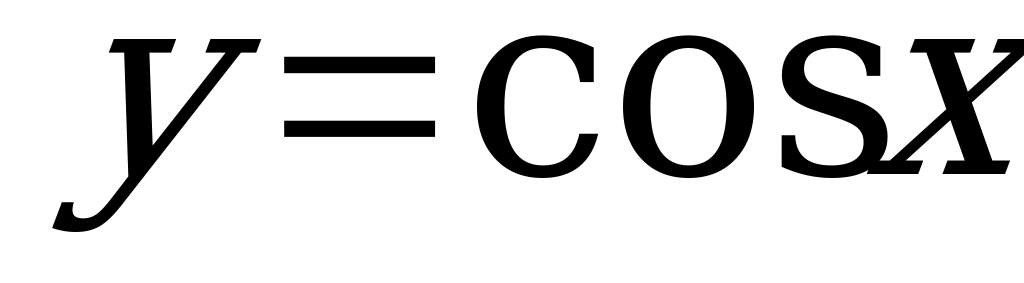 , называется функцией косинус.
, называется функцией косинус.
Область определения функции косинус – множество всех действительных чисел, т.е. D(cos) = R.
Областью значений функции косинус является отрезок [-1;1], т.е. 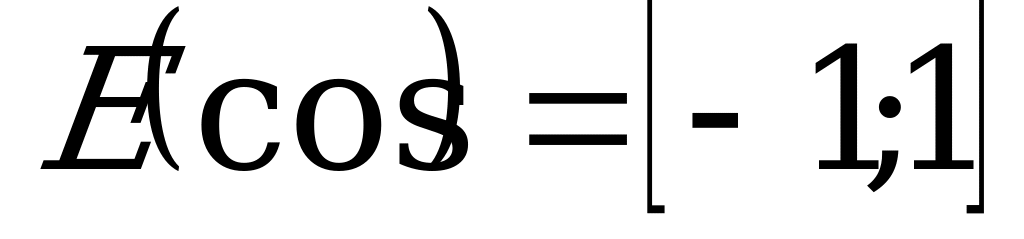 .
.
Косинус чётная функция, т.е. для любого x выполняется равенство cos (-x) = cos x.
Косинус периодическая функция с периодом T= 2π, т.е. для любого x выполняется равенство cos(x+2πn)=cos x, где n – произвольное целое число.
График косинуса называется косинусоида. (рис. 2).
y










2

1


0

x
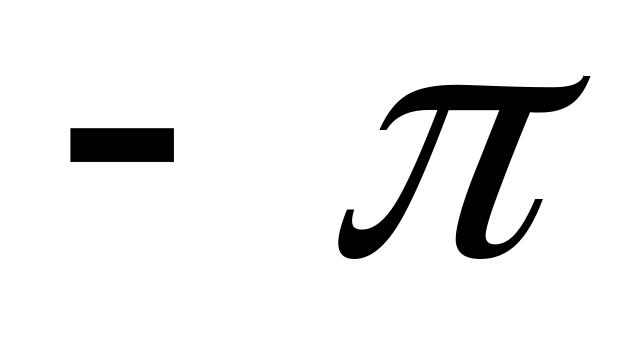
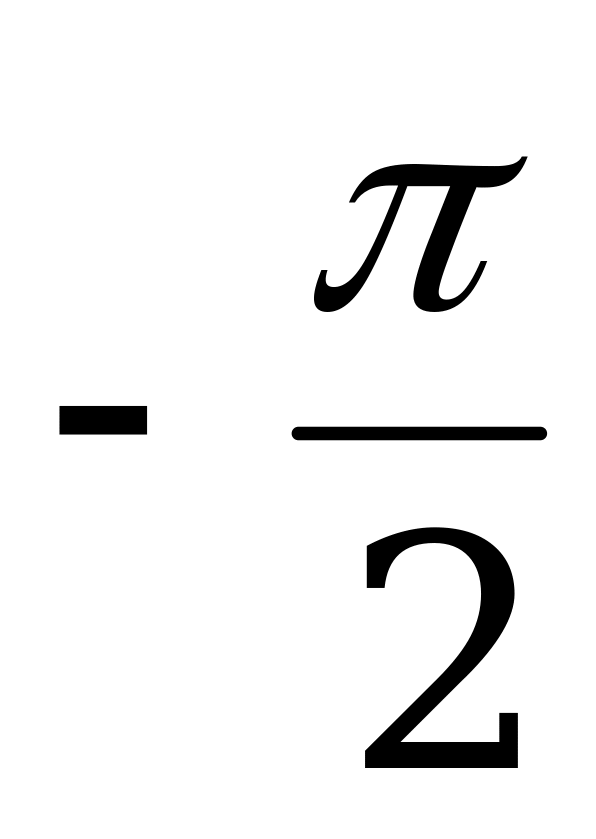
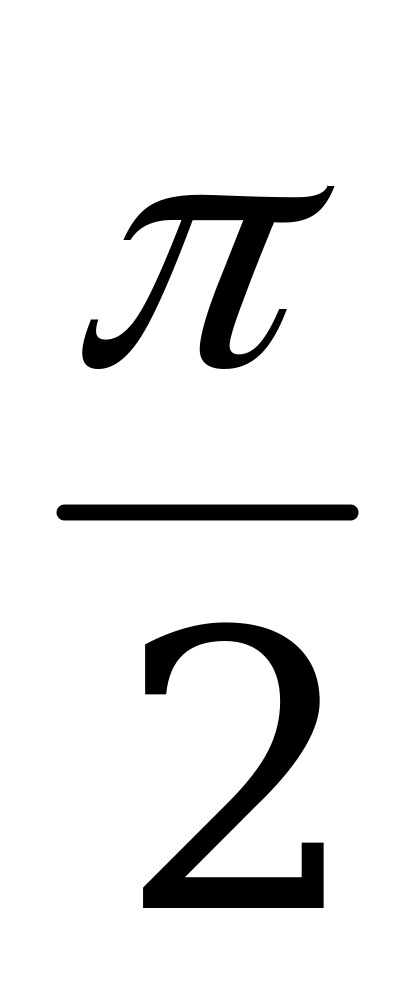

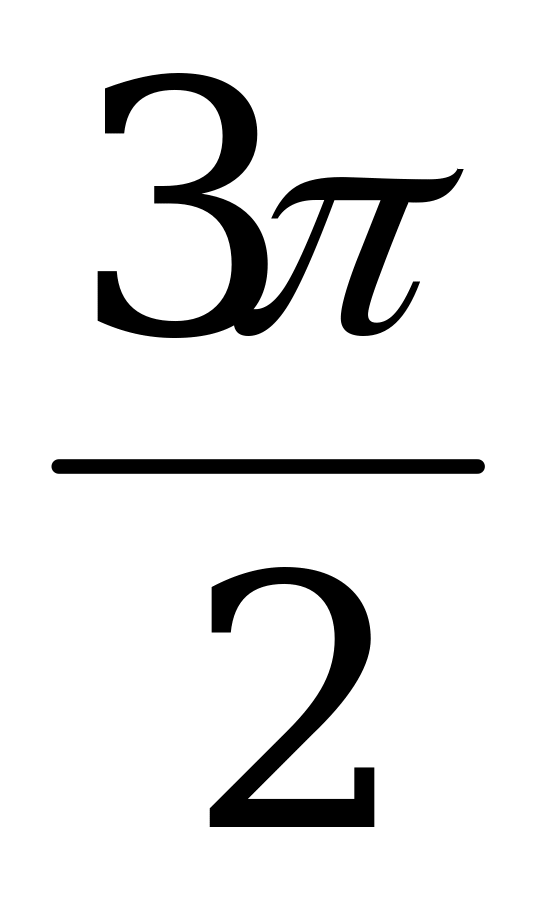
-1

-2


2.4. Функция тангенс.
Числовая функция, заданная формулой y = tg x, называется функцией тангенс.
Область определения функции тангенс – множество всех чисел x, для которых cos x ≠ 0, т.е. D(-tg) = 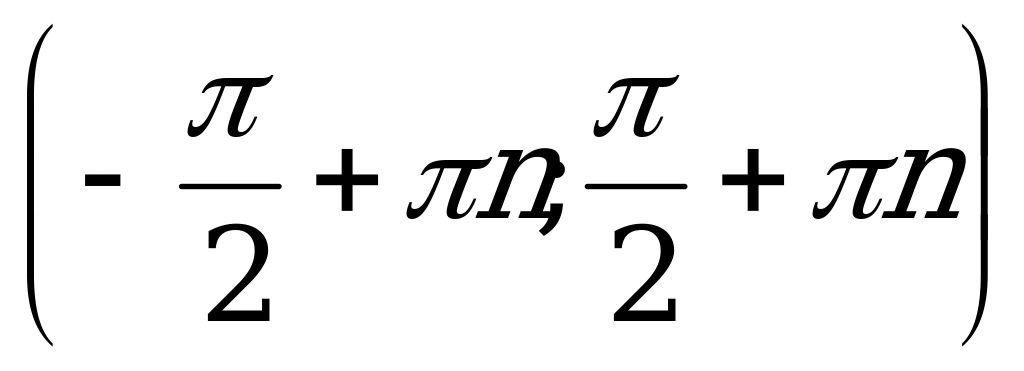 , где n є Z.
, где n є Z.
Область значения тангенса – все действительные числа, т.е. E(tg) = R
Тангенс является нечётной функцией, т.е. для любого x выполняется равенство tg(-x) = -tg x.
Тангенс периодическая функция с периодом Т = π, т.е. для любого x выполняется равенство tg(x + πn) = tg x, n є Z.
График тангенса называется тангенсоида.
y




















2

1

0

x
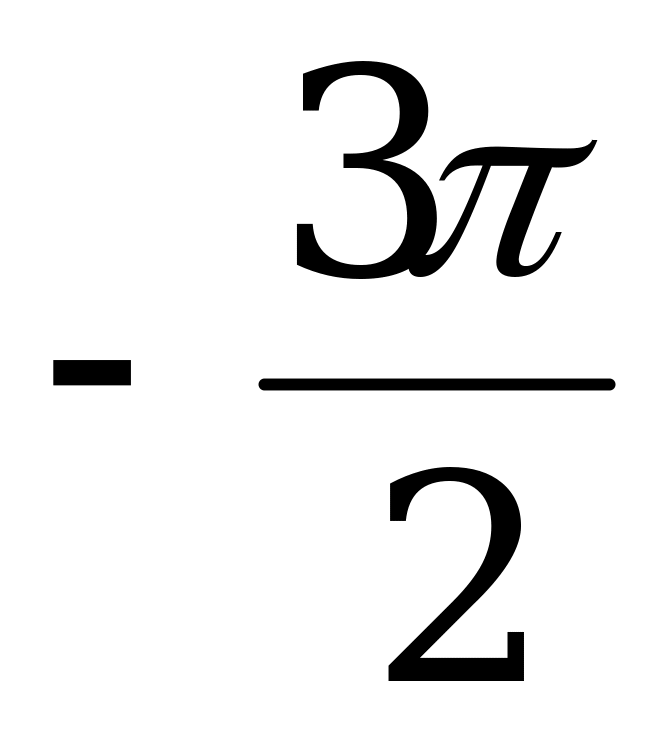
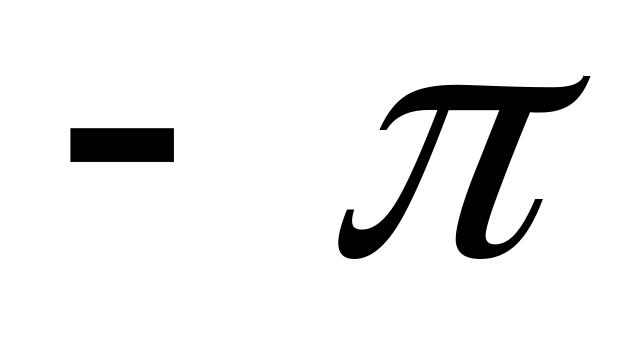
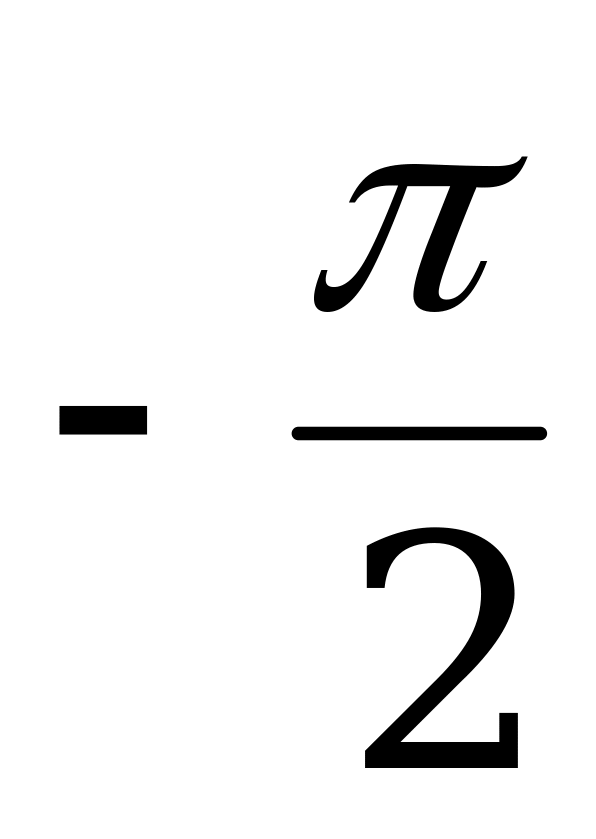
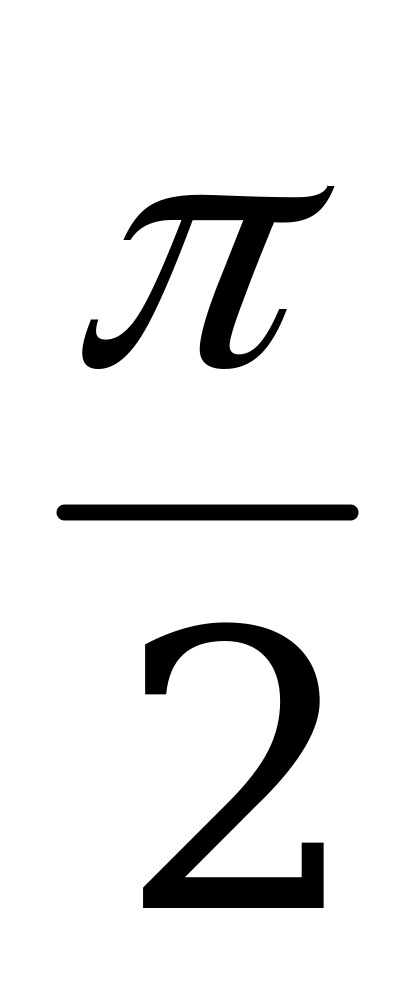

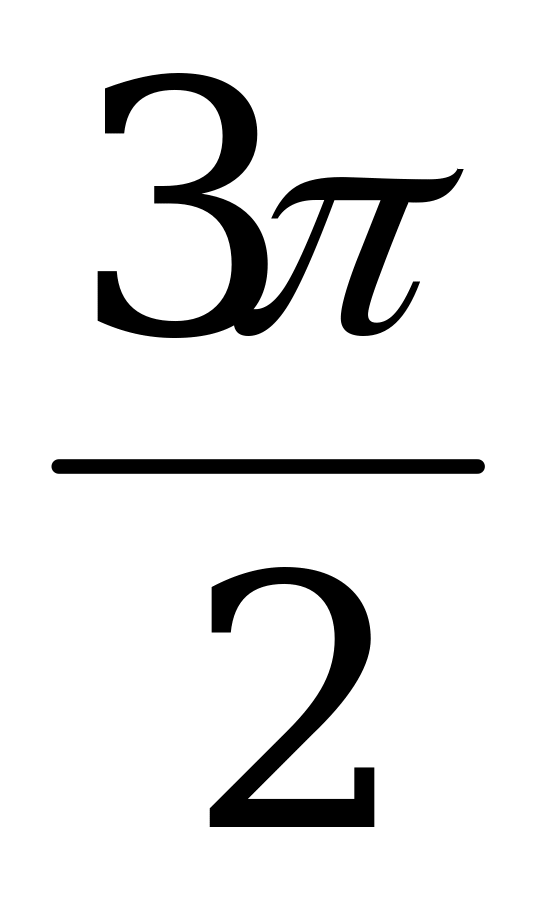

-1

-2


2.5. Функция котангенс.
Числовая функция, заданная формулой y =ctgx, называется функцией котангенс.
Область определения функции котангенс – множество всех чисел x, для которых sin x ≠ 0, т.е. D(ctg) = (πn; π + πn), где n є Z.
Область значений котангенса – все действительные числа, т.е.  R.
R.
Котангенс является нечётной функцией, т.е. для любого x выполняется равенство ctg(-x) = -ctg x.
Котангенс периодическая функция с периодом Т = π, т.е. для любого x выполняется равенство ctg(x + πn) = ctg x, где n є Z.
График котангенса называют котангенсоидой.
y

















2

1

0

x
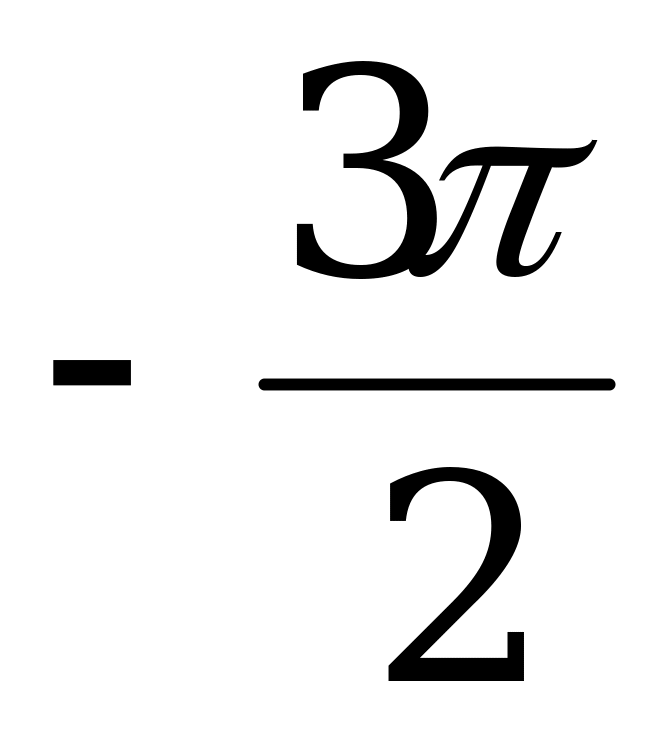
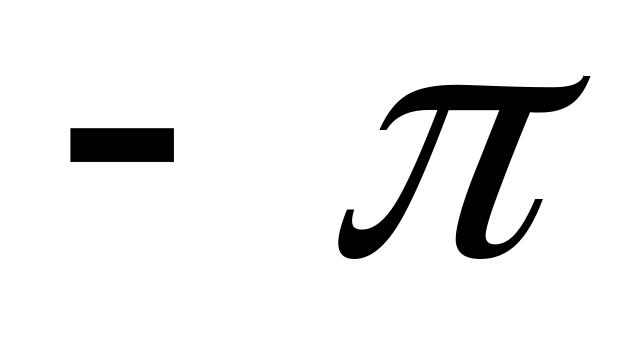
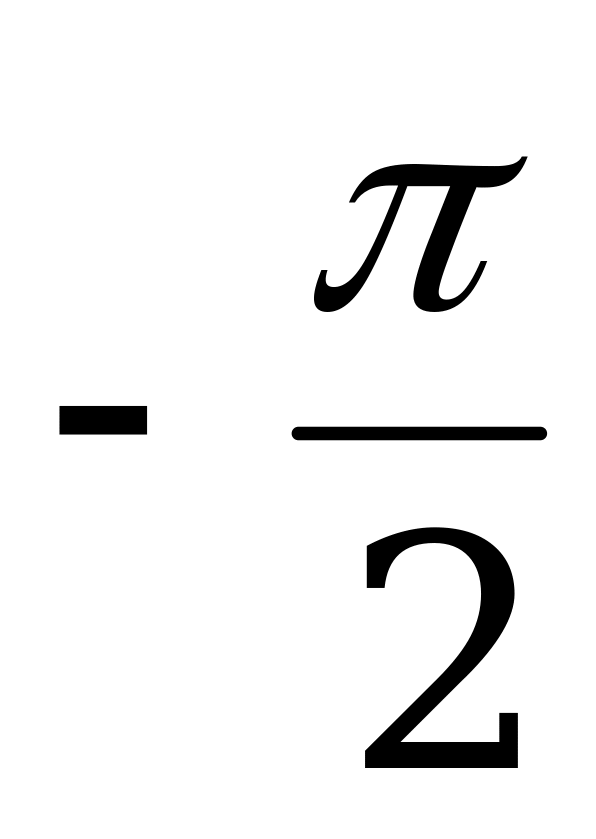
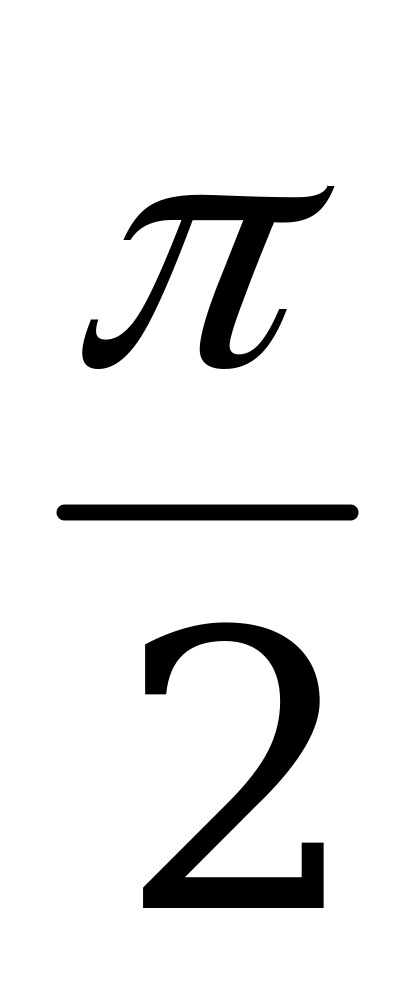

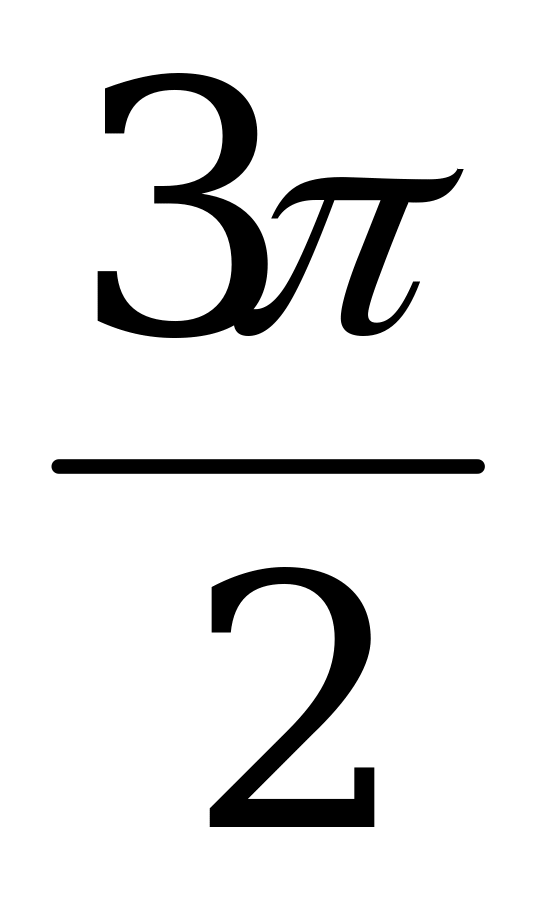
-1

-2


§ 3. Обратные тригонометрические функции.
Арксинус.
Справочный материал.
Арксинусом числа α называется такое число из отрезка 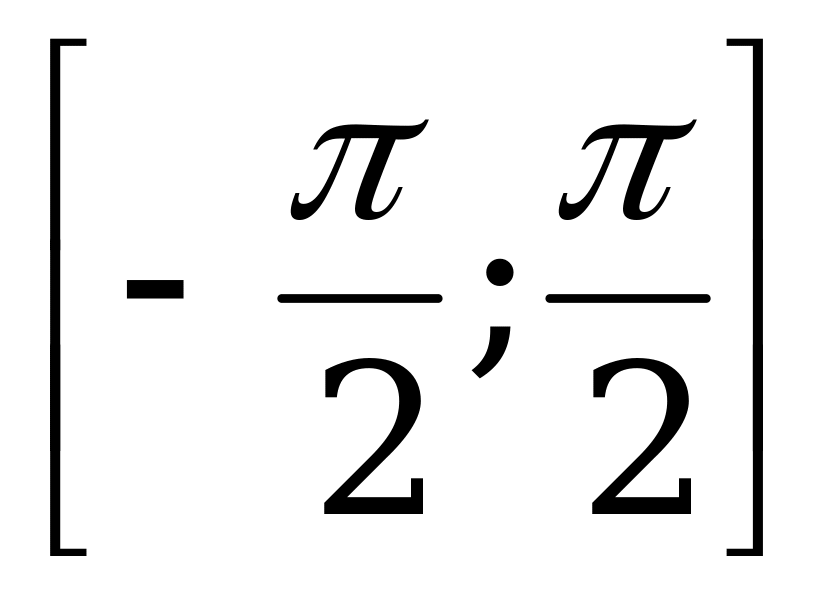 , синус которого равен α.
, синус которого равен α.
Упражнения с решениями.
Пример 1. Вычислите: а) 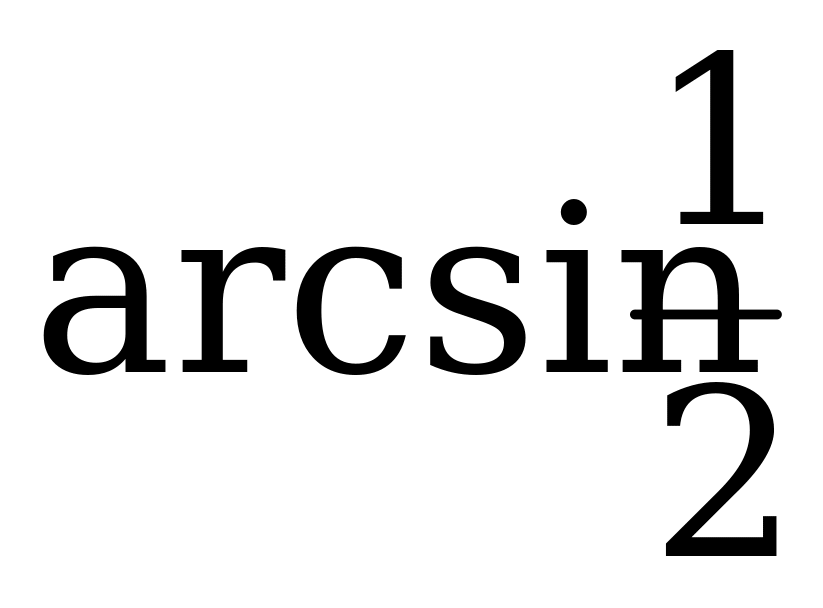 ; б)
; б) 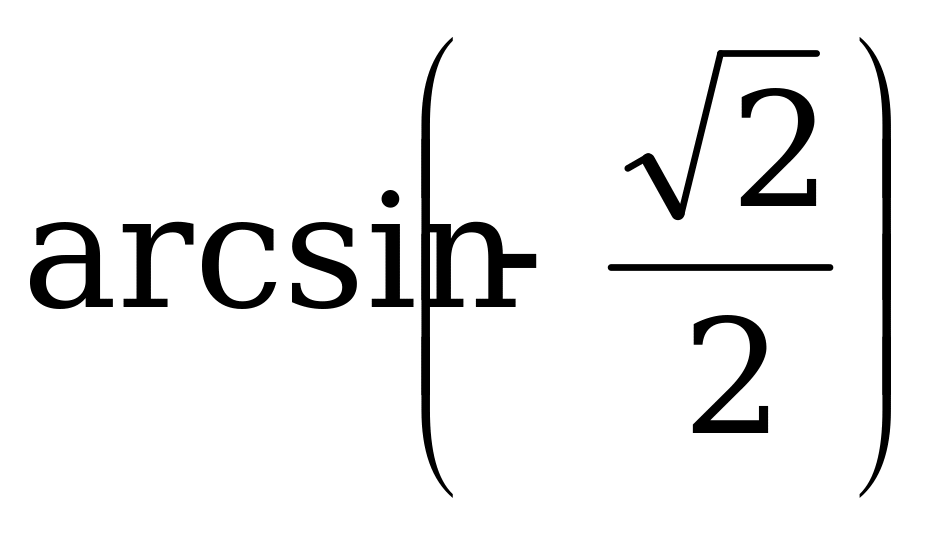 .
.
Решение. а) Так как 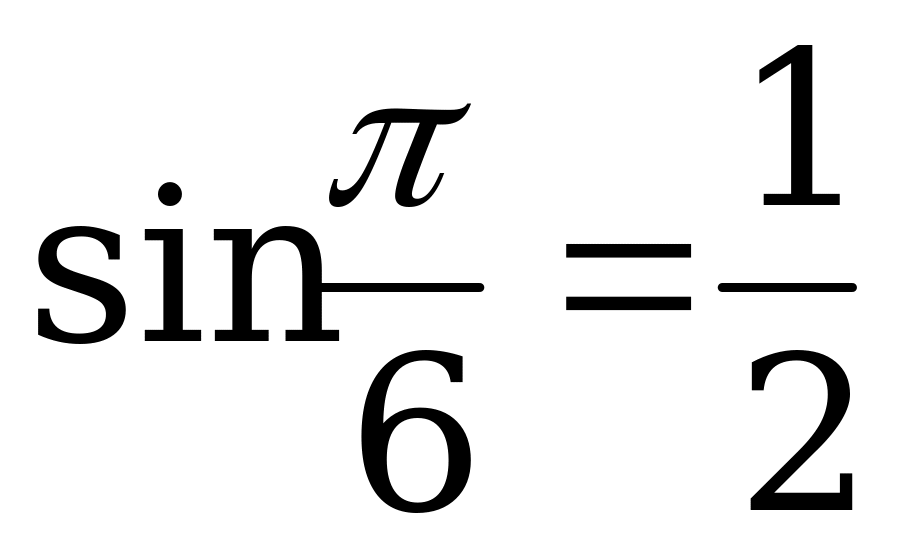 и
и 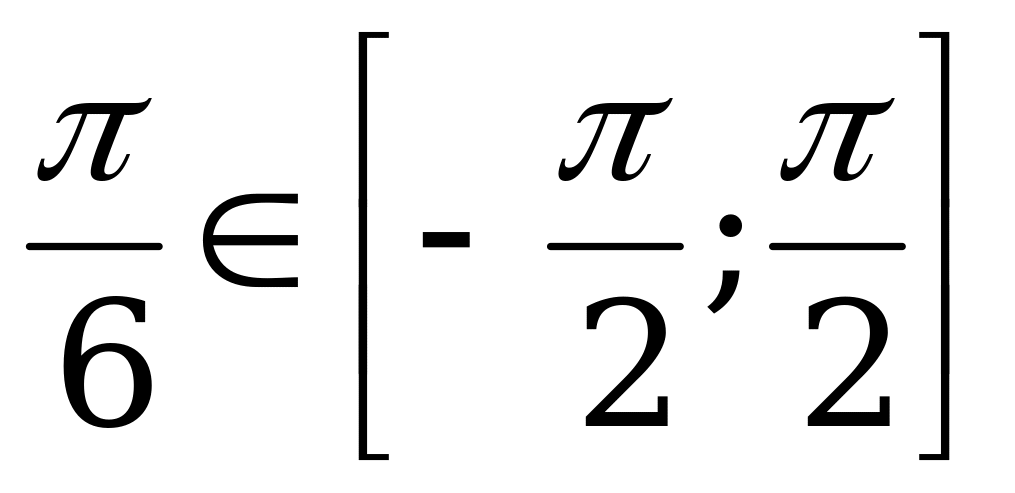 , то
, то 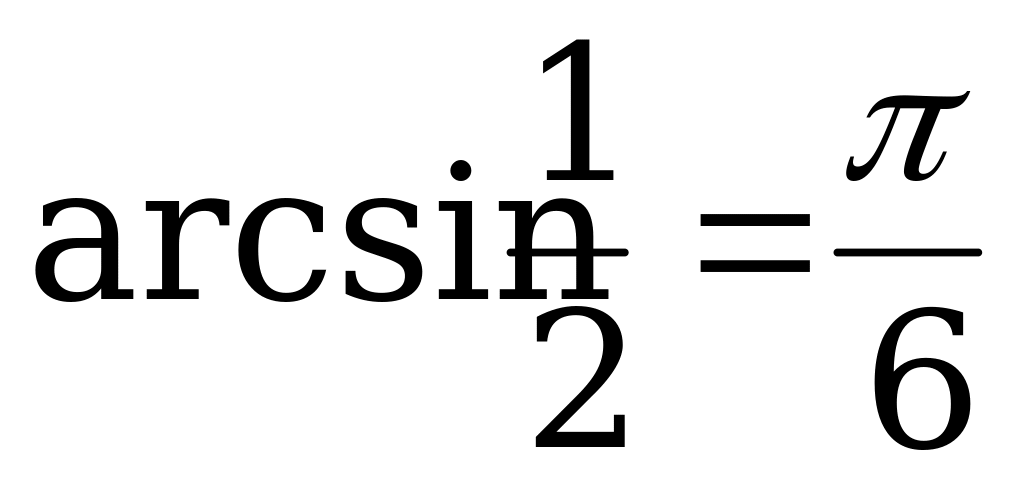 .
.
б) Так как 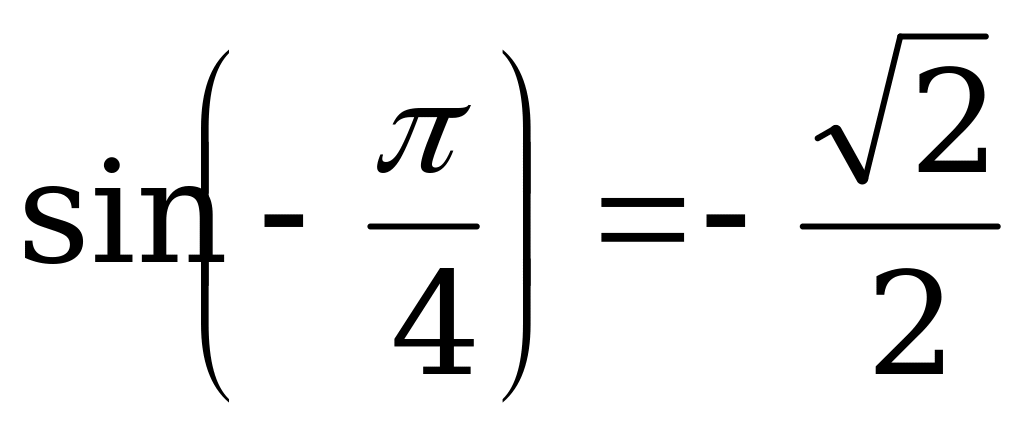 и
и 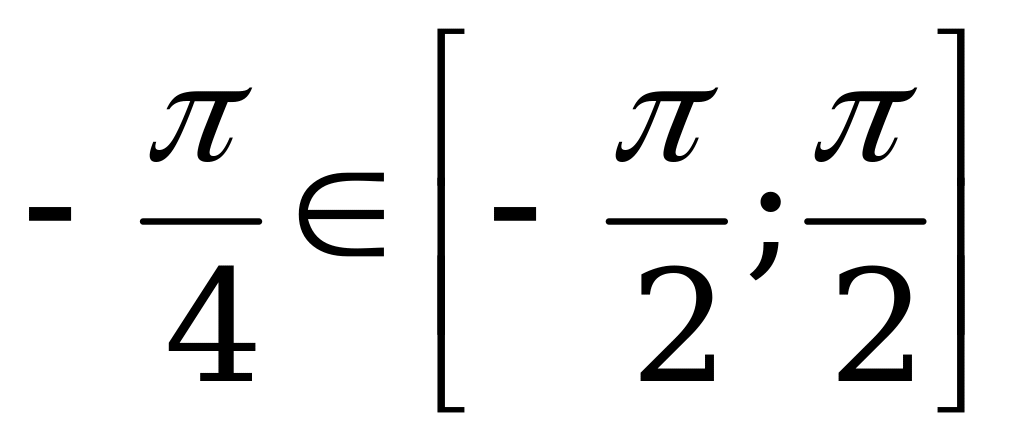 , то
, то 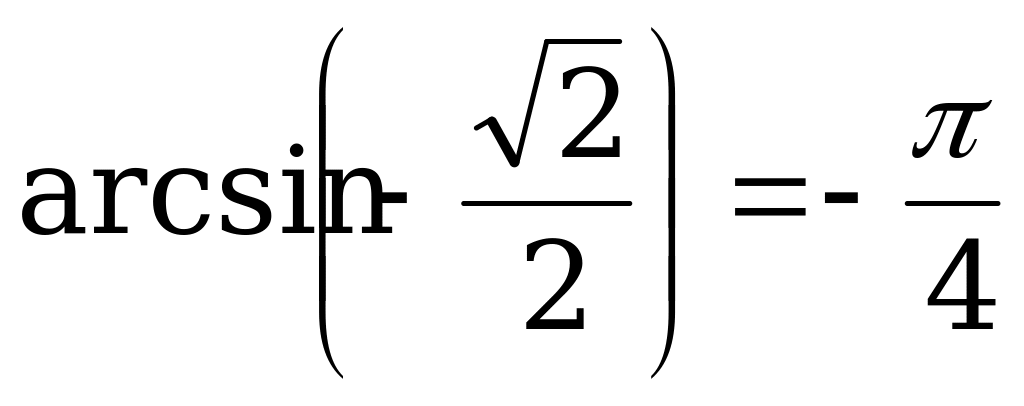 .
.
3.2. Арккосинус.
Справочный материал.
Арккосинусом числа α называется такое число из отрезка 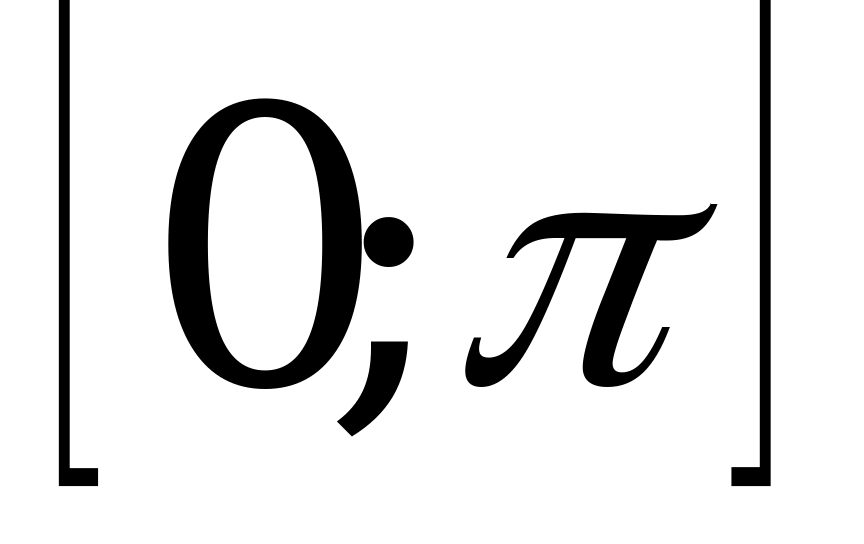 , косинус которого равен α.
, косинус которого равен α.
Упражнения с решениями.
Пример 2. Вычислите: а) 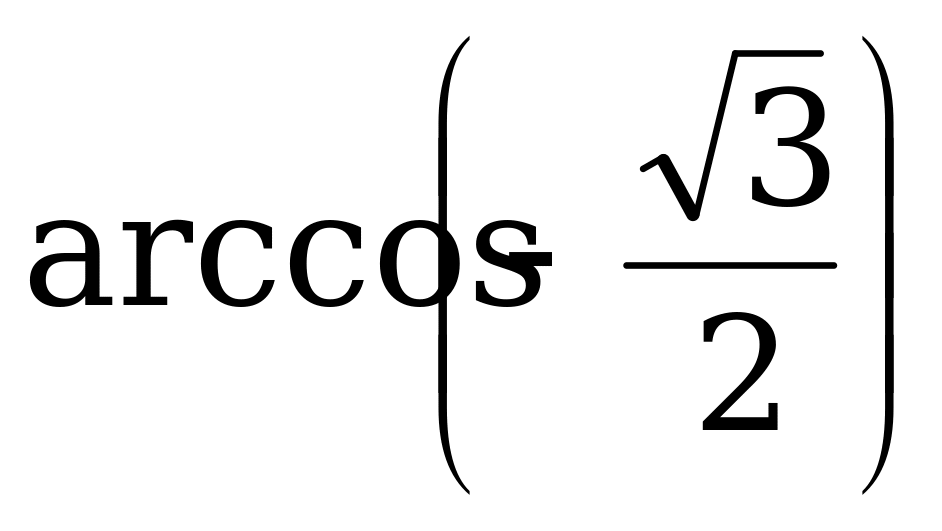 ; б)
; б) 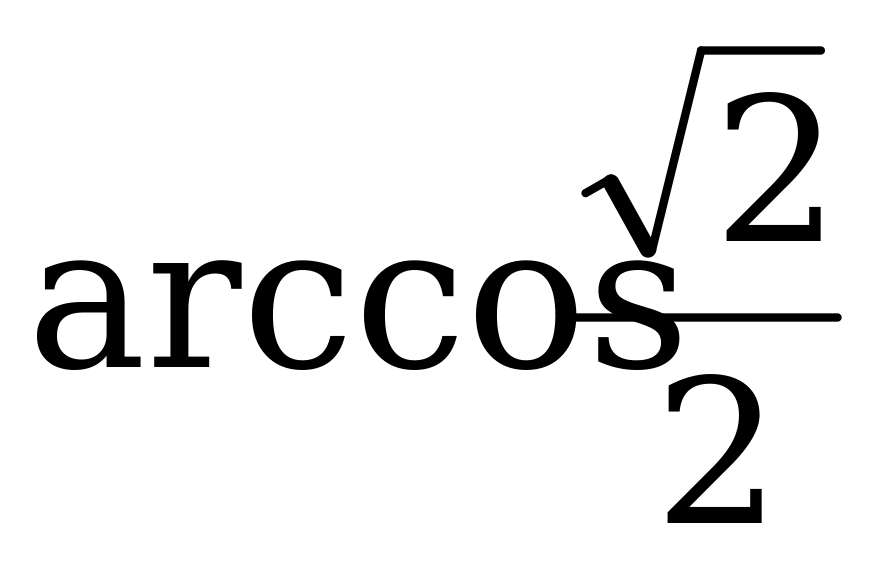 .
.
Решение. а) Так как 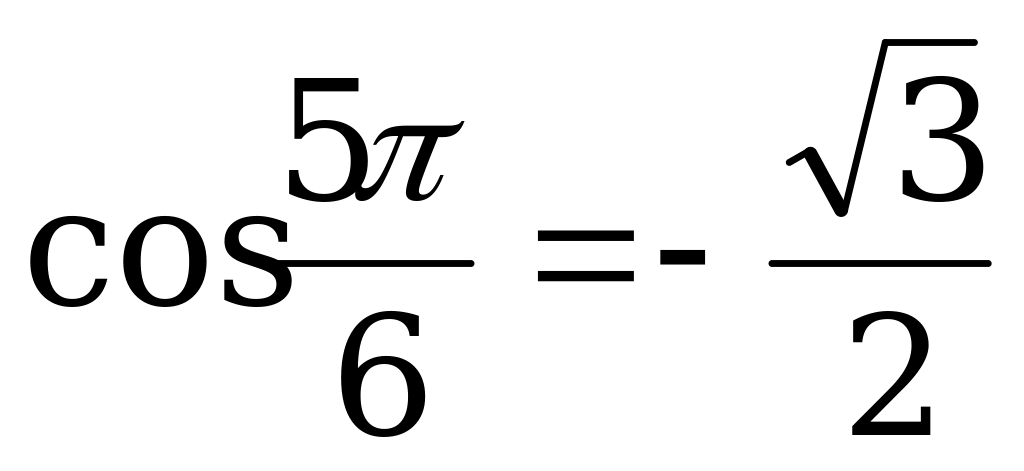 и
и 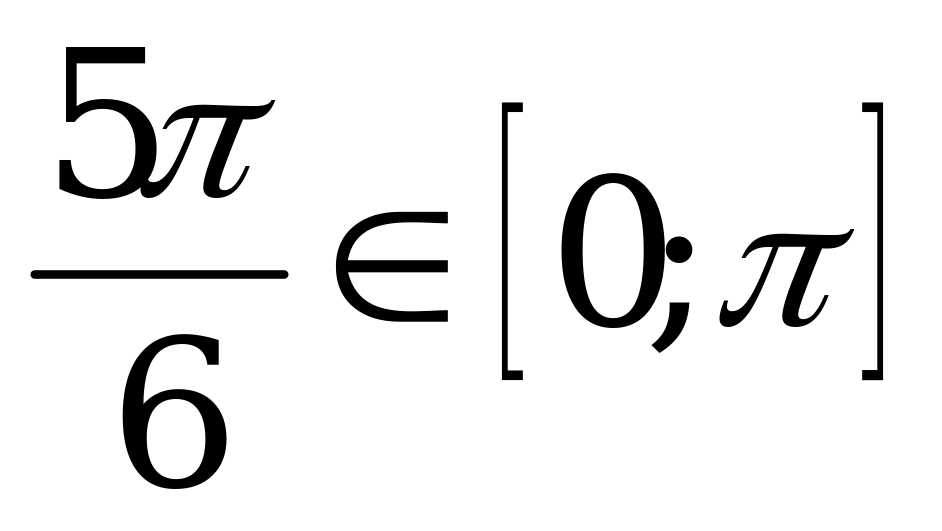 , то
, то 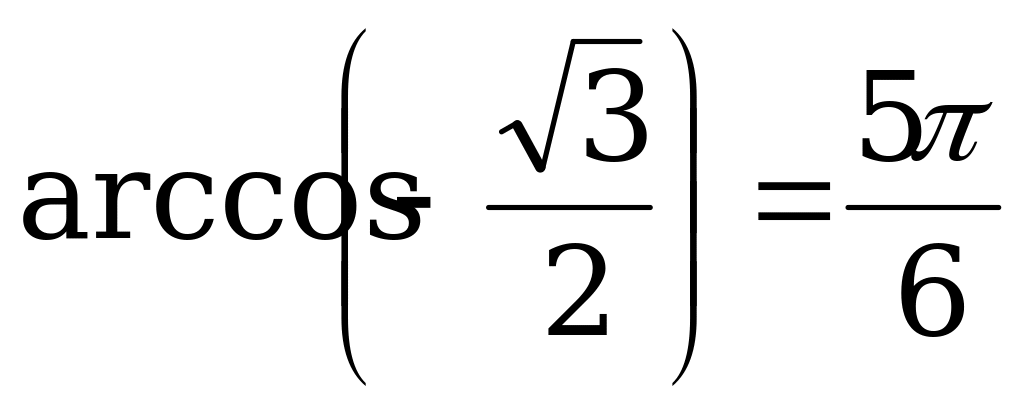 .
.
б) Так как 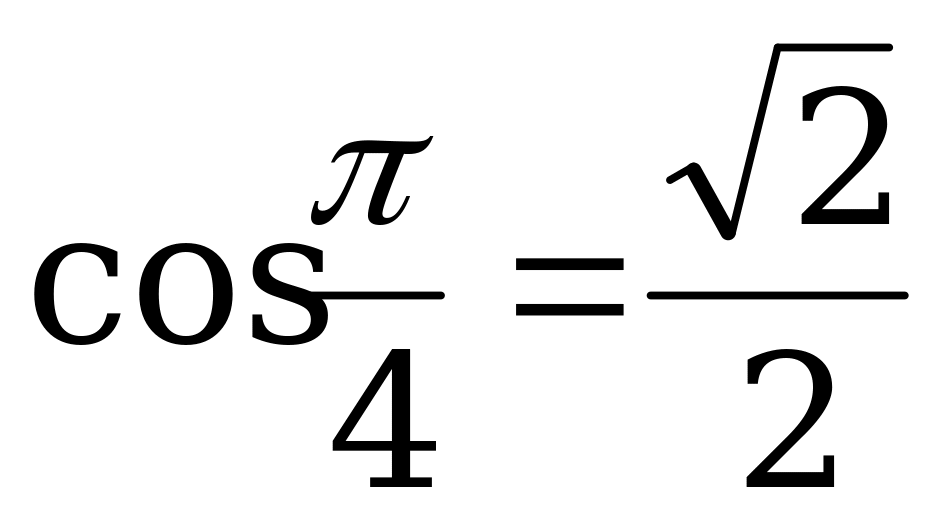 и
и 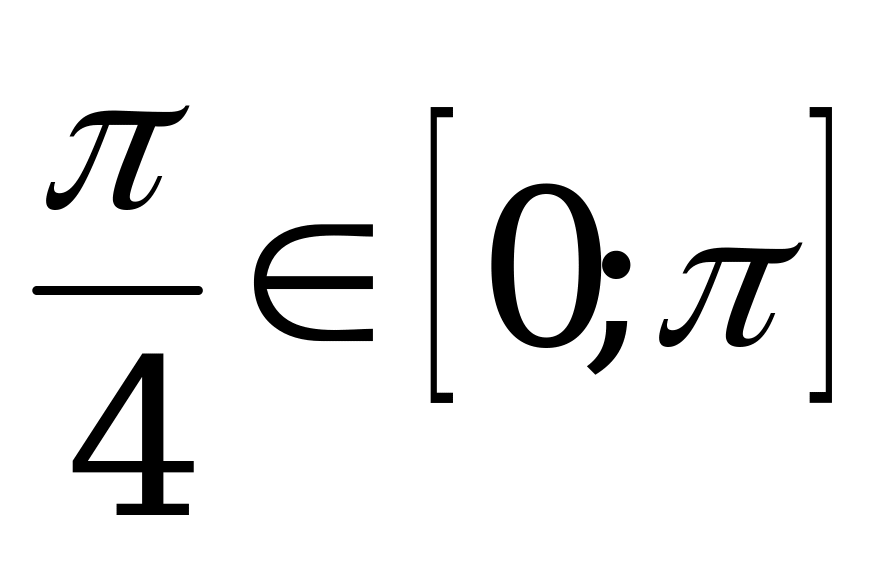 , то
, то 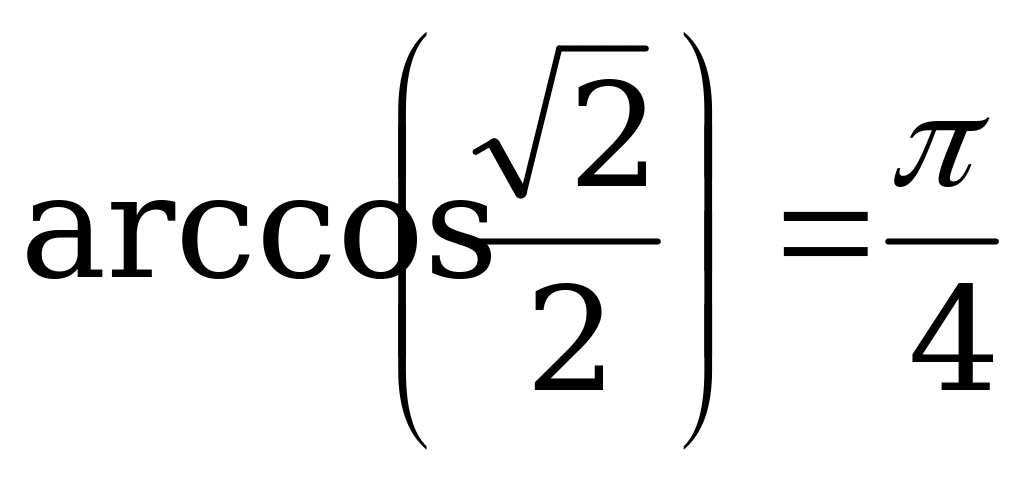 .
.
3.3. Арктангенс.
Справочный материал.
Арктангенсом числа α называется такое число из интервала 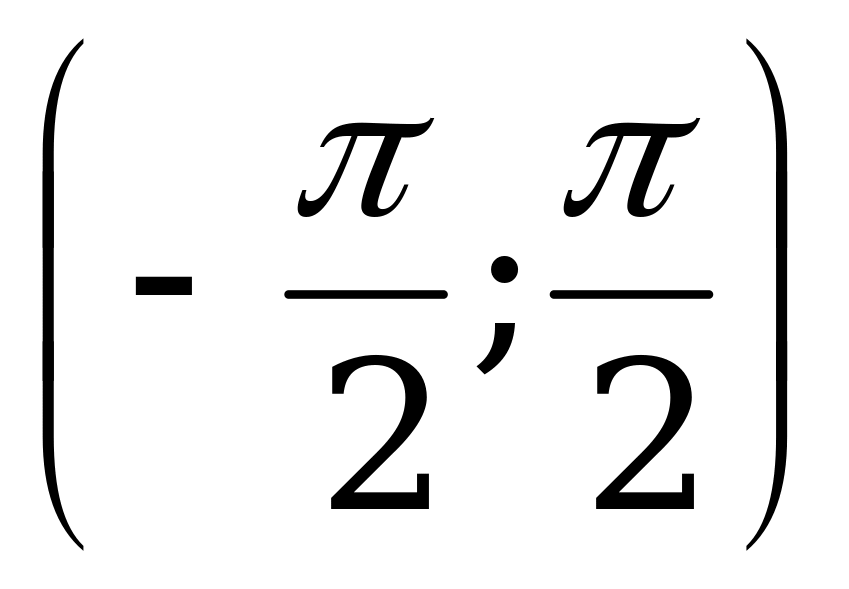 , тангенс которого равен α.
, тангенс которого равен α.
Упражнения с решениями.
Пример 3. Вычислите: а) 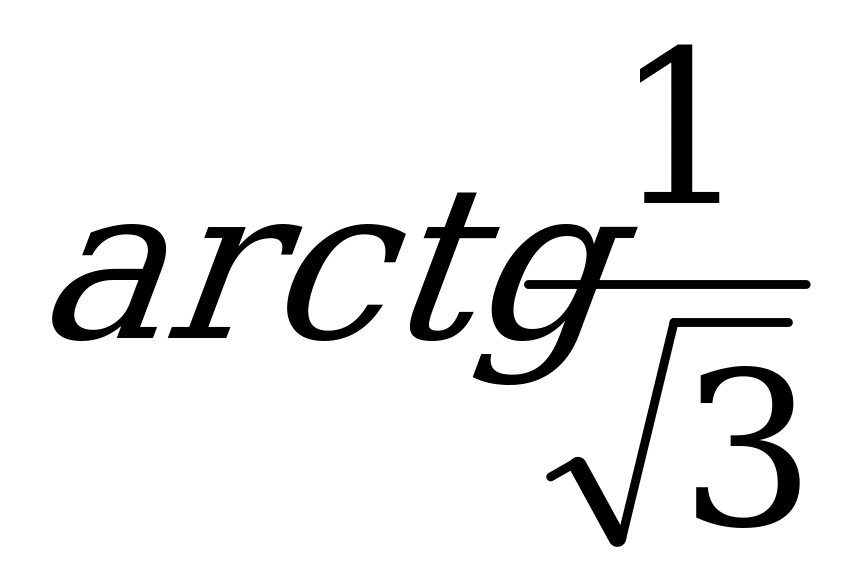 ; б)
; б) 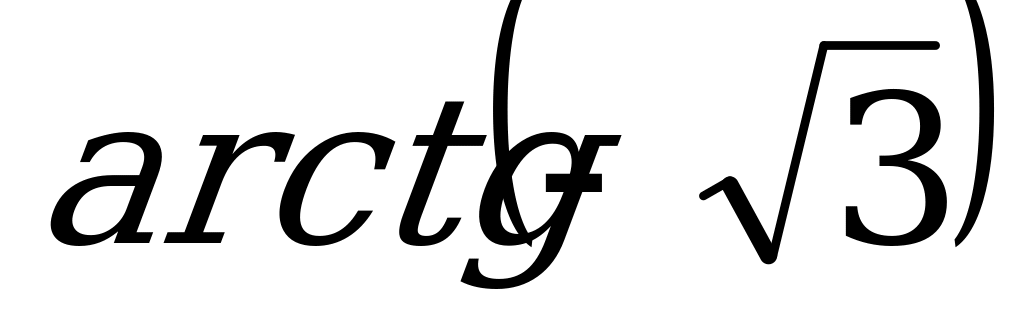 .
.
Решение. а) Так как 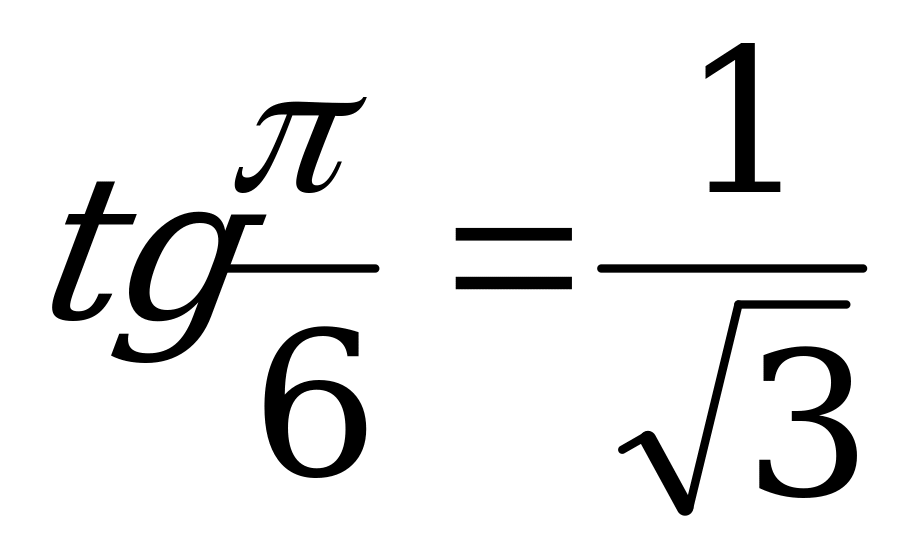 и
и 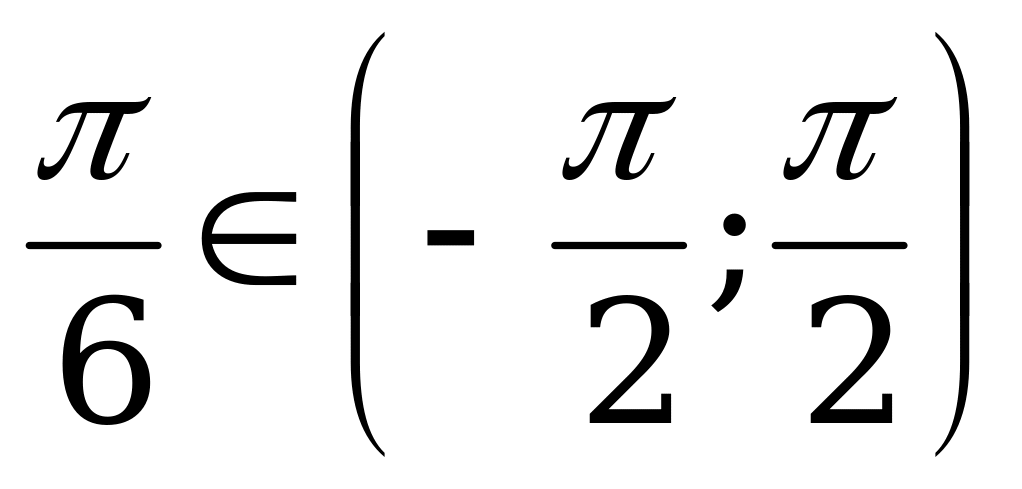 , то
, то 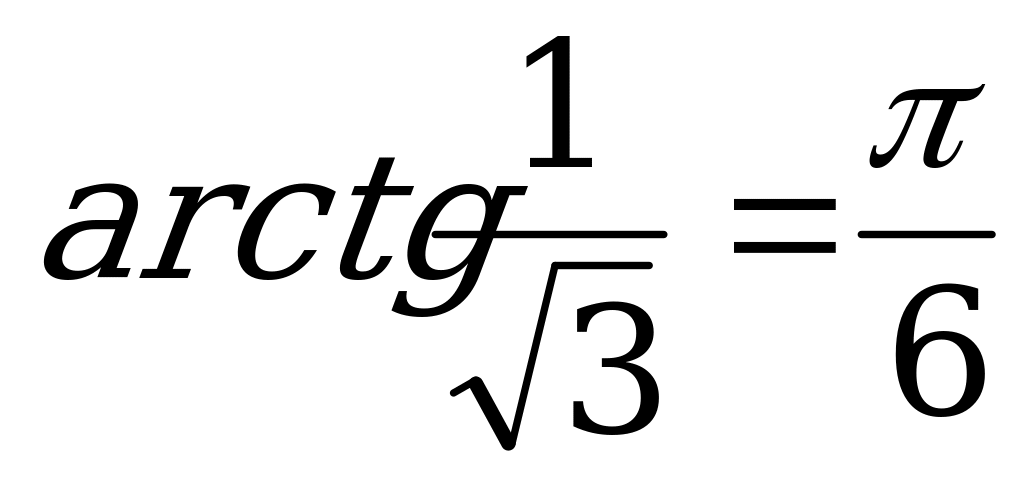 .
.
б) Так как 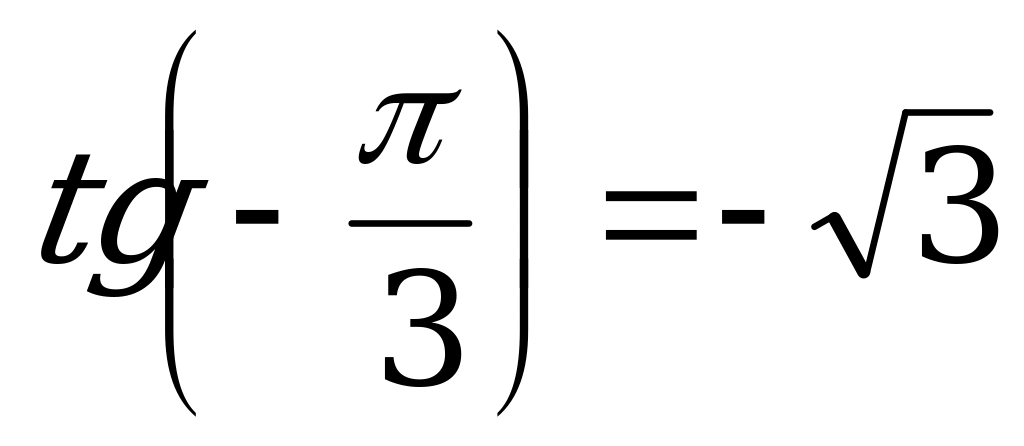 и
и 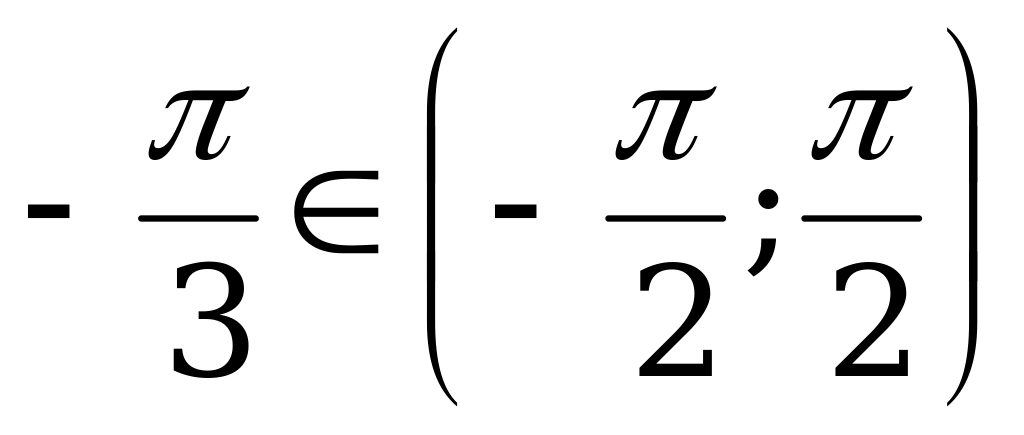 , то
, то 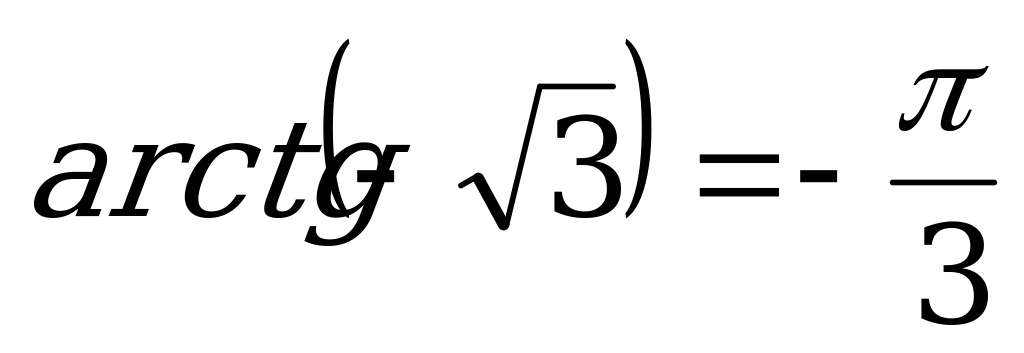 .
.
3.4. Арккотангенс.
Справочный материал.
Арккотангенсом числа α называется такое число из интервала 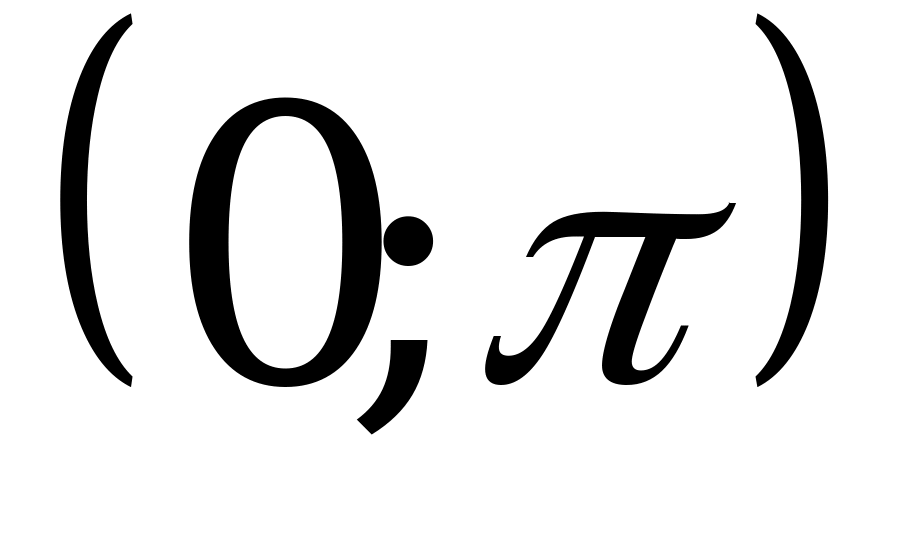 , котангенс которого равен α.
, котангенс которого равен α.
Упражнения с решениями.
Пример 4. Вычислите: а) 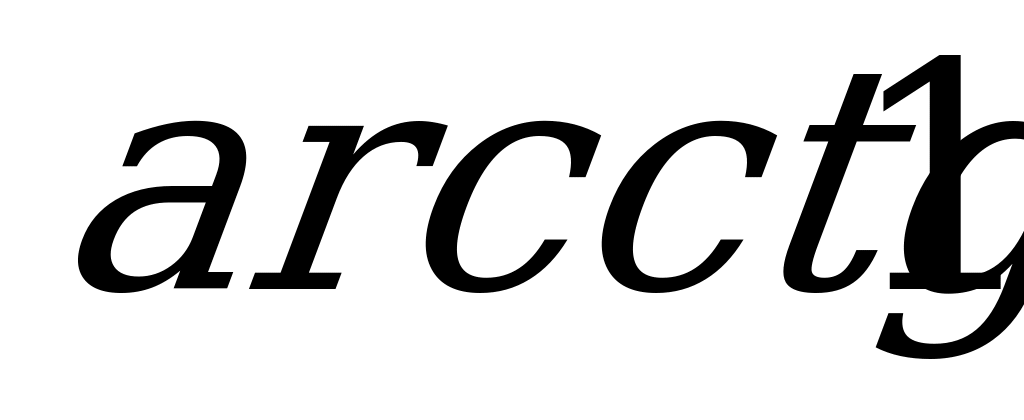 ; б)
; б) 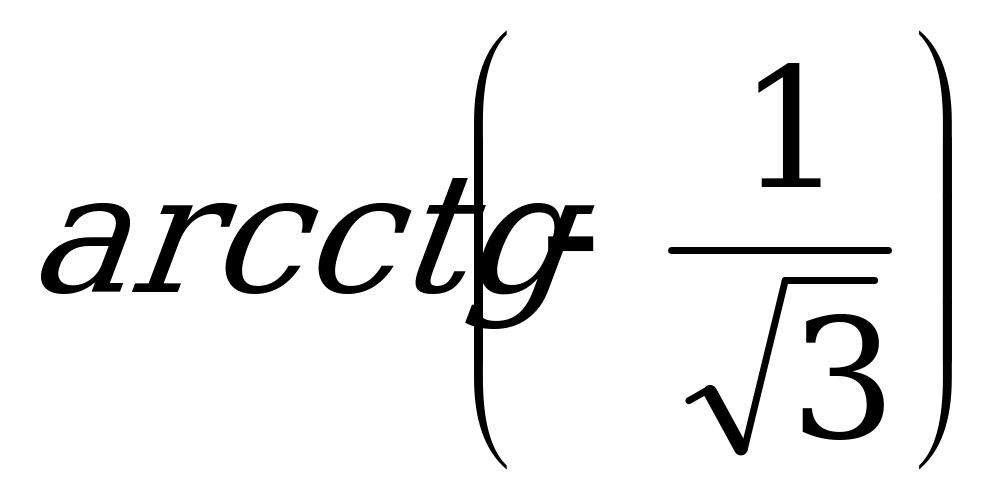 .
.
Решение. а) Так как 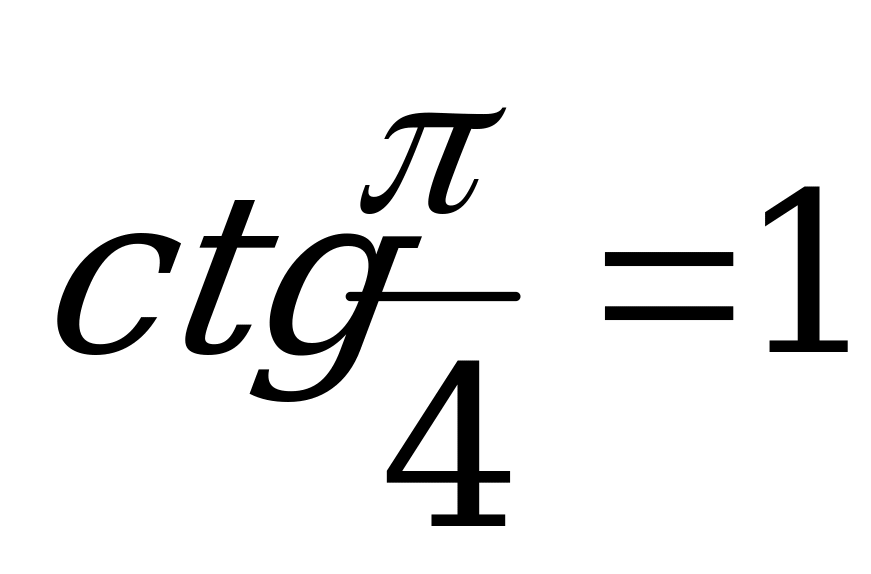 и
и 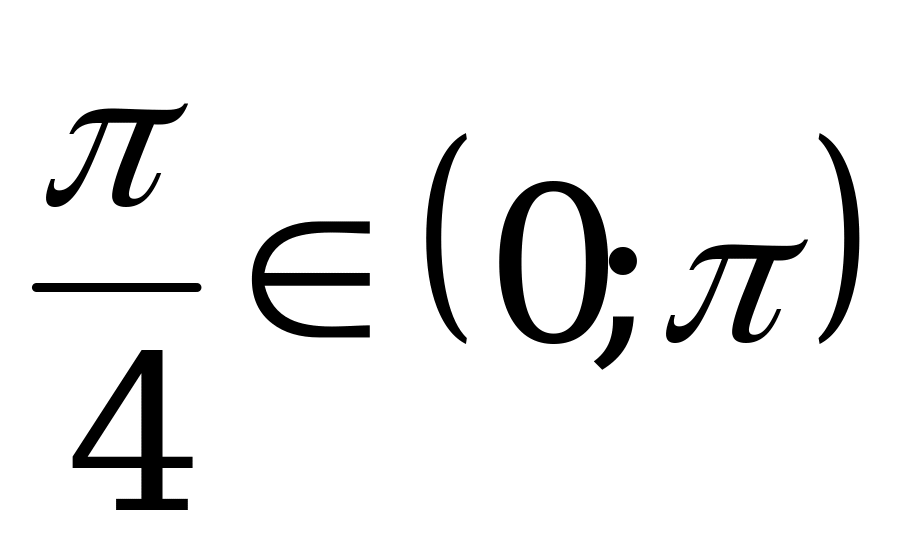 , то
, то 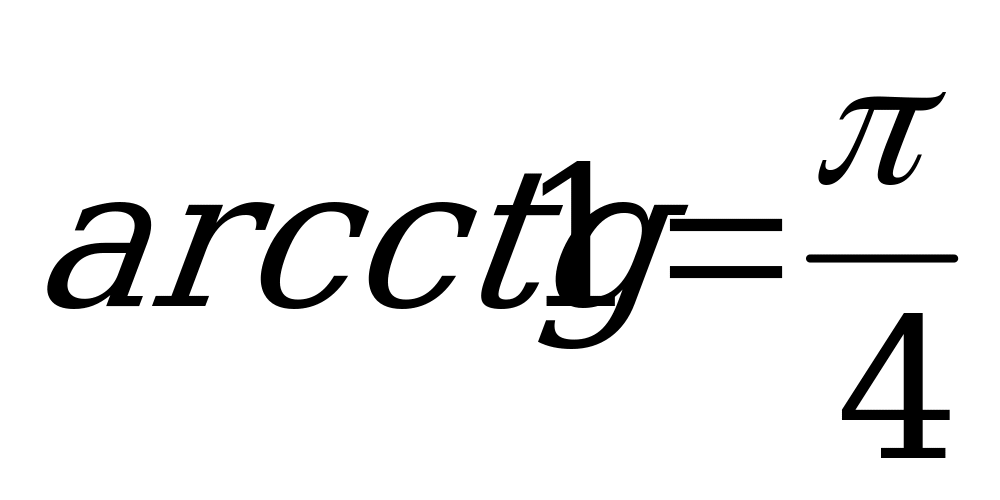 .
.
б) Так как 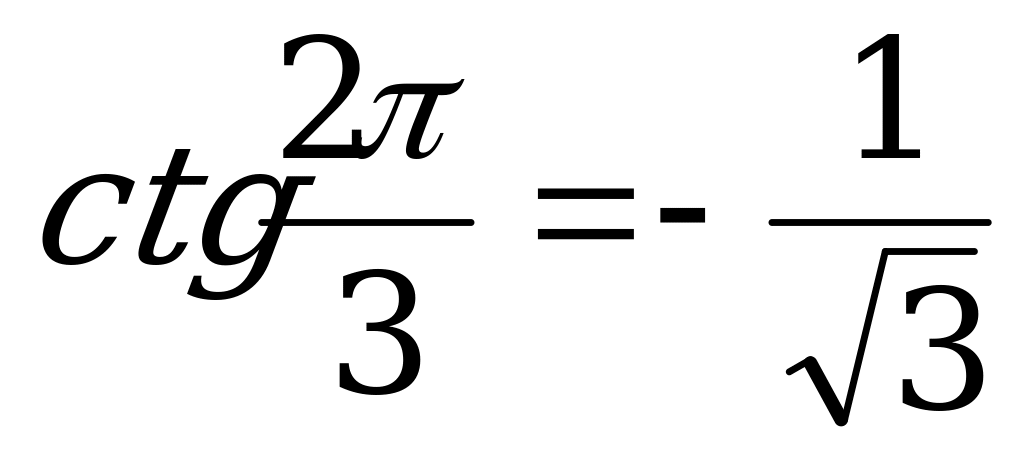 и
и 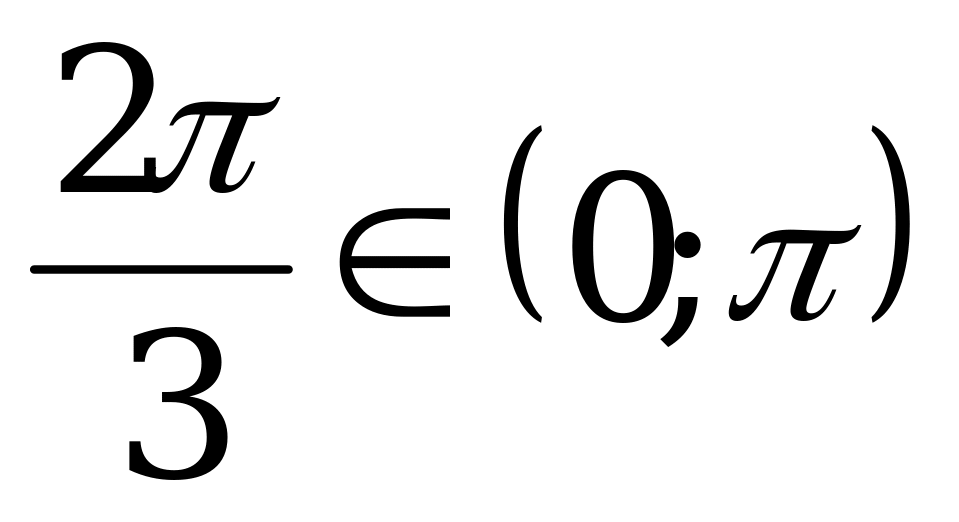 , то
, то 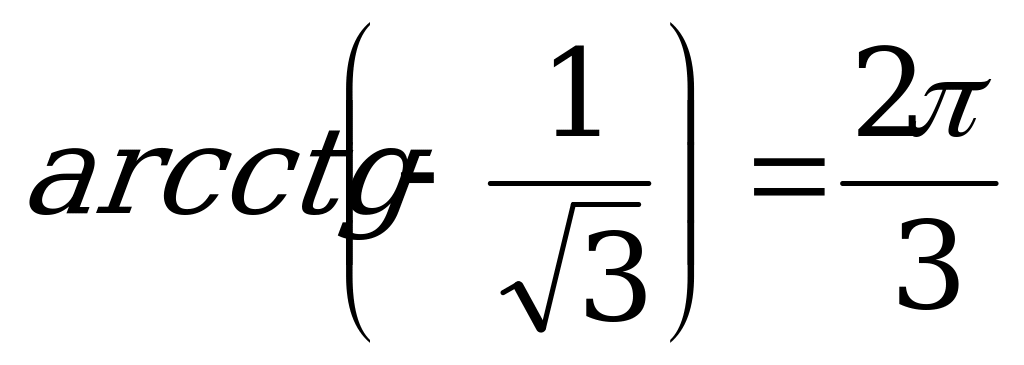 .
.
3.5. Свойства обратных тригонометрических функций.
Справочный материал.
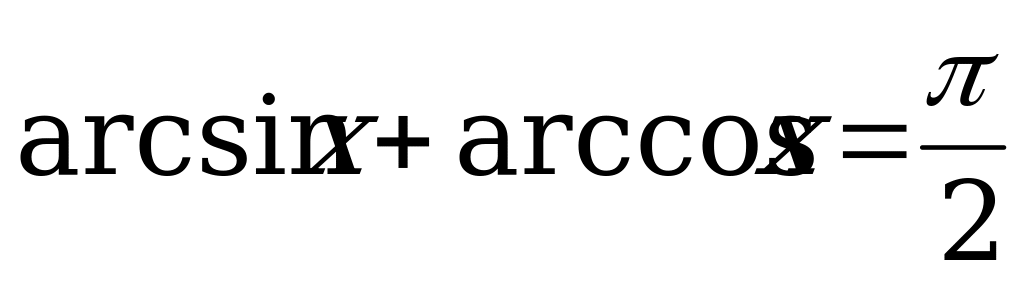 , если
, если 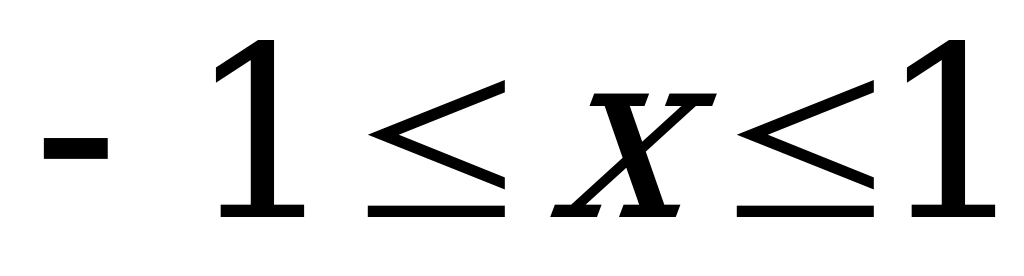 ; (1)
; (1)
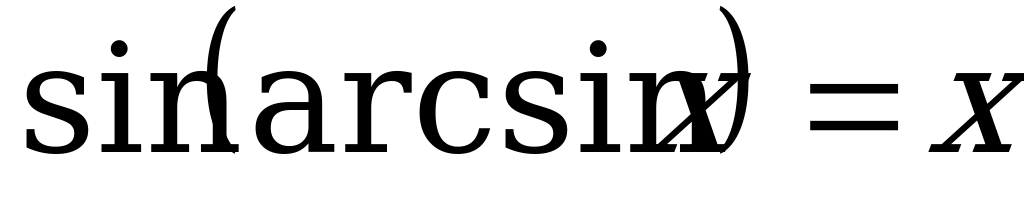 , если
, если 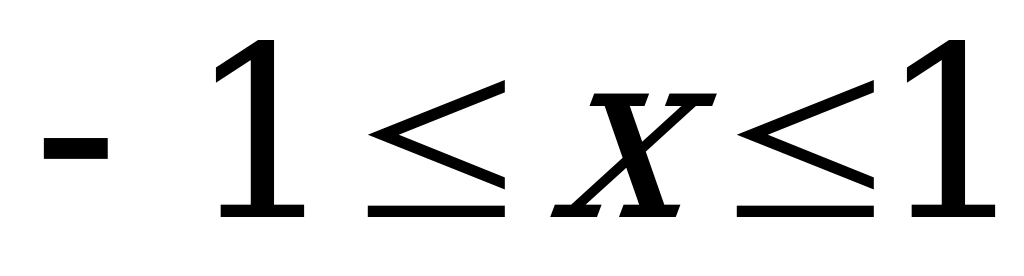 ; (2)
; (2)
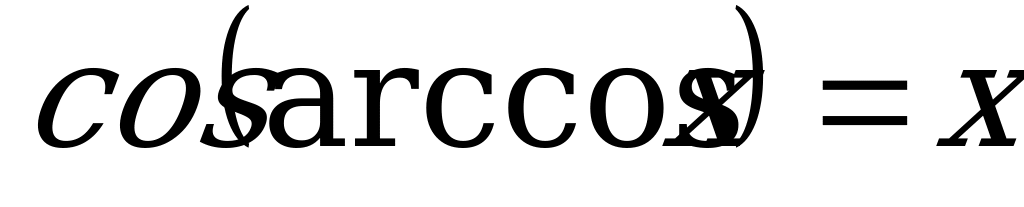 , если
, если 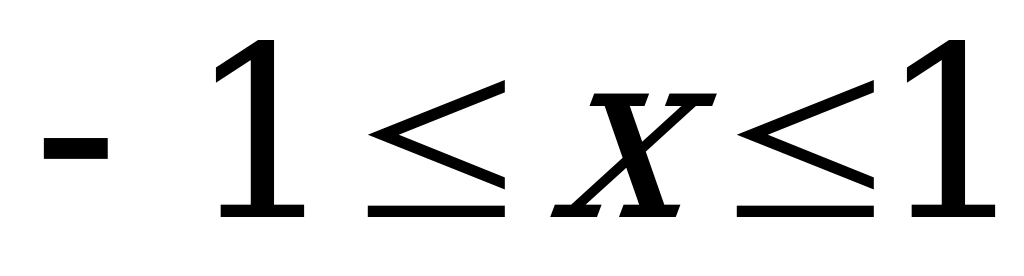 ; (3)
; (3)
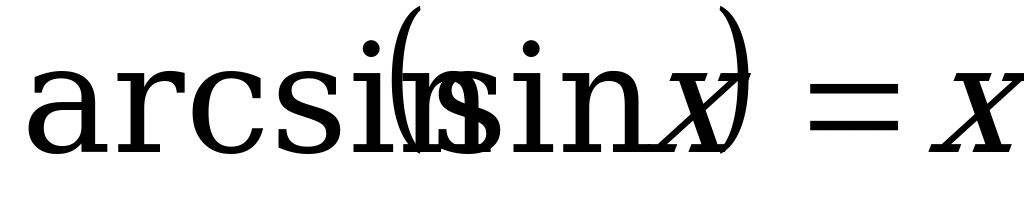 , если
, если 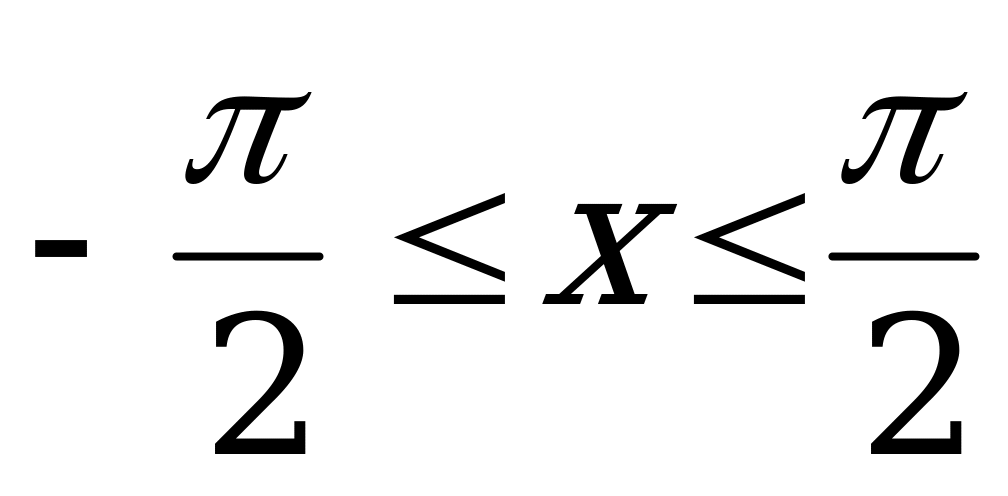 ; (4)
; (4)
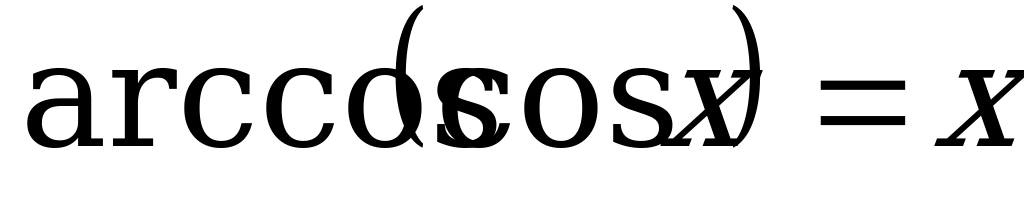 , если
, если 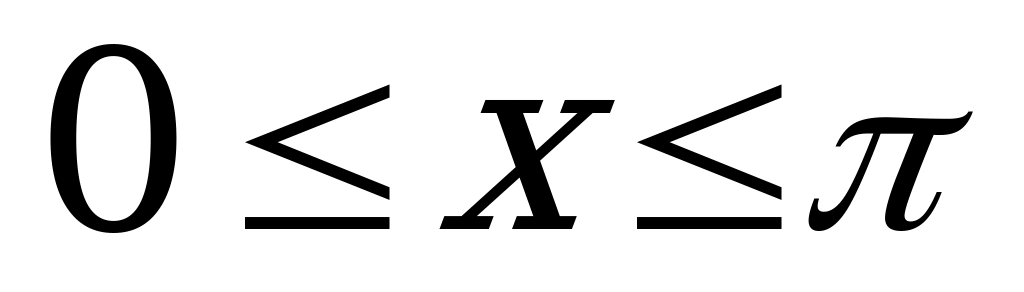 ; (5)
; (5)
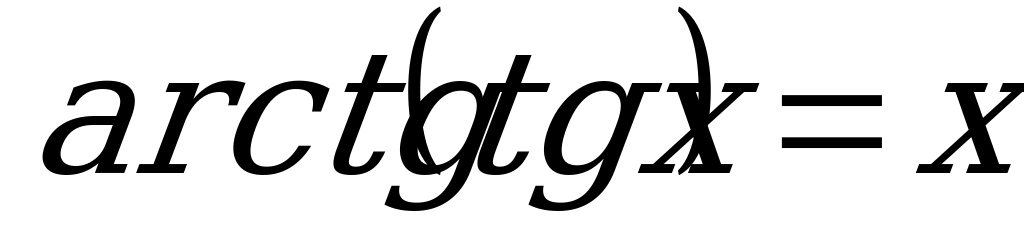 , если
, если 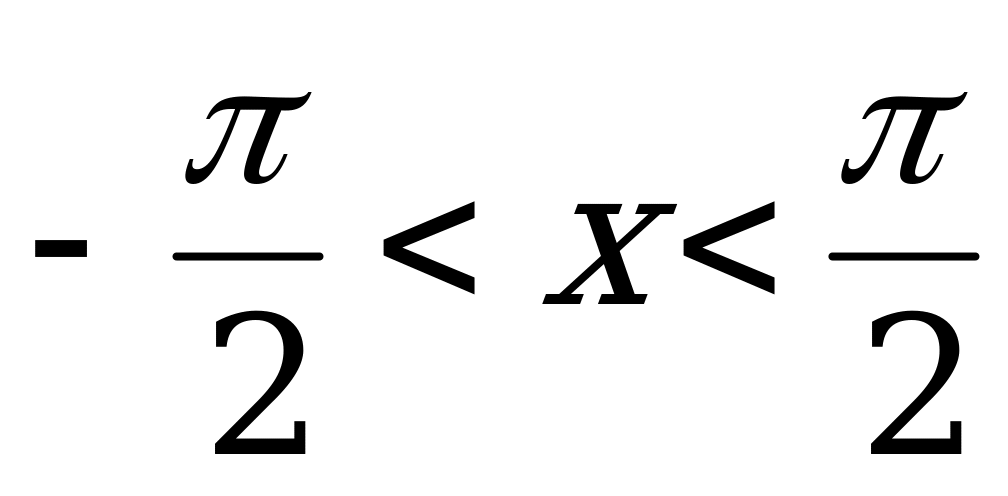 ; (6)
; (6)
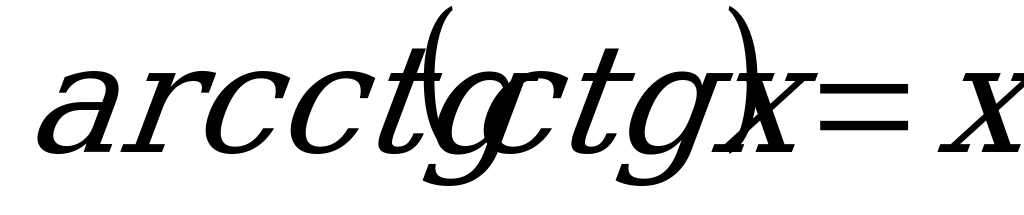 , если
, если 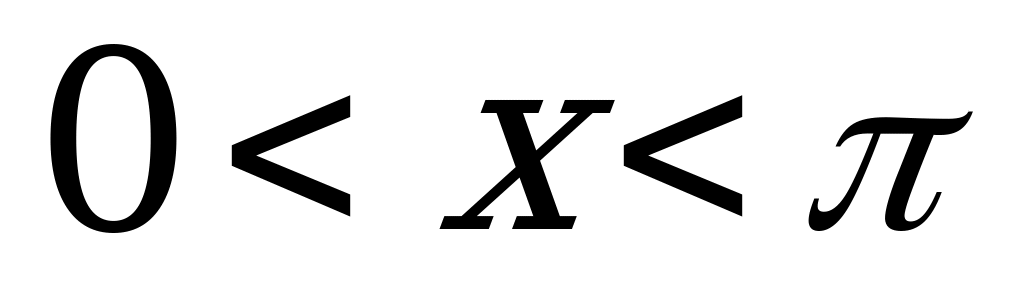 ; (7)
; (7)
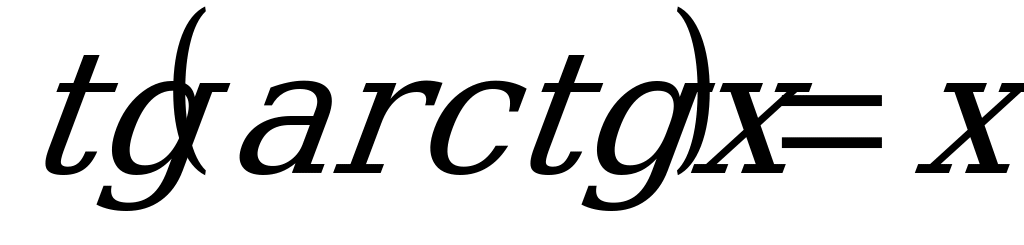 , где
, где 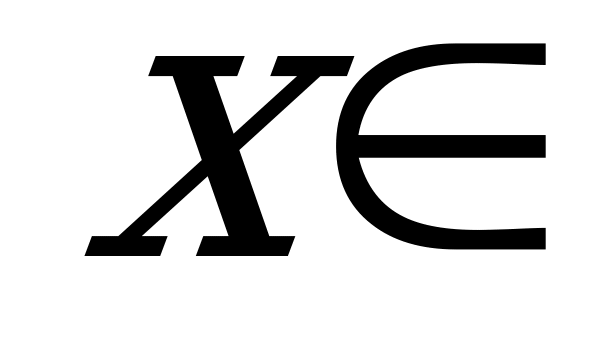 R. (8)
R. (8)
 , где
, где 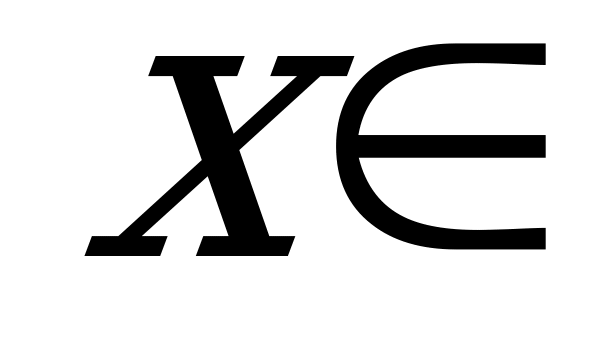 R. (9)
R. (9)
 ,где
,где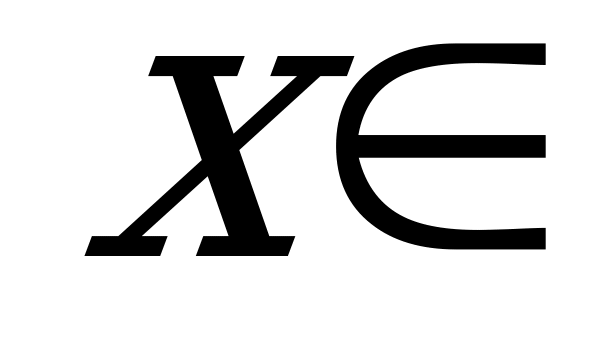 R. (10)
R. (10)
Упражнения с решениями.
Пример 5. Вычислите:
а) 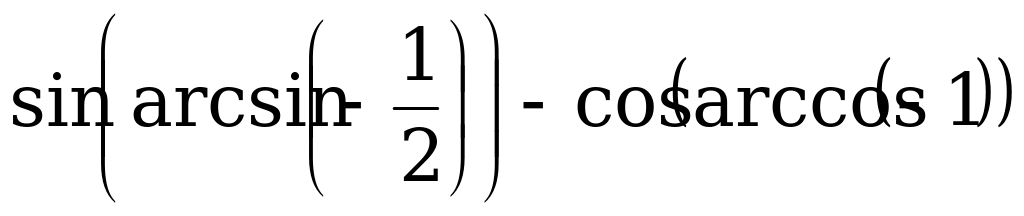 ;
;
б) 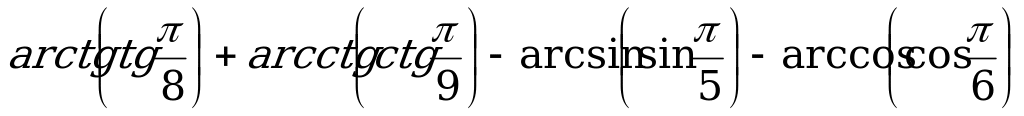 ;
;
в) 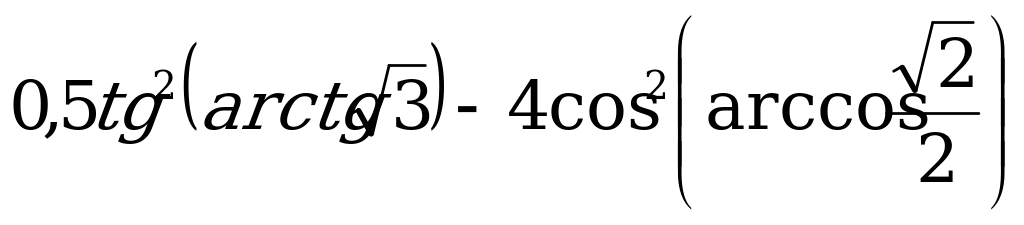 ;
;
г) 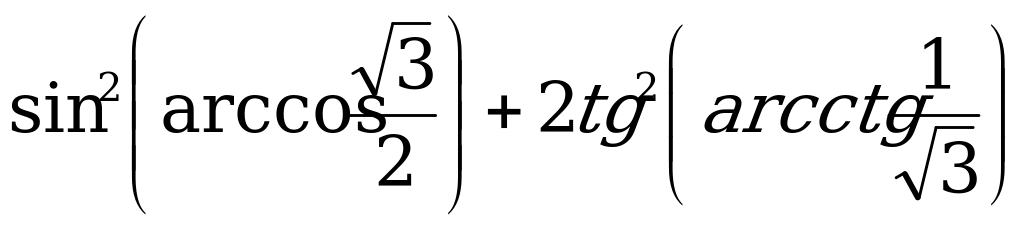 .
.
Решение а) Согласно тождествам (2) и (3) имеем:
 .
.
б) Согласно тождествам (4), (5), (6) и (7) имеем:
 .
.
в) Согласно формулам (3) и (8) имеем:
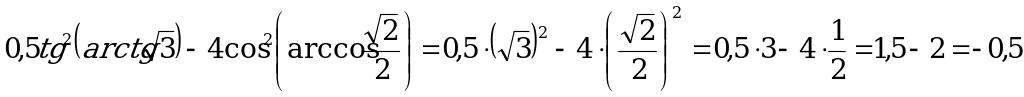 .
.
г) Так как 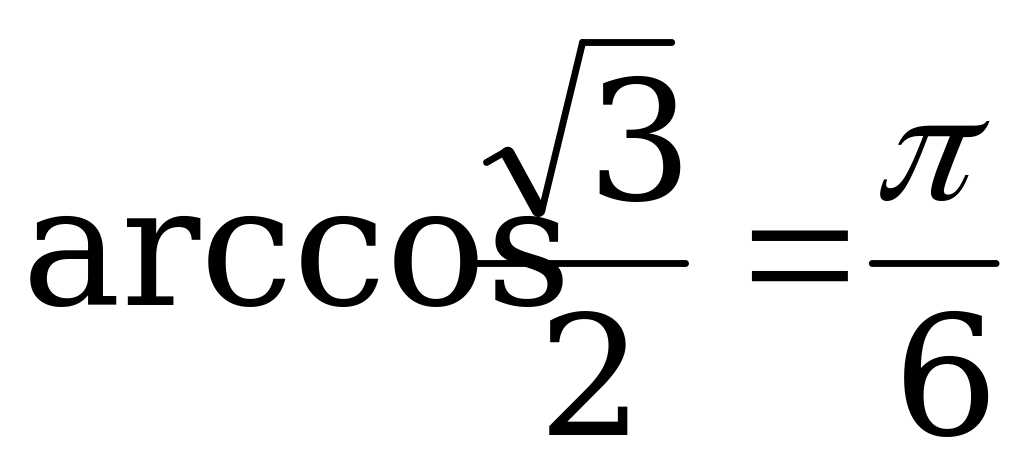 и
и 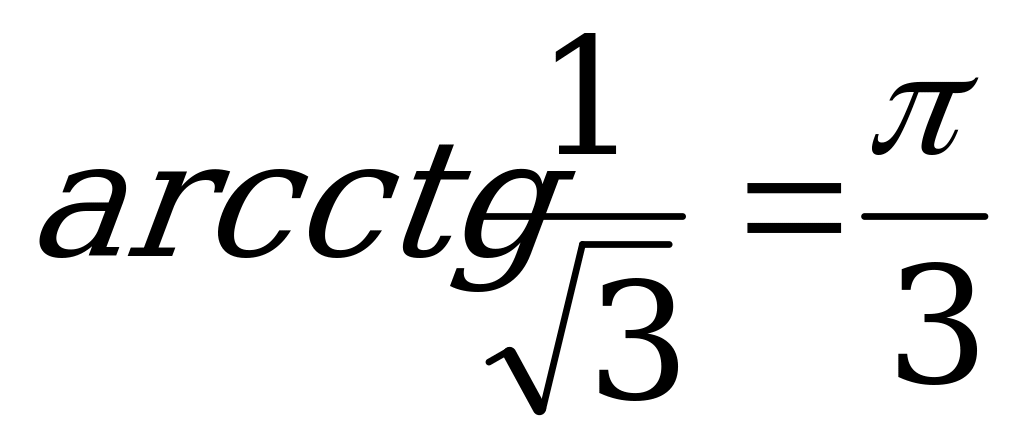 , то
, то
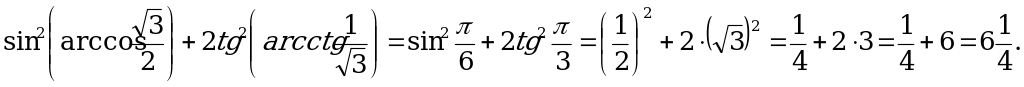
Самостоятельная работа №6.
Вариант №1.
Вычислите:
а) 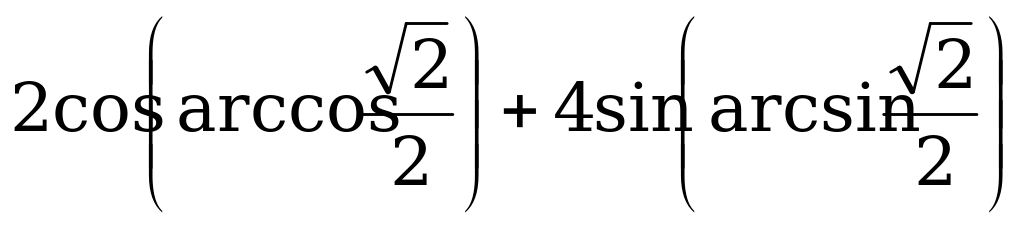 ;
;
б) 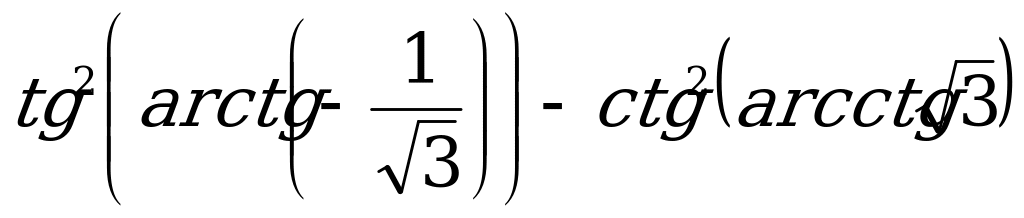 ;
;
в) 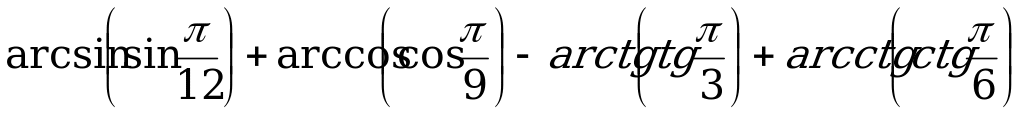 ;
;
г) 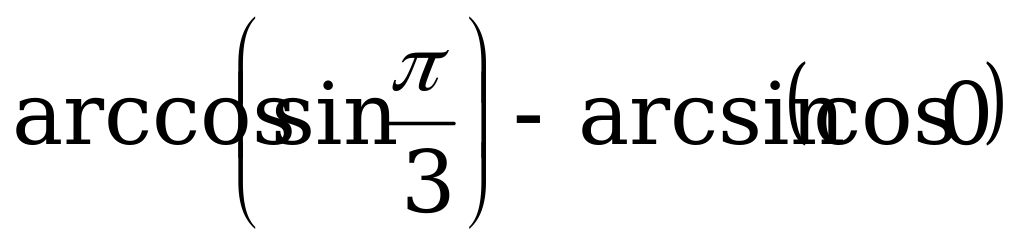 .
.
Вариант №2.
Вычислите:
а) 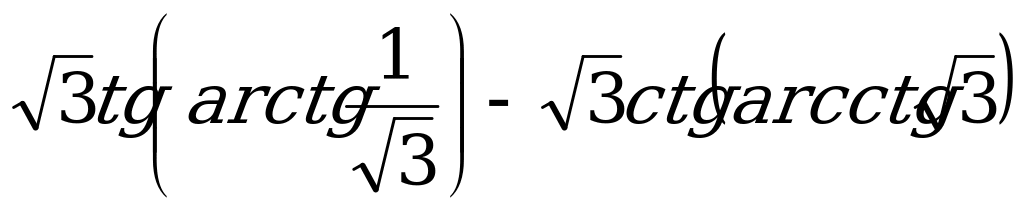 ;
;
б) 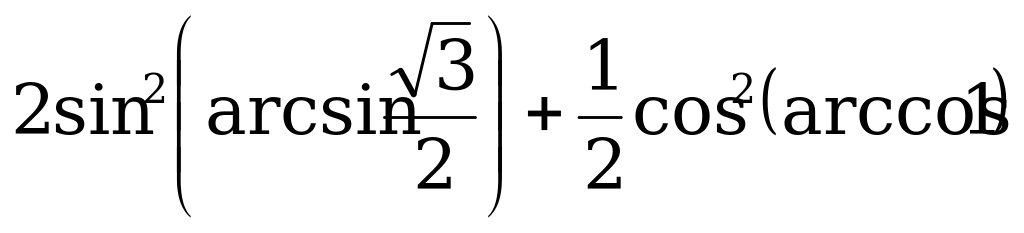 ;
;
в) 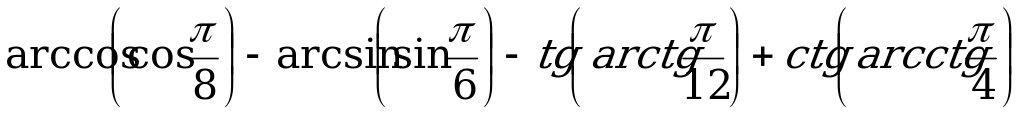 ;
;
г) 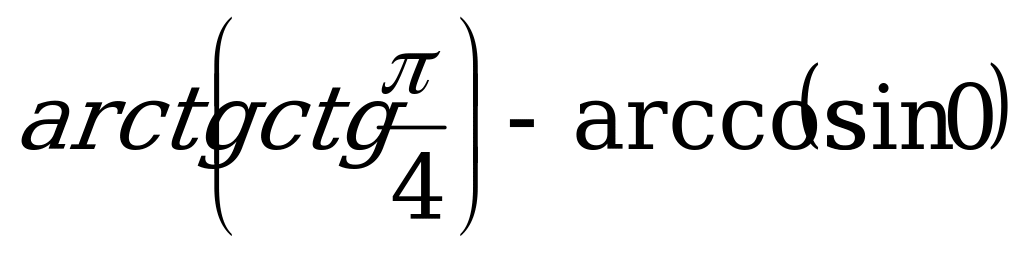 .
.
§4. Тригонометрические уравнения.
Простейшие тригонометрические уравнения.
Справочный материал.
Уравнения 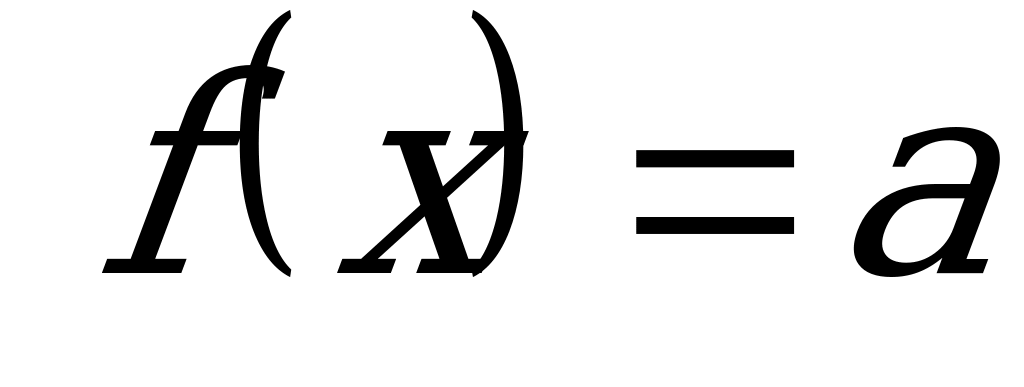 , где
, где 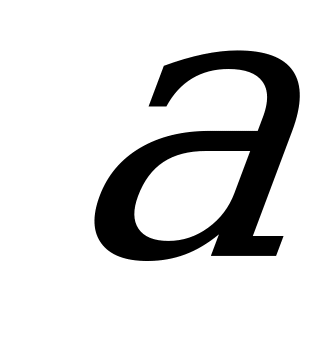 - данное число, а
- данное число, а 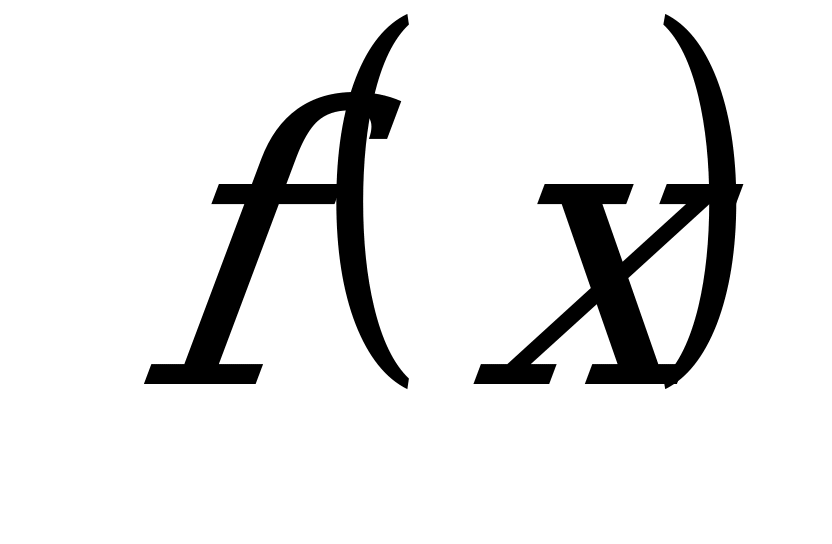 - одна из основных тригонометрических функций, называют простейшим тригонометрическим уравнением.
- одна из основных тригонометрических функций, называют простейшим тригонометрическим уравнением.
Уравнение 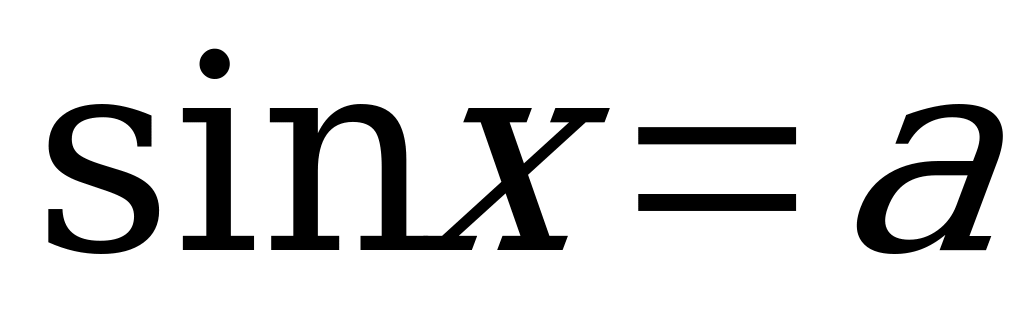 .
.
Данное уравнение имеет решение только при 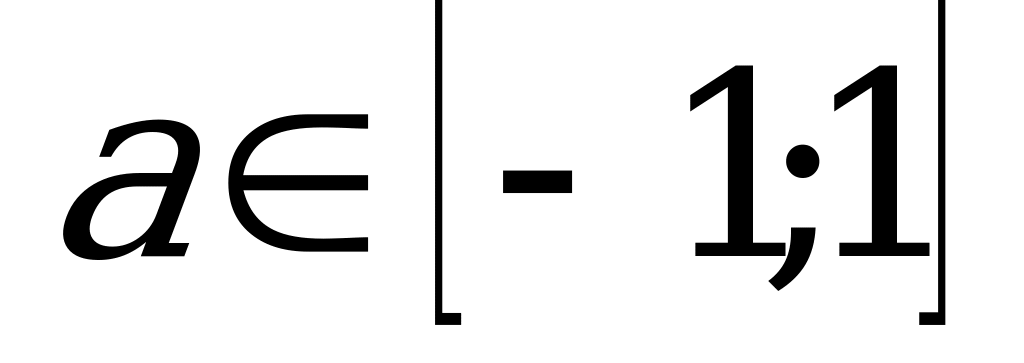 .
.
Формула корней уравнения 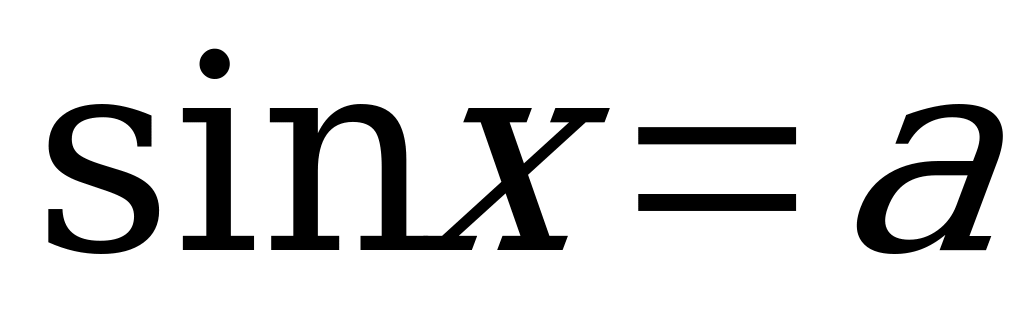 имеет вид:
имеет вид:
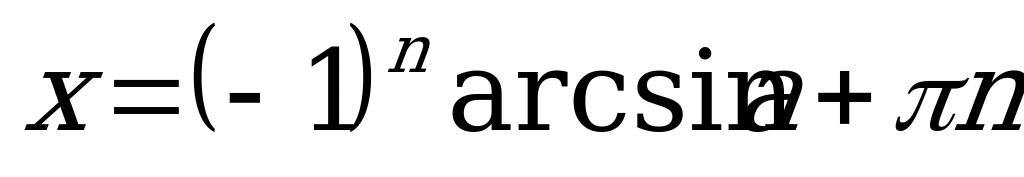 , где
, где  Z. (1)
Z. (1)
Уравнение 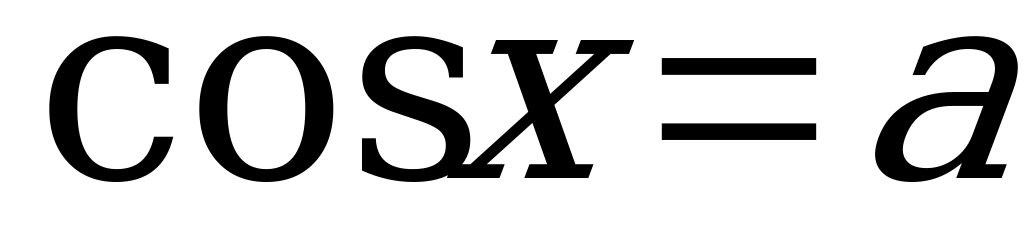 .
.
Данное уравнение имеет решение только при 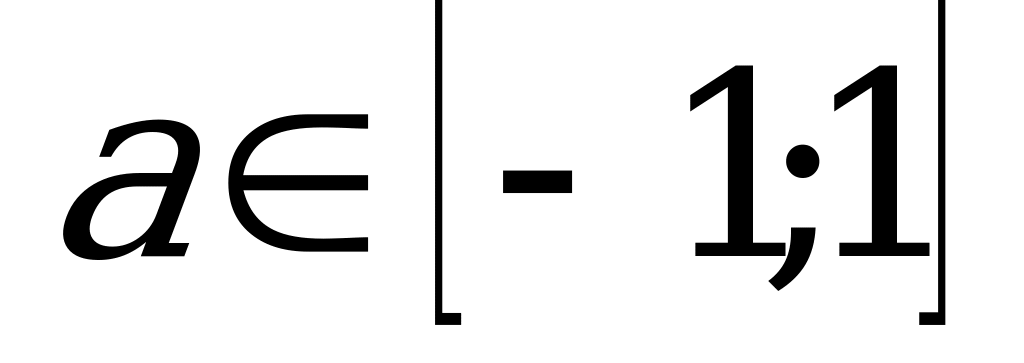 .
.
Формула корней уравнения 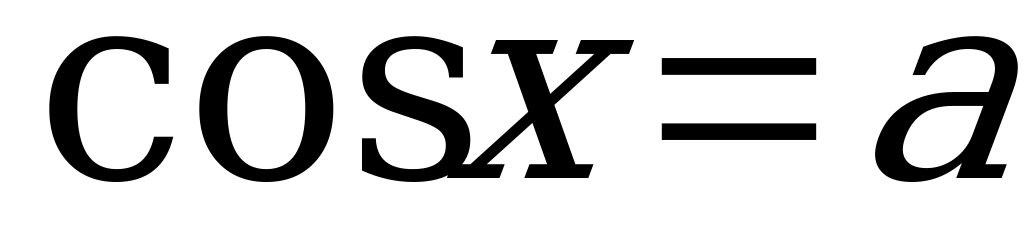 имеет вид:
имеет вид:
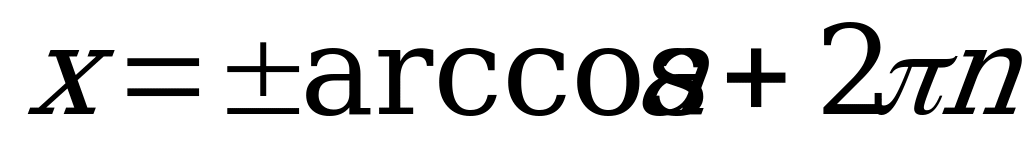 , где
, где  Z. (2)
Z. (2)
Уравнение 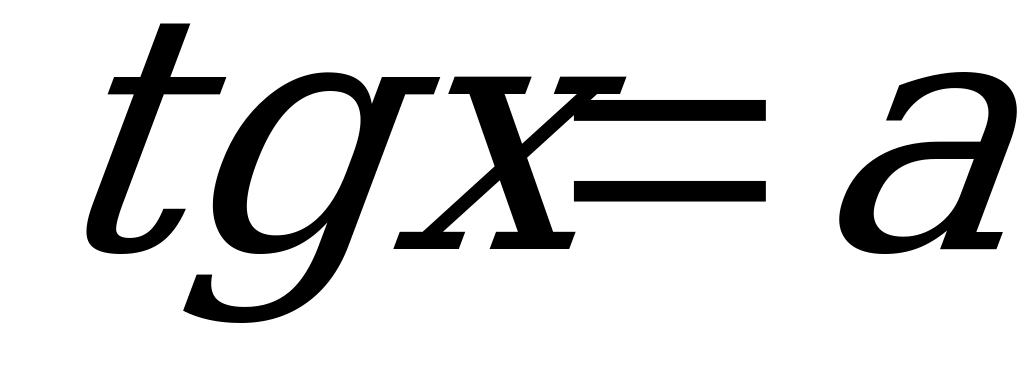 .
.
Данное уравнение имеет решение при любом 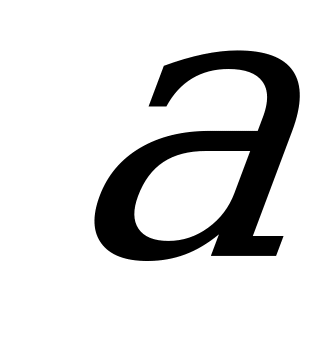 .
.
Формула корней уравнения 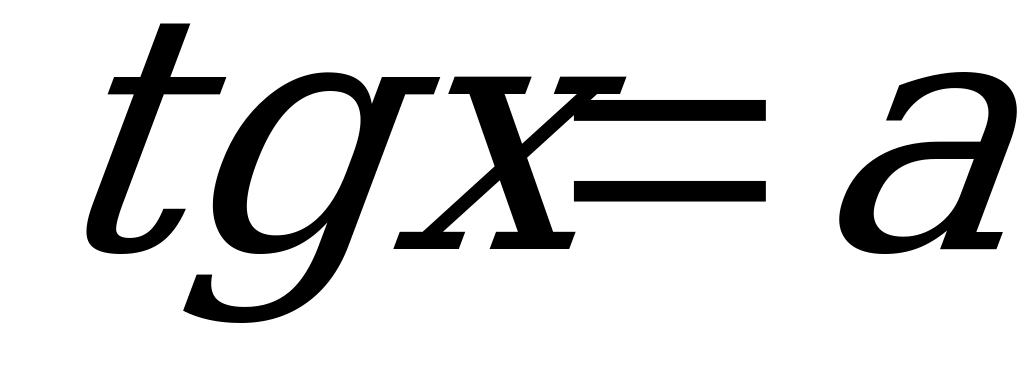 имеет вид:
имеет вид:
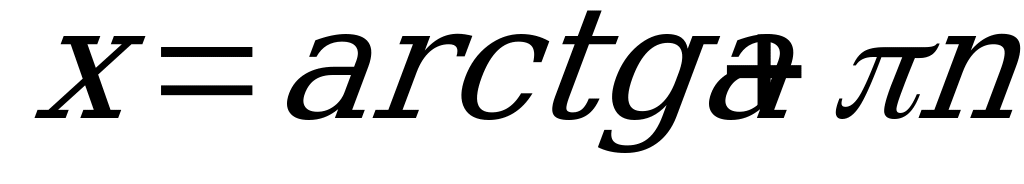 , где
, где  Z. (3)
Z. (3)
Уравнение 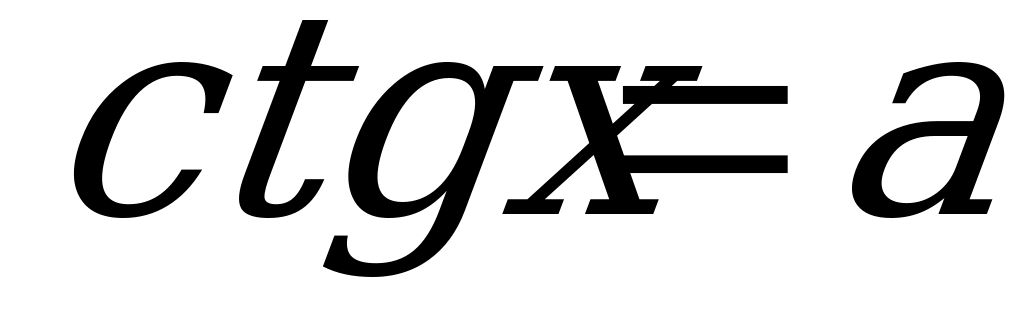 .
.
Данное уравнение имеет решение при любом 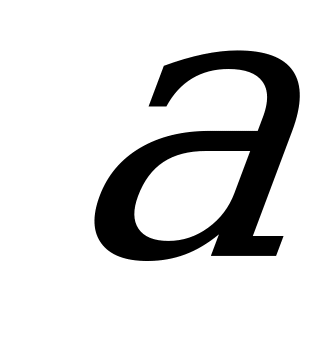 .
.
Формула корней уравнения 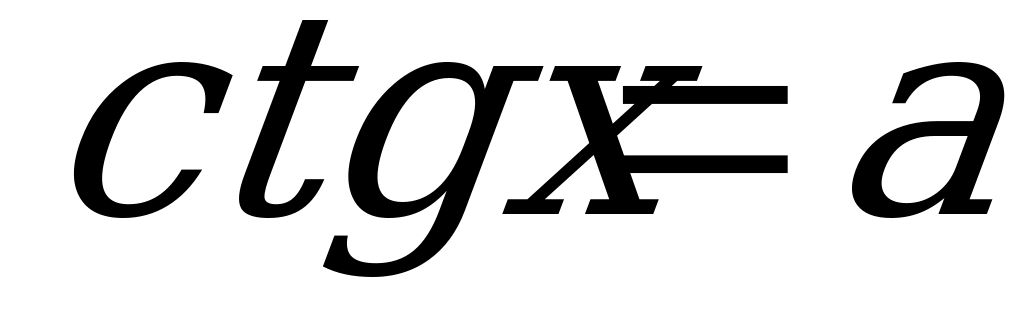 имеет вид:
имеет вид:
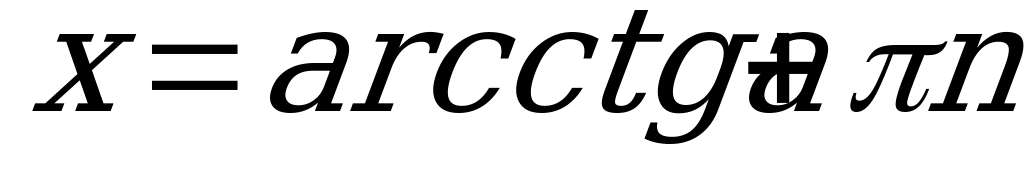 , где
, где  Z. (4)
Z. (4)
Упражнения с решениями.
Пример 1. Решите уравнения:
а) 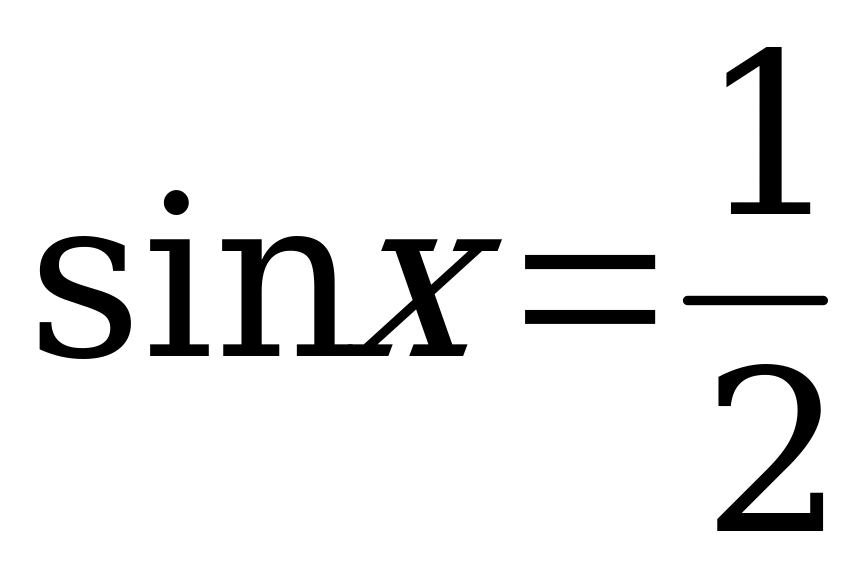 ; б)
; б) 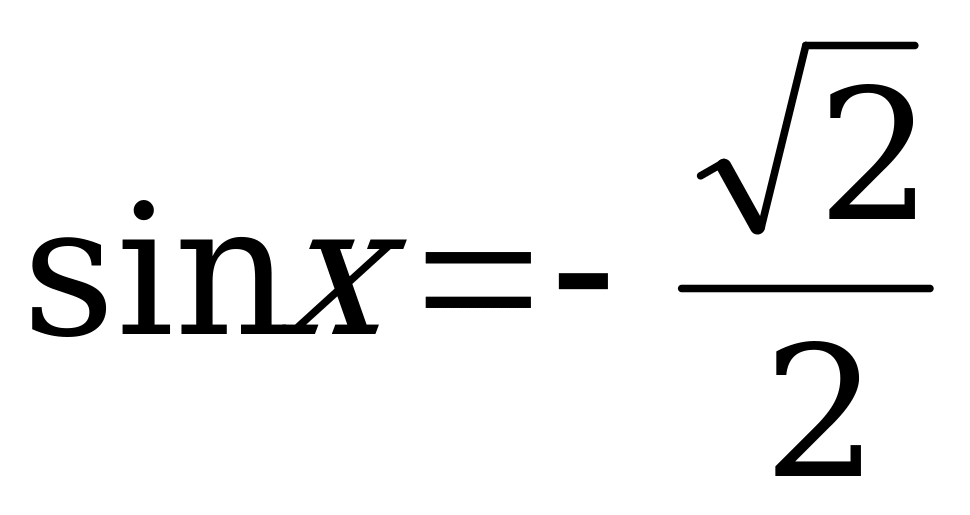 ; в)
; в) 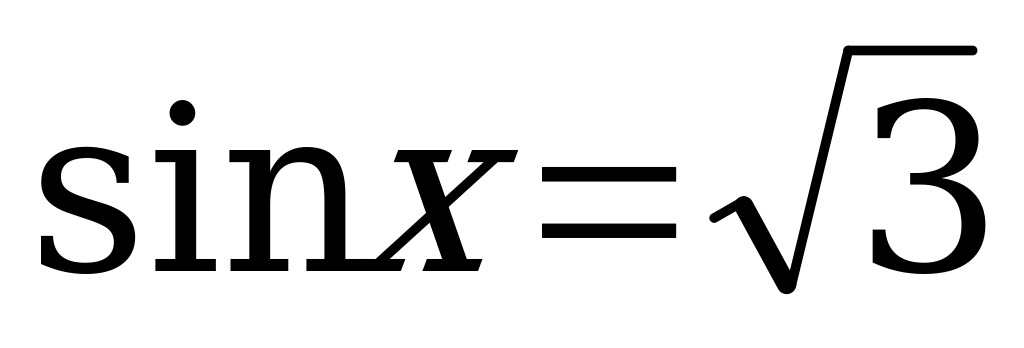 .
.
Решение: а) Решим уравнение 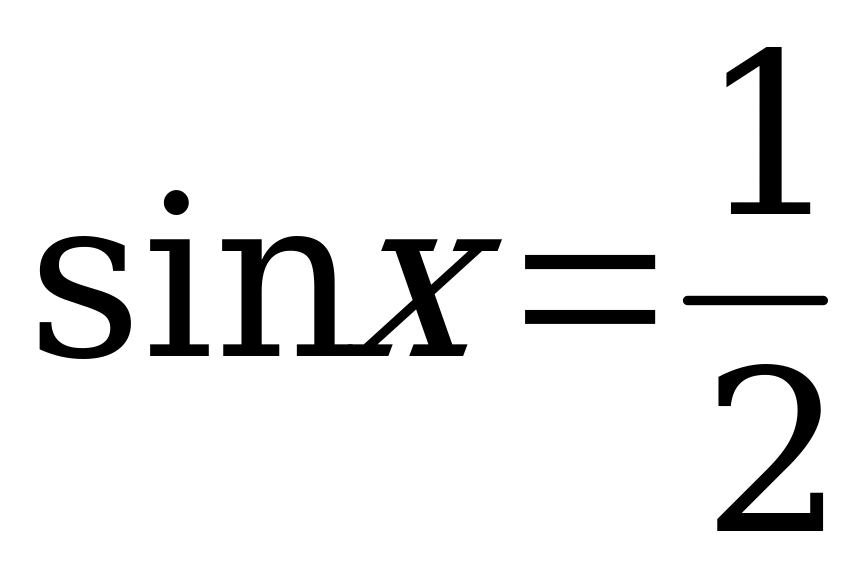 .
.
По формуле (1)
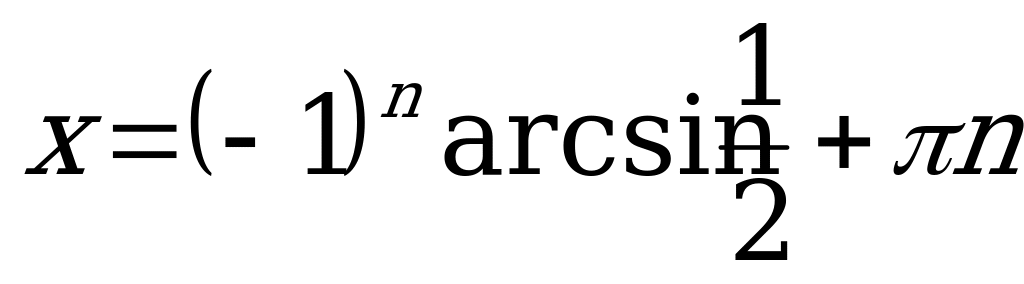 ,
, Z.
Z.
Так как 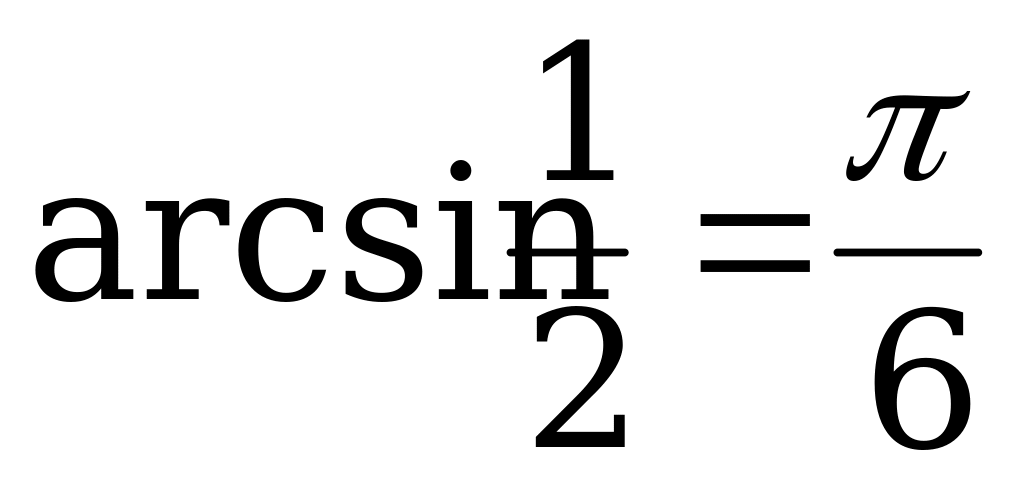 , то ответ имеет вид:
, то ответ имеет вид:
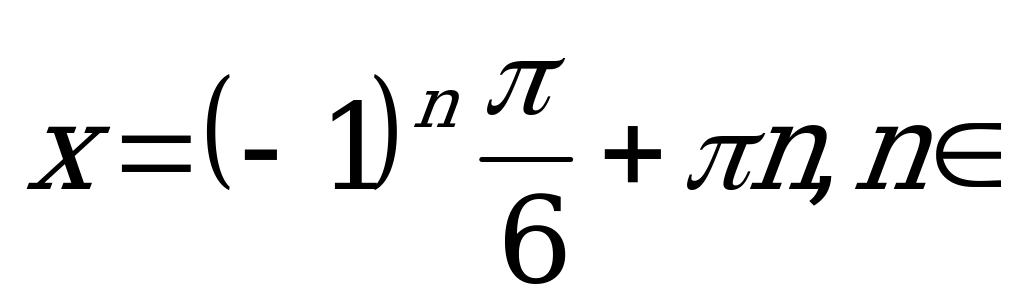 Z.
Z.
б) Решим уравнение 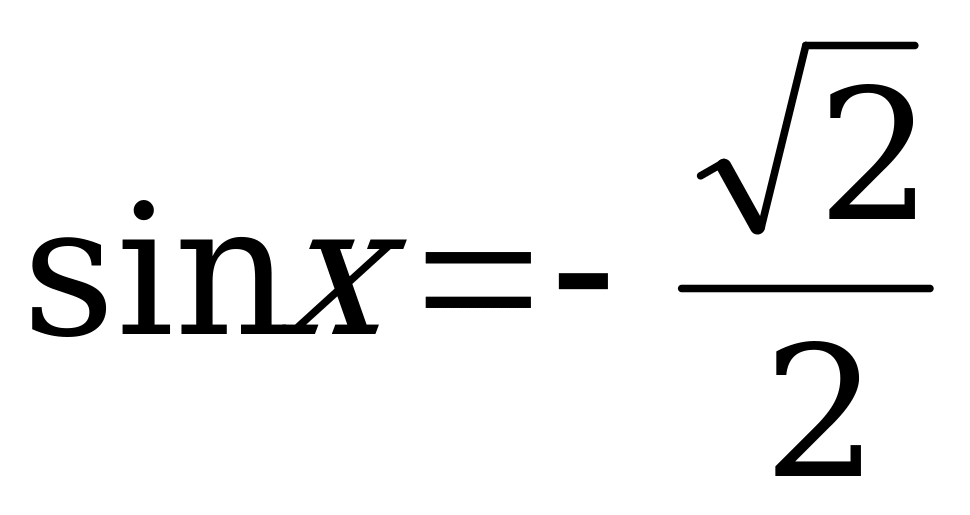 .
.
По формуле (1)
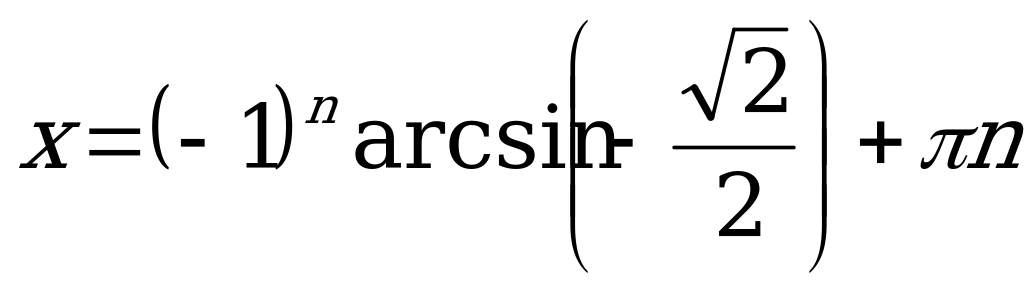 ,
, Z.
Z.
Так как 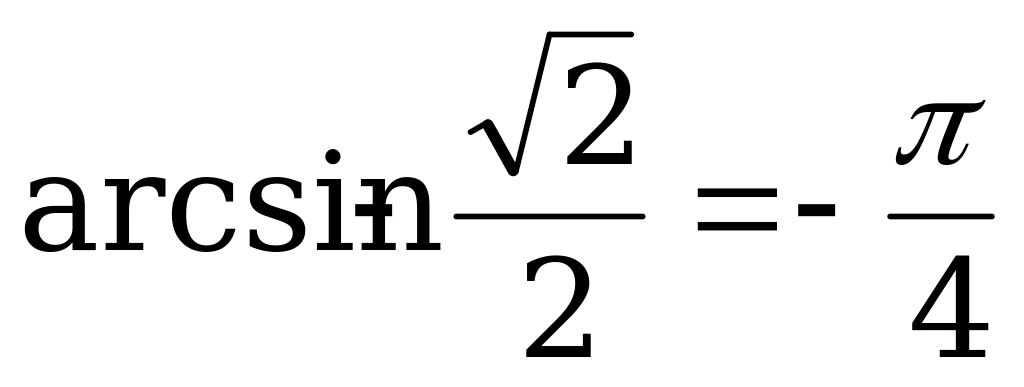 , то
, то
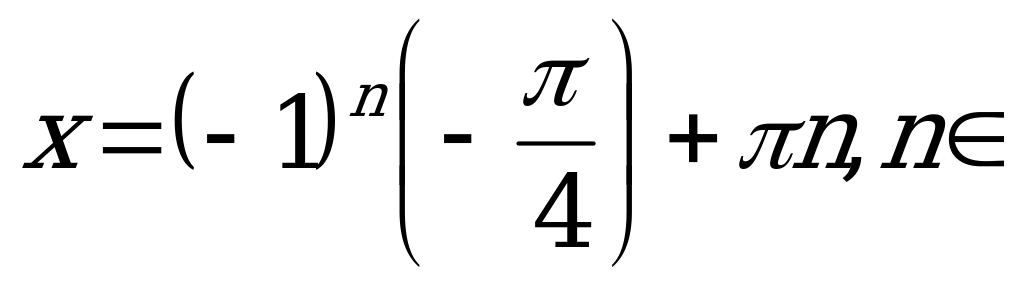 Z.
Z.
Так как 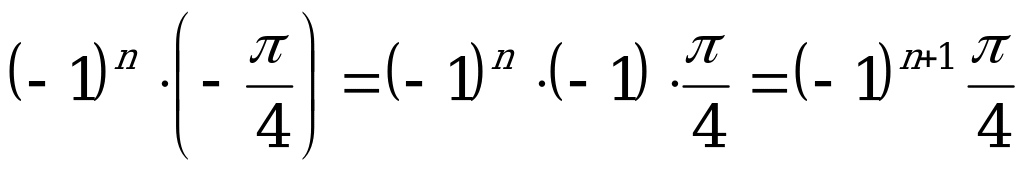 , то ответ имеет вид:
, то ответ имеет вид:
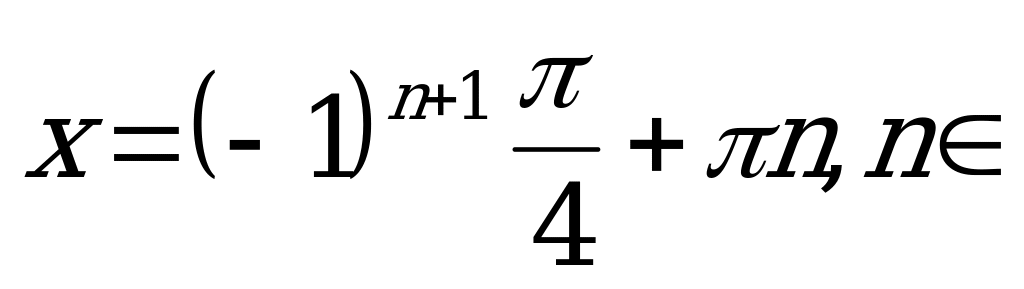 Z.
Z.
в) Решим уравнение: 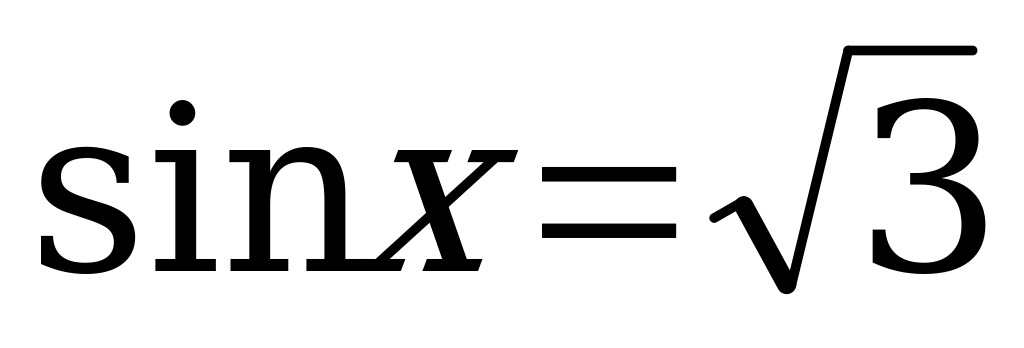 .
.
Так как 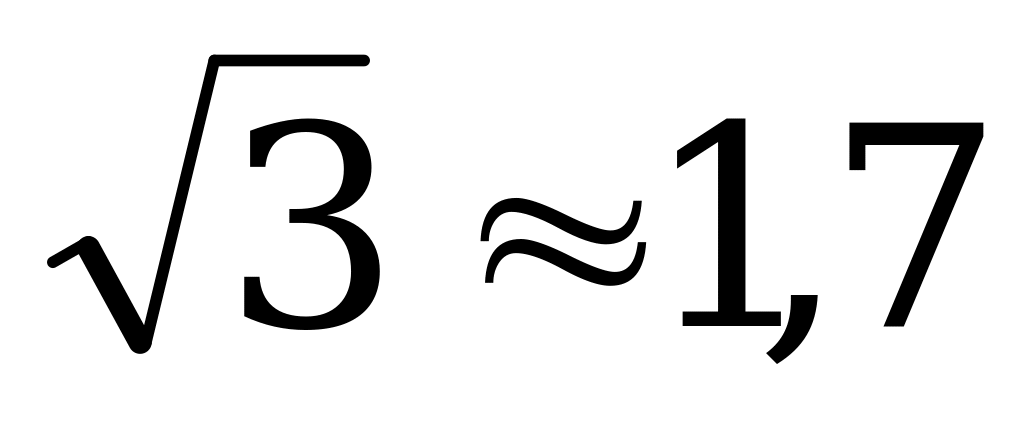 и 1,71, то
и 1,71, то 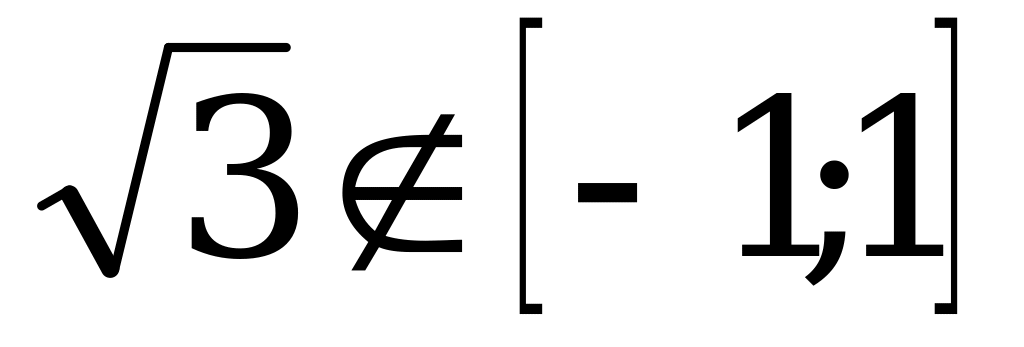 . Значит, уравнение
. Значит, уравнение 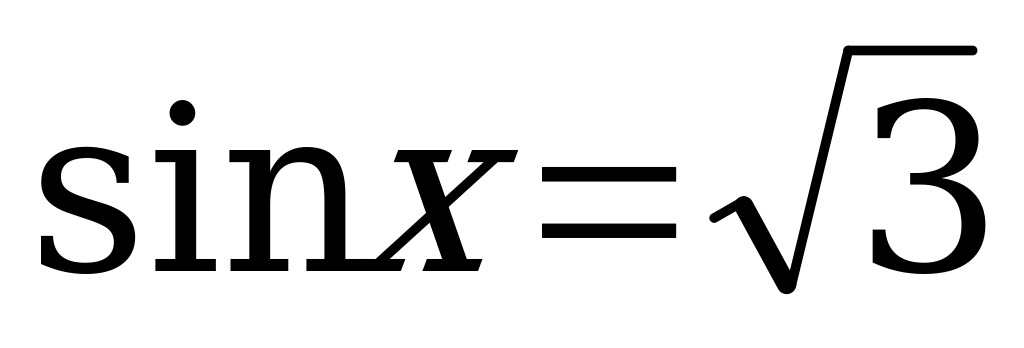 не имеет решения.
не имеет решения.
Пример 2. Решите уравнения:
а) 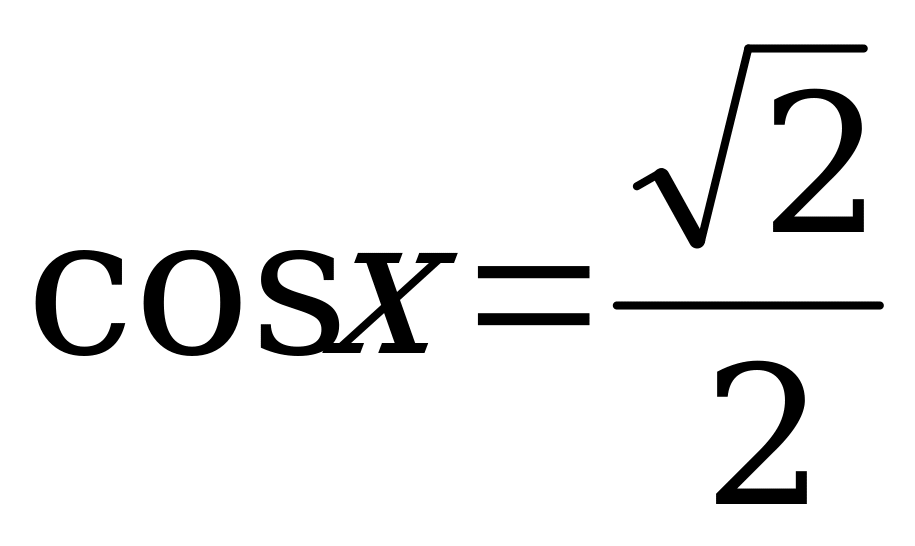 ; б)
; б) 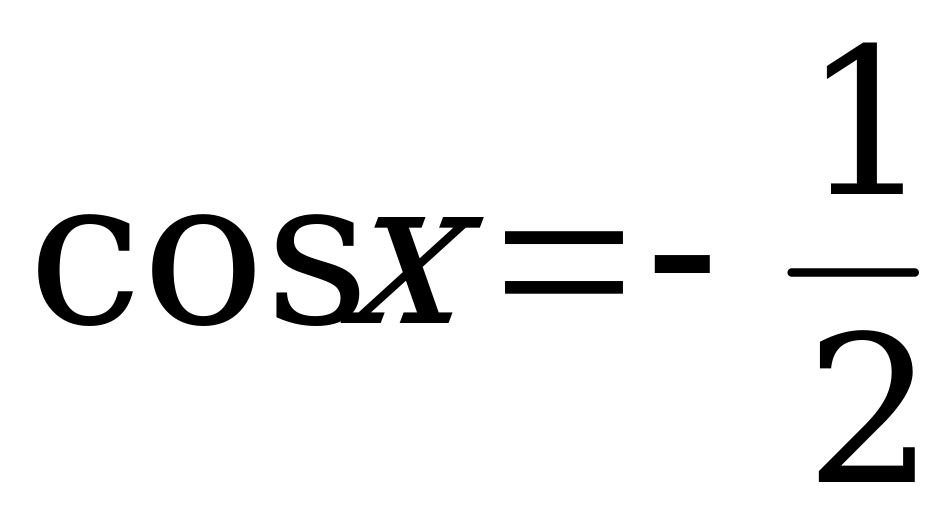 ; в)
; в) 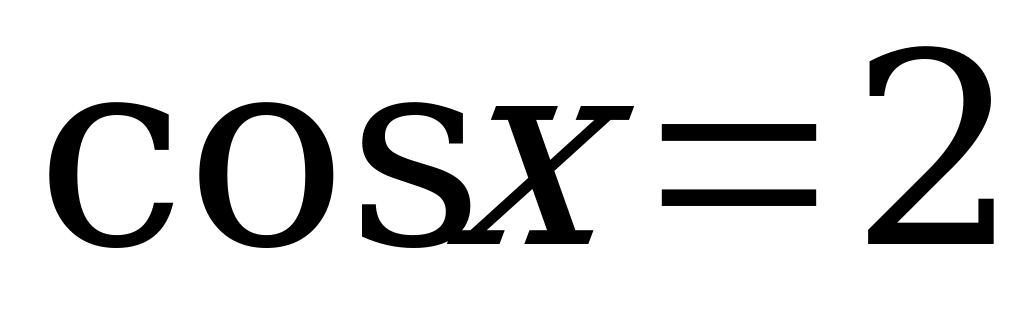 .
.
Решение. а) Решим уравнение 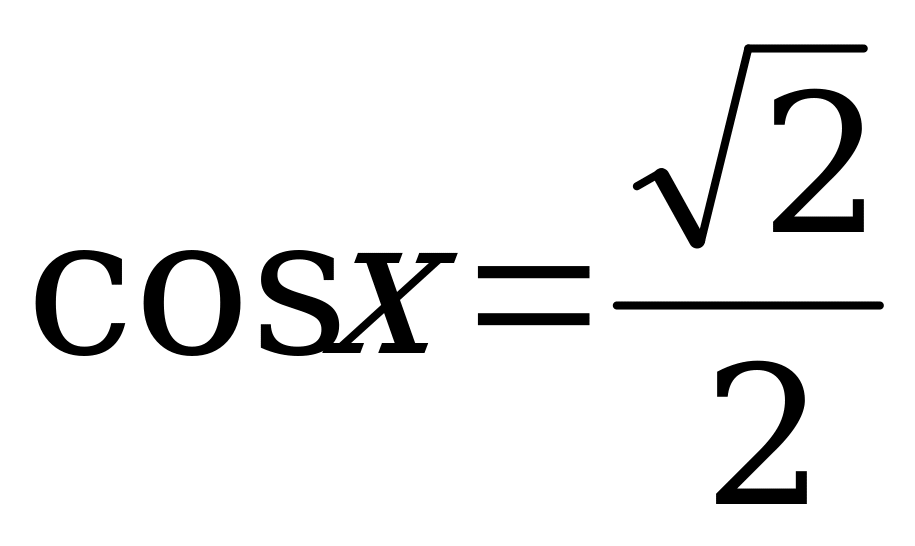 .
.
По формуле (2)
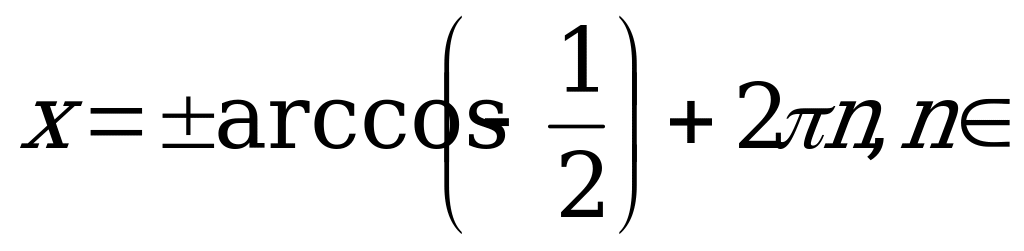 Z.
Z.
Согласно формуле (2) имеем:
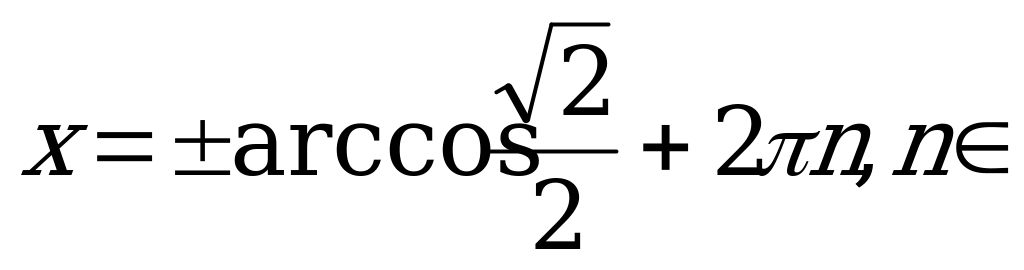 Z.
Z.
Так как 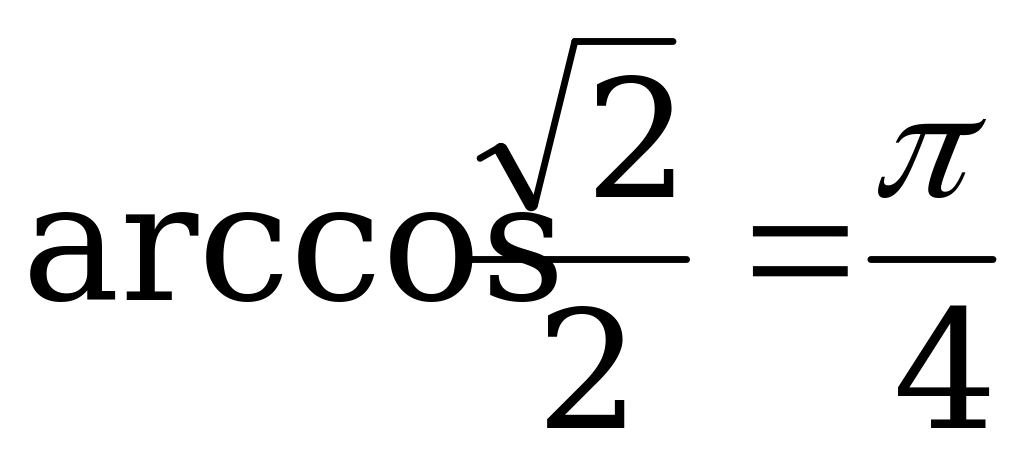 , то
, то
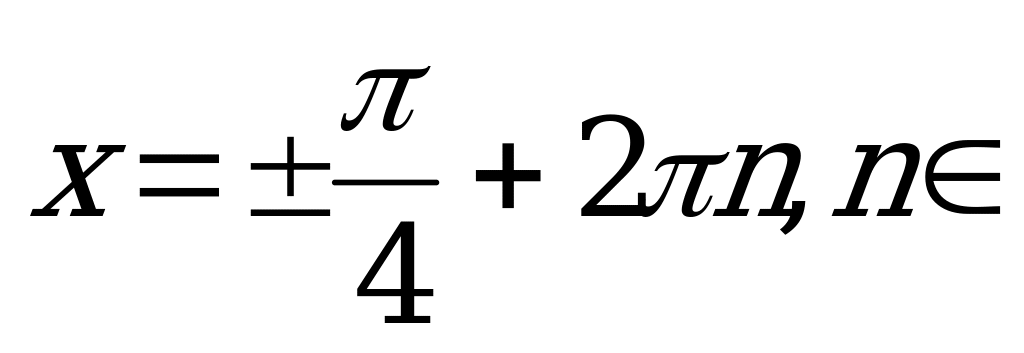 Z.
Z.
б) Решим уравнение 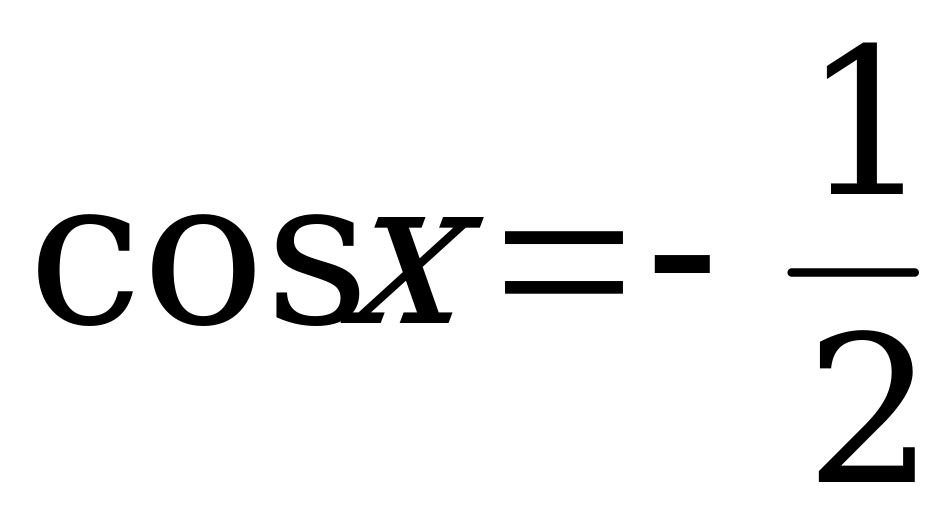 .
.
Так как 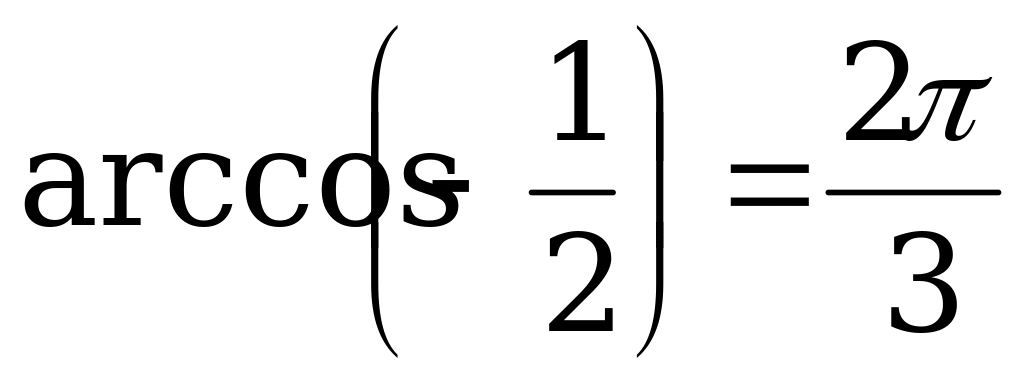 , то
, то
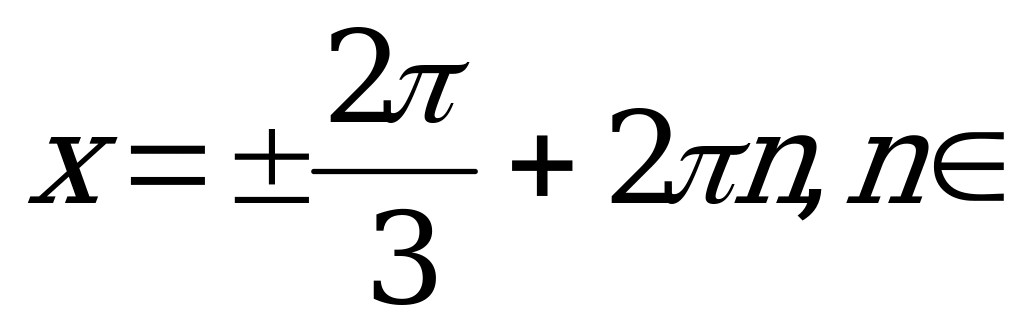 Z.
Z.
в) Решим уравнение 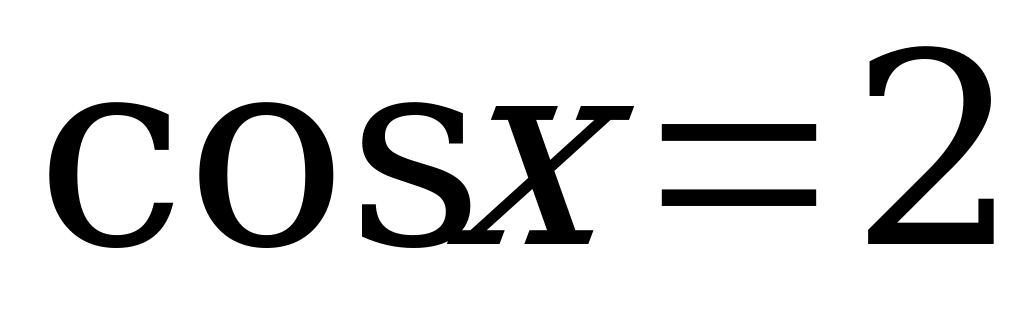 .
.
Так как 21, то уравнение 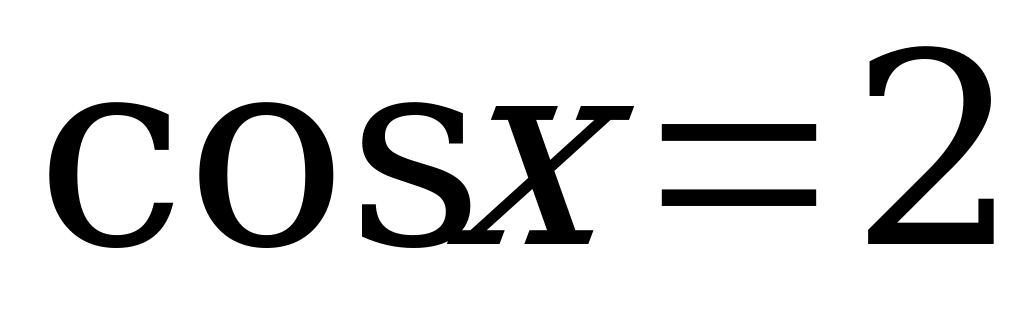 не имеет решения.
не имеет решения.
Пример 3. Решить уравнения:
а) 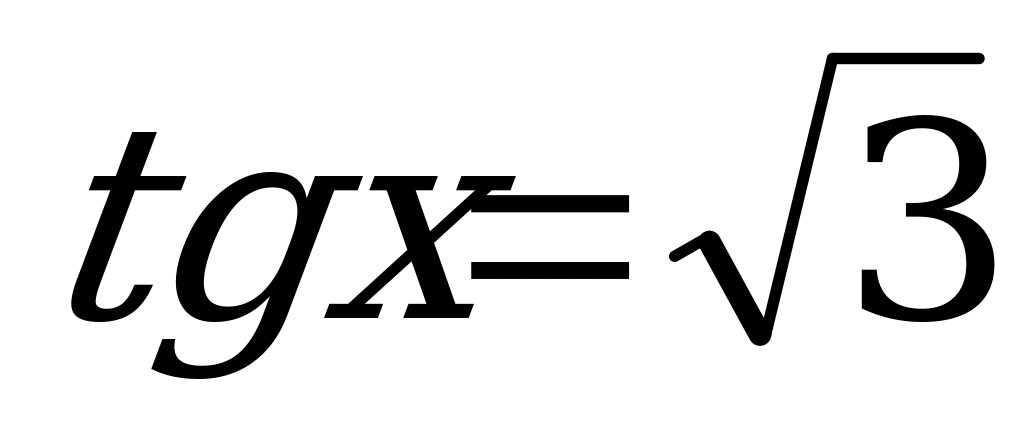 ; б)
; б) 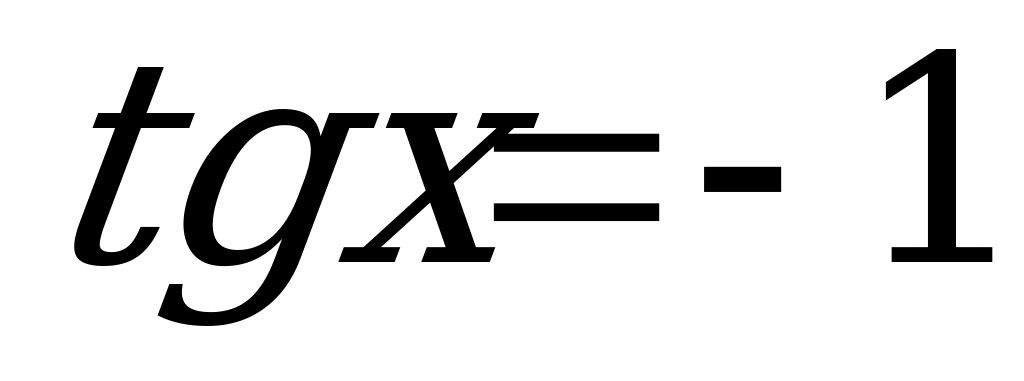 ; в)
; в) 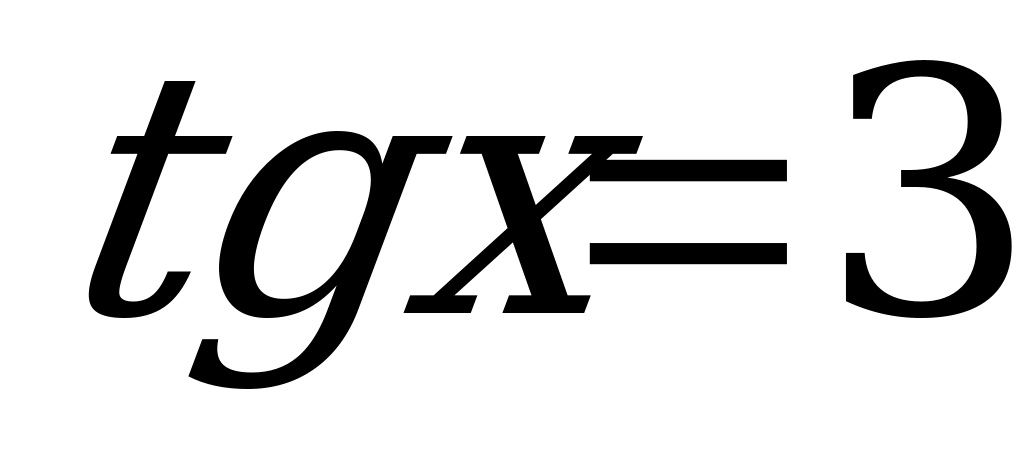 .
.
Решение: а) Решим уравнение 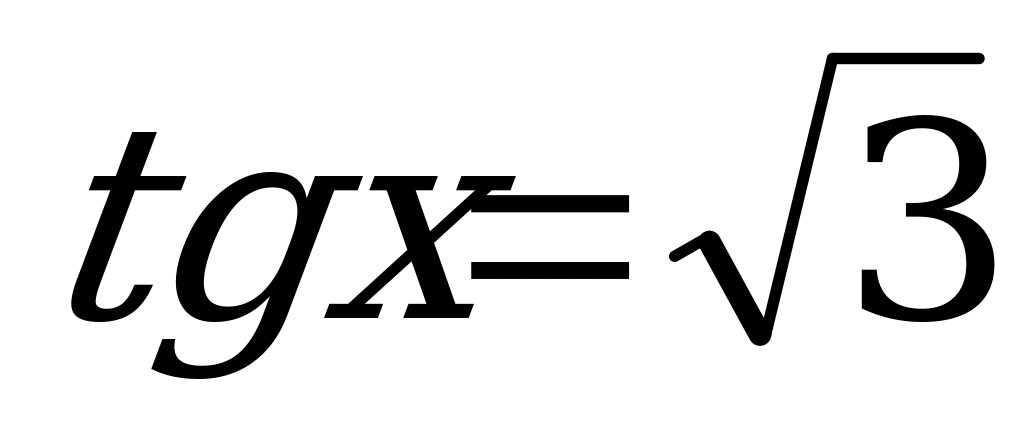 .
.
По формуле (3)
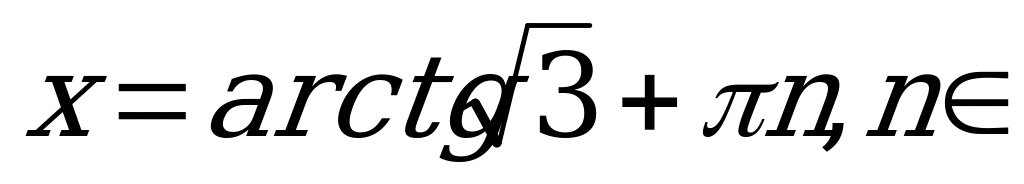 Z.
Z.
Так как 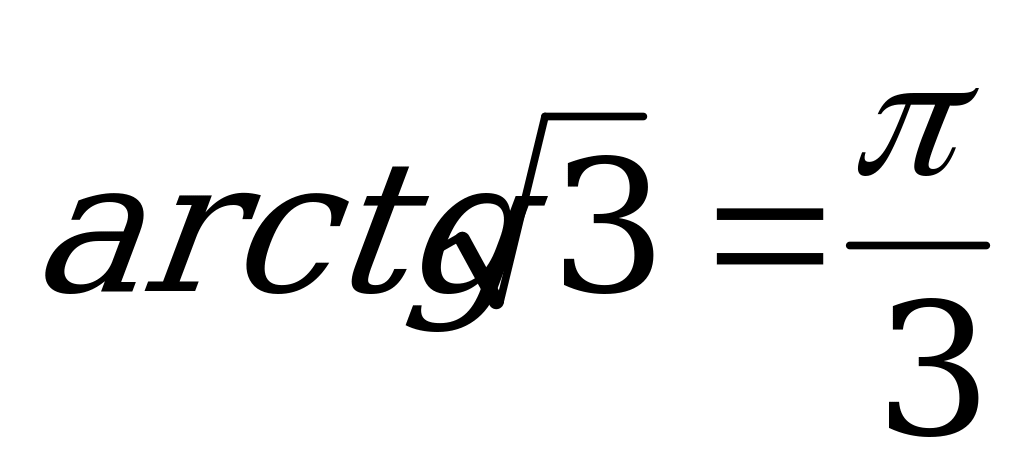 , то
, то
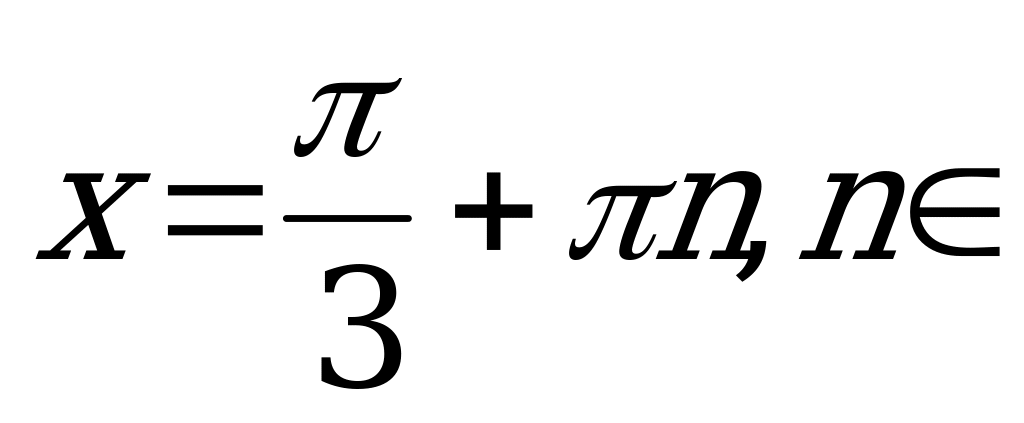 Z.
Z.
б) Решим уравнение 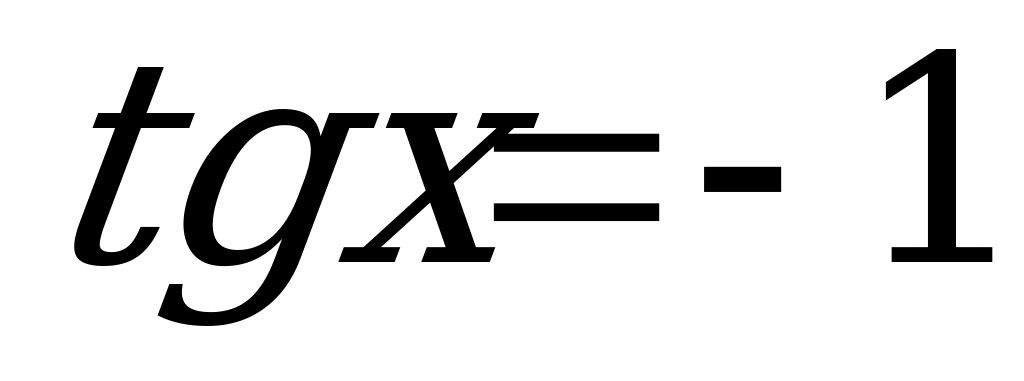 .
.
По формуле (3)
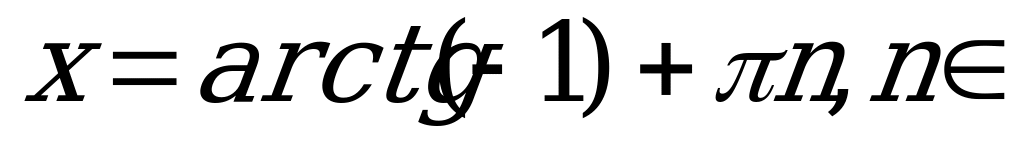 Z.
Z.
Так как 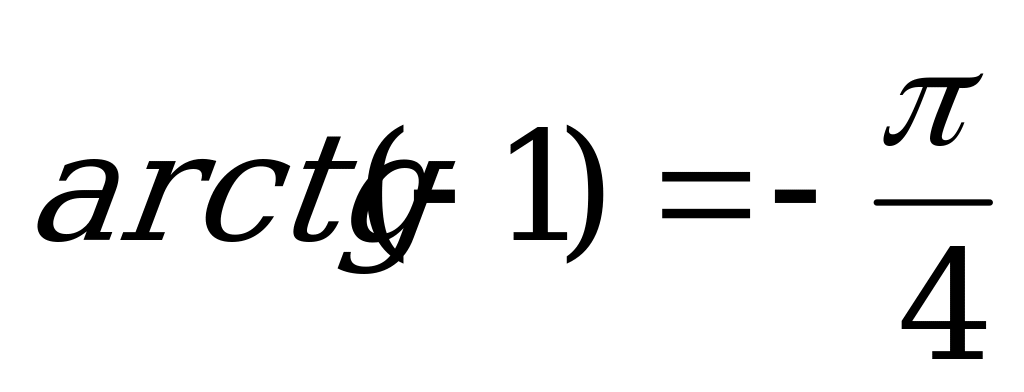 , то
, то
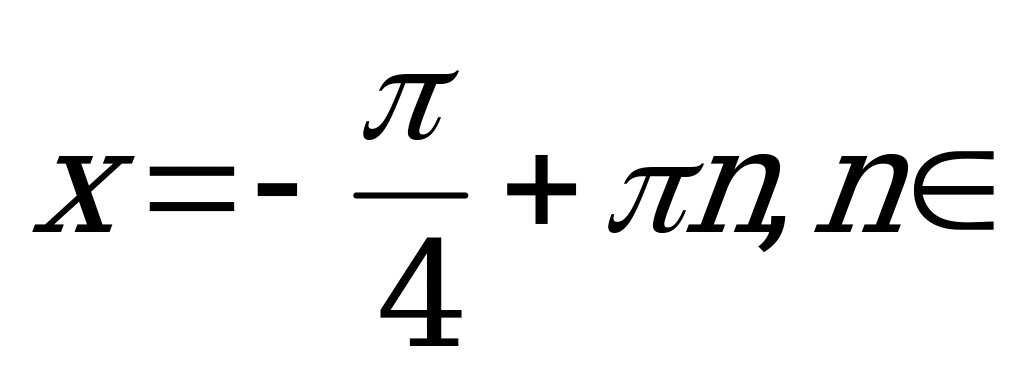 Z.
Z.
в) Решим уравнение 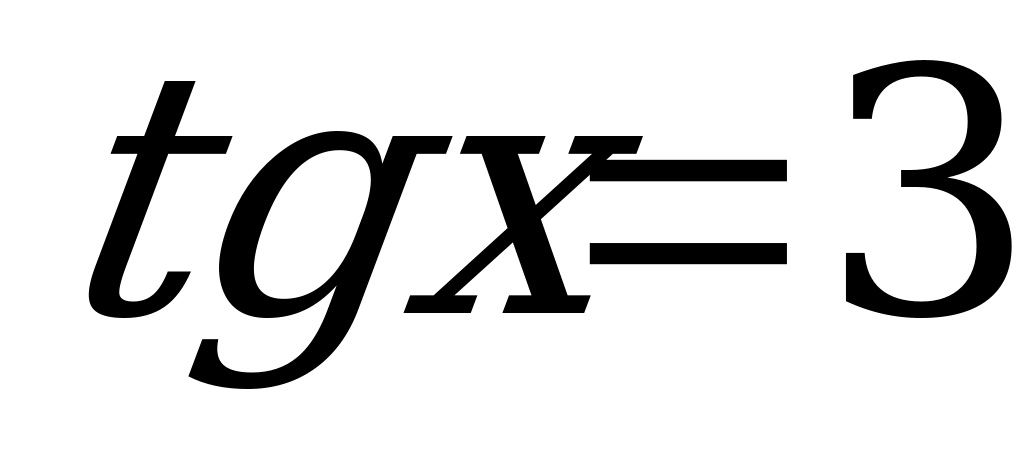 .
.
По формуле (3)
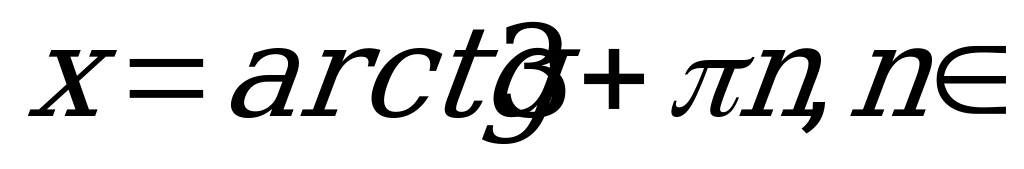 Z.
Z.
Пример 4. Решить уравнения:
а) 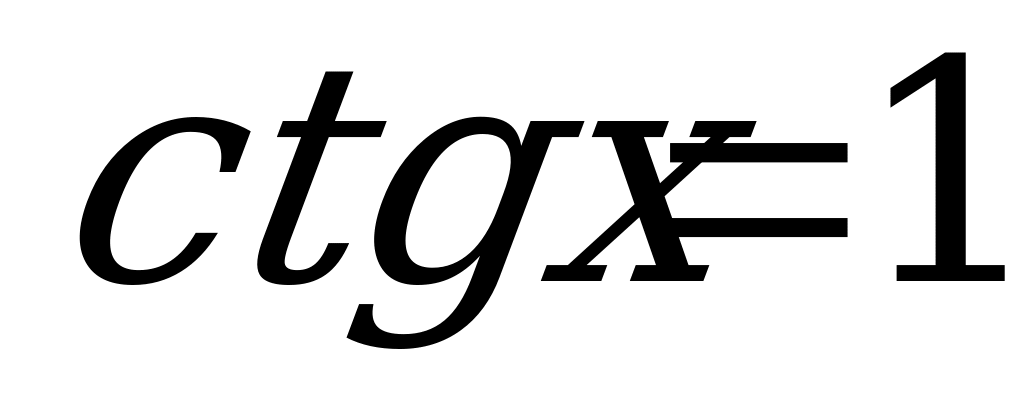 ; б)
; б) 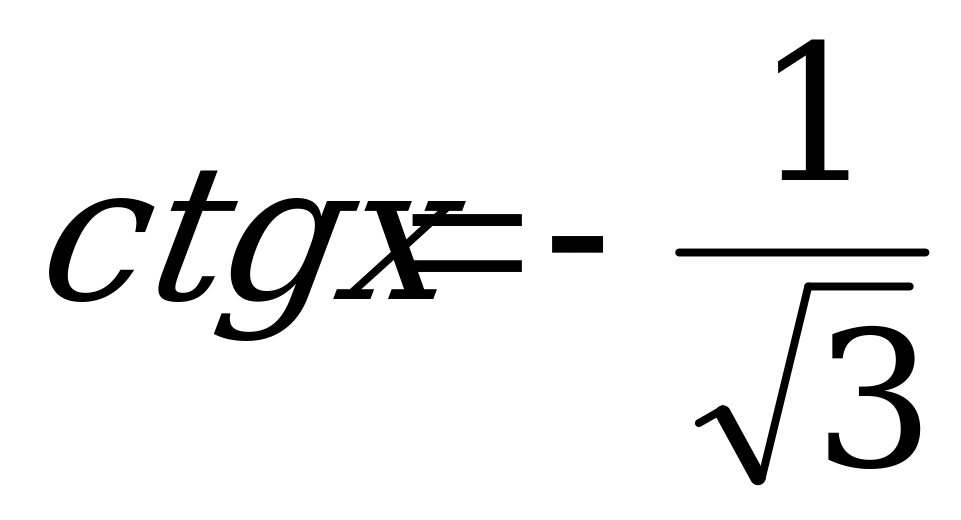 ; в)
; в) 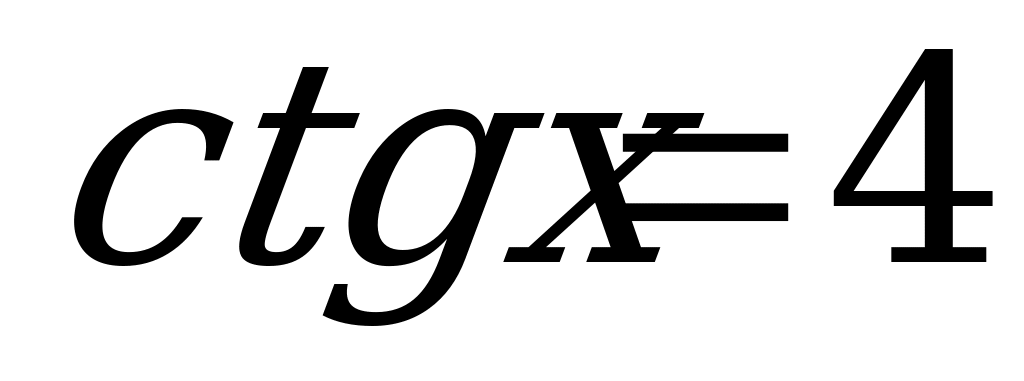 .
.
Решение: а) Решим уравнение 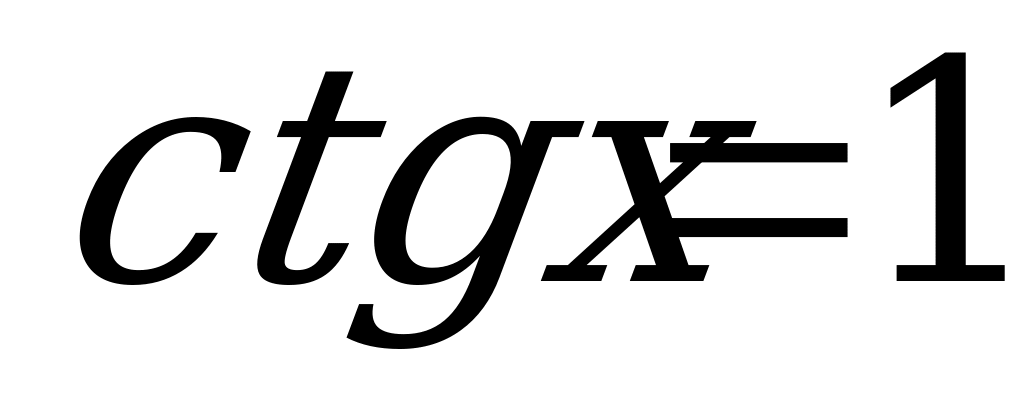 .
.
По формуле (4)
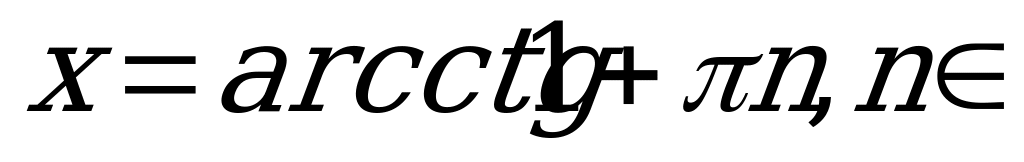 Z.
Z.
Так как 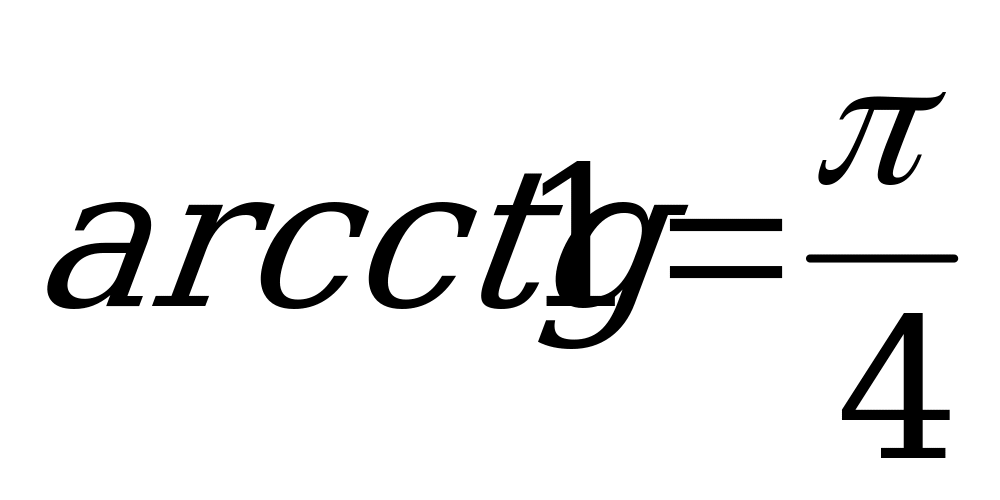 , то
, то
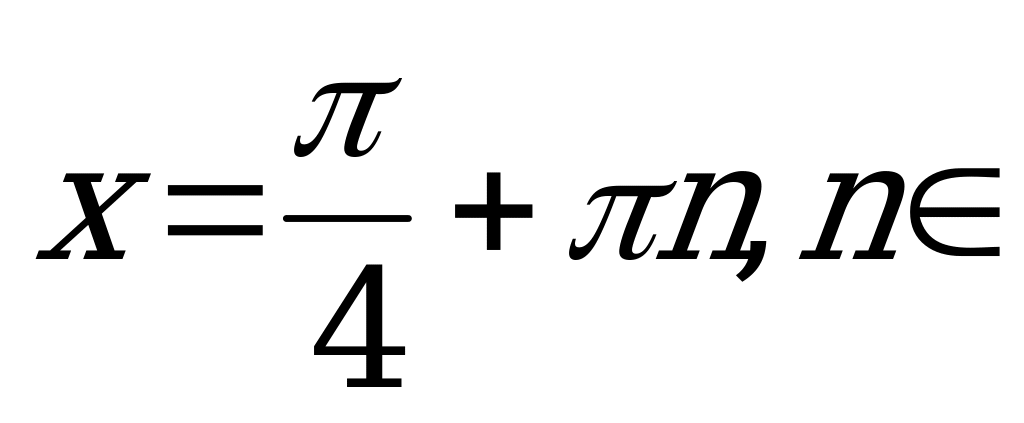 Z.
Z.
б) Решим уравнение 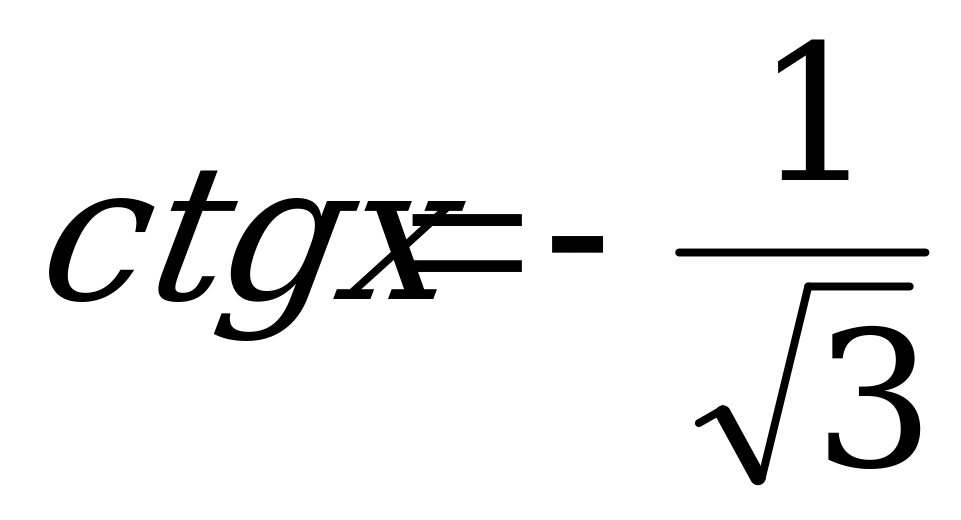 .
.
По формуле (4)
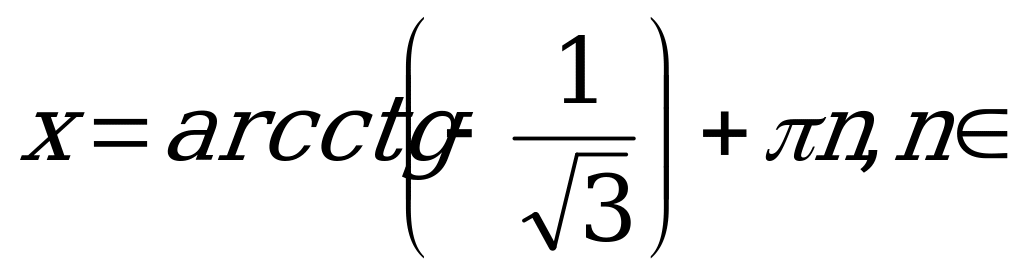 Z.
Z.
Так как 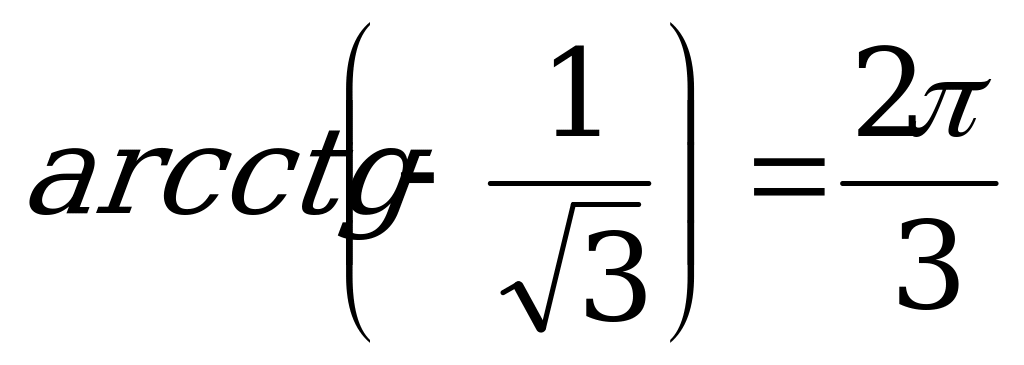 , то
, то
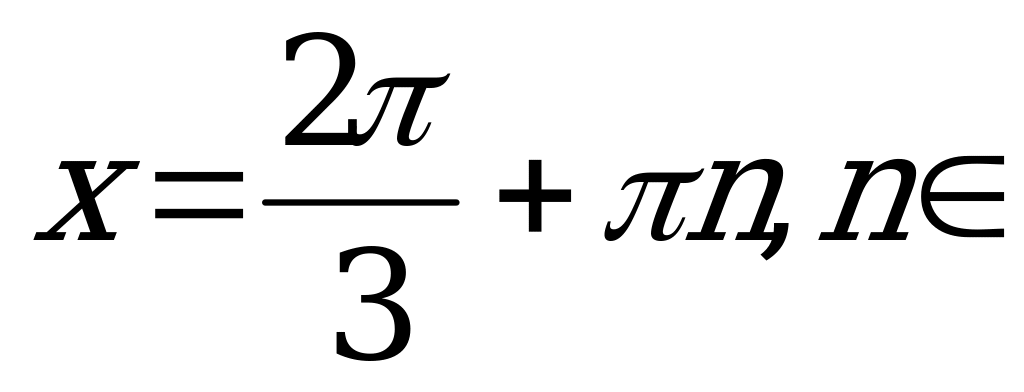 Z.
Z.
в) Решим уравнение 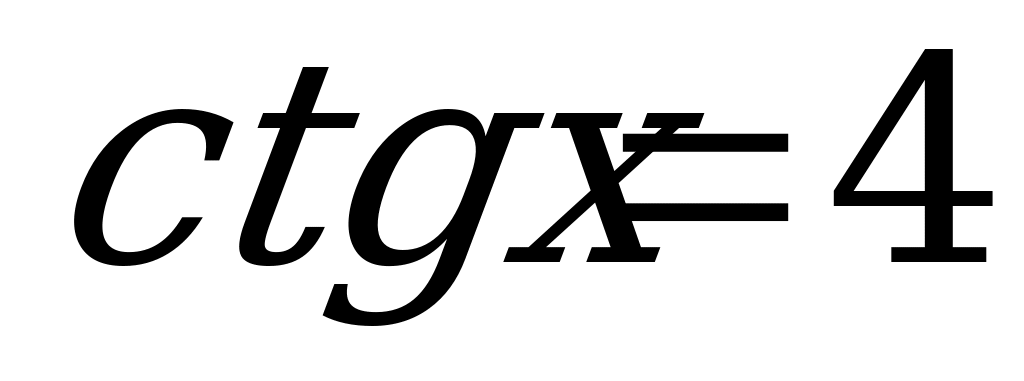 .
.
По формуле (4)
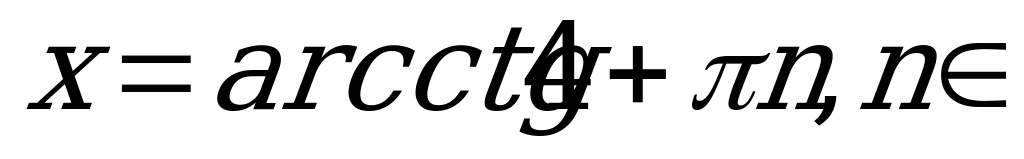 Z.
Z.
Частные случаи.
Справочный материал.
В частных случаях при 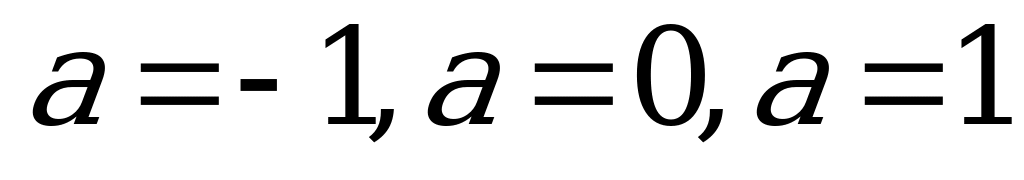 получаются следующие формулы:
получаются следующие формулы:
1) 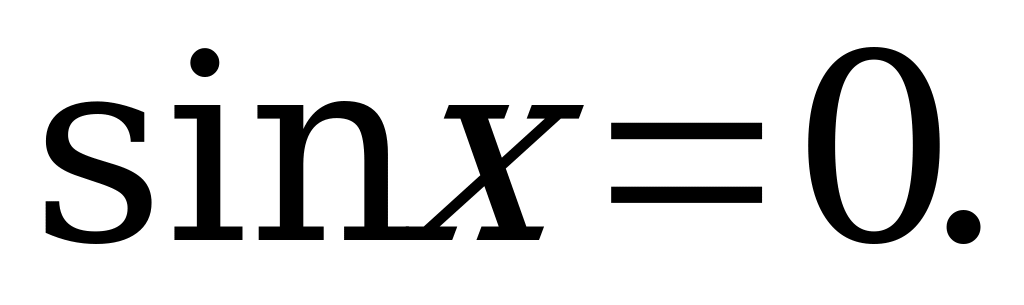
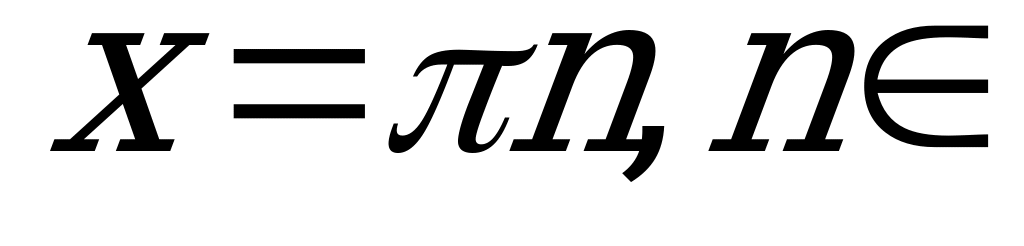 Z.
Z.
2) 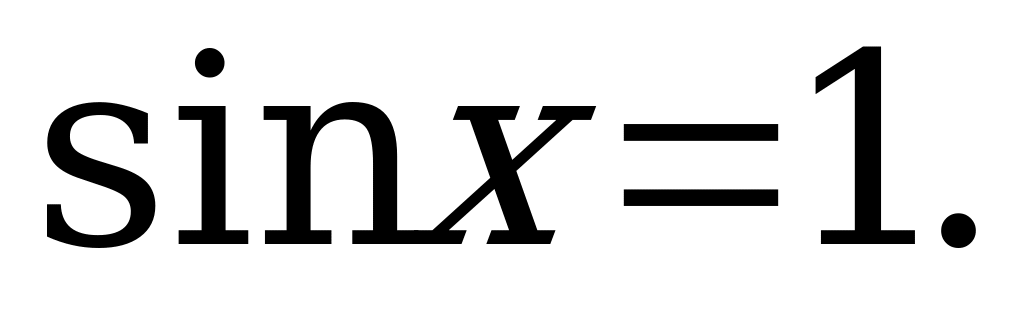
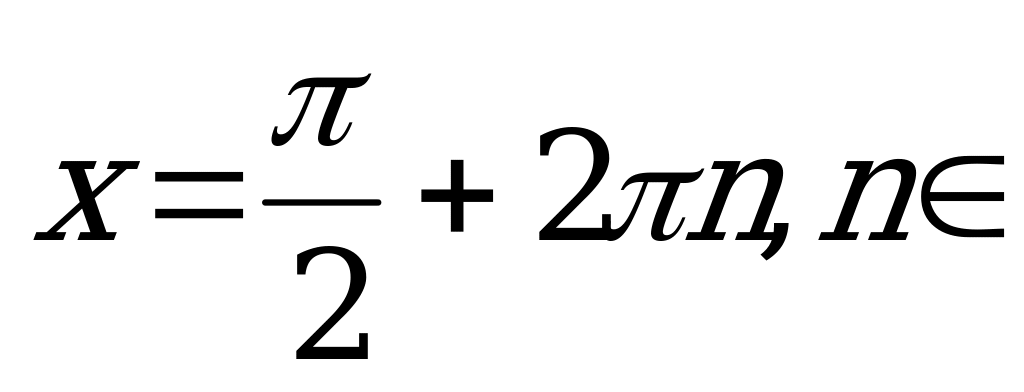 Z.
Z.
3) 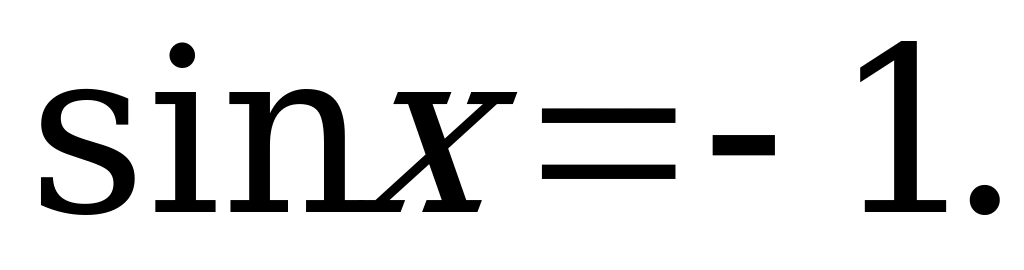
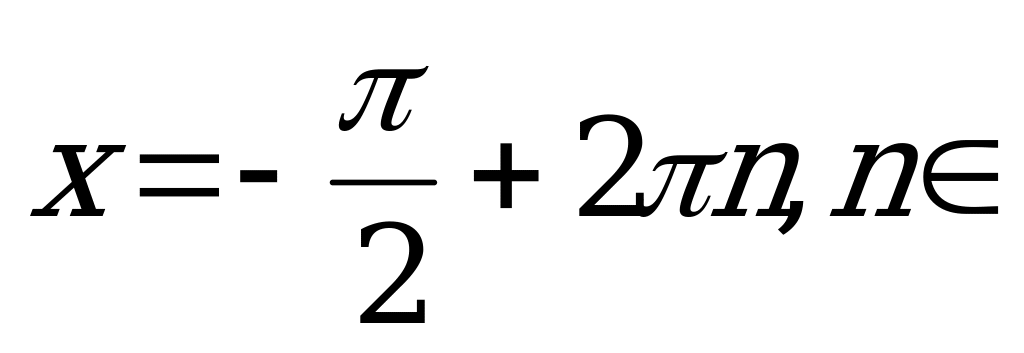 Z.
Z.
4) 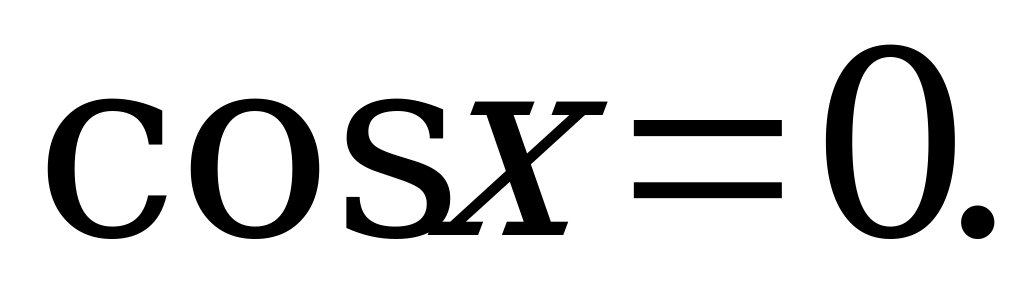
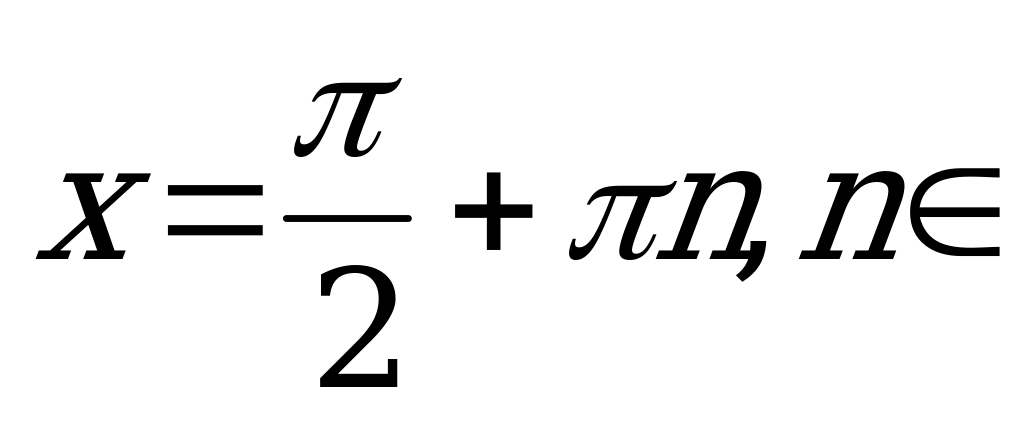 Z.
Z.
5) 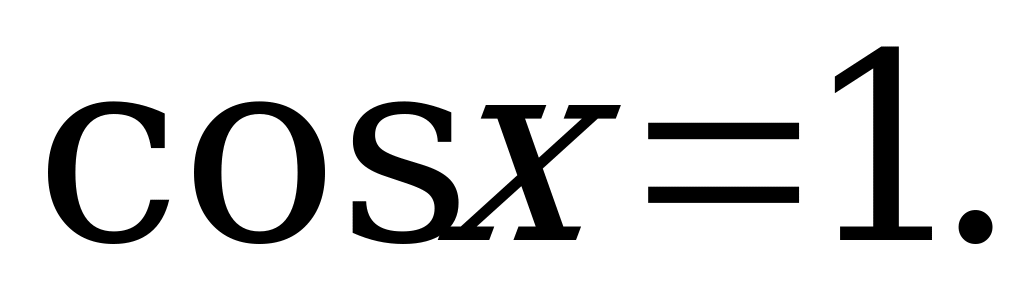
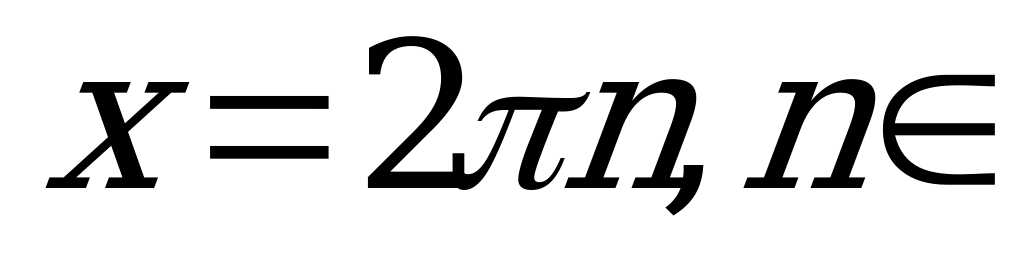 Z.
Z.
6) 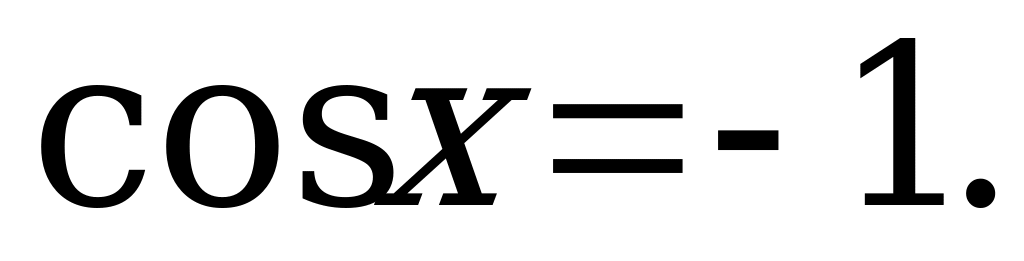
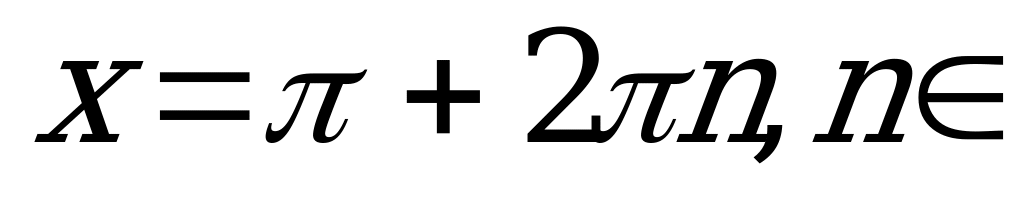 Z.
Z.
7) 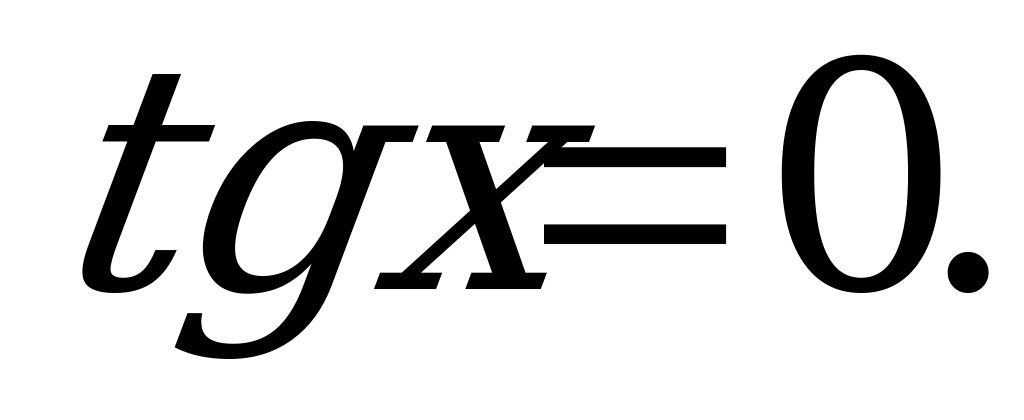
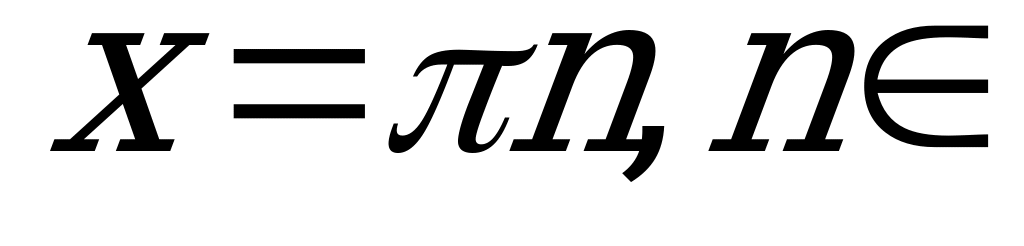 Z.
Z.
8) 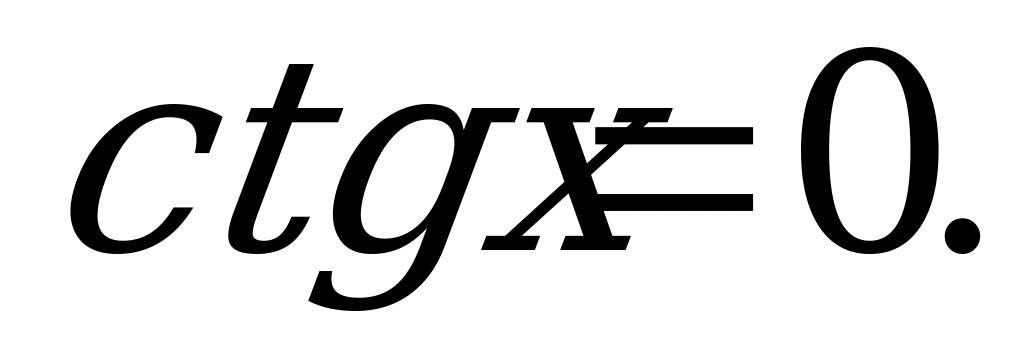
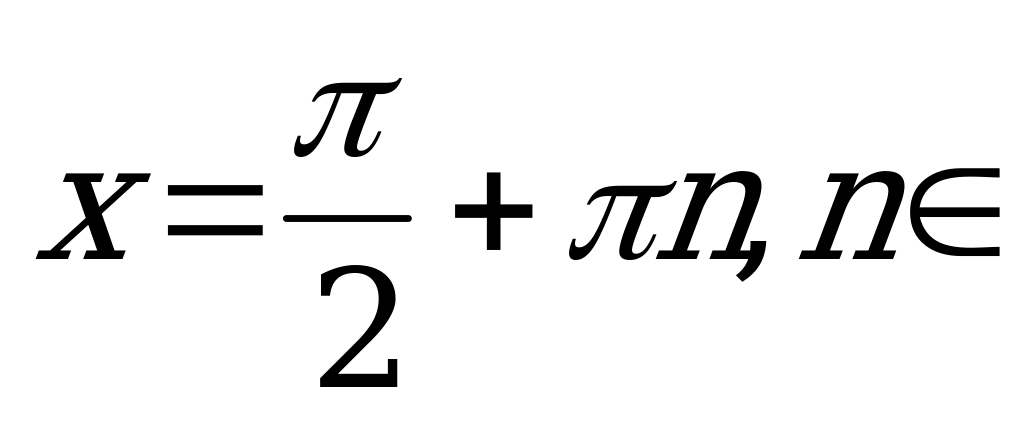 Z.
Z.
Уравнения вида
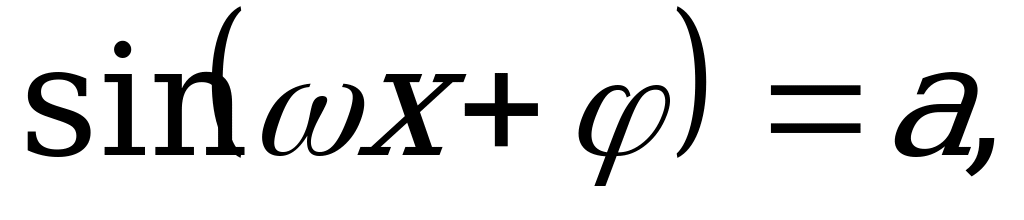
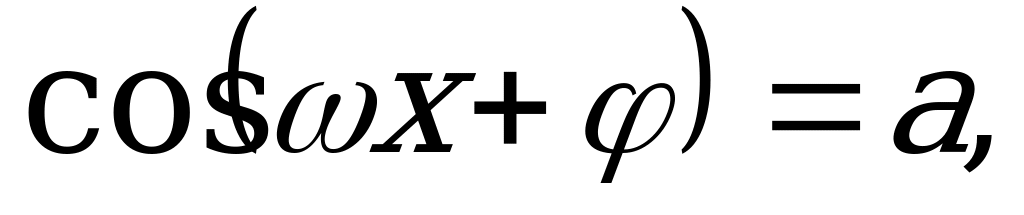
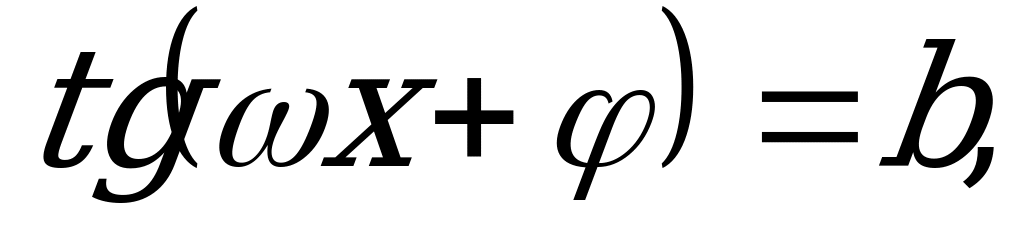
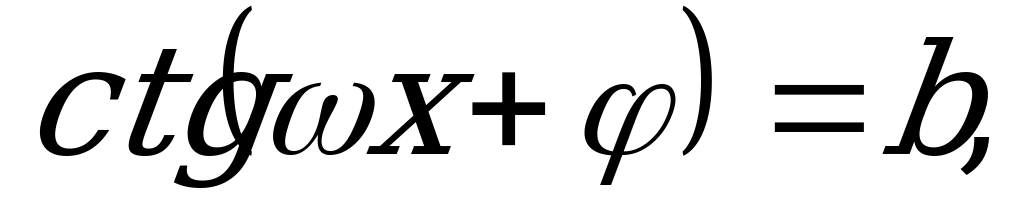 где
где 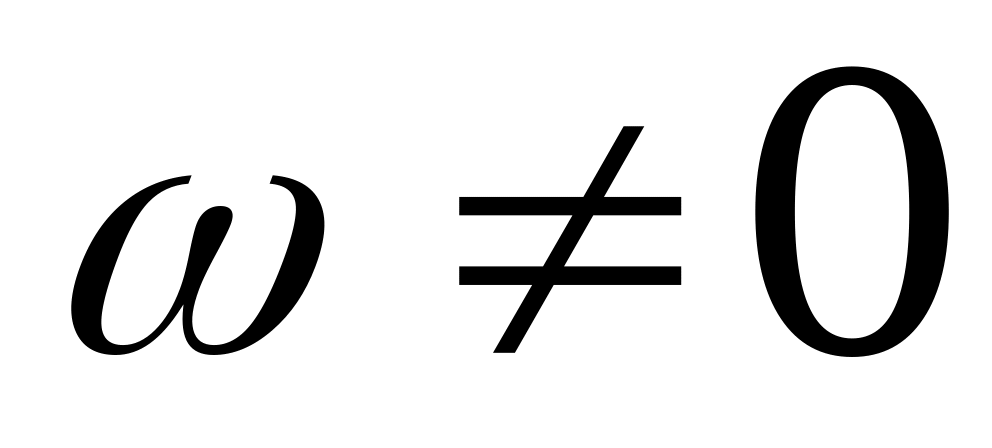
 ,
, 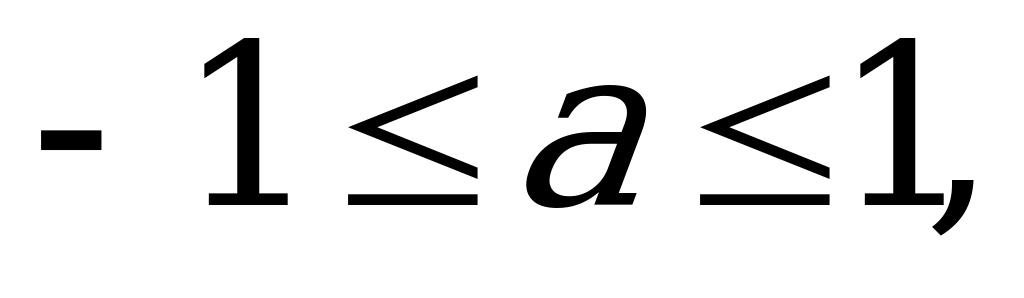
 и
и  - любые действительные числа, так же относятся к простейшим тригонометрическим уравнениям. Их следует решать по тем же формулам, заменив
- любые действительные числа, так же относятся к простейшим тригонометрическим уравнениям. Их следует решать по тем же формулам, заменив 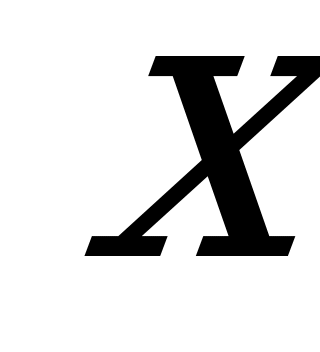 на
на 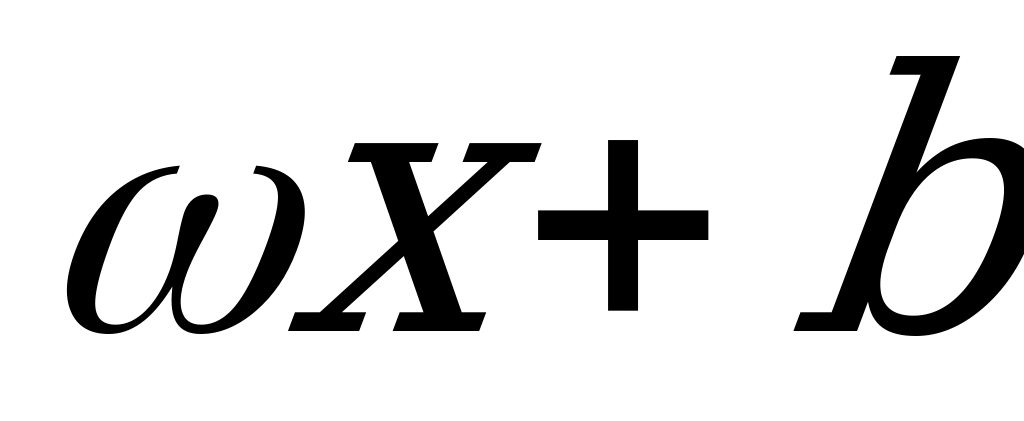 .
.
Упражнения с решениями.
Пример 5. Решить уравнения:
а) 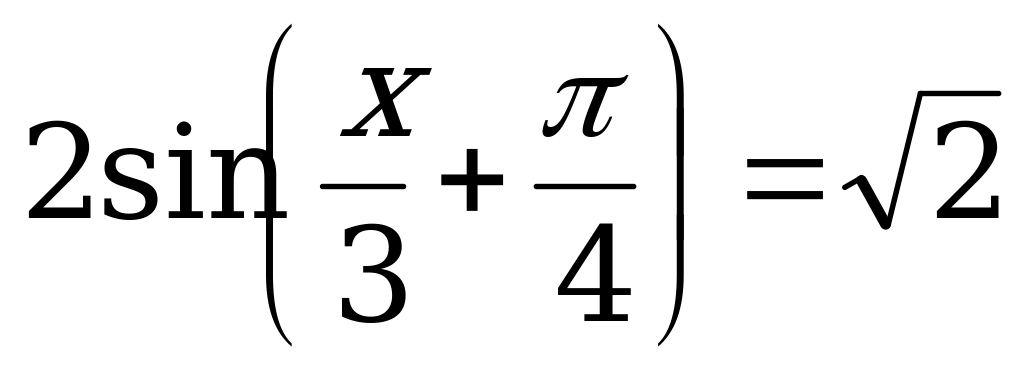 ; б)
; б) 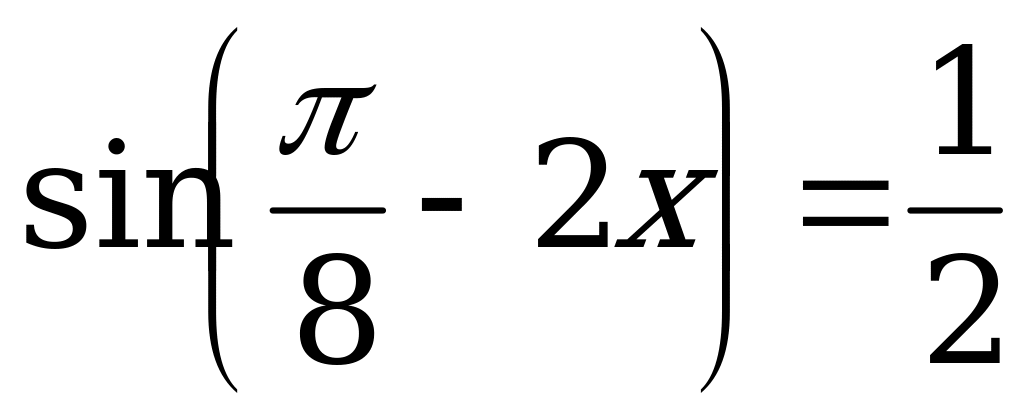 .
.
Решение. а) Решим уравнение 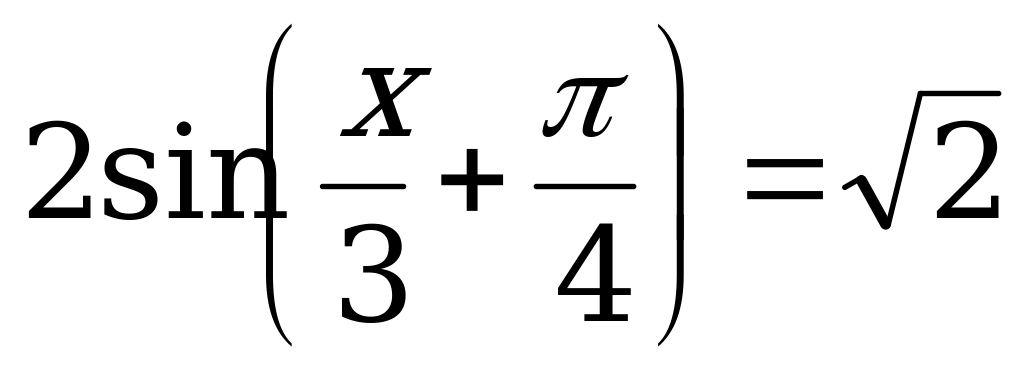 .
.
Разделим данное уравнение на 2, получим:
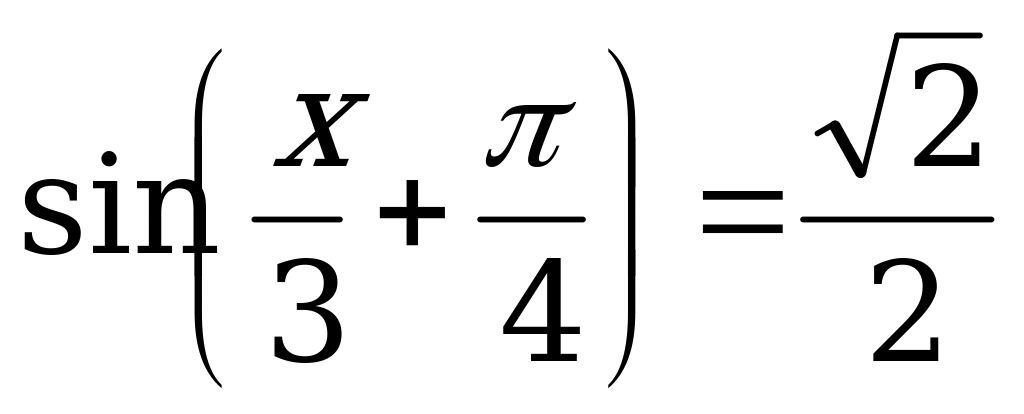 .
.
По формуле (1)
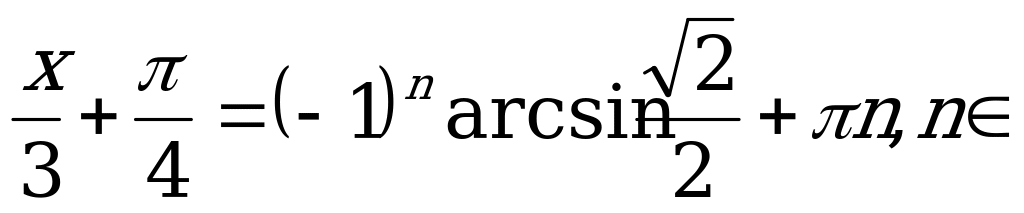 Z.
Z.
Так как 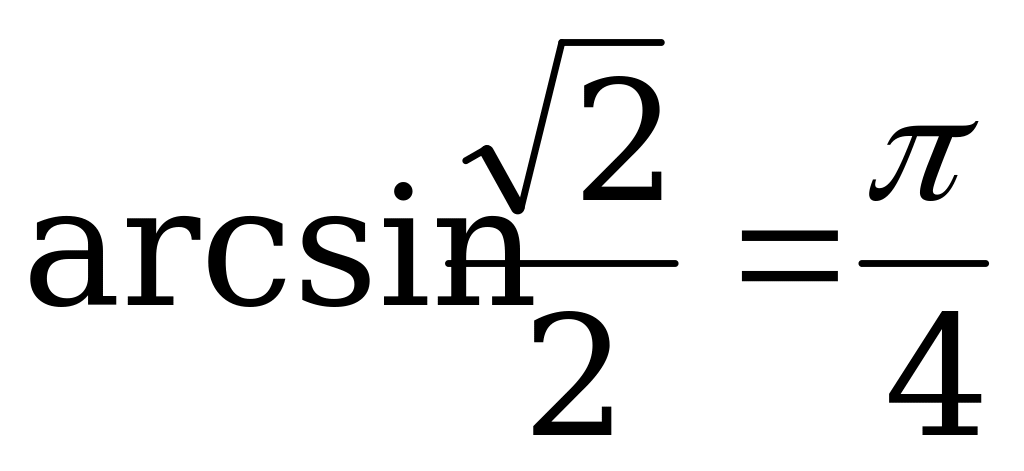 , то
, то

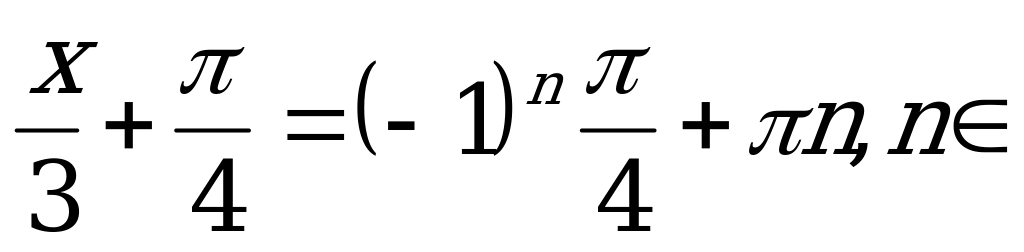 Z.
Z.

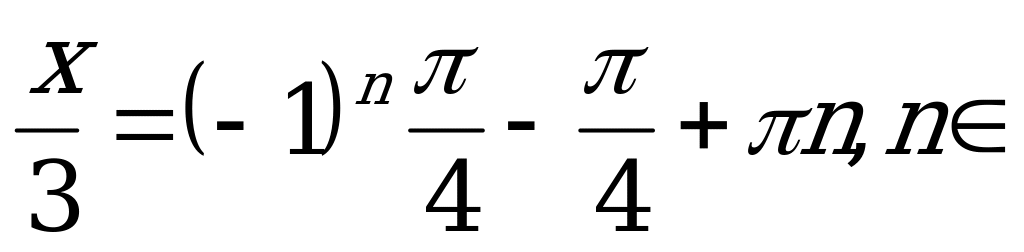 Z.
Z.
Умножим обе части равенства на 3 и запишем ответ:
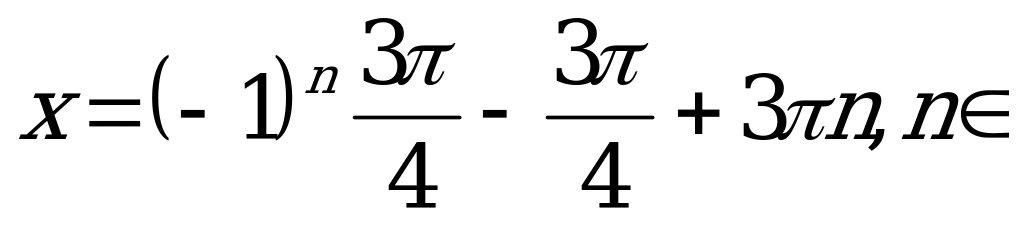 Z.
Z.
б) Решим уравнение 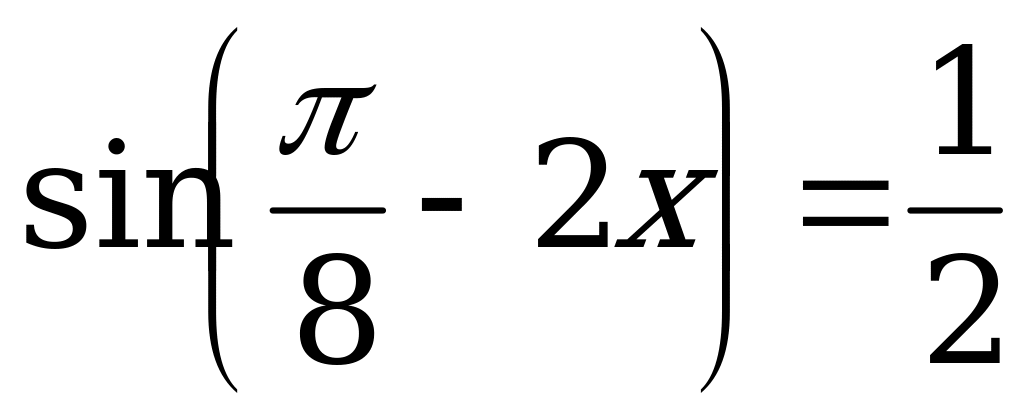 .
.
Так как синус нечётная функция, то
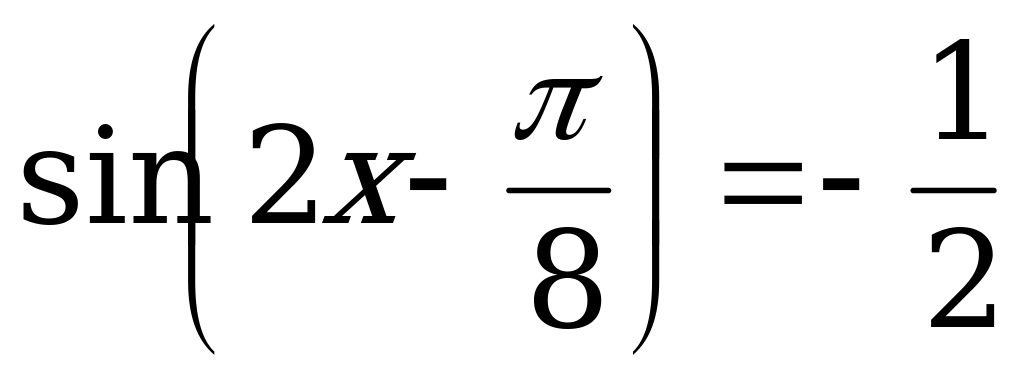 .
.
По формуле (1)
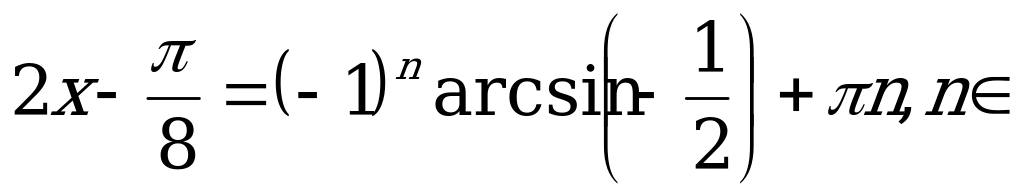 Z.
Z.
Так как 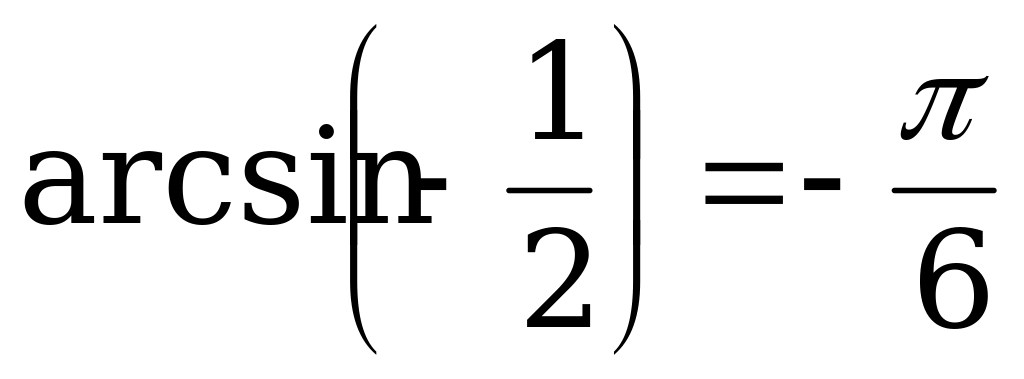 , то
, то
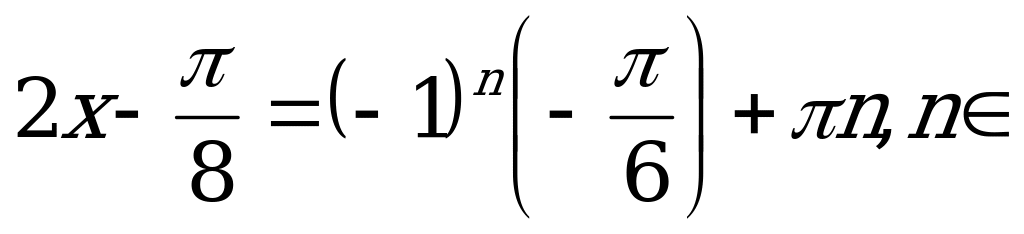 Z.
Z.
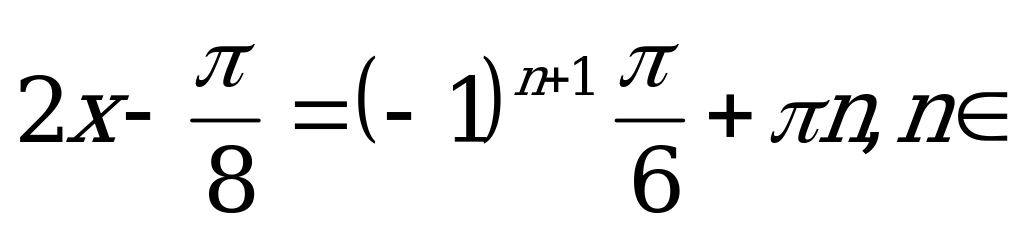 Z.
Z.
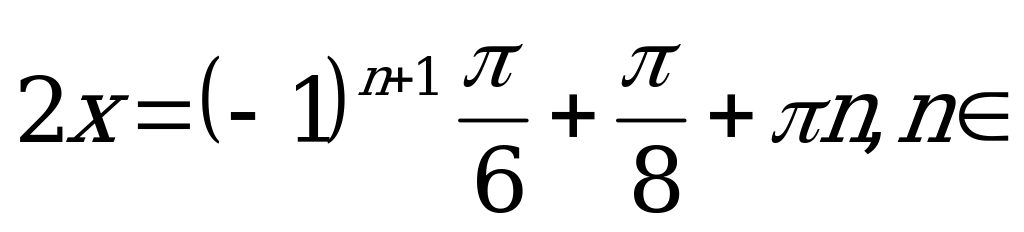 Z.
Z.
Разделим обе части равенства на 2 и запишем ответ:
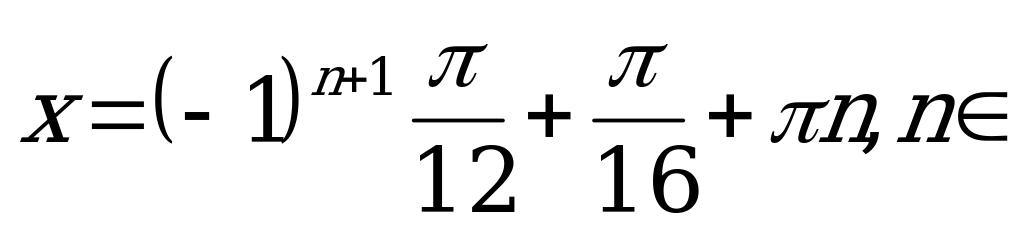 Z.
Z.
Пример 6. Решить уравнения:
а) 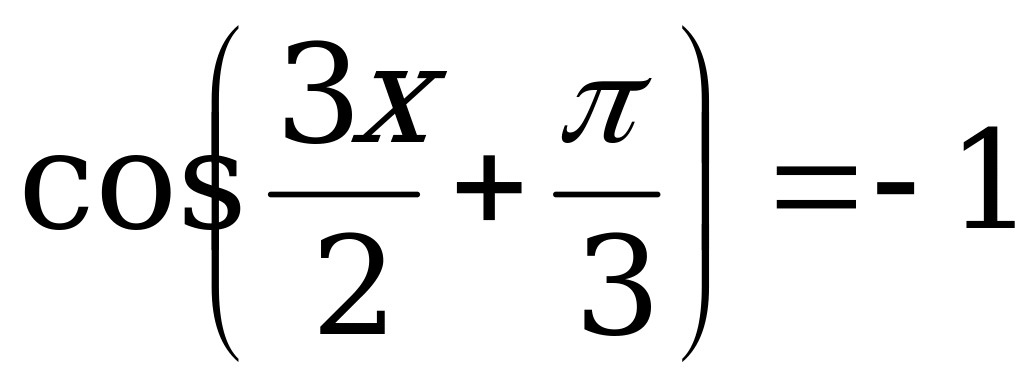 ; б)
; б) 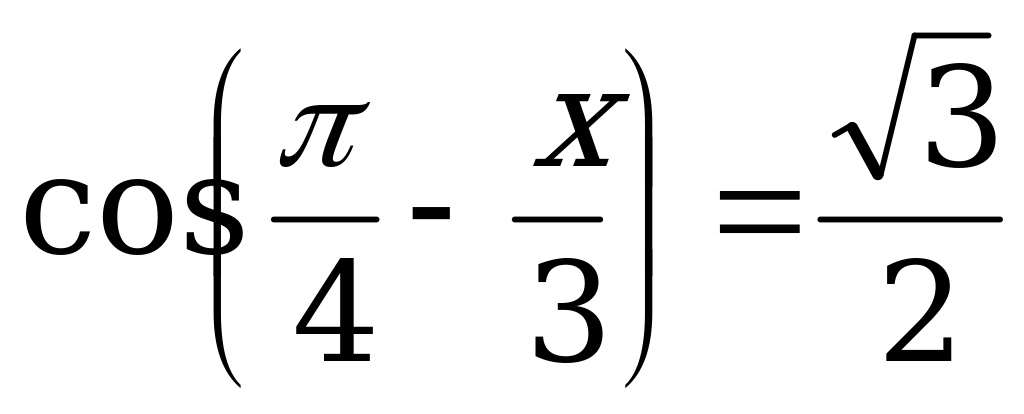 .
.
Решение. а) Решим уравнение 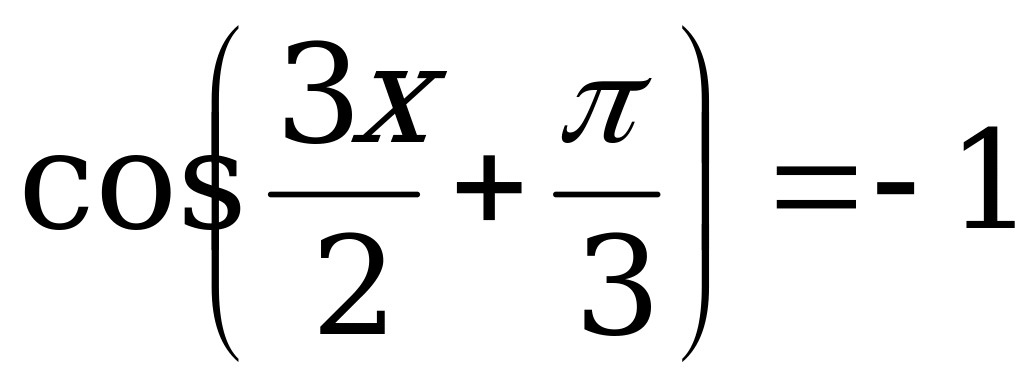 .
.
По формуле (10)

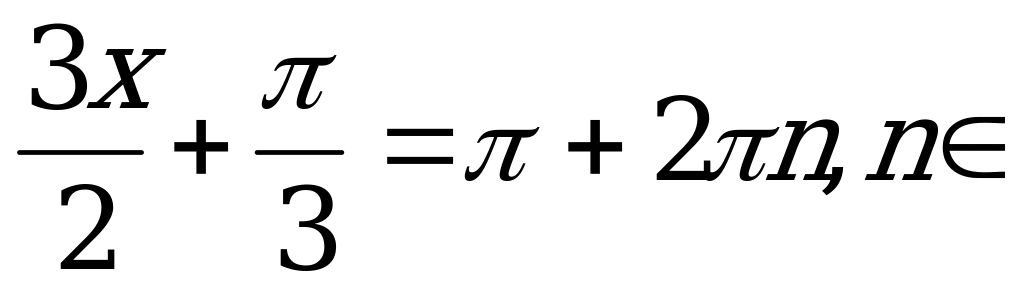 Z.
Z.
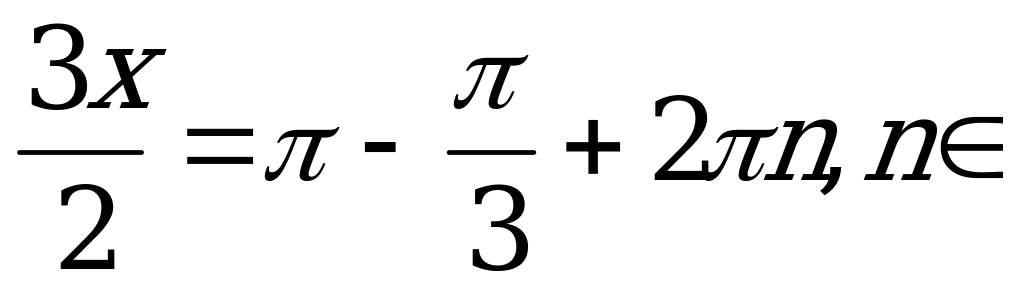 Z.
Z.
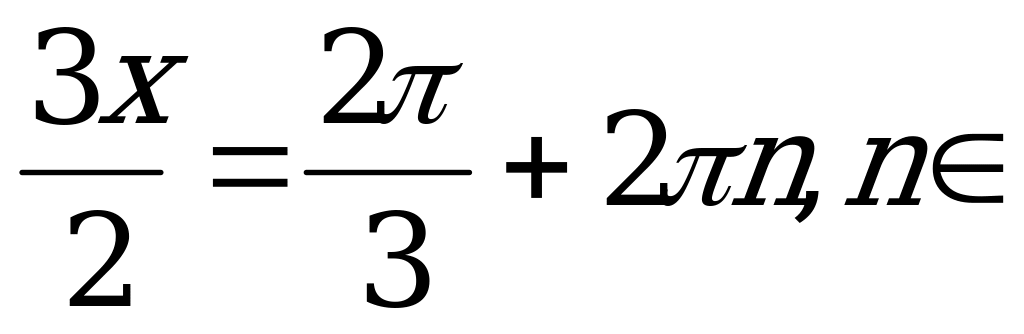 Z.
Z.
Умножим обе части равенства на 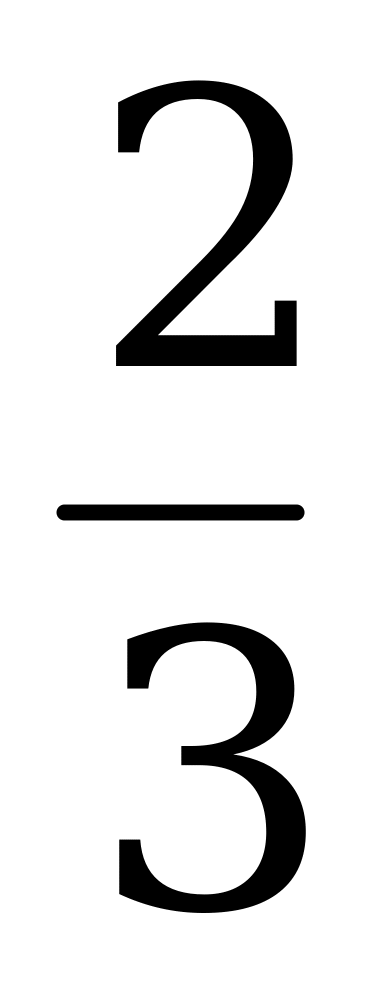 и запишем ответ.
и запишем ответ.
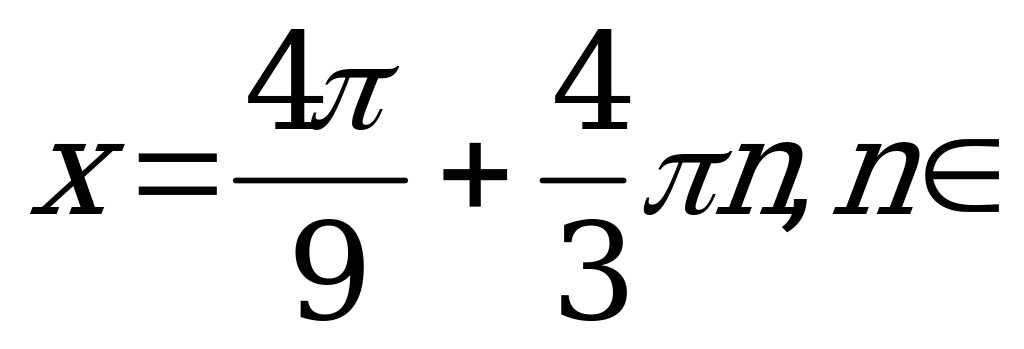 Z.
Z.
б) Решим уравнение 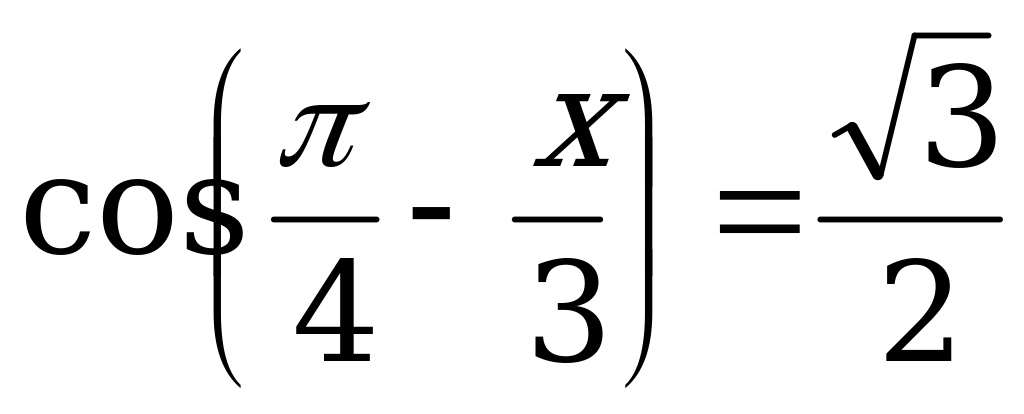 .
.
Косинус чётная функция. Значит
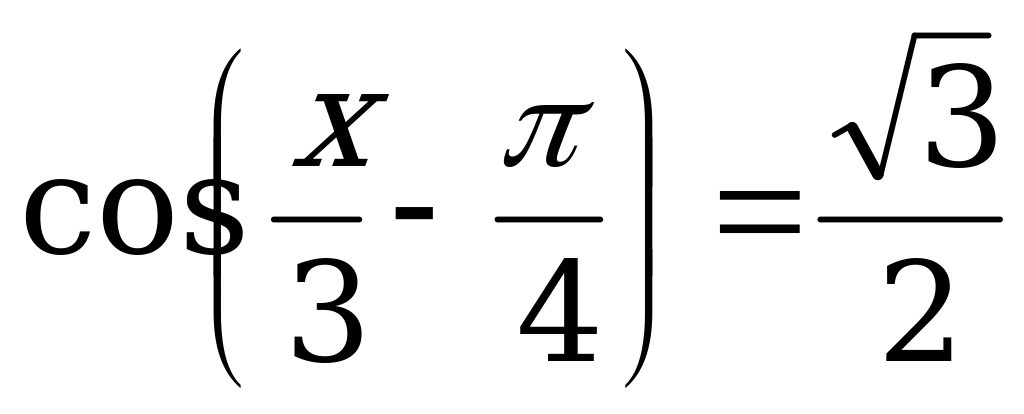 .
.
По формуле (2)
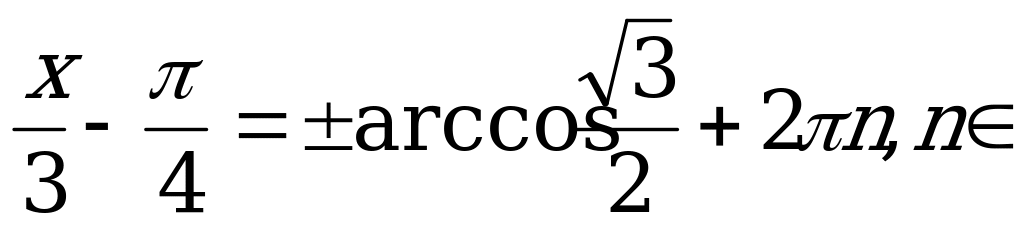 Z.
Z.
Так как 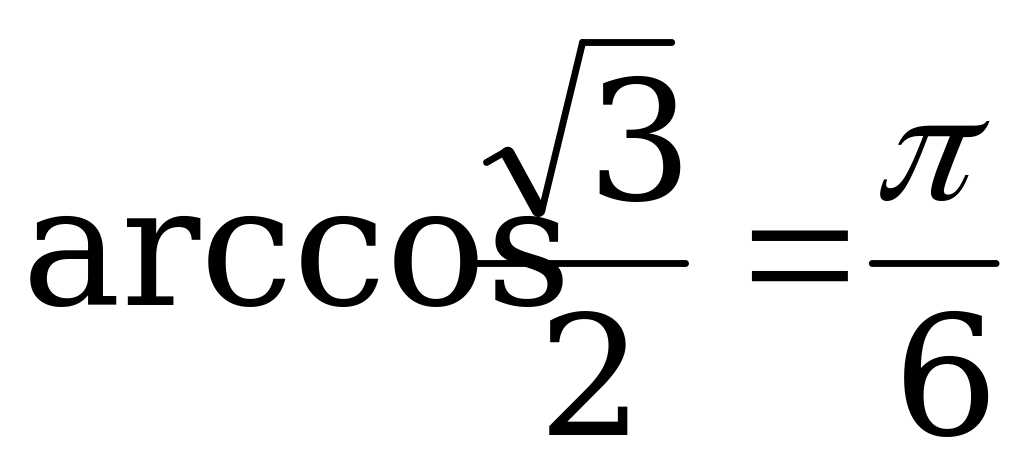 , имеем
, имеем
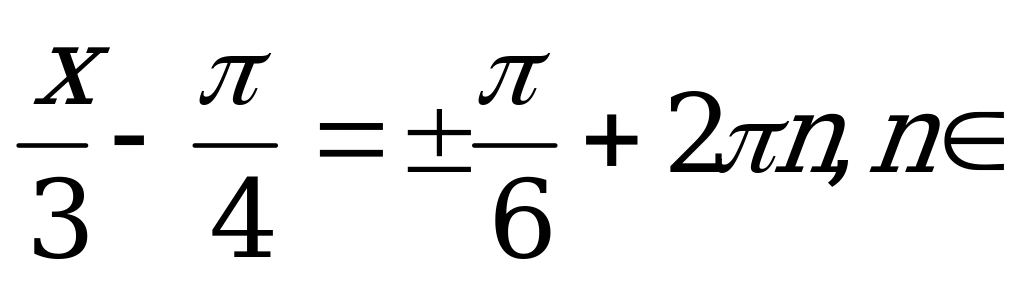 Z.
Z.
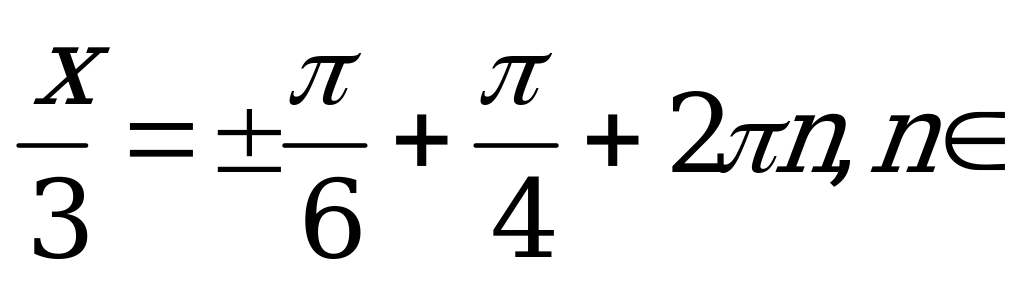 Z.
Z.
Умножим обе части равенства на 3 и запишем ответ:
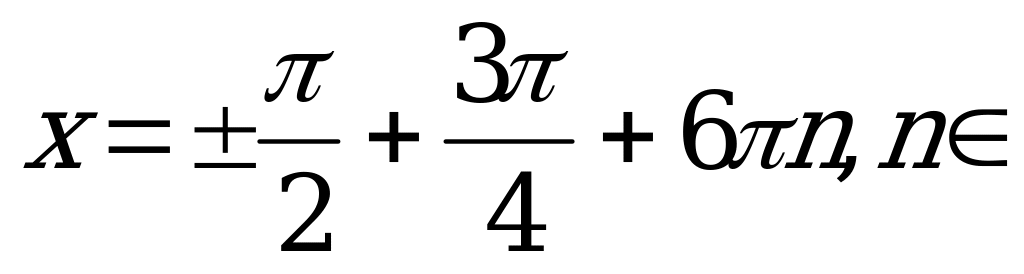 Z.
Z.
Пример 7. Решить уравнения:
а) 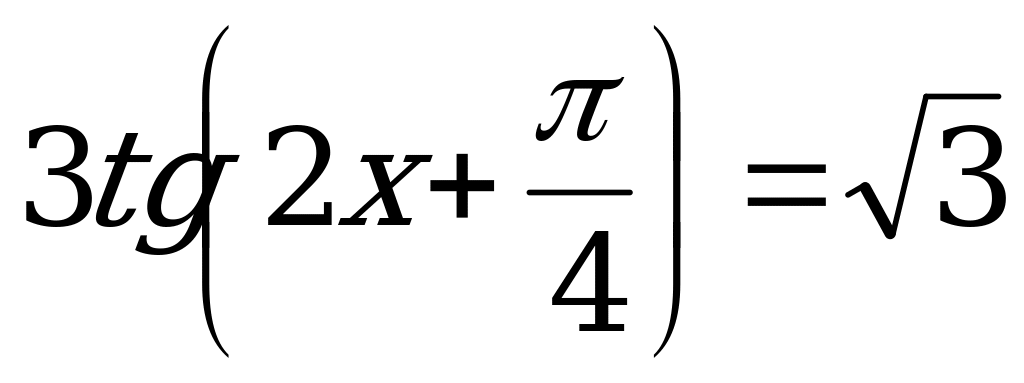 ; б)
; б) 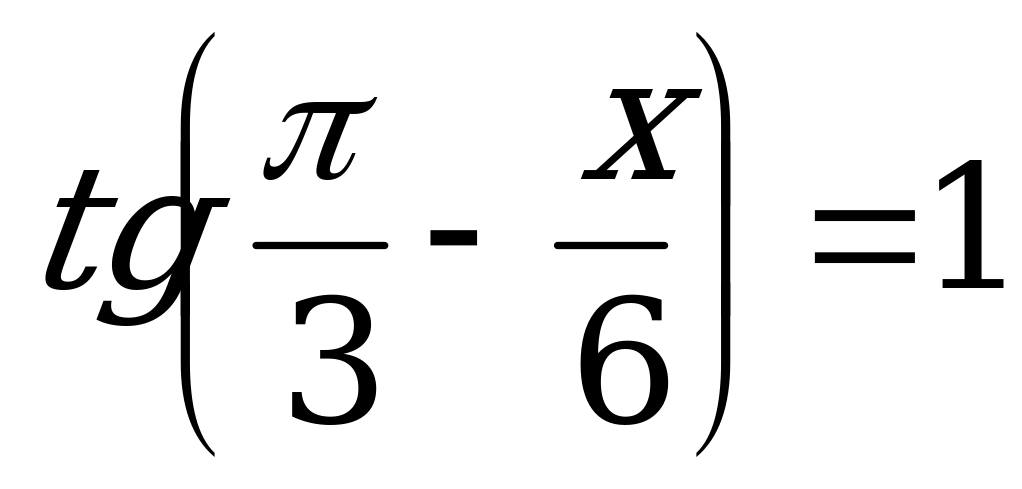 .
.
Решение. а) Решим уравнение 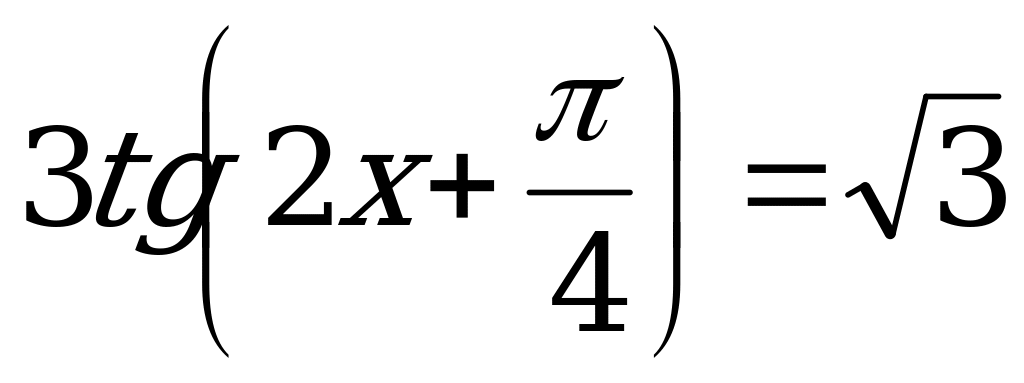 .
.
Данное уравнение разделим на 3.
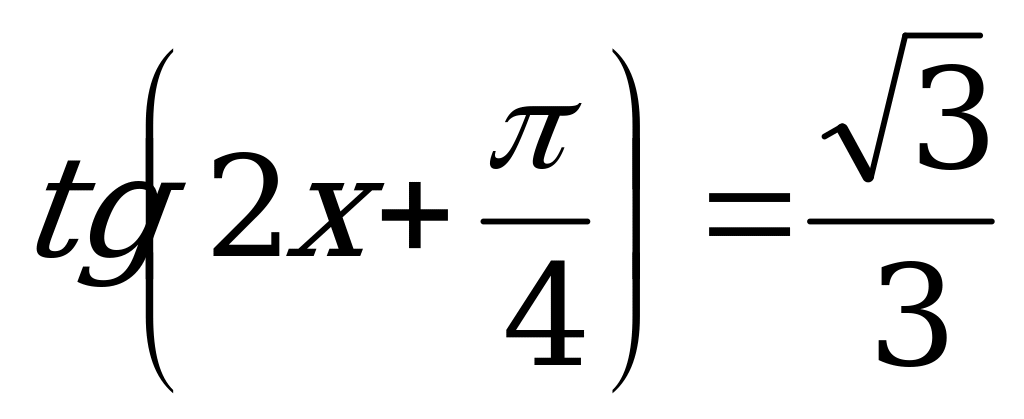 .
.
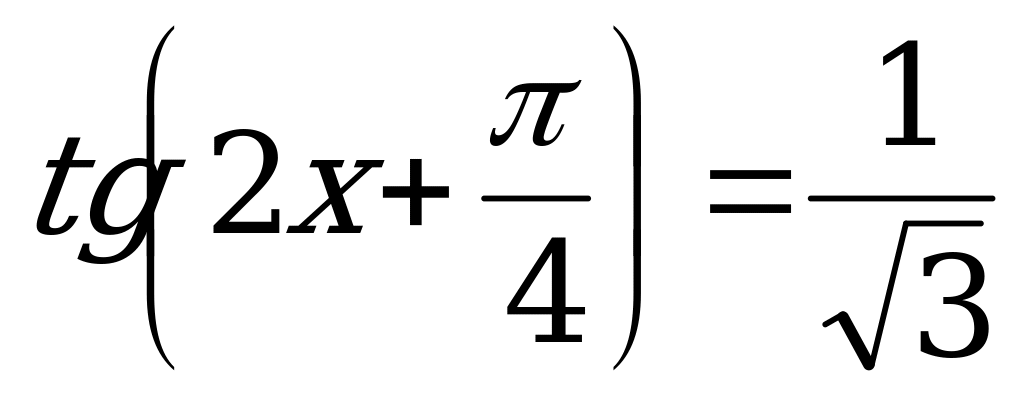 .
.
По формуле (3):
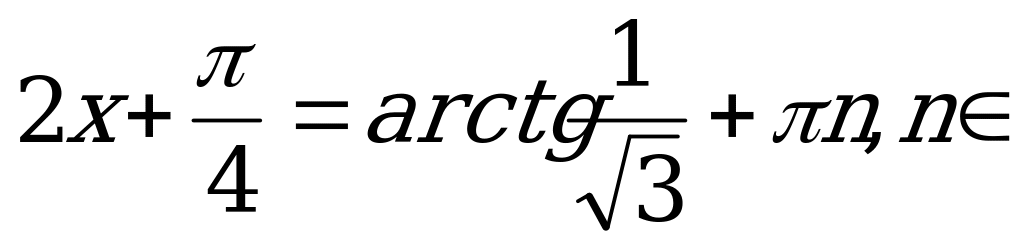 Z.
Z.
Так как 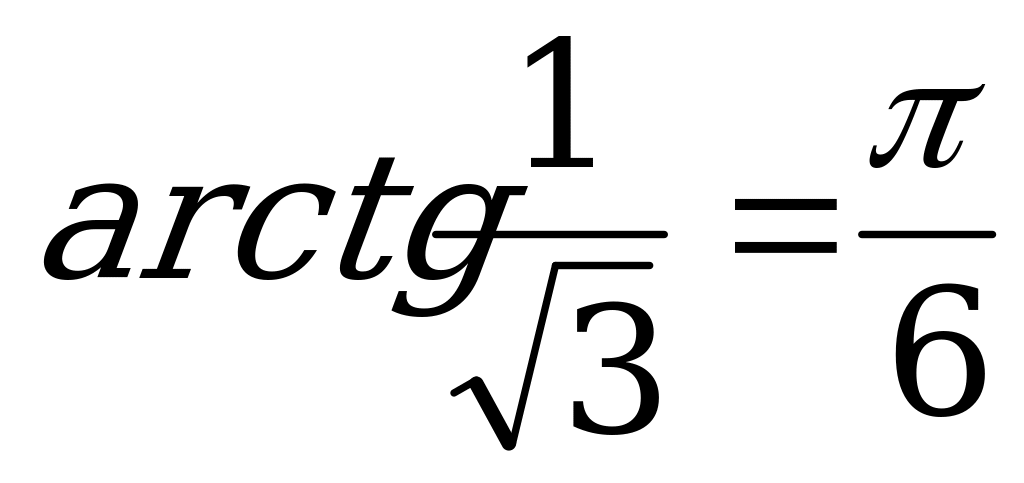 , то
, то
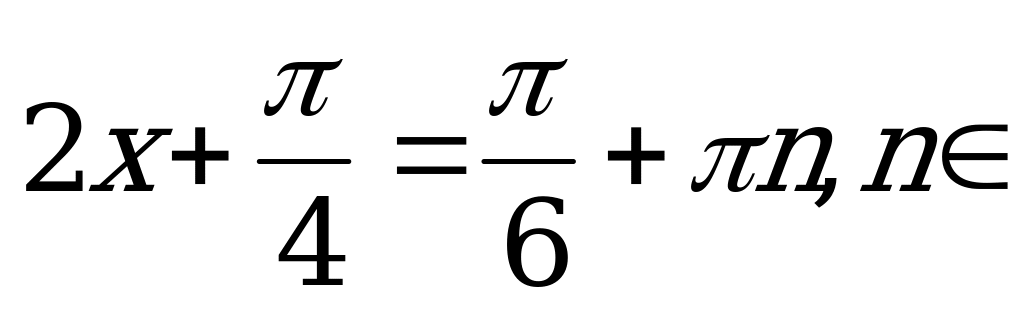 Z.
Z.
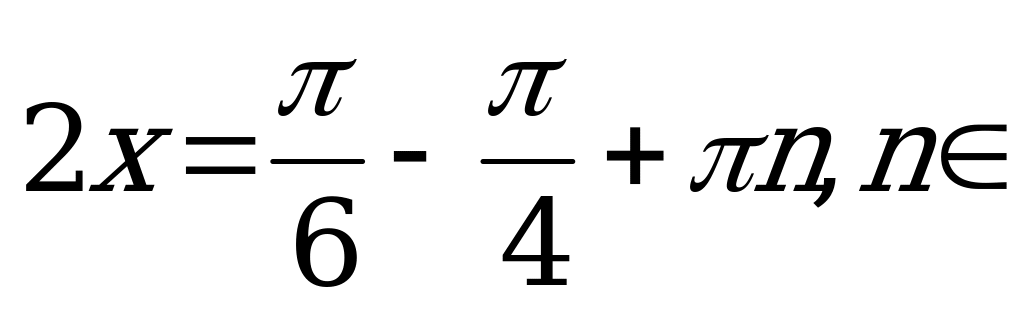 Z.
Z.
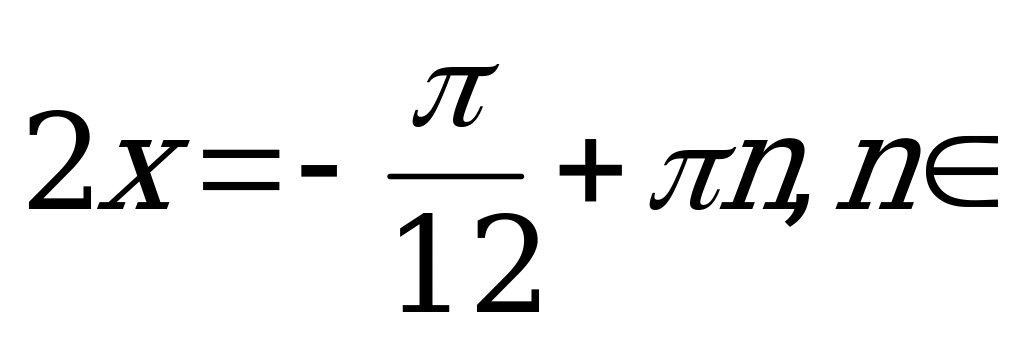 Z.
Z.
Разделим полученное равенство на 2 и запишем ответ.
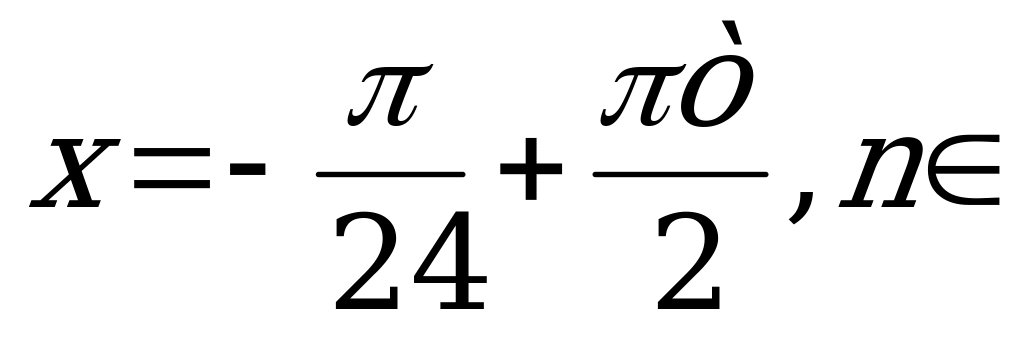 Z.
Z.
б) Решим уравнение 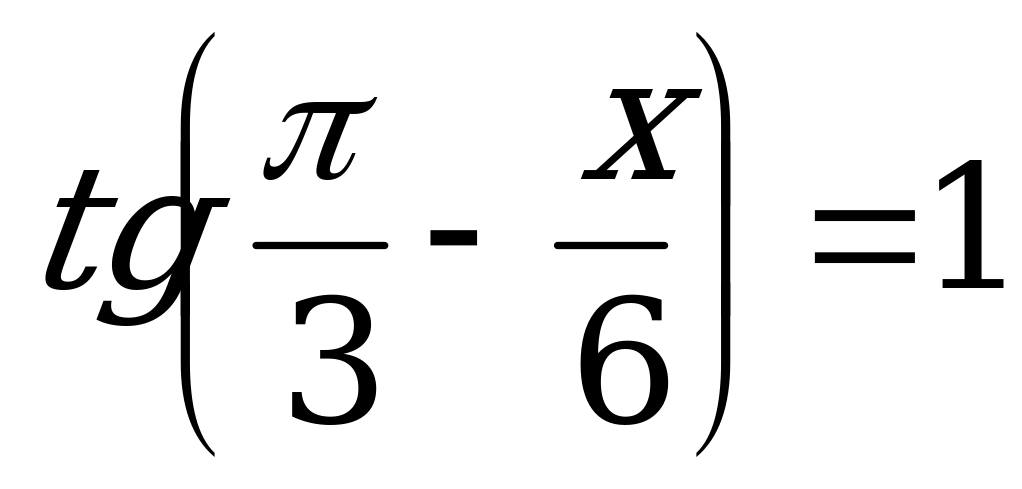 .
.
Функция тангенс нечётная. Поэтому:
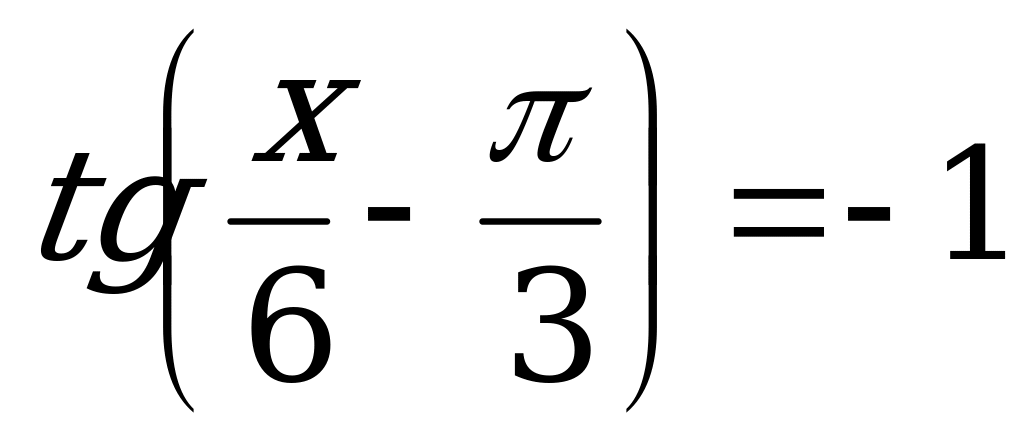 .
.
По формуле (3):
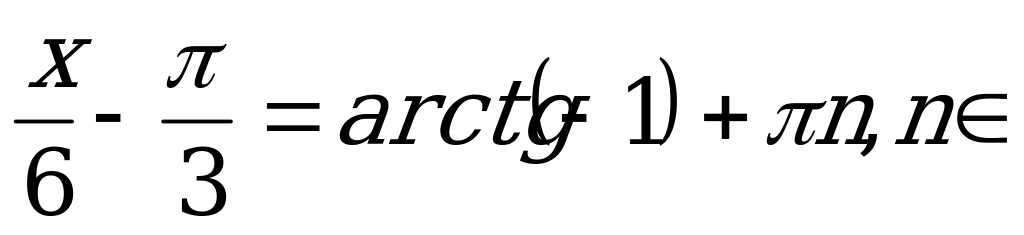 Z.
Z.
Так как 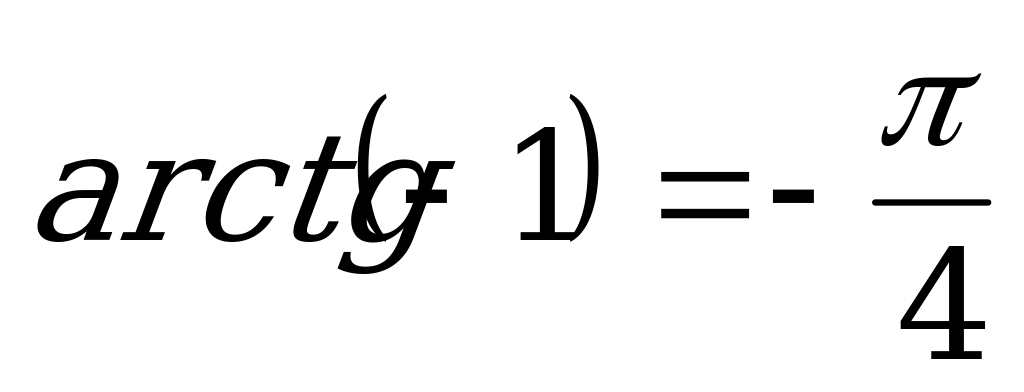 , то
, то
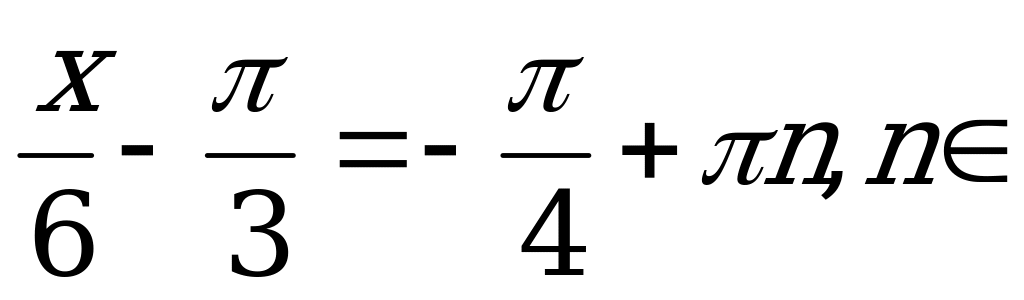 Z.
Z.
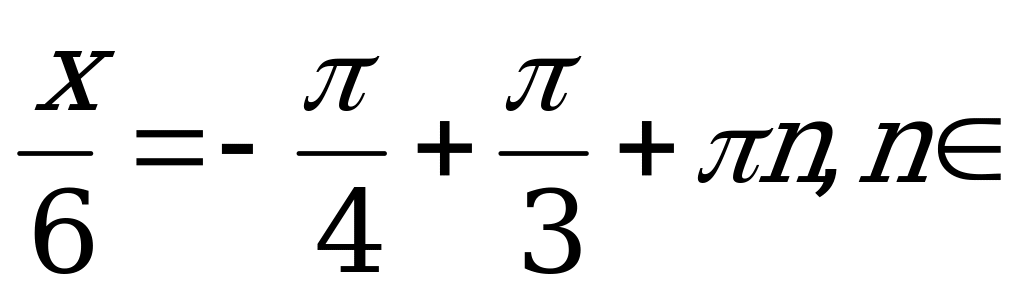 Z.
Z.
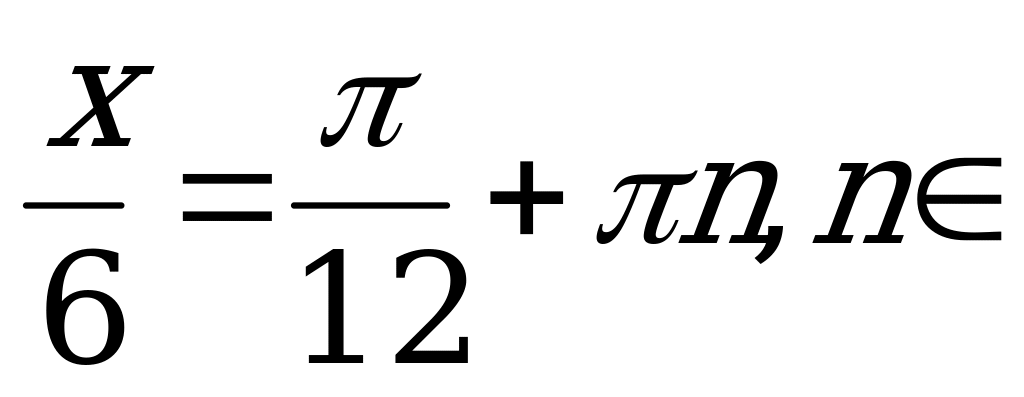 Z.
Z.
Умножим полученное равенство на 6 и запишем ответ.
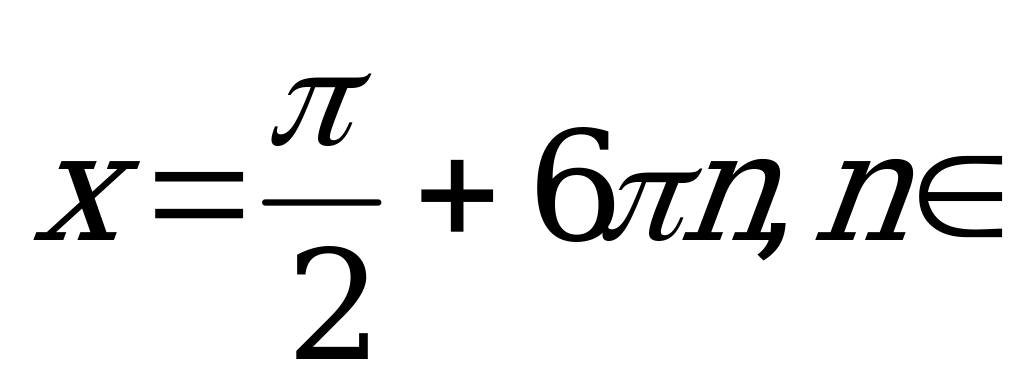 Z.
Z.
Пример 8. Решить уравнения:
а) 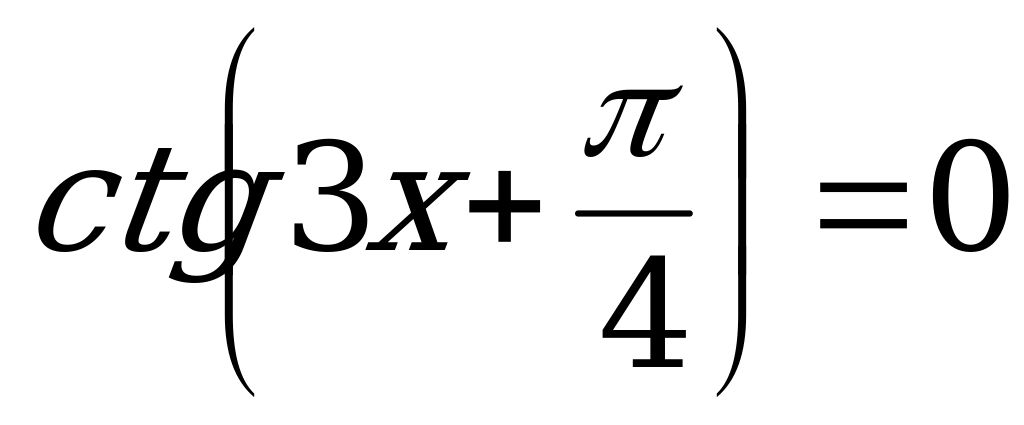 ; б)
; б) 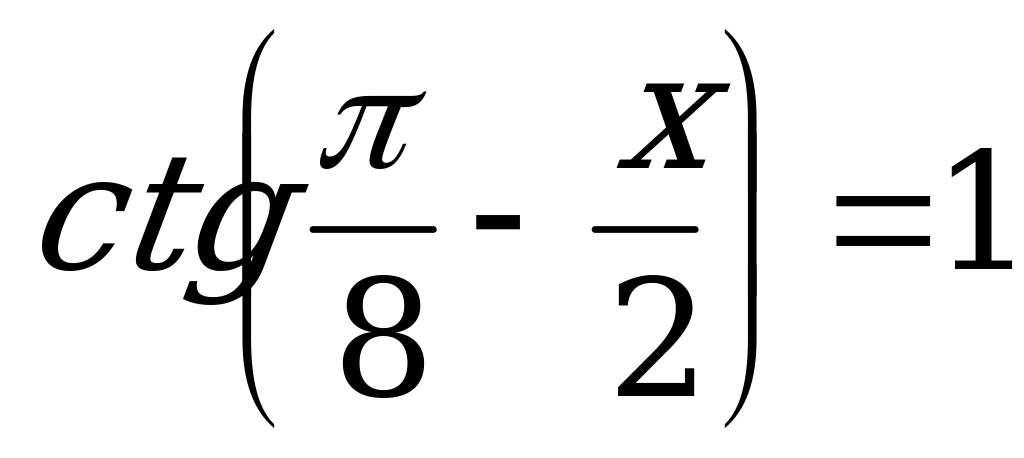 .
.
Решение. а) Решим уравнение 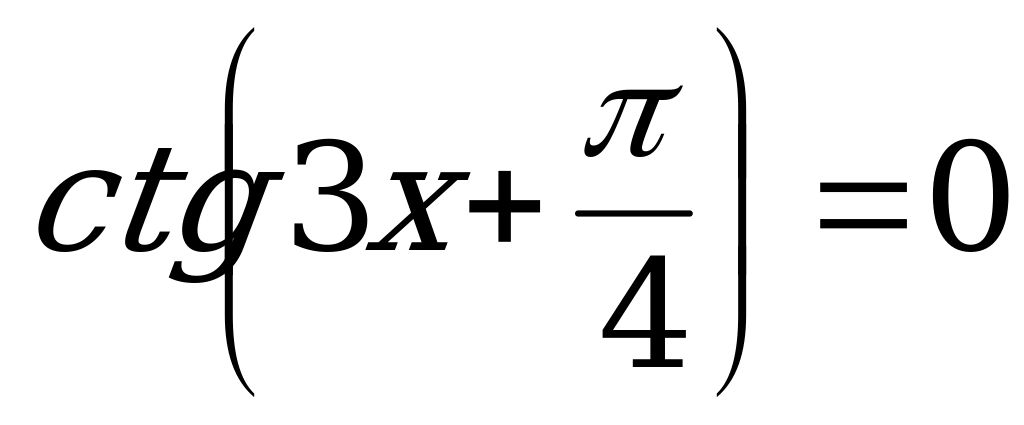 .
.
По формуле (12)
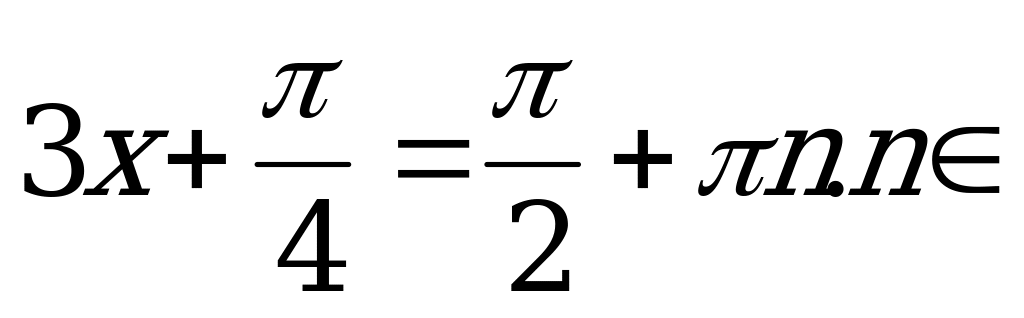 Z.
Z.
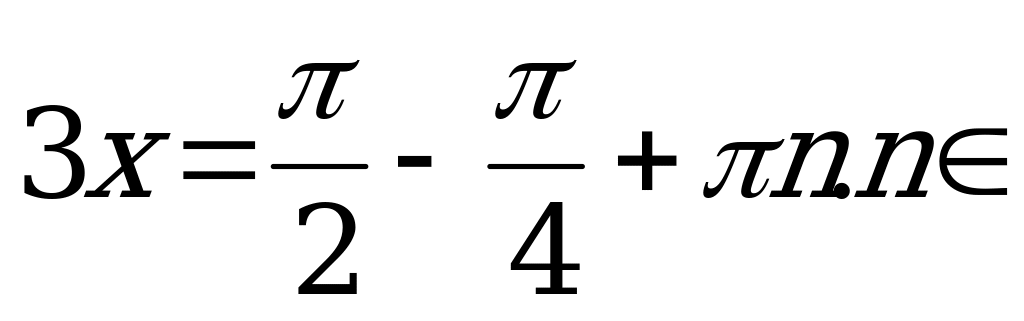 Z.
Z.
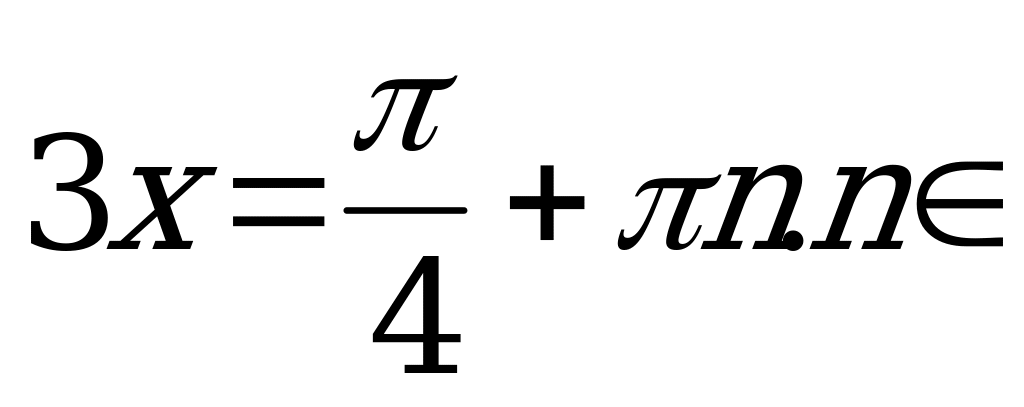 Z.
Z.
Разделим полученное равенство на 3 и запишем ответ.
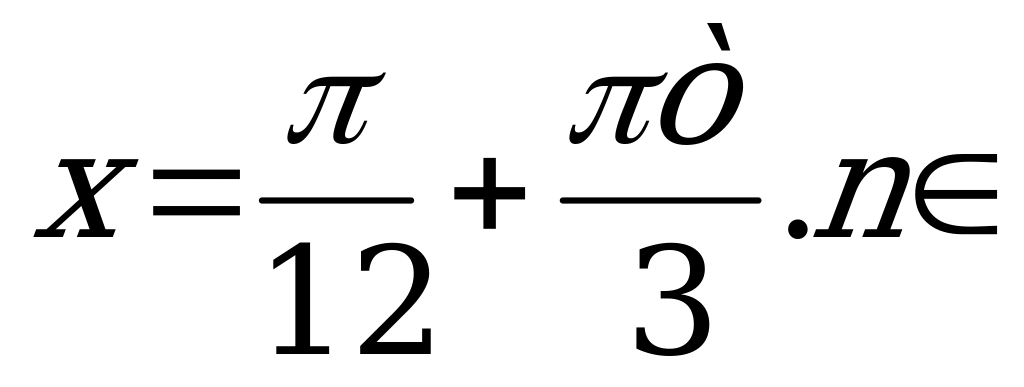 Z.
Z.
б) Решим уравнение 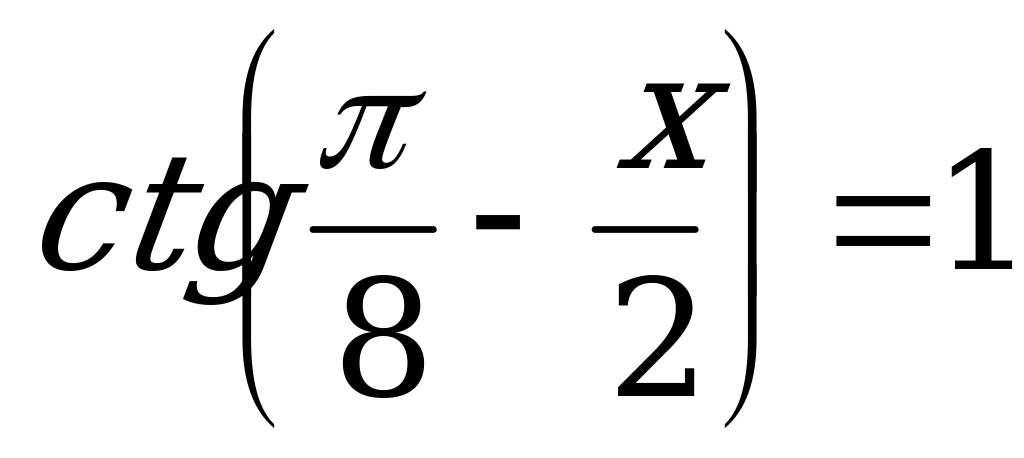 .
.
Функция котангенс нечётная. Поэтому:
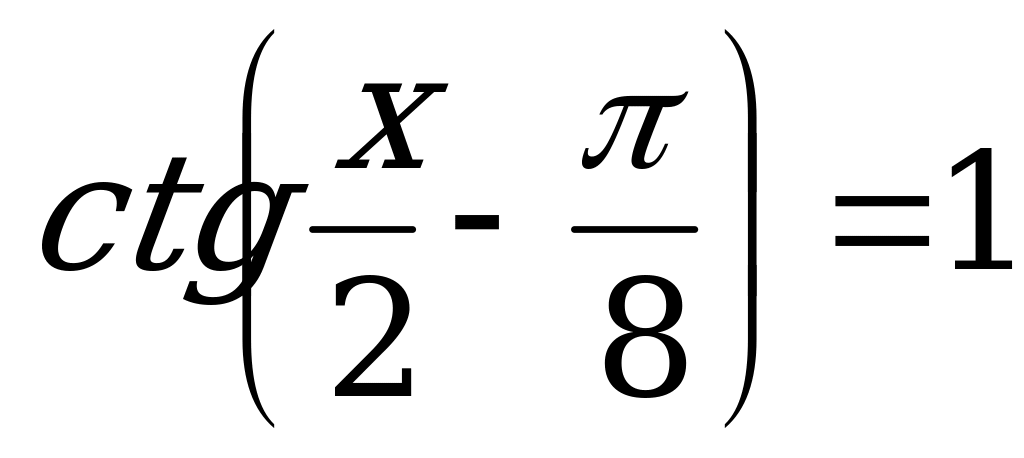 .
.
По формуле (4):
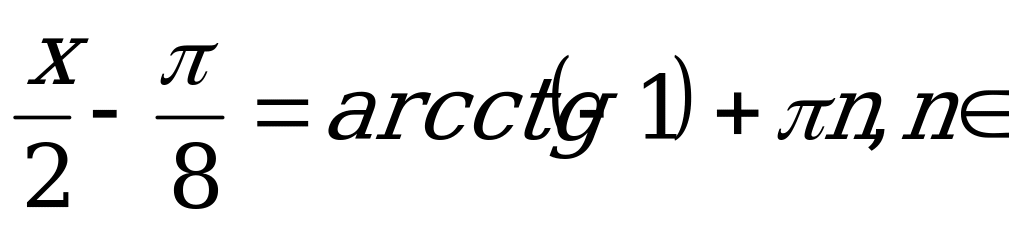 Z.
Z.
 Так как
Так как 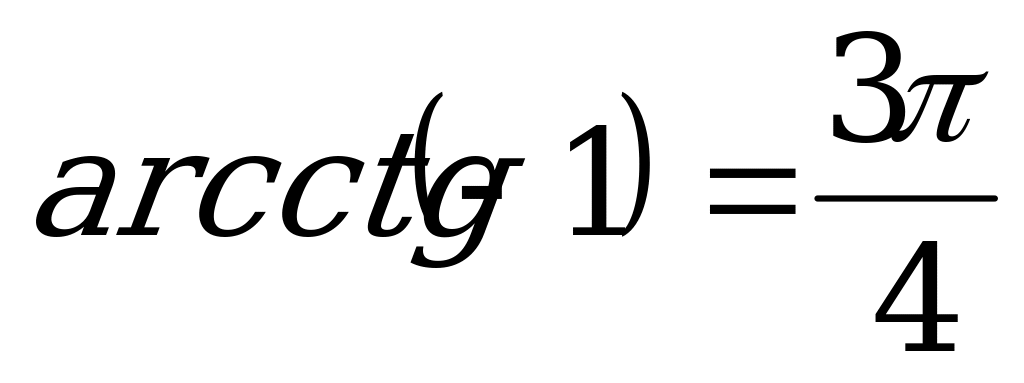 , то
, то
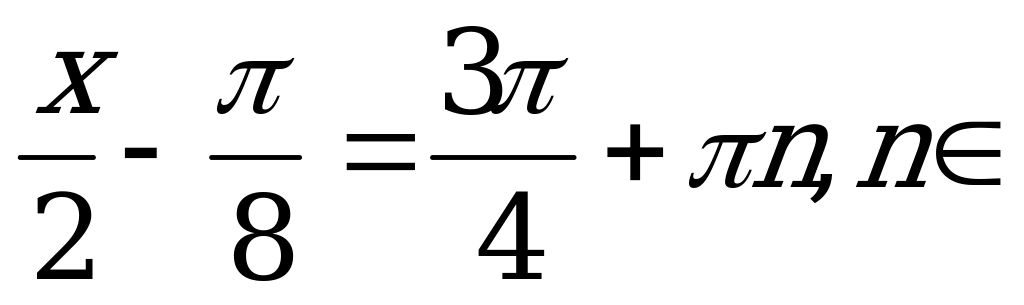 Z.
Z.
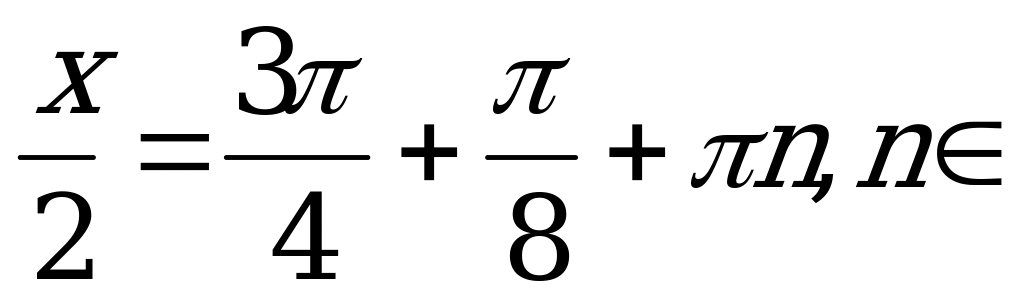 Z.
Z.
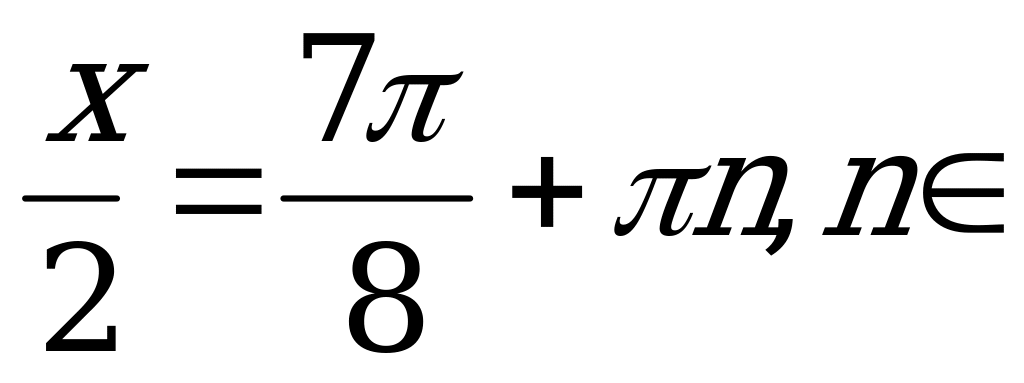 Z.
Z.
Умножим обе части равенства на 2 и запишем ответ.

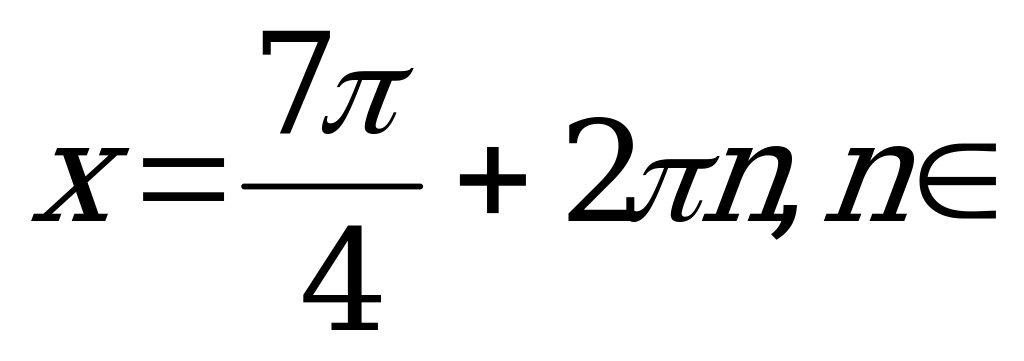 Z.
Z.
 Самостоятельная работа №7.
Самостоятельная работа №7.
Вариант №1.
Решить уравнения (1-16).
1. 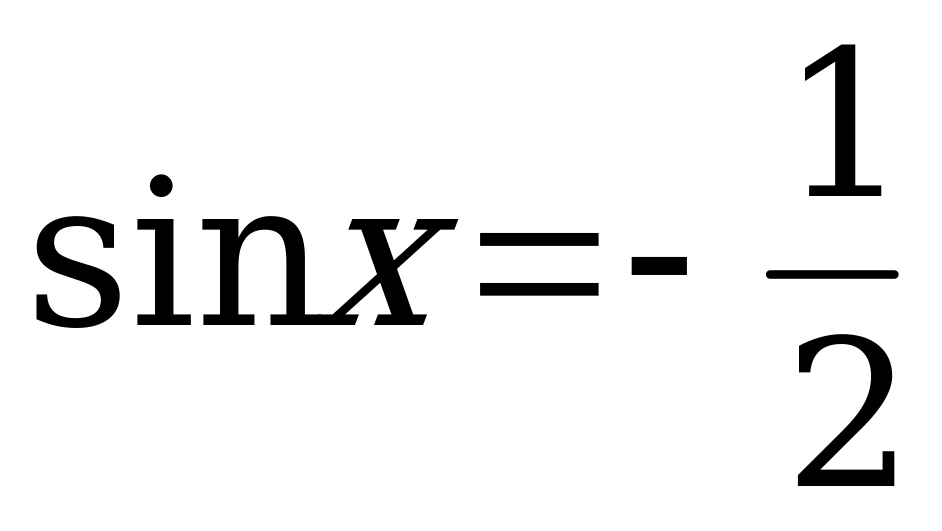 ; 9.
; 9. 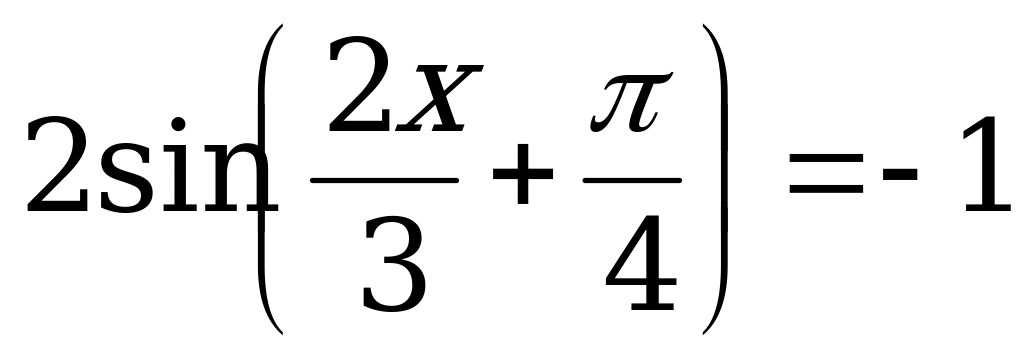 ;
;
2. 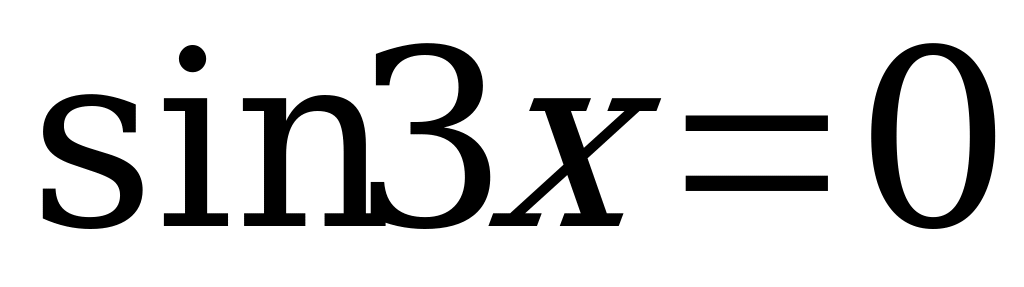 ; 10.
; 10. 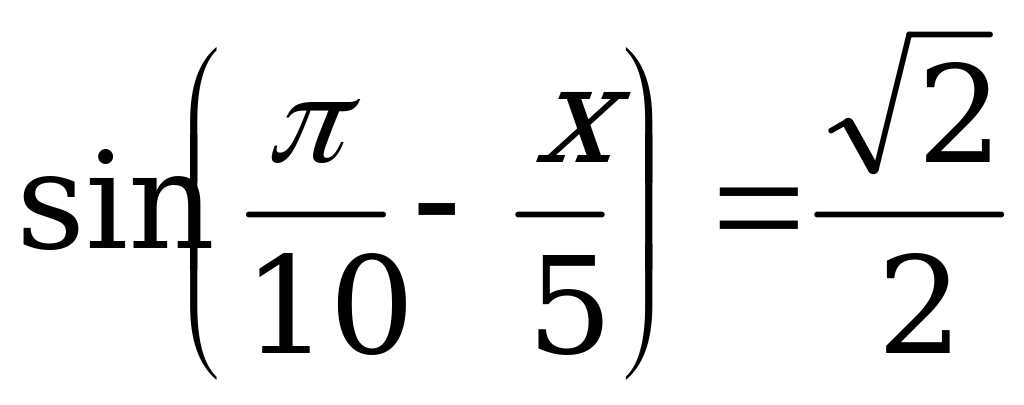 ;
;
3. 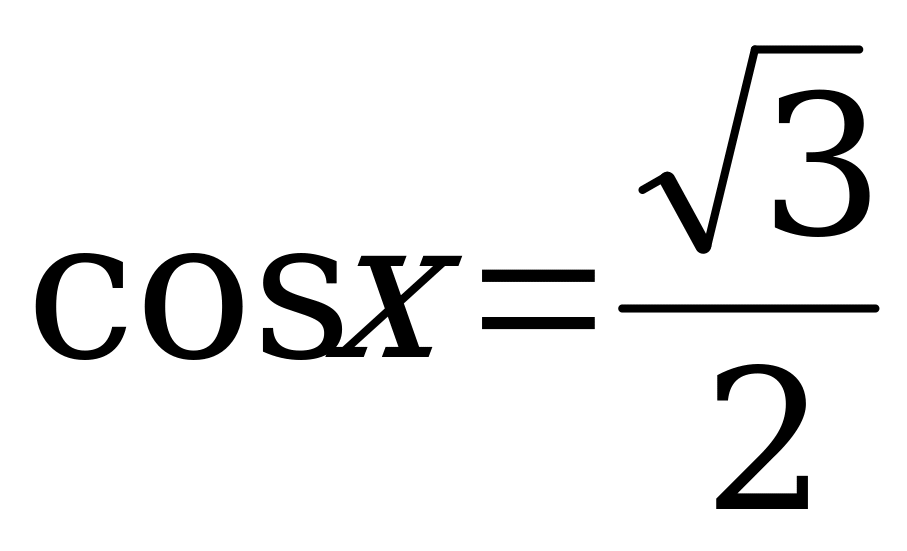 ; 11.
; 11. 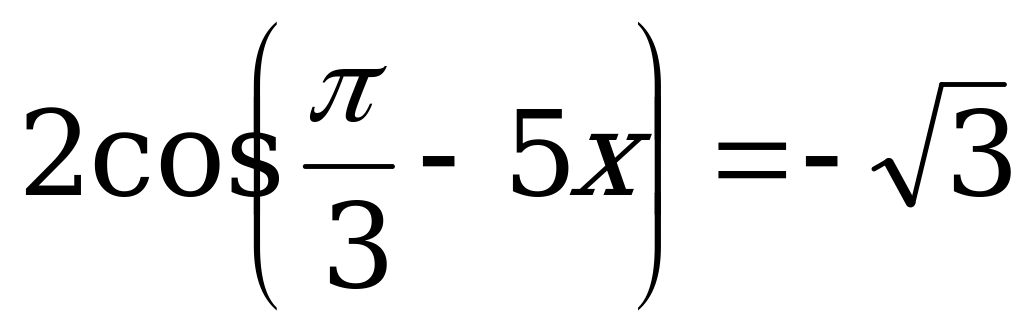 ;
;
4. 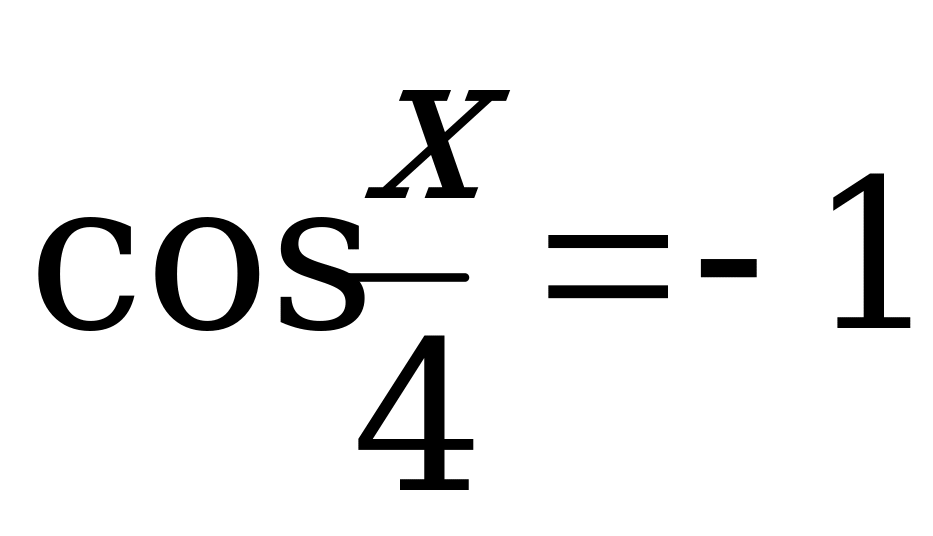 ; 12.
; 12. 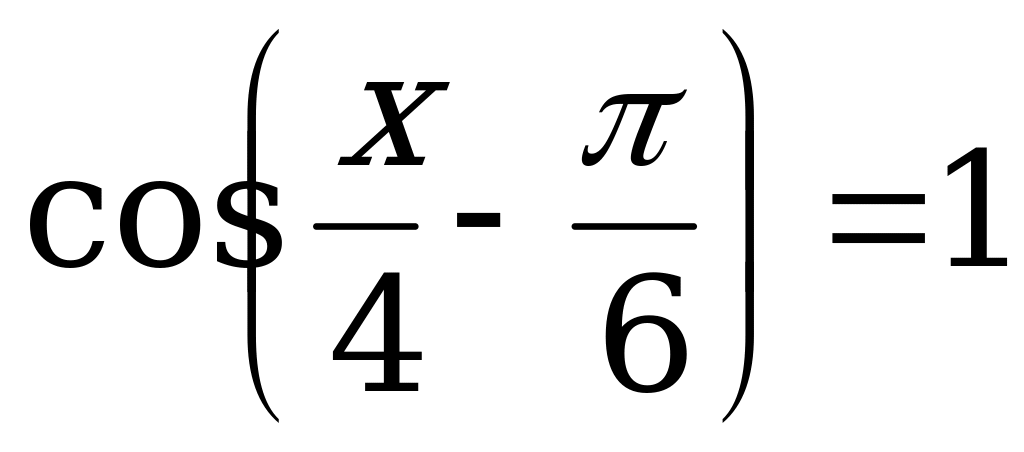 ;
;
5.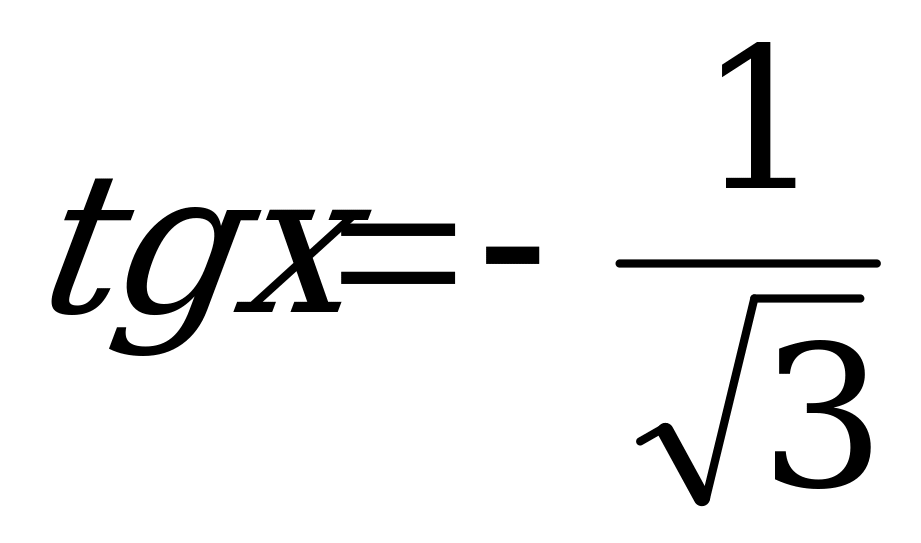 ; 13.
; 13. 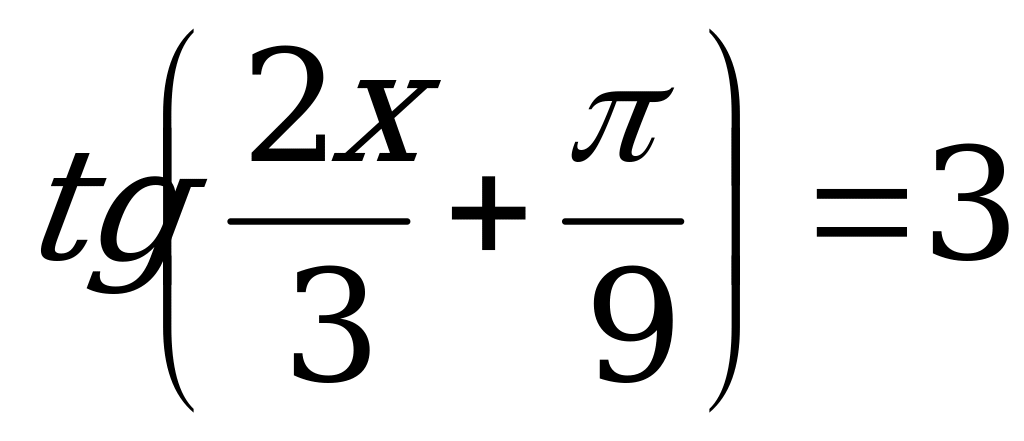 ;
;
6.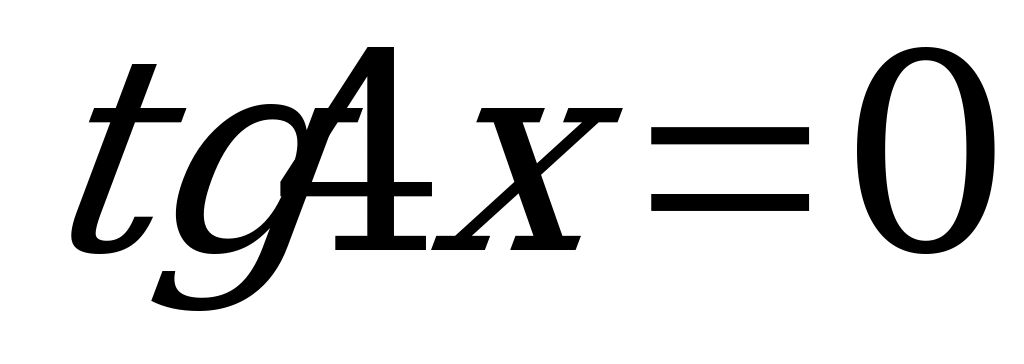 ; 14.
; 14. 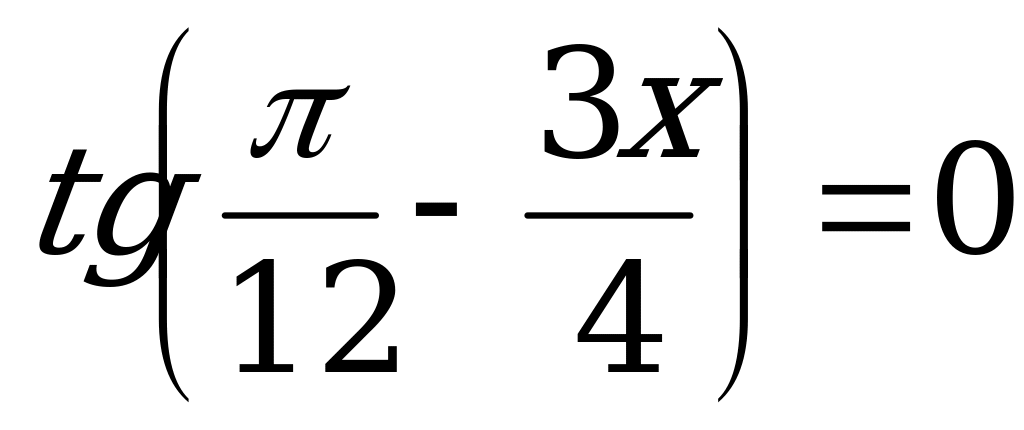 ;
;
7.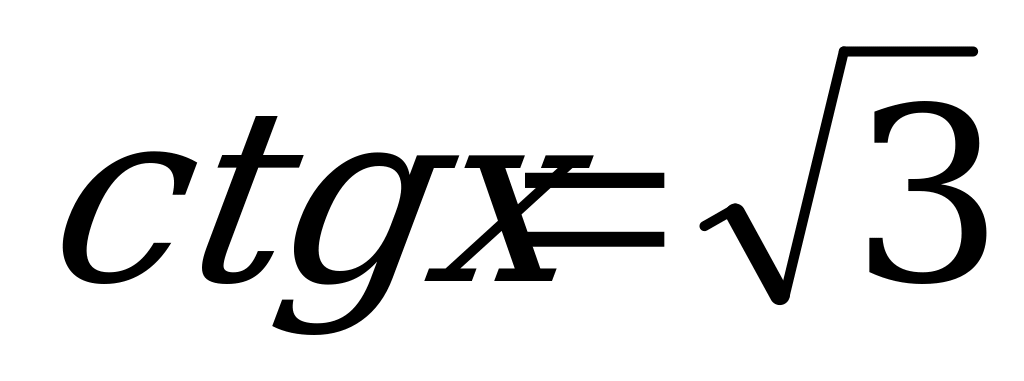 ; 15.
; 15. 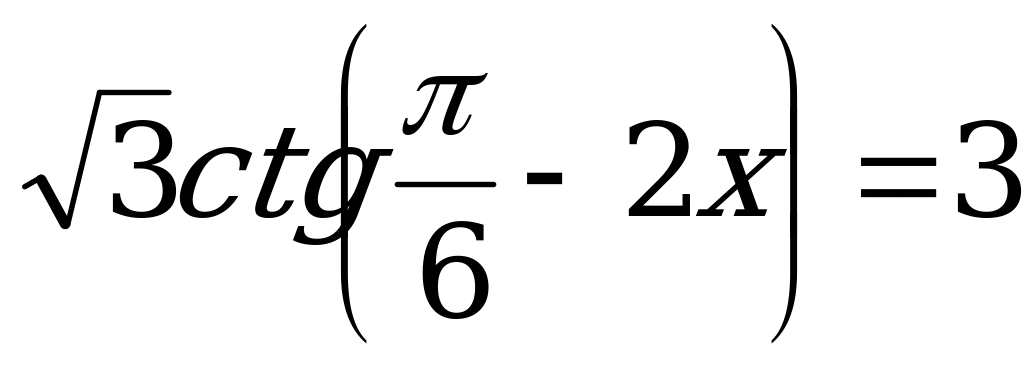 ;
;
8.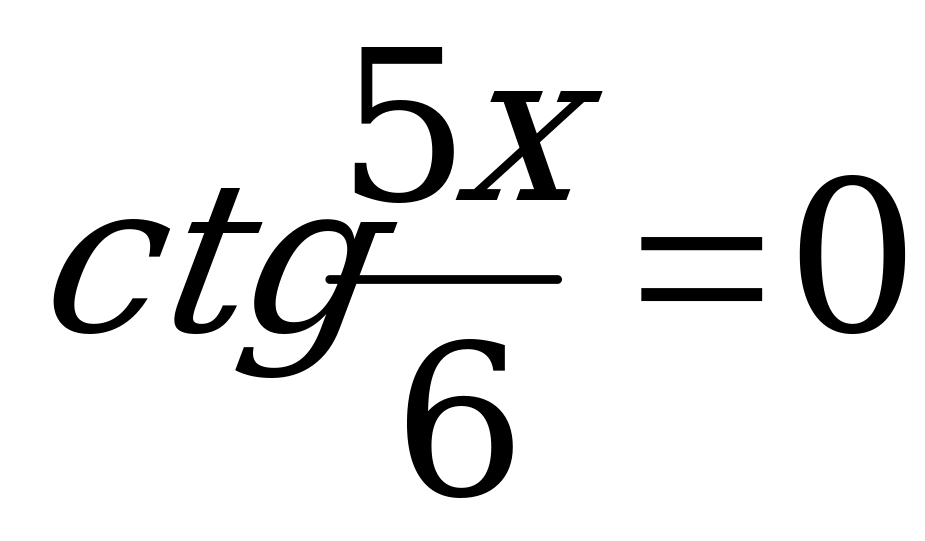 ; 16.
; 16. 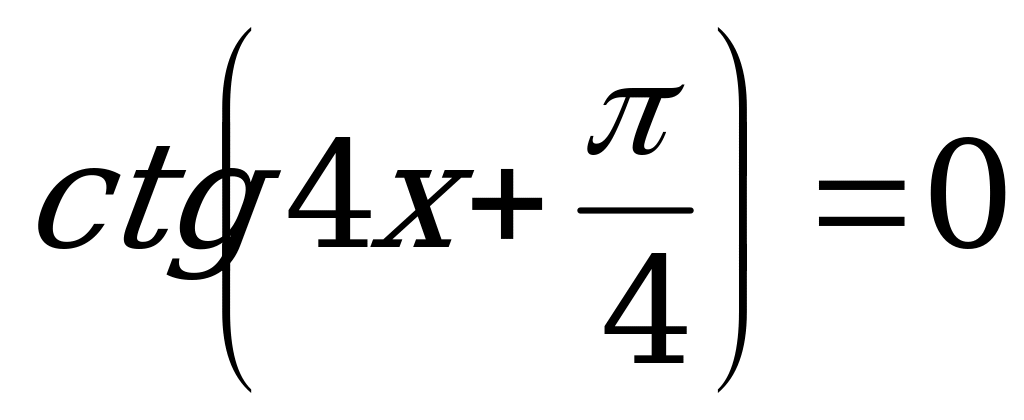 .
.
Вариант №2.
1. 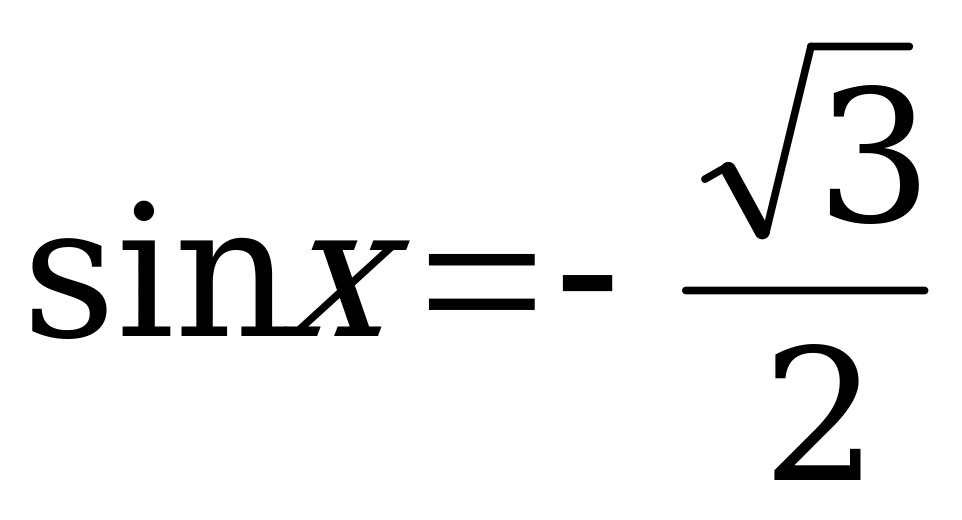 ; 9.
; 9. 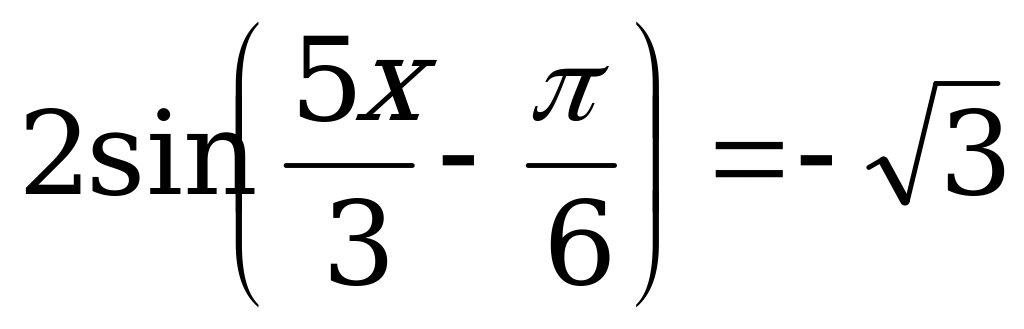 ;
;
2. 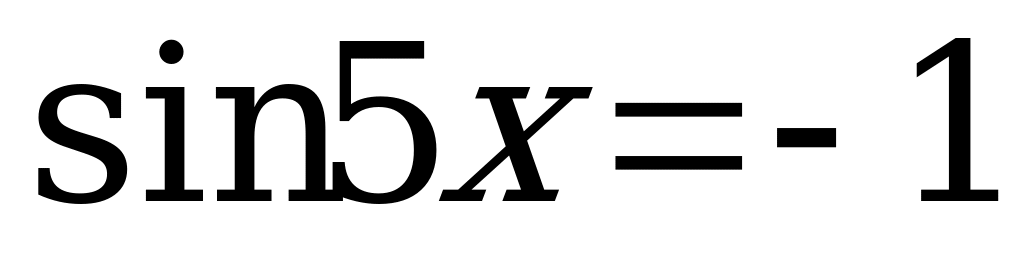 ; 10.
; 10. 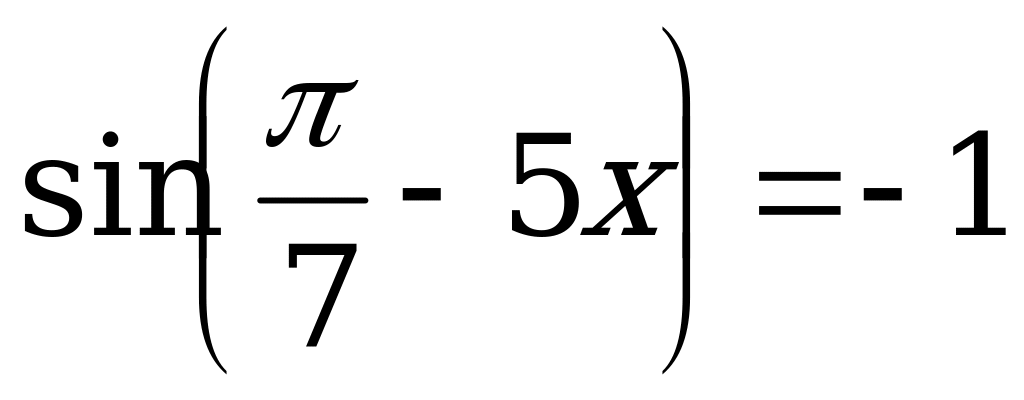 ;
;
3. 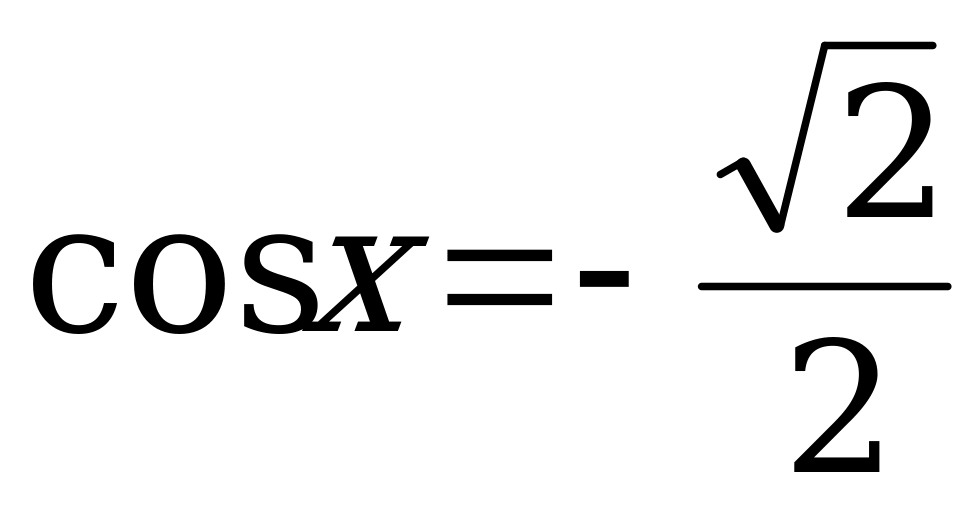 ; 11.
; 11. 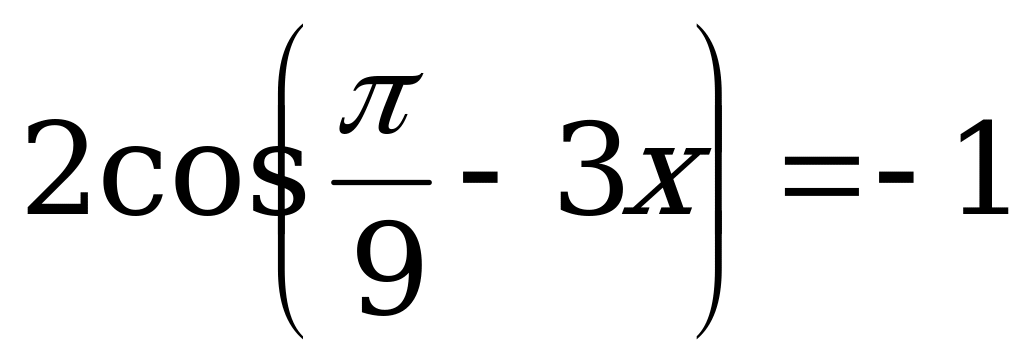 ;
;
4. 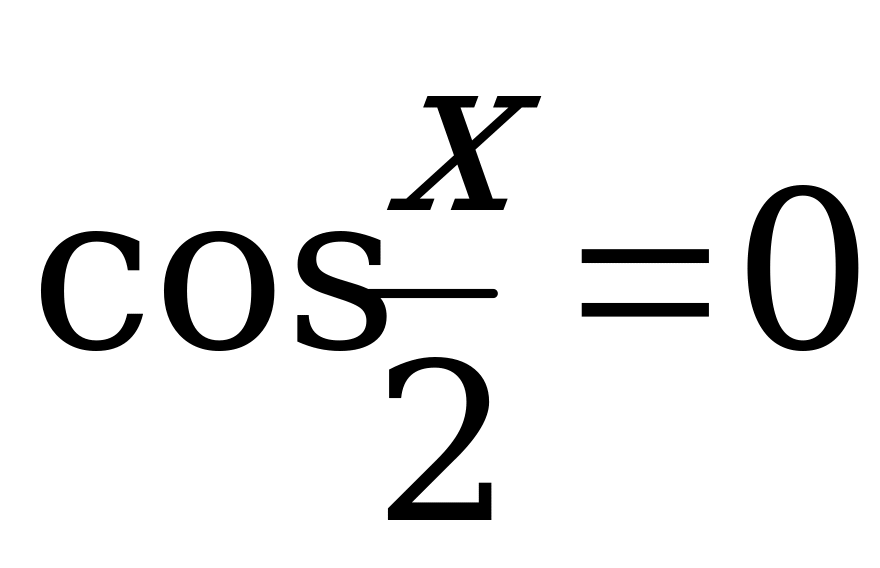 ; 12.
; 12. 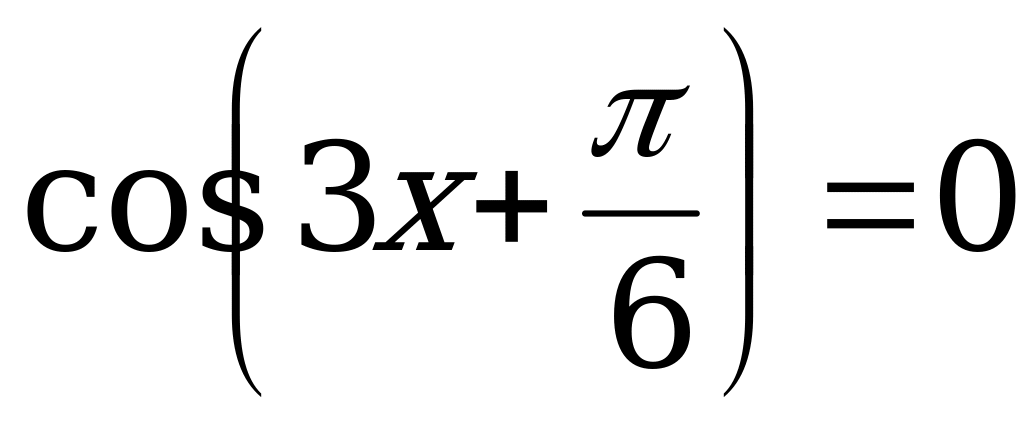 ;
;
5.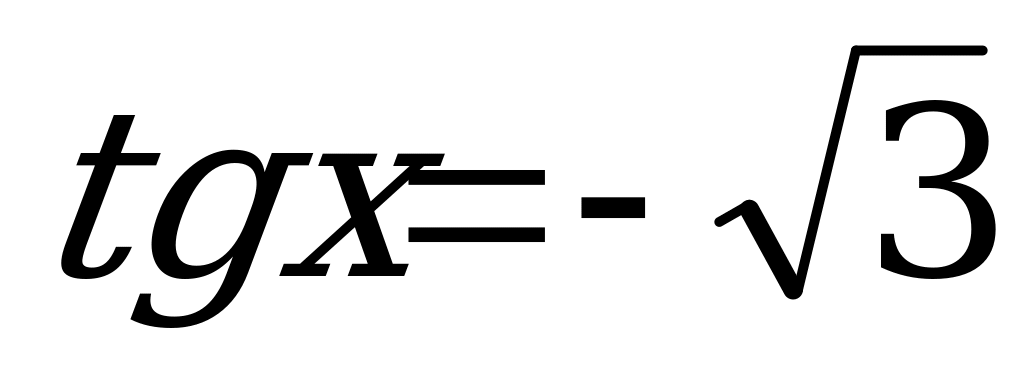 ; 13.
; 13. 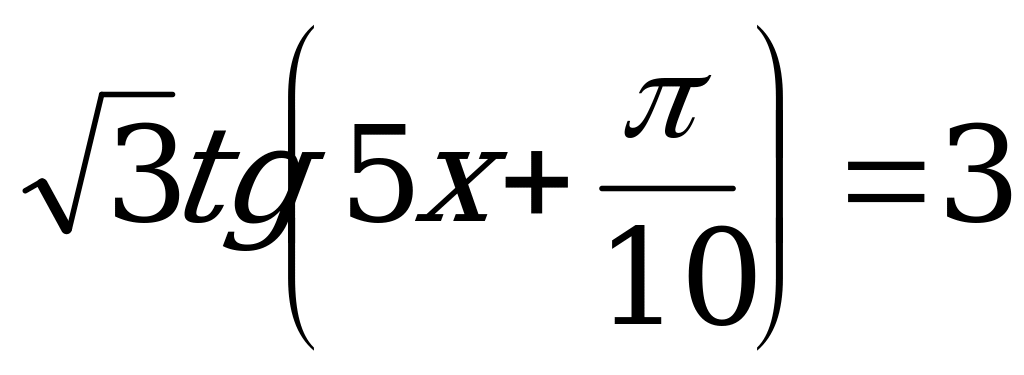 ;
;
6.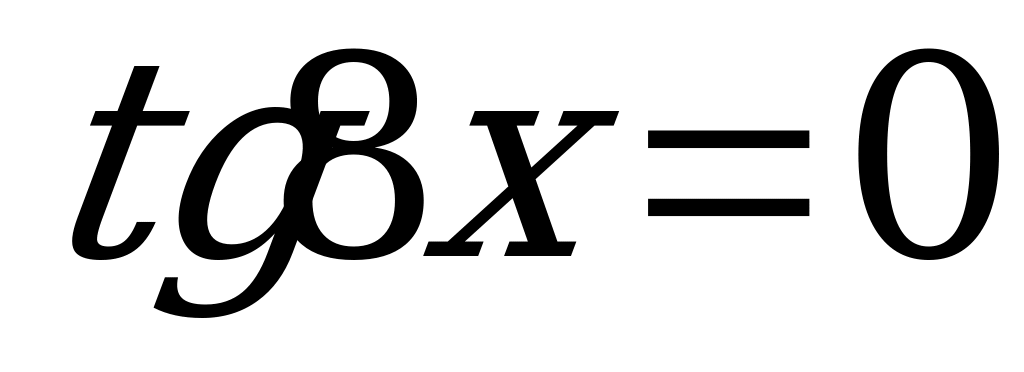 ; 14.
; 14. 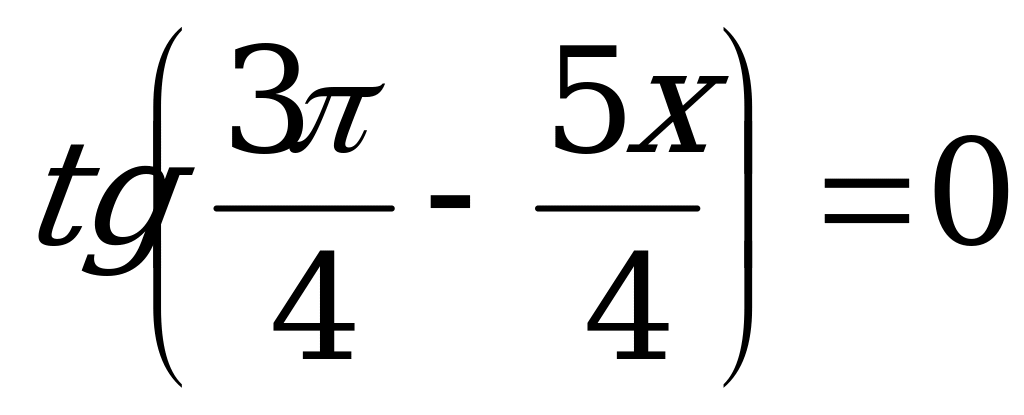 ;
;
7.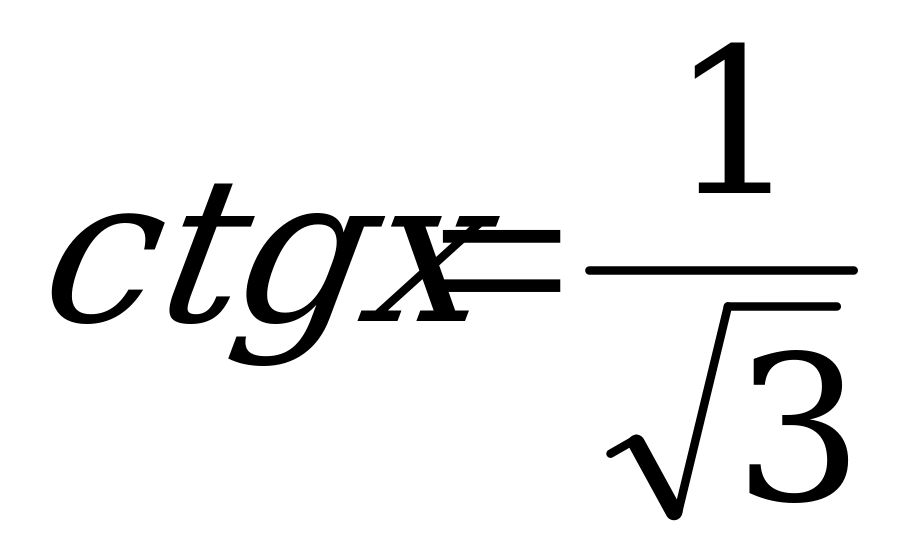 ; 15.
; 15. 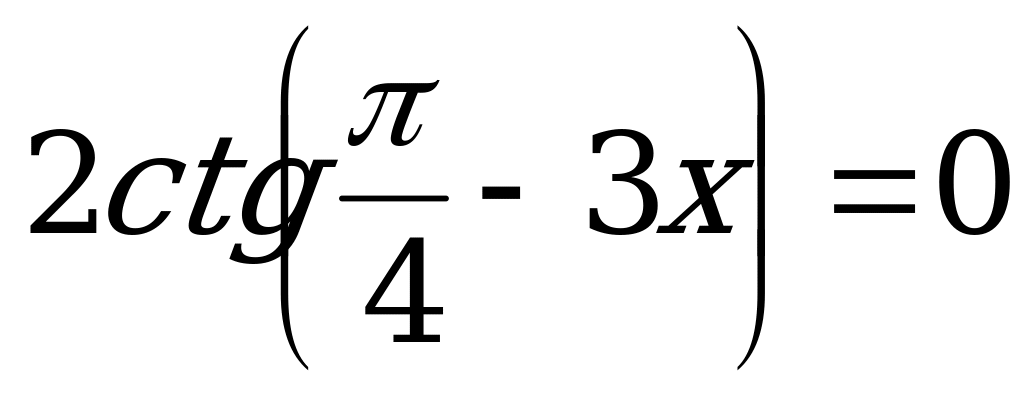 ;
;
8.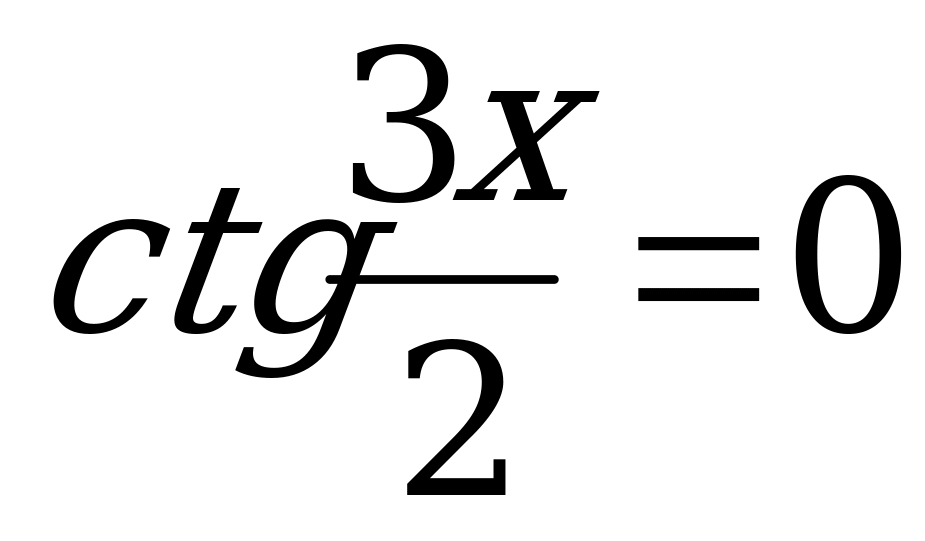 ; 16.
; 16. 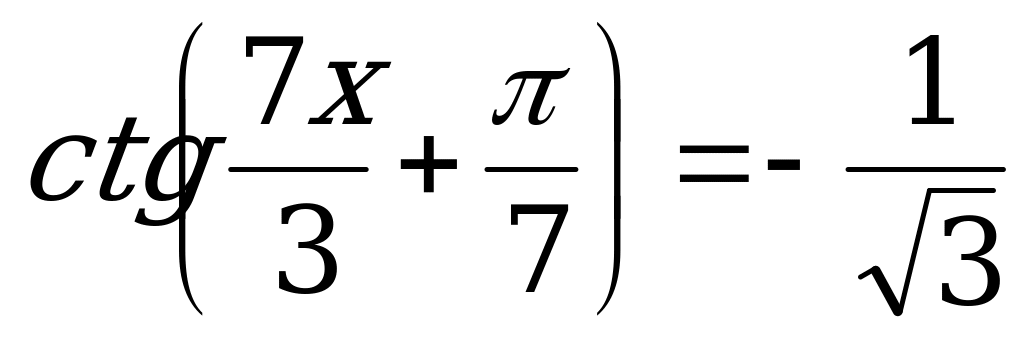 .
.
4.2. Тригонометрические уравнения, сводящиеся к простейшим заменой неизвестного.
Справочный материал.
Рассмотрим примеры решения уравнений, которые после введения нового неизвестного 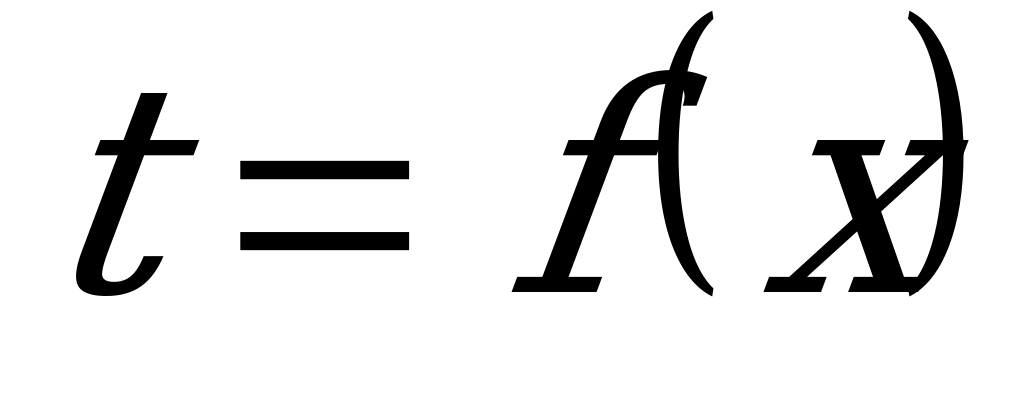 , где
, где 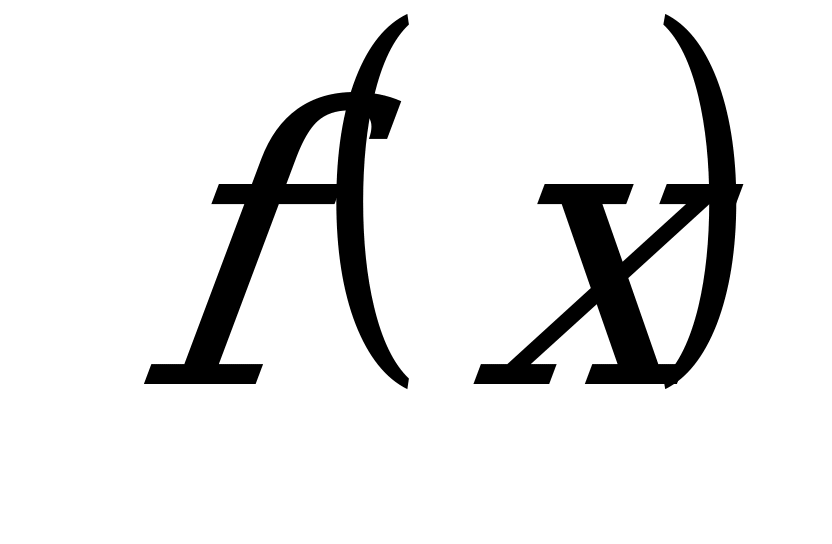 - одна из основных тригонометрических функций, превращаются в квадратные или рациональные уравнения с неизвестным
- одна из основных тригонометрических функций, превращаются в квадратные или рациональные уравнения с неизвестным 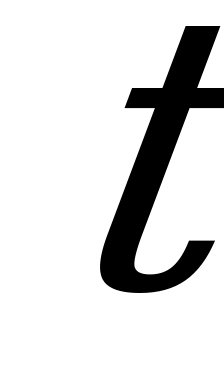 .
.
Упражнения с решениями.
Пример 1. Решить уравнение 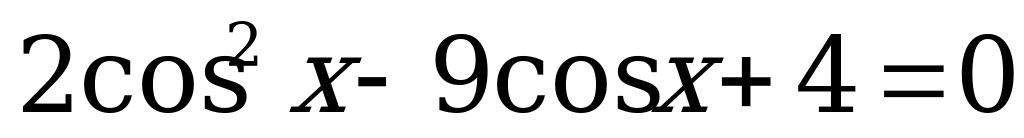 . (1)
. (1)
Решение. Введём новое неизвестное  . Тогда уравнение (1) превратиться в квадратное уравнение с неизвестным
. Тогда уравнение (1) превратиться в квадратное уравнение с неизвестным 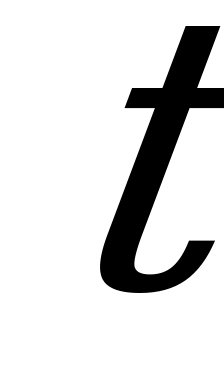 :
:
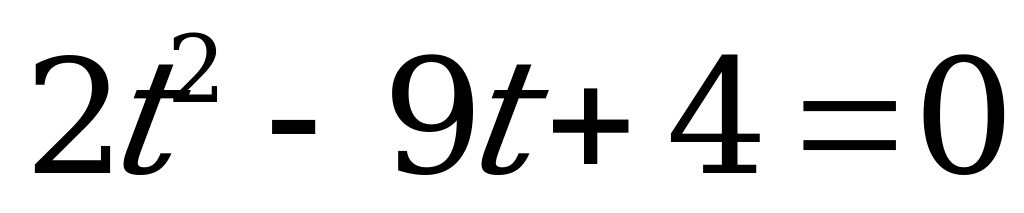 (2)
(2)
Найдём корни уравнения (2).
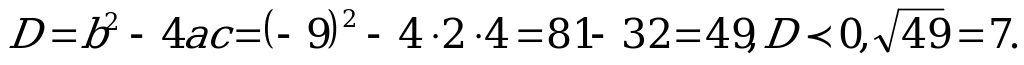
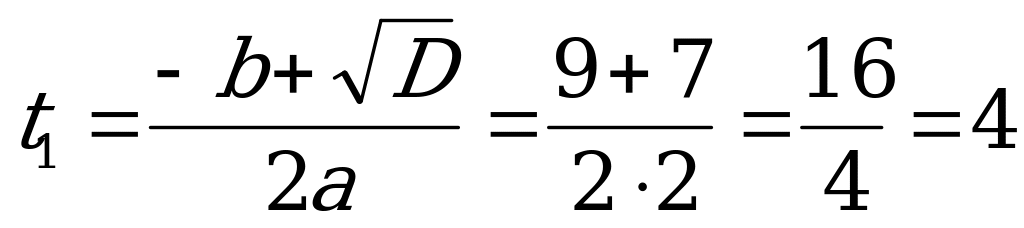 ;
; 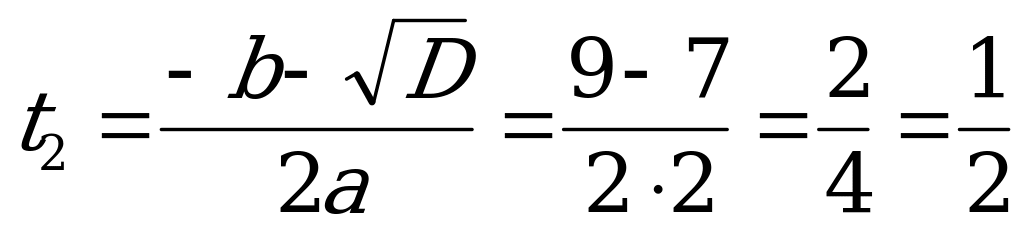 .
.
Следовательно:
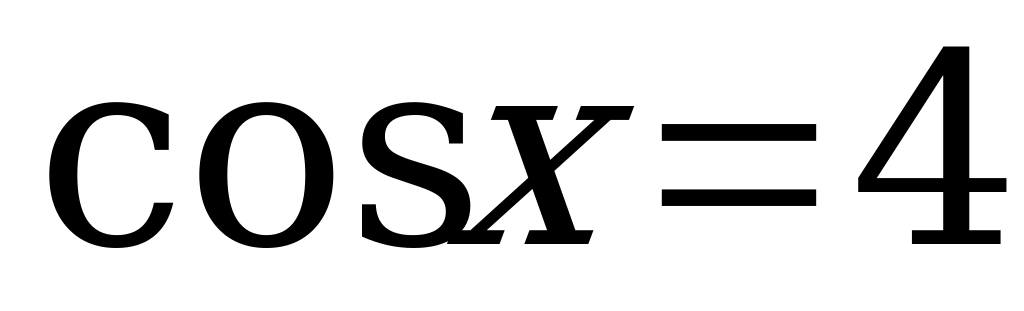 .
. 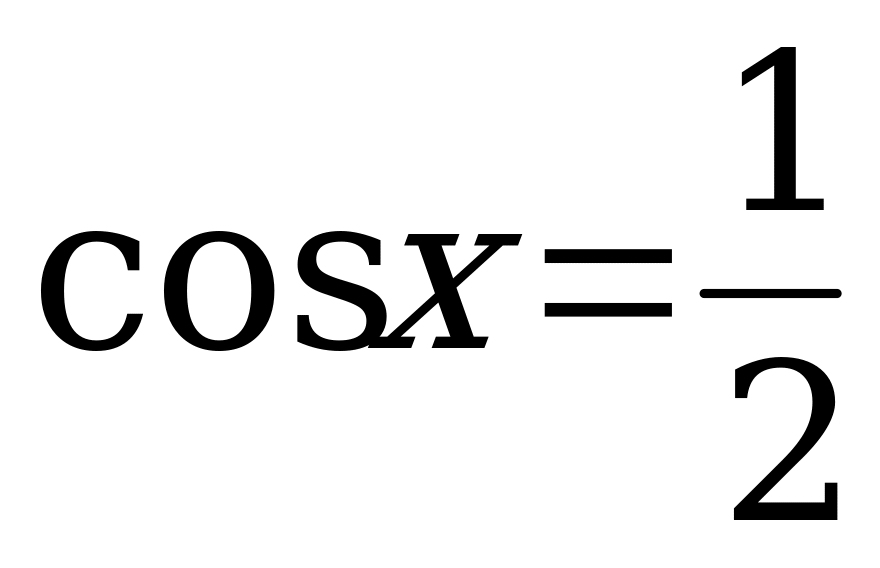 .
.
Решений нет, так как 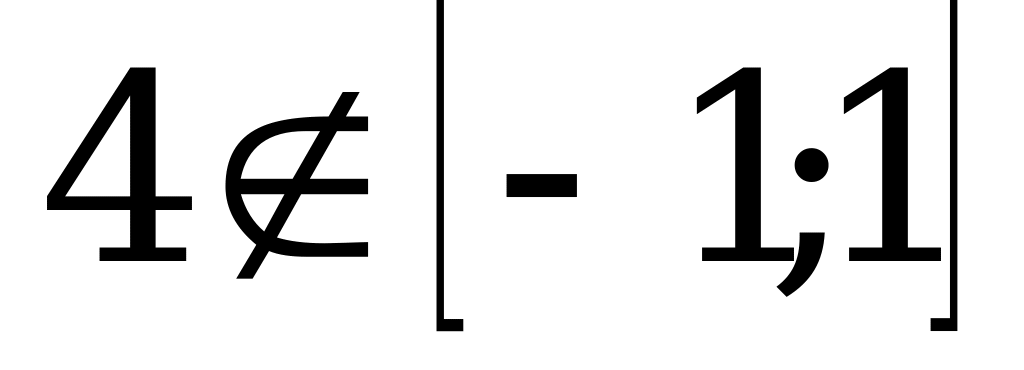
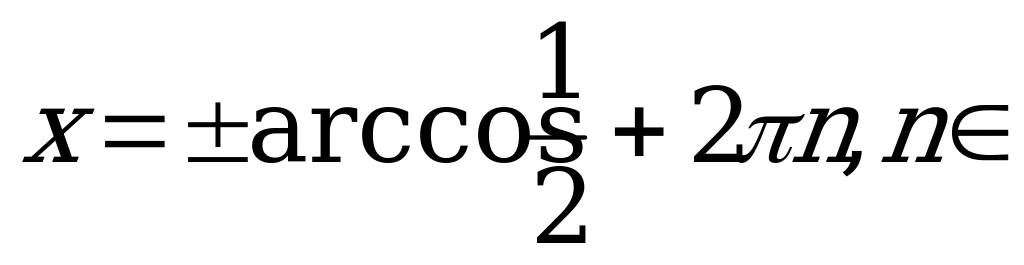 Z.
Z.
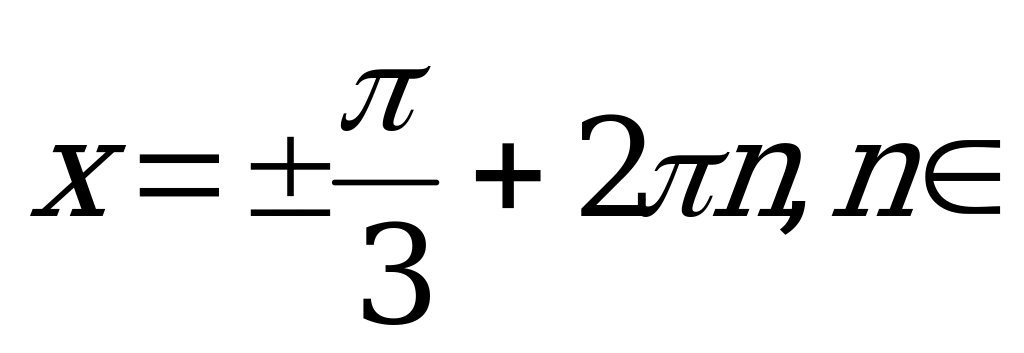 Z.
Z.
Ответ: 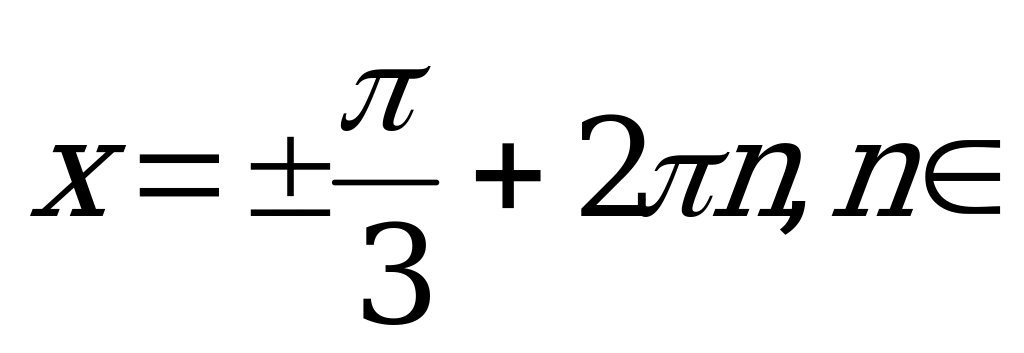 Z.
Z.
Пример 2. Решить уравнение 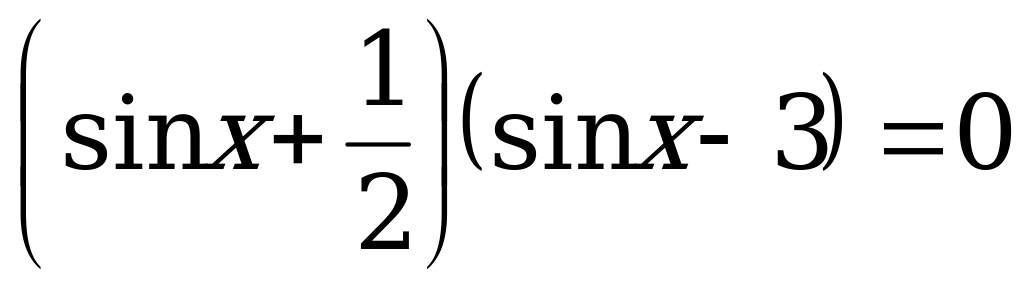 .
.
Решение. Заменим 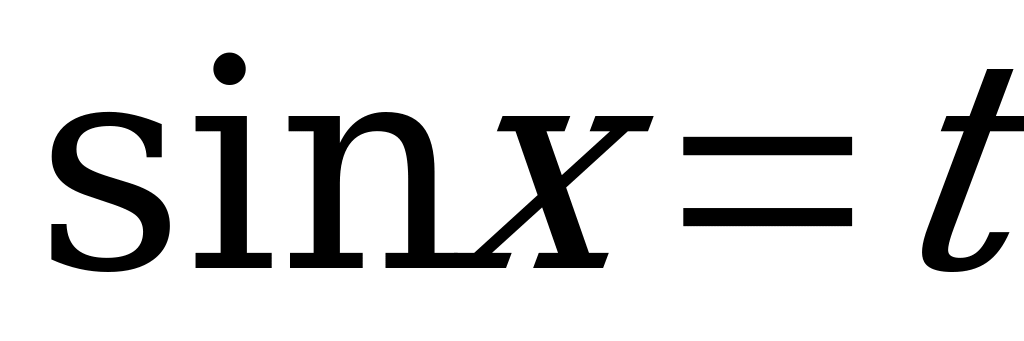 . Тогда:
. Тогда:
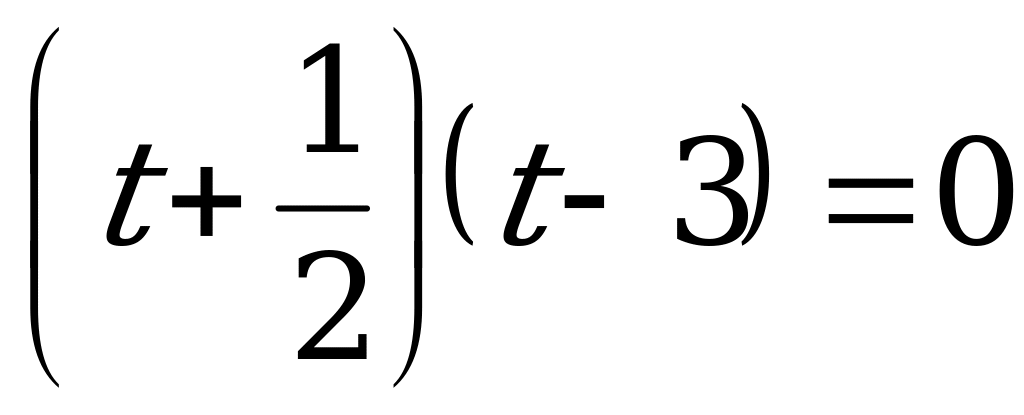 .
.
 или
или  .
.
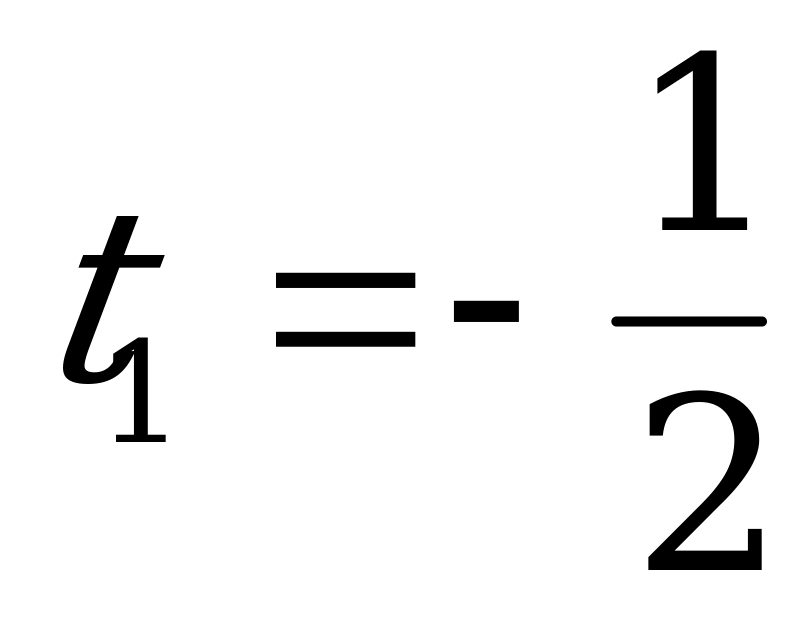 .
. 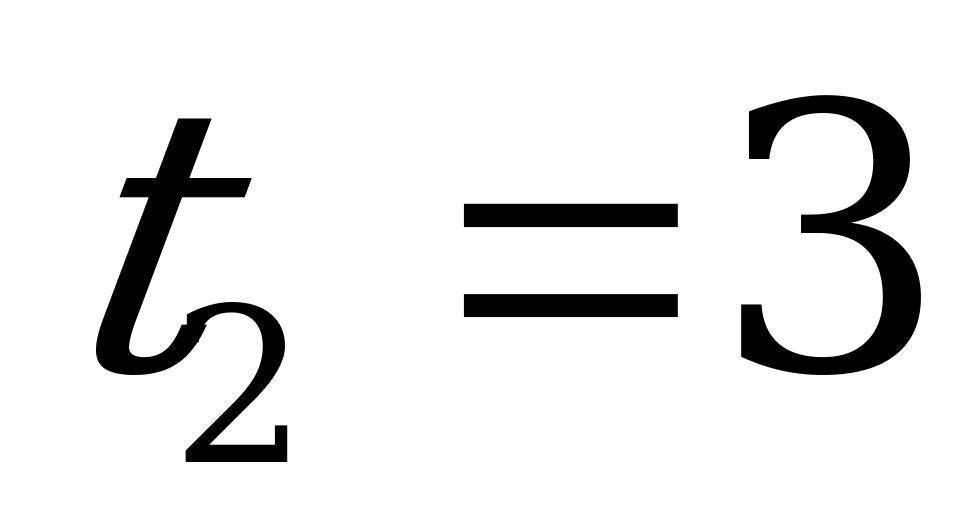 .
.
Следовательно:
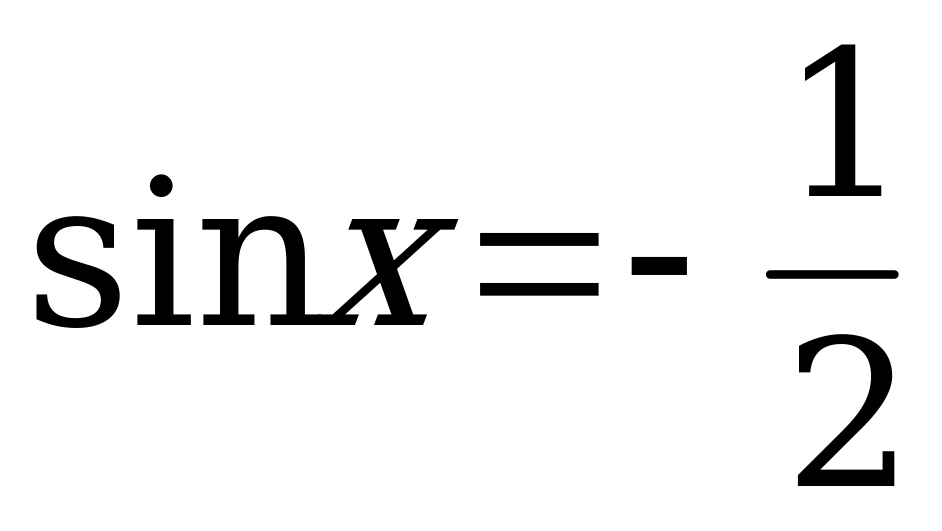 .
. 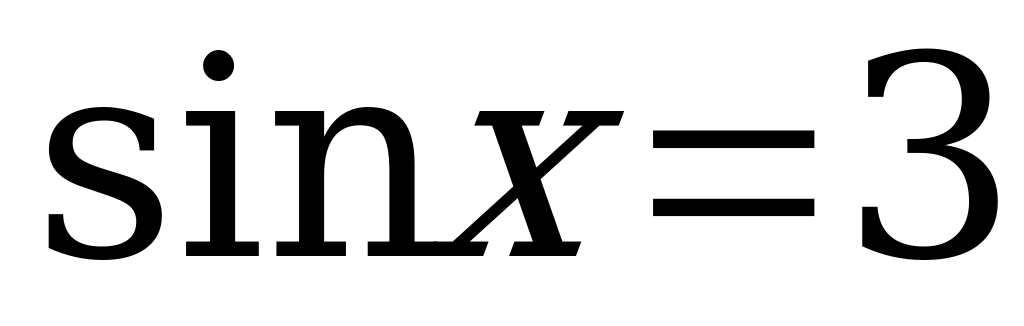 .
.
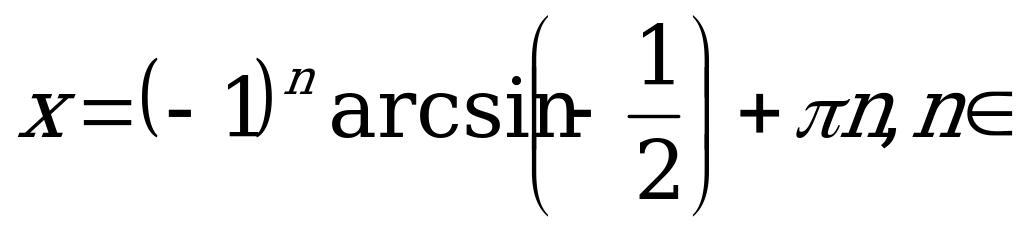 Z. Решений нет, так как
Z. Решений нет, так как
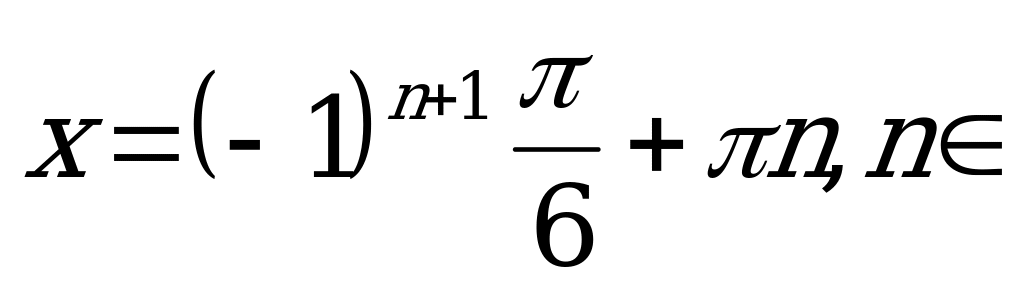 Z.
Z. 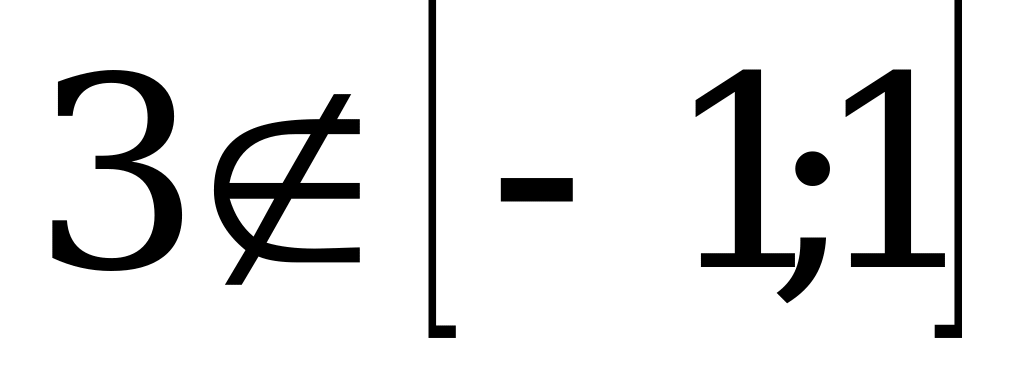 .
.
Ответ: 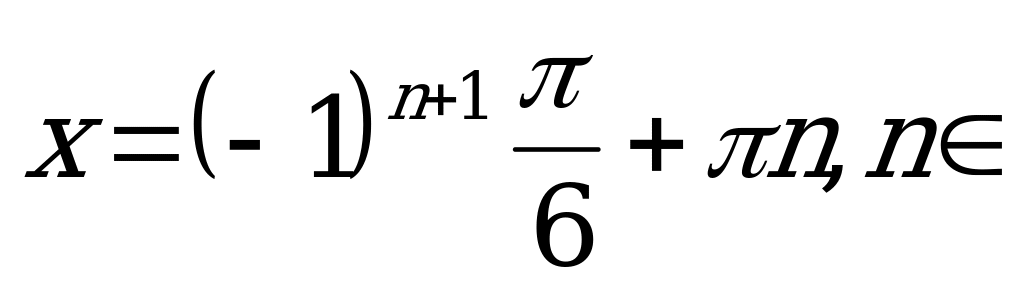 Z.
Z.
Пример 3. Решить уравнение 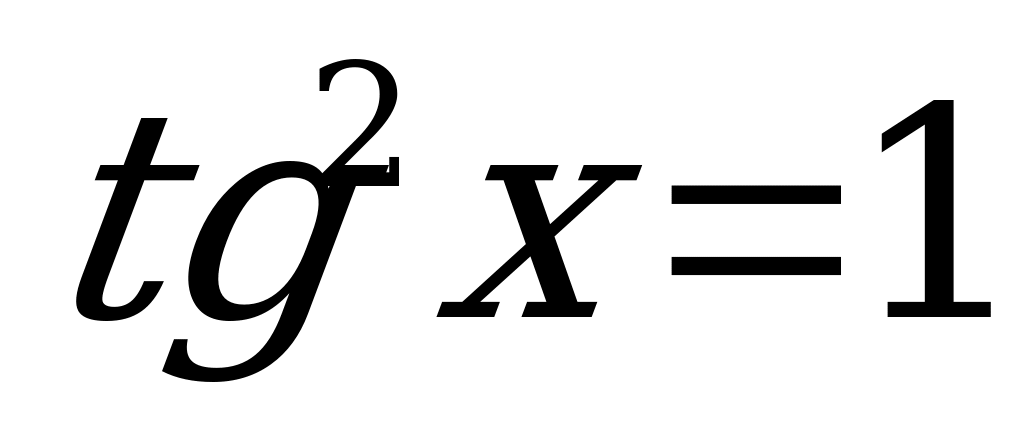 .
.
Заменим 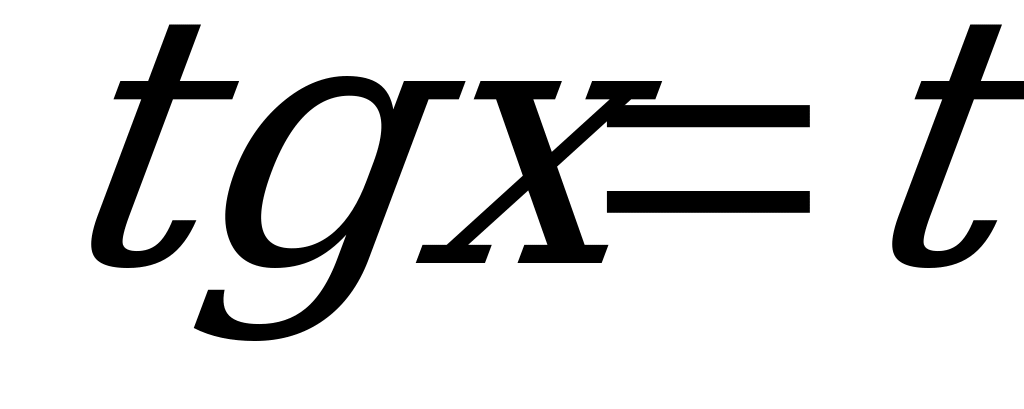 . Получим:
. Получим:
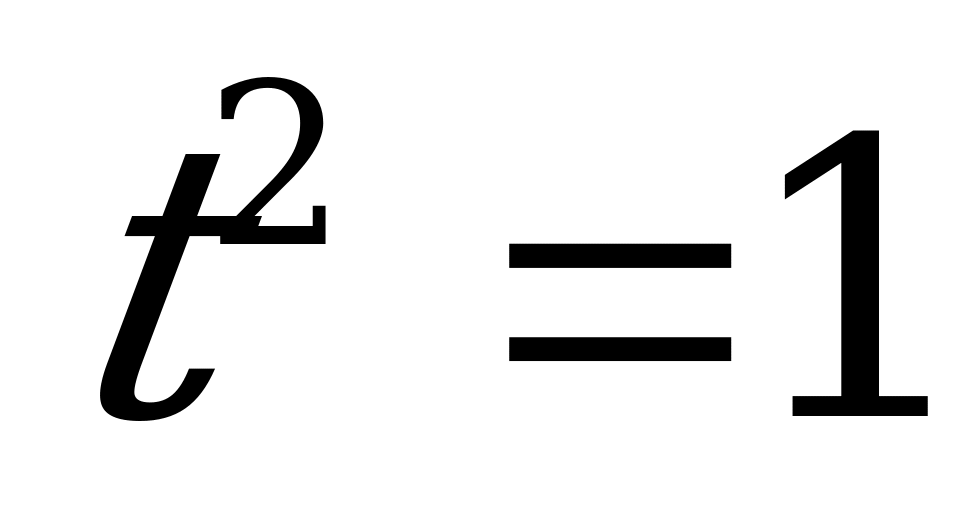 .
.
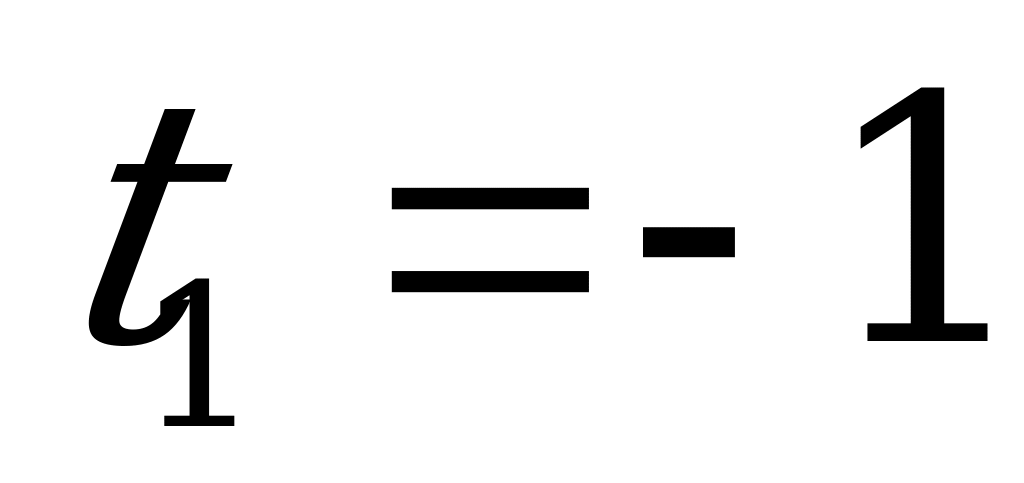 и
и 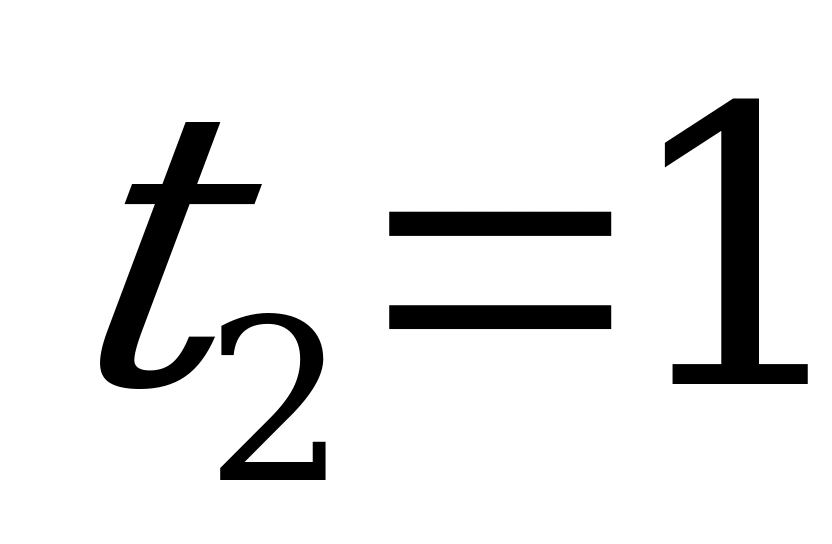 .
.
Следовательно:
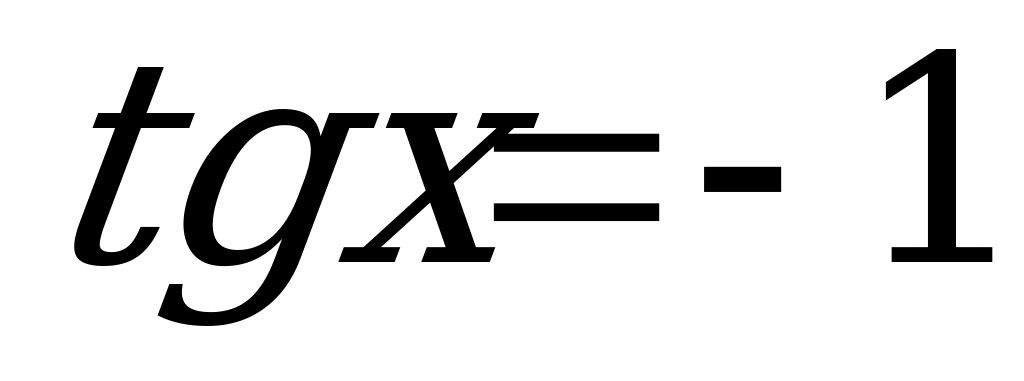 и
и 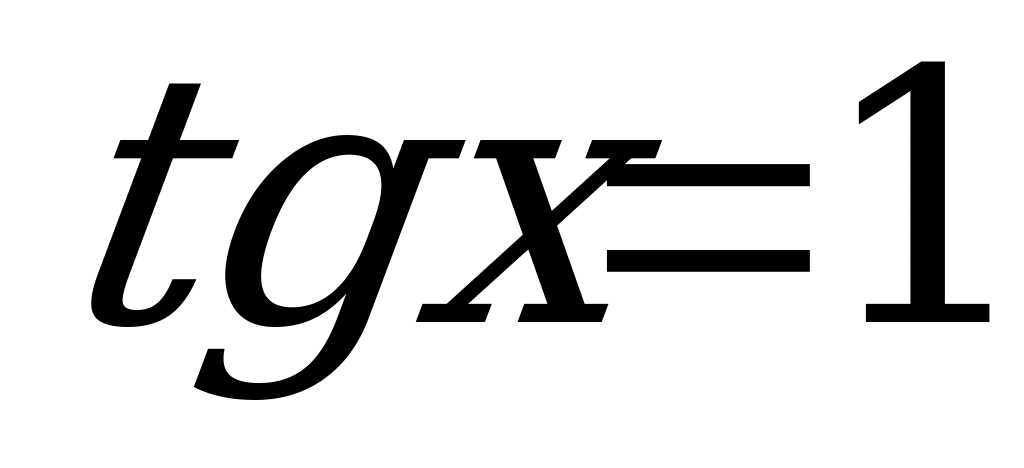 .
.
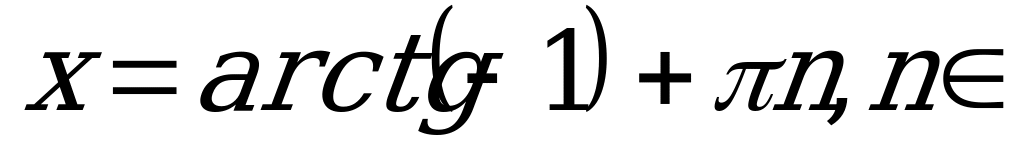 Z.
Z. 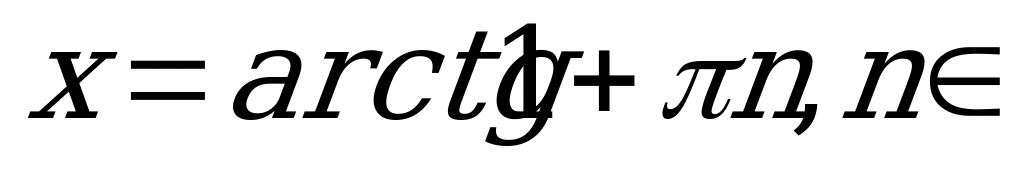 Z.
Z.
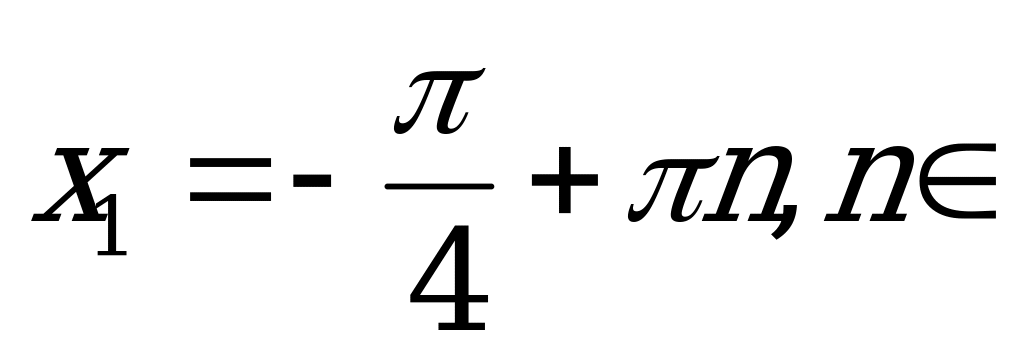 Z.
Z. 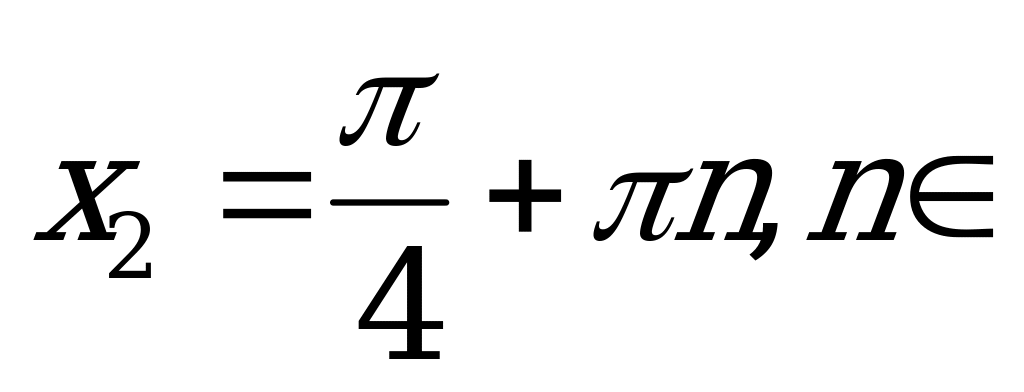 Z.
Z.
Ответ: 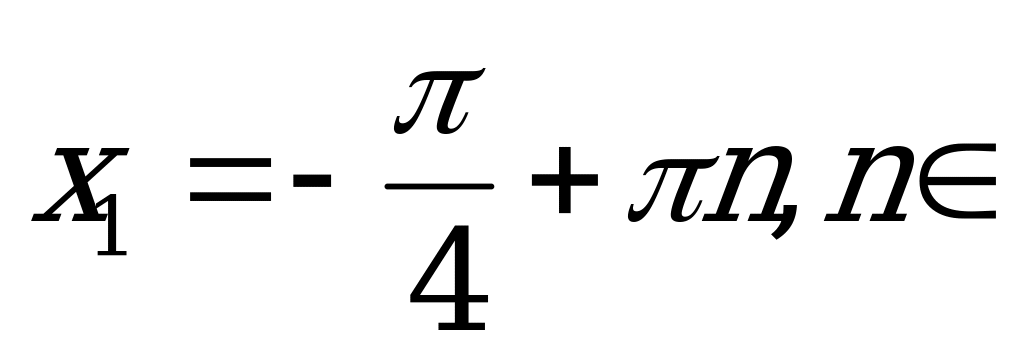 Z,
Z, 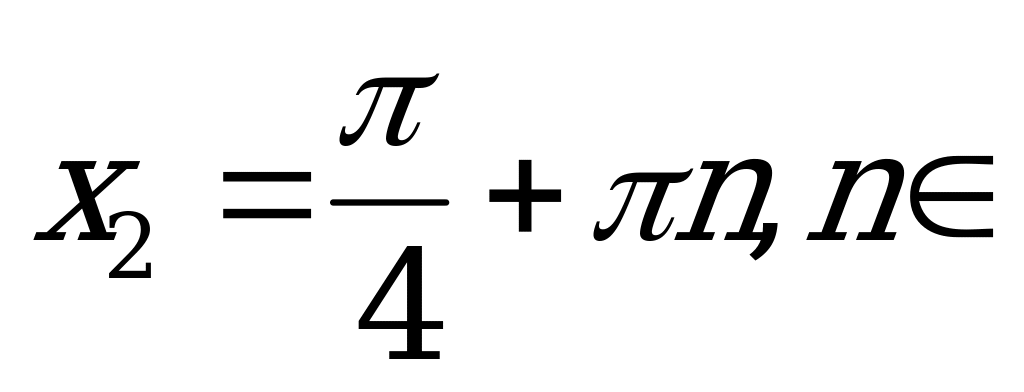 Z.
Z.
Самостоятельная работа №8.
Вариант №1.
Решить уравнения(1-4).
1) 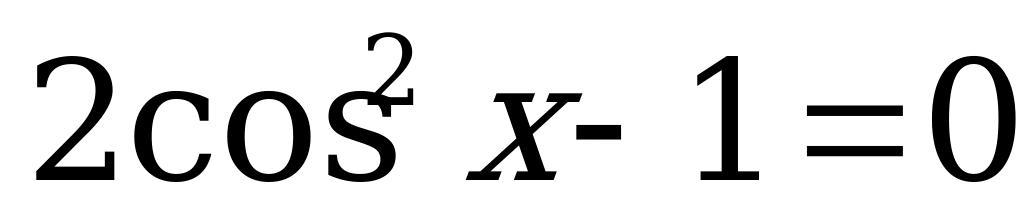 ;
;
2) 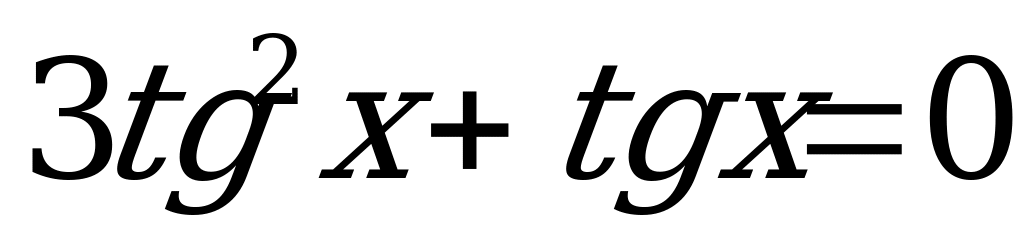 ;
;
3)  ;
;
4) 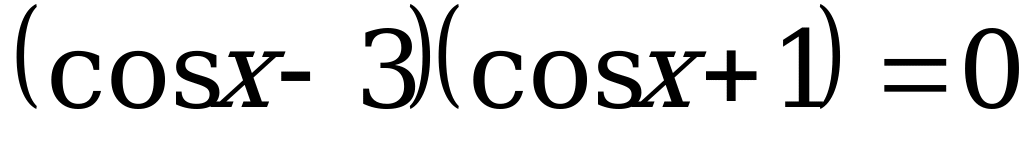 .
.
Вариант №2.
Решить уравнения(1-4).
1) 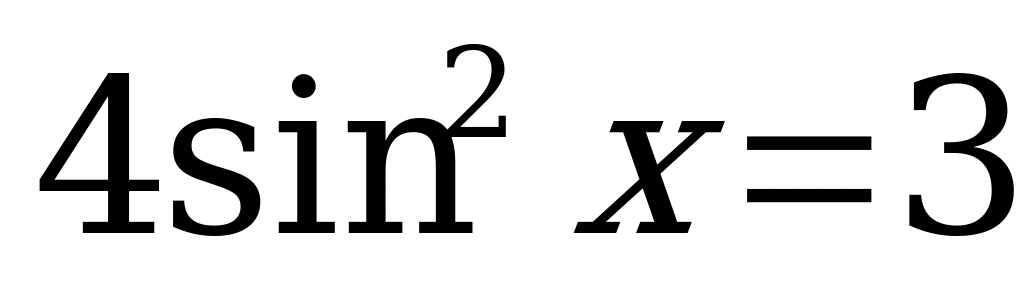 ;
;
2) 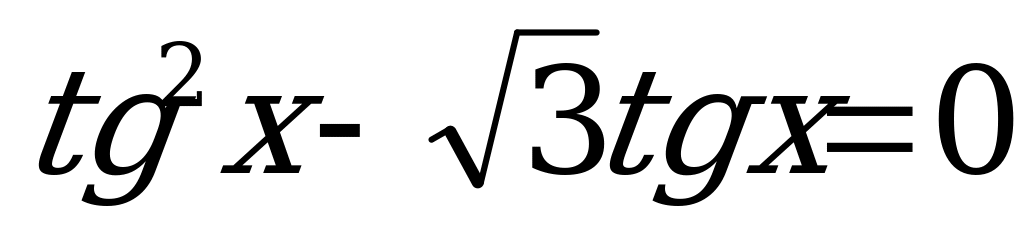 ;
;
3) 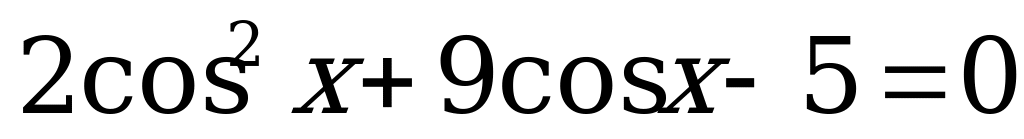 ;
;
4) 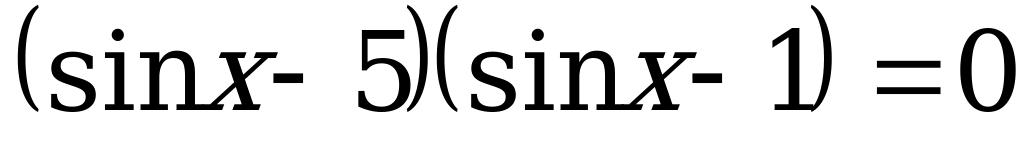 .
.
§5. Применение основных тригонометрических формул для  решения уравнений.
решения уравнений.
5.1. Применение основных тригонометрических тождеств.
Упражнения с решениями.
Пример 1. Решить уравнения:
а) 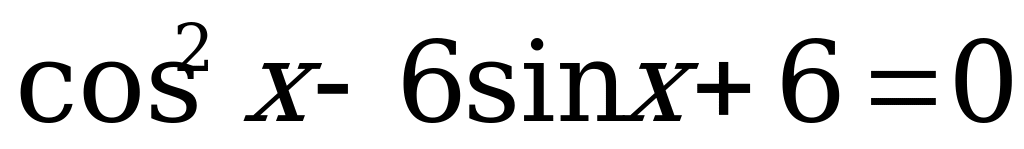 ;
;
б) 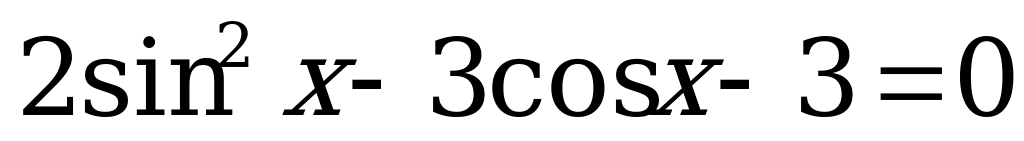 ;
;
в) 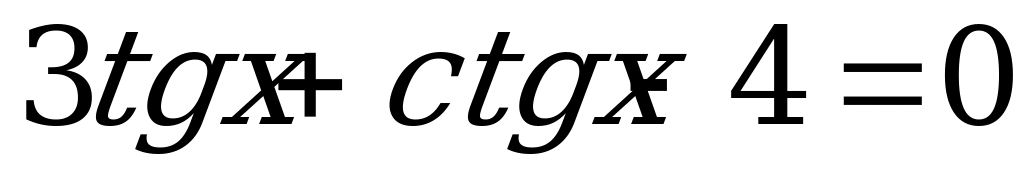 .
.
Решение.
а) Решим уравнение:
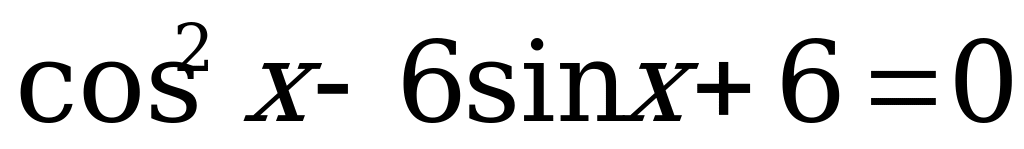 (1).
(1).
Применяя основное тригонометрическое тождество 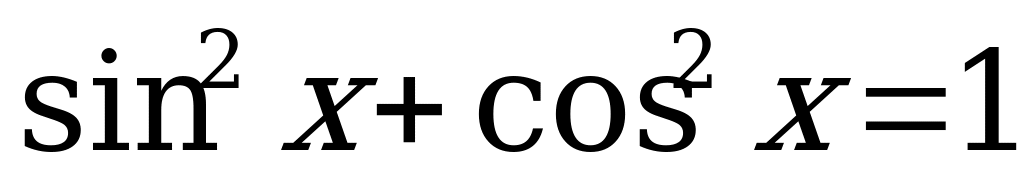 ,
,
произведём замену: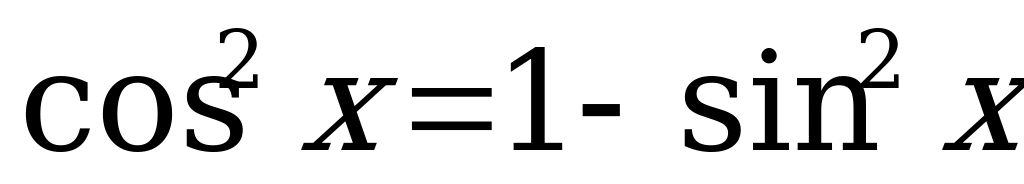 . Тогда уравнение (1) примет вид:
. Тогда уравнение (1) примет вид:
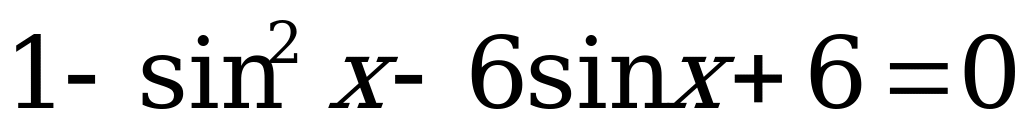 или
или
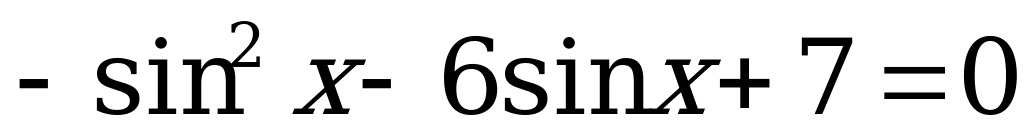 (2)
(2)
Введём новое неизвестное 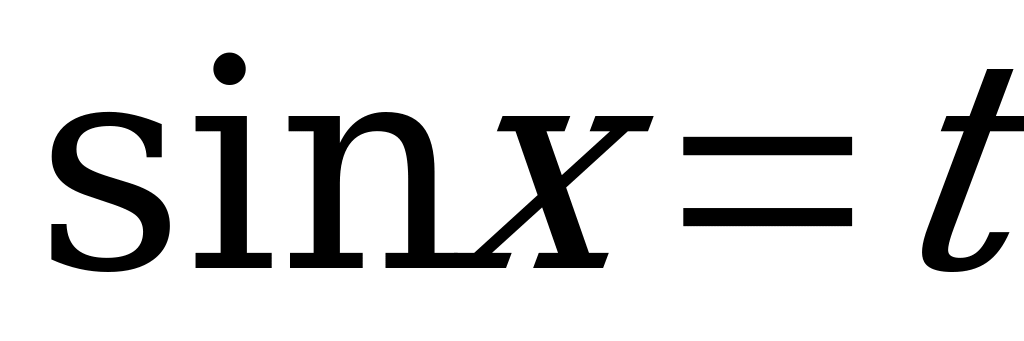 . Тогда уравнение (2) преобразуется в квадратное уравнение с неизвестным
. Тогда уравнение (2) преобразуется в квадратное уравнение с неизвестным 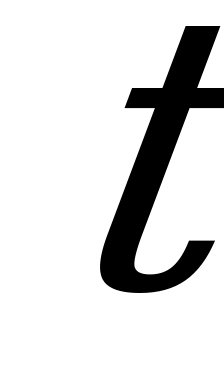 :
:
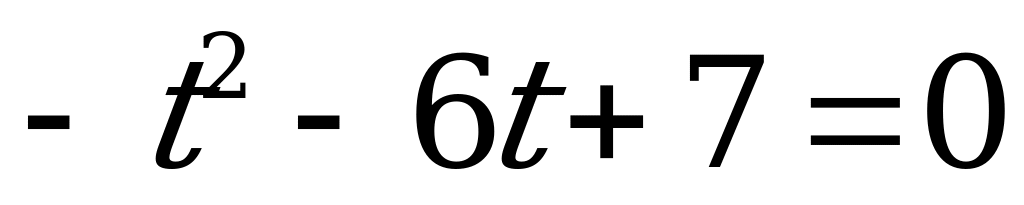 .
.
Разделим обе части уравнения на 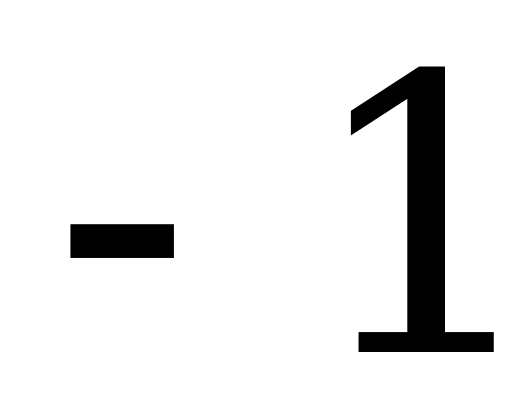 и получим приведённое квадратное уравнение:
и получим приведённое квадратное уравнение:
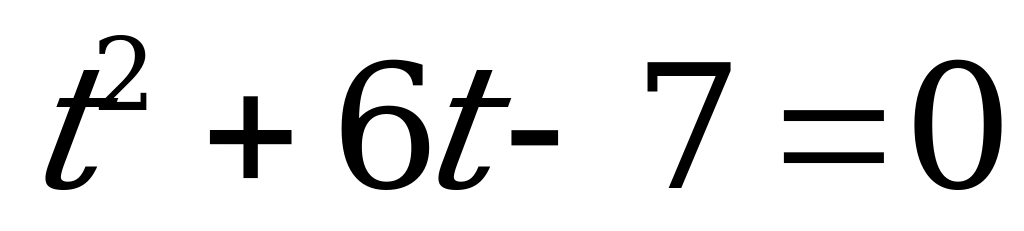 .
.
По теореме Виета:
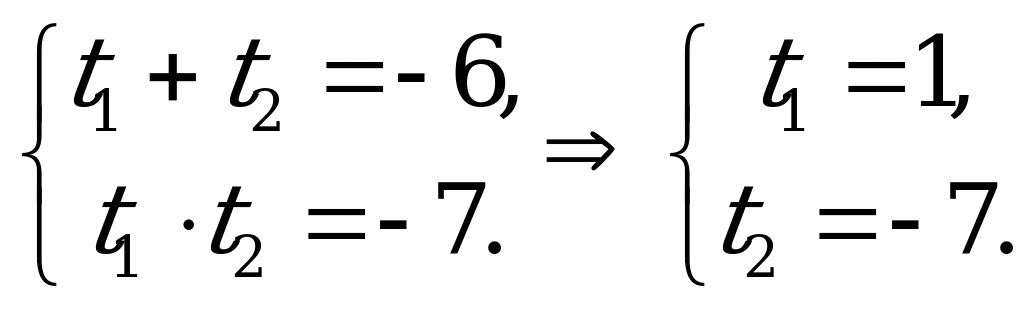
Следовательно:
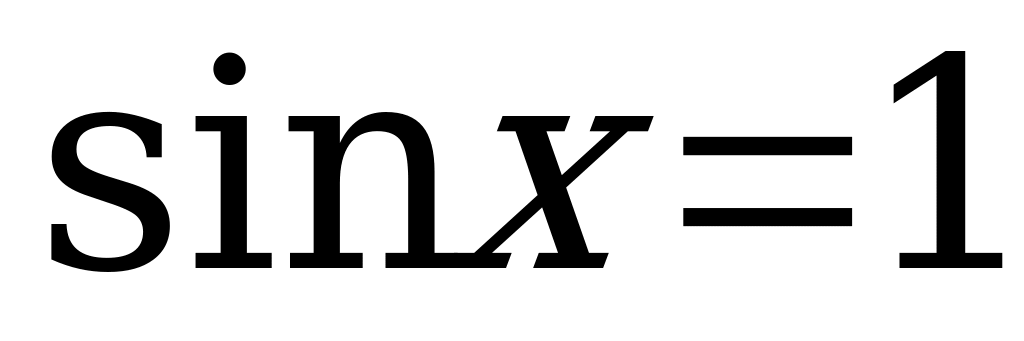 или
или 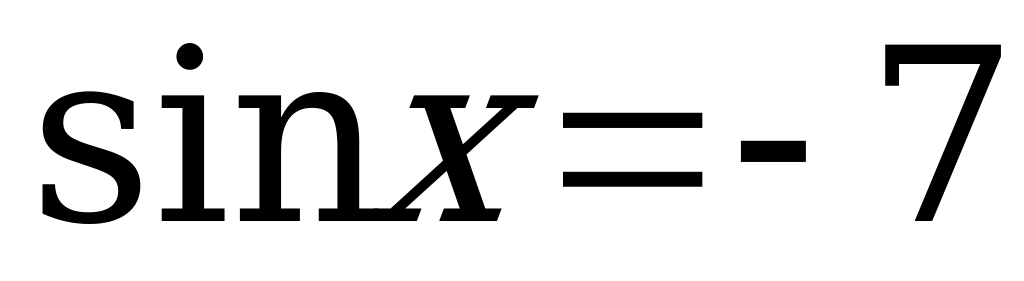
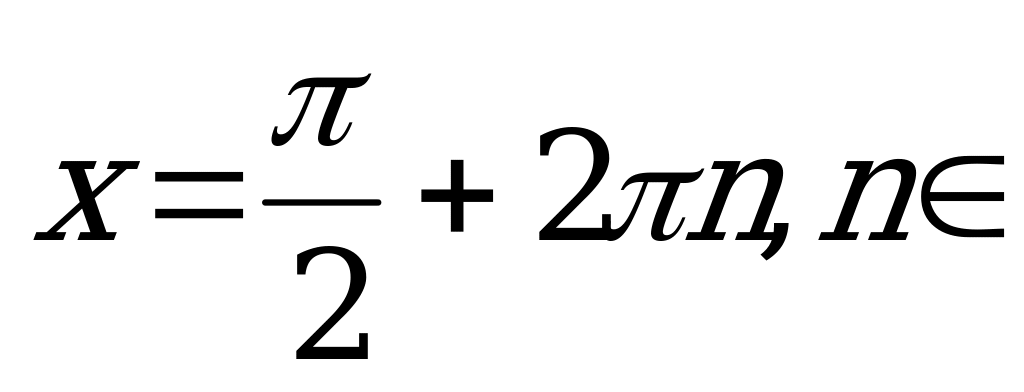 Z. Решений нет,
Z. Решений нет,
так как -7-1.
Ответ: 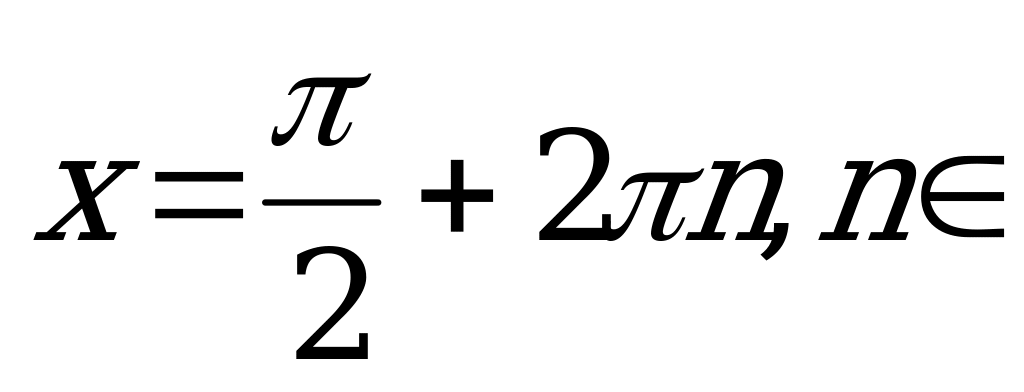 Z.
Z.
б) Решим уравнение:
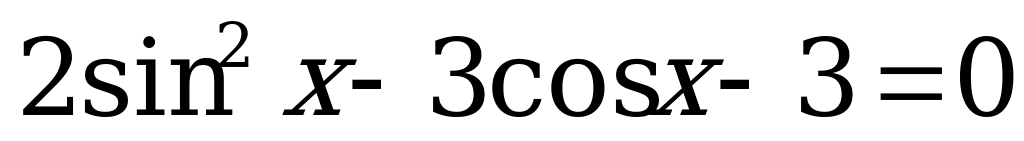 . (3)
. (3)
Применяя основное тригонометрическое тождество 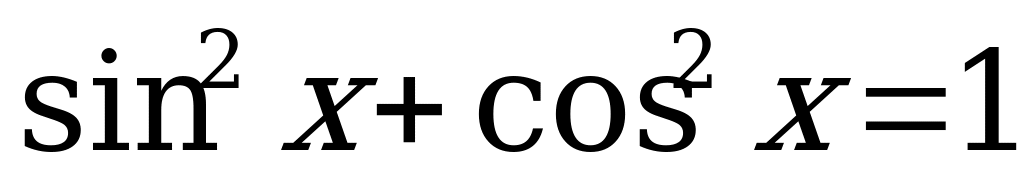 , произведём замену:
, произведём замену: 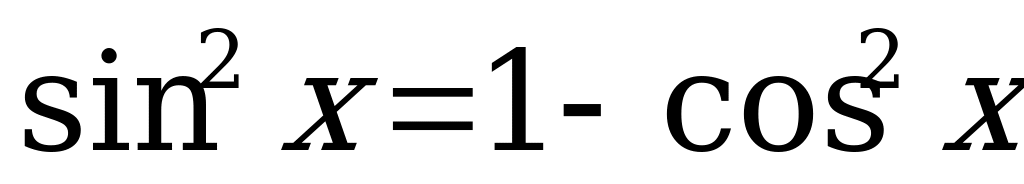 . Перепишем уравнение (3) в виде:
. Перепишем уравнение (3) в виде:
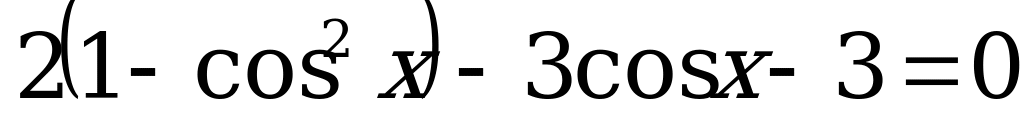 .
.
Раскроем скобки и соберём подобные слагаемые:
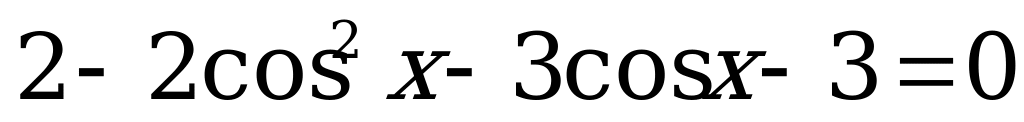 ,
,
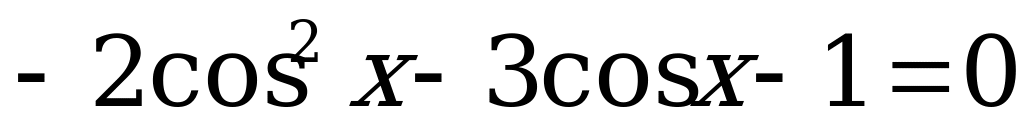 . (4)
. (4)
Введём новое неизвестное  . Тогда уравнение(4) примет вид:
. Тогда уравнение(4) примет вид:
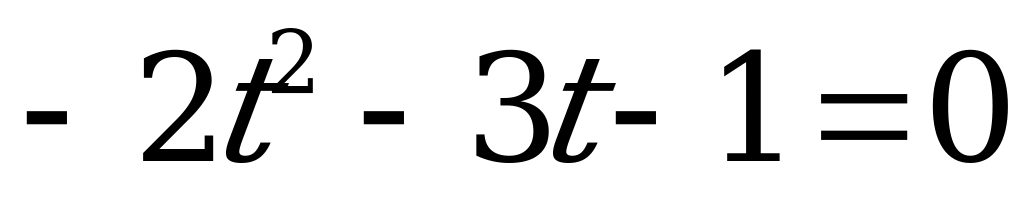 (5)
(5)
Найдём дискриминант и корни уравнения (5)
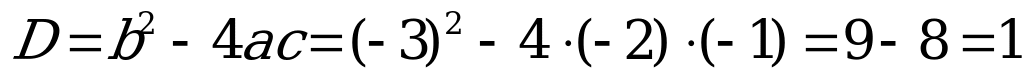 ,
,  .
.
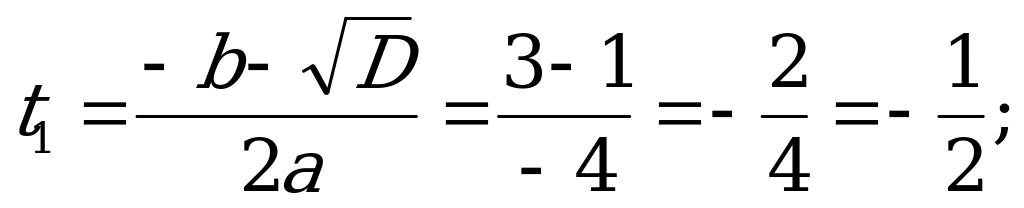
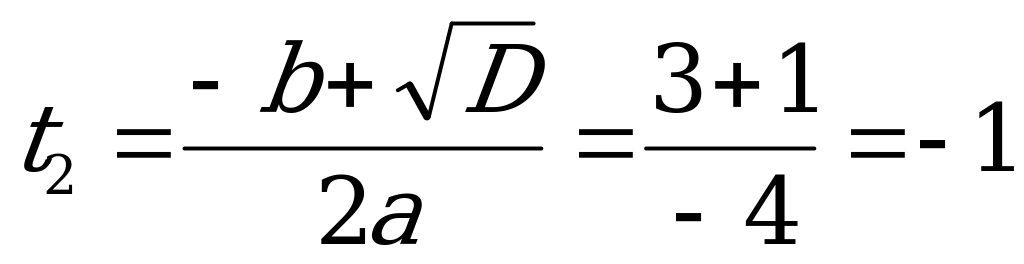 .
.
Следовательно:
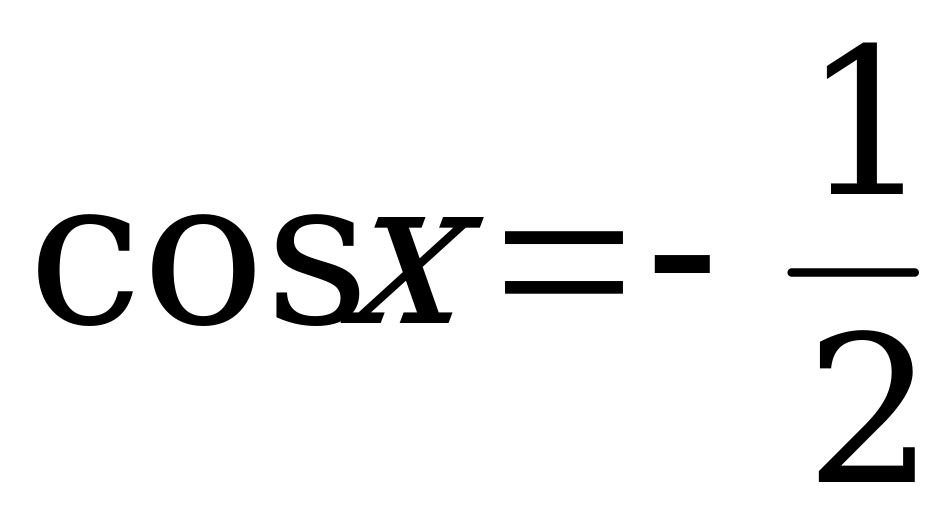 или
или 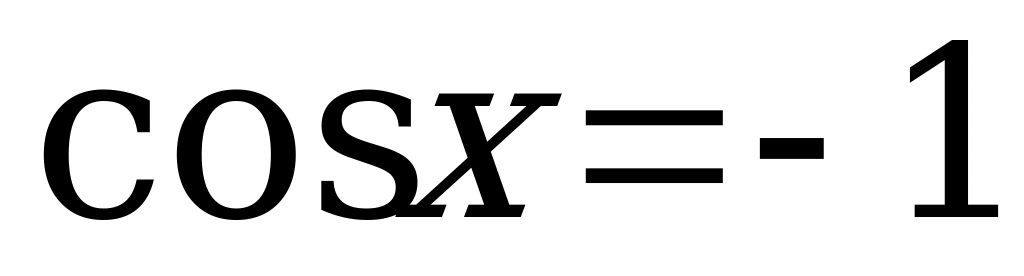
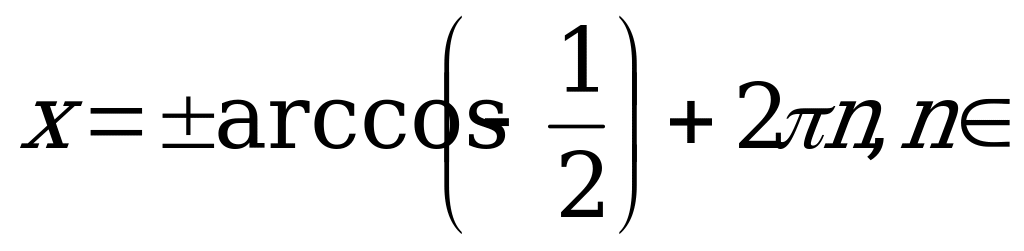 Z,
Z, 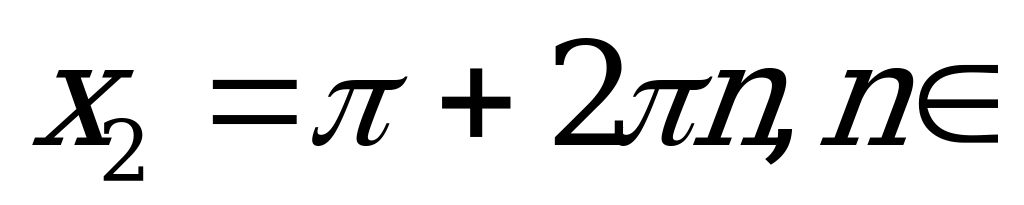 Z.
Z.
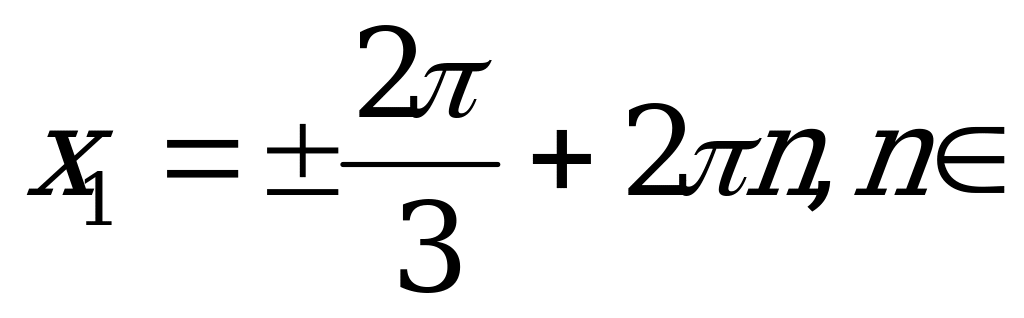 Z.
Z.
Ответ: 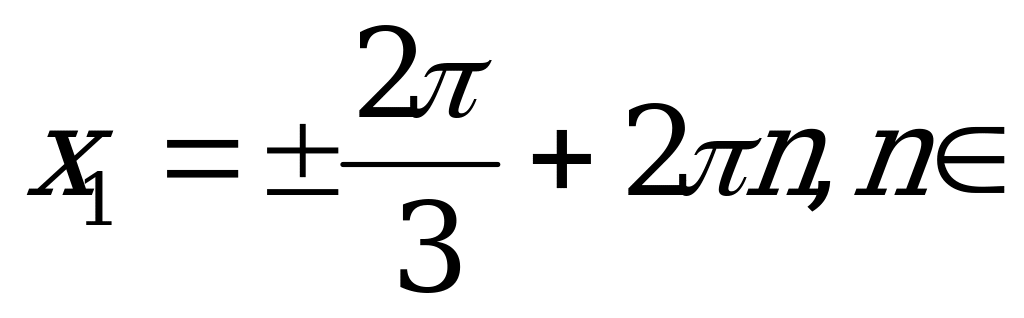 Z,
Z, 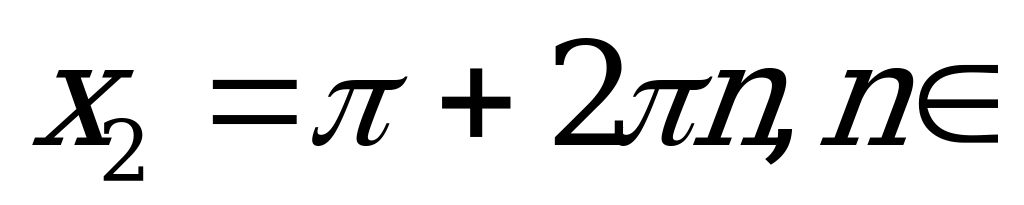 Z.
Z.
в) Решим уравнение
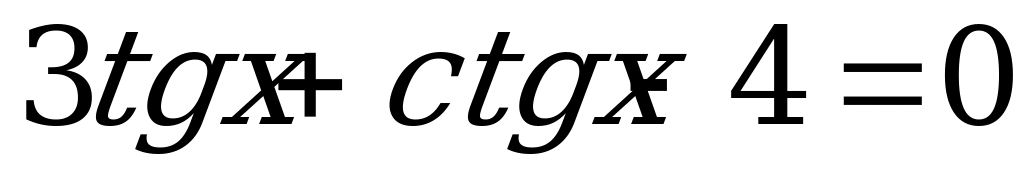 (6)
(6)
Из формулы 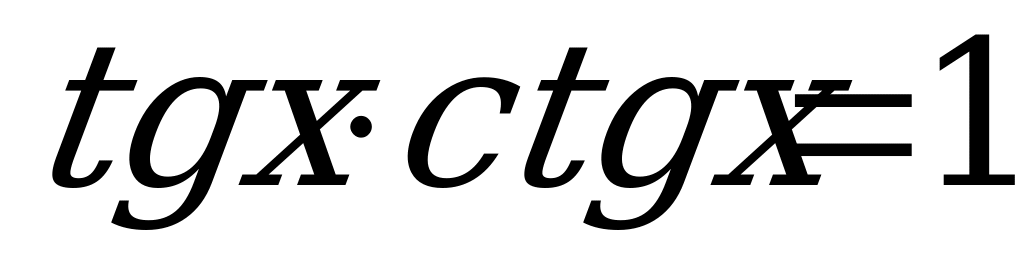 , следует что
, следует что 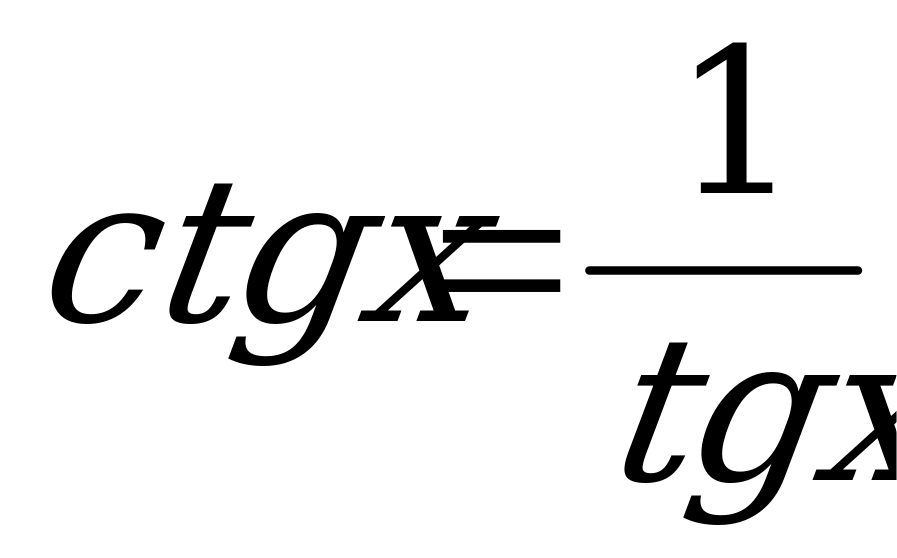 . Тогда уравнение (6) примет вид:
. Тогда уравнение (6) примет вид:
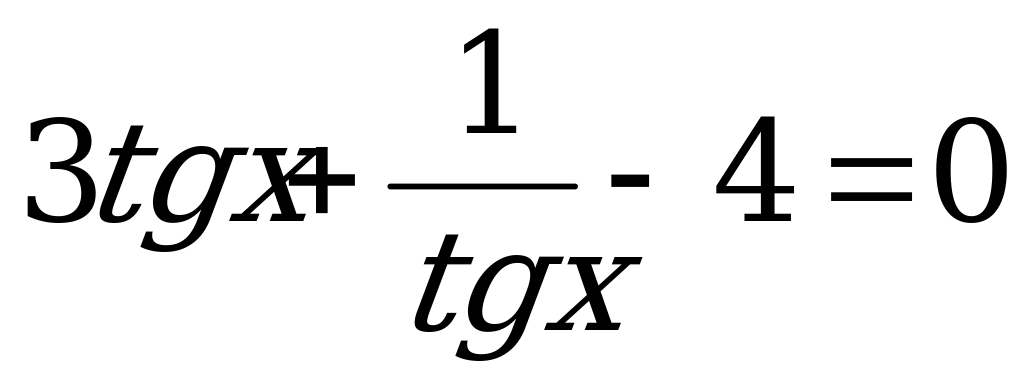 . (7)
. (7)
Введём новое неизвестное 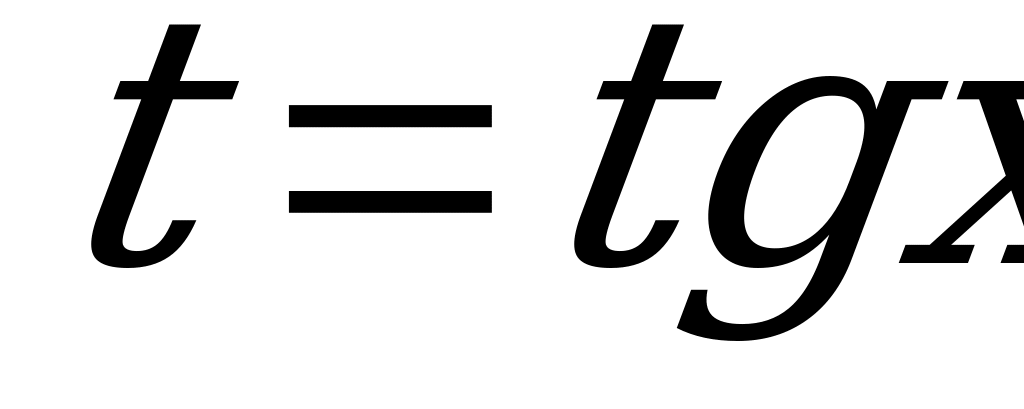 . Тогда уравнение (7) преобразуется в рациональное уравнение с неизвестным
. Тогда уравнение (7) преобразуется в рациональное уравнение с неизвестным 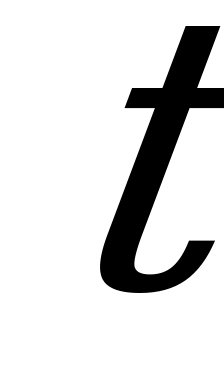 :
:
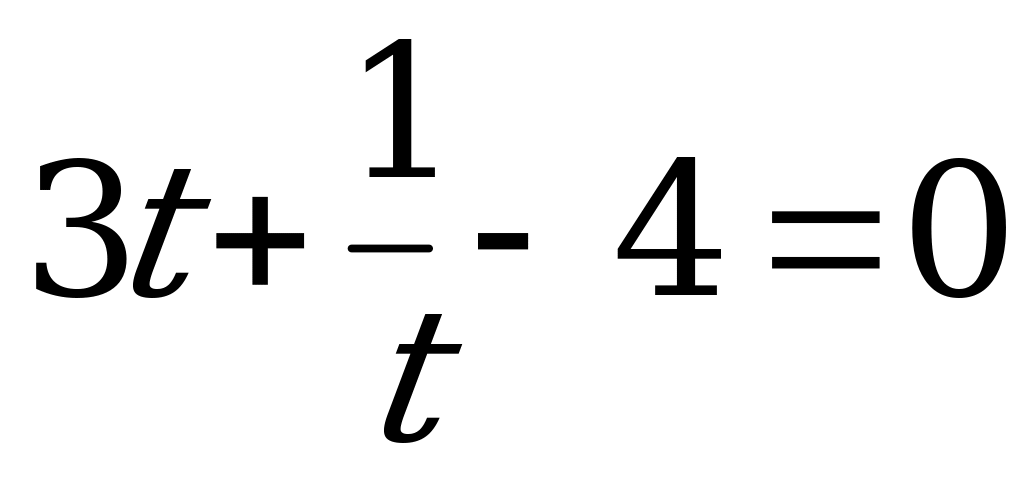 . (8)
. (8)
Умножим обе части уравнения (8) на неизвестное 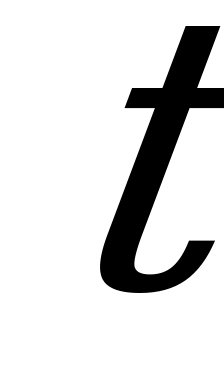 (при условии
(при условии 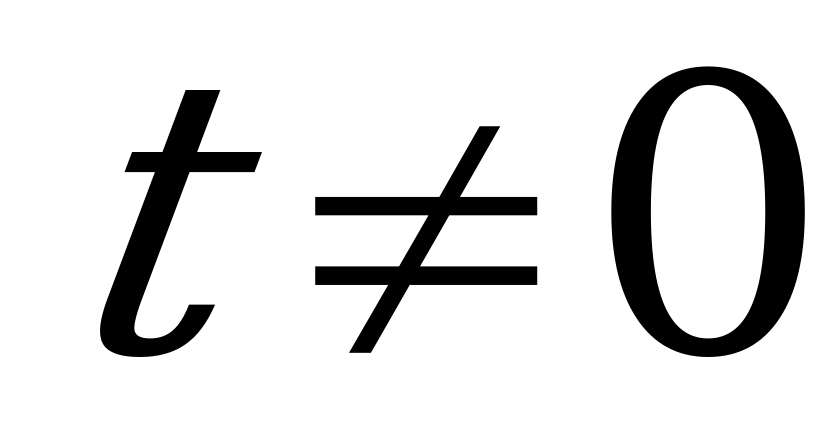 ):
):
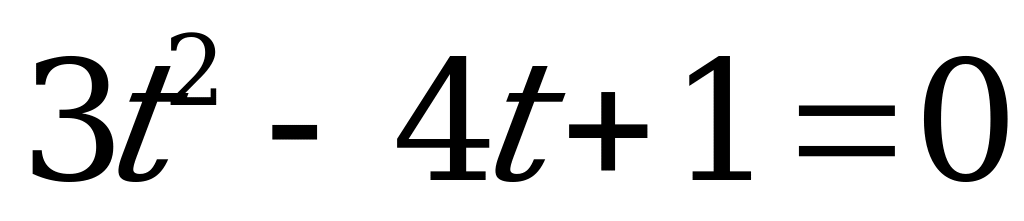 (9)
(9)
Найдём корни уравнения (9)
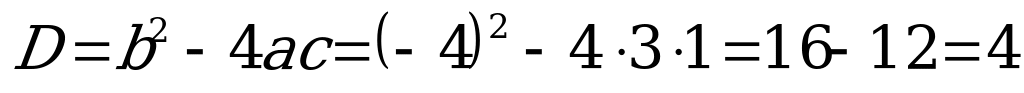 ,
, 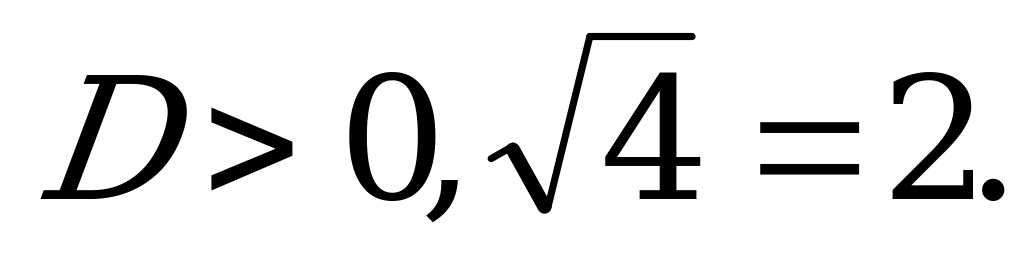 .
.
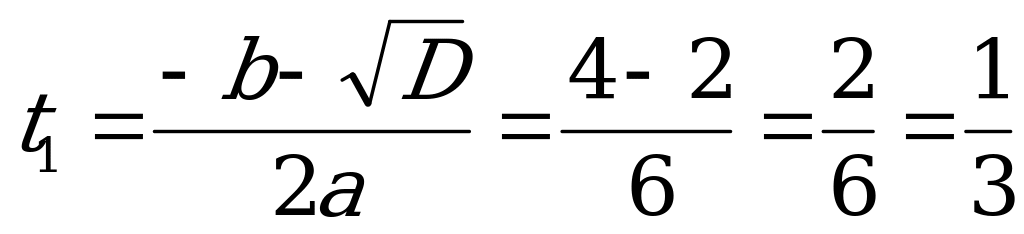 ;
; 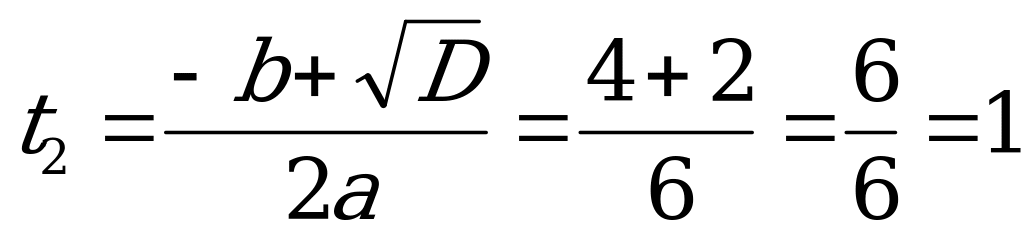 .
.
Следовательно:
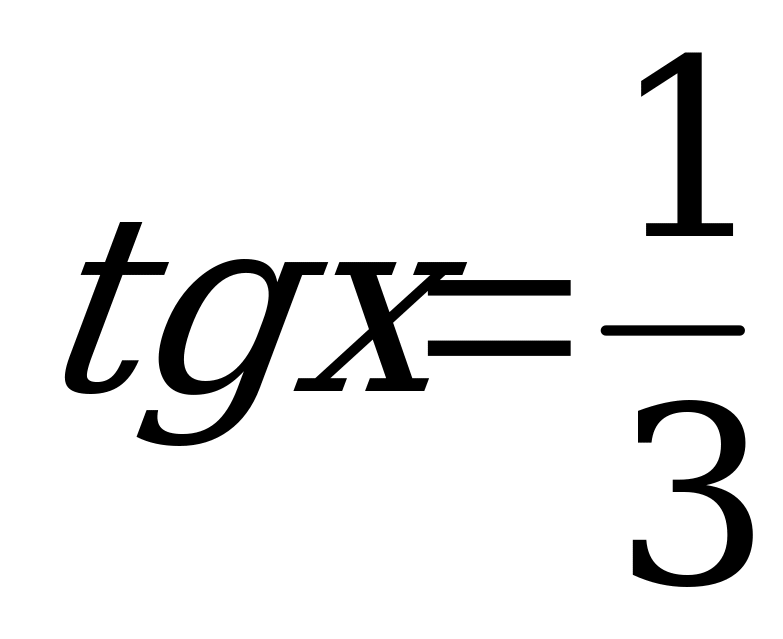 или
или 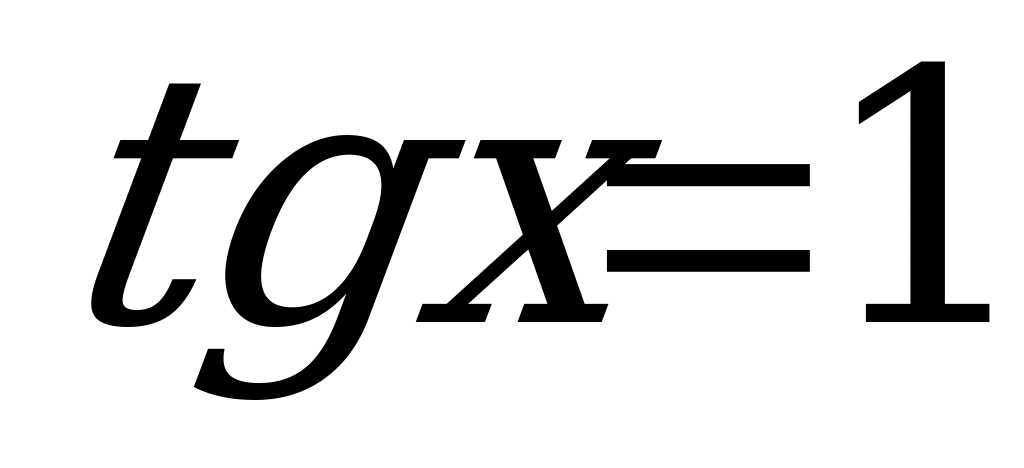 .
.
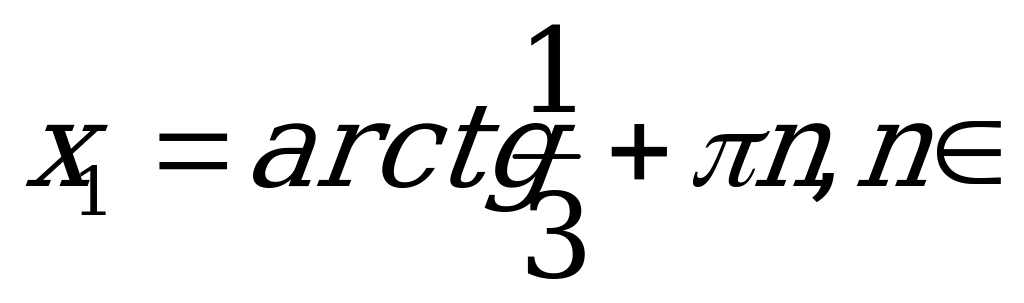 Z,
Z, 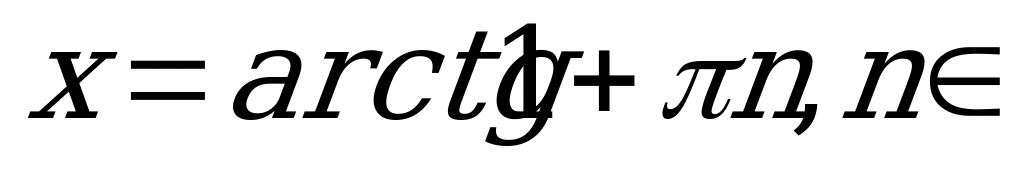 Z.
Z.

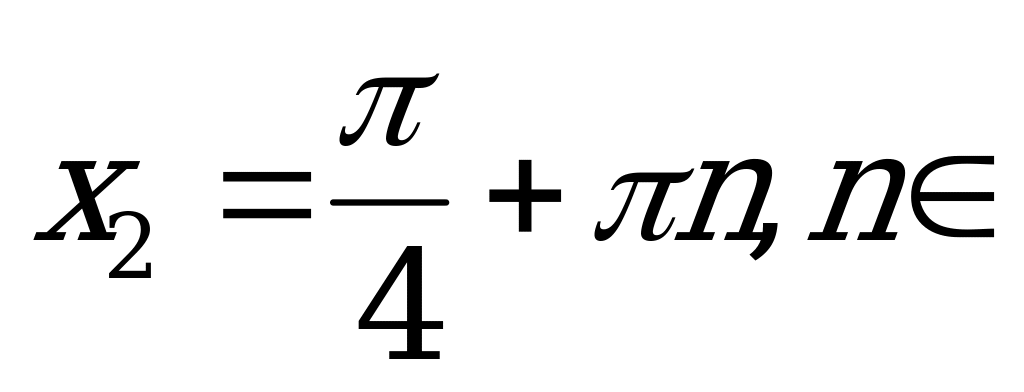 Z.
Z.
Ответ: 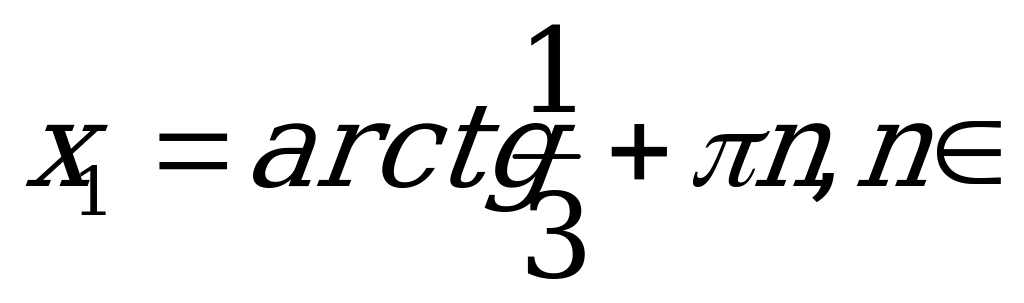 Z,
Z, 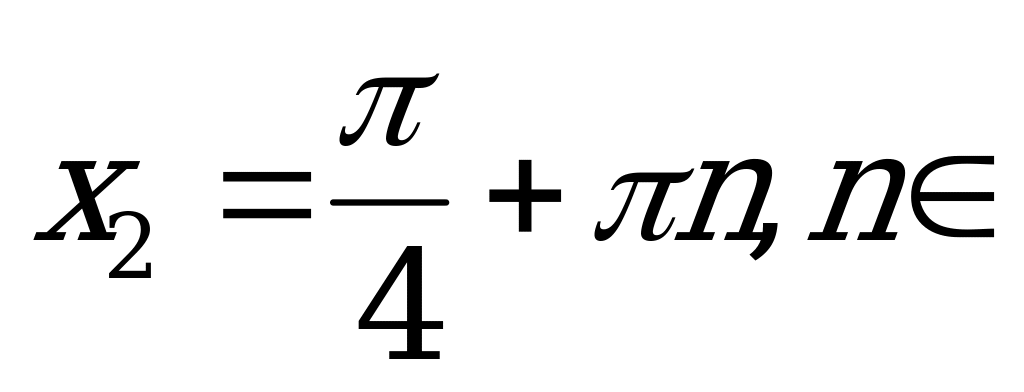 Z.
Z.
5.2. Применение формул приведения.
Упражнения с решениями.
Пример 2. Решить уравнения:
а) 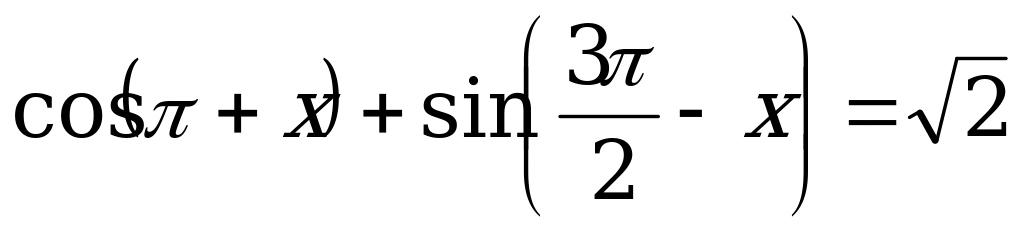 ;
;
б) 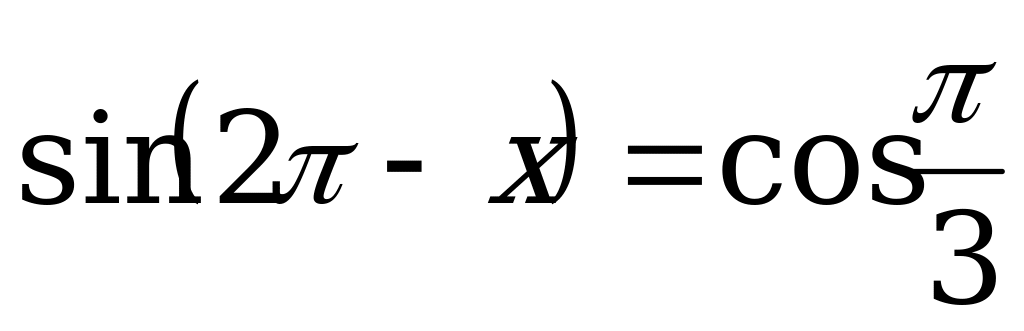 ;
;
в) 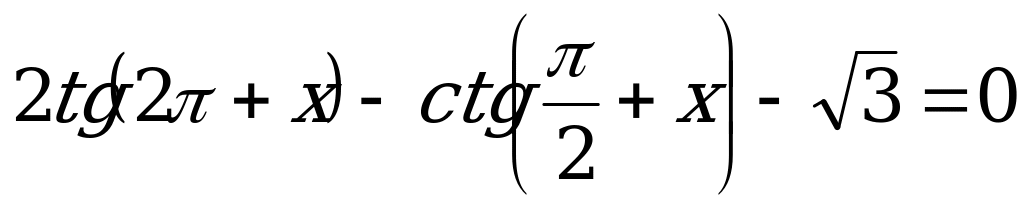 .
.
Решение. а) Решим уравнение 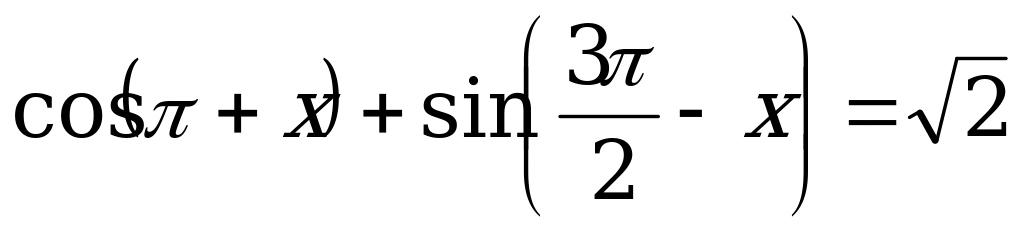 . (1)
. (1)
По формулам приведения:
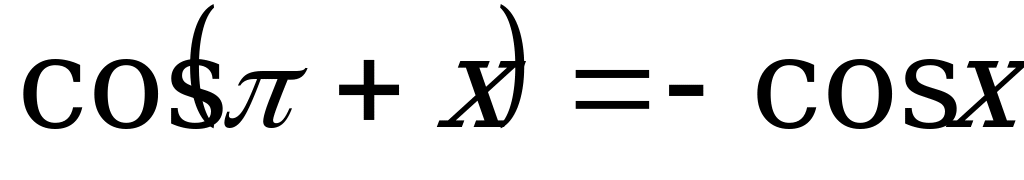 и
и 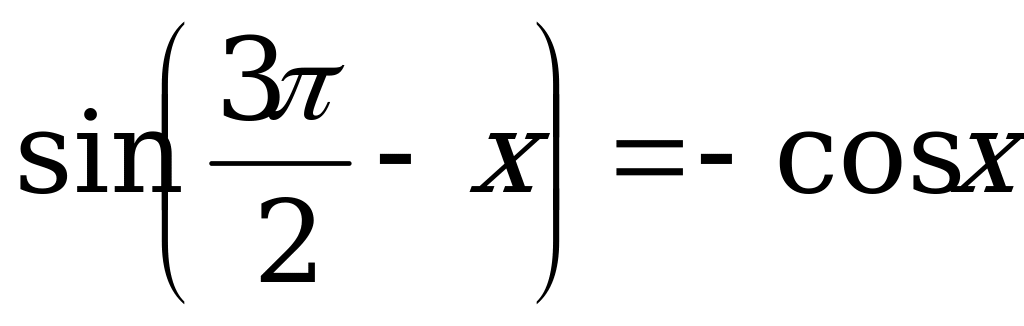 .
.
Тогда уравнение (1) перепишем в виде:
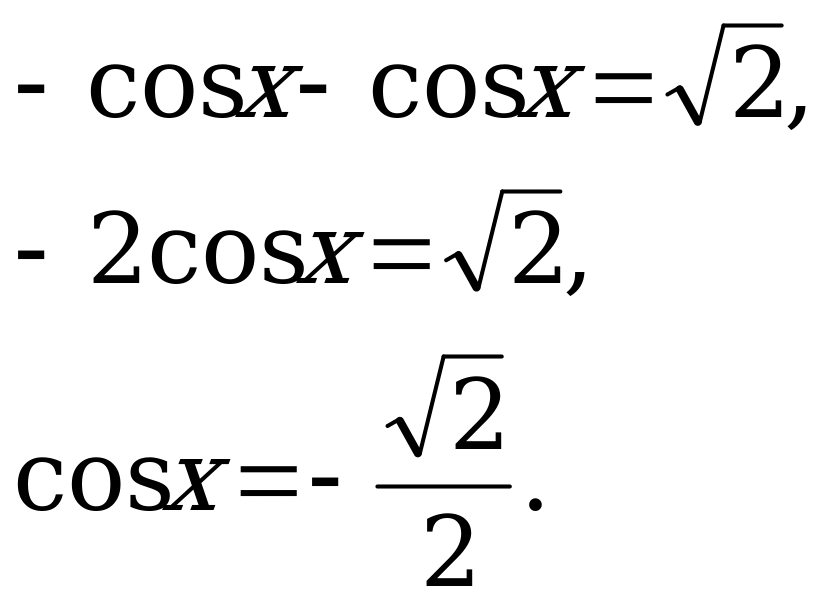
Получили простейшее тригонометрическое уравнение. Найдём его решение.


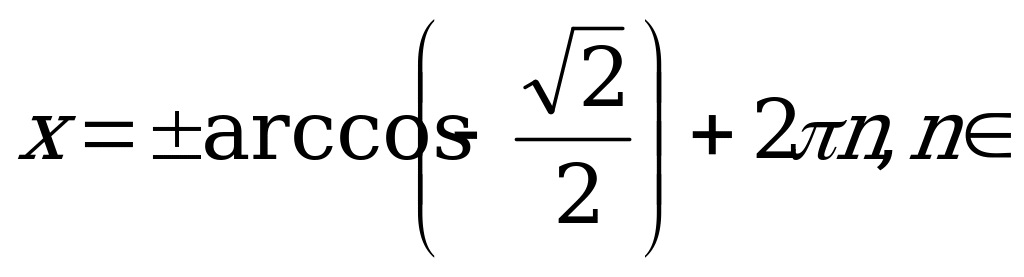 Z;
Z;
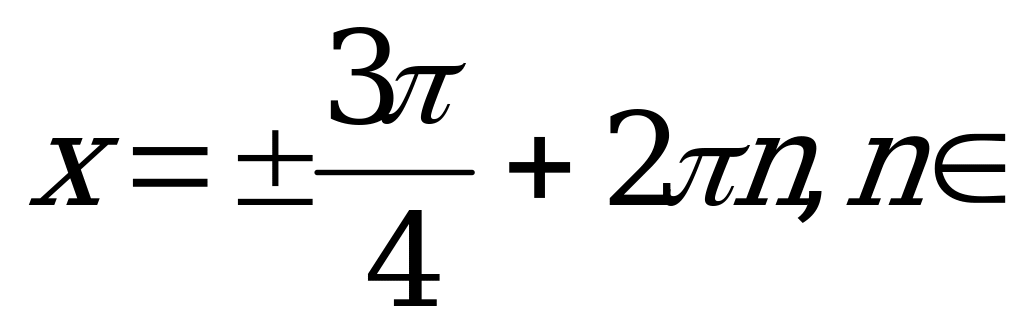 Z.
Z.
б) Решим уравнение 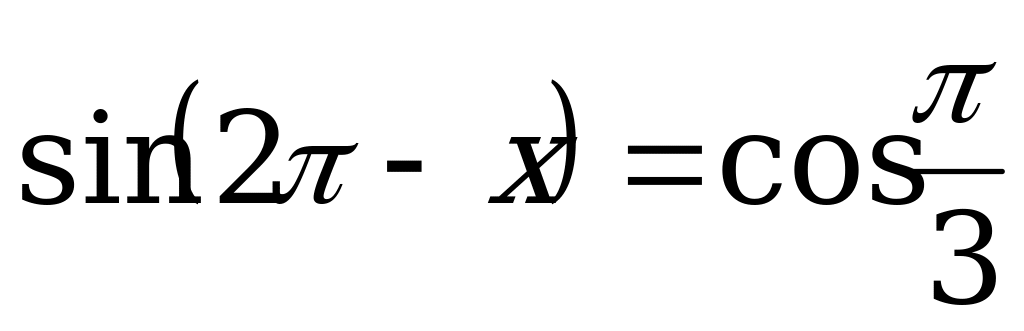 . (2)
. (2)
По формулам приведения: 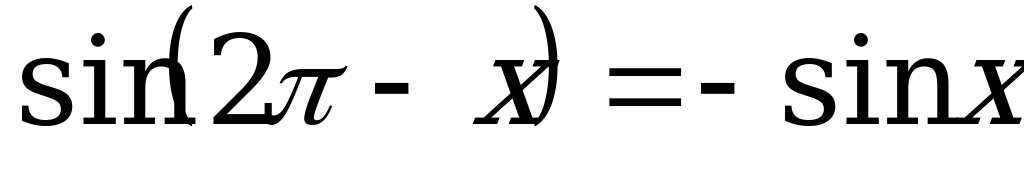 , а
, а 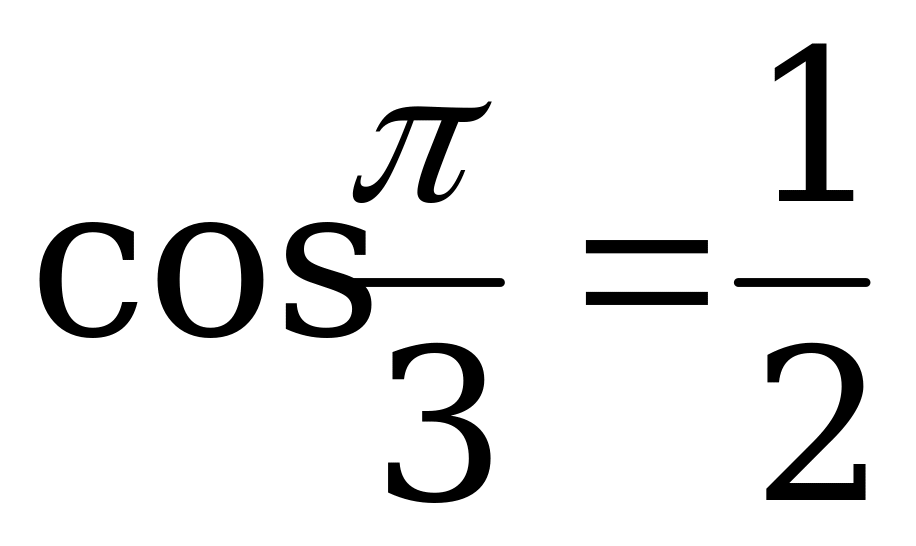 . Тогда уравнение (2) имеет вид:
. Тогда уравнение (2) имеет вид:
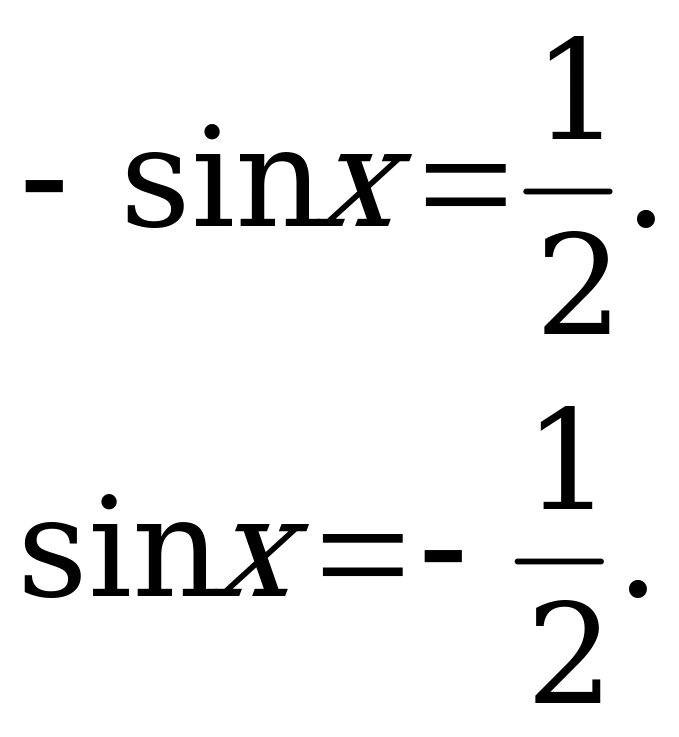
Получили простейшее тригонометрическое уравнение. Запишем его ответ.
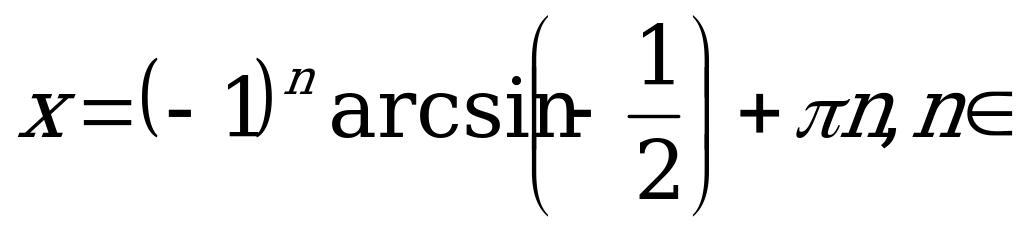 Z.
Z.
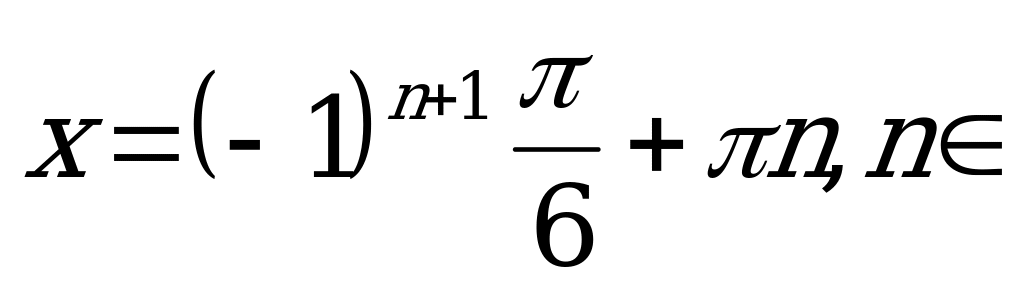 Z.
Z.
в) Решим уравнение 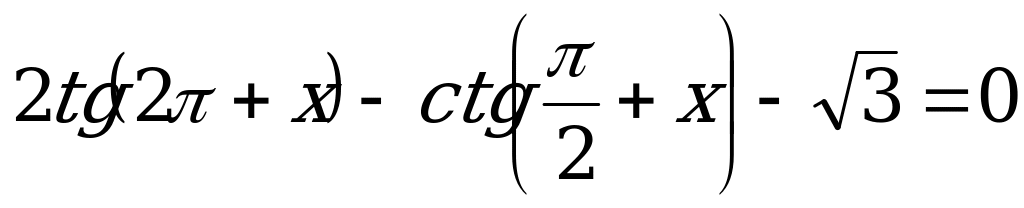 . (3)
. (3)
По формулам приведения: 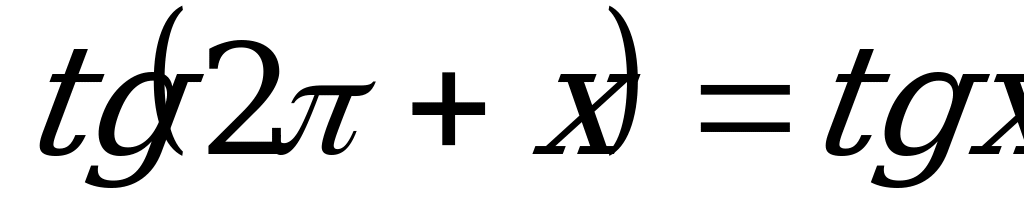 и
и 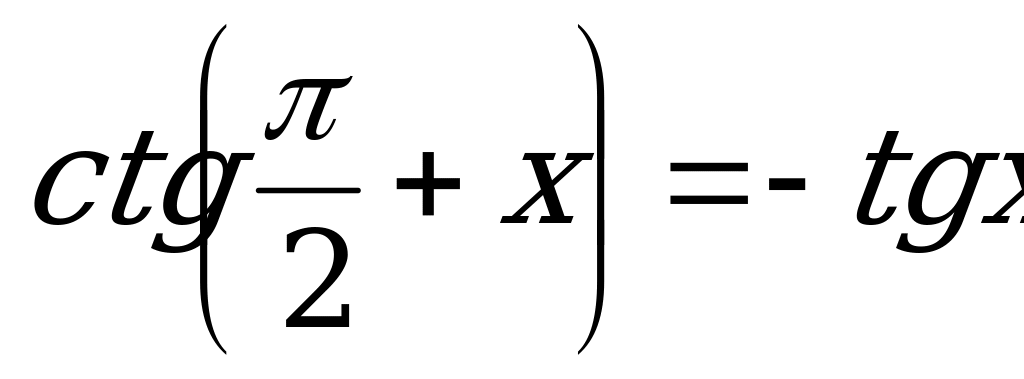 . Тогда уравнение (3) примет вид:
. Тогда уравнение (3) примет вид:
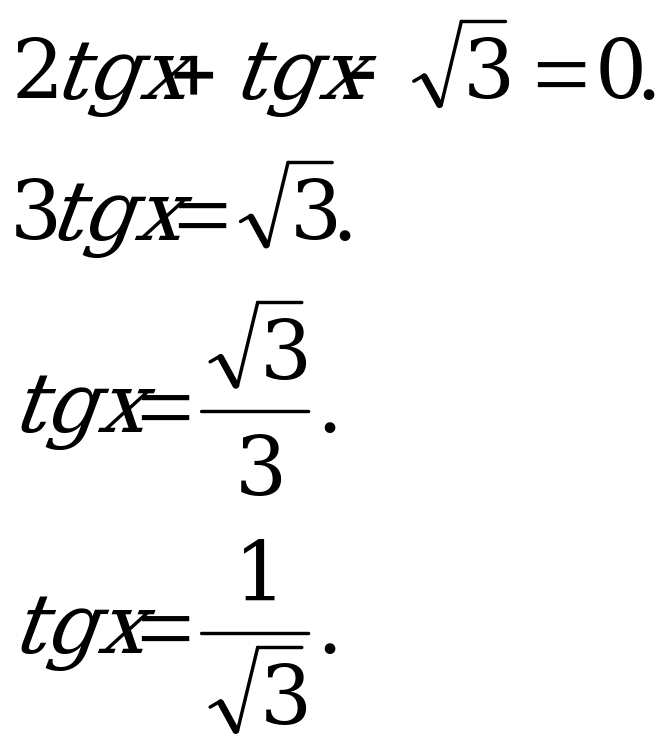
Получили простейшее тригонометрическое уравнение. Найдём его ответ.
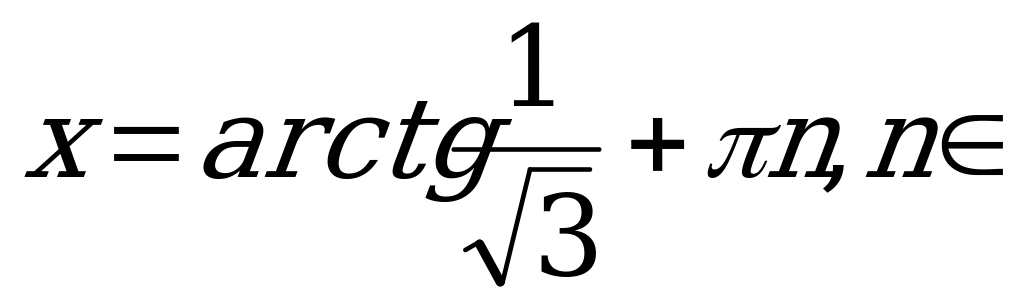 Z.
Z.
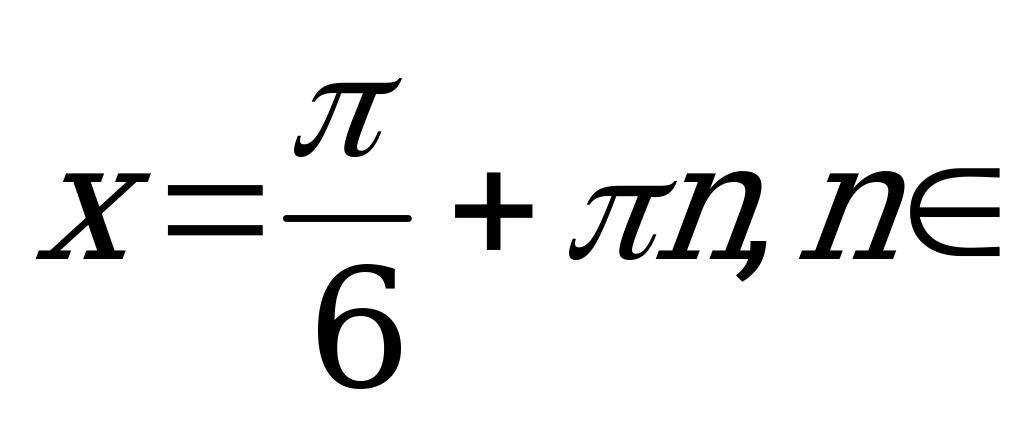 Z.
Z.
5.3. Применение формул двойного угла.
Упражнения с решениями.
Пример 3. Решить уравнения:
а) 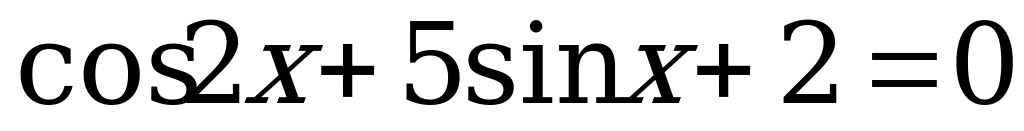 ;
;
б) 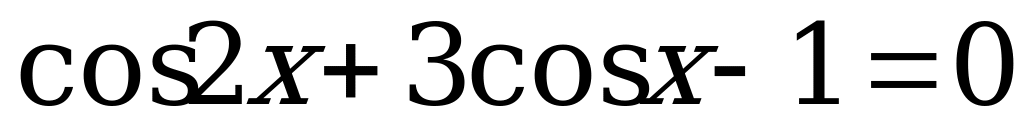 ;
;
в) 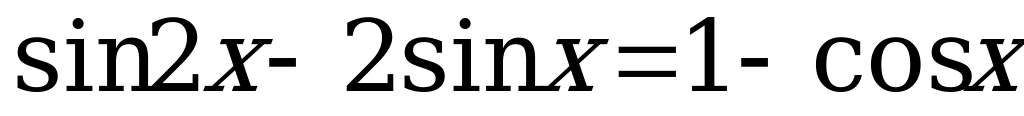 ;
;
г)  .
.
Решение.
а) Решим уравнение 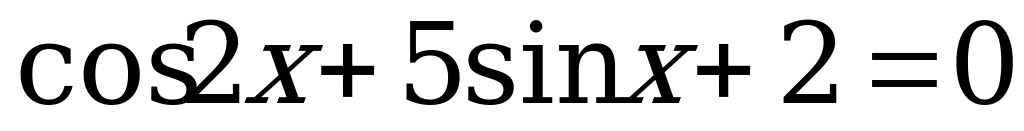 . (1)
. (1)
По формулам двойного угла 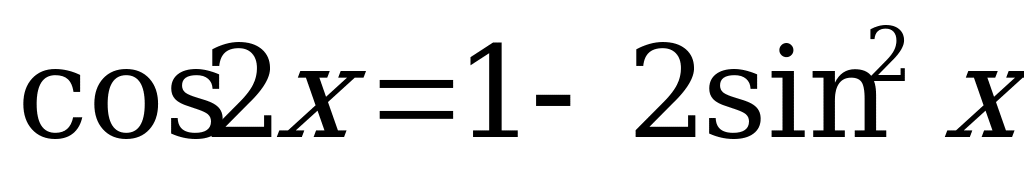 . Тогда уравнение (1) перепишем в виде:
. Тогда уравнение (1) перепишем в виде:

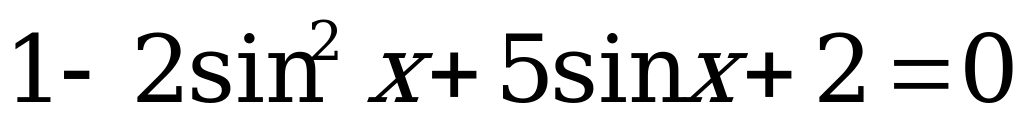 .
.
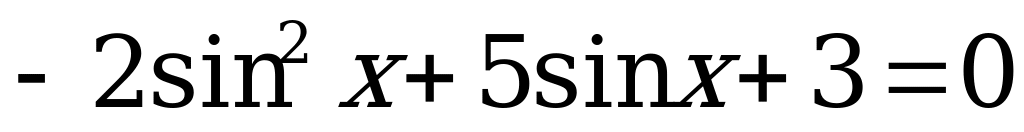 . (2)
. (2)
Заменим 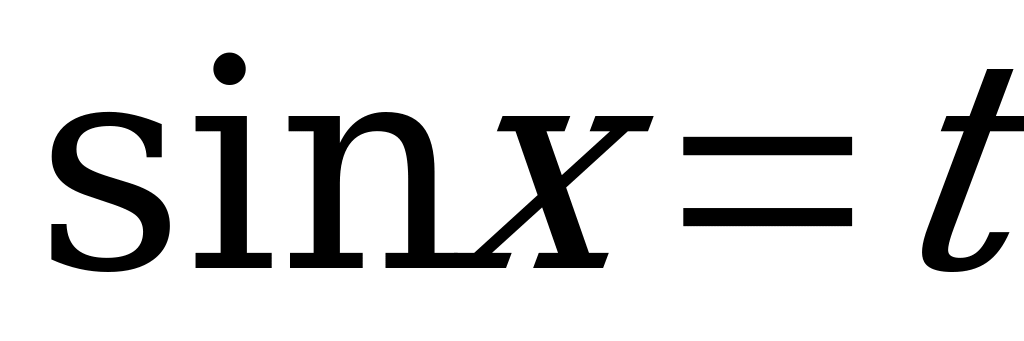 . Теперь уравнение (2) имеет вид:
. Теперь уравнение (2) имеет вид:
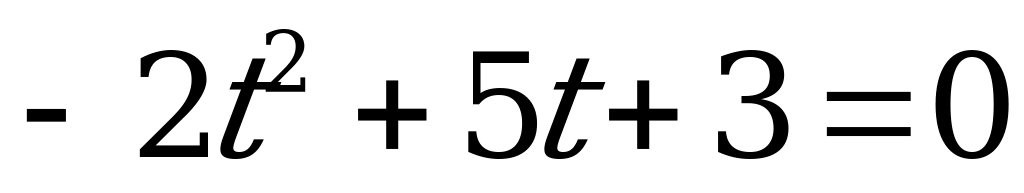 . (3)
. (3)
Найдём корни уравнения (3).
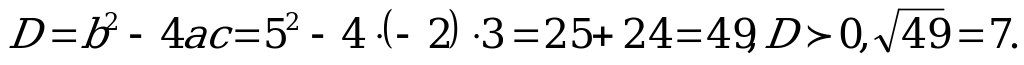
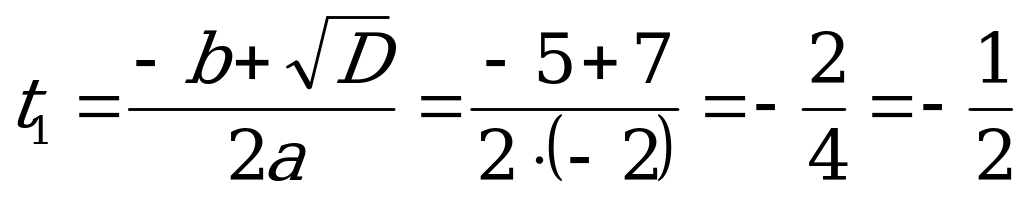 ;
; 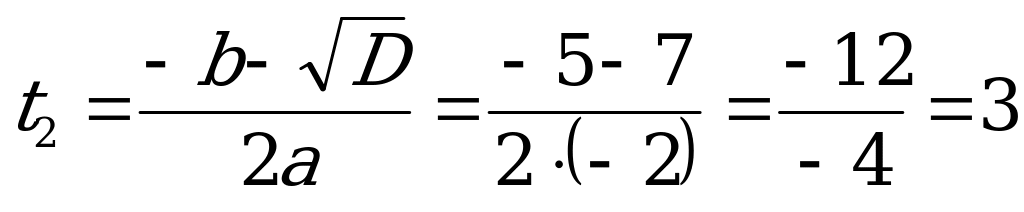 .
.
Следовательно:
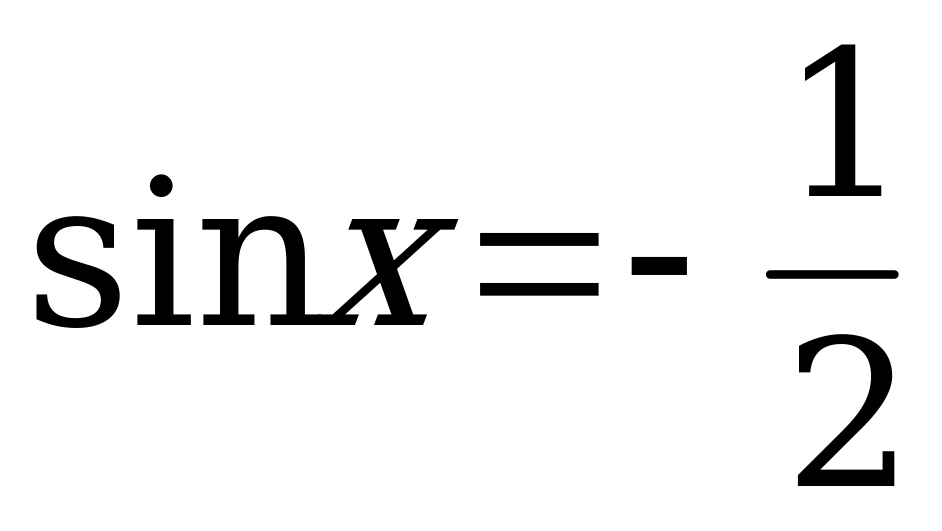 , и
, и 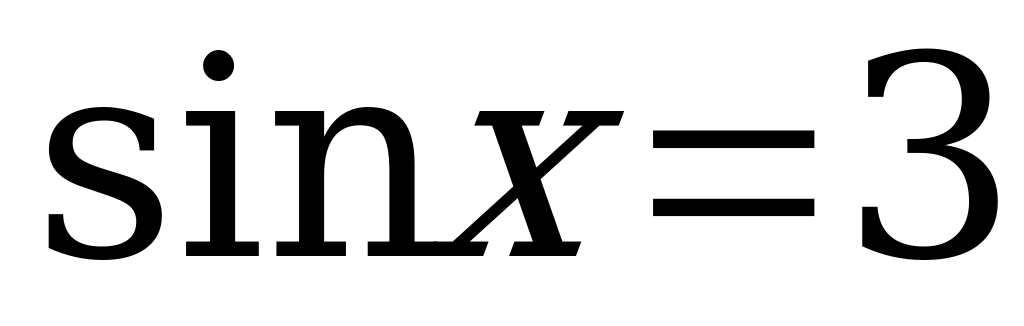 .
.
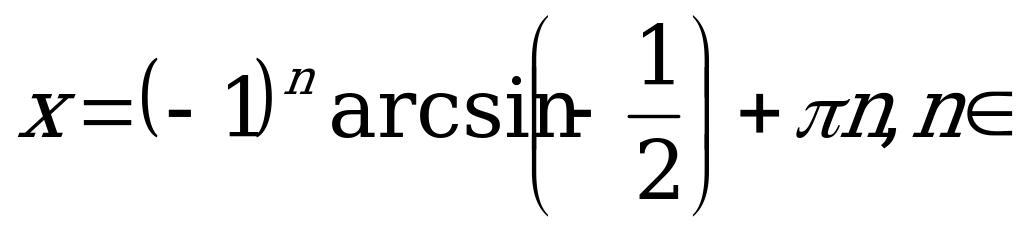 Z. Решений нет, так как
Z. Решений нет, так как 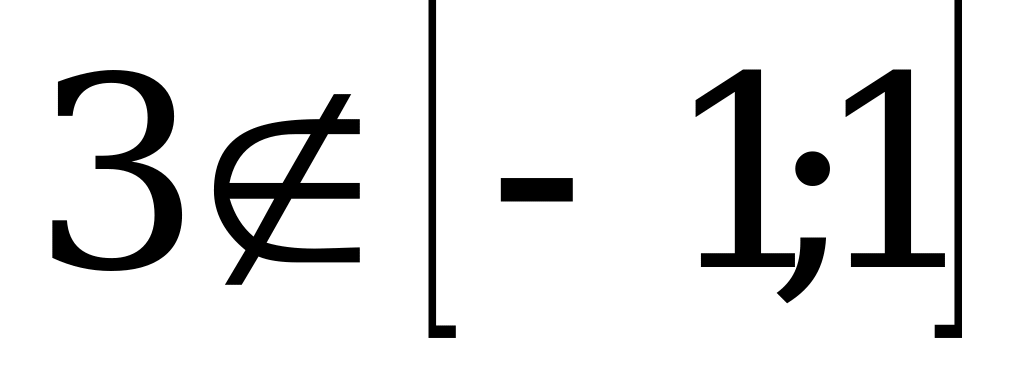 .
.
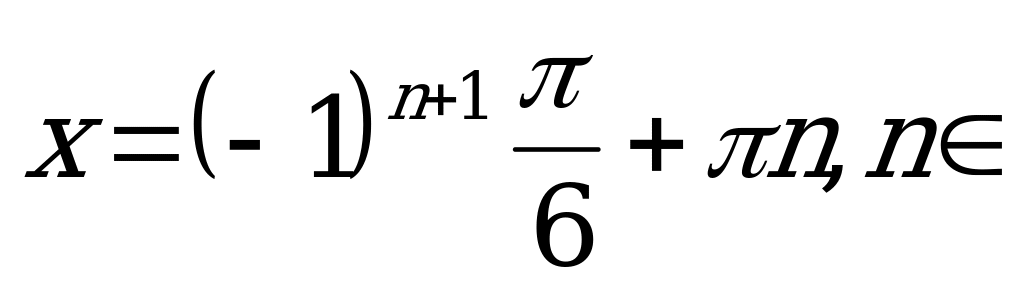 Z.
Z.
Ответ: 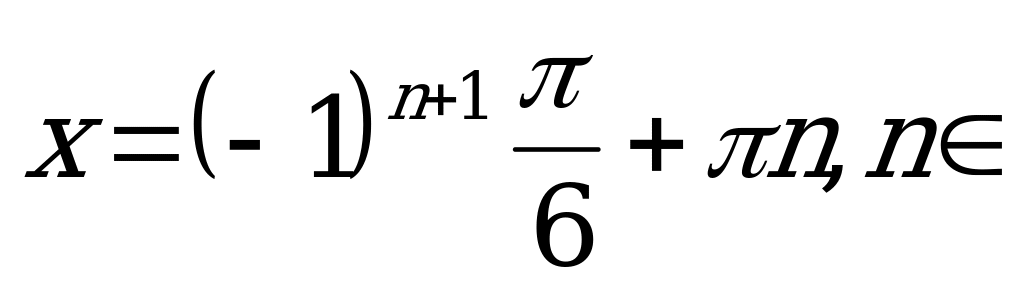 Z.
Z.
б) Решим уравнение 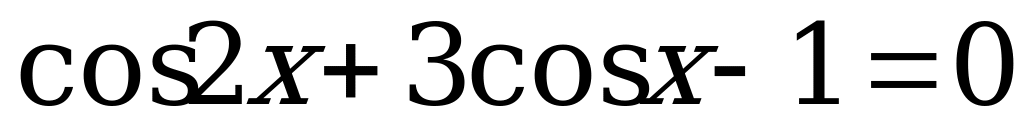 . (4)
. (4)
По формулам двойного угла 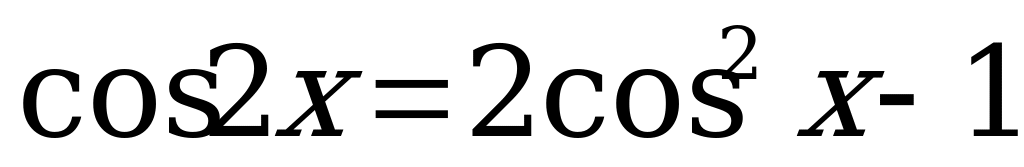 . Тогда уравнение (4) примет вид:
. Тогда уравнение (4) примет вид:
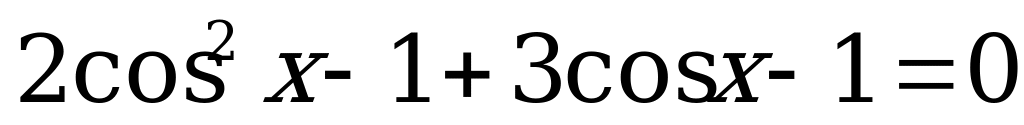 .
.

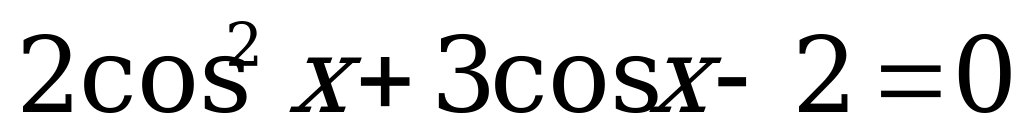 . (5)
. (5)
Введём новое неизвестное  . Тогда уравнение (5) станет квадратным уравнением с неизвестным
. Тогда уравнение (5) станет квадратным уравнением с неизвестным 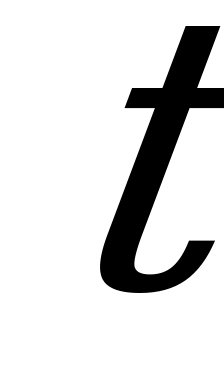 .
.
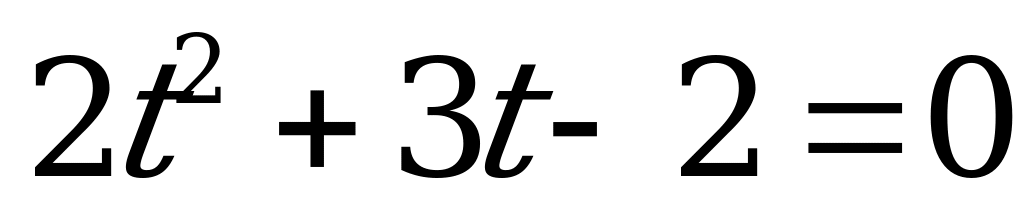 . (6)
. (6)
Найдём корни уравнения (6).
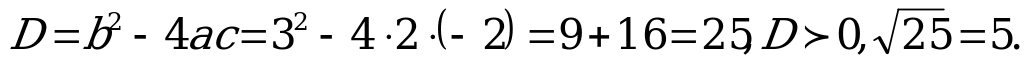
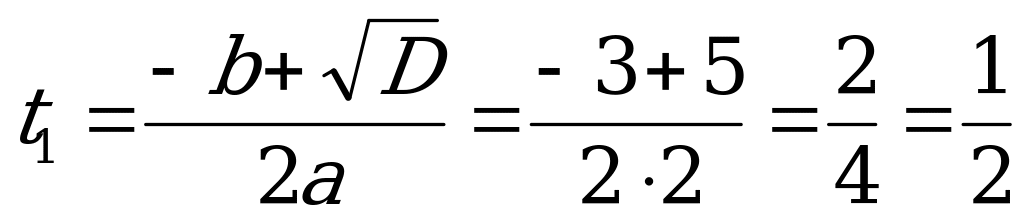 ;
; 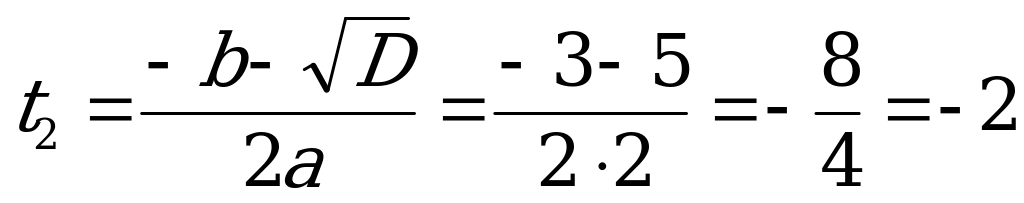 ;
;
Следовательно
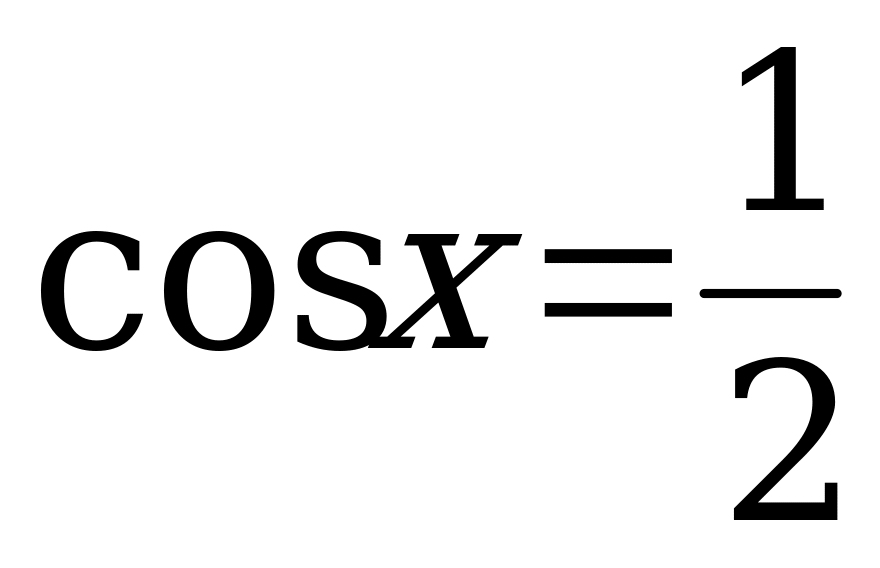 , и
, и 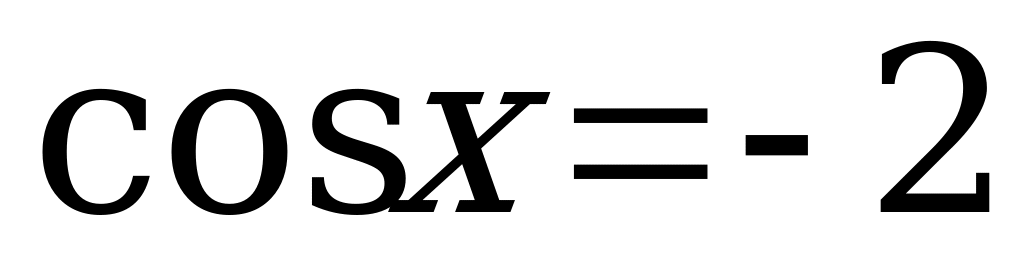 .
.
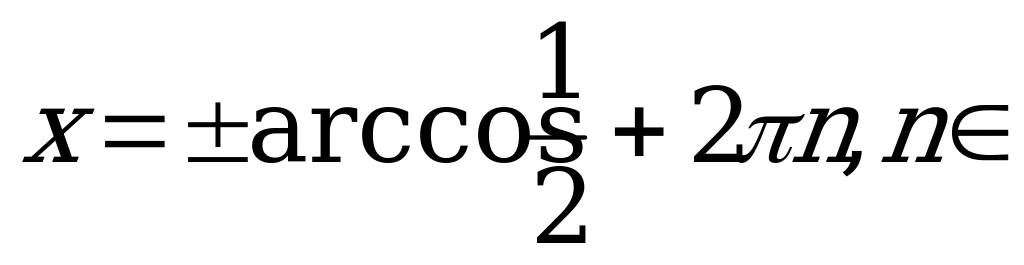 Z. Решений нет, так как
Z. Решений нет, так как 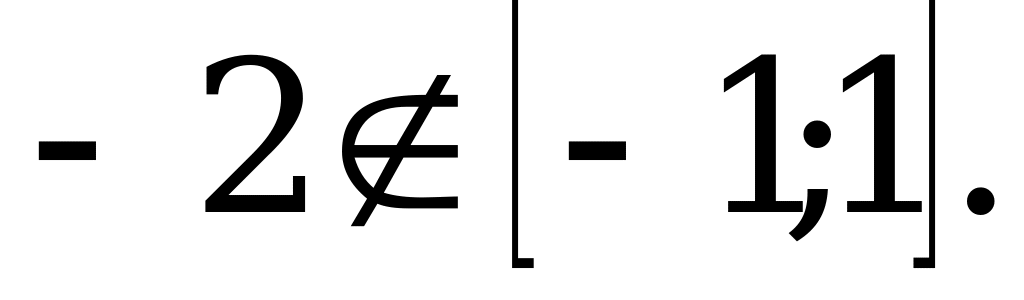
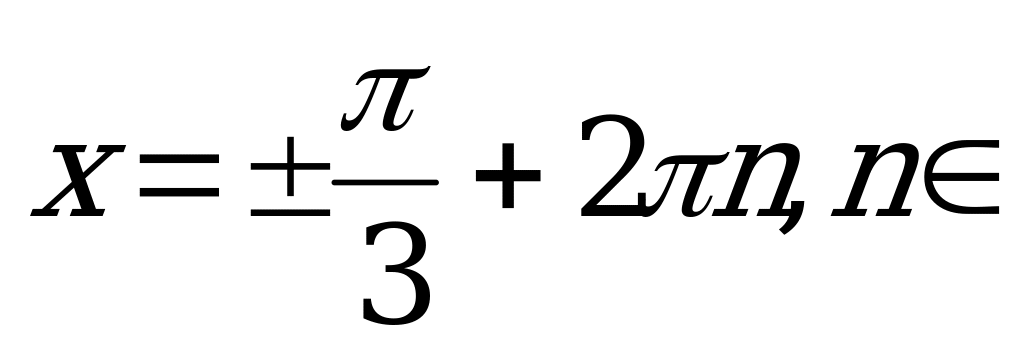 Z.
Z.
Ответ: 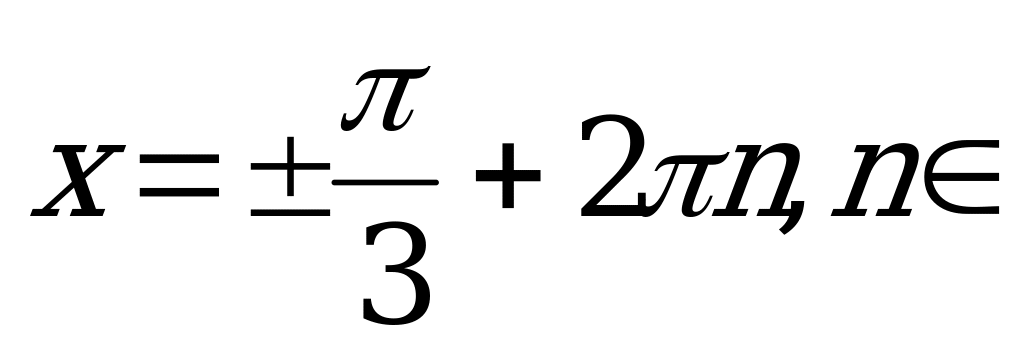 Z.
Z.
в) Решим уравнение 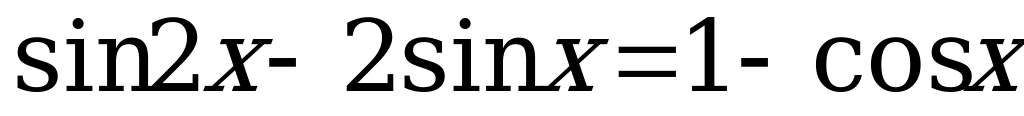 . (7)
. (7)
По формулам двойного угла 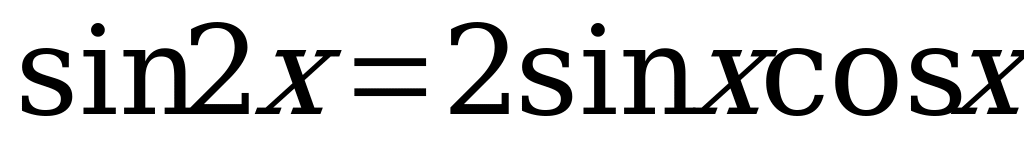 . Тогда уравнение (7) примет вид:
. Тогда уравнение (7) примет вид:
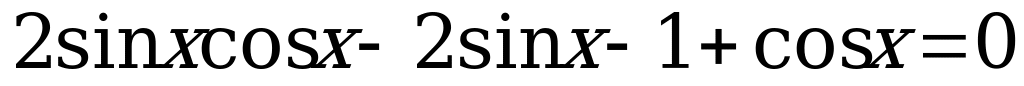 . (8)
. (8)
Сгруппируем в уравнение (8) первое слагаемое со вторым, а третье с четвёртым и вынесем за скобки общий множитель.
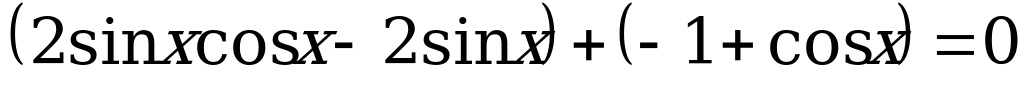 .
.
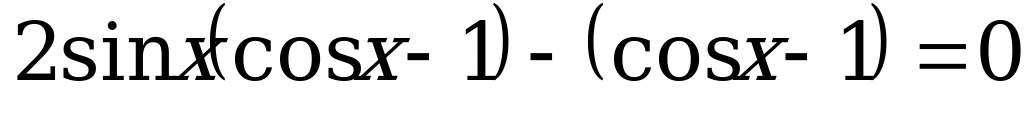 .
.
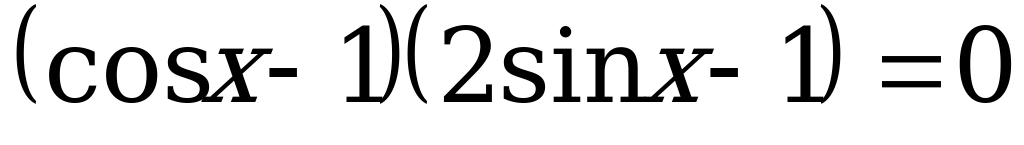 .
.
Приравняем каждый из множителей к нулю. В результате получим два простейших тригонометрических уравнения:
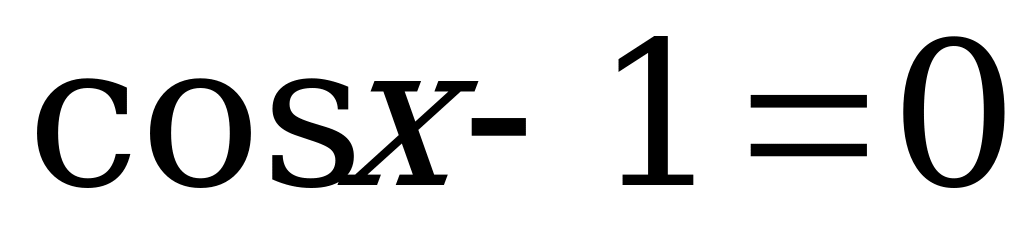 , или
, или 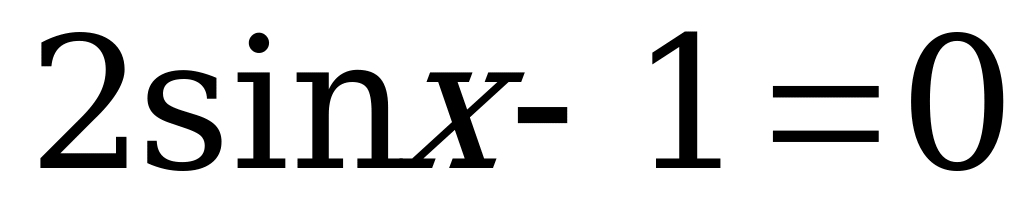 .
.
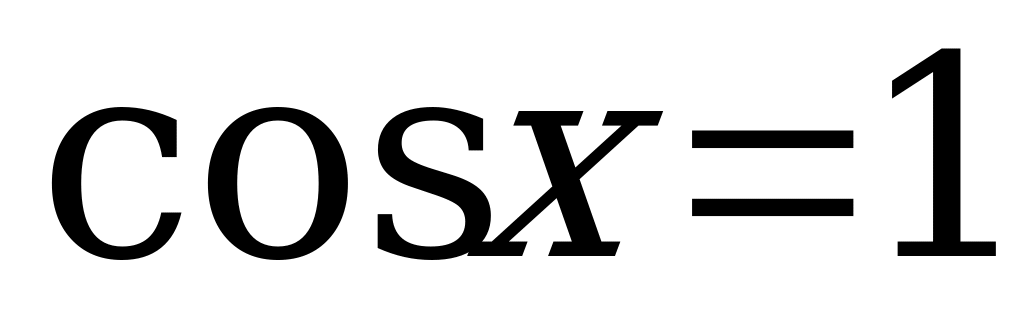 .
. 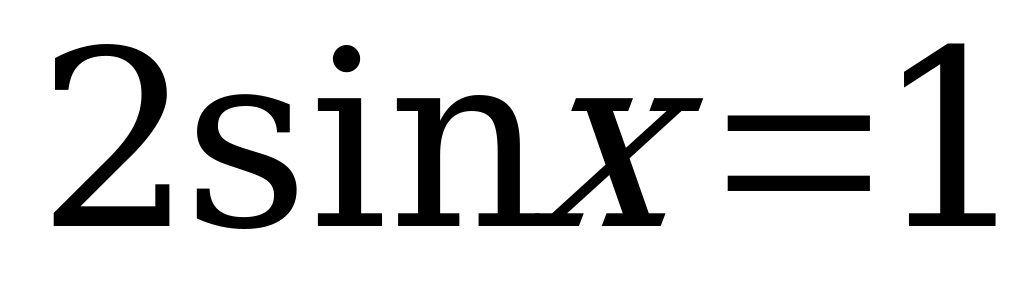 .
.
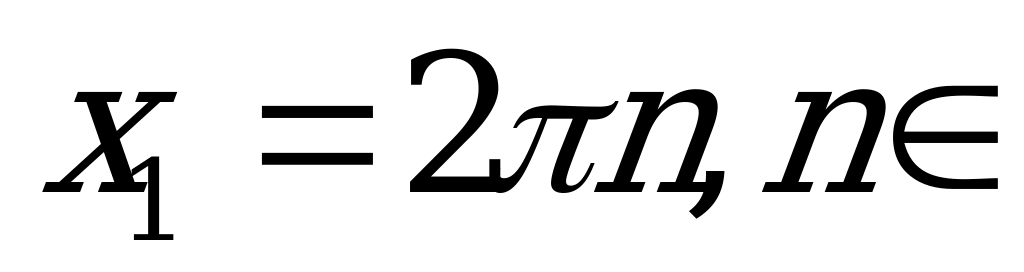 Z.
Z. 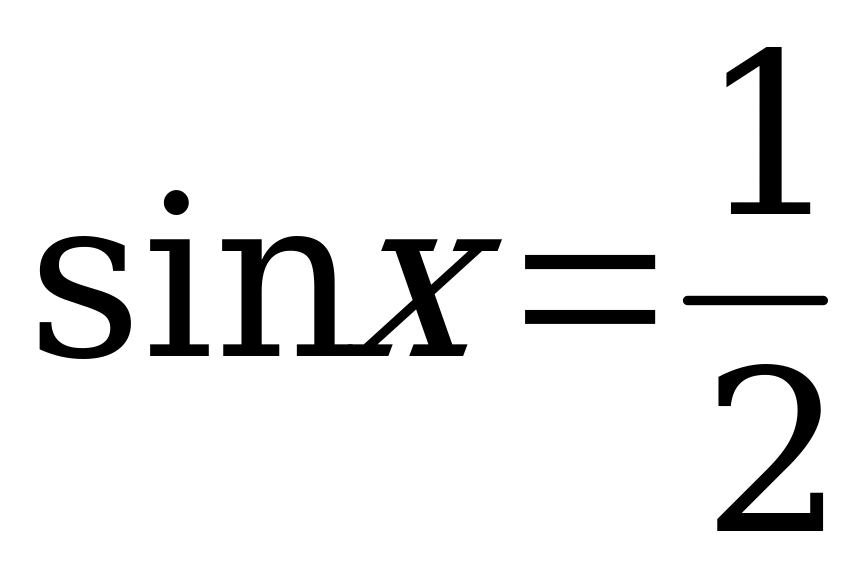 .
.
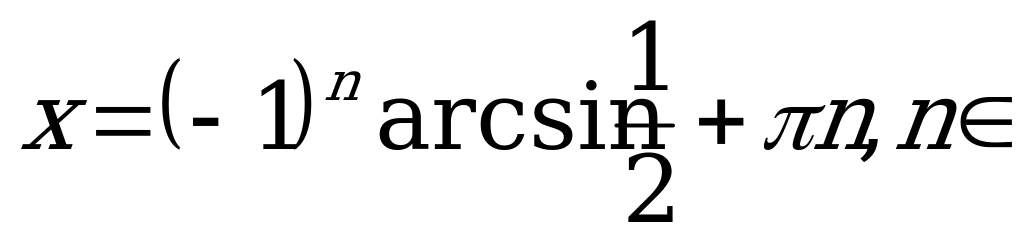 Z.
Z.
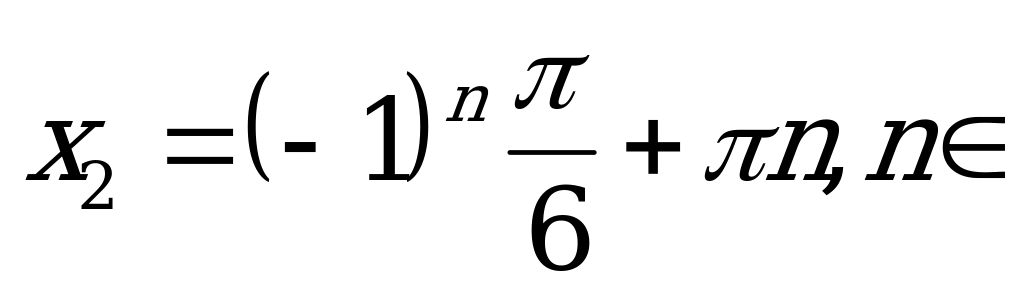 Z.
Z.
Ответ: 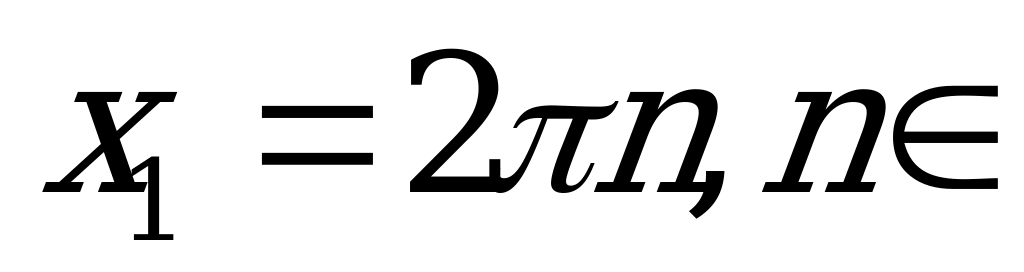 Z,
Z, 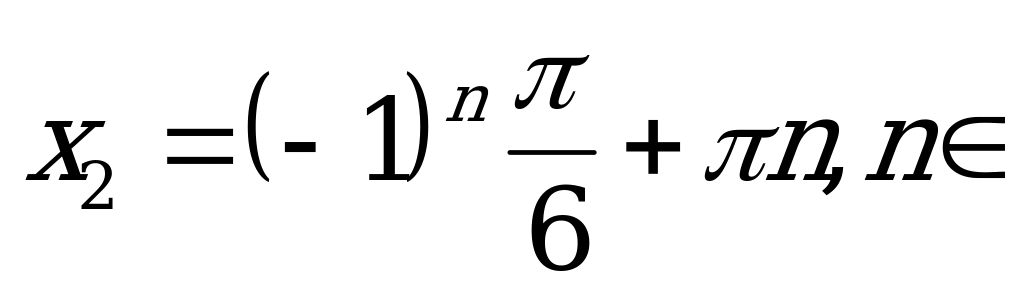 Z.
Z.
г) Решим уравнение  . (9)
. (9)
По формулам двойного угла 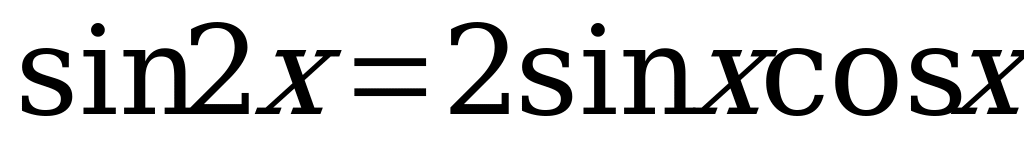 . Тогда уравнение (9) перепишем в виде:
. Тогда уравнение (9) перепишем в виде:
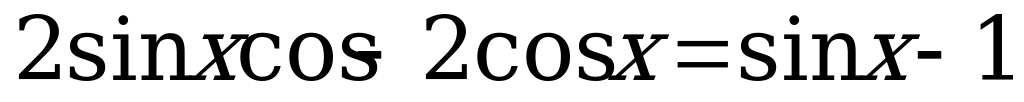 .
.
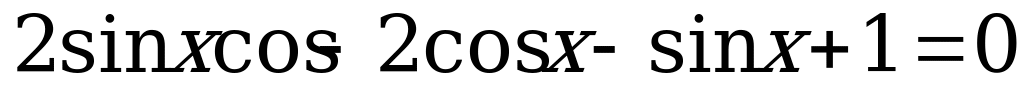 . (10)
. (10)
Сгруппируем в уравнение (10) первое слагаемое со вторым, а третье с четвёртым и вынесем общий множитель за скобки.

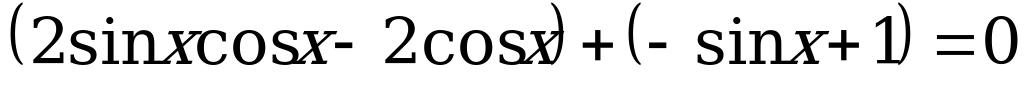 .
.
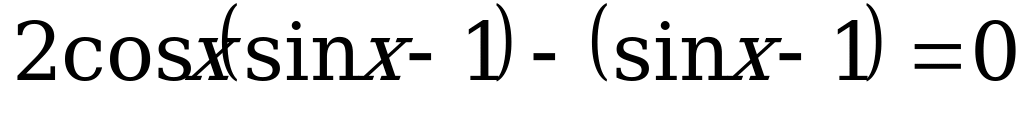 .
.
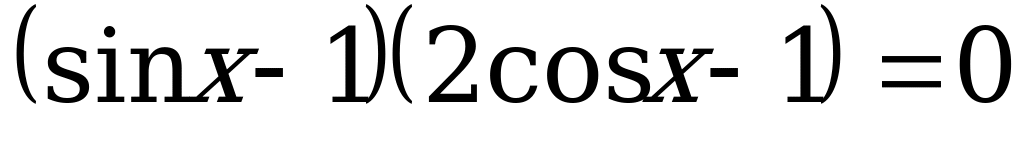 .
.
Тогда:
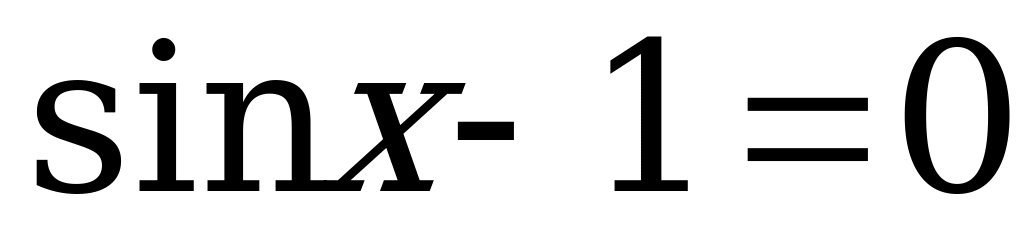 , или
, или 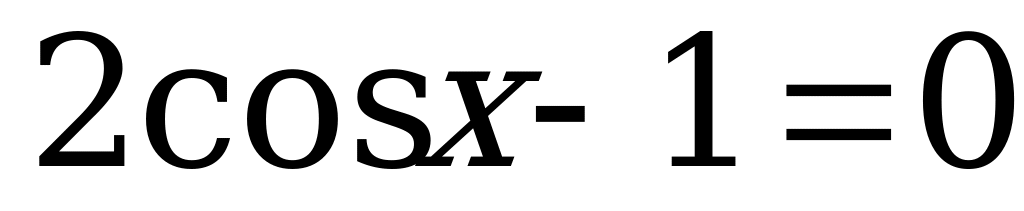 .
.
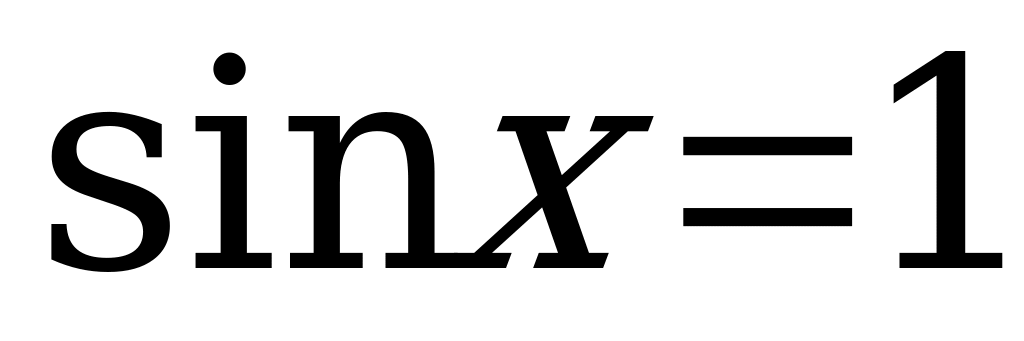 .
. 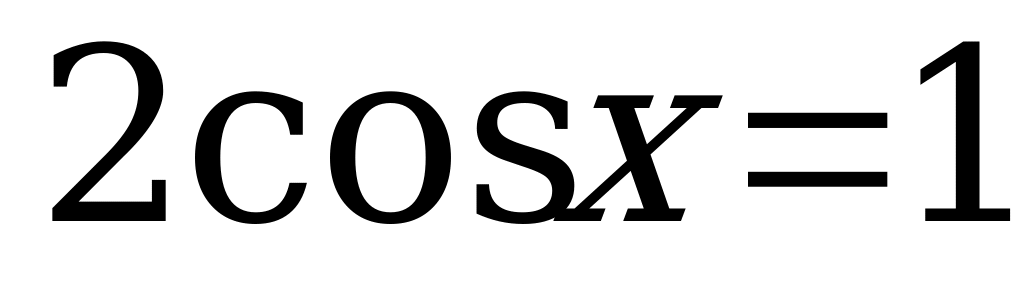 .
.
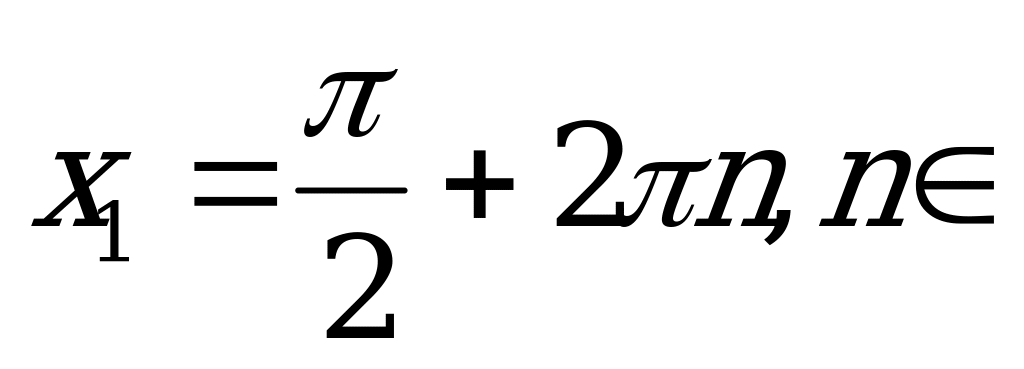 Z.
Z. 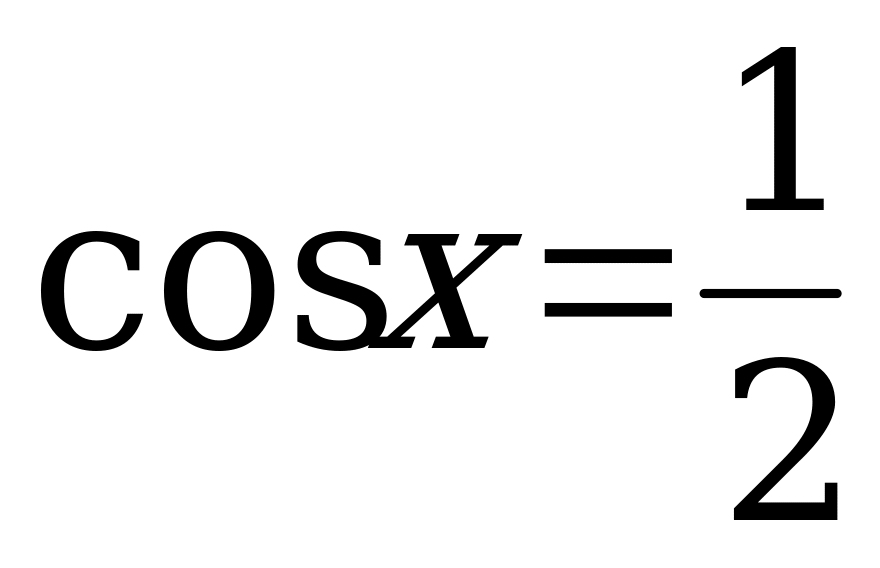 .
.
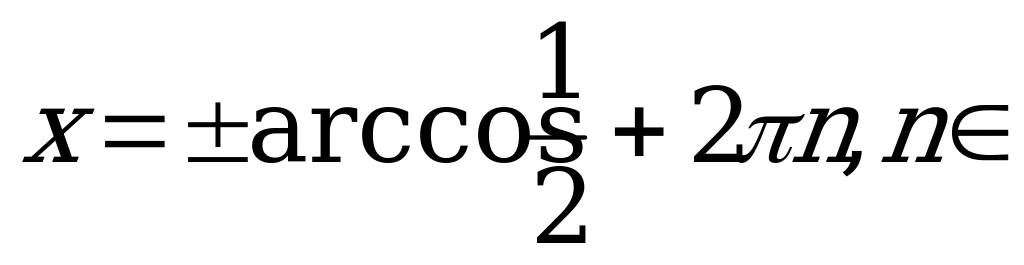 Z.
Z.
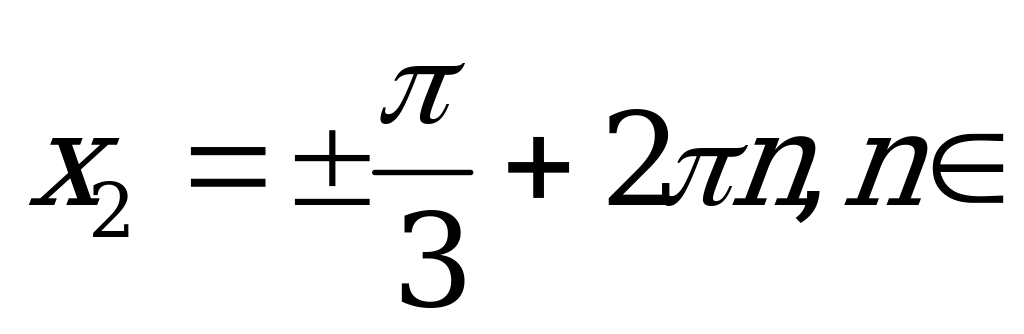 Z.
Z.
Ответ: 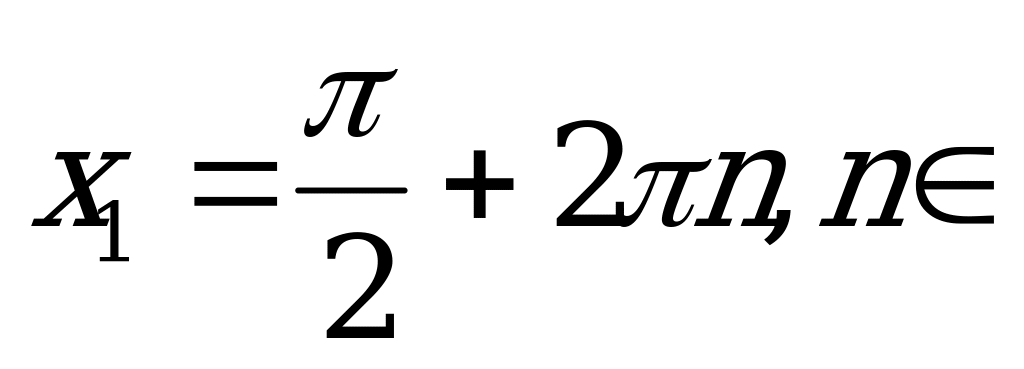 Z,
Z, 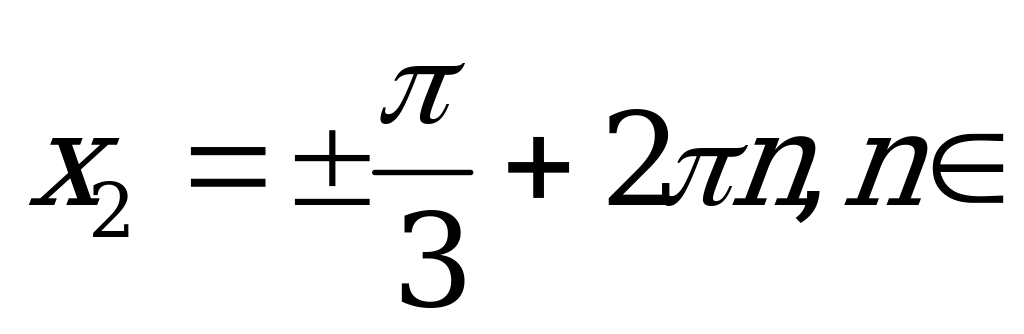 Z.
Z.
5.4. Однородные уравнения.
Справочный материал.
Уравнение вида 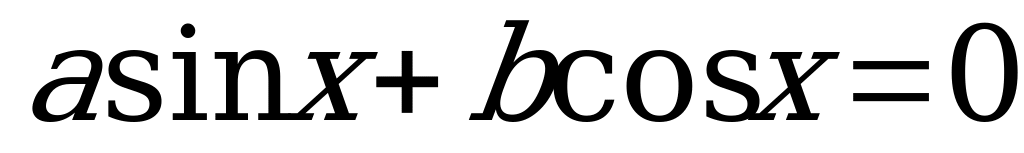 , где
, где 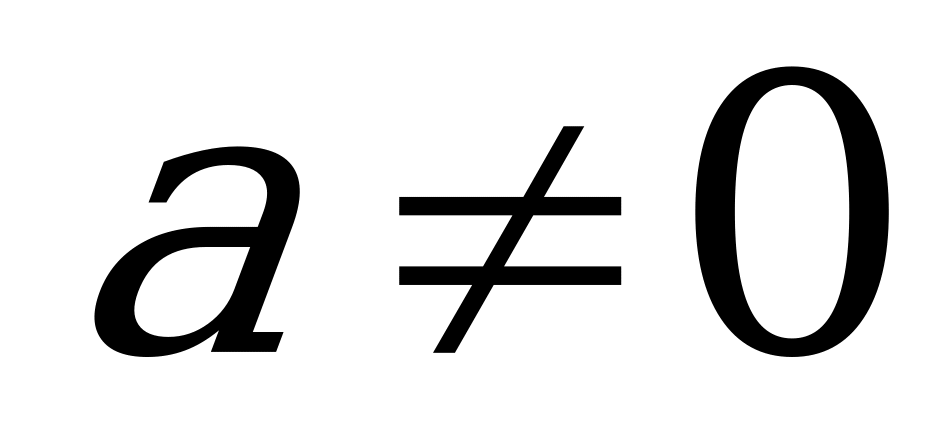 и
и 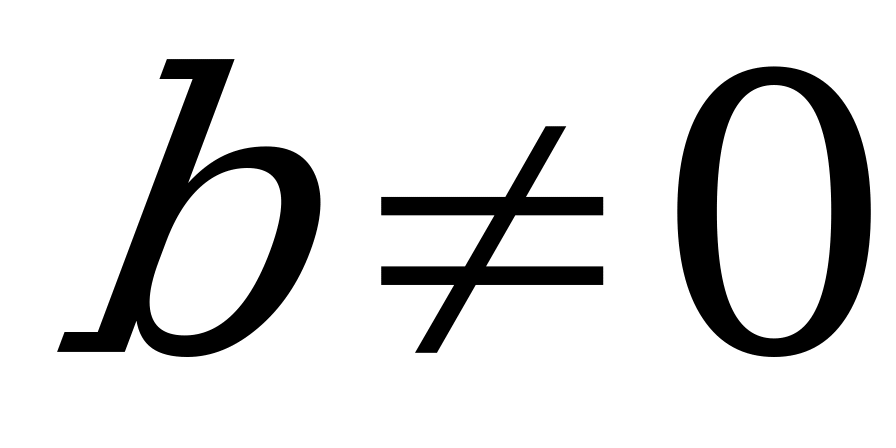 , называется однородным тригонометрическим уравнением первой степени. Данное уравнение решается делением обеих его частей на
, называется однородным тригонометрическим уравнением первой степени. Данное уравнение решается делением обеих его частей на 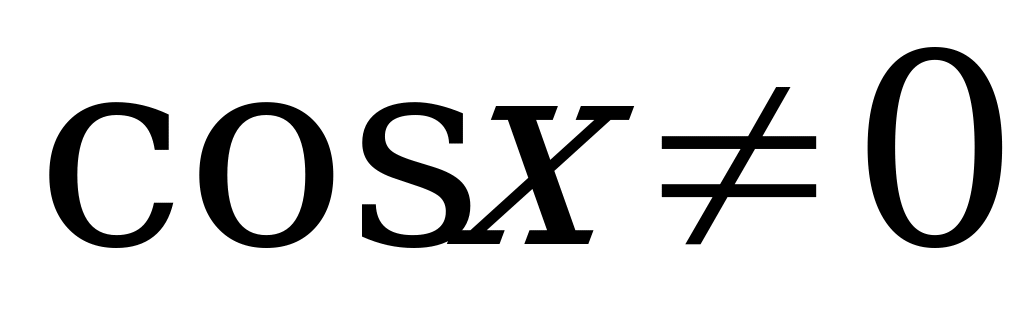 . В результате получается уравнение вида
. В результате получается уравнение вида 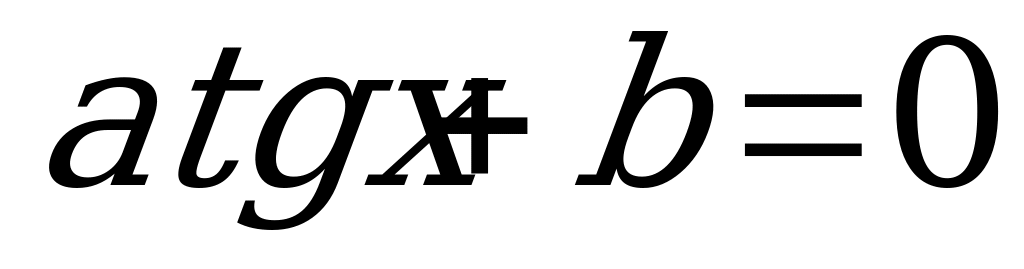 .
.
Упражнения с решениями.
Пример 1. Решить уравнение 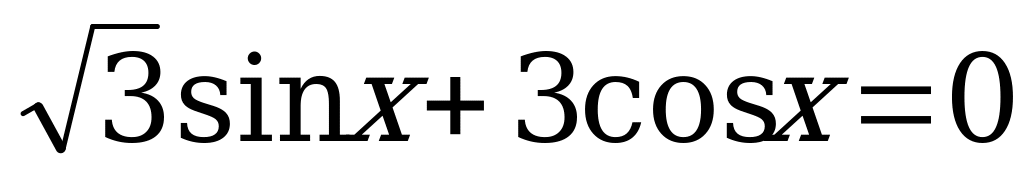 . (1)
. (1)
Решение. Разделив обе части уравнения (1) на 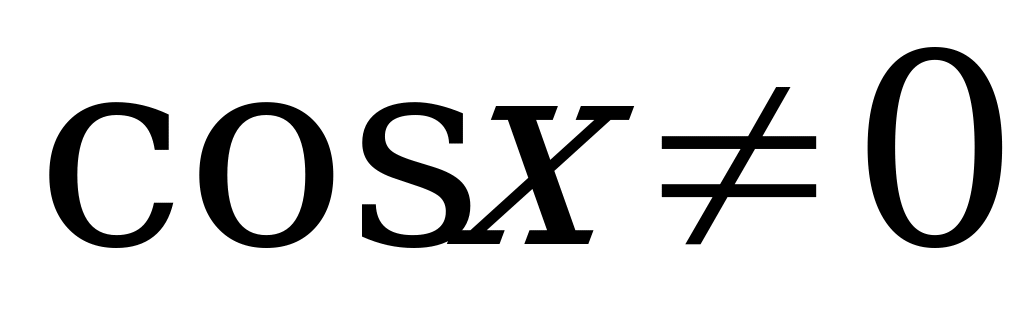 получим:
получим:
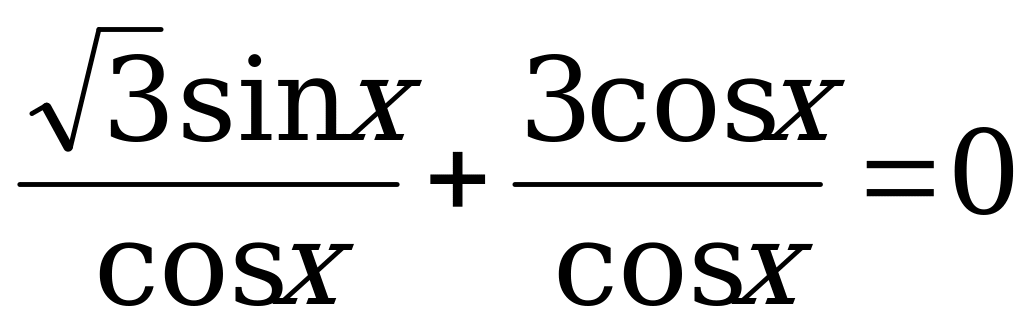 .
.
Так как 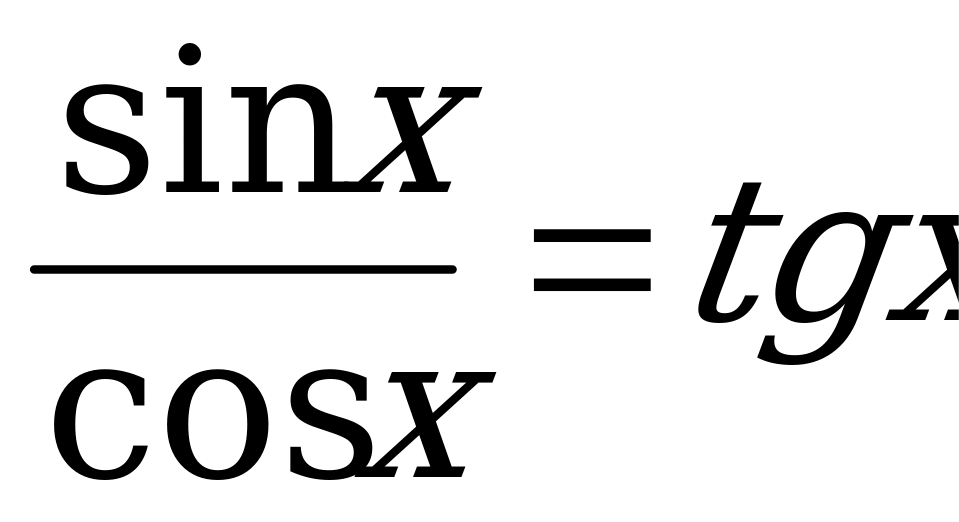 , то
, то
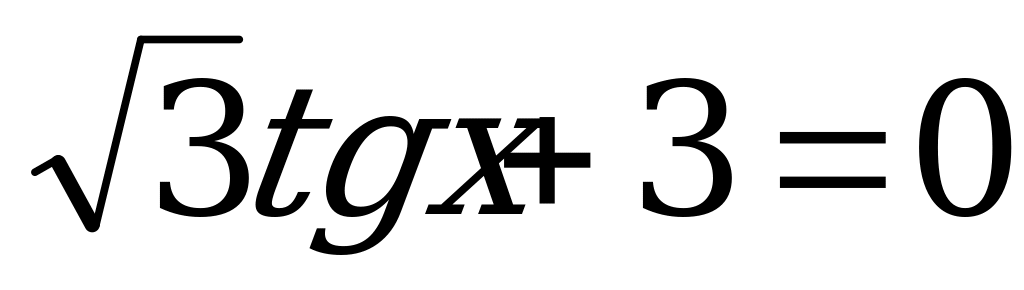 .
.
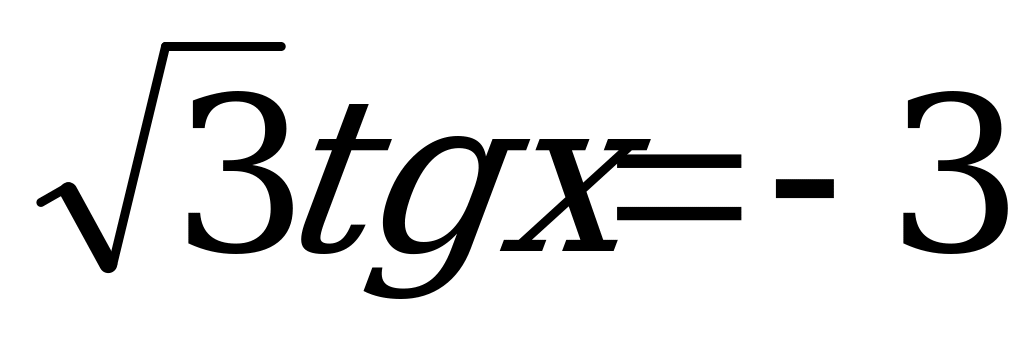 .
.
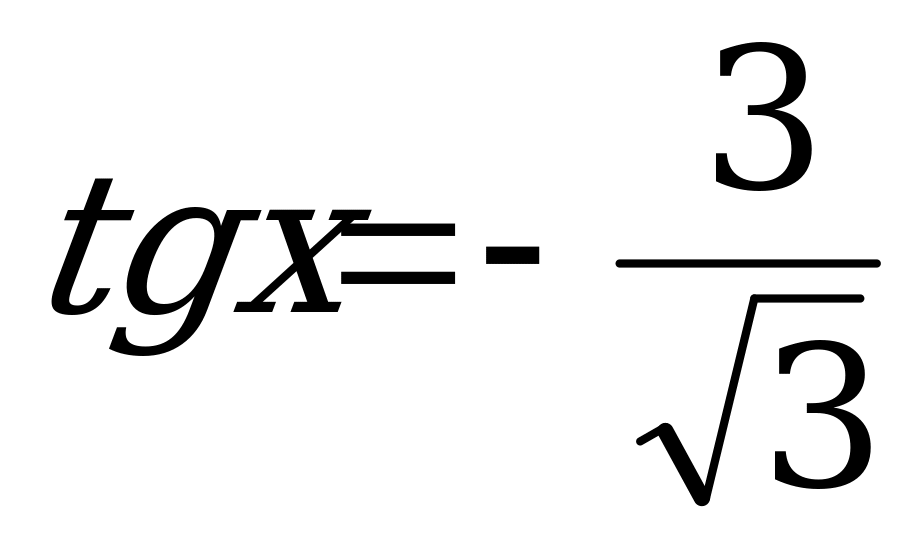 .
.
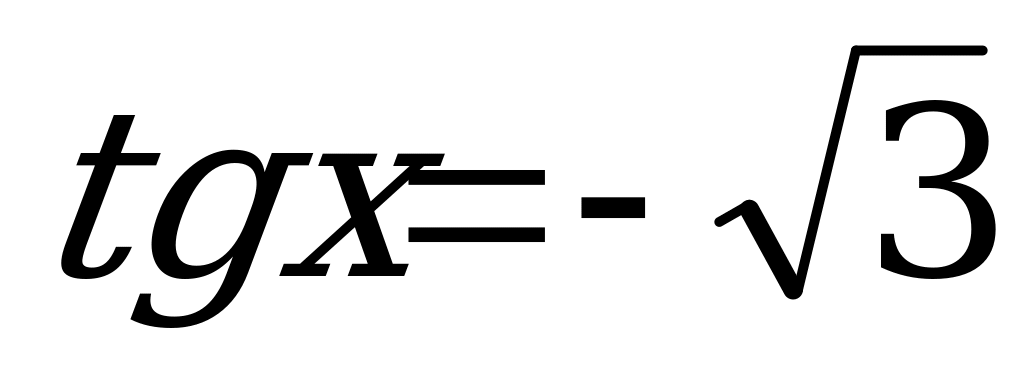 .
.
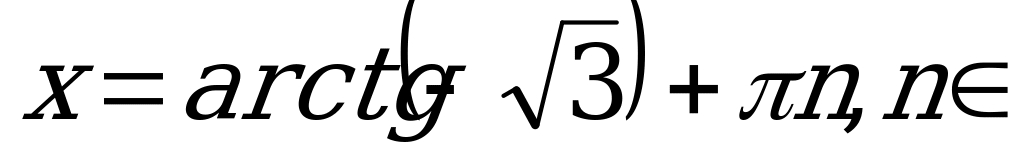 Z.
Z.
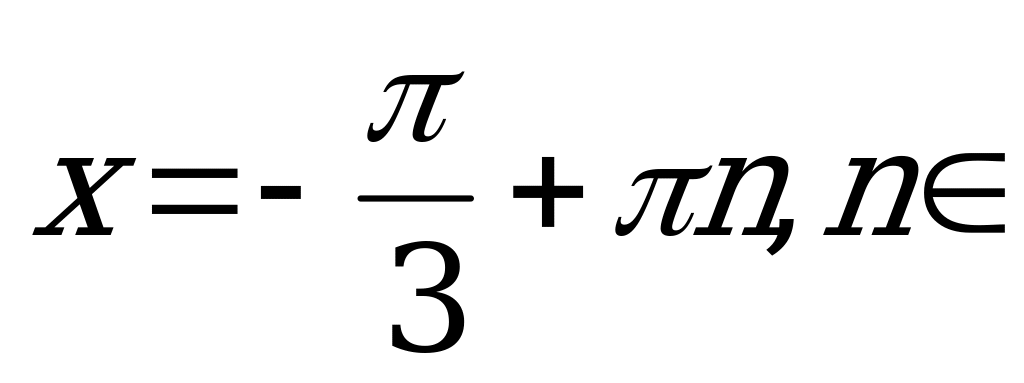 Z.
Z.
Ответ: 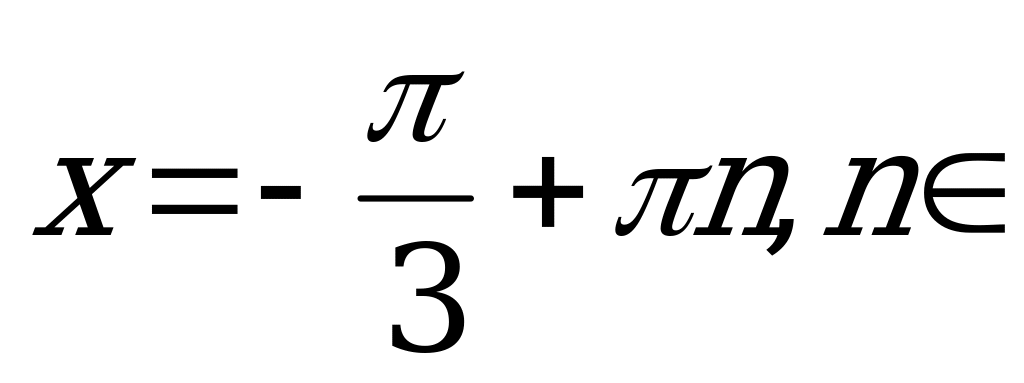 Z.
Z.
Справочный материал.
Уравнение вида
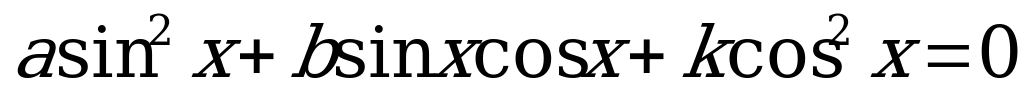 (2)
(2)
называется однородным тригонометрическим уравнением второй степени, если 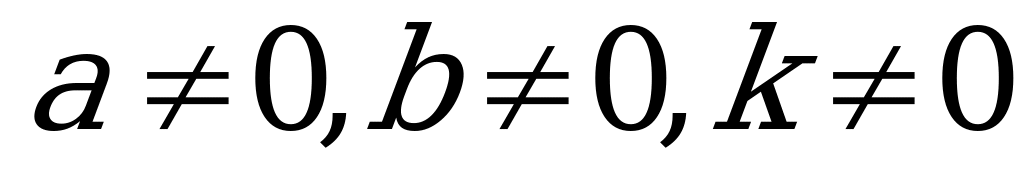 , или какие-либо два из них отличны от нуля.
, или какие-либо два из них отличны от нуля.
Если 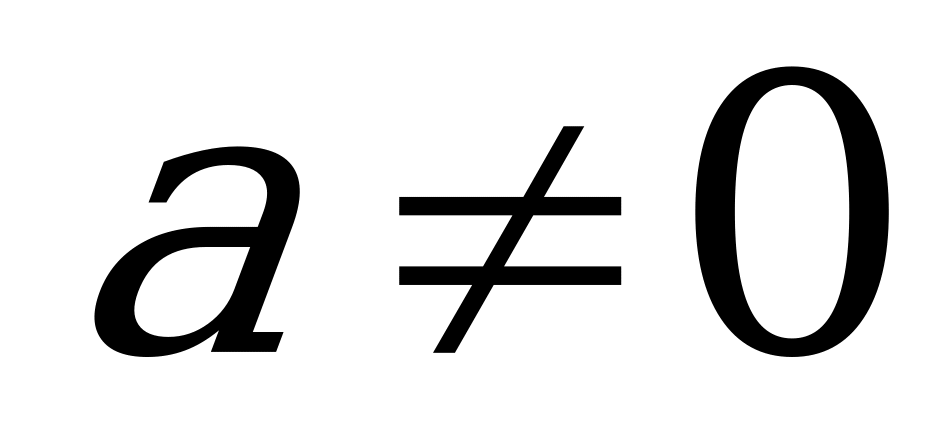 , то для решения уравнения (2) обе его части разделим на
, то для решения уравнения (2) обе его части разделим на 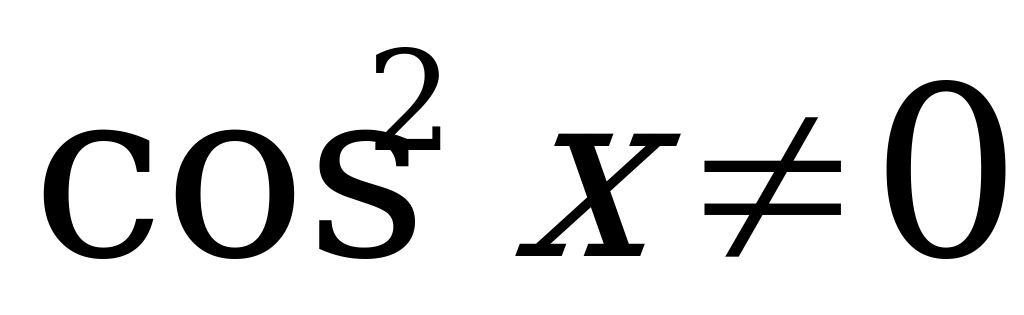 . В результате получим:
. В результате получим:
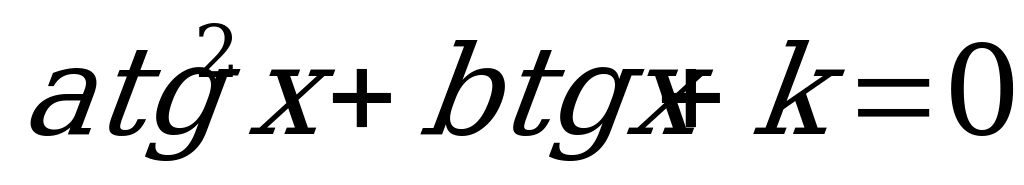 .
.
Если 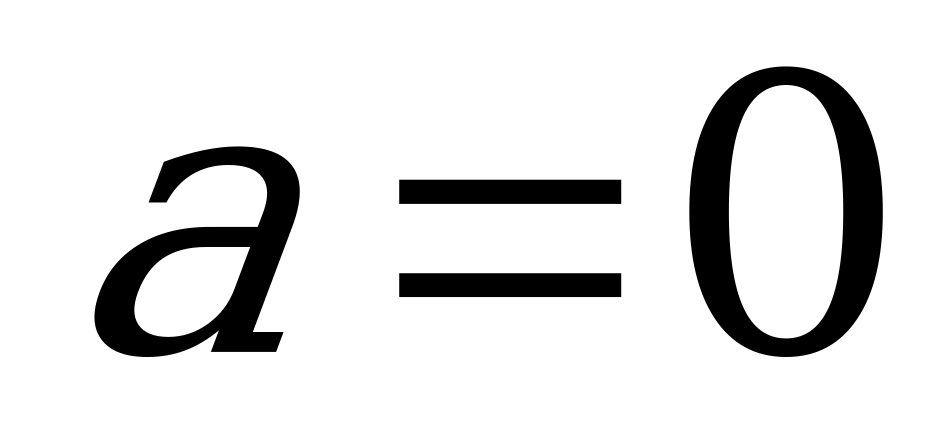 , то уравнение (2) примет вид:
, то уравнение (2) примет вид:
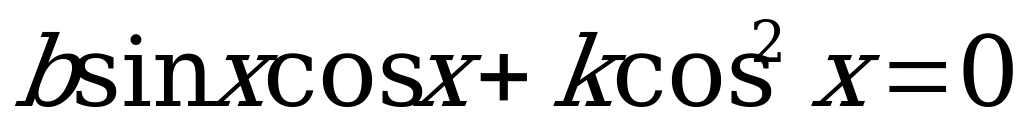 ,
,
которое решается разложением левой части на множители:
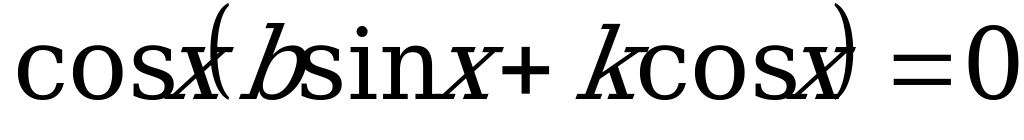 .
.
Пример 2. Решить уравнения:
а) 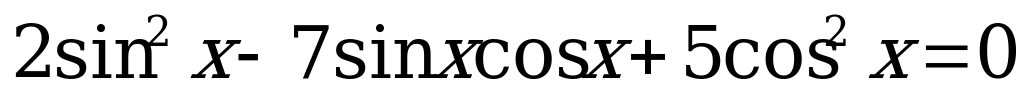 ;
;
б) 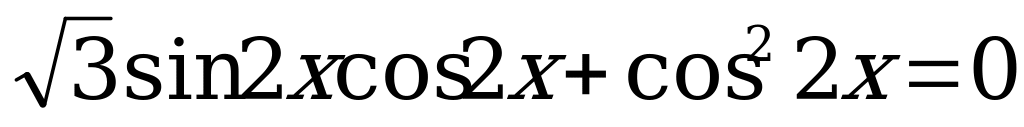 .
.
Решение. а) Решим уравнение 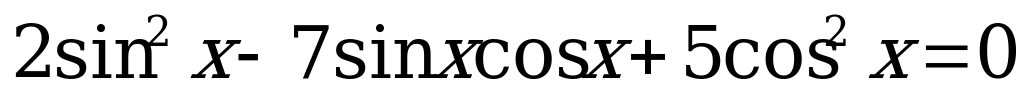 . (3)
. (3)
Так как 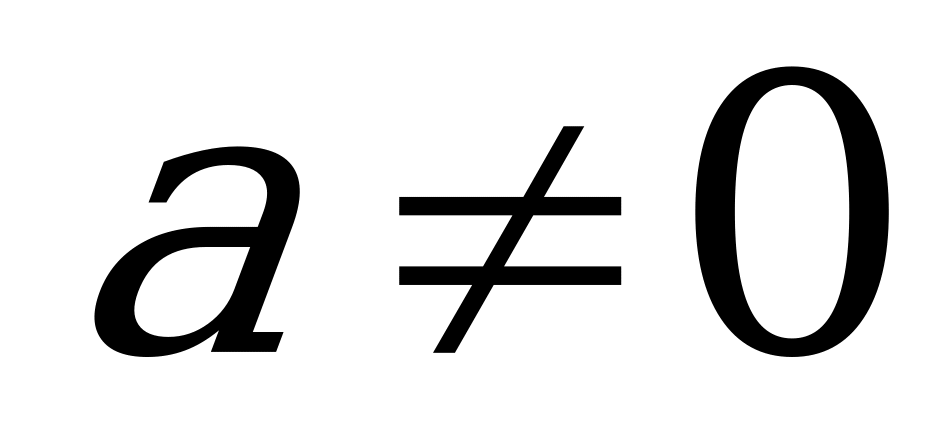 , то разделим обе части уравнения (3) на
, то разделим обе части уравнения (3) на 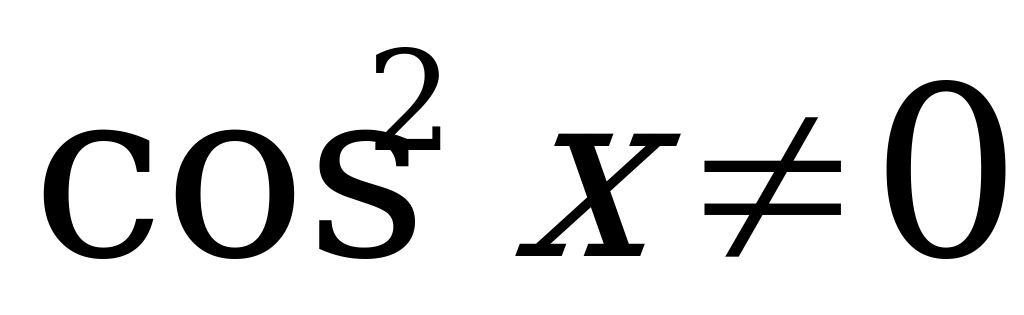 :
:
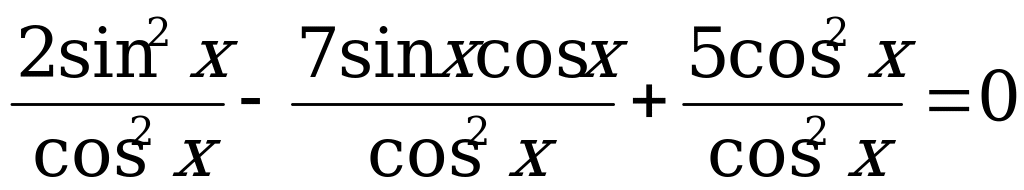 .
.
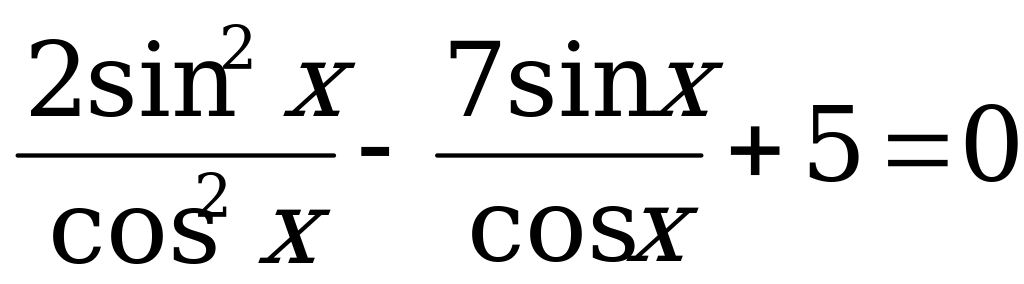 .
.
Так как 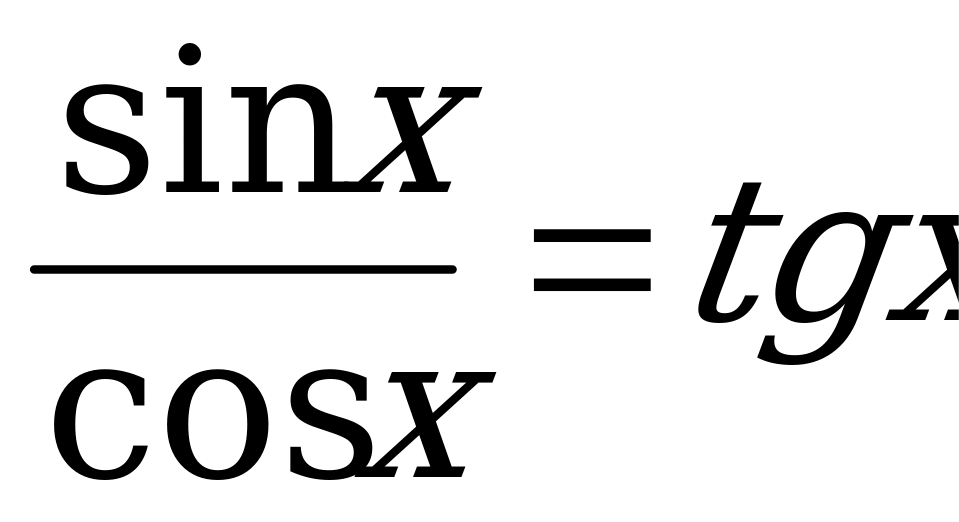 , то
, то
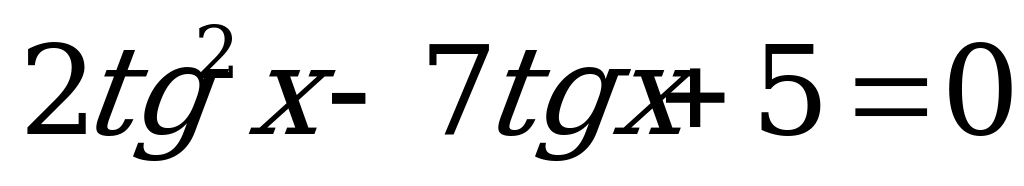 .
.
Введём новое неизвестное 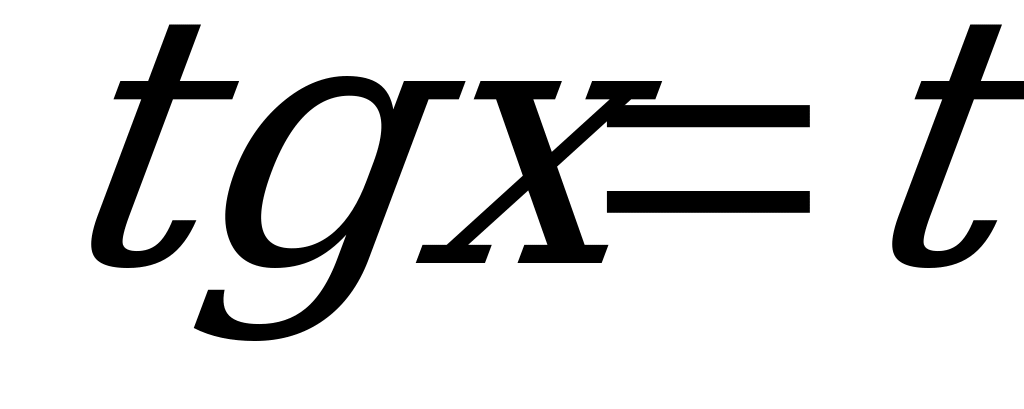 . В результате получим квадратное уравнение с неизвестным
. В результате получим квадратное уравнение с неизвестным 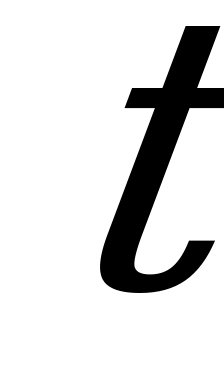

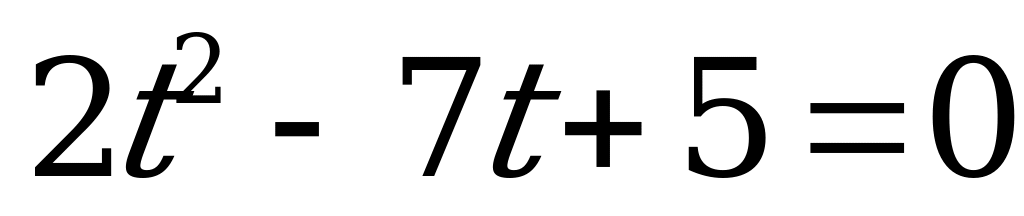 . (4)
. (4)
Найдём корни уравнения
б) Решим уравнение 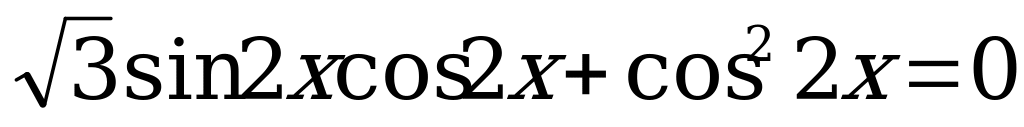 . (5)
. (5)
Разложим левую часть уравнения (5) на множители
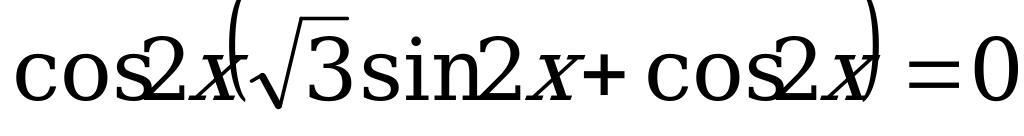 .
.
Тогда:
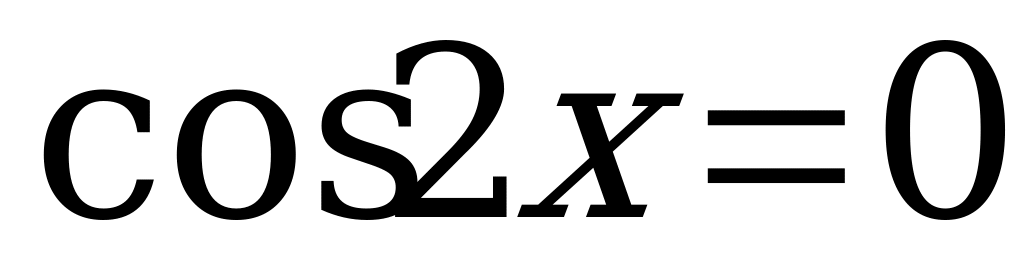 или
или 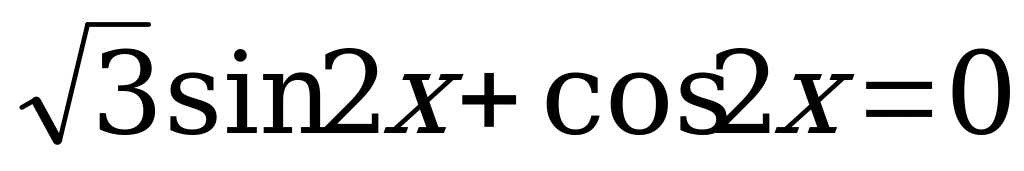 .
.
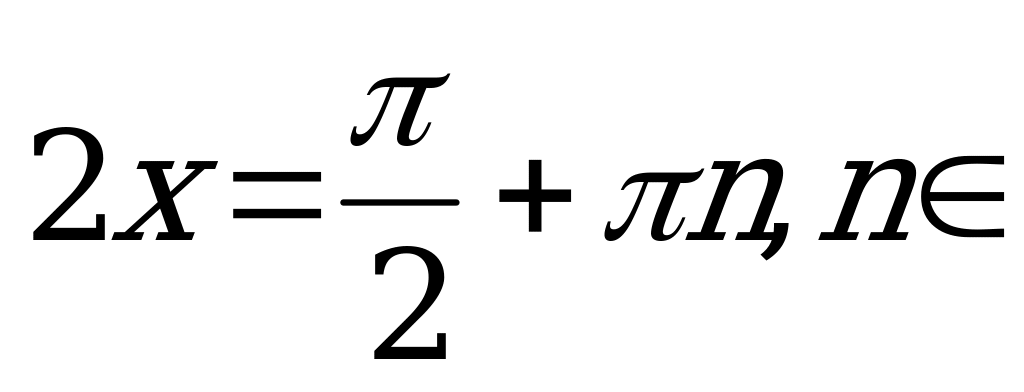 Z. Разделим обе части
Z. Разделим обе части
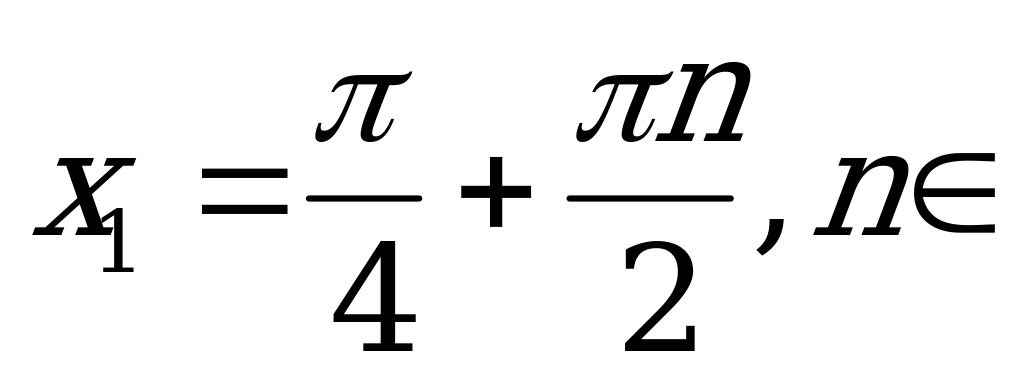 Z. уравнения на
Z. уравнения на 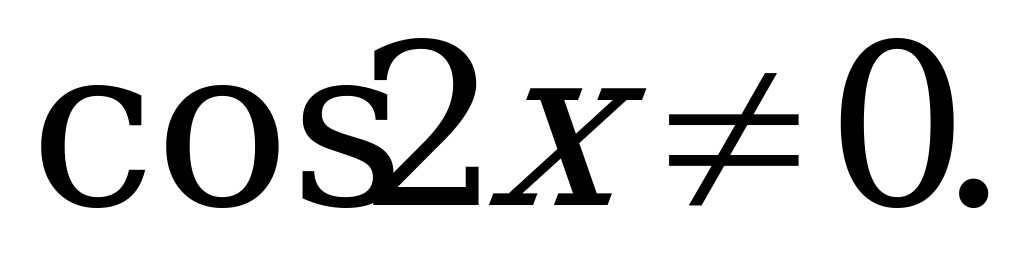
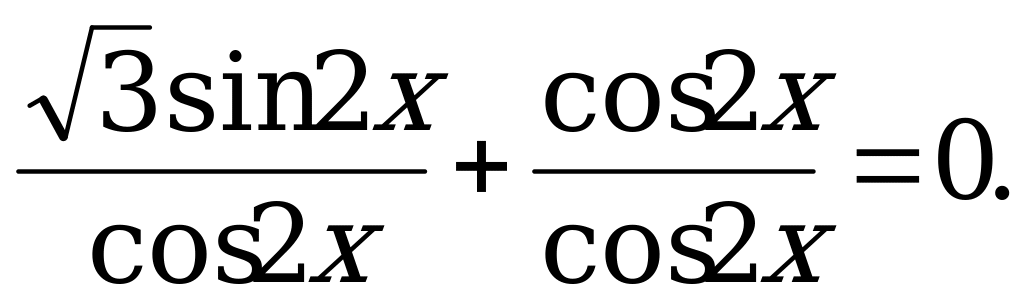
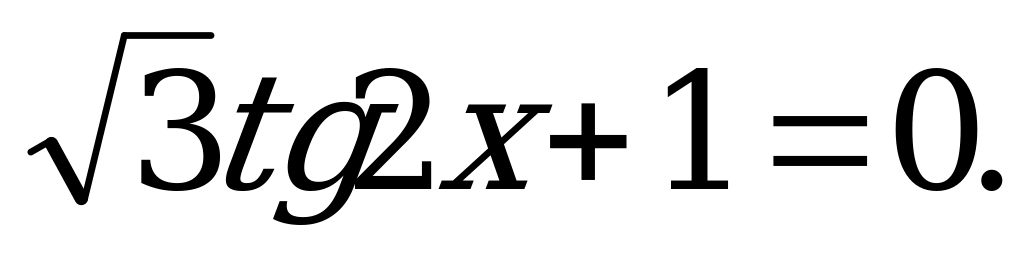
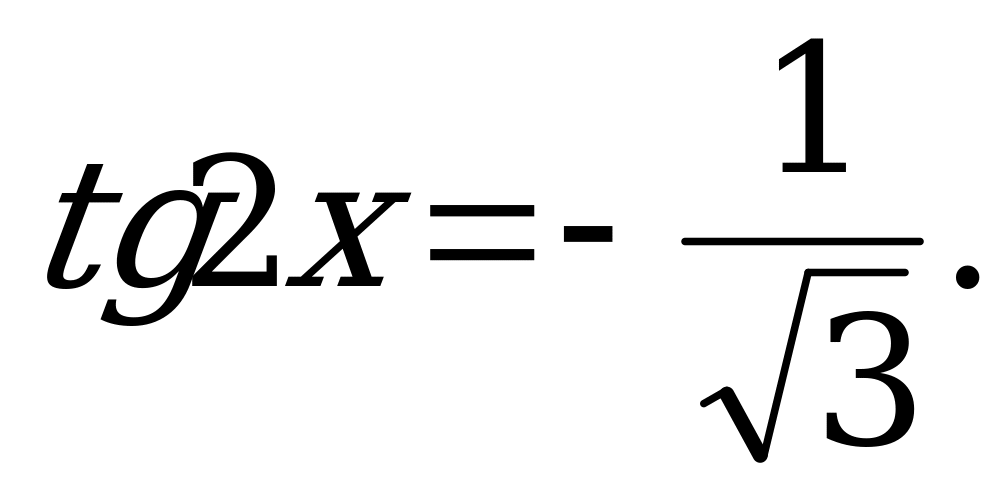
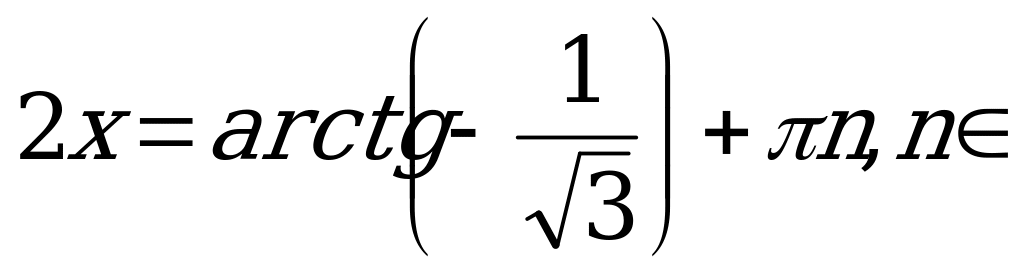 Z.
Z.
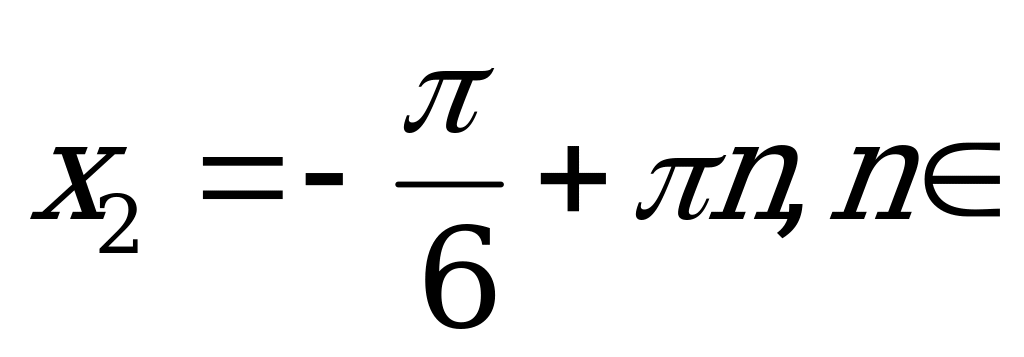 Z.
Z.
Ответ: 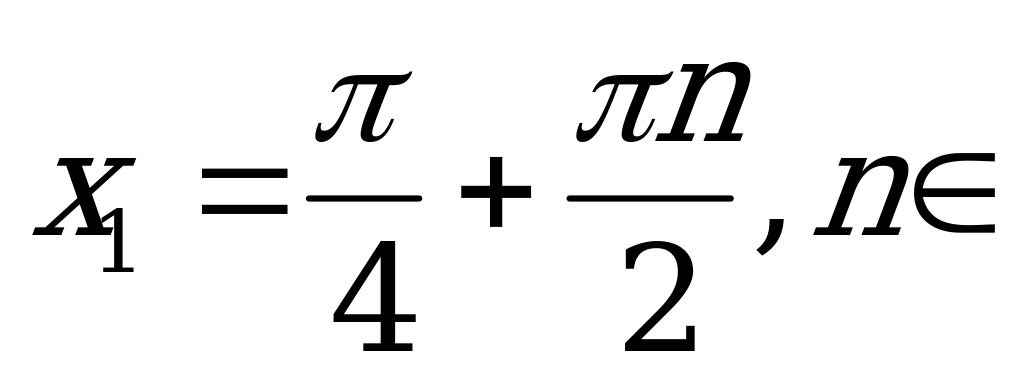 Z,
Z, 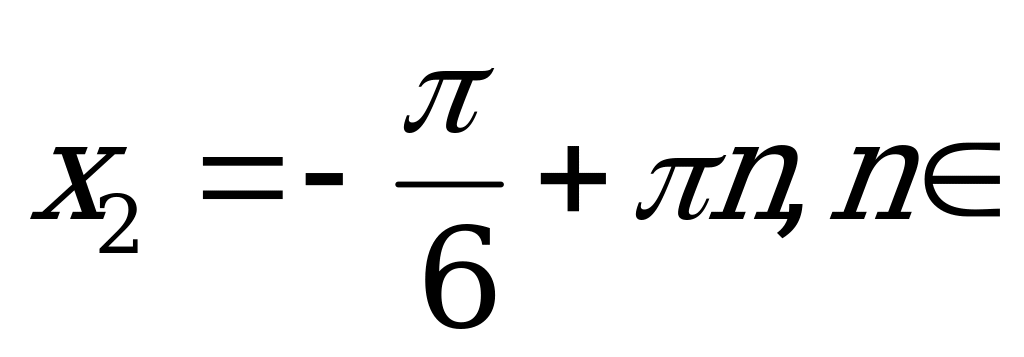 Z.
Z.
Самостоятельная работа №9.
Вариант №1.
Решить уравнения (1-7).
1) 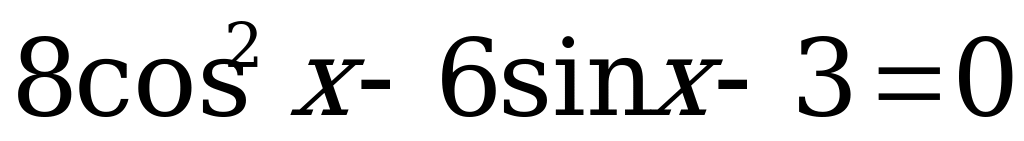 .
.
2) 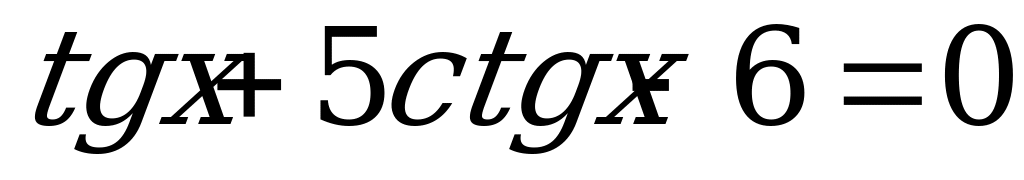 .
.
3) 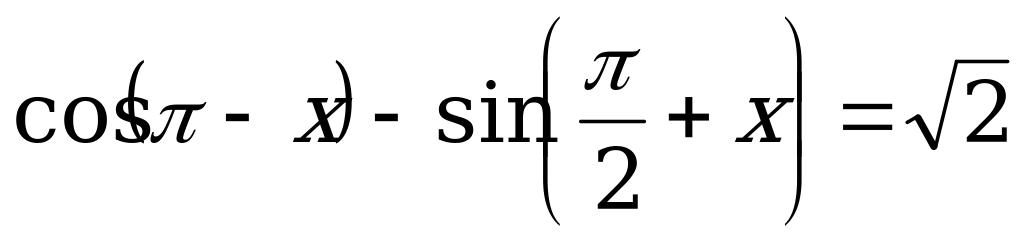 .
.
4) 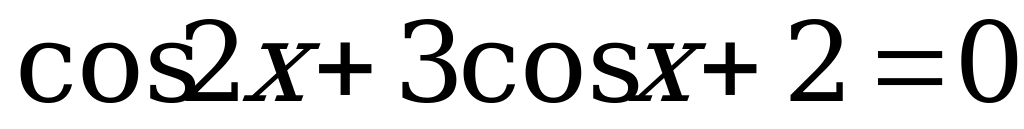 .
.
5)  .
.
6) 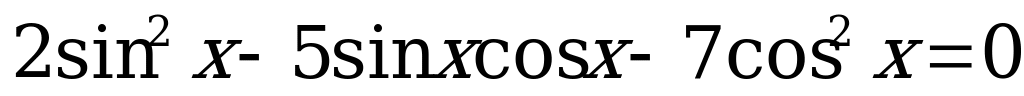 .
.
7) 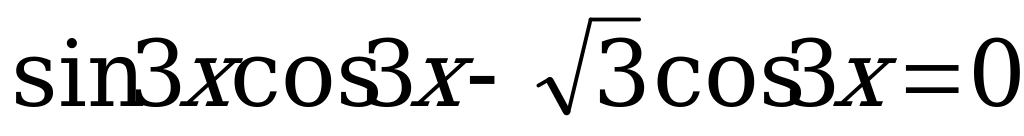 .
.
Вариант №2.
Решить уравнения (1-7).
1) 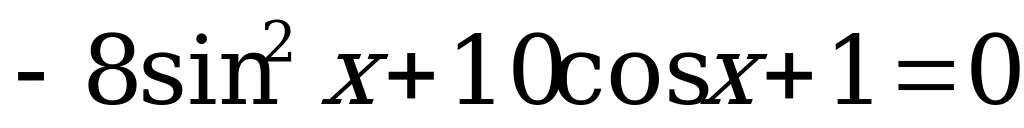 .
.
2) 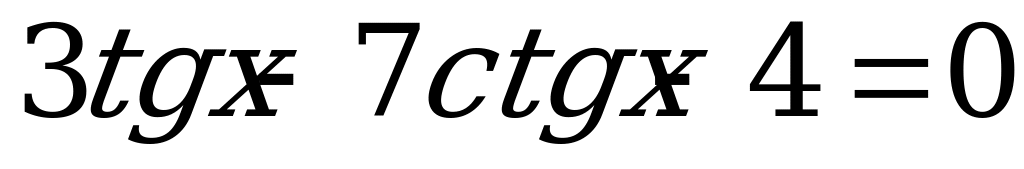 .
.
3) 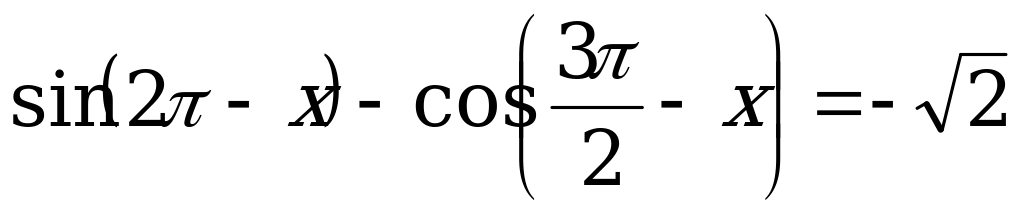 .
.
4) 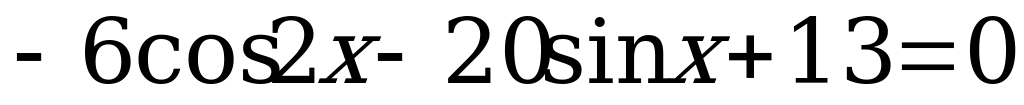 .
.
5) 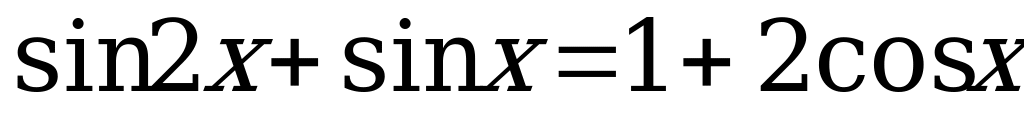 .
.
6) 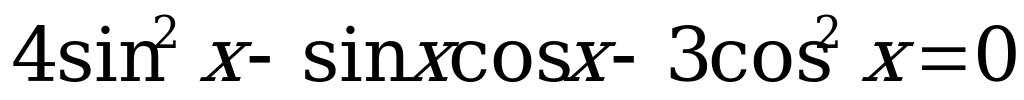 .
.
7) 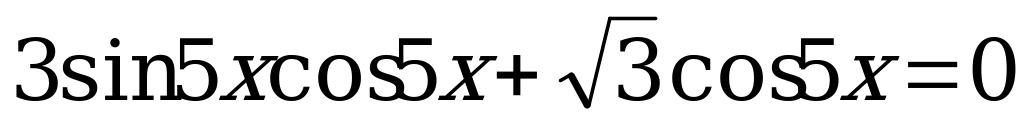 .
.
Список рекомендуемой литературы
Алимов Ш. А. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. — М., 2017.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2017.
Башмаков М. И. Математика: учебник для студ. учреждений сред. проф. образования. — М., 2018.
Башмаков М. И. Математика. Сборник задач профильной направленности: учеб. пособие для студ. учреждений сред. проф. образования. — М., 2018.
Башмаков М. И. Математика. Задачник: учеб. пособие для студ. учреждений сред. проф. образования. — М., 2018.
Башмаков М. И. Математика. Электронный учеб.-метод. комплекс для студ. учреждений сред. проф. образования. — М., 2018.
Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2018. Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2018.
Башмаков М. И. Алгебра и начала анализа, геометрия. 10 класс. — М., 2017.
Башмаков М. И. Математика (базовый уровень). 10 класс. Сборник задач: учеб. пособие. — М., 2018.
Башмаков М. И. Математика (базовый уровень). 11 класс. Сборник задач: учеб. пособие. — М., 2018.
Гусев В. А., Григорьев С. Г., Иволгина С. В. Математика для профессий и специальностей социально-экономического профиля: учебник для студ. учреждений сред. проф. образования. — М., 2018.
Колягин Ю. М., Ткачева М. В, Федерова Н. Е. и др. Математика: алгебра и начала математического анализа. Алгебра и начала математического анализа (базовый и углубленный уровни). 10 класc / под ред. А. Б. Жижченко. — М., 2018.
Колягин Ю. М., Ткачева М. В., Федерова Н. Е. и др. Математика: алгебра и начала математического анализа. Алгебра и начала математического анализа (базовый и углубленный уровни). 11 класс / под ред. А. Б. Жижченко. — М., 2018.
8








 адианная и градусная меры связанны зависимостью 1800 = π радиан; угол в n0 равен
адианная и градусная меры связанны зависимостью 1800 = π радиан; угол в n0 равен 

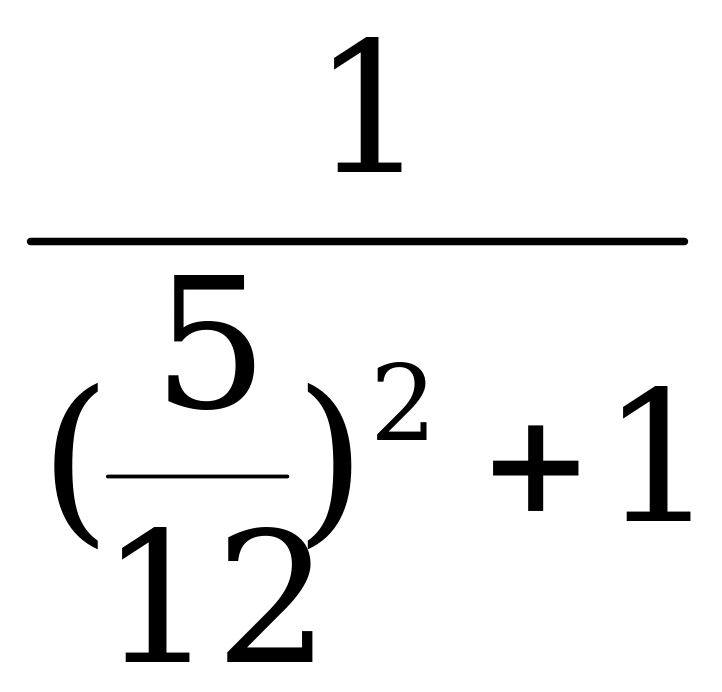 =
= 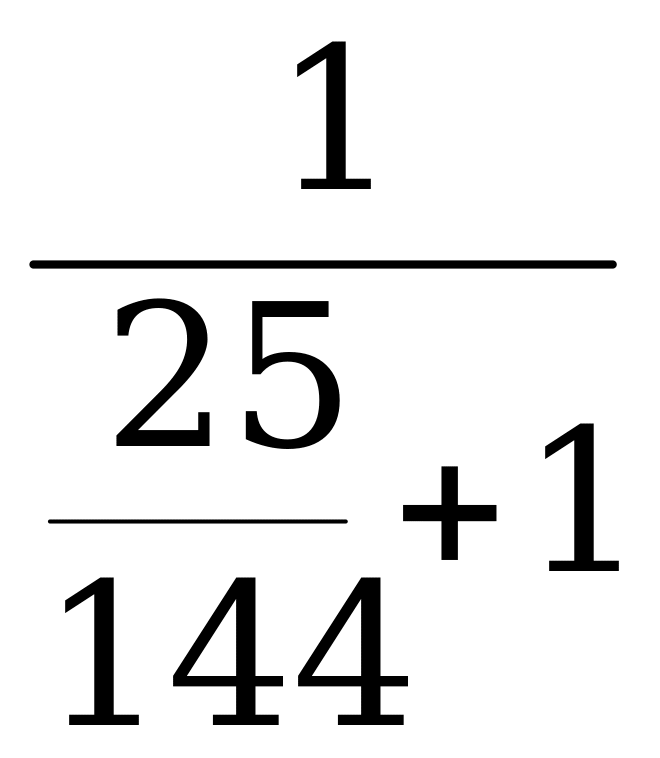 =
= 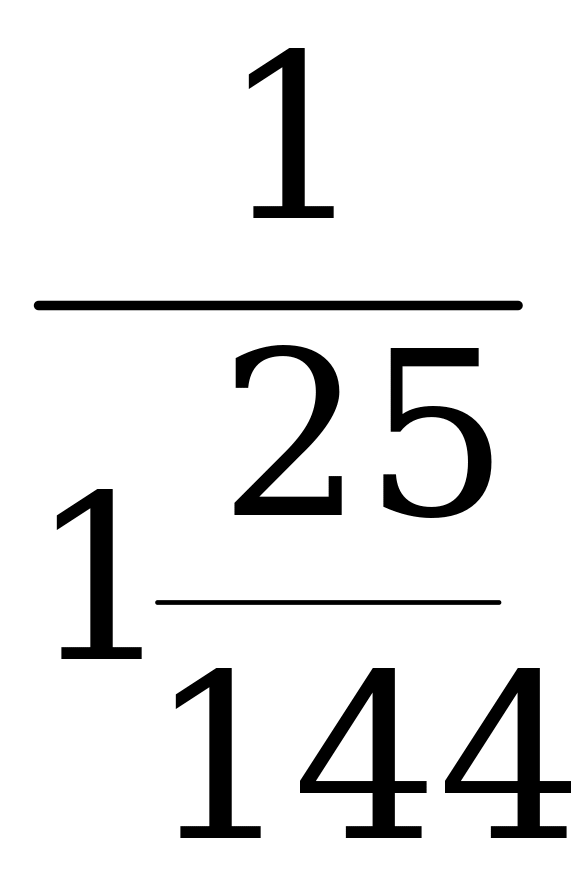 =
= 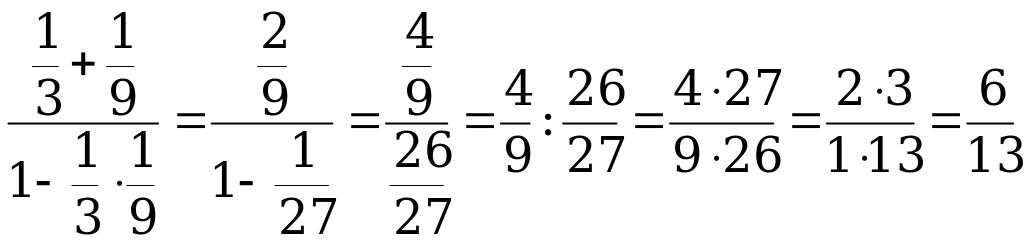 .
.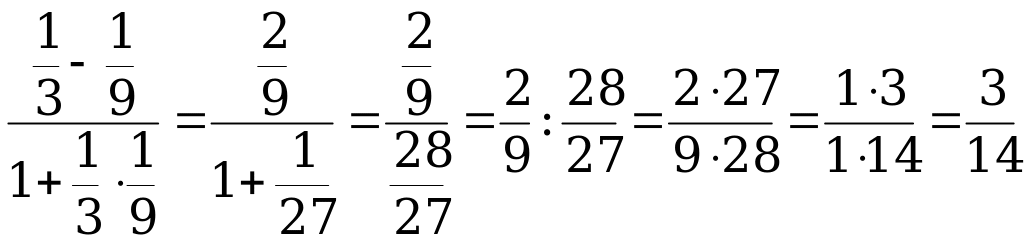 .
.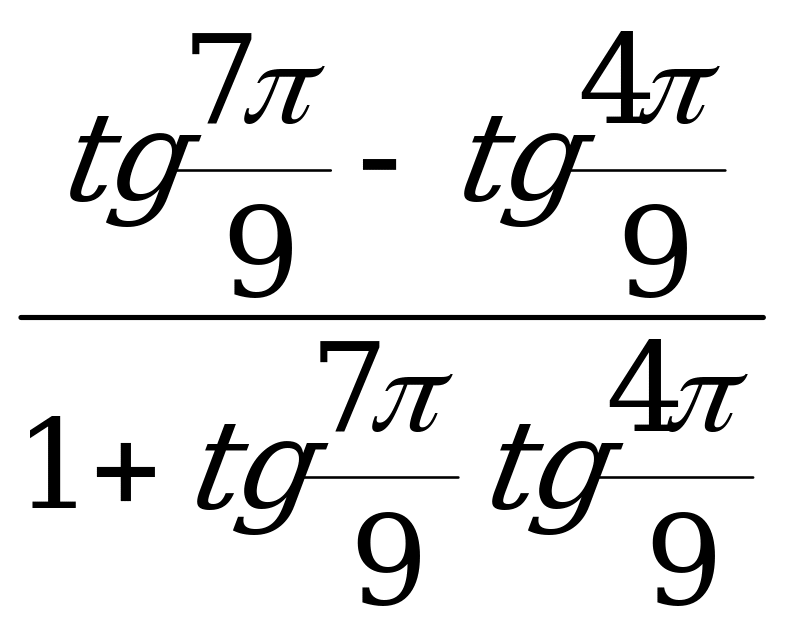 .
.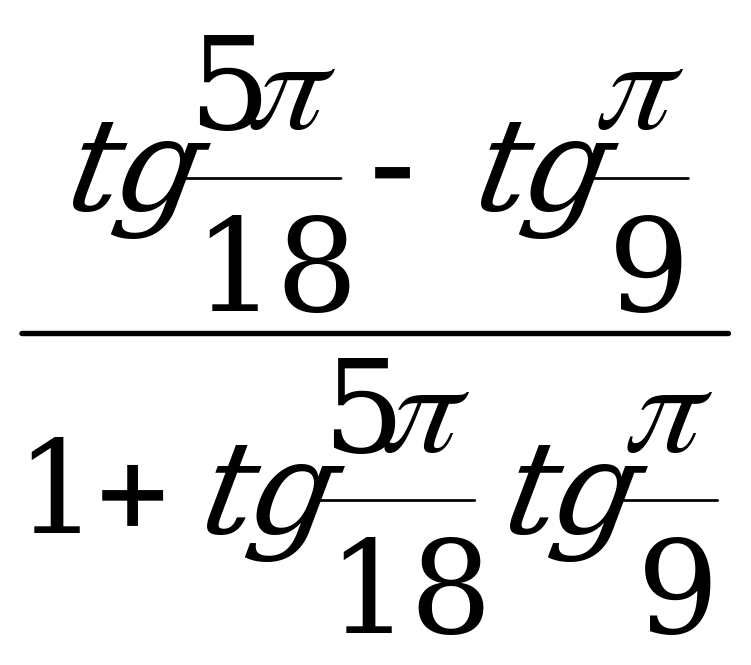 .
.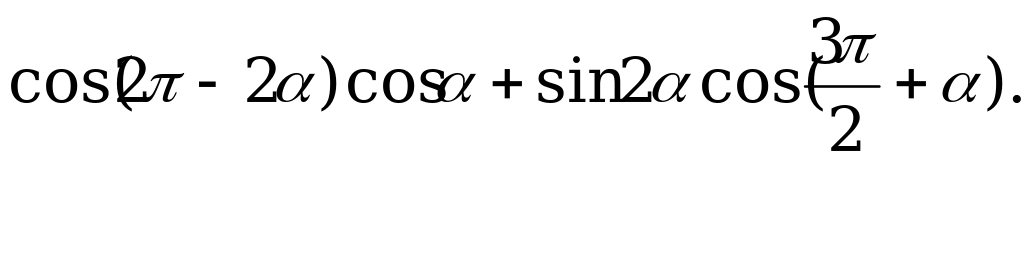
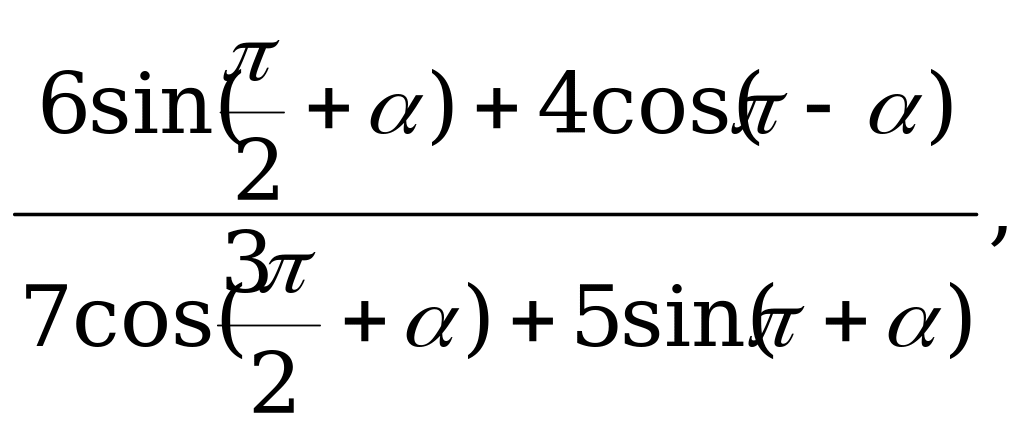 если
если 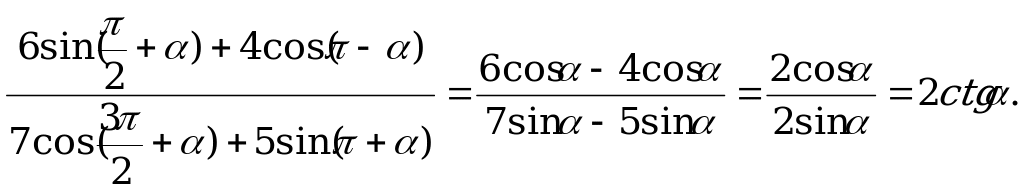
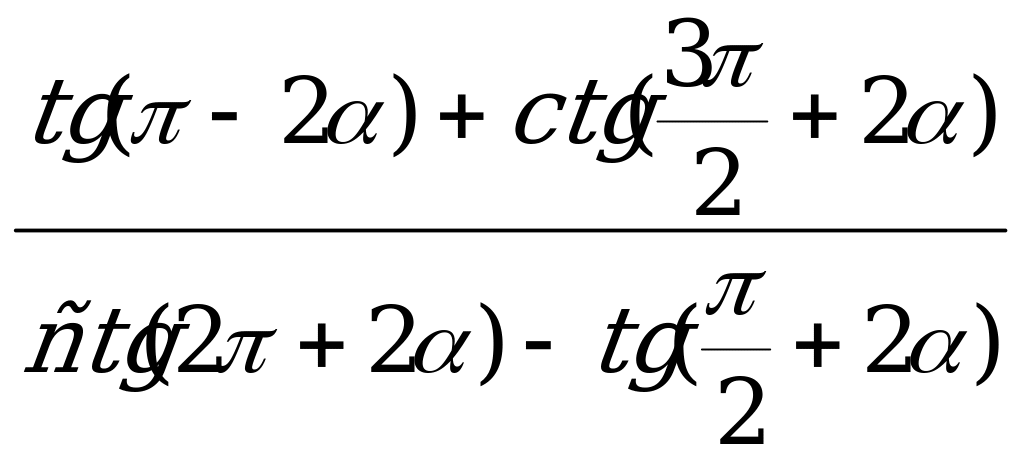 ,если
,если 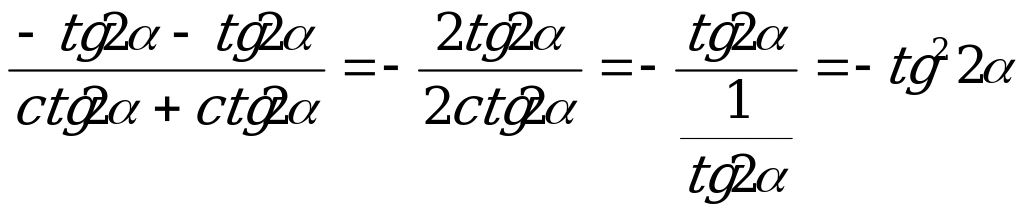 .
.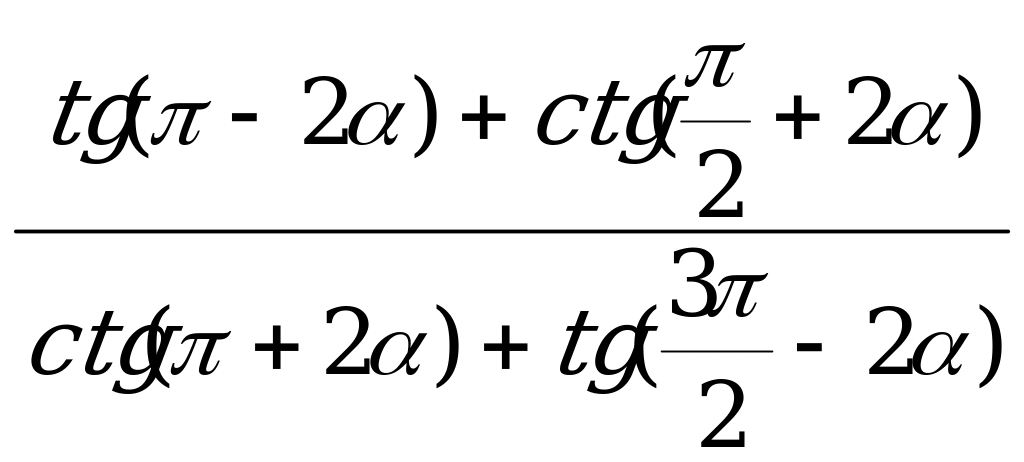 , если
, если 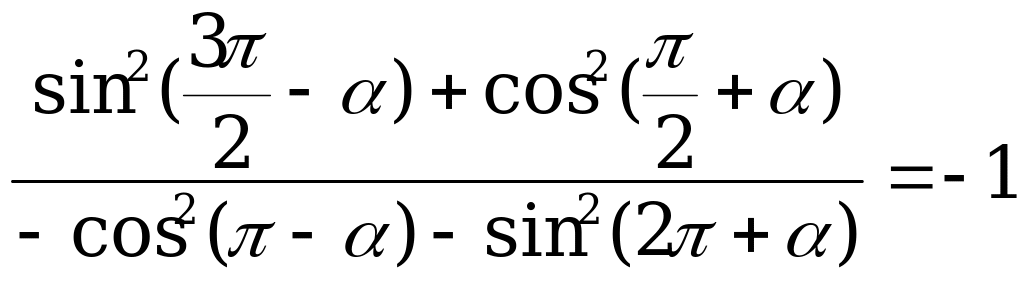 .
.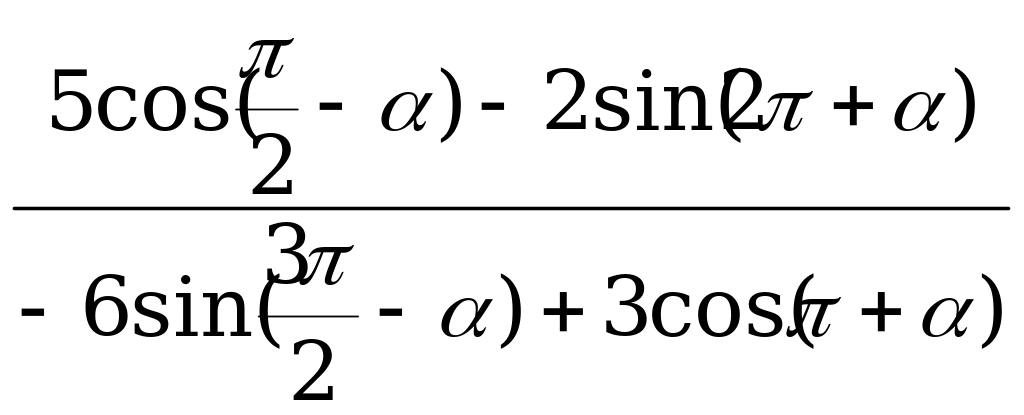 , если
, если 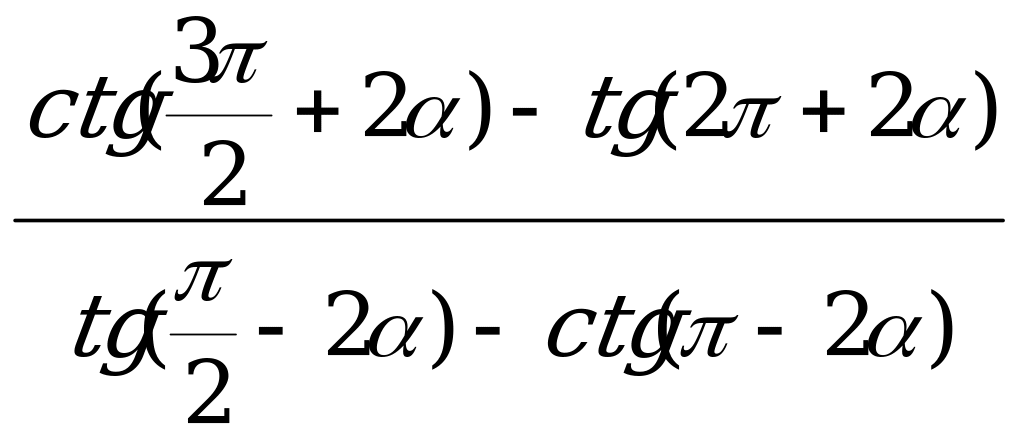
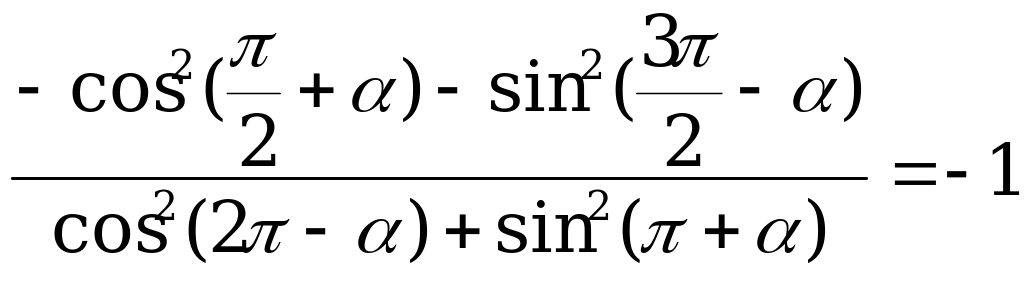 .
.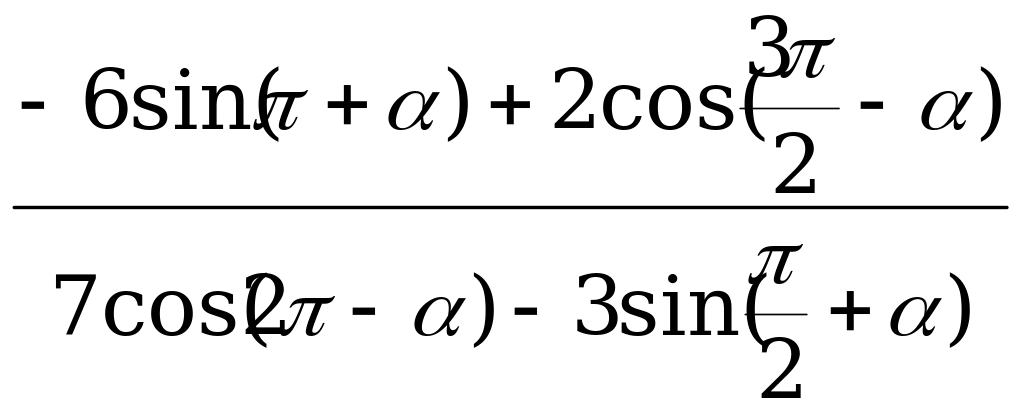 , если
, если 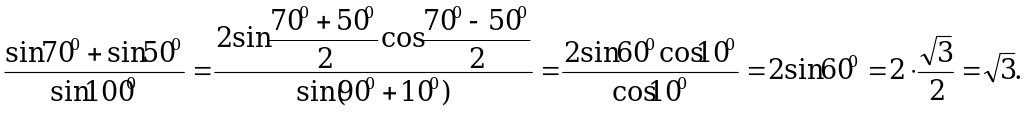 Пример 2. Вычислите
Пример 2. Вычислите 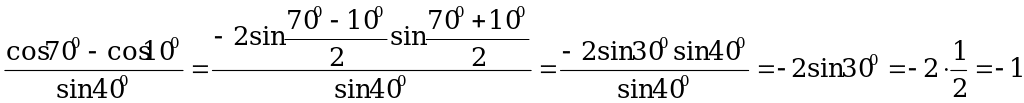
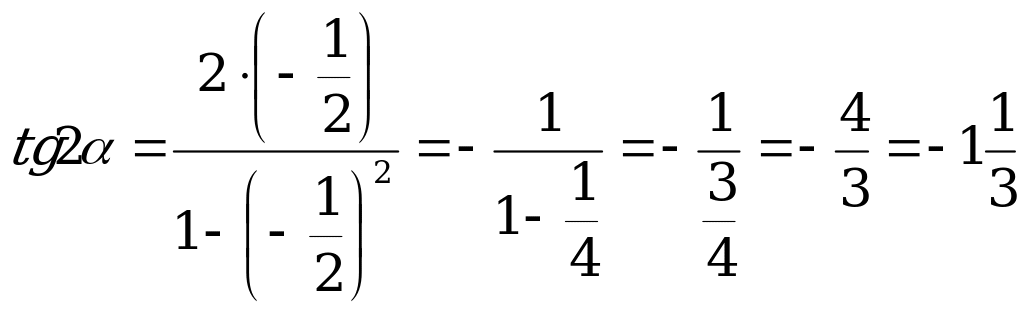 .
.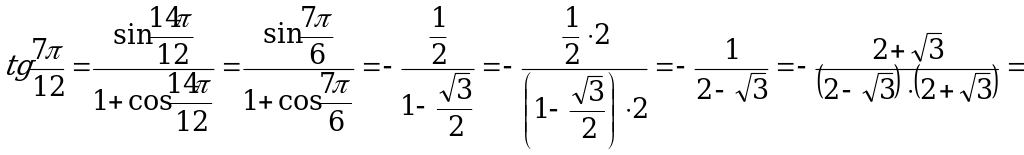
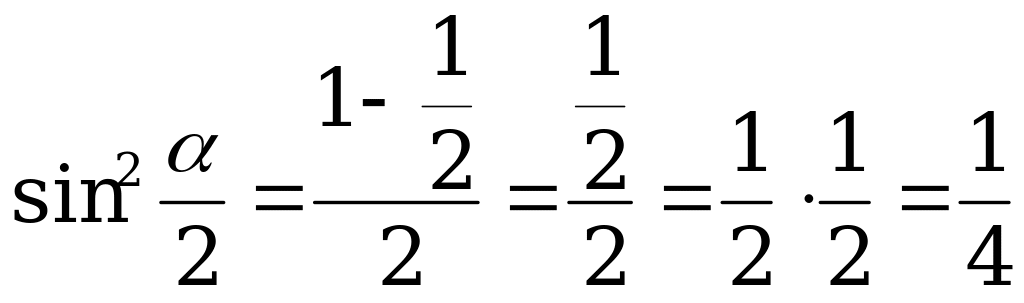 .
.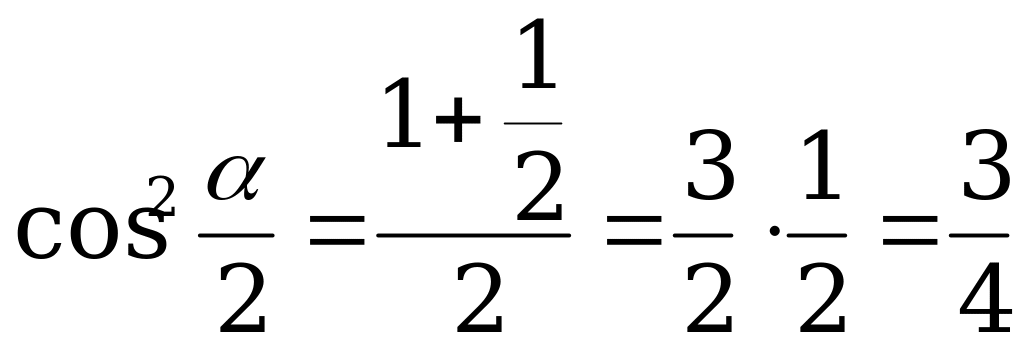 .
.













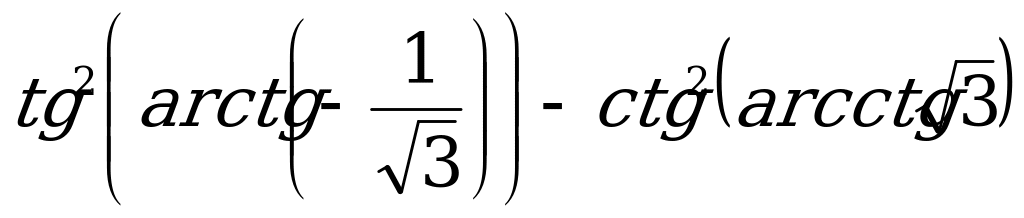 ;
;