Методические указания к практическим работам
По дисциплине «Инженерная графика»
(для заочников)
Преподаватель Грушникова Т.Н.
2020
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Методические указания к практическим работам по дисциплине «Инженерная графика» предназначены для студентов по специальности 15.02.15 «Технология металлообрабатывающего производства».
Цель методических указаний: оказание помощи студентам в выполнении практических заданий по дисциплине «Инженерная графика»
Методические указания содержат теоритические материалы и практические задания, которые позволят студентам закрепить теорию.
В результате выполнения практических заданий по дисциплине «Инженерная графика» студенты должны уметь:
- оформлять техническую документацию в соответствии с действующей нормативной базой;
В результате освоения дисциплины обучающийся должен знать:
- правила разработки и оформления технической документации, чертежей и схем;
- пакеты прикладных программ по инженерной графике при разработке и оформлении технической документации.
Перечень графических работ по инженерной графике
для студентов заочного отделения
| Графическая работа | Формат |
| Линии чертежа, шрифты (ГОСТ 2.303-68, ГОСТ 2.304-81) | А4 (297х210 мм) |
| Геометрические построения. Сопряжение | А4 |
| Геометрические тела и точки | А4 |
| Построение трех видов детали | А4 |
| Построение третьего вида детали по двум заданным (контрольная работа). | А4 |
Самостоятельная работа по изучению дисциплины
Прежде чем приступить к выполнению практического задания необходимо самостоятельно изучить учебный материал темы, ознакомиться с методическими указаниями к выполнению соответствующего практического задания.
Рекомендуется следующий порядок выполнения практического задания:
1. Прежде чем приступить к выполнению практического задания, необходимо кратко повторить теоретический материал по теме занятия.
2. Внимательно прочесть задание
3. Выбрать наиболее рациональные способы выполнения задания
4. Внимательно прочесть контрольные вопросы
5.Продумать последовательность выполнения задания.
Неаккуратное выполнение практического задания, несоблюдение принятой размерности, плохое выполнение эскизов, чертежей и схем могут послужить причиной снижения оценки за практическое занятие.
Методика выполнения контрольной работы.
Контрольная работа состоит из задачи, выполненной в виде чертежа. Чертеж выполняется на листе формата А4 (210 х 297) ГОСТ 2.301-68.Внутри формата наносится рамка поля чертежа на расстоянии от левой границы формата 20 мм, от трех других сторон — 5 мм. Рекомендуется выполнять изображения в контрольных заданиях в масштабе 1:1.
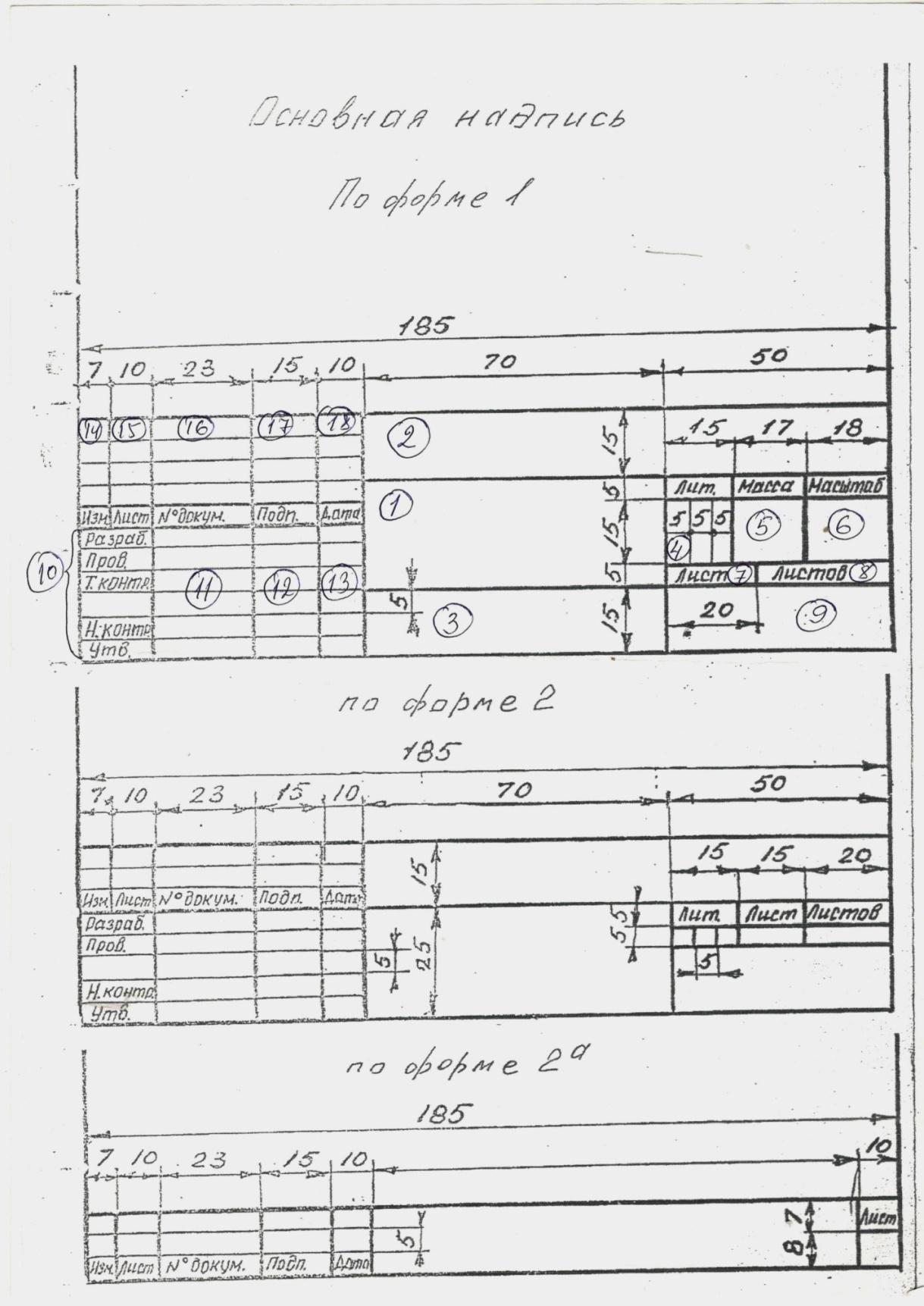
Чертеж сопровождается основной надписью по форме 1 ГОСТ 2.104-68 «Основные надписи».
Все построения при решении задач необходимо выполнять при помощи чертежных инструментов. Чертить следует остро наточенным твердым карандашом без нажима на него с тем, чтобы иметь возможность легко стирать резинкой неправильно проведенные линии.
Все линии проводятся ясно и четко, правильного строения и толщины в зависимости от их назначения в соответствии с ГОСТ 2.203-68.
Все буквенные и цифровые обозначения на чертеже, а также текст в основной надписи выполняются стандартным шрифтом типа Б с наклоном 75º по ГОСТ 2.304-81.
Необходимо внимательно прочитать методические указания. В методических указаниях приводятся содержание, порядок выполнения, рекомендации к выполнению и пример графического выполнения задачи.
Номер варианта задач определяется студентом по номеру в списке группы в учебном журнале. Выполненная контрольная работа передается в колледж Коломна на рецензию в полном объеме.
Перечень стандартов ЕСКД, изучаемых в курсе «Инженерная графика»
ГОСТ 2.104-68 ٭Основные надписи.
ГОСТ 2.109-73 Основные требования к чертежам.
ГОСТ 2.301-68* Форматы.
ГОСТ 2.302-68* Масштабы.
ГОСТ 2.303-68* Линии.
ГОСТ 2.304-81 Шрифты чертежные.
ГОСТ 2.307-68 Нанесение размеров и предельных отклонений.
ГОСТ 2.317-69 Аксонометрические проекции.
Практическая работа 1
Тема: Линии чертежа
Цель: Изучить типы линий, приобрести навыки выполнения линий по ГОСТ 2.303-68.
Порядок выполнения работы:
Задание выполняется по одному варианту на формате А4. Перечертить задание по образцу длина линий 160 мм.
Толщину и другие размеры линий выполнять в соответствии с ГОСТ 2.303-68. Размеры на чертеже не наносить. При проведении линий на чертеже нужно добиваться отношения толщин различных по типу линий, подбирать различного типа карандаши, выдерживать длину штрихов и промежутков между ними.
Выполнить окружности линиями различного типа радиусами R=30, R=40, R=50.
Центровые линии в центре окружности должны обязательно пересекаться своими штрихами. Штрихи должны выходить за пределы окружности на 3-4 мм.
Штриховку выполнить тонкими линиями под углом 45 параллельно, соблюдая расстояние между ними 2- 3 мм, изменяя направление штрихов для различных фигур
Задание
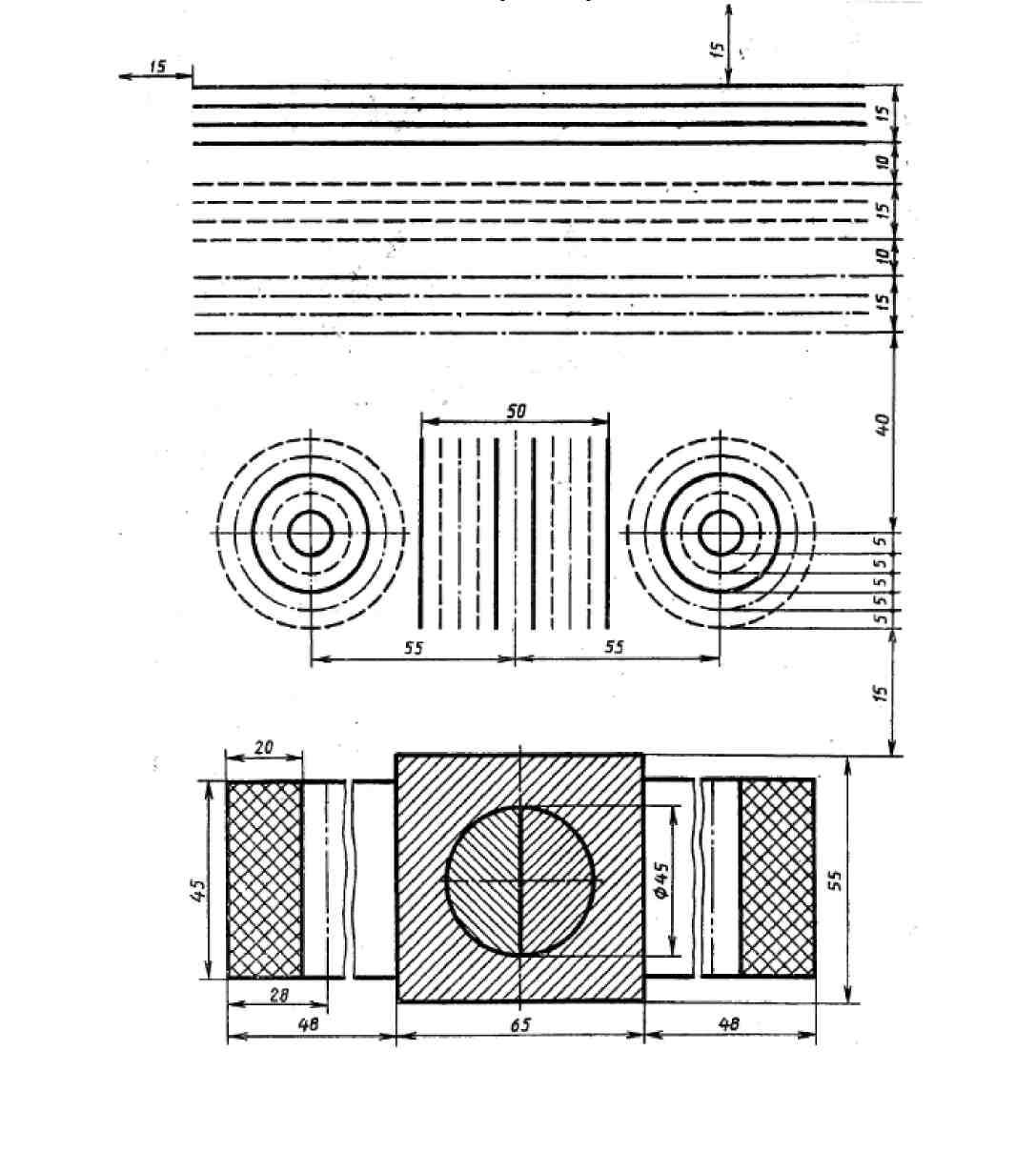
Контрольные вопросы:
1.В каких пределах выбирается толщина сплошной основной линии?
2.Каковы назначения сплошной тонкой линии и ее толщина?
Тема: Основная надпись
Цель: Научиться выполнять основную надпись по ГОСТ 2.104 – 68.
На формате А4 выполнить основную надпись по форме 1. Заполнить ее в соответствии с ГОСТ 2.104-68.
Теоретические сведения по теме: Построение аксонометрической проекции окружности.
Для наиболее наглядных изображений применяется прямоугольная изометрическая проекция (кратко - изометрия, от греч изо - равный, одинаковый). Положение аксонометрических осей этой проекции приведено на рисунке 1, а. Как видно из чертежа, оси проекции в изометрии располагаются под углом 120° друг к другу. При построении фигур размеры отрезков по осям х0 у0 z0 откладывают без изменения, т. е. действительные.

Рисунок 1
В том случае, когда действительные размеры берут только по двум осям (х0, z0), проекцию называют диметрической (от греч. ди - дважды). Положение осей диметрической проекции дано на рисунке 1, б.
Аксонометрические проекции многоугольников.
Построение аксонометрических проекций начинают с проведения осей. Параллельно им откладывают размеры отрезков.
Рассмотрим построение аксонометрических проекций плоских геометрических фигур, расположенных в горизонтальной плоскости. Построения даны в изометрической проекции.
Треугольник. Симметрично точке 00 (рисунок 2) по оси х0 откладывают отрезки С0А0 и 00Е0, равные половине стороны треугольника, а по оси у0 - его высоту 00С0. Полученные точки А0, B0 и С0 соединяют отрезками прямых.

Рисунок 2
Квадрат. По оси х0 от точки 00 (рисунок 3) откладывают отрезок а, равный стороне квадрата, вдоль оси у0 - также отрезок а. Затем проводят отрезки, параллельные отложенным.

Рисунок 3
Шестиугольник. По оси х0 вправо и влево от точки 00 (рисунок 4) откладывают отрезки, равные стороне шестиугольника. По оси у0 симметрично точке 00 откладывают отрезки, равные половине расстояния L между противоположными сторонами шестиугольника, т. е. L/2

Рисунок 4
Аксонометрическая проекция окружности.
В аксонометрической проекции окружность в общем случае проецируется в кривую, которую называют эллипсом. Эллипс - замкнутая плоская кривая. Ее строят с помощью лекал. Поскольку строить эллипсы трудно, при изображении окружности в аксонометрии их разрешается заменять овалами. Овал - кривая, очерченная дугами окружности.
Рассмотрим построение овала, представляющего изометрическую проекцию окружности. Овал удобно строить, вписывая его в ромб, который является изометрической проекцией квадрата. Построение выполняют в следующем порядке:
Строят ромб, сторона которого равна диаметру изображаемой окружности. Для этого через точку 00 проводят оси х0 и у0 (рисунок 5, а). На них от точки С0откладывают отрезки С01, С02 и т. д., равные радиусу изображаемой окружности. Через точки 1, 2, 3 и 4 проводят прямые, параллельные осям х0 и у0, получая на чертеже точки A, Б, С и D.
Для того чтобы вписать в ромб овал, из вершин тупых углов - точек В и А - проводят дуги. Их радиус R равен расстоянию от вершин тупых углов (точек Б и A) до точек 1, 2 или 3, 4 соответственно (рисунок 5, б). 
Рисунок 5
Через точки В и 1, В и 2 проводят прямые. При пересечении прямых В1 и В2 с большей диагональю ромба CD получают точки 01 и 02 (Рисунок 5, в). Эти точки будут центрами малых дуг. Их радиус R1 равен 011 (или 022). Дугами малого радиуса R1 соединяют большие дуги овала.
Теоретический материал по теме: Нанесение размеров.
Общие сведения. Для определения величины изображенного изделия или какой-либо его части по чертежу на нем наносят размеры.
Размеры разделяют на линейные и угловые. Линейные размеры характеризуют длину, ширину, толщину, высоту, диаметр или радиус измеряемой части изделия. Угловые размеры характеризуют величину углов. Линейные размеры на чертежах указывают в миллиметрах, но обозначение единицы измерения не выносят. Угловые размеры указывают в градусах, минутах и секундах.
Общее количество размеров на чертеже должно быть наименьшим, но достаточным для изготовления и контроля изделия.
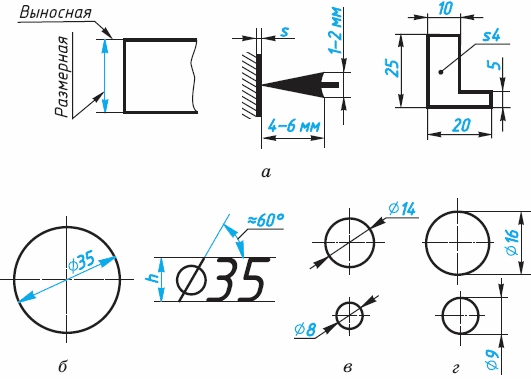
Рисунок 6
При создании чертежей приходится выполнять различные графические построения: делить на равные части отрезки и окружности, правила установлены стандартом. Назовем их, пользуясь полученными ранее сведениями.
Размеры на чертежах указывают с помощью выносных и размерных линий и размерных чисел. Сначала проводят выносныe линии перпендикулярно отрезку, размер которого указывают (рисунок 6, а). Затем на расстоянии 10 мм и более от контура детали проводят параллельную ему размерную линию. Она ограничивается с двух сторон стрелками (рисунок 6, а). Какой должна быть стрелка, показано на рисунке. Выносные линии выходят за концы стрелок размерной линии на 1...5 мм. Выносные и размерные линии проводят сплошной тонкой линией. Над размерной линией, ближе к ее середине, наносят размерное число.
Если на чертеже несколько размерных линий, параллельных друг другу, то ближе к изображению наносят меньший размер, чтобы выносные и размерные линии на чертеже не пересекались. Расстояние между параллельными размерными линиями выбирают от 7 до 10 мм, чтобы между ними размещались размерные числа, не касаясь этих линий.
Для обозначения диаметра перед размерным числом наносят специальный знак - кружок, перечеркнутый линией (рисунок 6, б). Если размерное число внутри окружности не помещается на рисунке, его выносят за пределы окружности, как показано на рисунке 6, в и г. Аналогично поступают при нанесении размера прямолинейного отрезка (см. рисунок 6, а, размер 5).
Для обозначения радиуса перед размерным числом пишут прописью латинскую букву R (рисунок 7, а). Размерную линию для указания радиуса проводят, как правило, из центра дуги и заканчивают с одной стороны стрелкой, упирающейся в точку дуги окружности.
При указании размера угла размерную линию проводят в виде дуги окружности с центром в вершине угла (рисунок 7, б).
Если размерная линия расположена вертикально (независимо от того, с какой стороны контура детали), то размерное число пишут слева от линии и читают снизу вверх (см. рисунок 6, а, размеры 25; 5). При наклонных размерных линиях цифры располагают над линией (см. рисунок 6, б, размер Ø35; рис. 19, а, размер R25). Если деталь имеет несколько одинаковых элементов, то на чертеже рекомендуется наносить размер лишь одного из них с указанием количества таких элементов. Например, запись на чертеже «3 отв. Ø10» означает, что в детали имеется три одинаковых отверстия диаметром 10 мм каждое.
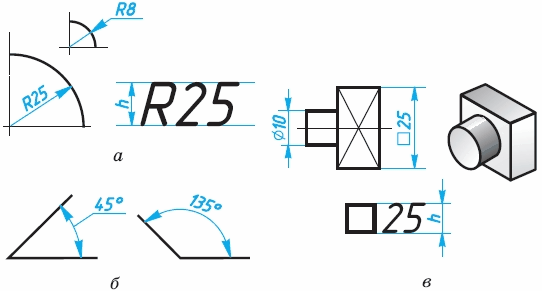
Рисунок 7
Перед размерным числом, указывающим сторону квадратного элемента, наносят знак квадрата (рисунок 7, в). При этом высота знака должна быть равна высоте цифр. При изображении плоских деталей в одной проекции толщина детали условно обозначается латинской строчной буквой s. Ее ставят перед размерным числом (см. рисунок 6, а, размер s4).
Теоретический материал по теме: Деление окружностей
На шесть равных частей окружность делят так. Приняв за центры дуг точки пересечения одного из диаметров с окружностью - А и В, проводят две дуги радиусом R, равным радиусу изображенной окружности (рисунок 8, а). Эти дуги пересекают окружность в четырех точках 1, 2, 3 и 4. Вместе с точками А и Б они делят окружность на шесть равных частей (рисунок 8, б). Ту же задачу можно решить при помощи угольника с углами 30° и 60° и линейки (рисунок 88, в).

Рисунок 8
На рисунке 9, а показано деление окружности на восемь равных частей. Для этой цели дуги 1-3, 3-5 и др. делят пополам точками 2, 4 и т. д. или делят на две равные части отрезки 1-3, 3-5 и т. д. Можно поступить так: провести через центр окружности две пары взаимно перпендикулярных диаметров (рисунок 9, б).
Рисунок 9
Теоретический материал по теме: Сопряжения линий
Сопряжением называется плавный переход от одной линии к другой. Для построения любого сопряжения дугой заданного радиуса нужно найти:
Центр сопряжения – центр, из которого проводят дугу;
Точки сопряжения (касания) – точки, в которых одна линия переходит в другую.
Центр сопряжения находится от точек сопряжения на одинаковых расстояниях, равных радиусу сопряжения R. Переход от прямой к окружности будет плавным в том случае, если прямая касается к окружности. Точка сопряжения К лежит на перпендикуляре, опущенном из центра О окружности к прямой (рисунок 10)
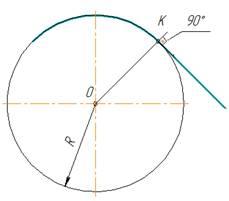
Рисунок 10
Переход от одной окружности к другой будет плавным, если окружности касаются.
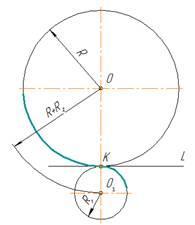
Различают два случая касания дуг окружностей: внешнее (рисунок 11) и внутреннее (рисунок 12).
При внешнем касании центры окружностей лежат по разные стороны от их общей касательной L (рисунок 11). Расстояние между их центрами ОО1 равно сумме радиусов окружностей R+R1 и точка касания лежит на прямой ОО1, соединяющей их центры.
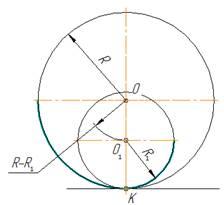
При внутреннем касании центры окружностей лежат по одну сторону от их общей касательной L. Расстояние между их центрами ОО1 равно разности их радиусов R-R1 и точка касания К окружностей лежит на продолжении прямой ОО1 (рисунок 12).
| 
| 
|
| Рисунок 11 | Рисунок 12 |
Сопряжение двух пересекающихся прямых
Даны пересекающиеся под прямым, острым и тупым углами прямые линии.
Требуется построить сопряжения этих прямых дугой заданного радиуса R.
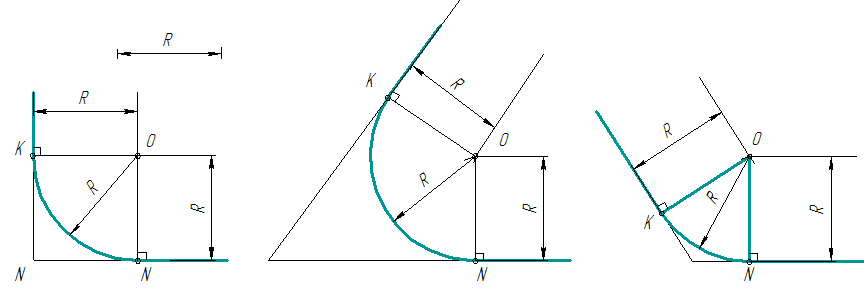
Рисунок 13
Для нахождения центра сопряжения проводят вспомогательные прямые, параллельные данным на расстоянии равном радиусу R. Точка пересечения этих прямых т.О и будет центом дуги сопряжения (рисунок 13).
Перпендикуляры, опущенные из центра дуги сопряжения т.О на данные прямые, определяют точки касания К и N.
Из точки О, как центра, описывают дугу заданного радиуса R.
Сопряжение двух окружностей дугой заданного радиуса
Заданы две окружности радиусом R1 и R2. Требуется построить сопряжение дугой заданного радиуса R.
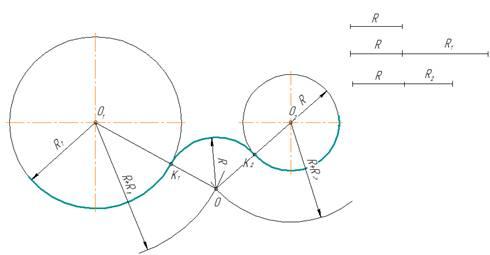
Рисунок 14
Внешнее касание
Для определения центра сопряжения О проводят вспомогательные дуги: из центра О1окружности радиусом R + R1 и из центра О2 окружности радиуса R + R2. Точка О пересечения этих дуг является центом сопряжения.
Соединяя центры О и О1, а так же О и О2 , определяют точки сопряжения (касания) К1 и К2.
Из центра О радиусом R проводят дугу сопряжения между точками К1 и К2
Внутреннее касание
При внутреннем касании выполняют те же построения, но дуги проводят радиусами
R -R1 и R - R2.

Рисунок 15
Смешанное касание

Рисунок 16
Центр сопряжения О находится в пересечении двух дуг, описанных из центра О1 радиусом R - R1 и из центра О2 радиусом R + R2
Примечание. При смешанном сопряжении центр О1 одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R , а центр О2 другой дуги – вне ее.
Практическая работа 2
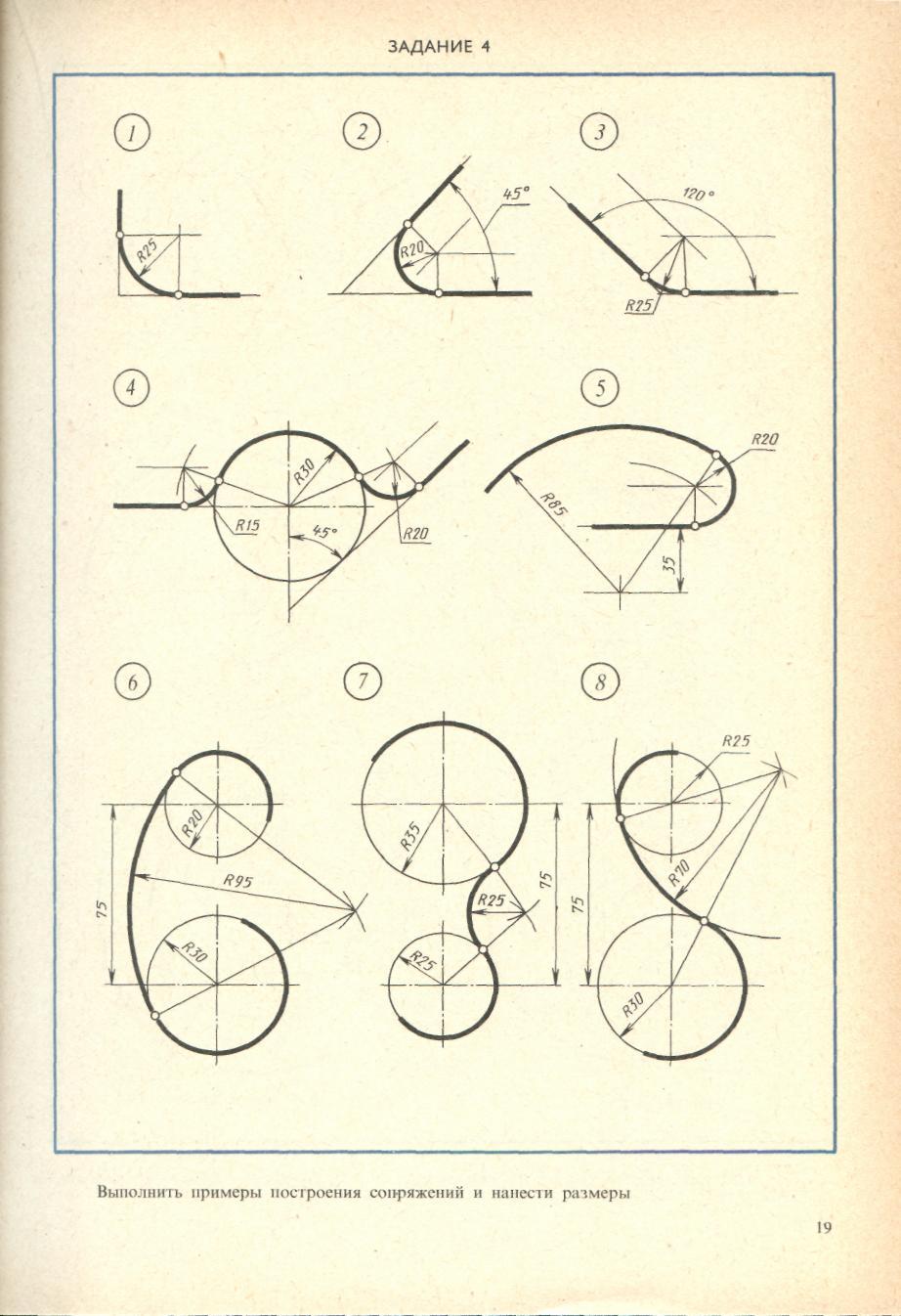
Тема: Построение сопряжений
Цель: Изучить типы сопряжений.
Порядок выполнения работы:
Вычертить сопряжения согласно заданию (упражнения 1, 2, 3, 6, 7, 8).
Теоретический материал по теме: Построение чертежа группы геометрических тел и точек на их поверхностях.
Вы уже познакомились с некоторыми геометрическими фигурами. Под фигурой понимают любую совокупность (множество) точек. Всякую сложную фигуру можно разделить на более простые.
Если все точки фигуры лежат в одной плоскости, фигуру называют плоской: треугольник, квадрат и др. Совокупность точек, расположенных в пространстве, образует пространственную фигуру: куб, цилиндр и др. Фигуры в пространстве называют телами.
Предметы, которые нас окружают, детали машин имеют, как правило, сложную реальную геометрическую форму. Однако, присмотревшись к ним внимательно, можно заметить, что некоторые из них состоят из одного или нескольких простых геометрических тел или их видоизмененных частей. Такими геометрическими телами, образующими форму предметов, являются призмы (рисунок 17, а), пирамиды (рисунок 17, б), цилиндры (рисунок 18, а), конусы (рисунок 18, б).

Рисунок 17
Рисунок 18
Форма каждого геометрического тела имеет свои характерные признаки. По ним мы отличаем призму от цилиндра, пирамиду от конуса и т. п. Эти признаки используются и при построении чертежей геометрических тел или состоящих из них предметов и деталей. Однако, прежде чем выполнять такие чертежи, выясним, какие правила положены в основу способов их построения.
Многогранники. Многогранником называют тело, поверхность которого состоит из плоских многоугольников. Таковы куб, призма, параллелепипед, пирамида и др.
Отдельные тела могут быть получены путем вращения прямой или кривой линии (образующей) вокруг какой-либо неподвижной линии (оси).
Это - тела вращения. Примерами их являются цилиндр, конус, сфера и др.
Поскольку форма большинства предметов представляет собой сочетание различных геометрических тел или их частей, для построения чертежей этих предметов необходимо знать, как изображается каждое геометрическое тело. Поэтому рассмотрим сначала построение чертежей и аксонометрических проекций простых тел. Это тем более необходимо, так как в сложной форме любого предмета всегда можно выделить простые геометрические тела, которые помогают представить форму предмета по его чертежу.
Изображение многогранников. Рассмотрим построение прямоугольных проекций призмы. Для примера возьмем треугольную (рисунок 19) и шестиугольную (рисунок 20) призмы. Их основания, параллельные горизонтальной плоскости проекций, изображаются на ней в натуральную величину, а на фронтальной и профильной плоскостях - отрезками прямых. Боковые грани изображаются без искажения на тех плоскостях проекций, которым они параллельны, и в виде отрезков прямых - на тех, которым перпендикулярны. Грани, наклонные к плоскостям, изображаются на них искаженными.
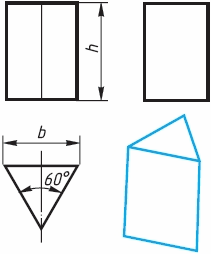
Рисунок 19
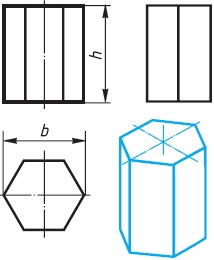
Рисунок 20
Размеры призм определяются их высотами и размерами фигур основания. Штрихпунктирными линиями на чертеже изображаются оси симметрии. Рассмотрим, как изображают на чертеже правильную четырехугольную пирамиду (рисунок 21). Основание пирамиды проецируется на горизонтальную плоскость проекций в натуральную величину. На нем диагоналями изображаются проекции боковых ребер. 
Рисунок 21
Фронтальная и профильная проекции пирамиды - равнобедренные треугольники. Размеры пирамиды определяются длиной b двух сторон ее основания и высотой h. Изображение тел вращения. Если круги, лежащие в основаниях цилиндра и конуса, расположены параллельно горизонтальной плоскости проекций, их проекции на эту плоскость будут также кругами (рисунок 22 и 23).
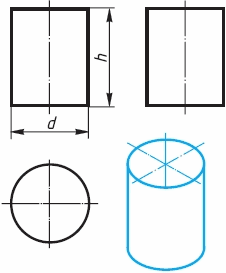
Рисунок 22
Рисунок 23
Фронтальная и профильная проекции цилиндра в данном случае - прямоугольники, а конуса — равнобедренные треугольники.
На всех проекциях следует наносить оси симметрии, с проведения которых и начинают выполнение чертежей цилиндра и конуса. Фронтальная и профильная проекции цилиндра одинаковы. То же можно сказать о проекциях конуса. Поэтому в данном случае профильные проекции на чертеже лишние. Кроме того, благодаря знаку диаметра Ø можно представить форму цилиндра и конуса даже по одной проекции. Отсюда следует, что в подобных случаях нет необходимости в трех проекциях. Размеры цилиндра и конуса определяются их высотой h и диаметром основания d.
Практическая работа 3
Тема: Построение проекций простейших геометрических тел (призмы, пирамиды, цилиндра, конуса), а также построения аксонометрических проекций
Цель: Изучить приемы построения проекций простейших геометрических тел.
Порядок выполнения работы:
На листе формата А4 выполнить комплексные чертежи: призмы, пирамиды, цилиндра и конуса, а также их аксонометрические проекции по следующим размерам
h = 70 мм и d = 50 мм. Нанести размеры.
Образец выполнения практической работы
Практическое задание 4
Тема: по аксонометрическим проекциям детали построить три вида детали.
Цель: Изучить приемы построения проекций деталей.
Порядок выполнения работы:
По аксонометрическим проекциям детали четко представить их форму. Построить три вида детали. Нанести размеры.
Методические рекомендации: при выполнении задания необходимо правильно расположить изображения на чертеже. На фронтальной плоскости проекций следует поместить то изображение, которое наиболее полно представляет основные формы и размеры модели (главный вид). Если изображаемая модель имеет плоскости симметрии, то ее чертеж начинают выполнять с проведения соответствующих осей симметрии. Если же плоскостей симметрии нет, то выполнение чертежа обычно начинают с изображения опорной поверхности, которая определяет вертикальное (или горизонтальное) расположение модели.
Чтобы обеспечить проекционную связь и лучше понять взаимное расположение отдельных элементов модели, рекомендуется все три изображения строить параллельно.
Комплексный чертеж модели следует выполнять в безосной системе (без нанесения на чертеже осей проекций). Перед окончательной обводкой чертежа линии связи удаляют и наносят размеры по ГОСТ 2.307–68.
Варианты заданий
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
В
Вариант 9
Вариант 10
Вариант 11
Вариант 12
Вариант 13
Вариант 14
Вариант 15
Вариант 16
Вариант 17
Образец выполнения работы:
Теоретический материал по теме: Построение третьего вида по двум заданным.
Построение третьего вида с помощью вспомогательной прямой.
Для того чтобы перенести размер ширины детали с вида сверху на вид слева, удобно воспользоваться вспомогательной прямой(рисунок а, б). Эту прямую удобнее провести справа от вида сверху под углом 45° к горизонтальному направлению.
Чтобы построить третью проекцию А3 вершины А, проведём через её фронтальную проекцию А2 горизонтальную прямую 1. На ней будет находиться искомая проекция А3. После этого через горизонтальную проекцию А1 проведём горизонтальную прямую 2 до пересечения ее со вспомогательной прямой в точке А0. Через точку А0 проведём вертикальную прямую 3 до пересечения с прямой 1 в искомой точке А3.
Аналогично строятся профильные проекции остальных вершин предмета.
После того как проведена вспомогательная прямая под углом 45О, построение третьей проекции также удобно выполнять с помощью рейсшины и треугольника (рис. 27б). Вначале через фронтальную проекцию А2 проведём горизонтальную прямую. Проводить горизонтальную прямую через проекцию А1нет необходимости, достаточно, приложив рейсшину, сделать горизонтальную засечку в точке А0 на вспомогательной прямой. После этого, немного сдвинув рейсшину вниз, прикладываем угольник одним катетом к рейсшине так, чтобы второй катет прошёл через точку А0, и отмечаем положение профильной проекции А3.
а б
Рисунок 1 - Построение третьей проекции по двум данным
Построение третьего вида с помощью базовых линий.
Для построения третьего вида необходимо определить, какие линии чертежа целесообразно принять за базовые для отсчёта размеров изображений предмета. В качестве таких линий принимают обычно осевые линии (проекции плоскостей симметрии предмета) и проекции плоскостей оснований предмета. Разберём на примере (рисунке 2) построение вида слева по двум данным проекциям предмета.
Рисунок 2 - Второй способ построения третьей проекции по двум данным
Сопоставив оба изображения, устанавливаем, что поверхность предмета включает в себя поверхности: правильной шестиугольной 1 и четырёхугольной 2 призм, двух цилиндров 3 и 4 и усечённого конуса 5. Предмет имеет фронтальную плоскость симметрии Ф, которую удобно принимать за базу отсчёта размеров по ширине отдельных частей предмета при построении его вида слева. Высоты отдельных участков предмета отсчитываются от нижнего основания предмета и контролируются горизонтальными линиями связи.
Форма многих предметов усложняется различными срезами, вырезами, пересечением составляющих поверхностей. Тогда предварительно нужно определить форму линий пересечения, построить их по отдельным точкам, вводя обозначения проекций точек, которые после выполнения построений могут быть удалены с чертежа.
Практическое задание 5 (контрольная работа)
Тема: по двум заданным проекциям детали построить третью проекцию (три вида детали).
Цель: Изучить приемы построения проекций деталей.
Порядок выполнения работы:
По двум заданным проекциям детали построить третью проекцию (три вида детали). Строить аксонометрическую проекцию детали не надо. Нанести размеры.
Варианты заданий
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
Вариант 11
Вариант 12
Вариант13
Вариант 14
Вариант 15
Образец выполнения задания:
Литература:
Бродский А.М., Фазлулин Э.М., Халдинов В.А. Инженерная графика - М.; Издательский центр «Академия», 2018.-399с.









































