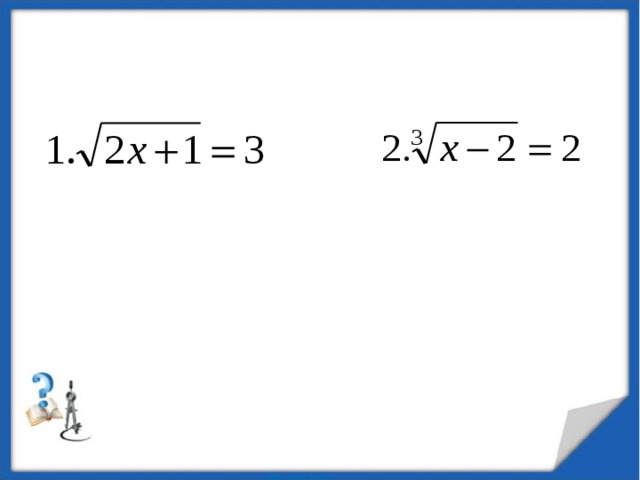| Этапы занятия | Задачи этапа | Деятельность преподавателя | Деятельность студента | УУД |
| 1.Организационный. (2мин) | Подготовка учащихся к работе на уроке: выработка на личностно значимом уровне внутренней готовности выполнения нормативных требований учебной деятельности. Создание благоприятного психологического настроя на работу. | Приветствие, проверка подготовленности к уроку, организация внимания. Здравствуйте. Прозвенел для нас звонок, Начинать пора урок. Мы немного повернёмся И друг другу улыбнёмся. Развернёмся и к гостям, Поприветствуем их там. А теперь не отвлекайтесь, За работу принимайтесь!
| Включаются в работу. | Личностные: определение общих для всех правил поведения. Регулятивные: включение в действие. Коммуникативные: планирование сотрудничества, готовность слушать и понимать речь других |
| 2. Актуализация знаний. (1мин) | Формирование мотива к деятельности на уроке. | Фронтальная беседа, показ значимости.
Нам вчера от студента 3 курса пришло письмо, давайте прочитаем это письмо. В нем говорится о том, что студент не может решить задачу.
| Отвечают на вопросы. | Личностные: установление связи между целью учебной деятельности и ее мотивом, самоопределение. Регулятивные: включение в действие, прогнозирование результата. Коммуникативные: планирование сотрудничества, готовность слушать и понимать речь других |
| 3. Постановка целей урока. (2мин) | Формирование мотива к достижению результата на уроке, обеспечение принятия целей урока учащимися, выработка на личностно значимом уровне внутренней готовности к достижению ожидаемого результата. | Постановка учебной проблемы. Создание условий для формулировки, осмысления и принятия цели урока и постановки учебных задач. «Начнем с задачи. (Преподаватель ставит перед обучающимися проблему: найти оптимальный способ решения задачи, а оптимальный способ решения задачи заключается в составлении иррационального уравнения). Задача: Повару - кондитеру нужно испечь праздничный пирог прямоугольной формы. Вычислите длину сторон пирога, если длина его диагонали равна 25 мм, а периметр - 70 см. Найдите оптимальный способ решения этой задачи. Перед вами проблема: найти оптимальный способ решения задачи. Вы предложили несколько способов. Но более оптимальный - это решение с помощью уравнения с которым мы сегодня познакомимся. Слайд 1 "Учиться можно только весело:
Чтобы переварить знания надо поглощать их с аппетитом"
А.Франц Поэтому предлагаю провести наше сегодняшнее занятие провести в «Математическом кафе». Рассмотрим меню на сегодня. (Группа делится на подгруппы. У каждый подгруппы, оценочные листы.) Слайд 2-3
| Осмысливают практическую значимость, формулируют цели урока, ставят учебные задачи. | Личностные: смыслообразование, самоопределение, выбор ценностей. Регулятивные: включение в действие, целеполагание, прогнозирование результата, волевая саморегуляция. Коммуникативные: планирование сотрудничества, готовность слушать и понимать речь других, умение выражать свои мысли. |
| 4. Подготовка к усвоению учебного материала. (5 мин) | Подготовка учащихся к эффективному усвоению учебного материала. Организация познавательной деятельности учащихся. | Организация повторения понятий, нужных для восприятия нового материала. « А чтобы познакомиться с этими уравнениями, давайте вспомним материал прошлого урока. Итак, настало время попробовать салат «Математический ералаш» под соусам из вопросов. Математический диктант «Да - НЕТ» Слайд 5- 7 | Активная познавательная деятельность: читают, ищут информацию, осмысливают практическую значимость. Выполняют математический диктант и делают взаимопроверку. | Личностные: смыслообразование, самоопределение. Регулятивные: включение в действие, волевая саморегуляция, оценка качества усвоения старого материала, применение методов информационного поиска, познавательная деятельность, умение строить речевые высказывания. Коммуникативные: планирование сотрудничества, готовность слушать и понимать речь других, умение выражать свои мысли. |
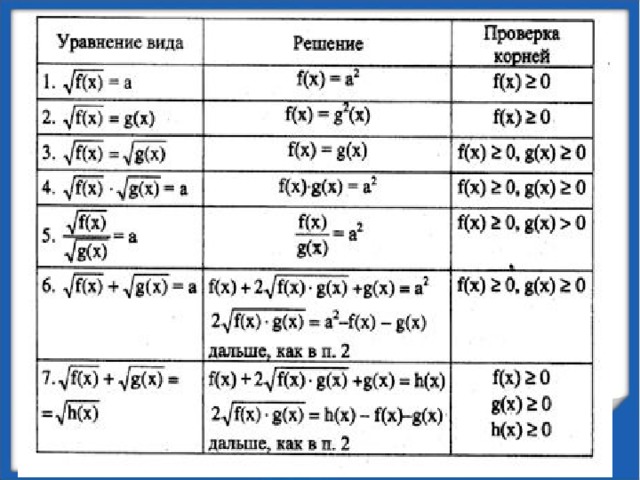
| 5. Усвоение новых знаний. (20мин) | Способствовать овладению методами решения уравнений, формированию алгоритмов решения, развитию логического мышления, умению говорить, объяснять, обосновывать выполняемые действия. | Организует восприятие новой темы, управляет осмыслением, усвоением: объясняет, выделяет главное, задает вопросы, ведет фронтальную беседу, отвечает на вопросы, обозначает алгоритмы, демонстрирует примеры решения различных типов. «Прошу вашего внимания на доску. Здесь расположены карточки, на которых записаны уравнения. Посмотрите внимательно и определите, какие уравнения вы уже умеете решать, а какие у вас вызывают затруднения? - Кто из вас может выйти к доске убрать карточки с уравнениями, которые вы можете решить и назвать их тип? Вывод: Остались карточки с уравнениями, которые вы еще не умеете решать. - Как называются числа, которые не выводятся из под корня? Ответ: Иррациональные. –Итак, как можно назвать тема нашего урока. Каждая группа предлагает свои варианты» Слад № 8-9 Тема нашего урока «Решение иррациональных уравнений» - Какие цели можно поставить ? (что такое ИУ, какие бывают, как решать?) Итак, смотрим на схему. Слайд №10-12. - Посмотрите на экран. Какие уравнения иррациональные? Слайд №13 - Как Решать ИУ? Рассмотрим два примера и составим алгоритм решения. 1. 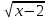 = 5 п - четная значит х - 2 0 = 5 п - четная значит х - 2 0 x-2 =25 x = 27 и х -2. 2. 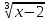 = 5 п - нечетная, = 5 п - нечетная, Х-2 = 125 Х = 127 . Алгоритм решение ИУ: смотрим на степень если четная то1, если нечетная то2. При решении иррациональных уравнений почти всегда необходимо избавиться от радикалов. Слайд №14. - Рассмотрим несколько видов ИУ. Слайд 15-18
| Выполняют учебные задачи: слушают лекцию, конспектируют, осмысливают, запоминают классификацию уравнений, запоминают алгоритмы решения, работают с учебником. | Личностные: смыслообразование, нравственно-этическое оценивание усваимого содержания Регулятивные: волевая саморегуляция, познавательная деятельность, знаково-символические действия, умение структурировать знания, смысловое чтение, извлечение необходимой информации из прослушанного текста, определение основной информации, умение сжать содержание текста, умение анализировать с целью выделения существенных признаков, умение устанавливать причинно-следственные связи. Коммуникативные: социальная компетентность-участие в коллективном обсуждении, планирование сотрудничества, готовность слушать и понимать речь других, умение выражать свои мысли. |
| 6. Проверка понимания, закрепление, самостоятельная работа. (10мин)
| Установить уровень усвоения, устранить пробелы в понимании, закрепить в памяти. | Организует деятельность учащихся по оценке усвоения, организует выявление уровня обязательного и возможного усвоения каждым учеником, организует деятельность по устранению пробелов в понимании, наблюдает, консультирует, корректирует. Переходим к следующему блюду пирог «Скороспелька». Каждая группа получает конверт с заданиями. Если вы правильно решите, то должны получить слова (работа в группах). Каждая группа выходит и пишет свои буквы, а в конце получим «Математика - царица наук!» - Рассмотрим три примера. Из каждой подгруппы выходит по одному студенту и решает у доски с комментарием. 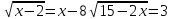 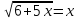
| Выделяют существенные признаки, соотносят факты с понятиями, выполняют самостоятельную работу, применяя полученные знания, могут консультироваться друг у друга и у учителя, устраняют пробелы в понимании. | Личностные: смыслообразование, самоопределение, нравственно-этическое оценивание усваимого содержания Регулятивные: волевая саморегуляция, знаково-символические действия, умение структурировать знания, выбор наиболее эффективных способов решения задач, извлечение необходимой информации из прослушанного текста, анализ, синтез, умение устанавливать причинно-следственные связи, контроль и оценка процесса и результатов деятельности, построение логической цепочки рассуждений, коррекция, применение методов информационного поиска Коммуникативные: социальная компетентность-участие в коллективном обсуждении, сотрудничество, готовность слушать и понимать речь других, умение выражать свои мысли. |
| 7. Подведение итогов урока. (3мин)
| Организовать анализ и самооценку успешности учебной деятельности, выявить качество и уровень овладения знаний, постановка цели последующей деятельности. | Организует самооценку успешности учебной деятельности
- А теперь используя полученные знания прорешаем задачу, которая была в начале урока. Слад №19 - Итак, вернемся к той схеме, которая была в начале урока. Какие уравнения называются Иррациональными?
Как решаются ИУ? Каждая группа оценивает свою работу на уроке. _ Что на уроке понравилась больше всего? - Что вызвало затруднение? (Студенты письменно отвечают на вопросы рефлексии ) Слайд 21-22 | Анализируют свою деятельность, соотносят уровень обязательного и реального усвоения учебного материала, ставят задачи последующей деятельности | Личностные: установление связи между целью и результатом, самоопределение. Регулятивные: контроль и оценка процесса и результатов деятельности, коррекция, оценка (осознание качества уровня усвоения), рефлексия способов и условий деятельности. Коммуникативные: социальная компетентность-участие в коллективном обсуждении, сотрудничество, готовность слушать и понимать речь других, умение выражать свои мысли. |
| 8. Домашнее задание. (2мин) | Объяснить методику выполнения домашнего задания. | Организует деятельность по усвоению методики выполнения домашнего задания. Учебник Алгебра и начала математического анализа. Под ред. А. Н. Колмагорова, 10-11 классы: с. 214-216, упр. 418, 422(б, в), (работа с приложением на электронном носителе), конспект учить. Нашу встречу хотело бы закончить с притчи."Жил мудрец, который знал все. Один человек захотел доказать, что мудрец знает не все. Зажав в ладонях бабочку, он спросил: "Скажи, мудрец, какая бабочка у меня в руках: мертвая или живая?” А сам думает: "Скажет живая – я ее мертвлю, скажет мертвая – выпущу”. Мудрец, подумав, ответил: "Все в твоих руках”.
|
| Личностные: установление связи между целью и результатом, самоопределение. Регулятивные: коррекция, оценка (осознание качества уровня усвоения). Коммуникативные: социальная компетентность-участие в коллективном обсуждении, сотрудничество, готовность слушать и понимать речь других, умение выражать свои мысли. |







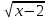
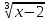 = 5 п - нечетная,
= 5 п - нечетная, 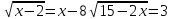
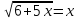




 0. 3. Если в n - четная, то а 0. 4. 5. Если в n - нечетная, то а любое. 6. Верно ли, что 25х 2 +40х+4 = (5х+2) 2 7. Верно ли, что 4х 2 +1-2х = (2х-1) 2; 8. 9. = ± 3" width="640"
0. 3. Если в n - четная, то а 0. 4. 5. Если в n - нечетная, то а любое. 6. Верно ли, что 25х 2 +40х+4 = (5х+2) 2 7. Верно ли, что 4х 2 +1-2х = (2х-1) 2; 8. 9. = ± 3" width="640"