МЕТОДИЧЕСКОЕ ПОСОБИЕ Для самостоятельной работы студентов По дисциплине: МАТЕМАТИКА Тема: «Комбинаторика» Специальность: 34.02.01 Сестринское дело Курс: 2

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ НОВОСИБИРСКОЙ ОБЛАСТИ «КУПИНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ»

МЕТОДИЧЕСКОЕ ПОСОБИЕ

Для самостоятельной работы студентов

По дисциплине: МАТЕМАТИКА

Тема: «Комбинаторика»

Специальность: 34.02.01 Сестринское дело Курс: 2

(базовой подготовки)

Купино

2016

Рассмотрено на заседании предметной цикловой

Методической комиссии по общеобразовательным дисциплинам,

общему гуманитарному и социально-экономическому, математическому и

естественно-научному циклу

Протокол № _____ от «_____» _________20____г.

Председатель ПЦМК: _____________

Автор – составитель: преподаватель математики высшей категории Тюменцева О.Н.

Купино

2016 г

Пояснительная записка к методическому пособию

Методическое пособие предназначено для изучения теоретических и практических знаний по теме.

Цель пособия – изучить основные понятия и правила комбинаторики и подготовиться к занятию по теме «Основные понятия комбинаторики».

Данное пособие рекомендовано для студентов первого и второго курсов специальности 34.02.01 Сестринское дело. Пособие содержит определение и правила комбинаторики, задания для самоконтроля.

Пособие направлено на формирование навыков самостоятельной работы с учебным материалом, формирование навыков решения задач, формирование и развитие творческого потенциала, повышение интереса к дисциплине.

Принципы сложения и умножения. Размещения, сочетания, перестановки

Выбором объектов и расположением их в том или ином порядке приходится заниматься чуть ли не во всех областях человеческой деятельности, например, конструктору, разрабатывающему новую модель механизма, ученому-агроному, планирующему распределение сельскохозяйственных культур на нескольких полях, химику, изучающему строение органических молекул, имеющих данный атомный состав.

С аналогичными задачами, получившими название комбинаторных, люди столкнулись в глубокой древности. Уже несколько тысячелетий назад в Древнем Китае увлекались составлением магических квадратов, в которых заданные числа располагали так, что их сумма по всем горизонталям, вертикалям и главным диагоналям была одной и той же. В Древней Греции подсчитывали число различных комбинаций длинных и коротких слогов в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые можно составить из частей особым образом разрезанного квадрата, и т.д.

Комбинаторные задачи возникали и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д. ( Например, задача о расстановке восьми ферзей на шахматной доске так, чтобы ни один из них не оказался под боем, об обходе всех полей доски шахматным конем и т.д.).

Комбинаторика становится наукой лишь в XVII в. – в период, когда возникла теория вероятностей. Чтобы решать теоретико-вероятностные задачи, нужно было уметь подсчитывать число различных комбинаций, подчиненных тем или иным условиям. После первых работ, выполненных в XVI в. итальянскими учеными Дж. Кардано, Н. Тартальей и Г. Галилеем, такие задачи изучали французские математики Б. Паскаль и П. Ферма. Первым рассматривал комбинаторику как самостоятельную ветвь науки немецкий философ и математик Г. Лейбниц, опубликовавший в 1666 г. работу «Об искусстве комбинаторики», в которой впервые появляется сам термин «комбинаторный». Замечательные достижения в области комбинаторики принадлежат Л. Эйлеру. Комбинаторными задачами интересовались и математики, занимавшиеся составлением и разгадыванием шифров, изучением древних письменностей. Теперь комбинаторика находит приложения во многих областях науки: в биологии, где она применяется для изучения состава белков и ДНК, в химии, механике сложных сооружений и т.д.

Комбинаторика-это раздел математики, в котором решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств.

Два основных принципа комбинаторики:

1. Принцип сложения:

Предположим, что та или иная задача решается любым из k методов, причем первый метод можно применить 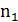_способами, второй - 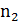_ способами, … , k-тый метод можно применить 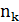_ способами. Тогда рассматриваемая задача решается (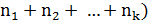_способами.

1. Принцип умножения:

Пусть требуется выполнить одно за другим какие-то k действий. Если первое действие можно выполнить 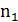_ способами, второе - 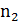_ способами, … , k-тое действие можно выполнить 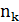_ способами, то все k действий вместе могут быть выполнены (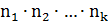_) способами.

Примеры.

1. В группе 30 человек, необходимо выбрать старосту и профорга. Сколькими способами можно это сделать?

2. Имеется 20 изделий первого сорта и 30 изделий второго сорта. Необходимо выбрать два изделия одного сорта. Сколькими способами можно это сделать?

Основные типы комбинаций:

1. Перестановки

Пусть имеется множество, содержащее три буквы: 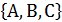_. Запишем все возможные комбинации из трех букв: ABC, ACB, BAC, BCA, CAB, CBA. Таких комбинаций 6. Заметим, что _

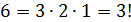Определение. Перестановкой из n элементов называется любое упорядоченное множество, в которое входят по одному разу все n различных элементов данного множества. Число перестановок n различных элементов будем обозначать _.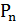

Теорема. Число перестановок n различных элементов равно n!, т.е.

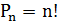
Примеры.

1. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что ни одна из них в числе не повторяется.

2. Вычислить: а) 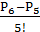_ ; б) _ ; в) _ .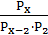

Замечание. Перестановки отличаются друг от друга только порядком

элементов.

1. Размещения

Пусть имеется множество, содержащее четыре буквы 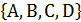_. Составим все возможные комбинации только из двух букв данного множества: AB, BA, AC, CA, AD, DA, BC, CB, BD, DB, CD, DC. Таких комбинаций получилось 12. Заметим, что _.

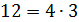Определение. Размещением из n элементов по m называется любое упорядоченное подмножество из m элементов множества, состоящего из n различных элементов. Число размещений из n элементов по m будем обозначать 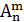_, где _.

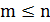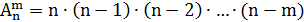
Теорема. Число размещений из n элементов по m равно 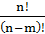_, т.е.

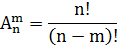
Примеры.

1. Сколько двузначных чисел можно составить из пяти цифр 1, 2, 3, 4, 5 при условии, что цифры в числе не повторяются.

2. Вычислить: а) 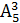_ ; б) 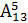_ ; в)_ .

Замечание. Размещения отличаются друг от друга самими элементами и порядком элементов.

1. Сочетания

Пусть имеется множество, содержащее четыре буквы 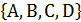_. Составим все возможные комбинации из двух букв, причем, не будем учитывать порядок элементов (т.е. комбинации AB и BA будем считать как одну комбинацию): AB, AC, AD, BC, BD, CD. Таких комбинаций получилось 6.

Определение. Сочетанием из n элементов по m называется любое подмножество из m элементов, которые принадлежат множеству, состоящему из n различных элементов.

Число сочетаний из n различных элементов по m будем обозначать _, где _.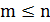

Теорема. Число сочетаний из n элементов по m равно _ , т.е.

Следствие. Число сочетаний из n элементов по (n-m) равно числу сочетаний из n элементов по m, т.е.

Теорема. Имеет место равенство (правило Паскаля)

Теорема. Имеет место равенство

Примеры.

1. Вычислить: а) _; б) _.

2. Сколькими способами можно выбрать трех дежурных из 30 человек в группе?

1. Решение задач.

1. Сколькими способами можно группу из 12 человек разбить на две подгруппы, в одной из которых должно быть не более пяти, а во второй – не более девяти человек?

2. Сколько существует вариантов опроса 11 учащихся на одном занятии, если ни один из них не будет подвергнут опросу дважды и на занятии может быть опрошено любое количество учащихся, причем, порядок, в котором опрашиваются учащиеся, безразличен?

3. Решить уравнение: а)._ ; б). _.

4. Вычислить: _

5. Решить систему уравнений: _

6. 30 учащихся обменялись друг с другом фото. Сколько всего фото было роздано?

Комбинации с повторениями

1. Перестановки с повторениями.

_ ,

где _, _ - число повторений i – го элемента.

1. Размещения с повторениями.

1. Сочетания с повторениями.

_.

Примеры.

1. Сколько разных «слов» можно составить из букв слова: а) «стена», б) «гамма»?

2. В продажу поступили открытки 10 разных видов. Сколькими способами можно образовать набор из 12 открыток?

3. Сколько разных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если одна и та же цифра может повторяться несколько раз?

1. Решение задач

1. В колоде 32 карты. Раздаются три карты. Сколько может быть случаев появления одного туза среди розданных карт?

2. Четыре студента сдают экзамен. Сколько может быть вариантов распределения оценок, если известно, что так или иначе все они сдали экзамен?

3. Сколько пятизначных чисел можно образовать из цифр 0 и 1?

4. Абитуриенту нужно сдать четыре экзамена и набрать не менее 17 баллов(«2» получать нельзя). Сколько существует разных наборов экзаменационных оценок, дающих ему право поступления?

5. Среди перестановок цифр 1, 2, 3, 4, 5 сколько таких, которые не начинаются цифрами 3 и 5?

6. Из цифр 1, 2, 3, 4, 5 составляются всевозможные пятизначные числа без повторяющихся цифр.

а). Сколько всего получится таких чисел?

б). Сколько среди них будут начинаться с цифры 5?

в). Сколько чисел будут оканчиваться комбинацией 41?

г). Сколько получится четных и сколько нечетных чисел?

д). Сколько получится чисел, кратных 3?

Приложение 1

«Расчет количества комбинаций»

Необходимые сведения из теории

1. ПРАВИЛА КОМБИНАТОРИКИ

   1. Правило суммы: Если некоторый объект А из совокупности объектов можно выбрать m способами, а другой объект В можно выбрать n способами, то объект либо A, либо B можно выбрать m + n способами.

   2. Правило произведения: Если некоторый объект А из совокупности объектов можно выбрать m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (AB) в указанном порядке может быть выбрана m·n способами.

2. ОСНОВНЫЕ ФОРМУЛЫ КОМБИНАТОРИКИ

   1. Размещения

Отличаются по составу и по порядку элементов.

Число размещений без повторений вычисляется по формуле:

Число размещений с повторениями вычисляется по формуле:

1. Перестановки

Отличаются по порядку элементов.

Число перестановок без повторений вычисляется по формуле:

Число перестановок с повторениями вычисляется по формуле:

где _ и

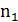_ – число повторений первого элемента,

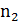_ – число повторений второго элемента и т.д.

1. Сочетания

Отличаются по составу и по порядку элементов.

Число сочетаний без повторений вычисляется по формуле:

Свойства сочетаний: _

_

Число сочетаний с повторениями вычисляется по формуле:

Задания

1. Вычислите:

а). _

б). _

в). _

г). _

д). _

е). _

2. Решить уравнения:

а). _

б). _

в). _

г). _

д). _

Приложение 2

Теория вероятностей и математическая статистика

Необходимые сведения из теории

1. ПРАВИЛА КОМБИНАТОРИКИ

1. Правило суммы: Если некоторый объектА из совокупности объектов можно выбрать m способами, а другой объект В можно выбрать n способами, то объект либо A, либо B можно выбрать m + nспособами.

2. Правило произведения: Если некоторый объектА из совокупности объектов можно выбрать m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (AB) в указанном порядке может быть выбрана m_n способами.

1. ОСНОВНЫЕ ФОРМУЛЫ КОМБИНАТОРИКИ

   1. Размещения

Отличаются по составу и по порядку элементов.

Число размещений без повторений вычисляется по формуле:

Число размещений с повторениями вычисляется по формуле:

1. Перестановки

Отличаются по порядку элементов.

Число перестановок без повторений вычисляется по формуле:

Число перестановок с повторениями вычисляется по формуле:

где _ и

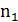_ – число повторений первого элемента,

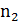_ – число повторений второго элемента и т.д.

1. Сочетания

Отличаются по составу и по порядку элементов.

Число сочетаний без повторений вычисляется по формуле:

Свойства сочетаний: _

_

Число сочетаний с повторениями вычисляется по формуле:

З

Задания.

1. Сколько можно изготовить различных трехцветных флажков, если использовать следующие цвета: белый, синий, красный, желтый, зеленый, черный?

2. Сколькими способами можно распределить шесть проводников по шести вагонам, если за каждым вагоном закрепляется один проводник?

3. На семь сотрудников выделено четыре одинаковые путевки в дом отдыха. Сколькими способами их можно распределить?

4. Для полета на Марс необходимо укомплектовать следующий экипаж космического корабля: командир корабля, первый его помощник, второй помощник, два бортинженера и один врач. Командующая тройка может быть отобрана из числа 25 готовящихся к полету летчиков, два бортинженера – из числа 20 специалистов, в совершенстве знающих устройство космического корабля, и врач – из числа 8 медиков. Сколькими способами можно укомплектовать экипаж исследователей?

1. Сколькими способами восемь различных книг можно расставить на одной полке так, чтобы: а) две определенные книги оказались рядом; б) две определенные книги не оказались рядом.

2. Сколько существует способов размещения 10 шариков в два ящика, чтобы в одном оказалось не более 4, а в другом – не более 8 шариков.

3. Сколько можно составить слов из букв слова «математика».

Ответы: 1) 120; 2) 720; 3) 35; 4) 20 976 000; 5) а) 10 080; б) 30 240; 6) 375; 7) 151 200.

1. СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1. Апанасов П.Т., Орлов М.И. Сборник задач по математике: Учеб.пособие для техникумов. – М.: Высш. шк., 1987. – 303с.: ил.

2. Бычков А. Г. Сборник задач по теории вероятностей, математической статистики и методам оптимизации: учебное пособие. – М.: ФОРУМ. 2008. – 224с.: ил. – («Профессиональное образование»)

3. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учеб.пособие. – 2 – е изд., перераб. и доп. – М.: Наука. Гл. ред. физ.–мат. лит., 1989. – 576 с.: ил.

4. Калинина В.Н., Панкин В.Ф. Математическая статистика: Учеб. для студ. сред. спец. учеб. заведений. – 3-е изд., испр. –М.: Высш. шк.., 2001.- 336 с.: ил.

5. Кочетков Е.С., Смерчинская С.О., Соколов В.В. Теория вероятностей и математическая статистика: Учебник. – М.: ФОРУМ: ИНФРА – М, 2003. – 240 с.: ил. – (Серия «Профессиональное образование»)

10