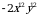| 2 | Постановка цели и задач урока.
Мотивационно-целевой этап урока. | Постановка цели и задач урока. Сообщение обучающимся целей предстоящей работы.
Учитель предлагает обучающимся предположить тему урока.
Для этого учитель демонстрирует на доске запись примеров и предлагает обучающимся классифицировать их: Приложение 1. 
Учитель предлагает обучающимся попытаться классифицировать по блокам представленные произведения и числа. Предполагаемые вопросы: Что можно отнести к блоку «Число»? Какие элементы относятся к пройденной теме «Степень с натуральным показателем? С одинаковым основанием, разным основанием?» Какие из элементов знакомы? Какие не знакомы? Почему? Что можно сказать про элементы, которые относятся к неизвестному блоку? | Обучающиеся акцентируют внимание на предстоящей работе.
Вместе с учителем пытаются сформулировать тему сегодняшнего урока.
Предполагаемые ответы: - Числа это количественная величина, поэтому к числу можно отнести -100, 144, 12, 9, 36. - Ранее мы проходили свойства степеней с натуральным показателям, выполняли умножение, деление, возведение в степень чисел с одинаковыми основаниями. - К третьему блоку можно отнести выражения, которые представляет собой произведение букв, чисел и букв в степени и чисел в степени.
| умение задавать вопросы в соответствии с требованиями и задачами коммуникации, касающихся предстоящих учебных действий. | поиск и выделение необходимой информации; структурирование знаний; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности. | составление плана и последовательности действий; предвосхищение результата предстоящей работы на уроке; планирование учебного сотрудничества с учителем и сверстниками; определение цели, функций участников, способов взаимодействия; постановка вопросов;
|
| 3 | Поисково-исследователь-ский. | Учитель обращает внимание на то, что к третьему блоку на доске относятся выражения вида, где представлено произведение букв, чисел. И делает акцент на том, что ученики будут изучать выражения такого вида, Учитель предлагает обучающимся с опорой на пройденный материал, ознакомится с принципами построения нового. Для этого учитель предлагает ознакомиться с конкретным буквенным выражением и изучить его составляющие. 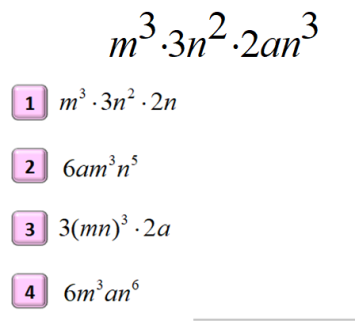 Учитель предлагает разобрать составляющие произведения. Задает наводящие вопросы: -Что в произведении можно выделить? Если ли в ним числа? -Если ли в произведении одинаковые основания в степени? -Все ли основания одинаковые? -Есть ли переменные без степеней? Учитель открывает на доске тайну темы урока. И говорит обучающимся, что сегодня мы изучим «Одночлены» Учитель предлагает открыть тетрадь и записать структурное определение. | Обучающиеся внимательно изучают представленные модели, получившиеся методом исключения. Делают вывод исключительно по внешнему виду выражения о его составе.
Изучают пример, который предлагает учитель. Пытаются ответить на поставленные вопросы, полагаясь на собственный опыт и знания предыдущей темы. Предполагаемые ответы: - В данном буквенном выражении есть две разные переменные - В произведении есть числа; - В произведении есть переменные в степени и т.д. | инициативное сотрудничество в поиске и сборе информации; управление поведением партнера контроль, коррекция, оценка его действий; умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации;
| выбор наиболее эффективных способов решения задач в зависимости от конкретных условий; извлечение необходимой информации из прослушанных текстов различных жанров; определение основной и второстепенной информации; постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем творческого и поискового характера;
| п рогнозирование - предвосхищение результата и уровня усвоения знаний, его временных характеристик; рогнозирование - предвосхищение результата и уровня усвоения знаний, его временных характеристик; составление модели и последовательности действий работы с ней в виде задающих ее координат; внесение необходимых дополнений и коррективов модель задачи в процессе ее создания или усовершенствования |
| 4 | Первичное усвоение новых знаний. | Учитель предлагает обучающимся зарисовать структурную схему определения «Одночлена» Одночленом называют алгебраическое выражение, которое представляет собой произведение чисел и переменных, возведённых в степень с натуральными показателями. Схема: 

Учитель предлагает решить задачу, полагаясь на пройденный материал и только что записанное определение: Задание на доске: 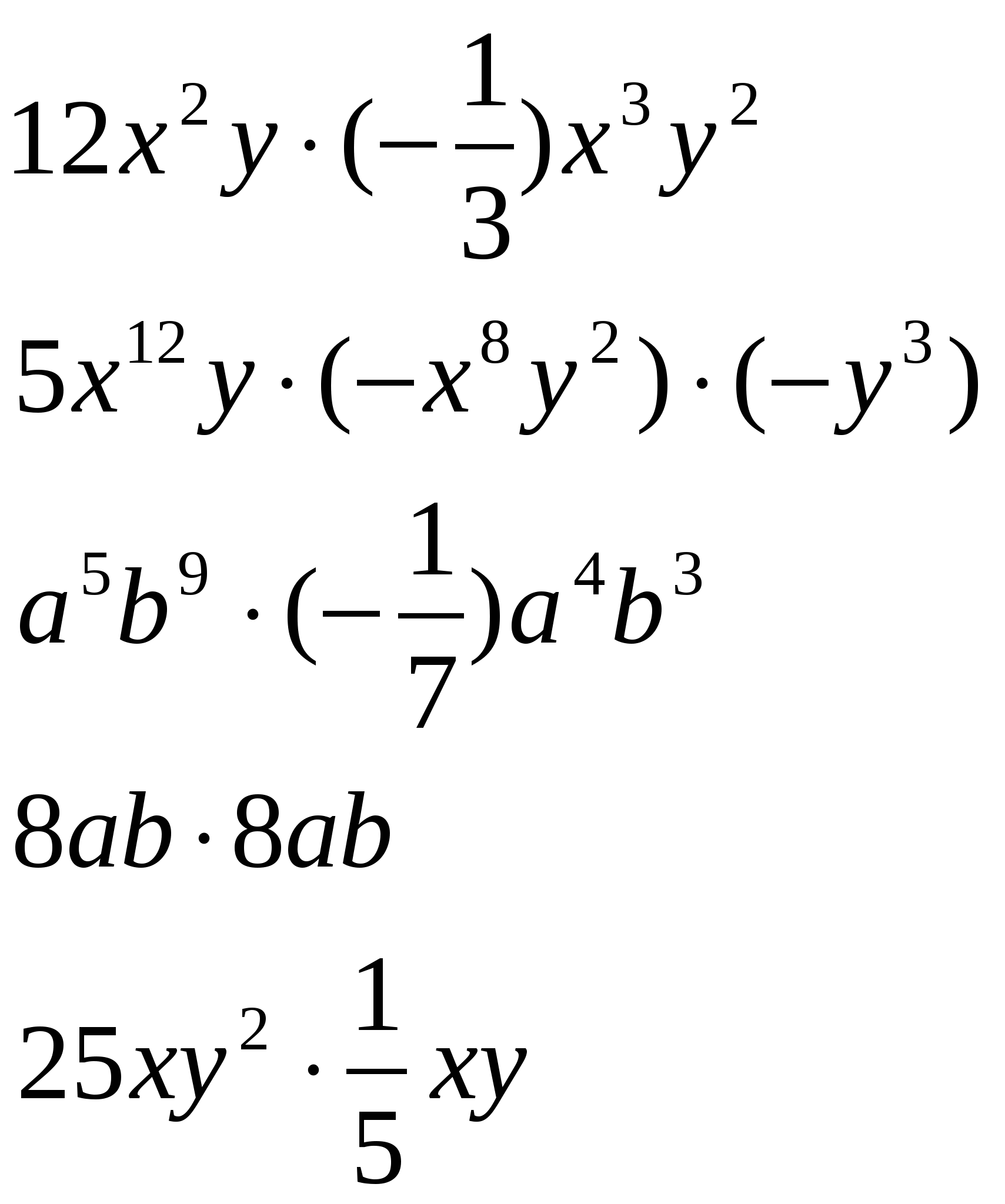
Учитель спрашивает обучающихся, обозначив проблем. Скажите, можем ли мы поменять местами имеющиеся переменные так, чтобы что-то упростить?
А если можем поменять множители, то что получится? В буквенном выражении меняем множители для того, чтобы видеть, что и как можно упростить, посчитать или использовать свойства степеней. 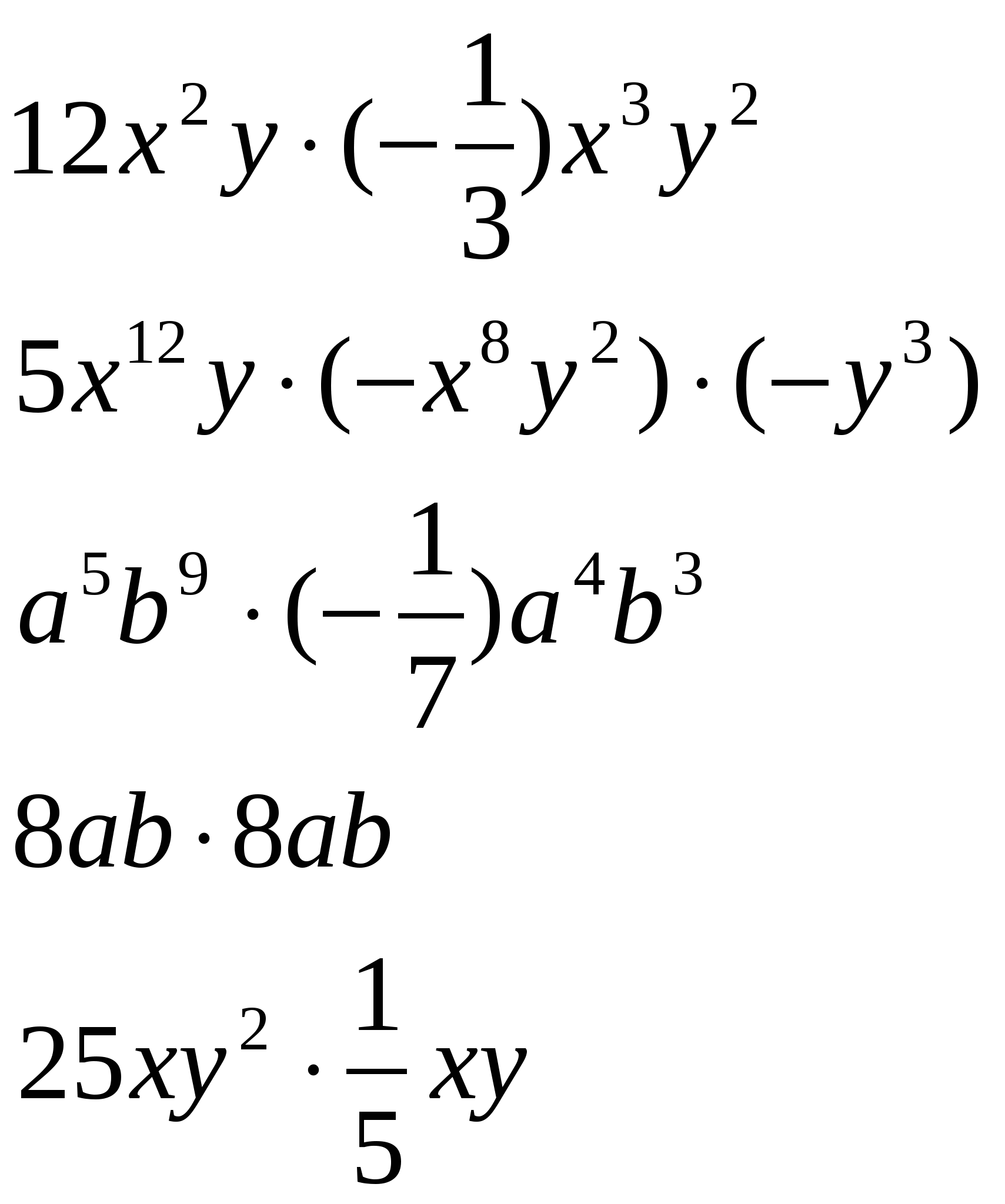
Учитель вводит определение стандартного вида одночлена: 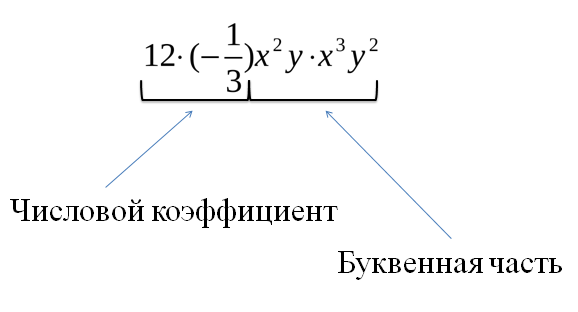
Учитель структурой определения проговаривает алгоритм упрощение одночлена: Любой одночлен можно записать в стандартном виде. Для этого нужно: 1.перемножить все числовые множители и поставить полученное произведение на первое место; 2.перемножить все имеющиеся степени с одним буквенным основанием; 3.перемножить все имеющиеся степени с другим буквенным основанием и т.д. Учитель предлагает обучающимся вспомнить об уже знакомых одночленах, которые приведены к стандартному виду: 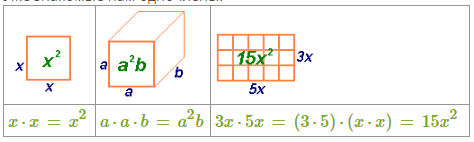
Учитель вводит определение степени одночлена. Учитель вводит определение нуль - одночлена. Вывод: у одночлена коэффициент может быть нулевой, а у буквенных множителей всегда есть степени, больше нуля и нуль включая. Предлагает обучающимся изучить схему на доске: 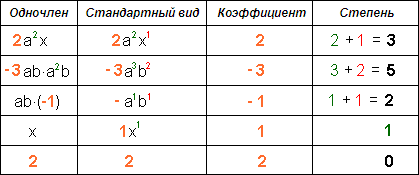
| Обучающиеся изучают структуру определения и задают вопросы.
С учителем разбирают правило, выделяя все существенные свойства определения
Формируют вопросы по решению задач. Можно ли менять множители в буквенном выражении и зачем?
Отвечают на вопросы. От перестановки множителей - произведение не меняется. Значит, можем.
Обучающиеся изучают алгоритм представления одночлена к стандартному виду. Выделяют существенные свойства. Определяют понятие коэффициент одночлена.
Обучающиеся внимательно изучают представленные модели, закрепляя понятий аппарат визуальным изображением.
Обучающиеся записывают определения. Предвосхищают свои результаты деятельности по решению задач.
Обучающиеся внимательно изучают схему, слушая комментарии учителя. Задают вопросы. | — планирование учебного сотрудничества с учителем и сверстниками — определение цели, функций участников, способов взаимодействия; — постановка вопросов — инициативное сотрудничество в поиске и сборе информации; — управление поведением партнера контроль, коррекция, оценка его действий; — умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации; — разрешение разногласий по поводу решения задач – выявление, идентификация проблемы, поиск и оценка альтернативных способов разрешения ситуации, принятие решения и его реализация
| — выбор наиболее эффективных способов решения задач в зависимости от конкретных условий; — извлечение необходимой информации из прослушанных текстов различных жанров; определение основной и второстепенной информации; — постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем творческого и поискового характера; — установление причинно-следственных связей; — самостоятельное создание способов решения проблем творческого и поискового характера; — выбор оснований и критериев для сравнения, сериации, классификации объектов; — синтез - составление целого из частей, в том числе самостоятельное достраивание с восполнением недостающих компонентов; — преобразование объекта из одной формы в модель, где выделены существенные характеристики объекта пространственно- графическая или знаково-символическая; — преобразование модели с целью выявления общих законов, определяющих данную предметную область
| — определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий; — внесение необходимых дополнений и корректив в план и способ действия в случае расхождения эталона, реального действия и его результата; – предвосхищение результата и уровня усвоения знаний; – контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона |
| 5 | Практико-ориентированный | Учитель предлагает обучающимся на доске несколько задач на отработку алгоритма. Задание. Представить произведение в стандартном виде. Указать степень одночлена и его коэффициент. 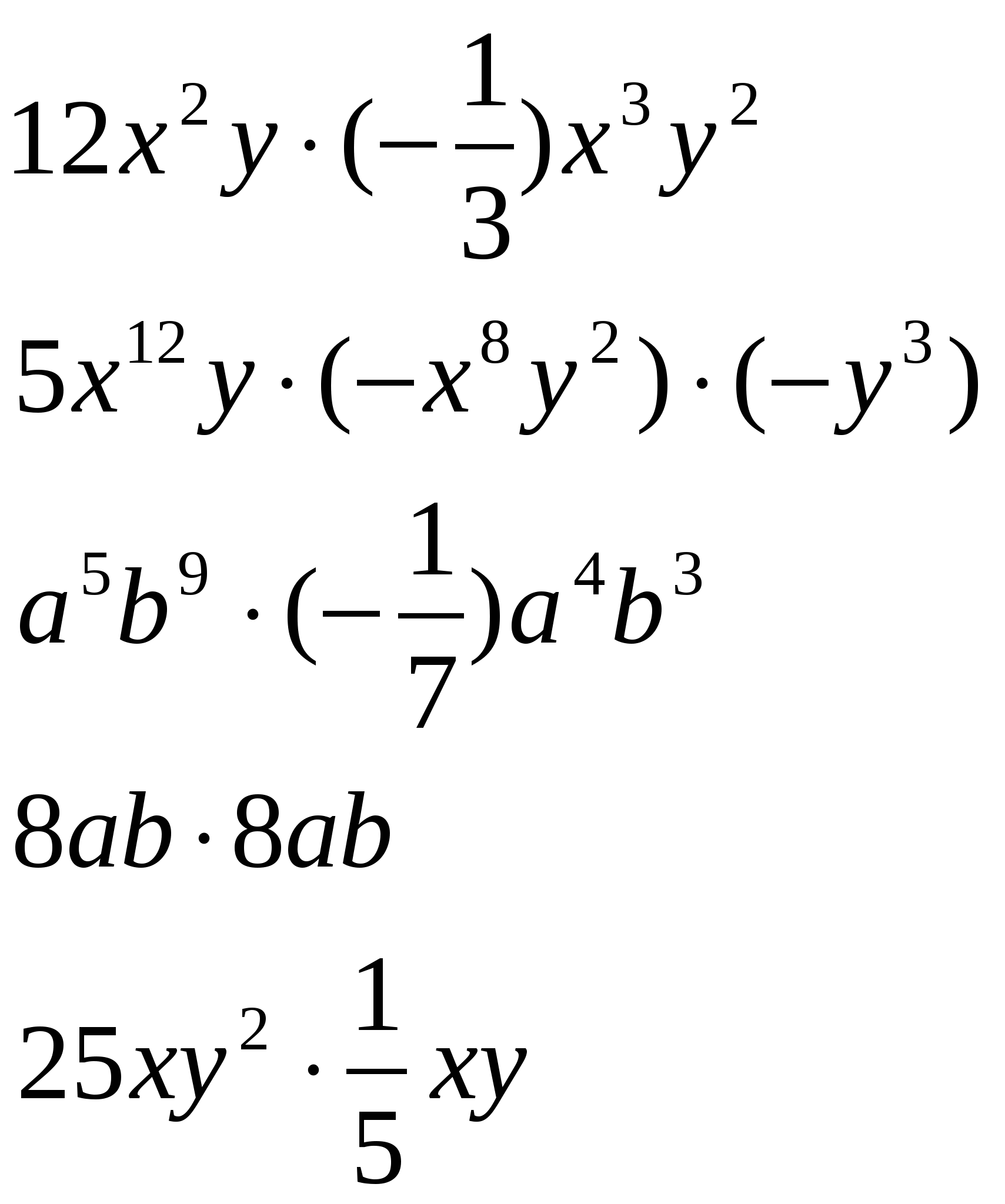
Учитель совместно с учениками разбирают у доски 4 примера.
Учитель может предложить решение задач в парах с взаимопроверкой у доски, отмечая ошибки и недостатки в усвоении нового материала.
Учитель определяет трудности в решении, уделяет внимание на правила и алгоритмы, упрощающие понимание и сводящие пример к минимуму ошибок и исключение ее появления. | Изучают условие задачи. Акцентируют внимание на теоретическую информацию, необходимую для решения данного задания: Что такое коэффициент? Что есть степень одночлена? Что есть одночлен?
1 ситуация. У доски производят решение 4 ученика, пытаясь сделать первые шаги к пояснению и решению задач на одночлены.
2 ситуация. Ученики работают в парах, осуществляя взаимопроверку после завершения решения. | — планирование учебного сотрудничества с учителем и сверстниками - определение цели, функций участников, способов взаимодействия; — постановка вопросов - инициативное сотрудничество в поиске и сборе идей; — формирование ИКТ компетенции. | — постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем творческого и поискового характера. — выделение существенных характеристик объекта пространственно- графическая или знаково-символическая форма представления задания; — синтез - составление целого из частей, в том числе самостоятельное достраивание с восполнением недостающих компонентов; — установление причинно-следственных связей; | — прогнозирование - предвосхищение результата и уровня усвоения знаний, его временных характеристик; — составление модели и последовательности действий работы с ней в виде задающих ее координат; – внесение необходимых дополнений и коррективов модель задачи в процессе ее создания или усовершенствования; |
| 6 | Контрольно-оценочный | Учитель предлагает обучающимся решить задачи с учебника: № 269 (4-6); №271 (5,6); № 274. Учитель предлагает небольшую самостоятельную работу по карточкам. Задание: Определите степень и коэффициент одночлена, предварительно упростив его. Приложение 2. | Обучающиеся решают задачи совместно с учителем у доски на оценку. Задают вопросы. Обсуждают способы разрешения учебной ситуации. | — формирование ИКТ компетенции; — строить грамотно вопрос в соответствии с задачами коммуникации
| — синтез - составление целого из частей, в том числе самостоятельное достраивание с восполнением недостающих компонентов; — установление соответствия компонентов, задающих логическую составляющую: сложение фрагментов в одно целое, сопоставление одному объекту другой, интерпретация
| — прогнозирование - предвосхищение результата и уровня усвоения знаний, его временных характеристик.
|
| 7 | Рефлексивно-обобщающий | Учитель осуществляет опрос в конце урока: - О чем мы сегодня говорили? -Что называют одночленом? -Что называется коэффициентом одночлена? - Что называют степенью одночлена? - Что называют нуль - одночленом? - Что называют стандартным видом одночлена?
Осуществляет рефлексию образовательно деятельности, подводит итоги. Определяет домашнее задание: решить тест. Приложение 3. | Обучающиеся отвечают на вопросы анкеты. Записывают домашнее задание. Осуществляет рефлексию своей деятельности на уроке через анализ собственных затруднений и деятельности коллектива, группы в целом как в процессе, так и в итоге. | — постановка вопросов в соответствии с задачами коммуникации. | — самостоятельное выделение и формулирование познавательной цели.
| — планирование — определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий. |








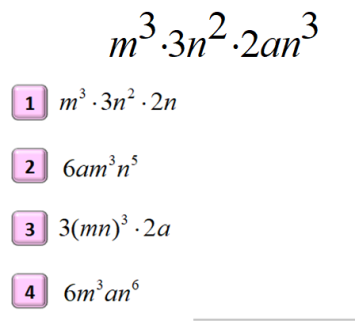
 рогнозирование - предвосхищение результата и уровня усвоения знаний, его временных характеристик;
рогнозирование - предвосхищение результата и уровня усвоения знаний, его временных характеристик;




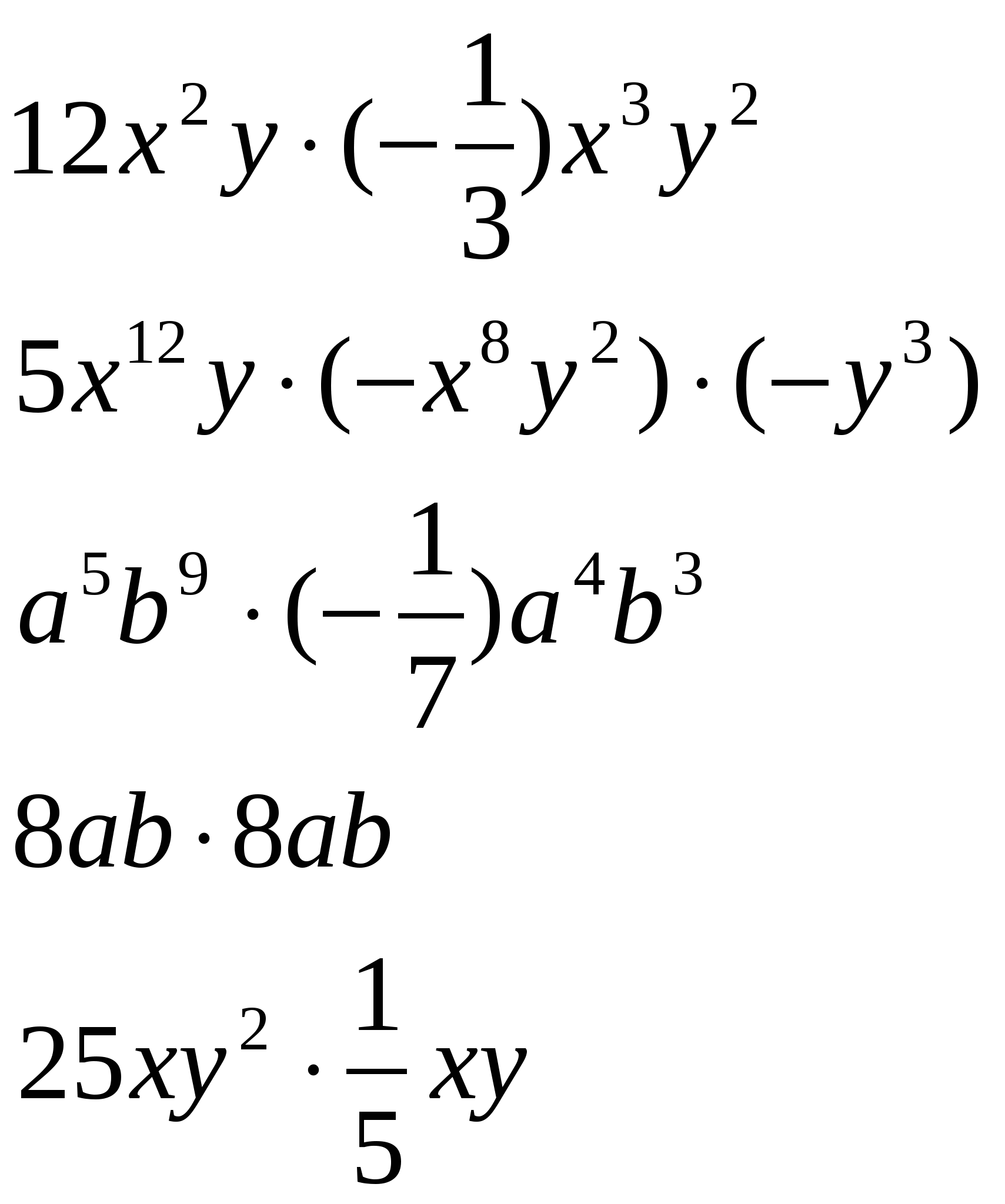

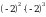 .
.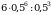 .
.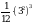 .
.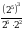 .
.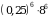 .
.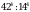 .
.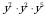 .
. 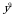 2)
2) 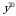 3)
3) 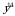 4)
4) 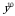
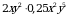
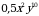 2)
2) 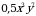 3)
3) 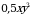 4)
4) 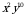
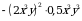
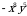 2)
2) 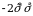 3)
3) 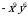 4)
4) 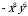
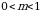 . Из данных чисел выберите наибольшее
. Из данных чисел выберите наибольшее 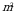 2)
2) 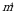 3)
3) 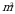 4)
4) 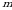
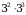 .
.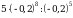 .
.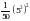 .
.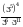 .
.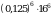 .
.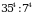 .
.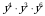 .
. 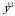 2)
2) 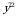 3)
3) 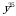 4)
4) 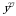
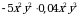 .
. 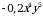 2)
2) 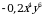 3)
3) 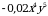 4)
4) 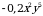
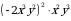 .
. 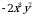 2)
2) 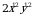 3)
3)