Модуль
по физической химии
Урок №1: Фазовое равновесие.
Закон действия масс является законом для гомогенных систем, однако на практике часто приходится иметь дело с гетерогенными системами, в которых вещества находятся в различных агрегатных состояниях.
Равновесие в гетерогенных системах рассматривается применительно закона равновесия фаз или правила фаз (выведенное американским ученым Д. Гиббсом в 1873-1876 г.). Оно устанавливает, при каких условиях (температуре, давлении, концентрациях веществ) отдельные однородные участки гетерогенных систем (фазы) находятся в состоянии термодинамического равновесия.
Молекулы жидкостей и твердых тел при любой температуре могут переходить в газообразную фазу. Переход жидкости в газообразную фазу называется испарением, обратный процесс – конденсацией.
Переход вещества из твердой фазы в газообразную, минуя жидкую фазу – сублимация (возгонка), обратный процесс – десублимация.
Возможен переход твердого вещества в жидкое состояние – плавление, а наоборот – кристаллизация. Все эти процессы, при которых вещества без изменения химического состава вещества переходом из одного агрегатного состояния в другое, называются фазовым переходом.
Основные понятия
Фаза (Ф) – однородные участки системы, отделенные друг от друга видимыми поверхностями раздела.
(Система, состоящая из воды и льда – две фазы (Ф=2): одна жидкая, вторая – твердая.
Смесь газов в закрытом сосуде – система состоит из одной фазы (Ф=1).
Насыщенный раствор соли в воде – 3х фазная система: твердая соль, жидкость, пар над раствором).
Гетерогенная система – система, состоящая из нескольких фаз.
Гомогенная система – состоящая из одной фазы.
Между фазами гетерогенной системы установиться равновесие, которое называется фазовым равновесием.
(Примером может служить наступление равновесия в системе насыщенный раствор соли – в равновесии находятся жидкий раствор и кристаллы. Скорость растворения в такой системе равна скорости кристаллизации.)
Гетерогенная система может состоять из одного или нескольких компонентов.
Компонент (К) – независимая часть системы, которая может быть выделена и существовать самостоятельно.
Для физических реакций или систем, в которых не идут химические реакции, число компонентов равно числу составных частей, входящих в систему (числу химически индивидуальных веществ).
Например, в системе водного раствора хлорида натрия два компонента: вода и хлорид натрия. К=2.
В системе, состоящей из трех различных фаз

Вещество одно H2O К=1.
Для химических реакций (когда в системе идет реакция) число компонентов равно числу составных частей минус число реакций, протекающих между этими веществами.

К=3. Реакция одна.
К = 3 – 1 = 2.

В реакции:
К=4. Реакция 1.
К = 4 – 1 = 3.
Если менять условия p, t, концентрацию в гетерогенной системе, равновесие будет смещаться.
Но эти параметры можно менять без смещения равновесия.
Например, если Т=const, сжимать насыщенный пар (давление увеличивается), то пар будет конденсироваться, все равно система состоит из 2х фаз: пар и жидкость.
Число условий, которые можно менять произвольно, не меняя числа и вида фаз, называется числом степеней свободы (С).
Соотношение между числом и видом фаз называется правилом фаз.
С = К – Ф + 2
Ф + С = К + 2
Число фаз + число степеней свободы = числу компонентов плюс 2.
С – число степеней свободы.
К – число компонентов.
Ф – число фаз.
Если С = 1, т.е. степень свободы равна 1 – одновариантные системы.
С = 2 двухвариантные системы.
С = 0 безвариантная система.
Пример 1. Определить степень свободы для систем, состоящих:
А) раствор KNO3 и раствор NaNO3 в присутствии кристаллов KNO3 и кристаллов NaNO3 и паров Н2О. Система физическая.
Число веществ KNO3, NaNO3, Н2О равно трем.
К=3.
Число фаз: жидкая, пары воды, две твердые KNO3 и NaNO3. Ф = 4.
С = 3 – 4 + 2 = 1.
Одновариантная система.
Б) Раствор обеих солей в присутствии льда, кристаллов KNO3, NaNO3 и
паров Н2О.
К=3. Ф=5.
С = 3 – 5 + 2 = 0.
Безвариантная система.
В) Раствор обеих солей в присутствии льда и паров Н2О.
К=3. Ф=3.
С = 3 – 3 +2 = 2.
Двухвариантная система (можно из 2 параметра Т, концентрацию).
Пример 2. При сплавлении молей КСl и NaNO3 идет реакция.

Определить степень свободы, если жидкий расплав находится в равновесии с кристаллами NaNO3.
К = 4 – 1 = 3.
Ф = 2 (жид. и кр.).
Так как система состоит из жидкой и твердой фазы
С = К – Ф + 1
С = 3 – 2 + 1 = 2. Двухвариантная система.
Пример 3.
Вычислить максимальное число фаз и число степеней свободы для однокомпонентной системы.
К = 1.
С = К – Ф +2.
Предположим фаз = 1.
К = 1. Ф = 1.
С = 1 – 1 + 2= 2.
К = 1. Ф = 2.
С = 1 – 2 + 2= 1.
К = 1. Ф = 3.
С = 1 – 3 + 2= 0.
Для однокомпонентной системы максимальное число фаз равно трем, а степень свободы двум.
Урок №2: Однокомпонентные системы.
Диаграмма состояния воды.
В однокомпонентной системе (гетерогенной) фазы состоят из одного вещества (т.е. фаз несколько: пар, лед, жидкость, а вещество одно: вода, или S, Fe, FgNO3). На однокомпонентных системах, не содержащих примеси, изучаются физические и химические свойства веществ.
В однокомпонентной системе число равновесных фаз не может быть больше трех:
▲ При большем числе фаз число степеней свободы будет отрицательным, что не имеет физического смысла.
Предположим, что Ф = 1 (лед, вода, пар).
Если К = 1 ,Ф = 1, С = К – Ф + 2 = 1 – 1 + 2 = 2.
1) С = 2.
В этом случае можно изменять и температуру, и давление без нарушения равновесия, причем изменение одного параметра не вызовет изменения другого.
Если К = 1, Ф = 2, С = 1 – 2 + 2 = 1.
Ф = 2 (лед ↔ пар, вода ↔пар, лед ↔ вода и т.д.)
2) С = 1.
В этом случае можно изменить только один параметр без нарушения равновесия, при этом второй параметр изменяется в зависимости от первого.
3) С = 0.
Наступает равновесие, которое характеризуется определенными параметрами (р и Т) и ни один из них не может быть изменен без нарушения равновесия системы.
Вывод: в однокомпонентной системе: 1) наибольшее число фаз равно трем; 2) степенно свободы равна 2 (изменять возможно t, p, а концентрация остается неизменной величиной).
Рассмотрим графическую зависимость фазового состояния однокомпонентных систем, например, воды от внешних условий (p и T).
С = К + 2 – Ф
Т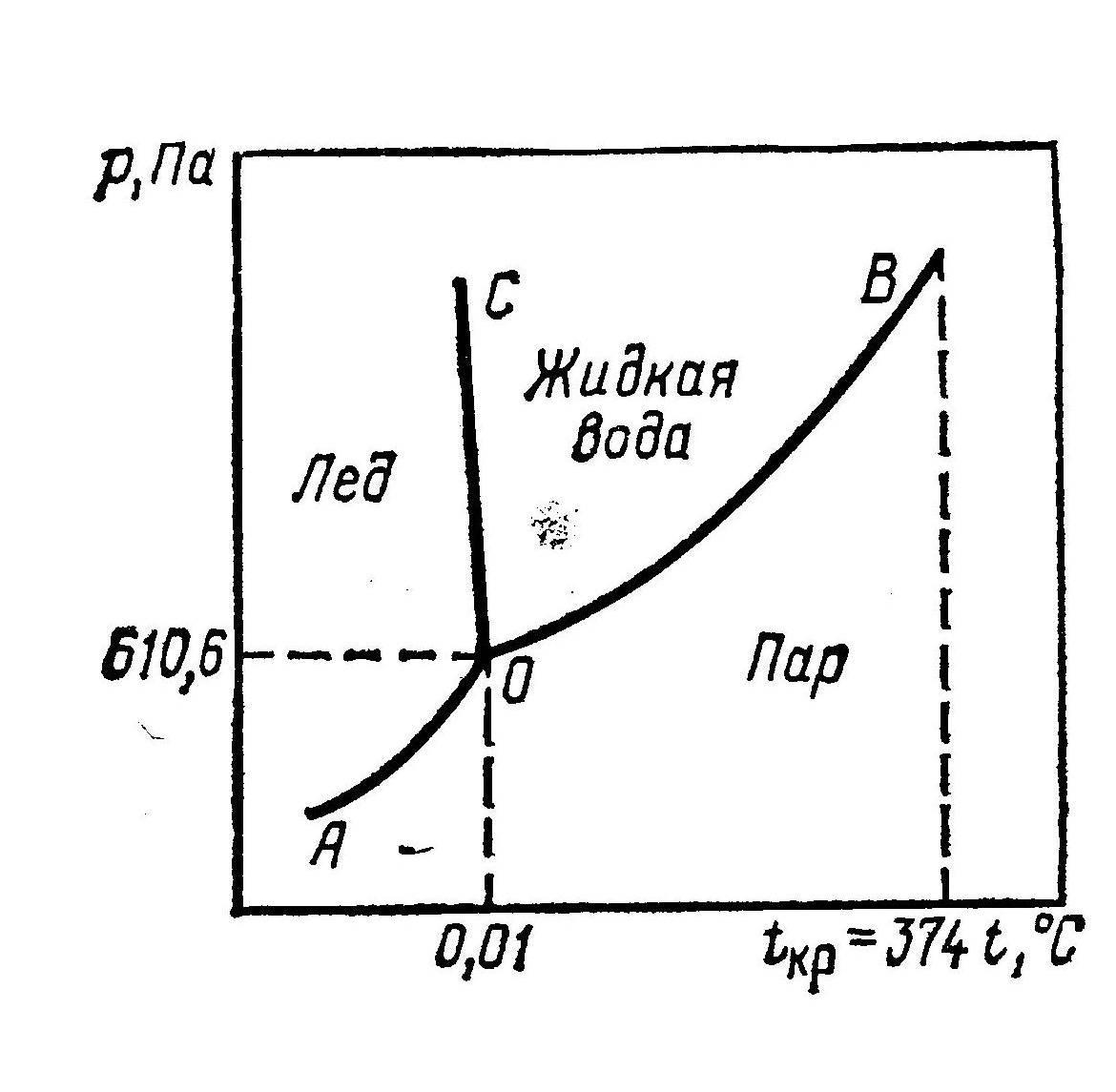 акие графики называются фазовые диаграммы или диаграммы состояния. Их строили на основе экспериментальных данных.
акие графики называются фазовые диаграммы или диаграммы состояния. Их строили на основе экспериментальных данных.
На диаграмме состояния воды имеются три линии АО, ВО, СО, пересекающиеся в точке О и разделяющие всю систему на 3 части.
Кривая АО выражает зависимость (изменение) давления насыщенного пара над льдом (повышение) от температуры. По кривой видно, что давление над льдом небольшое и растет с повышением температуры. При температуре точки «О» лед плавится и превращается в воду.
ОВ – показывает зависимость давления насыщенного пара над жидкой водой от температуры (или ее можно характеризовать как зависимость температуры кипения от давления).
Кривая ОВ обрывается при ординате t = 3740 С – это критическая температура воды, а при более высокой температуре жидкая вода не может существовать.
Кривую ОС можно определить как зависимость температуры плавления льда (или замерзания жидкой воды) от давления.
Она имеет небольшой наклон влево т.е. с повышением давления температура уменьшается. Такой ход кривой характерен только для веществ (вода, Ag, Bi), т.к. это связано с тем, что при затвердевании их объем увеличивается (вода в бутылке, когда замерзнет, может разорвать ее).
У большинства же веществ при затвердевании объем уменьшается и кривая ОС будет смещена вправо.
На графике выделяются три области:
1) АОС – область льда (вода может быть только в виде льда при p и t, лежащих в этой области).
2) ВОС – область жидкой воды.
3) АОВ – область пара.
В се кривые пересекаются в точке О, которая соответствует равновесию трех фаз:
се кривые пересекаются в точке О, которая соответствует равновесию трех фаз:
(На данной диаграмме масштаб не выдержан)
Точка «О» получила название тройной точки и координаты ее строго определены. Для этой точки рассмотрим систему, в которой компонентов К = 1 (вода), фаз Ф = 3. Ни один из параметров менять нельзя, иначе равновесие сместится.
По правилу фаз число степеней свободы равно:
С = 1 + 2 – 3 = 0
Если возьмем точки, лежащие на кривых, тогда для этих точек К = 1, а фаз Ф = 2. Например,

С = 1 + 2 – 2 = 1.
Значит можно менять произвольно только один параметр, но чтобы сохранить равновесие, который тоже будет меняться в зависимости от первого.
Для точек А или В, С, лежащих в любой из областей, К = 1, Ф = 1.
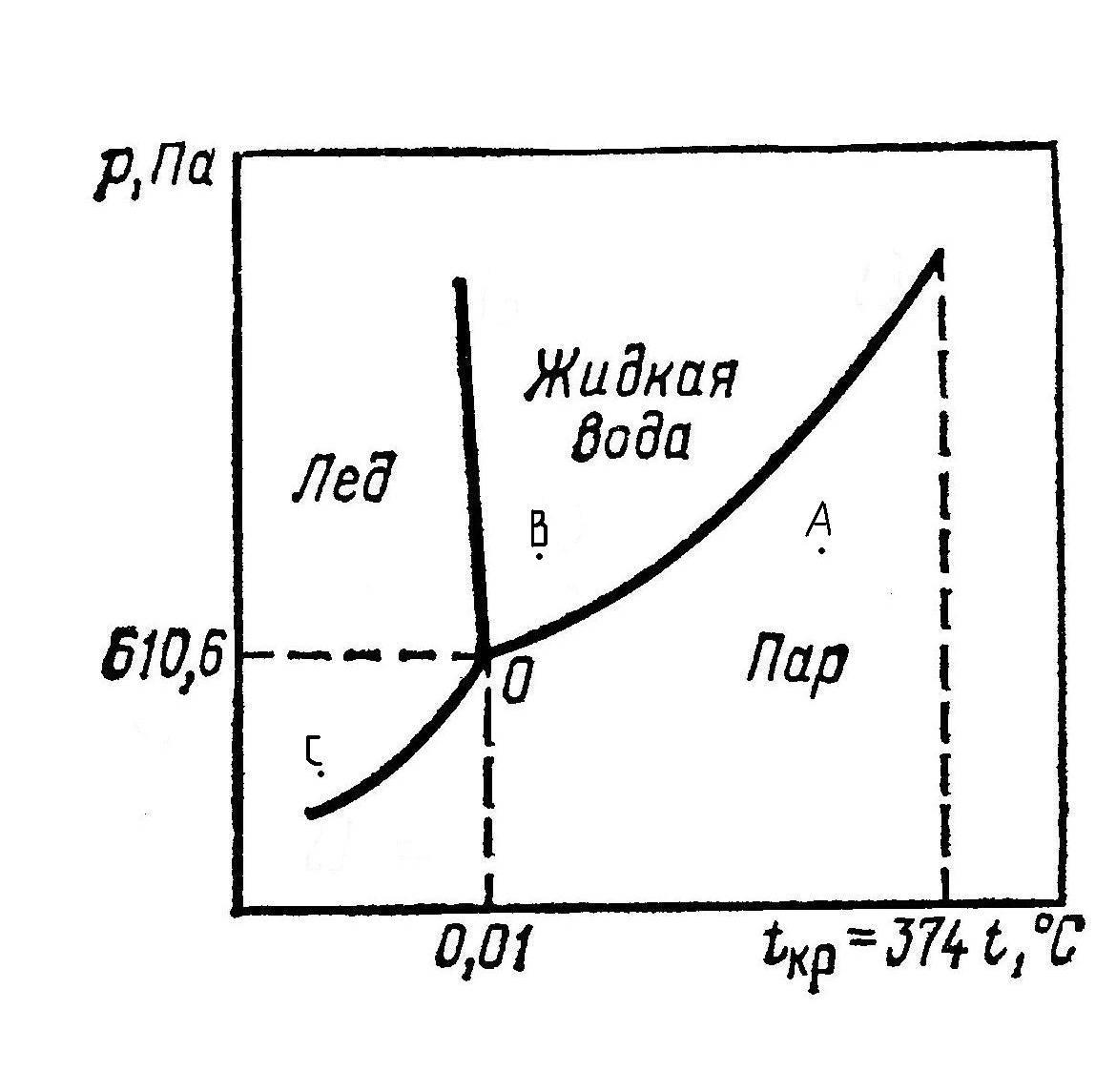
Число степеней свободы С = 1 + 2 – 1 = 2, т.е. в известных пределах можно менять значение двух факторов (р, t) независимо друг от друга, не изменяя числа фаз.
При температуре, соответствующей точке «О», лед плавится и превращается в жидкую воду.
Наибольшее давление насыщенного пара наблюдается при критической температуре воды (3740 С) и равно 2,212*107 Н/м2.
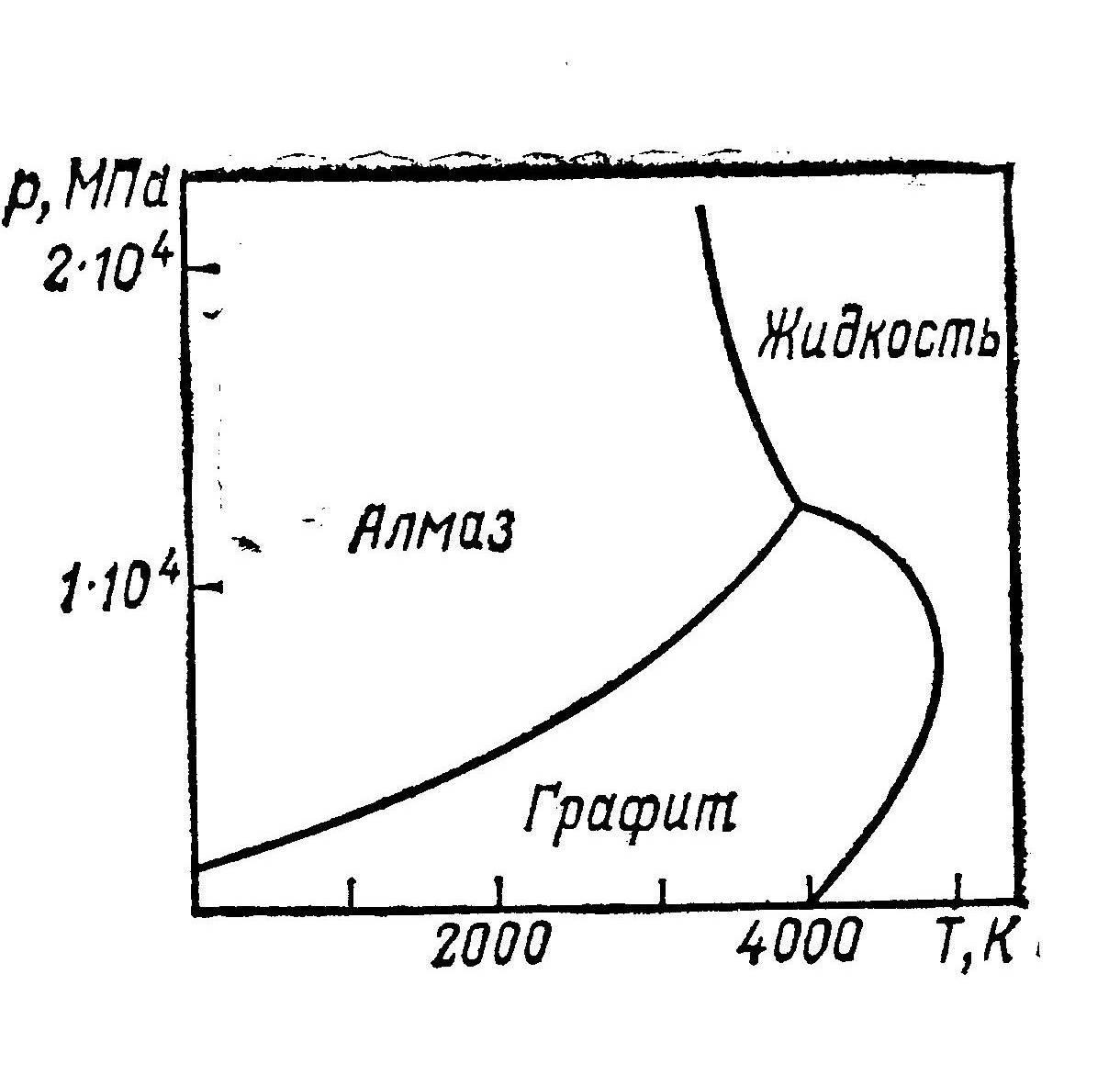
Примером относительно простой фазовой диаграммы с двумя кристаллическими фазами может служить диаграмма состояния углерода. Углерод встречается в двух кристаллических формах – в виде алмаза и графита. Эти две формы образовались при медленном охлаждении магмы – жидкой массы, находящейся в глубинных слоях земной коры. При высоких температуре и давлении из растворенного в магме углерода кристаллизовался алмаз – более устойчивая кристаллическая форма при этих условиях. По мере охлаждения магмы температура и давление понижались до таких значений, при которых кристаллизация алмаза прекращалась и начиналась кристаллизация графита. В принципе, алмаз в обычных условиях представляет собой неустойчивую форму углерода, не успевшую при охлаждении магмы превратиться в графит. При давлении же свыше 6000 МПа и температурах 1500-2000 К графит превращается в алмаз. На этом основано получение искусственных алмазов.
Урок №3:Равновесие в двухкомпонентных системах.
Примером двухкомпонентной системы являются сплавы из двух металлов, или расплавы солей.
К = 2 С = 2 + 2 – Ф
К = 2 Ф = 1 С = 2 + 2 – 1 = 3
К = 2 Ф = 2 С = 2 + 2 – 2 = 2
К = 2 Ф = 3 С = 2 + 2 – 3 = 1
К = 2 Ф = 4 С = 2 + 2 – 4 = 0.
Наибольшее число фаз, находящихся в равновесии в 2х-компонентной системе равно 4 (например, 2 твердые фазы одного и второго компонента, жидкая форма и пар).
Наибольшее число степеней свободы равно 3 при Ф = 1 – температура, давление, концентрация одного из компонентов (С1), концентрация второго компонента, зависящая от первой и находится из уравнения С2 = 100% - С1 (концентрацию выражают в мольных или весовых долях, %).
В общем случае для построения диаграммы состояния 2х-компонентной системы пользуются тремя осями координат: t, p, c. При этом получаются пространственные модели.
При изучении конденсированных систем, состоящих только из жидких и твердых фаз.
Фактор давления можно не учитывать и если исследование проводится при атмосферном давлении, колебания которого незначительны.
В этом случае построение фазовых диаграмм упрощается (плоское изображение в координатах: температура – концентрация).
Примером конденсированных 2х-космпонентных систем служит сплав из двух нелетучих металлов.
Главный метод изучения сплавов – термический анализ.
Проводим термический анализ сплавов висмута (Bi) с кадмием (Сd). Имеем ряд образцов состава:
100% Bi
90% Bi и 10% Cd
80% Bi и 20% Cd
60% Bi и 40% Cd
10% Bi и 90% Cd
100% Cd
Каждый из образцов расплавляют и затем медленно охлаждая регистрируют температуру расплава через определенные промежутки времени термометром. По полученным данным строят кривые охлаждения.
Кривая 1 характеризует охлаждение чистого Bi. Вначале температура понижается (происходит охлаждение расплавленного висмута).
Кривые охлаждения сплавов и диаграмма Bi – Cd.
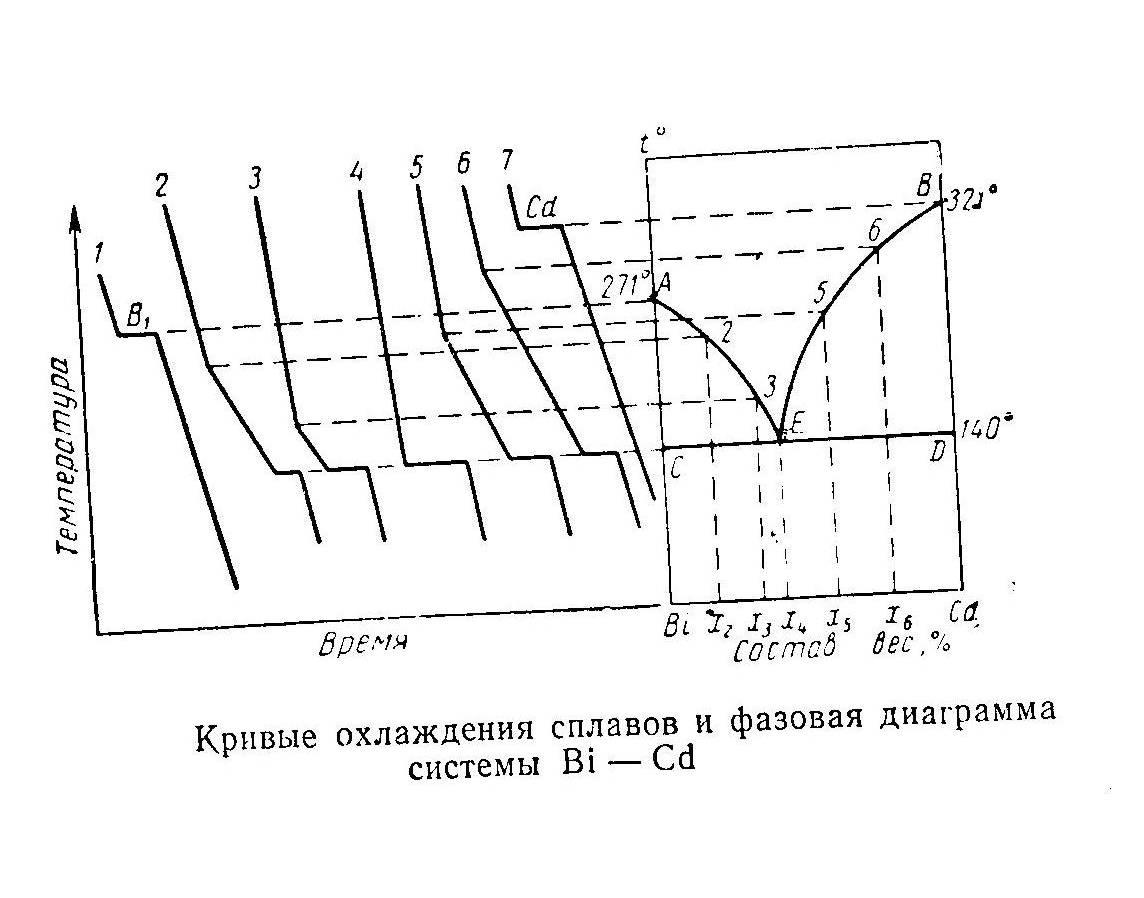
При 2710 С Bi начинает кристаллизоваться: температура при этом постоянная.
Постоянная температура при отвердевании связана с безвариантностью системы.
Ф = 2 (жидкая и твердая). С = К + 1 – Ф = 1 + 1 – 2 = 0.
После того, как весь Bi отвердеет, температура понижается равномерно, происходит охлаждение отвердевшего металла.
Кривая 7 – кривая охлаждения чистого Сd t = 3210 C (аналогично кривой №1).
Кривые 2, 3, 4, 5, 6 характеризуют остывание сплавов различного состава.
Кривая 2. Вначале t падает, охлаждается жидкий сплав. При некоторой t скорость охлаждения становится меньшей, так как в жидкости появляются первые кристаллы висмута, и выделяющаяся при этом теплота кристаллизации частично компенсирует охлаждение жидкого сплава. По мере охлаждения из жидкого сплава все больше выделяется кристаллов висмута и увеличивается содержание кадмия в жидкой фазе. При достижении определенной температуры и состава жидкой фазы наряду с висмутом начинает кристаллизоваться и кадмий. Температура при этом остается постоянной до тех пор, пока полностью не отвердеет сплав. После этого начинается равномерное охлаждение застывшего сплава.
Кривая 3. Подобным же образом происходит охлаждение сплава 3, однако начало кристаллизации висмута из жидкого сплава (точка излома) наблюдается при более низкой t, чем у сплава 2.
При охлаждении сплавов 5 и 6 из жидкой фазы первоначально выпадают кристаллы кадмия.
Из сопоставления кривых охлаждения 2, 3, 5 и 6 видно, что процесс кристаллизации сплавов не происходит при какой-то одной постоянной температуре, а захватывает определенный интервал. При этом начало кристаллизации сплавов различного состава наблюдается при различных температурах, окончательное отвердевание их происходит при одной и той же температуре (1400).
Исключение Кривая 4. Она имеет такую же форму как и у чистых металлов. При охлаждении такого сплава вплоть до 1400 кристаллизация не происходит. При 1400 из жидкой фазы в виде кристаллов одновременно начинают выпадать оба компонента, причем состав выпадающей твердой фазы одинаков с составом жидкого сплава. Этот сплав, который обладает наиболее низкой температурой кристаллизации, называется эвтектическим.
При температуре эвтектики в равновесии находятся 3 фазы:
Кристаллы Cd
Кристаллы Bi
Жидкий сплав
Число компонентов К = 2.
С = К + 1 – Ф = К + 1 – 3 = 0.
Эвтектика механическая смесь, она неоднородна и состоит из мелких кристаллов одного и другого компонента.
▲ Одновременная кристаллизация обоих компонентов мешает образованию крупных кристаллов.
Температура окончания кристаллизации всех сплавов одинакова и лежит на одной прямой СD.
Это линия, отвечающая температурам полного отвердевания, называется линией солидуса. (Солидус – твердый, плотный).
Область диаграммы выше линии АЕВ характеризует жидкие сплавы всевозможного состава.
Правило фаз для этой области:
Ф = 1 (жидкая фаза)
С = К + 1 – Ф = 2 + 1 – 1 = 2.
Т.е. как бы не изменялись состав сплавов и температура, количество фаз остается прежней (одна фаза).
Кривая АЕВ, отвечающая температуре начала кристаллизации, называется линией ликвидуса.
Область ниже прямой СD составляет твердый сплав Bi и Cd.
Точка Е выражает состав и температура плавления эвтектического сплава .
(60% Bi + 40% Сd)
При этом Ф = 3. С = 0.
Поле АЕС – область сплавов с содержанием Cd менее 40%, отвечает одновременному сосуществованию в равновесии жидких расплавов переменного состава с кристаллами висмута.
В этом случае Ф = 2, С = 1, т.е. т.а. до известного предела определенной t соответствует строго определенный состав жидкой фазы, находящейся в равновесии с кристаллами.
Поле ВЕD – область сплавов с содержанием Cd более 40%, характеризует равновесие жидких сплавов различного состава с кристаллами Сd при определенной температуре.
Точка А является температурой плавления чистого висмута.
Точка В – температура плавления чистого Cd.
По мере добавки к Bi кадмия или Cd висмута температура плавления металлов понижает t плавления понижается.
Всякая примесь, находящаяся в веществе, снижает его t плавления.
Линия BЕ - процесс кристаллизации Cd из жидких сплавов.
Одновременно линии АЕ и ВЕ указывают как изменяется состав жидкой фазы по мере кристаллизации Bi и Cd.
При 1400 состав твердой фазы одинаков с составом жидкого сплава.
Вид, подобный диаграмме Сd – Bi ….. вещества, неограниченно растворимые в жидком состоянии и не образующие между собой химических соединений и твердых растворов (Pb – Ag, Al - Si).
Руководствуясь диаграммами плавкости, можно подбирать состав сплавов, обладающих определенной температурой плавления (низкой или высокой).
Если из данной пары веществ нужно получить сплав с низкой температурой плавления, то компоненты берут в таком соотношении, в каком они находятся в эвтектическом сплаве.
По диаграмме можно также определять состав сплавов, обладающих наиболее высокими температурами плавления, хорошими механическими свойствами (мелкозернистые эвтектические сплавы), области устойчивости и распада образующихся химических соединений, твердых растворов, условия образования новых кристаллических модификаций и т. д. Фазовые диаграммы состояния широко используют при получении различных сплавов, при расчетах состава шлаков, шихты для получения стекла, цемента, огнеупорных материалов.
Диаграммы состояния применяют также для нахождения состава сплава, предварительно точно определив его температуру плавления (т. е. для целей анализа). При этом очень важно, чтобы в данной смеси не присутствовали примеси посторонних веществ, которые могут исказить результаты анализа.
В Советском Союзе в области изучения фазовых равновесий работал крупнейший ученый и выдающийся деятель отечественной промышленности Н. С. Курнаков (1860—1941 гг.). Изучение Н. С. Курнаковым равновесий в различных солевых системах способствовало выяснению условий кристаллизации солей в природе, что дало возможность научно эксплуатировать солевые богатства нашей страны. Н. С. Курнаковым совместно с учениками были решены такие важные солевые проблемы, как проблемы извлечения глауберовой соли Na2SO4•10Н2О из вод залива Каспийского моря — Кара-Богаз-Гола, проблема переработки соликамского карналлита KCl • MgCl2 • 6H2O с целью извлечения из него чистого хлористого калия и получения фосфорно-аммиачно-калиевых концентрированных удобрений в формах, легко усваиваемых растениями, и многие другие.
Тестовый контроль знаний по теме: Фазовые переходы»
| Основные понятия | Определение понятия |
| 1. Одновариантная система | Температуры плавления льда от давления |
| 2. Безвариантная система | А) С=2 Б)С=3 В)С=2 Ф=3 Ф=2 Ф=2 |
| 3. В однокомпонентной системе наибольшее число фаз и степень свободы равны | В этом случае можно изменить температуру и давление без нарушения равновесия, причем изменение одного параметра не вызовет изменения другого |
| 4. Кривая АО выражает зависимость | В этом случае можно изменять только один параметр без нарушения равновесия, при этом второй параметр изменяется в зависимости от первого |
| 5. Двухвариантная система | Давления насыщенного пара на жидкой водой от температуры |
| 6. Кривая ОВ выражает зависимость | В системе наступает равновесие, которое характеризуется определенными параметрами и ни один из них не может быть изменен без нарушения равновесия |
| 7. Кривая ОС выражает зависимость | Давления насыщенного пара над льдом от температуры |
| 8. Кривая ОС наклонена влево в следствии того, что происходит | А) тройственной С=1 Б) тройной С=0
В) третичной С=2 |
| 9. Точка «0» называется и имеет степень свободы равную | А)М Б)Е В)О |
| 10. Для какой точки диаграммы состояния воды характерны следующие параметры: К=1, Ф=2, С=1 | А) понижение давления при уменьшении температуры Б) повышение давления при повышении температуры В) повышение давления при уменьшении температуры |
| 11. Решите задачу. Определите степень свободы для следующих систем: а) лед ↔вода↔пар
б) NH4OH↔NH3↔H2O Ж I Ж |
|
ТЕСТОВЫЙ ОПРОС ПО ТЕМЕ: «ФАЗОВЫЕ ПЕРЕХОДЫ, ПРАВИЛО ФАЗ»
Дополнение:
1) Переход твердого вещества в жидкое называется
2) Переход вещества из одного агрегатного состояния в другое называется
3![]() ) Переход жидкости в газообразное состояние называется
) Переход жидкости в газообразное состояние называется
Переход вещества из твердой фазы в газообразную минуя жидкую фазу
называется
Однородные участки системы отделенные друг от друга видимыми
поверхностями раздела называются
Переход газообразного вещества в жидкое состояние называется
Независимая часть системы, которая может быть выделена и существовать
самостоятельно называются
Система, состоящая из нескольких фаз называются
Число условий которые можно менять произвольно не меняя числа и вида фаз
называются и определяется по формуле
Определить вариантность систем:
состоящей из растворов серной и азотной кислот в присутствии
кристаллов льда и паров воды.
AgNO3 + NaCl ↔AgCl↓ + NaNO3
р-р р-р к-р р-р











 акие графики называются фазовые диаграммы или диаграммы состояния. Их строили на основе экспериментальных данных.
акие графики называются фазовые диаграммы или диаграммы состояния. Их строили на основе экспериментальных данных. се кривые пересекаются в точке О, которая соответствует равновесию трех фаз:
се кривые пересекаются в точке О, которая соответствует равновесию трех фаз:













