МР комбинированного занятия для преподавателя "Основы интегрального исчисления. Неопределённый интеграл".

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

НОВОСИБИРСКОЙ ОБЛАСТИ

«БАРАБИНСКИЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ»

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

КОМБИНИРОВАННОГО ЗАНЯТИЯ ДЛЯ ПРЕПОДАВАТЕЛЯ

ДИСЦИПЛИНА «МАТЕМАТИКА»

Раздел 1. Математический анализ

Тема 1.6. Основы интегрального исчисления. Неопределённый интеграл

Специальность

31.02.01 Лечебное дело

Курс – первый

2016

Одобрена на заседании цикловой методической комиссии _________________ Протокол №___от_______________________ Председатель___________________________ Разработчик: О.А. Потемкина

Оглавление

Выписка из рабочей программы дисциплины «Математика» для специальности 31.02.01 Лечебное дело 3

Методический лист 4

Примерная хронокарта занятия 5

Приложение 1 6

Мотивация 6

Информационно-справочный материал 6

Неопределённый интеграл, понятия, свойства 6

Таблица неопределённых интегралов 8

Методы интегрирования 9

Задания для закрепления метода применения таблицы неопределённых интегралов 9

Задания для закрепления метода замены переменной и по частям 11

Простейшие приложения неопределённого интеграла 13

Выписка из рабочей программы дисциплины «Математика»
для специальности 31.02.01 Лечебное дело

Тема 1.6. Основы интегрального исчисления. Неопределённый интеграл	Содержание учебного материала	2
	Основы интегрального исчисления. Первообразная и неопределённый интеграл. Основные свойства неопределённого интеграла. Таблица неопределённых интегралов. Методы интегрирования. Решение прикладные задач в области профессиональной деятельности.		1,2
	Лабораторные работы	‑
	Практические занятия 5) Первообразная, неопределённый интеграл	2
	Контрольные работы	‑
	Самостоятельная работа обучающихся Выполнение упражнений, работа с тестами на тему «Основы интегрального исчисления» Работа с учебником [1, стр. 82-88]; [1, стр. 116, задание №22, вариант 10]	2

Методический лист

Вид занятия – комбинированное занятие

Продолжительность – 90 мин.

Требования к результатам освоения темы в соответствии с ФГОС по специальности среднего профессионального образования 31.02.01 Лечебное дело:

В результате изучения темы обучающийся должен уметь:

• решать прикладные задачи в области профессиональной деятельности;

В результате изучения темы обучающийся должен знать:

• значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы;

• основные математические методы решения прикладных задач;

• основы интегрального исчисления.

Цели занятия:

1. Учебные цели:

• формировать знание основ интегрального исчисления и основных математических методов решения прикладных задач;

• способствовать расширению знаний о значении математики в профессиональной деятельности и при освоении профессиональной образовательной программы.

2. Развивающие цели:

способствовать

• формированию умения организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество (ОК 2);

• развитию математического кругозора, мышления и речи, внимания и памяти.

3. Воспитательные цели:

• способствовать пониманию студентом сущности и социальной значимости своей будущей профессии, проявления к ней устойчивого интереса (ОК 1).

Методы обучения: объяснительно-иллюстративный, репродуктивный.

Место проведения занятия: аудитория колледжа.

Интегративные связи: физика, информатика и все предметы, где используется математический аппарат.

Литература:

1. Гилярова М.Г. Математика для медицинских колледжей. – Ростов н/Д: Феникс, 2011. – 410, [1] с. – (Медицина)

2. Математика: учеб. пособие / В.С. Михеев [и др.]; под ред. Н.М. Демина. – Ростов н/Д : Феникс, 2009. – 896 с. – (Среднее профессиональное образование).

Оснащение занятия:

1. Доска

2. Раздаточный материал

Домашнее задание:

1. Конспект

2. Работа с учебником [1, стр. 82-88];

Примерная хронокарта занятия

№	Наименование этапа	Время	Цель этапа	Деятельность		Оснащение
				преподавателя	студентов
1	2	3	4	5	6	7
	Организационный этап	1	Организация начала занятия. Проверка посещаемости и внешнего вида студентов. Сообщение темы и плана занятия.	Отмечает отсутствующих студентов в журнале. Сообщает тему и план занятия.	Староста называет отсутствующих студентов.	Журнал
	Мотивационный этап:	1	Развитие интереса к новой теме. Формирование у студентов способности понимать сущность и социальную значимость своей будущей профессии, проявления к ней устойчивого интереса (ОК 1).	Объясняет студентам важность изучения данной темы	Слушают, задают вопросы	МР Приложение 1
	Цели занятия	1	Установка приоритетов при изучении темы	Озвучивает цели занятия	Слушают, записывают в тетрадь тему занятия	Методический лист МР
	Изложение нового материала	60	Формирование знания об основах интегрального исчисления и основных математических методах решения прикладных задач; Расширение знаний о значении математики в профессиональной деятельности и при освоении профессиональной образовательной программы.	Излагает новый материал.	Слушают, записывают, задают вопросы по ходу объяснения материала.	Приложение 1
	Закрепление материала	25	Закрепление и осмысление полученных знаний. Заложение основ умения организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество. (ОК 2)	Инструктирует и контролирует выполнение заданий, обсуждает правильность ответов	Выполняют задания, слушают правильные ответы после выполнения, вносят коррективы	Приложение 1
	Задание для самостоятельной внеаудиторной работы студентов	1	Закрепление знаний. Развитие математического кругозора, мышления, внимания и памяти.	Дает задание для самостоятельной внеаудиторной работы студентов.	Записывают задание	Методический лист
	Подведение итогов занятия	1	Подведение итога занятия	Подводит итоги занятия.	Слушают, анализируют.	Журнал

Приложение 1 Мотивация

Интегральное исчисление, раздел математики, в котором изучаются свойства и способы вычисления интегралов и их приложения. Интегральное исчисление тесно связано с дифференциальным исчислением и составляет вместе с ним одну из основных частей математического анализа (или анализа бесконечно малых). Центральными понятиями интегрального исчисления являются понятия определённого интеграла и неопределённого интеграла функций одного действительного переменного.

Вместе с дифференциальным исчислением оно составляет основу аппарата математического анализа, а значит способствовать расширению знаний о значении математики в профессиональной деятельности и при освоении профессиональной образовательной программы.

Интегральное исчисление возникло из рассмотрения большого числа задач естествознания и математики. Важнейшие из них – физическая задача определения пройденного за данное время пути по известной, но, быть может, переменной скорости движения и значительно более древняя задача вычисления площадей и объемов геометрических фигур.

Информационно-справочный материал Неопределённый интеграл, понятия, свойства

Как в самой математике, так и в других дисциплинах — физике, электротехнике, механике и т.д. — часто приходится решать задачу обратную дифференцированию, т.е. восстанавливать саму функцию.

Действие, посредствам которого по некоторой функции производной находится сама функция, называется интегрированием.

Примеры

1. Скорость тела при переменном движении изменяется по закону v = 2t. Требуется найти пройденный телом s путь за промежуток времени от t = t₁ , до t = t₂.

Здесь, так как , по данной производной функции требуется найти саму функцию s = f(t).

2. Изменение массы вещества при радиоактивном распаде пропорционально времени распада и его первоначальной массе, т.е. dm = -kmdt, т = f(t)-?

3. Угловой коэффициент касательной в данной точке некоторой линии k = 2х. Найти уравнение этой линии.

Очевидно, решение этой задачи сводится к нахождению функции у = f(x), производная которой задана, т.е. у'=2х.

Рассмотрим алгоритм решения подобных задач. Принято решение записывать так:

1-я задача: s = ;

2-я задача: т = -;

3-я задача: у = .

Здесь — математический знак, который обозначает операцию, восстанавливающую функцию по ее производной.

В общем виде = f(x) + C.

Совокупность первообразных для функции F(x) (или дифференциала F(x)dx) называется неопределенным интегралом и обозначается символом . Неопределённым интегралом потому, что С – произвольная постоянная интегрирования (может быть любым числом).

Элементы неопределённого интеграла:

F(x) — подынтегральная функция;

F(x)dx- подынтегральное выражение;

f(x) — искомая, называемая первообразной, функция;

С — произвольная постоянная.

Без доказательства примем следующие свойства неопределённых интегралов.

1. Постоянный множитель можно выносить за знак неопределённого интеграла или вносить под его знак:

= a.

2. Неопределённый интеграл от суммы конечного числа функций равен сумме интегралов от каждой функции:

3. Производная от неопределённого интеграла равна подынтегральной функции, а дифференциал – подынтегральному выражению:

.

4. Неопределённый интеграл от дифференциала некоторой функции равен этой функции с точностью до константы:

.

Таблица неопределённых интегралов

Методы интегрирования

1. Применение таблицы неопределённых интегралов

А) Интегрировать можно сразу, используя формулу соответ­ствующего табличного интеграла:

1)	4)
2)	5)
3)	6)

Б) Приводим к одному или нескольким табличным интегралам, если предварительно воспользоваться свойствами 1 или 2:

1)

2)

3)

B) Приводится к одному или нескольким табличным интегралам после соответствующих тождественных преобразований над подынтегральной функцией и применения свойств.

1)

2)

3)

4)

Задания для закрепления метода применения таблицы неопределённых интегралов

1. ; 2. ;

3. ;

4. 5. ; 6.

7. 8.

2. Интегрирование методом замены переменной

Рассмотрим интегралы — ; ;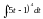

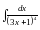
Оказывается, первых два интеграла можно найти методом непосредственного интегрирования, возводя двучлены под интегралами соответственно в 5-ю и 4-ю степени, но процесс будет весьма громоздким. Третий интеграл никакими преобразованиями вообще нельзя привести к табличным.

Для нахождения таких интегралов и подобных им применяется метод замены переменной.

Сущность интегрирования методом замены переменной заключается в преобразовании интеграла в интеграл , который находится по какой-либо из основных формул интегрирования.

Для нахождения интеграла заменяем переменную х новой переменной и с помощью постановки х = w(u), затем связываем дифференциалы переменных х, и и получаем .

После того как первообразная по новой переменной будет найдена, необходимо вернуться к старой переменной.

Примеры

;

;

.

3. Интегрирование по частям

Как в самой математике, так и в других дисциплинах (электротехнике, радиотехнике, гидроаэродинамике) встречается ряд интегралов, которые никакими преобразованиями к табличным не приводятся.

Для их нахождения знаменитым математиком Эйлером был предложен новый метод — интегрирование по частям. Его суть заключается в следующем: в вышеуказанных интегралах выра­жения под интегралом представляют собой произведения какой-либо одной функции на дифференциал другой, т.е. udv. Эйлер показал, что в этом случае

Это и есть формула интегрирования по частям.

Задания для закрепления метода замены переменной и по частям

1.

2.

3. ; 4.

4. Интегрирование рациональных дробей

Рациональной дробью называется дробь вида , где Рп(х) и Qm(x) — многочлены соответственно n-й и m-й степе­ни.

Рациональная дробь называется правильной, если n т, и неправильной, если пт.

Всякую неправильную рациональную дробь с помощью деления числителя на знаменатель можно представить в виде суммы многочлена и правильной рациональной дроби. Поэтому интегрирование рациональных дробей сводится к интегрированию правильных рациональных дробей.

Для интегрирования правильной рациональной дроби её представляют как сумму простейших дробей, т.е. дробей вида и , где квадратный трехчлен не имеет действительных корней, а т и п — положительные числа.

Рассмотрим примеры, где покажем, как на практике осуществлять разложение правильных рациональных дробей в сумму простейших дробей.

1.

Решение. Разложим на множители: х² + 5х + 4 = (х - 1)(х + 4). В этом случае подынтегральная функция раскладывается на простейшие дроби таким образом:

где А и В — коэффициенты, подлежащие определению.

Умножив обе части равенства на общий знаменатель и отбрасывая затем этот знаменатель, получим 2х +1 = А(х - 4) + В(х -1) = 2х +1 = (А + В)х - (4А + В).

Приравняв коэффициенты при одинаковых степенях х, по­лучим систему уравнений

Т.о., .

Теперь находим искомые интегралы:

2.

Решение. Разложим на множители: = x(х²+3x+2)=x(x‑1)(х -2), тогда подынтегральная функция раскладывается на простейшие дроби таким образом:

Далее, имеем

или

Приравняв коэффициенты при одинаковых степенях х, по­лучим систему уравнений

Т.о.,

Решите самостоятельно

3.; 4.

Простейшие приложения неопределённого интеграла

Восстановление функции по заданной производной или дифференциалу – задача неопределённая, так как определяет множество первообразных функций у = f(x) + C , которые отличаются друг от друга постоянным слагаемым С.

С может принимать любые числовые значения, если на первообразную не наложено никаких начальных условий. Чтобы из множества первообразных функций выделить одну определённую функцию, должны быть заданы начальные условия.

Под начальными условиями понимается задание частных значений х и у для первообразной
у = f(x) + C, по которым находится определённое значение C, удовлетворяющее этим начальным условиям.

Примеры

1. Найти функцию, производная которой а)у' = Зх² - 6х + 2; б)y’=3x²+2x+C .

2. Найти функцию, производная которой у' = 2х - 3 , если при х = 2 эта функция принимает значение, равное 6.

Решение. Имеем у' = 2х - 3 или у = х²-3х + С.

Вычислим С при заданных значениях х = 2 и у = 6 . Подставив в выражение для функции эти значения, получим 6 = 2²-3-2 + С=С = 8.

Итак, функция, удовлетворяющая заданным начальным условиям, имеет вид у = х² – 3х + 8 .

1. Найти уравнение линии, если угловой коэффициент касательной в каждой её точке равен 2х.

Решение. Согласно условию к = 2х.

Известно, что k = tgа = у' , следовательно, у = х²+С.

Мы нашли совокупность (семейство) кривых, для которых угловой коэффициент касательной в любой точке равен 2х. Эти кривые отличаются друг от друга на постоянное слагаемое С.

При С = 0 получим параболу у = х² с вершиной в начале координат, при С = 2 – параболу
у = х²+2 с вершиной в точке (0; 2), при С = -2 — параболу у = х² - 2 с вершиной в точке (0;-2) и т.д.

1. Найти уравнение линии, проходящей через точку А(2;-1), если угловой коэффициент касательной к прямой в каждой точке равен 2х - 4.

Решение. Согласно условию к = 2х - 4;  у = х² – 4х + С.

Линия проходит через точку А , значит, её координаты обращают уравнение в тождество, т.е. -1 = 2² - 4 - 2 + С  С = 3.

Таким образом, искомое уравнение имеет вид у = х² - 4х + 3 .

5. Скорость прямоугольного движения точки измеряется по закону v = 3t² - 2t. Найти закон её движения.

Решение. Известно, что скорость прямоугольного движения точки равна производной от пути S по времени t, т.е. v = S’(t) следовательно, s = = t³ -t² + С .

6. Скорость прямолинейного движения точки измеряется по закону v = 3t² + 4. Найти закон движения S, если за время t = 2 с точка прошла 20 м.

Решение. Так как v = S’(t), то  S=t³ + 4t + С.

Используя начальные условия, найдём 20=2³ + 4 – 2 + С  C=4.

Итак, закон движения точки имеет вид s = t³ + 4t + 4.
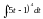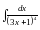
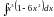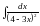