МР комбинированного занятия для преподавателя "Предел функции".

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

НОВОСИБИРСКОЙ ОБЛАСТИ

«БАРАБИНСКИЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ»

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

КОМБИНИРОВАННОГО ЗАНЯТИЯ ДЛЯ ПРЕПОДАВАТЕЛЯ

ДИСЦИПЛИНА «МАТЕМАТИКА»

Раздел 1. Математический анализ

Тема 1.3. Предел функции

Специальность

060101 Лечебное дело

Курс – первый

2013

Одобрена на заседании цикловой методической комиссии _________________ Протокол №___от_______________________ Председатель___________________________ Разработчик: О.А. Потемкина

Оглавление

Выписка из рабочей программы дисциплины «Математика» 4

Методический лист 5

Примерная хронокарта занятия 6

Приложение 1 8

Контроль знаний по теме: 8

«Значение математики в профессиональной деятельности. Функции» 8

Приложение 2 9

Доклад на тему: «Из истории развития понятия предела функции» 9

Приложение 3 10

Информационно-справочный материал по теме: «Предел функции» 10

Приложение 4 15

Закрепление материала 15

Приложение 5 16

Контроль знаний 16

Приложение 6 18

Задания для самостоятельной внеаудиторной работы студентов 18

Выписка из рабочей программы
дисциплины «Математика»

для специальности 060101 Лечебное дело

Наименование разделов и тем	Содержание учебного материала, лабораторные и практические работы, самостоятельная работа обучающихся, курсовая работа (проект)		Объем часов	Уровень освоения
1	2		3	4
Раздел 1.	Математический анализ		45
Тема 1.3. Предел функции	Содержание учебного материала		2
		Значение математики в профессиональной деятельности при проведении диагностических исследований, при проведении контроля эффективности лечения. Предел функции в точке. Основные свойства пределов. Предел функции на бесконечности. Решение прикладные задач в области профессиональной деятельности		1,2
	Лабораторные работы		‑
	Практические занятия 1) Предел функции. Методы вычисления пределов		2
	Контрольные работы		‑
	Самостоятельная работа обучающихся Выполнение упражнений, поиск информации в периодической печати и сети Internet при подготовке доклада «Использование информационно-коммуникационных технологий в профессиональной деятельности», работа с обучающими тестами на тему «Пределы» Повторение материала по конспектам теоретического занятия; [1, стр. 46, задание №6, контрольные вопросы]		2

Методический лист

Вид занятия – комбинированный урок

Продолжительность – 90 мин.

Требования к результатам освоения темы в соответствии с ФГОС по специальности среднего профессионального образования 060101 Лечебное дело:

В результате изучения темы обучающийся должен уметь:

• решать прикладные задачи в области профессиональной деятельности;

В результате изучения темы обучающийся должен знать:

• значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы;

• основные математические методы решения прикладных задач;

• основы дифференциального исчисления.

Цели занятия:

1. Учебные цели:

• рассмотреть понятие бесконечно малой и бесконечно большой функции, предела функции;

• рассмотреть методы раскрытия неопределённостей вида ;

• уяснить возможность использования предела функции при решении экономических, физических, биологических и медицинских задач;

• получить и закрепить навыки нахождения предела функции.

2. Развивающие цели:

способствовать

• формированию умений применять приемы сравнения, обобщения, выделения главного;

• развитию математического кругозора, мышления и речи, внимания и памяти.

3. Воспитательные цели: способствовать формированию культуры общения, внимания, интереса к предмету, способствовать пониманию студентом сущности и социальной значимости своей будущей профессии, проявления к ней устойчивого интереса.

Методы обучения: объяснительно-иллюстративный, репродуктивный.

Место проведения занятия: аудитория колледжа.

Интегративные связи: физика, геометрия и все предметы, где используется математический аппарат

Литература:

1. Гилярова М.Г. Математика для медицинских колледжей. – Ростов н/Д: Феникс, 2011. – 410, [1] с. – (Медицина)

2. Математика: учеб. пособие / В.С. Михеев [и др.]; под ред. Н.М. Демина. – Ростов н/Д : Феникс, 2009. – 896 с. – (Среднее профессиональное образование).

Оснащение занятия:

1. Доска

2. Раздаточный материал

3. Проектор

4. Мультимедиа

Домашнее задание:

1. Повторение материала по конспектам теоретического занятия

2. Работа с учебником [1, стр. 34-38]

Примерная хронокарта занятия

№	Наименование этапа	Время	Цель этапа	Деятельность			Оснащение
				преподавателя	студентов
1	2	3	4	5	6	7
	Организационный этап	2	Организация начала занятия. Проверка посещаемости и внешнего вида студентов. Сообщение темы и плана занятия.	Отмечает отсутствующих студентов в журнале. Сообщает тему и план занятия.	Староста называет отсутствующих студентов.	Журнал
	Актуализация опорных знаний	3	Ориентация на глубину усвоения знаний, систематизация материала	Проверка качества выполнения Д/з (фронтальный опрос, работа у доски)	Отвечают на вопросы по Д/з.	Эталоны ответов
	Контроль знаний по предыдущей теме	10	Оценка уровня сформированности знаний	Инструктирует и проводит контроль	Выполняют письменную проверочную работу	Приложение 1
	Мотивационный этап	5	Развитие интереса к новой теме	Объясняет студентам важность изучения данной темы	Слушают, задают вопросы	Приложение 2
	Цели занятия	2	Установка приоритетов при изучении темы	Озвучивает цели занятия	Слушают, записывают в дневник новую тему	Методический лист МР теоретического занятия
	Изложение нового материала План: Бесконечно малые и бесконечно большие функции, действия над ними Понятие бесконечно малых и бесконечно больших функций; Действия над бесконечно малыми и бесконечно большими функциями; Предел функции, теоремы о пределах Понятие, символика; Теоремы о пределах функций; Два замечательных предела	30	Формирование знаний, понимания сущности и социальной значимости своей будущей профессии	Излагает новый материал	Слушают, читают материал на слайдах, записывают	Приложение 3 Мультимедиа
	Выполнение заданий для закрепления знаний	25	Закрепление и осмысление полученных знаний	Инструктирует и контролирует выполнение заданий, обсуждает правильность ответов	Выполняют задания, слушают правильные ответы после выполнения, вносят коррективы	Приложение 4
	Предварительный контроль новых знаний	10	Оценка эффективности занятия и выявление недостатков в новых знаниях	Инструктирует и проводит контроль	Выполняют задания	Приложение 5
	Задание для самостоятельной внеаудиторной работы студентов	2	Формирование и закрепление знаний	Дает задание для самостоятельной внеаудиторной работы студентов, инструктирует о правильности выполнения	Записывают задание	Приложение 6
	Подведение итогов занятия	1	Подведение итога занятия	Выставляет оценки, комментируя ошибки, сделанные в ходе работы	Слушают, обсуждают, анализируют.	Журнал

Приложение 1 Контроль знаний по теме: «Значение математики в профессиональной деятельности. Функции»

1 вариант

1. Какую зависимость между переменными принято называть функциональной, или функцией?

2. Как символически записывается функция в математике?

3. Приведите примеры функций заданных аналитически.

4. Сформулируйте и запишите условия возрастания функции на промежутке?

5. Дайте определений нечётной функции. Приведите примеры.

6. Как располагаются графики чётных функций?

7. Найдите точки пересечения графика функции с осями координат.

8. Найдите область определения функции:

а) ; б)

9. Исследуйте функции на чётность:

2 вариант

1. Как в математике называют независимую переменную?

2. Какие способы задания функции вы знаете?

3. Запишите условия убывания функции на промежутке?

4. Дайте определений чётной функции и приведите примеры.

5. Как располагаются графики нечётных функций?

6. Перечислите наиболее распространённые виды функций.

7. Найдите точки пересечения графика функции с осями координат.

8. Найдите область определения функции:

1. ; б)

9. Исследуйте функции на чётность:

;

Приложение 2 Доклад на тему:
«Из истории развития понятия предела функции»

Предел — одно из важнейших понятий математики.

Определение предела впервые появилось в XVII пеке. Число А называется пределом величины х, если в процессе своего изменения х неограниченно приближается к А.

Однако математики XVII и XVIII веков не ставили своей задачей построить стройную теорию пределов. Эта задача была поставлена и решена лишь в XIX веке.

Обозначение lim — сокращение латинского слова limes (межа, граница); например, если мы говорим «значение стремится к чему-либо», то мы приближаем его к границе.

Термин «предел» ввел И. Ньютон. Рассказ о происхождении терминологии, принятой в дифференциальном исчислении, был бы не полон без понятия бесконечно малой. Бесконечно малые играют важную роль в математическом анализе, который поэтому часто называют также анализом бесконечно малых.

В развитии теории пределов принимали участие И. Ньютон, Г. Лейбниц, Ж. Даламбер (1717-1783), Л. Эйлер. Современная теория предела основана на строгом определении предела, данном О. Коши (1789-1857), и была существенно продвинута работами математиков К. Вейерштрасса (1815-1897) и Б. Больцано (1781-1848).

Теория пределов является базовой для основных теорий высшей математики: дифференцирования, интегрирования и дифференциальных уравнений.

Большая заслуга в развитии теории пределов принадлежит французскому математику Коши (1789—1857). Он развил теорию пределов и положил ее в основу построения одного из важнейших разделов математики — математического анализа.

Огюстен Луи Коши не только дал четкое определение основным понятиям математического анализа — пределу, непрерывности функции, сходимости ряда и т.д., но и внес неоценимый вклад в развитие математики. Он установил точные условия сходимости ряда Тейлора к данной функции и провел различие между сходимостью этого ряда вообще и его сходимостью к данной функции. Ввел понятие радиуса сходимости степенного ряда, дал определение интеграла как предела сумм, доказал сущес­твование интегралов от непрерывных функций. Нашел выражение аналитической функции в виде интеграла по контуру (интеграл Коши) и вывел из этого представления разложение функции в степенной ряд. Таким образом, он развил теорию функций комплексного переменного: используя интеграл по контуру, нашел разложение функции в степенной ряд, определил радиус сходимости этого ряда, разработал теорию вычетов, а также ее при­ложения к различным вопросам анализа и т.д. В теории дифференциальных уравнений Коши впервые поставил общую задачу о нахождении решения дифференциаль­ного уравнения с заданными начальными условиями (называемую с тех пор задачей Коши), дал способ ин­тегрирования дифференциальных уравнений в частных производных первого порядка. Коши занимался также геометрией (теорией многогранников, поверхностями 2-го порядка), алгеброй (симметрическими многочлена­ми, свойствами определителей), теорией чисел (теоремой Ферма о многоугольных числах, законом взаимности). Ему принадлежат исследования по тригонометрии, меха­нике, теории упругости, оптике, астрономии. Коши был членом Лондонского королевского общества, Петербург­ской академии наук и ряда других академий Европы.

Научные работы Коши посвящены арифметике, те­ории чисел, алгебре, математическому анализу, диффе­ренциальным уравнениям, механике, математической физике и т.д. Всего Коши написал свыше 800 работ, полное собрание его сочинений содержит 27 томов.

Приложение 3 Информационно-справочный материал по теме:
«Предел функции»

1. Бесконечно малые и бесконечно большие функции, действия над ними

1.1. Бесконечно малые и бесконечно большие функции

Пусть дана некоторая функция у = f(x). Напомним, что лю­бая функция связывает между собой, по крайней мере, две пере­менных величины, одну из которых обозначают через х и счита­ют независимой переменной, другую переменную обозначают через у, она зависит определённым образом от х.

Такую функциональную зависимость считают в математике функцией одной независимой переменной и записывают так:

у=f(x).

Предположим, что мы построили график этой функции и по­лучили линию, изображённую на рис. 1.

Возьмём далее некоторое сколь угодно малое положительное число эпсилон (0,5; 0,1; 0,01; 0,001,... т.д.), например, = 0,5 .

Изобразим его отрезком 1 кл., который отложим на оси OY (см. рис. 1).

Очевидно, что данная функция в процессе своего изменения может стать равной этому числу при некотором значении ар­гумента х = х₀, а при всех остальных значениях х х₀ она будет становиться всё меньше и меньше него.

Такие функции называются бесконечно малыми (сокращён­но: Б.М.Ф.).

Примеры

1. Атмосферное давление, в зависимости от высоты от по­верхности земли, — также функция бесконечно малая;

2. Скорость движущегося по инерции тела (при выключенном двигателе) является бесконечно малой функцией и т.д.

Бесконечно малые функции обозначаются малыми буквами греческого алфавита: α, β, , и т.д.

Пусть задана другая функция y = F(x), график которой представлен на рис. 2.

Возьмём далее сколь угодно большое число B(10,100,1000,...), например В = 100.

Изобразим его отрезком (100 ед. = 10 кл.), кото­рый отложим на оси OY (см. рис. 2).

Из рис. 2 видно, что при некотором значении аргумента х = х₀ данная функция достигает значения В и в дальнейшем она стано­вится всё больше и больше В.

Функцию y = F(x) и ей подобные называют бесконечно большими функциями (сокращённо Б.Б.Ф.)

Бесконечно большие функции обозначаются большими бук­вами латинского алфавита: F(x), Q(x), G(x)... и т.д. или проcтo F,Q,G,R, ....

В качестве примера Б.Б.Ф. можно назвать расстояние, прой­денное Землёй при её движении вокруг Солнца за время от мо­мента образования Солнечной системы до настоящего времени.

Попробуйте самостоятельно привести примеры Б.Б.Ф.

1.2. Действия над бесконечно малыми и бесконечно большими функциями

Бесконечно малые функции можно:

1) складывать, причём сумма конечного числа бесконечно малых функций есть функция бесконечно малая, т.е.:

α + β + ;

2) вычитать, при этом разность двух бесконечно малых функ­ций есть функция бесконечно малая, т.е.:

;

3) умножать:

а) бесконечно малую функцию на число а. В этом случае ка­ким бы большим а ни было:

α·а = , т.е. Б.М.Ф.;

б) бесконечно малые функции на бесконечно малые, в результате получается бесконечно малая функции, т.е.:

α·.

Примечание.

Если α, — бесконечно малые функции, то

α· — Б.М.Ф. 2-го порядка,

α· — Б.М.Ф. 3-го порядка и т.д.;

4) делить:

а) , т.е. при делении Б.М.Ф. на любое действительное число получается Б.М.Ф.; на языке цифр это будет выглядеть так: = 0;

б) {y,k,F}, т.е. при делении бесконечно малой функции на бесконечно малую функцию частным будет или бесконечно ма­лая функция, или какое-либо постоянное число, или бесконечно большая функция; на языке цифр запишем это действие так:

в) при делении числа на Б.М.Ф. частное будет представлять Б.Б.Ф., т.е.: ; на языке цифр:

5) бесконечно малые функции можно возводить в степень с любым показателем, при этом получится Б.М.Ф. 2-го, 3-го и т.д. порядков, т.е.:

6) из Б.М.Ф. можно извлекать корни любого показателя, в итоге получится Б.М.Ф., т.е.: .

Над бесконечно большими функциями можно произво­дить все действия, что и над бесконечно малыми функциями:

1. Сложение.

При этом сумма конечного числа бесконечно больших функ­ций будет функцией бесконечно большой, т.е.: F + Q + R + ... + G = M;

2. Вычитание.

При этом действии разность может дать бесконечно большую или бесконечно малую функцию, т.е.: F – Q =[G,α].

На языке цифр эту разность запишем так: ∞ — ∞ = [∞,0];

Умножение:

а) произведение Б.Б.Ф. на любое даже сколь угодно малое число есть Б.Б.Ф., т.е. F·a = Q.

На языке цифр: а·∞ = ∞;

б) произведение конечного числа бесконечно больших функ­ций есть функция бесконечно большая, т.е.: F·Q·R·...·G = M;

4. Деление (запишите словами самостоятельно):

а) . На языке цифр: ∞/α = ∞; б) ; а/F = α. На языке цифр: а / ∞ = 0;

b) = {G; α; k}. На языке цифр: ∞ / ∞ = ∞; к; 0;

5. Возведение в степень: ,т.е.: ∞ⁿ = ∞; 6. Извлечение корней: .

2. Предел функции, теоремы о пределах

2.1. Предел функции, понятия, символика

Пусть дана некоторая функция у = f(x), которая графически представляет собой линию, изображённую на рис. 3.

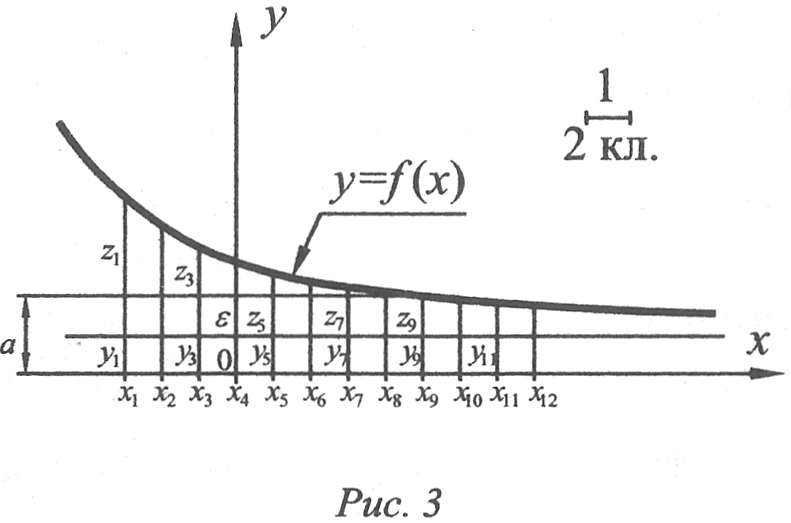
Возьмём далее некоторое число а, изобразим его отрезком, например,(4кл.=2ед.), т.е. а = 2, который отложим на оси OY; через конец этого отрезка проведём прямую, параллельную оси абсцисс.

Теперь найдём разности между соответствующими значениями функции и числа, которые будем обозначать через z; получим:

Эти значения также представим в виде отрезков.

Из рисунка нетрудно сделать вывод, что значение z_i. зависит от х, т.е. z = g(x).

Если мы возьмём сколь угодно малое значение ε, например, ε = 0,5, и отложим его на оси OY (см. рис. 3), то очевидно, что функция z = g(x) может достигнуть значения ε (при х = х₀ = х₁₀), а дальше становится меньше этого ε; это значит, что функция z=g(x) является функцией бесконечно малой.

Таким образом, мы получили, что у — а или, что то же самое, можно записать

y – а = α.

Следует отметить, что разность между значениями у и чис­лом а может быть и отрицательной, если у — а — возрастающая, а так как ε всегда больше ну­ля, то будем оценивать модуль разности | у – а|.

Итак, для заданной функции у = f(x) и числа а получаем следующее соотношение

|у-а| или |у-а| = α.

Определение.

Если разность между значениями некоторой функции у = f(x) и постоянным числом а, взятая по модулю, является бесконечно малой функцией, то число а является пределом функ­ции у = f(x), что принято записывать так:

Так как это соотношение начинает выполняться при некото­ром значении аргумента х = х₀, то наличие предела у функции записывают следующим образом:

или

Справедливо обратное утверждение:

Итак, что же такое предел функции?

Пределом функции, если он есть, является некоторое число; очевидно, что для каждой функции это число своё, свой предел.

У каждой ли функции есть предел?

Оказывается, не у каждой. Так, у бесконечно больших функ­ций предела нет; вернее, он есть, но выражается очень большим числом, что принято записывать так: = ∞.

Классическое определение предела функции (для сколь угодно малых положительных чисел δ u ε).

Пределом функции у = f(x) называется число а при х → х₀, если для любого сколь угодно малого числа ε 0 найдётся такое значение δ0, что |f(х)-а| при 0x — x₀| δ.

Символически определение записывается так: .

2.2. Теоремы о пределах функций

Теорема 1 (об единственности предела).

Если функция имеет предел, то он единственный.

Теорема 2 (о пределе суммы п функций).

Предел суммы конечного числа функций равен сумме преде­лов каждой функции в отдельности.

Теорема 3.

Предел разности двух функций равен разности пределов функций уменьшаемой и вычитаемой.

Теорема 4.

Предел произведения конечного числа функций равен произ­ведению пределов от каждой функции в отдельности.

Из данной теоремы следует:

Следствие 1.

Постоянный множитель можно выносить за знак предела или вносить под знак.

Пример.

Следствие 2.

Предел от степени некоторой функции равен степени предела этой функции.

Т.е.

Пример.

Следствие 3.

Предел от корня n-го показателя некоторой функции равен корню этого показате­ля из предела этой функции, т.е. .

Теорема 5.

Предел частного от деления двух функций равен частному пределов функций делимой и делителя.

Следствие

Предел от логарифма некоторой функции равен логарифму от предела этой функции, т.е.

2.3. Два замечательных предела

Их называют замечательными потому, что с их помощью, описывается множество явлений и процессов, происходящих в природе, технике и обществе.

Первый замечательный предел. Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице, .

Второй замечательный предел. (Число e).

Последовательность имеет предел, заключенный между 2 и 3.

Можно доказать, что функция у = , х (-∞, 0) (0, + ∞) при х → ∞ стремится к е:

е =

Пусть = α (α -1) , тогда е = или е = , где е = 2,7182818284... .

При определении предела некоторой функции, задан­ной аналитически, при х → а или х →∞, +∞, -∞, при формальной подстановке этой величины в качестве ар­гумента в формулу можно получить неопределенности

вида: , , 0·∞, ∞ -∞, ∞°, 0^∞ или 1^∞.

В этом случае нельзя судить о существовании предела и используют некоторые приемы для раскрытия неопределенности. Например, сокращение дроби, умножение на сопряженное выражение, использование замечательных пределов и т.д.

Приложение 4 Закрепление материала

Вычислите пределы:

Вариант I

1)

2)

3)

4)

5)

6)

7)

8)

9)

Вариант II

1)

2)

3)

4)

5)

6)

7)

8)

9)

Приложение 5 Контроль знаний

1– вариант

Выполните тестовые задания:

1. Значение, равное 2, имеют два из приведенных ниже пределов …

1)

2)

3)

4)

2. Функция имеет разрыв в двух точках …

1) –1

2) 0

3) 1

4) 2

3. Область определения функции является интервал …

1) (;7

2) (;7)

3) (7;+)

4) 7;+)

4. Значение предела равно …

1)

2)

3) 0

4) 

5. Предел равен числу е в степени …

1) 2

2) 10

3)

4)

2– вариант

Выполните тестовые задания:

1. Значение предела равно …

1)

2)

3) 0

4) 

2. Предел равен …

1) –32

2) 4

3) –4

4) 32

3. Предел , если параметр t принимает значение, равное …

1) –4

2)

3) –0,25

4) 4

4. Установите соответствие между пределами и их значениями …

1)	1) 2
2)	2)
3)	3) 1

5. Значение предела равно …

1) 0,7

2) 

3) 7

4) 0

Эталоны ответов

	1	2	3	4	5
1 вариант	1,2	1,2	1	2	2
2 вариант	2	4	4	1–1 2–2 3–3	1

Приложение 6 Задания для самостоятельной внеаудиторной работы студентов

1. Подготовить доклад на тему:

   1. Исаак Ньютон;

   2. Готфрид Лейбниц;

2. Ответы на контрольные вопросы:

1. Дайте определение предела функции.

2. Перечислите основные свойства пределов функций.

3. Какие вам известны приемы вычисления пределов функций?

4. Какие известны способы раскрытия неопределеннос­ти вида ?

5. Какие известны, способы раскрытия неопределеннос­ти вида ?

6. Дайте определение бесконечно малой величины.

7. Дайте определение бесконечно большой величины.

8. Что такое первый замечательный предел?

9. Что такое второй замечательный предел?

10. Как используется теория пределов?