

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 25.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Была в сети 11.04.2022 10:34

Касымова Умзахрат Шарабутдиновна
учитель математики
34 года
Местоположение
Россия, Буйнакск
Нахождение значения степени
Категория:
Алгебра
23.03.2022 21:21
© 2022, Касымова Умзахрат Шарабутдиновна 273 0








 называется внесением множителя под знак радикала.
называется внесением множителя под знак радикала.

 , где a, b — рациональные числа, называются подобными. Их можно прибавлять и отнимать:
, где a, b — рациональные числа, называются подобными. Их можно прибавлять и отнимать: Заметим, что равенство
Заметим, что равенство  не выполняется. В этом можно убедиться на таком примере:
не выполняется. В этом можно убедиться на таком примере:
 5 2)67в
5 2)67в 4 3)97n
4 3)97n 3 4) b75 5)34n5
3 4) b75 5)34n5
 4 8)57nm
4 8)57nm 3 9) ab35 10)45n5
3 9) ab35 10)45n5
 b0,6 2)a-5,6·
b0,6 2)a-5,6·  a0 3) а-2,2·а0,2
a0 3) а-2,2·а0,2 ,4 4)с-2.4·
,4 4)с-2.4· ,4 9)с-2.4·
,4 9)с-2.4·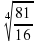 +
+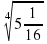 Б)
Б)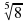 ∙
∙ 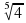



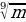 5
5 4 3)9
4 3)9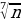 3 4) b
3 4) b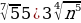
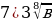 4 8)5
4 8)5 3 9) ab
3 9) ab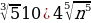
 b0,6 2)a-5,6
b0,6 2)a-5,6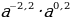 ,4 4)с-2.4
,4 4)с-2.4 ,4 9)с-2.4
,4 9)с-2.4



















