СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 12.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Была в сети 11.04.2022 10:34

Касымова Умзахрат Шарабутдиновна
учитель математики
34 года
Местоположение
Россия, Буйнакск
Степень с целым отрицательным показателем
Категория:
Алгебра
21.03.2022 14:10
© 2022, Касымова Умзахрат Шарабутдиновна 284 1


 ; в) (–11)–2; г)
; в) (–11)–2; г) 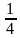 = , т.е (2 ∙ 3)-2 = (свойство 4).
= , т.е (2 ∙ 3)-2 = (свойство 4).