Нахождение расстояния от точки до плоскости методом объемов.

Расстояние от точки до плоскости

Задачи на нахождение расстояния от точки до плоскости ( типовые задачи С2)

Подготовила:

учитель математики

МОУ «Гимназия №1»

г. Железногорска Курской области

Агашкова Н.А.

План проведения занятий.

• Нахождение расстояния от точки до плоскости по определению. Построение перпендикуляра к плоскости на основании признака перпендикулярности прямой и плоскости.
• Нахождение расстояния от точки до плоскости по определению. Построение перпендикуляра к плоскости на основании признака перпендикулярности прямой и плоскости.
• Нахождение расстояния от точки до плоскости. Построение перпендикуляра к плоскости на основании свойства перпендикулярных плоскостей.
• Нахождение расстояния от точки до плоскости. Построение перпендикуляра к плоскости на основании свойства параллельности прямой и плоскости.

• Нахождение расстояния от точки до плоскости методом объемов.

• Нахождение расстояния от точки до плоскости методом координат.
• Решение одной задачи разными методами.

Метод объемов

Методом объемов мы называем приравнивание двух подходящих выражений для объёма, в результате чего удаётся вычислить искомую величину (расстояние или угол).

Метод объемов можно использовать, вычисляя:

• расстояние от точки до плоскости;

• угол между прямой и плоскостью;
• угол между плоскостями;
• расстояние между скрещивающимися прямыми.

С идейной точки зрения метод объемов весьма прост. Все, что здесь нужно, - это найти подходящую треугольную пирамиду и аккуратно провести вычисления. Правда, вычислений обычно получается несколько больше, чем в методах, рассмотренных выше. Но тут уж ничего не поделаешь – за простоту метода приходится платить.

Замечательный факт состоит в том, что при вычислении объема треугольной пирамиды можно в качестве основания выбрать любую ее грань. Это используется при нахождении расстояния от точки до плоскости; нужно лишь представить искомое расстояние как высоту подходящей пирамиды.

А именно, предположим, что нам нужно найти расстояние от некоторой точки C до некоторой плоскости ABD.

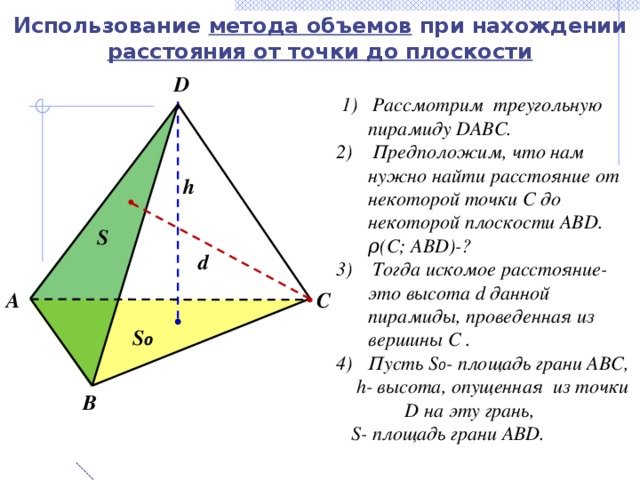
Использование метода объемов при нахождении расстояния от точки до плоскости

D

1) Рассмотрим треугольную пирамиду DABC.

2) Предположим, что нам нужно найти расстояние от некоторой точки C до некоторой плоскости ABD. ρ(С; ABD)-?

3) Тогда искомое расстояние- это высота d данной пирамиды, проведенная из вершины С .

• Пусть S ₀ - площадь грани ABC,

h- высота, опущенная из точки D на эту грань,

S- площадь грани ABD.

h

S

d

C

А

S ₀

B

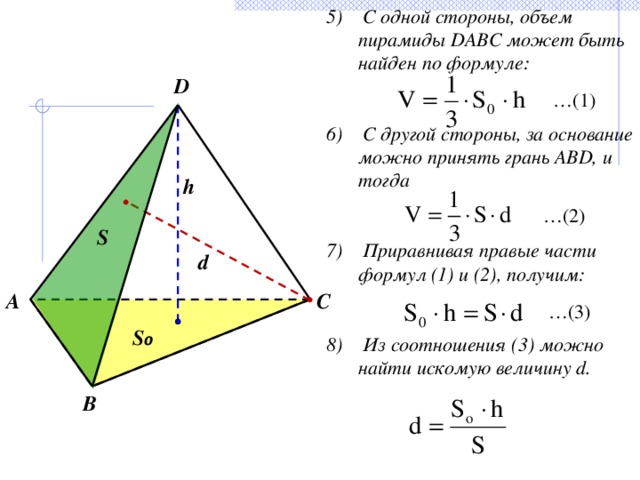
5) С одной стороны, объем пирамиды DABC может быть найден по формуле:

6) С другой стороны, за основание можно принять грань ABD, и тогда

7) Приравнивая правые части формул (1) и (2), получим:

8) Из соотношения (3) можно найти искомую величину d.

D

… (1)

h

… (2)

S

d

А

C

… (3)

S ₀

B

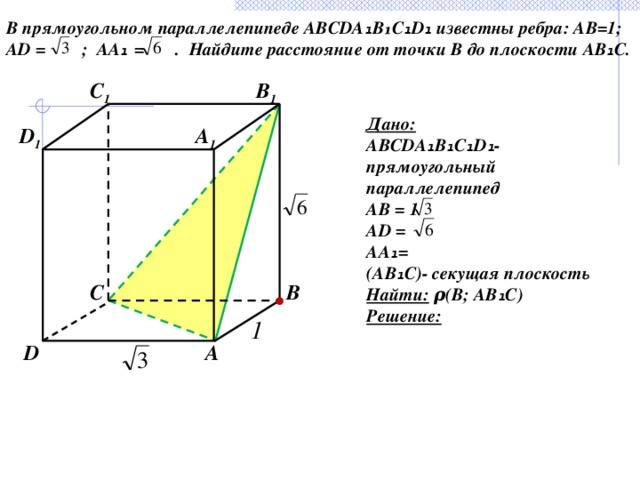
В прямоугольном параллелепипеде ABCDA ₁ B₁C ₁ D ₁ известны ребра: АВ=1;

AD = ; АА ₁ = . Найдите расстояние от точки В до плоскости АВ ₁ С.

C 1

B 1

Дано:

ABCDA ₁ B ₁ C ₁ D ₁ - прямоугольный параллелепипед

АВ = 1

AD =

АА ₁ =

(АВ ₁ С)- секущая плоскость

Найти: ρ(В; АВ ₁ С)

Решение:

A 1

D 1

C

B

1

D

А

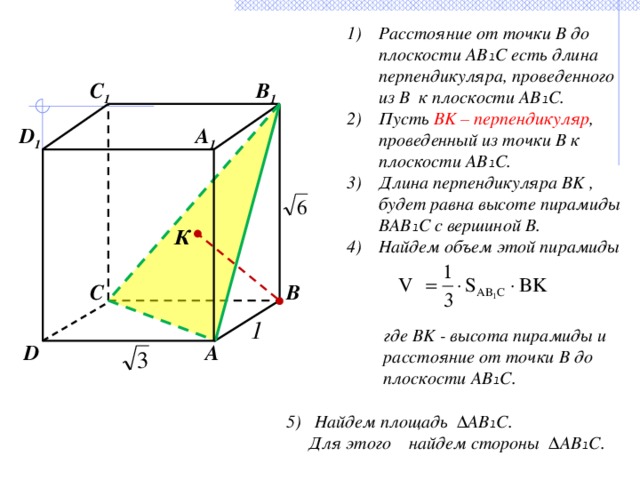
• Расстояние от точки B до плоскости AB ₁ C есть длина перпендикуляра, проведенного из B к плоскости AB ₁ C.
• Пусть BK – перпендикуляр , проведенный из точки B к плоскости AB ₁ C.
• Длина перпендикуляра BK , будет равна высоте пирамиды BAB ₁ C с вершиной B.
• Найдем объем этой пирамиды

B 1

C 1

D 1

A 1

К

B

C

1

где BK - высота пирамиды и расстояние от точки В до плоскости АВ ₁ С.

А

D

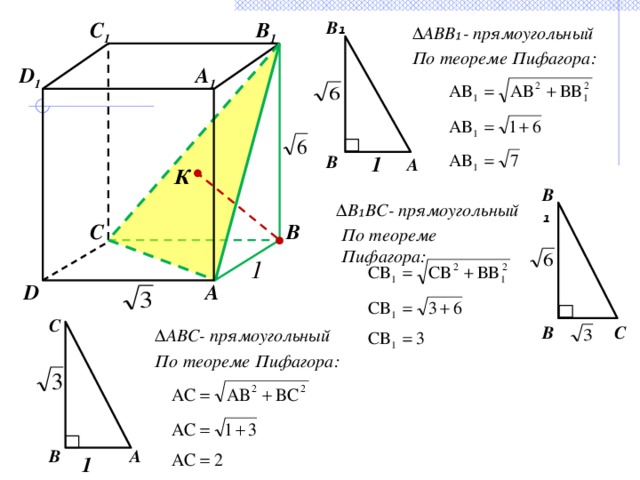
5) Найдем площадь ∆АВ ₁ С.

Для этого найдем стороны ∆АВ ₁ С.

В ₁

C 1

B 1

∆ АВВ₁- прямоугольный

По теореме Пифагора:

A 1

D 1

В

1

А

К

В ₁

∆ В₁ВС- прямоугольный

C

B

По теореме Пифагора:

1

А

D

С

С

В

∆ АВС- прямоугольный

По теореме Пифагора:

В

А

1

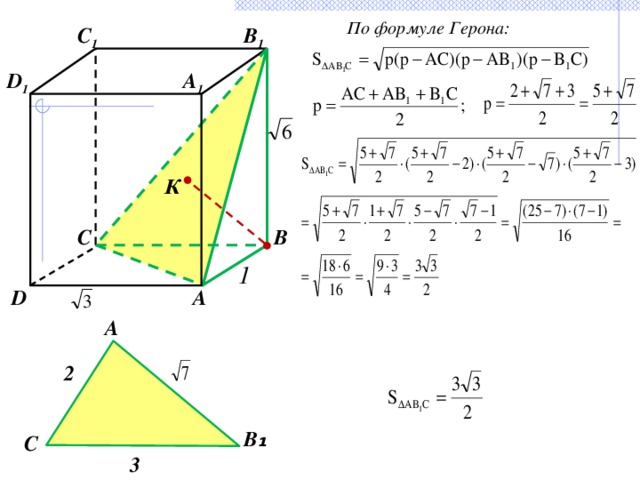
По формуле Герона:

B 1

C 1

D 1

A 1

К

C

B

1

D

А

А

2

В ₁

С

3

А

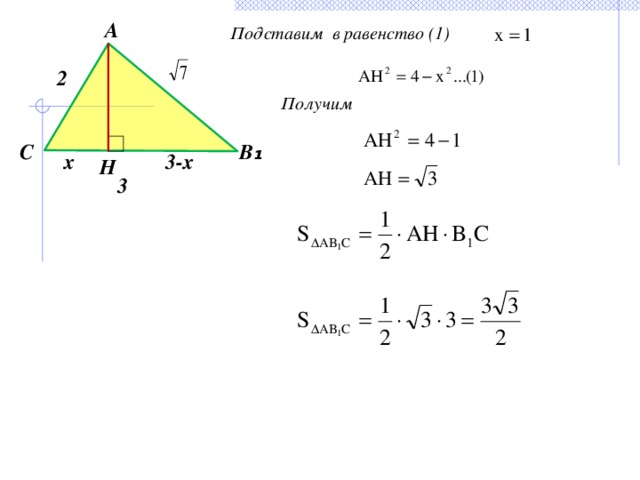
Второй способ вычисления площади ∆AB ₁ C

1) Проведем высоту АН

2

2) Пусть НС = х

В ₁ H = 3- x

В ₁

С

3) ∆АНС - прямоугольный

По теореме Пифагора:

х

3-х

Н

3

4) ∆AHB ₁ - прямоугольный

5) Приравнивая правые части равенств (1) и (2), получим:

По теореме Пифагора:

А

Подставим в равенство (1)

2

Получим

В ₁

С

х

3-х

Н

3

Третий способ вычисления площади ∆AB ₁ C

А

2

По теореме косинусов найдем

С

В ₁

3

Итак,

Подставим в формулу площади, получим

… (1)

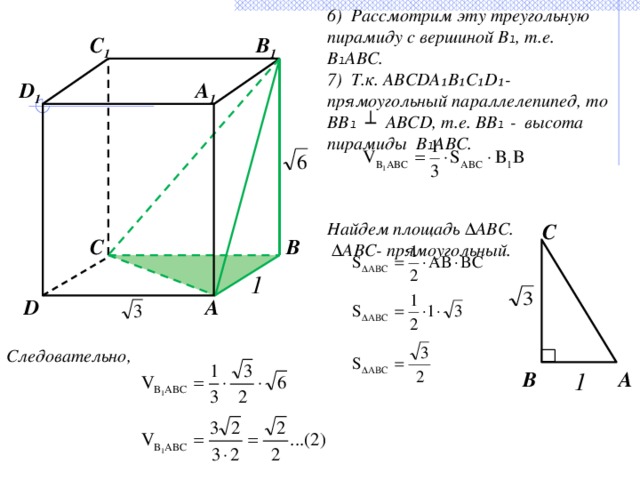
6) Рассмотрим эту треугольную пирамиду с вершиной В ₁ , т.е. В ₁ АВС.

7) Т.к. ABCDA₁B₁C₁D₁- прямоугольный параллелепипед, то ВВ ₁ ┴ ABCD, т.е. ВВ ₁ - высота пирамиды В ₁ АВС.

Найдем площадь ∆АВС.

∆ АВС- прямоугольный.

B 1

C 1

A 1

D 1

С

B

C

1

D

А

Следовательно,

1

B

А

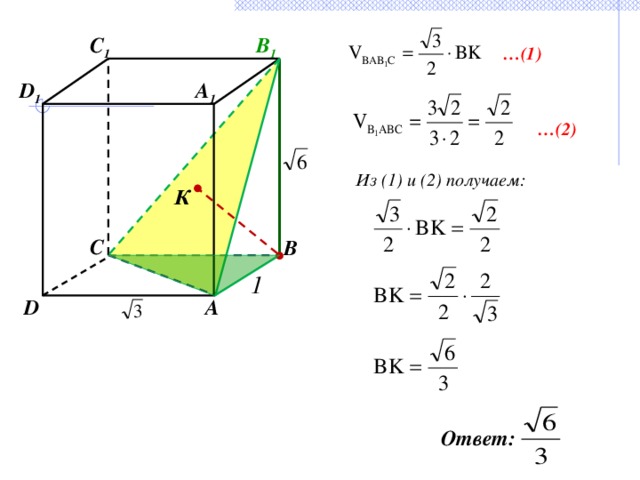
B 1

C 1

… (1)

D 1

A 1

… (2)

Из (1) и (2) получаем:

Ответ:

К

C

B

1

D

А

Метод объемов легко справляется с задачами, решить которые прежними методами было бы затруднительно.

Почему при решении этой задачи прежними методами мы столкнулись бы с проблемами? Дело в том, что в пирамиде АВСВ ₁ отсутствует симметрия – все ребра пирамиды имеют различную длину. Соответственно, к проекции точки В на плоскость АВ ₁С не так-то просто «подобраться». Но методу объемов, как видите, данная трудность нипочем – мы нашли искомую высоту, даже не выясняя, куда именно проектируется точка В.

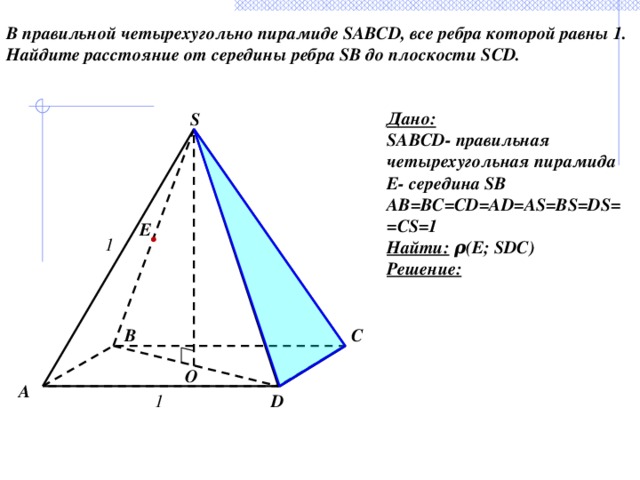
В правильной четырехугольно пирамиде SABCD, все ребра которой равны 1. Найдите расстояние от середины ребра SB до плоскости SCD.

Дано:

S

SABCD- правильная четырехугольная пирамида

Е- середина SB

AB=BC=CD=AD=AS=BS=DS=

=CS=1

Найти: ρ(Е; SDC)

Решение:

E

1

B

C

O

A

D

1

15

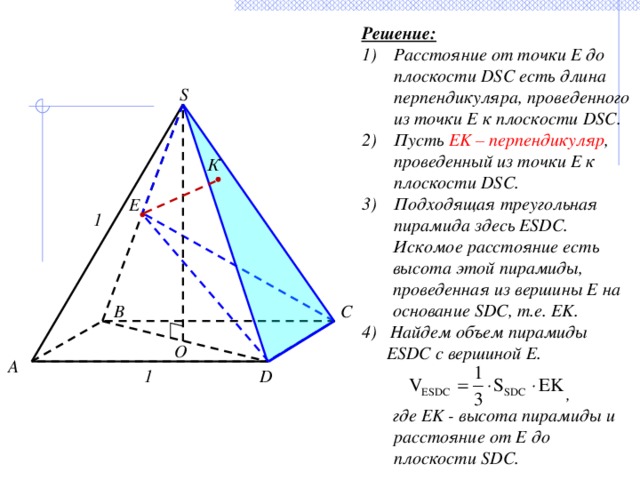
Решение:

• Расстояние от точки E до плоскости DSC есть длина перпендикуляра, проведенного из точки E к плоскости DSC.
• Пусть EK – перпендикуляр , проведенный из точки E к плоскости DSC.
• Подходящая треугольная пирамида здесь ESDC.

Искомое расстояние есть высота этой пирамиды, проведенная из вершины Е на основание SDC, т.е. EK.

4) Найдем объем пирамиды ESDC с вершиной Е.

,

где EK - высота пирамиды и расстояние от Е до плоскости SDC.

S

К

E

1

C

B

O

A

D

1

18

5) Найдем площадь ∆SDC.

∆ SDC- правильный, т.к. все ребра пирамиды равны.

- площадь правильного треугольника.

Следовательно,

6) Итак,

S

К

E

1

B

C

O

A

… (1)

D

1

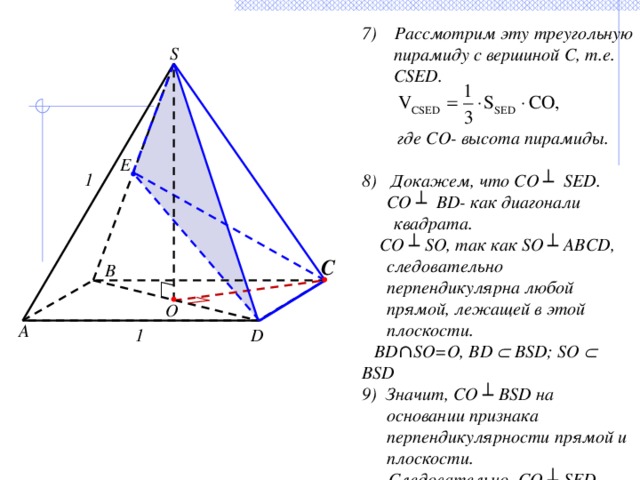
7) Рассмотрим эту треугольную пирамиду с вершиной С, т.е. CSED.

где СО- высота пирамиды.

8) Докажем, что СО ┴ SED.

СО ┴ BD- как диагонали квадрата.

СО ┴ SO, так как SO ┴ ABCD, следовательно перпендикулярна любой прямой, лежащей в этой плоскости.

BD∩SO=O, BD  BSD; SO  BSD

9) Значит, СО ┴ BSD на основании признака перпендикулярности прямой и плоскости.

Следовательно, СО ┴ SED.

S

E

1

C

B

O

A

1

D

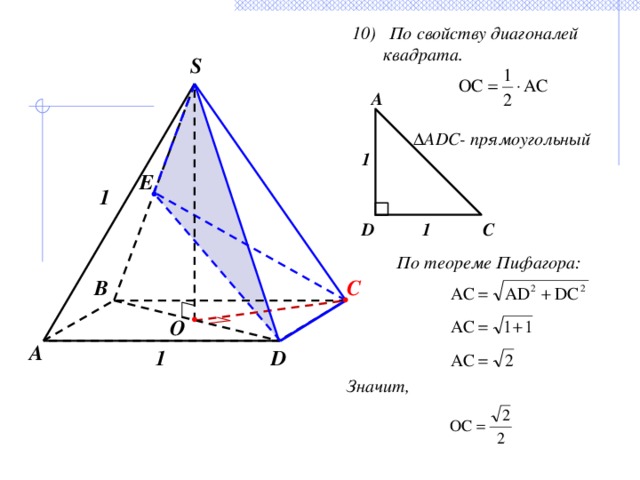
10) По свойству диагоналей квадрата.

S

А

∆ ADC- прямоугольный

1

E

1

D

C

1

По теореме Пифагора:

B

C

O

A

D

1

Значит,

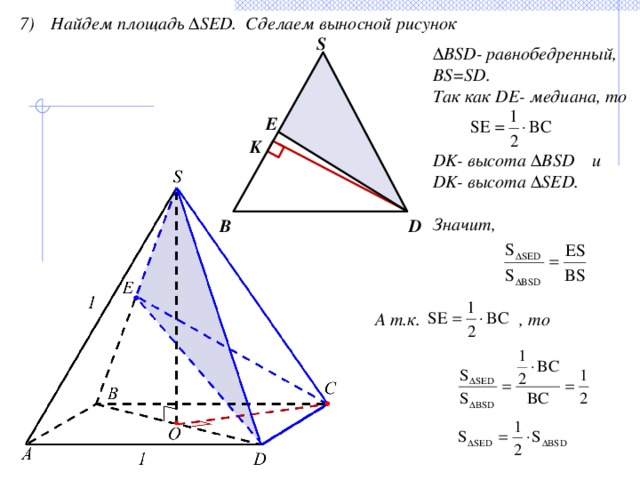
• Найдем площадь ∆SED. Сделаем выносной рисунок

S

∆ BSD- равнобедренный,

BS=SD.

Так как DE- медиана, то

DK- высота ∆BSD и

DK- высота ∆SED.

Значит,

E

K

B

D

А т.к. , то

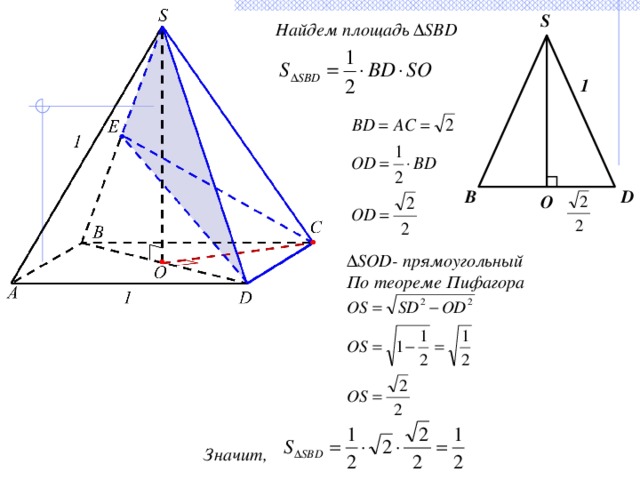
S

Найдем площадь ∆SBD

1

B

D

O

∆ SOD- прямоугольный

По теореме Пифагора

Значит,

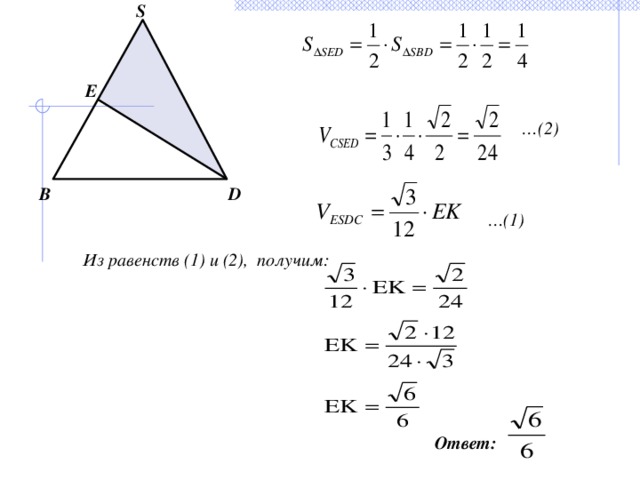
S

E

… (2)

B

D

… (1)

Из равенств (1) и (2), получим:

Ответ:

Задачи для самостоятельного решения

• В правильной шестиугольной призме ABCDEFA ₁ B ₁ C ₁ D ₁ E ₁ F ₁ , все ребра которой равны 1, найдите расстояние от точки А до плоскости BFA ₁ .

Ответ:

• В правильной шестиугольной пирамиде SABCDEF, стороны основания равны 1, а боковые ребра равны 2, найдите расстояние от точки А до плоскости SCE.

Ответ:

• В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние от точки А до плоскости SBF

Ответ:

• В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точка Е- середина ребра SB. Найдите расстояние от точки В до плоскости ACE.

Ответ: 0,5

• В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от точки А до плоскости SCD. Ответ:

• В правильной пирамиде SABCDEF, стороны основания которой равны 1, а боковые стороны (ребра) равны 2, найдите расстояние от точки А до плоскости SDE. Ответ:

• В единичном кубе ABCDA ₁ B ₁ C ₁ D ₁ найдите расстояние от точки А до плоскости BDC ₁ .

Ответ: