бюджетное учреждение профессионального образования
«Радужнинский политехнический колледж»
НАУКА О РЕШЕНИИ УРАВНЕНИЙ
| Автор: | Ильина Лидия Элхановна 26 группа, профессия «Делопроизводитель»
|
| Руководитель: | Озерова Руфина Кунакбаевна, Преподаватель математики и информатики
|
2018 год
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ…………………………………………………..…………………………….…..2
ГЛАВА 1. ИСТОРИЯ НАУКИ ОБ УРАВНЕНИЯХ............................................................3
1.1. Из истории уравнений..........................................................................................................3
1.2. Из истории рациональных уравнений................................................................................3
1.3. Из истории иррациональных уравнений............................................................................5
1.4. Из истории логарифмических уравнений...........................................................................6
1.5. Из истории тригонометрических уравнений......................................................................7
ГЛАВА 2. ИССЛЕДОВАНИЕ МЕТОДОВ РЕШЕНИЯ УРАВНЕНИЙ...........................9
2.1. Решение рационального уравнения......................................................................................9
2.1.1. Первый способ решения рационального уравнения по алгоритму...............................9
2.1.2. Второй способ решения рациональных уравнений методом введения новой переменной...................................................................................................................................10
2.2. Решение иррациональных уравнений................................................................................12
2.2.1. Первый способ решения иррационального уравнения методом возведения в квадрат..........................................................................................................................................12
2.2.2. Второй способ решения иррационального уравнения методом введения новой переменной...................................................................................................................................12
2.3. Решение логарифмических уравнений...............................................................................13
2.3.1. Первый способ решения логарифмического уравнения функционально-графическим методом.........................................................................................................................................13
2.3.2. Второй способ решения логарифмического уравнения методом потенцирования..13
2.3.3. Третий способ решения логарифмического уравнения способов введения новой переменной...................................................................................................................................14
2.4. Решение тригонометрических уравнений..........................................................................15
2.4.1. Первый способ решения тригонометрического уравнения методом введения новой переменной...................................................................................................................................15
2.4.2. Второй способ решения тригонометрического уравнения методом разложения на множители....................................................................................................................................15
ЗАКЛЮЧЕНИЕ………………………………………………………............................….….16
ЛИТЕРАТУРА…………………………………………...............................................................4
ВВЕДЕНИЕ
Актуальность работы заключается в том, что на уроках математики мы очень часто встречаемся с решением уравнений. Поэтому каждый учащийся должен уметь верно и рационально решать то или иное уравнение, что также пригодится и при решении более сложных задач. Практически все, что окружает современного человека – это все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих уравнений сводится к различным способам решения их, которые необходимо научиться использовать.
Цель данной работы:
Изучить историю возникновения уравнений.
Исследовать различные методы уравнений.
Гипотеза:
Уравнения имеют различные методы решения, которые мы могли ещё не изучать или же забыть.
Основной проблемой является незнание всевозможных методов решения, что затрудняет учащегося при решении и нахождении ответа.
Задачи:
Изучить литературу по данной теме
Исследовать методы решения уравнений
Объектом исследования являются различные уравнения.
Предмет исследования: разнообразные методы решения уравнений.
Методы исследования: анализ материала, описание, обобщение, вывод.
Практическая ценность работы заключается в том, что полученные результаты позволят создать методическое пособие не только для учащихся, но и для преподавателей.
ГЛАВА 1. ИСТОРИЯ НАУКИ УРАВНЕНИЙ
1.1. Из истории уравнений
Алгебра появилась в связи с решением различных задач с помощью уравнений. Обычно в задачах требуется найти одну либо несколько искомых значений, зная при всем этом показатели некоторых действий, которые были произведены над разыскиваемыми и данными величинами. Подобные задачки сводятся к решению 1-го либо системы нескольких уравнений, к нахождению неизвестных при помощи алгебраических действий над данными величинами. В алгебре исследуются общие характеристики действий над величинами.
Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны около 4000 лет назад в Древнем Вавилоне. В клинописных текстах встречаются решения как неполных, так и полных квадратных уравнений с применением алгебраической записи. Правила решения этих уравнений совпадают по факту с современными, но непонятно, каким образом дошли вавилоняне до данного правила. Практически все найденные до настоящего времени клинописные тексты приводят лишь задачки с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Невзирая на высочайший уровень развития алгебры в Вавилоне не использовалось понятие отрицательного числа, и отсутствовали общие способы решения квадратного уравнения.
Не наименьшую роль, чем квадратные уравнения, играют в математике и ее приложениях уравнения третьей и по более больших степеней.
1.2. Из истории рациональных уравнений
Уже в древности люди поняли, как важно научиться решать алгебраические уравнения вида а0хn+а1хn-1+…+аn=0 — ведь к ним сводятся очень многие и очень разнообразные вопросы практики и естествознания (конечно, здесь можно сразу предполагать, что а0, так как иначе степень уравнения на самом деле не n, а меньше). Уместно напомнить, что сам термин «алгебра» происходит от названия сочинения Мухаммеда аль-Хорезми, (Мухаммед из Хорезма) «Аль-джебр аль-мукабала», в котором излагались решения такого уравнения при n=1 и n=2.
Уравнения первой степени с одной переменной решали уже в Древнем Египте и в Древнем Вавилоне. Вавилонские писцы умели решать и уравнения второй степени. Евклид находил уравнения второй степени геометрически. Для математиков, уже умевших решать уравнения первой и второй степени, хотелось научиться решать уравнения третьей степени. Одним из самых первых этим вопросом заинтересовался таджикский ученый Омар Хоийен (1048-1122). Омар Хоийен придумал очень сложные, но красивые способы геометрических построений для отыскания неизвестного. Но и для практического использования они очень неудобны.
Многим, разумеется, приходила в голову заманчивая мысль найти и для любой другой степени n2 формулы, которые выражали бы корни уравнения через его коэффициенты с помощью четырех арифметических действий – сложения, вычитания, умножения, деления – и извлечения корней или радикалов, то есть, говоря более кратко, решали бы уравнение в радикалах.
Однако «мрачное средневековье» оказалось как нельзя более мрачным и в отношении обсуждаемой задачи – в течение целых семи столетий требуемых формул никто не сыскал. Только в 16 веке итальянским математикам удалось продвинуться дальше – найти формулы для n=3 и n=4.
Были периоды, когда начинало казаться, что сил человеческого ума недостаточно для решения этой задачи. Томас Торквемада–глава инквизиции в Испании, монах-доминиканец – считал, что решение таких уравнений волей бога изъято из возможностей человеческого разума. И когда один из его друзей, математик по имени Паоло Вальмес, неосторожно сказал Торквемаде, что он, Вальмес, умеет решать уравнения даже четвертой степени, Торквемада бросил его в тюрьму, а затем отправил на костер за «борьбу с божественной волей». Вальмес никому не успел сообщить о своем открытии. Это было в конце 15 века.
1.3. Из истории иррациональных уравнений
Термин «рациональное» (число) происходит от латиноамериканского слова ratio – отношение, которое является переводом греческого слова «логос» в отличие от рациональных чисел. Числа, выражающие отношение несоизмеримых величин, были названы еще в древности иррациональными, т.е. нерациональными (по-гречески «алогос»). Сначала термины «рациональный» и «иррациональный» относились не к числам, а к соизмеримым и не соизмеримым величинам, которые пифагорейцы называли выразимыми и невыразимыми. Теодор Киренский же симметричными и ассимметричными. В V-VI вв. римские авторы Капелла и Кассиодор переводили эти термины на латынь словами rationalis и irrationalis. Термин «соизмеримый» (commensurabilis) ввел в первой половине VI в. другой римский автор - Боэций.
Древнегреческие математики классической эпохи пользовались только рациональными числами (вернее целыми, дробными и положительными). В своих «Началах» Евклид излагает учение об иррациональностях чисто геометрически.
Математики Индии, Ближнего и Среднего Востока, развивая алгебру, тригонометрию и астрономию, не могли обойтись без иррациональных величин, которые, длительное время не признавали за числа. Греки называли иррациональную величину, например, корень из квадратного числа, «алогос» – невыразимое словами. Позже европейские переводчики с арабского на латынь перевели это слово латинским словом surdus – глухой. В Европе термин surdus - глухой впервые появился в середине XII в. у Герарда Кремонского, известного переводчика математических прозведений с арабского на латынь. Затем же у итальянского математика Леонардо Фабоначчи и других европейских математиков, вплоть до XVIII в. Правда уже в XVI в. Отдельные ученые, в первую очередь итальянский математик Рафаэль Бомбелли и нидерландский математик Симон Стевин считали понятие иррационального числа равноправным с понятием рационального числа. Стевин писал: «Мы приходим к выводу, что не существует никаких абсурдных, иррациональных, неправильных, необъяснимых или глухих чисел, но что среди чисел существует такое совершенство и согласие, что нам надо размышлять дни и ночи над их удивительной закономерностью».
Еще до Бомбелли и Стевина многие ученые стран Среднего Востока в своих трудах употребляли иррациональные числа как полноправные объекты алгебры. Более того, комментируя «Начала» Евклида и исследуя общую теорию отношения Евдокса, Омар Хайям уже в начале XII в. теоретически расширяет понятие числа до положительного действительного числа. В том же направлении много было сделано крупнейшим математиком XIII в. ат-Туси.
1.4. Из истории логарифмических уравнений
Логарифмы были придуманы для ускорения и упрощения вычислений. Идея логарифма, т. е. идея выражать числа в виде степени одного и того же основания, принадлежит Михаилу Штифелю. Но в его времена математика была не столь развита и идея логарифма не нашла своего развития. Логарифмы были изобретены позже шотландским учёным Джоном Непером(1550-1617) и швейцарцем Иобстом Бюрги(1552-1632). Первым опубликовал работу Непер в 1614г. под названием «Описание удивительной таблицы логарифмов», теория логарифмов была дана в достаточно полном объёме, а способ вычисления логарифмов дан наиболее простой. Поэтому заслуги Непера в изобретении логарифмов больше, чем у Бюрги. Он работал над таблицами одновременно с Непером, но долгое время держал их в секрете и опубликовал лишь в 1620г. Идеей логарифма Непер овладел около1594г., хотя таблицы опубликовал через 20 лет. Первые таблицы на русском языке были изданы в 1703г. при участии замечательного педагога 18в. Л. Ф Магницкого. Леонард Эйлер первым стал рассматривать логарифмирование как действие, обратное возведению в степень, он ввёл в употребление термины «основание логарифма» и «мантисса». Бригс составил таблицы логарифмов с основанием 10. Десятичные таблицы более удобны для практического употребления, теория их проще, чем у логарифмов Непера. Поэтому десятичные логарифмы иногда называют бригсовыми. Термин «характеристика» ввёл Бригс.
Дошедшие до нас источники говорят, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако нигде не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: «Смотри!», «Делай так!», «Ты правильно нашел». В этом смысле исключением является «Арифметика» греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений.
Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово «аль-джебр» из арабского названия этого трактата – «Китаб аль-джебер валь-мукабала» («Книга о восстановлении и противопоставлении») – со временем превратилось в хорошо знакомое всем слово «алгебра», а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.
1.5. Из истории тригонометрических уравнений
Зарождение тригонометрии относится к глубокой древности. Еще за долго до новой эры вавилонские ученые умели предсказывать солнечные и лунные затмения. Это позволяет сделать вывод о том, что им были известны некоторые простейшие сведения из тригонометрии. Постепенно в геометрии и астрономии установились понятия синуса, косинуса, тангенса угла.
Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во II в. до н. э. Он является автором первых тригонометрических таблиц. Эти таблицы до нас не дошли, но они вошли в сочинения "великое построение" (Альмагест) знаменитого александрийского астронома Клавдия Птолемея жившего во второй половине II в. до н. э.
Эти таблицы являются таблицами значений удвоенного синуса половины соответствующего центрального угла. В них были даны значения хорд для всех углов (через каждые пол градуса) от 0° до 180°. Однако надо иметь в виду, что в древней Греции тригонометрия не выделялась в «самостоятельную науку», а считалась частью астрономии.
Важный вклад в развитие тригонометрии был внесен индийской математикой в период V-X1I в. н. э. Индийские математики стали вычислять не полную хорду, как это делали греки, а ее половину (то есть «линию синусов»). Линия синусов именовалась ими «архаджива», что буквально означало «половина тетивы лука». Индийцы составили таблицу синусов, в которой были даны значения полухорд, измеренных частями (минутами) окружности для всех углов от 0° до 90° (через каждые 3°45'). Эти таблицы были точнее таблиц Птолемея.
В XI-XIII вв. в трудах математиков Средней Азии, Закавказья, Ближнего Востока и Индии началось формирование тригонометрии как отдельной науки. И в дальнейшем потребности географии и военного дела способствовали развитию тригонометрии, как науки. Особенно усиленно тригонометрия развивалась в средние века, а в первую очередь на юго-востоке. В Индии (Ариабхата, Брамагупта, Бхаскара), в Узбекистане, Азербайджане и Таджикистане (Насирад-Дин ат-Туси, ал-Каши, ал-Бируни), в Арабии (Ахмад, ибн-Абдаллах, ал-Баттани). Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насирад-Дину Мухаммаду ат-Туси, написавшему «Трактат о полном четырехугольнике». Работы ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела математики. Однако в их трудах еще не было необходимой символики, и поэтому развитие тригонометрии происходило медленно.
С XV в. и в Европе появляются работы, посвященные вопросам тригонометрии. Немецкий ученый Иоганн Мюллер, известный в науке под именем Региомонтан, издал труд «Пять книг о треугольниках всех видов», сыгравший важную роль в развитии тригонометрии. Здесь дано систематическое изложение тригонометрии как самостоятельной научной дисциплины. Региомонтан составил таблицы синусов с точностью уже до 10-7. В его таблицах радиус круга принимался за 107 вместо числа кратного 60, то есть, по сути, был совершен переход от шестидесятеричной системы измерения к десятичной. В 1696 г. появился труд Варфоломея Питискуса «Тригонометрия, или Краткий обзорный трактат о решении треугольников».
В XV-XVII в. в Европе было составлено и издано несколько тригонометрических таблиц. Над их составлением работали крупнейшие ученые: Н. Коперник, И. Кеплер, Ф. Вието и др. В России первые тригонометрические таблицы были изданы в 1703 г. при участии .
Таким образом, тригонометрия возникла на геометрической основе, имела геометрический язык и применялась к решению геометрических задач. Развитие алгебраической символики позволило записывать тригонометрические соотношения в виде формул; применение отрицательных чисел позволило рассматривать направленные углы и дуги и распространить понятие тригонометрических линий (определенных отрезков в круге) для любых углов. В этот период создалась база для изучения тригонометрических функций как функций числового аргумента, основа аналитической теории тригонометрических (круговых) функций. Аналитический аппарат, позволяющий вычислять значения тригонометрических функций с любой степенью точности, был разработан Ньютоном.
Современный вид тригонометрия получила в трудах великого ученого, члена Российской академии наук Л. Эйлера. Эйлер стал рассматривать значения тригонометрических функций как числа – величины тригонометрических линий в круге, радиус которого принят за единицу («тригонометрический круг» или «единичная окружность»). Эйлер дал окончательное решение о знаках тригонометрических функций в разных четвертях, вывел все тригонометрические формулы из нескольких основных, установил несколько неизвестных до него формул, ввел единообразные обозначения. Именно в его трудах впервые встречаются записи sin α, cos α, tg α, ctg α. Он также открыл связь между тригонометрическими и показательной функциями от комплексного аргумента. На основании работ Л. Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности.
ГЛАВА 2. ИССЛЕДОВАНИЕ МЕТОДОВ РЕШЕНИЯ УРАВНЕНИЙ
Решение рационального уравнения
2.1.1. Первый способ решения рационального уравнения по алгоритму
Вспомним, что такое рациональное выражение с одной переменной алгебраическое выражение, составленное из чисел и переменной x с помощью операций сложения, вычитания, умножений, деления и возведения в целую степень. Если r(x) рациональное выражение, то уравнение r(x) = 0 называют рациональным уравнением.
На практике удобнее пользоваться несколько более широким толкованием термина «рациональное уравнение»: это уравнение вида h(x) = q(x), где h(x) b q(x) рациональные выражения.
Раньше мы могли решить не любое рациональное уравнение, а только такое, которое в результате различных преобразований и рассуждений сводилось к линейному уравнению. Дальше наши возможности стали значительно шире: мы сможем решить рациональное уравнение, которое сводится не только к линейному, но и к квадратному уравнению.
Пример 1.
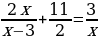
Решение. Перепишем уравнение в виде
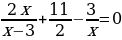
При этом, как обычно, использоваться тем, что равенства A=B и A-B=0 выражают одну и ту же зависимость между A и B. Это позволяет нам перенести член 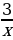 в левую часть уравнения с противоположным знаком.
в левую часть уравнения с противоположным знаком.
Выполним преобразование левой части уравнения:
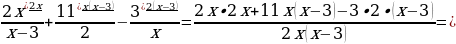
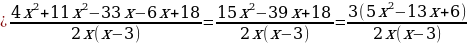
Таким образом, преобразовали заданное уравнение к виду
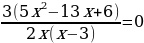
Вспоминаем условия равенства дроби нулю: 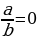 тогда и только тогда, когда одновременно выполняются два соотношения:
тогда и только тогда, когда одновременно выполняются два соотношения:
1) числитель дроби равен нулю (a = 0);
2) знаменатель дроби от нуля (b ≠ 0).
Приравняв нулю, числитель дроби в левой части уравнения, получим:
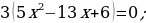
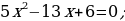
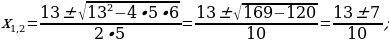
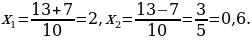
Остается проверить выполнение второго указанного выше условия. Соотношение b≠0 означает для уравнения, что 2x(x-3)≠0, т.е. x≠0, x≠3. Значение x1=2 x2=0,6 указанным соотношениям удовлетворяют и потому служат корнями уравнения, а вместе с тем и корнями заданного уравнения.
Ответ: 2; 0,6.
Алгоритм решения рационального уравнения
1. Перенести все члены уравнения в одну часть.
2. Преобразовать эту часть уравнения к виду алгебраической дроби 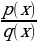 .
.
3. Решить уравнение p(x)=0 .
4. Для каждого корня уравнения p(x)=0 сделать проверку: удовлетворяет ли оно условию q(x) ≠ 0 или нет. Если да, то это корень заданного уравнения; если нет, то это посторонний корень и в ответ его включать не следует.
Если среди корней числителя окажется такое число, при котором знаменатель дроби обращается в нуль, то такое число корнем уравнения не может быть, его называют посторонним корнем и в ответ не включают.
2.1.2. Второй способ решения рациональных уравнений методом введения новой переменной
Пример 2.
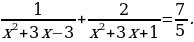
Решение.
Здесь дважды встречается одно и то же выражение x2+3x. Значит, имеет смысл ввести новую переменную y=x2+3x. Это позволит переписать уравнение в более простом и приятном виде:
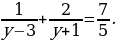
А теперь решаем по алгоритму решения рационального уравнения:
Перенесем все члены уравнения в одну часть:
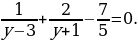
Преобразуем левую часть уравнения:
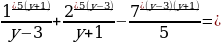
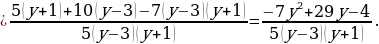
Итак, преобразовали заданное уравнение к виду
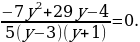
3) Из уравнения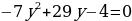 находим:
находим: 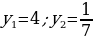 .
.
4) Выполняем проверку найденных корней с помощью условия 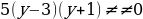 . Оба корня этому условию удовлетворяют.
. Оба корня этому условию удовлетворяют.
Квадратное уравнение относительно новой переменной y решено: 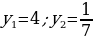 .
.
Поскольку 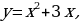 а y, как установили, принимает два значения: 4 и
а y, как установили, принимает два значения: 4 и 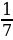 , ещё предстоит решить два уравнения:
, ещё предстоит решить два уравнения: 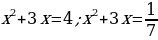 . Корнями первого уравнения являются
. Корнями первого уравнения являются 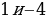 , а корнями второго числа
, а корнями второго числа 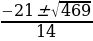 .
.
Ответ: 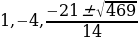 .
.
Пример 3.
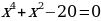
Решение. Введем новую переменную 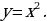 Так как
Так как 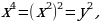 то заданное уравнение можно переписать в виде:
то заданное уравнение можно переписать в виде:
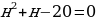
Квадратное уравнение, корни которого найдем, используя известные формулы: 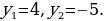
Но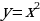 , значит, задача свелась к решению двух уравнений:
, значит, задача свелась к решению двух уравнений:
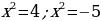
Из первого уравнения: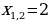 . Второе не имеет корней.
. Второе не имеет корней.
Ответ: 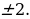
Уравнения вида: 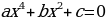 называют биквадратным уравнением («Би» два, т.е. как бы дважды квадратное уравнение).
называют биквадратным уравнением («Би» два, т.е. как бы дважды квадратное уравнение).
2.2. Решение иррациональных уравнений
Если в уравнении переменная содержится под знаком квадратного корня, то уравнение называют иррациональным.
2.2.1. Первый способ решения иррационального уравнения методом возведения в квадрат
Пример 4.
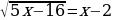 .
.
Решение. Возведем обе части уравнения в квадрат:
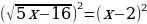 .
.
Далее получаем:
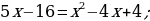
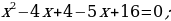
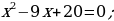
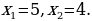
Проверка. Подставим 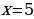 в уравнение, получим:
в уравнение, получим: 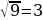 верное равенство. Подставим
верное равенство. Подставим 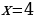 в уравнение, получим:
в уравнение, получим: 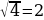 верное равенство. Следовательно, оба значения являются корнями уравнения.
верное равенство. Следовательно, оба значения являются корнями уравнения.
Ответ: 4; 5.
2.2.2. Второй способ решения иррационального уравнения методом введения новой переменной
Пример 5.
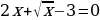
Решение. Вводим новую переменную 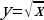 . Тогда получим:
. Тогда получим: 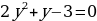 квадратное уравнение переменной y. Находим корни:
квадратное уравнение переменной y. Находим корни: 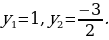
Выходят два уравнения:
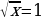 ;
; 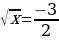 .
.
Из первого уравнения находим x=1, второе уравнение не имеет корней.
Ответ: 1.
2.3. Решение логарифмических уравнений.
Логарифмическими уравнениями называют уравнения вида 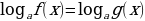 , где a положительное число, отличное от 1, и уравнения, сводящиеся к этому виду.
, где a положительное число, отличное от 1, и уравнения, сводящиеся к этому виду.
2.3.1. Первый способ решения логарифмического уравнения функционально-графическим методом
Пример 6.
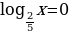 .
.
Изображаем график функции 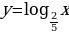
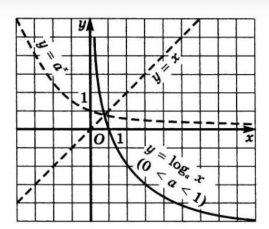
Уравнение 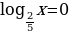 имеет один корень
имеет один корень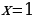 т.к. график функции
т.к. график функции 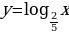 пересекает ось x в единственной точке (1;0)
пересекает ось x в единственной точке (1;0)
Ответ: 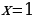 .
.
2.3.2. Второй способ решения логарифмического уравнения методом потенцирования
Пример 7.
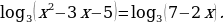
Решение.
1)Потенцируем (т.е. освобождаемся от знаков логарифмов) уравнение
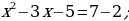
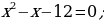
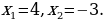
Проверяем найденные корни по условиям, определяющим ОДЗ:
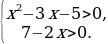
Значение 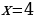 не удовлетворяет этой системе неравенств (достаточно заметить, что
не удовлетворяет этой системе неравенств (достаточно заметить, что 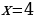 не удовлетворяет второму неравенству системы), т.е.
не удовлетворяет второму неравенству системы), т.е. 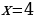 посторонний корень для заданного уравнения. Значение
посторонний корень для заданного уравнения. Значение 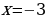 удовлетворяет обоим неравенствам системы, а потому
удовлетворяет обоим неравенствам системы, а потому 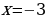 корень заданного уравнения.
корень заданного уравнения.
Ответ: 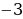
2.3.3. Третий способ решения логарифмического уравнения способов введения новой переменной.
Пример 8.
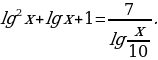
Решение.
Так как 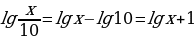 , то заданное уравнение можно переписать так:
, то заданное уравнение можно переписать так: 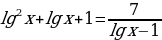 .
.
Вводим новую переменную: 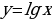 ; тогда уравнение примет следующий вид:
; тогда уравнение примет следующий вид:
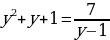 .
.
Находим:
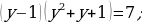
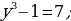
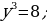
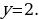
Значение удовлетворяет условию 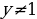 .
.
Итак, 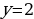 . Но
. Но 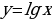 , значит, осталось решить простейшее логарифмическое уравнение
, значит, осталось решить простейшее логарифмическое уравнение 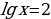 , откуда находим:
, откуда находим: 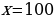 .
.
Ответ: 100
2.4. Решение тригонометрических уравнений
2.4.1. Первый способ решения тригонометрического уравнения методом введения новой переменной
Пример 9.
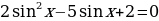
Решение.
Введем новую переменную: 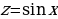 . Тогда уравнение примет вид
. Тогда уравнение примет вид
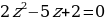 ,
,
откуда находим: 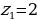 ,
, 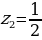 .
.
Значит, либо 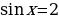 , либо
, либо 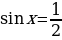 . Первое уравнение не имеет корней, а из второго находим:
. Первое уравнение не имеет корней, а из второго находим:
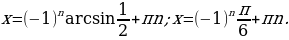
Ответ: 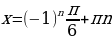 .
.
2.4.2. Второй способ решения тригонометрического уравнения методом разложения на множители
Пример 10.
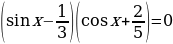 .
.
Решение.
Задача сводится к решению совокупности уравнений:
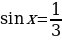 ;
; 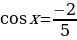 .
.
Из этих уравнений находим соответственно:
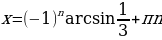 ;
; 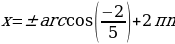 .
.
Ответ: 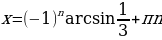 ;
; 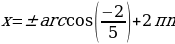 .
.
ЗАКЛЮЧЕНИЕ
Изучение компьютеризации как феномена человеческой деятельности имеет огромное значение в науке. Компьютер стал неотъемлемой частью человеческой жизни и прочно вошел во все ее сферы. Первой целью нашего исследования было изучение влияния компьютеризации на человеческую деятельность. В ходе работы мы выяснили, что наряду с положительными аспектами, компьютеризация профессионально-трудовой деятельности принесла и проблемы.
Наша гипотеза полностью подтвердилась результатами исследования: большинство опрашиваемых согласились с тем, что компьютеризация профессионально-трудовой деятельности облегчает работу, развивает творческое мышление. Вместе с тем, негативно влияет на здоровье и нервную систему, возникает зависимость от компьютерной техники. Компьютерная неграмотность является основной проблемой среди большинства испытуемых. Новизна нашего исследования состоит в том, что мы создали методическое пособие для устранения проблемы компьютерной неграмотности. Это было второй целью нашего исследования, которая также была достигнута в ходе работы.
Созданная методичка несет в себе практическое значение: результаты нашего исследования могут быть использованы в разных сферах профессионально-трудовой деятельности, отдельными пользователями для устранения пробелов в знаниях программ MS Office и Интернет, на уроках информатики и других дисциплин, тесно связанных с компьютерными технологиями.
Таким образом, мы пришли к следующему выводу: компьютеризация – неизбежный процесс современного общества, поэтому мы должны научиться решать проблемы, которые он в себе несет.
СПИСОК ЛИТЕРАТУРЫ
Алгебра / Под ред. А.Г. Мордковича. М., 2013;
Алгебра и начала математического анализа 10-11 / Под ред. А.Л. Колмогоровым, А.М. Абрамовым, Ю.П. Дубницыным. М., 2008;
Интернет-ресурсы
http://plasma.karelia.ru/~ekostq/PUBLIC/IntSrIzm_NEW/page5/page2.html
http://www.follow.ru/article/117
http://seozar.ru/katalog-statej/moj-kompyuter/moj-kompyuter/0001/kompyuterizaciya-obshchestva-xxi-veka-plyusy-i-minusy.php
http://www.irbis.vegu.ru/repos/924/HTML/0015.HTM
http://book.kbsu.ru/theory/chapter9/1_9.html







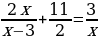
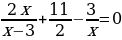
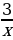 в левую часть уравнения с противоположным знаком.
в левую часть уравнения с противоположным знаком.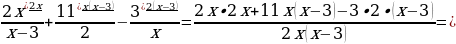
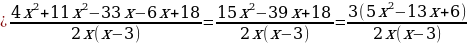
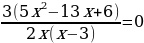
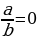 тогда и только тогда, когда одновременно выполняются два соотношения:
тогда и только тогда, когда одновременно выполняются два соотношения: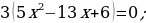
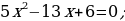
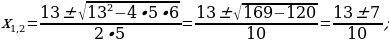
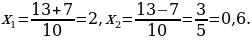
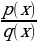 .
.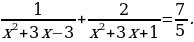
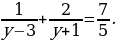
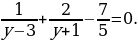
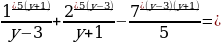
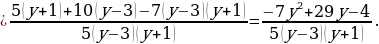
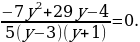
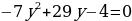 находим:
находим: 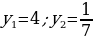 .
.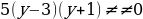 . Оба корня этому условию удовлетворяют.
. Оба корня этому условию удовлетворяют.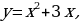 а y, как установили, принимает два значения: 4 и
а y, как установили, принимает два значения: 4 и 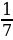 , ещё предстоит решить два уравнения:
, ещё предстоит решить два уравнения: 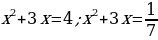 . Корнями первого уравнения являются
. Корнями первого уравнения являются 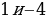 , а корнями второго числа
, а корнями второго числа 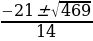 .
.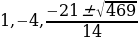 .
.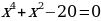
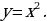 Так как
Так как 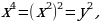 то заданное уравнение можно переписать в виде:
то заданное уравнение можно переписать в виде: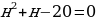
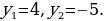
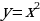 , значит, задача свелась к решению двух уравнений:
, значит, задача свелась к решению двух уравнений: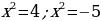
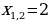 . Второе не имеет корней.
. Второе не имеет корней.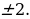
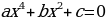 называют биквадратным уравнением («Би» два, т.е. как бы дважды квадратное уравнение).
называют биквадратным уравнением («Би» два, т.е. как бы дважды квадратное уравнение).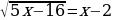 .
.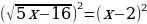 .
.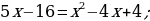
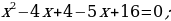
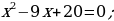
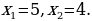
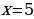 в уравнение, получим:
в уравнение, получим: 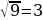 верное равенство. Подставим
верное равенство. Подставим 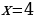 в уравнение, получим:
в уравнение, получим: 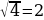 верное равенство. Следовательно, оба значения являются корнями уравнения.
верное равенство. Следовательно, оба значения являются корнями уравнения.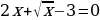
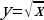 . Тогда получим:
. Тогда получим: 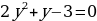 квадратное уравнение переменной y. Находим корни:
квадратное уравнение переменной y. Находим корни: 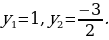
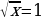 ;
; 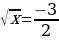 .
.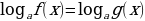 , где a положительное число, отличное от 1, и уравнения, сводящиеся к этому виду.
, где a положительное число, отличное от 1, и уравнения, сводящиеся к этому виду.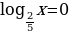 .
.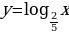

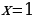 т.к. график функции
т.к. график функции 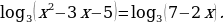
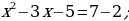
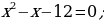
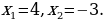
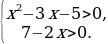
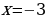 удовлетворяет обоим неравенствам системы, а потому
удовлетворяет обоим неравенствам системы, а потому 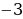
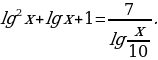
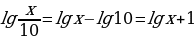 , то заданное уравнение можно переписать так:
, то заданное уравнение можно переписать так: 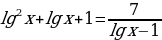 .
.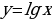 ; тогда уравнение примет следующий вид:
; тогда уравнение примет следующий вид: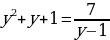 .
.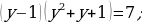
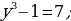
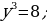
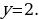
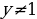 .
.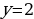 . Но
. Но 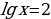 , откуда находим:
, откуда находим: 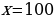 .
.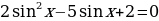
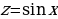 . Тогда уравнение примет вид
. Тогда уравнение примет вид 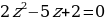 ,
,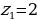 ,
, 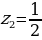 .
.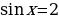 , либо
, либо 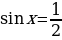 . Первое уравнение не имеет корней, а из второго находим:
. Первое уравнение не имеет корней, а из второго находим: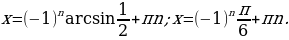
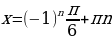 .
.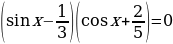 .
.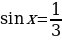 ;
; 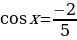 .
.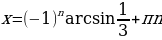 ;
; 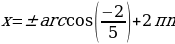 .
.









