Необратимость процессов в природе

Конспект урока "Первый закон термодинамики. Необратимость процессов в природе"

В одном из прошлых уроков мы выяснили следующее: изменить внутреннюю энергию тела можно путем совершения работы или путем теплопередачи. Сразу хотелось бы сказать, что первый закон термодинамики — это, фактически применение закона сохранения энергии к тепловым процессам. Напомним еще раз формулировку этого закона: никакая энергия не возникает и исчезает. Она переходит из одной формы в другую.

Таким образом, общее количество энергии в природе неизменно. В открытие закона сохранения энергии внесли вклад многие ученые, но, как правило, выделяют троих: открыли закон Роберт Маайер и Джеймс Джоуль (в честь которого названа единица измерения энергии), однако наиболее точную формулировку этому фундаментальному закону дал Герман Гельмгольц.

Итак, первый закон термодинамики гласит: изменение внутренней энергии системы тел при переходе из одного состояния в другое равно сумме работы внешних сил, совершенной над системой и количества теплоты, переданного этой системе:

Сразу заметим, что изменение внутренней энергии изолированной системы равно нулю. Действительно: на изолированную систему не действуют внешние силы, и изолированной системе не передается тепло. Довольно часто, при изучении первого закона термодинамики рассматривают не работу внешних сил над системой, а работу самой системы. Как мы уже убедились на прошлых уроках, работа внешних сил над системой равна работе системы с противоположным знаком. Тогда мы можем сформулировать закон несколько иначе: количество теплоты, которое получает система равно сумме изменения внутренней энергии системы и работы, совершаемой системой:

Исходя из первого закона термодинамики, можно заключить, что создание вечного двигателя невозможно. Под вечным двигателем подразумевается некий двигатель, способный совершать работу без потребления энергии от внешних источников. В этом случае, количество теплоты, которое получает система должно быть равно нулю. Тогда уравнение, описывающее первый закон термодинамики, преобразуется:

Из него мы видим, что вся работа в случае вечного двигателя должна совершаться за счет внутренней энергии. Поскольку внутренняя энергия рано или поздно иссякнет, двигатель рано или поздно перестанет работать.

Необходимо отметить, что на сегодняшний день все же существуют некие модели, похожие на вечный двигатель. Например, для его создания можно использовать колесо с полыми спицами. В эти спицы вставляются одинаковые цилиндрические магнитики, а по обе стороны от колеса ставятся большие постоянные магниты, повернутые разными полюсами к колесу.

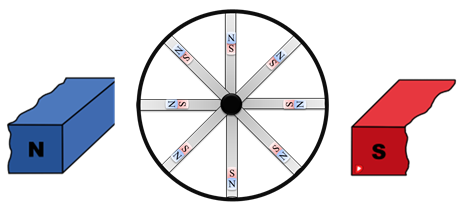
В результате, один магнит отталкивает магнитики внутри спиц, а другой — притягивает. Это приводит к смещению магнитиков на одну сторону, то есть к смещению центра тяжести. Таким образом, колесо может постоянно вращаться. Конечно, этот механизм тоже не будет работать вечно, поскольку магниты могут размагнититься, да и существует износ механических деталей. Существует множество подобных вариаций так называемых, вечных двигателей, которые работают, используя магнитные поля и силу притяжения. Однако, на сегодняшний день ни одна из таких моделей не признана действительно работающим вечным двигателем.

Еще один вопрос, который мы сегодня рассмотрим — это необратимость процессов в природе. Можно привести ряд примеров: скажем, яблоко может упасть с яблони, но оно никогда самопроизвольно не залетит обратно на яблоню. Котел, который мы нагреваем с помощью сжигания, дров не может внезапно начать отдавать энергию обратно дровам, а сам начать остужаться. Если вы вытопили печь, то она, несомненно, будет остывать, отдавая свое тепло дому. Не может произойти такого, чтоб вся комната начала остывать, а печка бы снова раскалилась. Если вы уроните стакан, то он вполне может разбиться о пол, но вот самопроизвольно восстановиться из осколков стакан не сможет. Можно продолжать приводить подобные примеры до бесконечности, но все они говорят нам о том, что макроскопические процессы в природе протекают в определенном направлении. В обратном направлении они могут протекать только в случае внешнего воздействия, но такие процессы уже нельзя будет назвать самопроизвольными. Отличной демонстрацией невозможности обратимости процессов может послужить практически любое видео в обратной перемотке. В соответствии с подобными наблюдениями, был сформулирован второй закон термодинамики. Мы используем формулировку Рудольфа Клаузиуса: невозможно перевести тепло от более холодной системе к более горячей при отсутствии других одновременных изменений в обеих системах или в окружающих телах.

Таким образом, второй закон термодинамики указывает направление протекания процессов, что уже говорит о том, что природные процессы необратимы.

Рассмотрим еще один пример, который позволяет статистически обосновать необратимость тепловых процессов.

Как вы знаете, находясь в сосуде газ занимает весь объем сосуда. Если отодвинуть поршень, увеличив объем, то газ, незамедлительно расширится. Но вот сжаться сам по себе он не сможет.

Чтобы газ самопроизвольно сжался нужно, чтобы все его молекулы оказались в одной половинке сосуда. Мы не будем сейчас объяснять, как рассчитывается вероятность такого события, а просто приведем числа:

Смело можно сказать, что эта вероятность практически нулевая. Да и без расчетов вы понимаете, что такие события никогда не происходят в реальности. Например, какова вероятность того, что пылинки в вашей комнате полностью покроют одну половину стола, а на другую половину не попадут вообще? Или какая вероятность того, что человек, случайно переставляющий шахматные фигуры, сможет обыграть Гарри Каспарова? Ответ на этот вопрос может быть только один: такие события попросту невероятны.

Одним из фундаментальных законов природы является закон сохранения и превращения энергии. Его частным случаем в применении к термодинамическим системам является первый закон (первое начало) термодинамики. С его помощью можно делать важные заключения о характере протекающих процессов. В этом видеоуроке мы поговорим о применении первого начала термодинамики к различным процессам, при которых одна из физических величин, характеризующих состояние идеального газа, остаётся неизменной.

Первый закон термодинамике имеет практическое применение к различным процессам в физике, например, позволяет вычислить идеальные параметры газа при разнообразных тепловых и механических процессах. Помимо сугубо практичного применение можно этому закону найти применение и философское ведь что ни говорите, но первый закон термодинамики является выражением одного из самых общих законов природы – закона сохранения энергии. Еще Еклезиаст писал, что ничто ни откуда не появляется и никуда не уходит, все пребывает вечно, постоянно трансформируясь, в этом и кроется вся суть первого закона термодинамики.

С помощью первого закона термодинамики можно делать важные заключения о характере протекающих процессов. Рассмотрим различные процессы, при которых одна из физических величин, характеризующих состояние газа, остаётся неизменной (то есть изопроцессы). Естественно, что для простоты мы будем считать газ идеальным одноатомным.

Пусть газ находится в цилиндрическом сосуде, закрытом неподвижным поршнем. Что произойдёт, если мы начнём подводить теплоту к газу? Если пренебречь тепловым расширением сосуда, то объём газа остаётся практически неизменным, хотя давление газа увеличивается. Следовательно, работа силы давления газа равна нулю. А это, согласно первому закону термодинамики, означает, что при изохорном процессе всё передаваемое газу количество теплоты идёт на увеличение его внутренней энергии:

Очевидно, что если теплота отводится от газа, то изменение внутренней энергии отрицательно и внутренняя энергия газа уменьшается.

Мы уже с вами знаем, что изменение внутренней энергии идеального одноатомного газа прямо пропорционально изменению его абсолютной температуры и не зависит от других макроскопических параметров системы:

Следовательно, при изохорном процессе количество теплоты также пропорционально изменению абсолютной температуры:

С другой же стороны, количество теплоты, переданное термодинамической системе, прямо пропорционально её массе и изменению абсолютной температуры:

В записанной формуле c_V — это удельная теплоёмкость газа при постоянном объёме. Давайте подставим записанное уравнение в предыдущую формулу:

Сократив полученное выражение на массу газа и изменение его температуры, получим, что удельная теплоёмкость газа при изохорном процессе обратно пропорциональна его молярной массе:

Теперь предположим, что наш сосуд с газом под поршнем находится в термостате (напомним, что это устройство, в котором поддерживается постоянная температура). Если теперь, например, мы с помощью внешнего устройства начнём медленно перемещать поршень в сосуде так, чтобы объём газа увеличивался, то работа силы давления расширяющегося газа будет положительной. При одинаковой первоначальной температуре термостата и газа теплопередачи не происходит. Положительная работа силы давления расширяющегося газа совершается за счёт уменьшения его внутренней энергии, а значит, и температуры. Но как только температура газа начинает уменьшаться, тут же возникает теплопередача от термостата газу. При медленном перемещении поршня в сосуде температура газа успевает выровняться, а реально происходящий процесс близок к изотермическому.

Значит, и внутренняя энергия идеального одноатомного газа остаётся постоянной, а её изменение равно нулю:

Отсюда следует, что при изотермическом процессе всё подведённое к газу количество теплоты идёт на совершение газом работы:

Если же внешнее устройство обеспечивает медленное уменьшение объёма газа в сосуде, то работа газа будет отрицательной. А это приводит к увеличению внутренней энергии и, следовательно, температуры газа. В результате возникает теплопередача от газа термостату.

Что касается теплоёмкости газа при изотермическом процессе, то она стремится к бесконечности (предлагаем вам самостоятельно доказать это):

Теперь предположим, что наш газ находится в цилиндрическом сосуде, закрытом поршнем, который может свободно перемещаться. Будем изобарно нагревать газ (напомним, что изобарный процесс — это процесс, протекающий при постоянном давлении). Очевидно, что в этом случае газ будет нагреваться, расширяться и совершать работу, то есть будет изменяться его внутренняя энергия. Следовательно, при изобарном процессе подведённое к газу количество теплоты частично расходуется на увеличение внутренней энергии системы и частично на совершение работы силой давления газа при его расширении:

Распишем величины, входящие в формулу, согласно их определению:

Величина c_p — это удельная теплоёмкость газа при постоянном давлении.

Преобразуем формулу для работы газа. Для этого запишем уравнение Клапейрона — Менделеева для двух его состояний (а мы вправе это сделать, так как масса газа и его химический состав в ходе процесса не изменялись):

Теперь вычтем из второго уравнения первое:

Сравнивая последнее уравнение с формулой для работы, находим, что работа газа прямо пропорциональна изменению его абсолютной температуры:

Перепишем первое начало термодинамики для изобарного процесса с учётом наших рассуждений:

Полученное равенство разделим на массу газа и изменение его температуры:

Сравнивая полученное равенство с выражением для удельной теплоёмкости газа при постоянном объёме, видим, что удельная теплоёмкость газа при постоянном давлении всегда больше его удельной теплоёмкости при постоянном объёме:

Это объясняется тем, что при постоянном давлении часть подводимой энергии расходуется на совершение силой давления газа работы при расширении.

Расширение жидких и твёрдых тел при нагревании при постоянном давлении значительно меньше, чем газов. Поэтому их работа при расширении намного меньше, чем изменение внутренней энергии. Следовательно, их удельные теплоёмкости слабо зависят от характера процесса (с_р ≈ с_V).

А теперь давайте представим, что мы смогли теплоизолировать цилиндр с газом и предоставили ему возможность самопроизвольно расширяться. Очевидно, что при этом газ будет совершать положительную работу. Но за счёт чего? Ведь теплообмен с окружающей средой отсутствует, то есть теплота не подводится (Q = 0).

Процесс, протекающий без теплообмена термодинамической системы с окружающей средой, называется адиабатным процессом.

Из первого закона термодинамики следует, что работа газа при адиабатном процессе совершаться только за счёт убыли его внутренней энергии:

Таким образом, при адиабатном расширении газ совершает работу и сам охлаждается. И наоборот, при адиабатном сжатии работа совершается над газом и он нагревается. А так как при адиабатном процессе количество теплоты равно нулю, то и удельная теплоёмкость газа также равна нулю:

На практике адиабатный процесс осуществляется главным образом не за счёт теплоизоляции (нельзя окружить систему оболочкой, которая абсолютно не допускает теплопередачи), а за счёт скорости протекания процесса. Например, когда вы открываете охлаждённую газировку, то можете заметить облачко тумана, которое растекается из горлышка бутылки. Объясняется это тем, что при адиабатном расширении происходит уменьшение температуры газа и, как следствие, происходит конденсация пара.

Адиабатный процесс, как и все изопроцессы, можно наглядно представить в виде графика зависимости давления газа от его объёма. График адиабатного процесса в координатах (p, V), называется адиабатой.

R= - молярная газовая постоянная

Вопрос 1. Приведите пример действия первого закона термодинамики.

Ответ. В качестве примера можно привести газ в сосуде. Если сообщить ему какое-то количество теплоты, оно пойдет на увеличение внутренней энергии газа в сосуде. 

Вопрос 2. Сформулируйте первый закон термодинамики.

Ответ. В любой изолированной системе запас энергии остается постоянным.

Вопрос 3. Как еще можно сформулировать первый закон термодинамики?

Ответ. Вот разные формулировки первого закона термодинамики:

1. Количество теплоты, полученное системой, идет на изменение внутренней энергии системы, а также на совершение работы против внешних сил.

2. Невозможен вечный двигатель первого рода (двигатель, совершающий работу без затраты энергии).

Вопрос 4. Что такое изопроцесс? Какие есть изопроцессы?

Ответ. По определению:

Изопроцесс – это термодинамический процесс, при котором один из параметров системы (давление, объем, температура, энтропия) остается неизменным.

Изопроцесс может быть:

• изотермическим (T=const);

• изобарным (P=const);

• изохорным (V=const);

• Адиабатическим (отсутствует теплообмен с окружающей средой).

Вопрос 5. При каком изопроцессе газ не совершает работу?

Ответ. При изохорном.