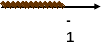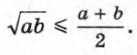Открытый урок по алгебре на тему:
«Неравенства с одной переменной»
8 класс
Цель урока: продолжить формирование умения решать неравенства с одной переменной путем перехода к равносильному неравенству
Планируемые образовательные результаты:
Предметные: знать понятия: «неравенство с переменной», «решение неравенства с переменной», «линейное неравенство», «равносильное неравенство», «равносильное преобразование неравенства», знать правила решения неравенств; уметь решать линейные неравенства и отображать множество его решений на координатной прямой.
Личностные: формирование ответственного отношения к успешной учебной деятельности.
Метапредметные:
регулятивные: уметь ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку;
коммуникативные: уметь формулировать свои мысли на математическом уроке, организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками;
познавательные: уметь выполнять упражнения по правилу, алгоритму, формулировать правило по многократно повторенному алгоритму
Тип урока: урок открытия нового знания
Оборудование: компьютер, проектор, интерактивная доска, презентация к уроку, раздаточный материал
Ход урока.
1. Самоопределение к деятельности (организационный момент)
Учитель проверяет готовность класса, приветствует детей, высказывает добрые пожелания детям; предлагает пожелать друг другу удачи, озвучивает эпиграф к уроку:
«Математика учит преодолевать трудности и исправлять собственные ошибки» (Декарт)
Учитель сообщает о раздаточном материале: Оценочный лист, карточки для графического диктанта
Предлагает проверить домашнюю работу с соседом по парте. Обучающиеся проверяют работу, исправляют ошибки (если есть), обращаются к классу, если нет единства в решении.
2. Актуализация знаний и способов действий
Учитель предлагает выполнить графический диктант. До начала диктанта, если необходимо, то на нижней строчке карточки для графического диктанта пронумеровать номера вопросов от 1 до 10 (для удобства)
Графический диктант
Выясните, верны ли утверждения. Если утверждение верное, то заполните клеточку так
 , если же утверждение неверное, то так
, если же утверждение неверное, то так  .
.
Главное требование: каждый следующий ответ должен начинаться в клетке так, чтобы в результате получился именно непрерывный графический рисунок.
Верно ли утверждение, что если x 5 и y -3, то x+y 2?
Является ли неравенство 2х – 15 4х + 7 строгим?
Принадлежит ли отрезку [- 6; - 2] число -6,5?
Является ли число -5 решением неравенства 4+2х 0?
Верно ли, что решением неравенства 5х – 1 24 является x Î (5; +¥)?
Верно ли, что решением неравенства 3х £ 5 является x Î (- ¥; 2]?
Изображением решения неравенства 5х 30 служит 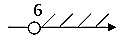 ?
?
Верно ли, что неравенству x 3,2 соответствует открытый числовой луч
(3,2; +¥) ?
Существует ли целое число, принадлежащее отрезку [-3,9; -3,5]?
При любом ли значении переменной a верно неравенство а² +2 0?
Один из учеников выходит к доске и изображает получивший графический рисунок
Правильный ответ
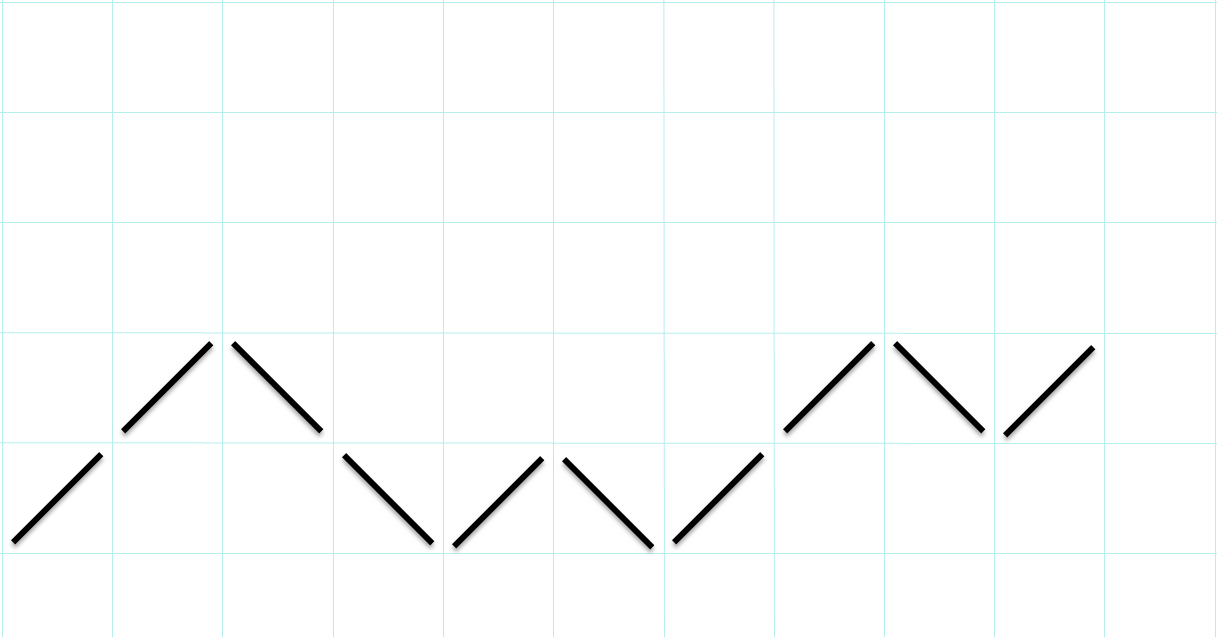
Учитель просит обучающихся посчитать количество верных ответов в выполненном графическом диктанте и занести набранное количество баллов в свой оценочный лист (за каждый правильный ответ – 0,5 балла)
Учитель предлагает выполнить задания устного характера, за каждый правильный ответ обучающиеся получают 1 балл.
Устный счет
Укажите все целые числа, принадлежащие полуинтервалу [-5; 3) (-5; -4; -3; -2; -1; 0; 1; 2)
Укажите какое-либо число из интервала (-5,6 ; -5,1)
Принадлежит ли отрезку [-2; 15] число 14,99? (да)
Укажите наименьшее целое число, являющееся решением неравенства 8 – 2х (5)
Является ли число - 5,2 решением неравенства -3х+5 ≤ - 4 ? (нет)
При каких значениях х выражение 2х – 1 принимает положительные значения? (при x 0,5)
Найди ошибку
1. Х Ответ: (-∞;9]
2. y ≤ 5,5 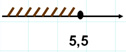 Ответ: [-∞;5,5]
Ответ: [-∞;5,5]
3. n -2 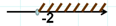 Ответ: (-∞;-2]
Ответ: (-∞;-2]
4. k ≤ -2,1 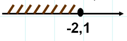 Ответ: (-∞; -2,1)
Ответ: (-∞; -2,1)
3. Определение и поставка учебных задач
В тетрадях записывают дату, классная работа.
На интерактивной доске появляется задание
Решить неравенство
4(2 - 5х) – 3(4 + х) 18 – х
Что это за неравенство?
Чем неравенство отличается от тех, что вы умеете решать?
Учитель предлагает определить тему урока
Озвучивают и записывают тему урока «Решение неравенств с одной переменной»
Предлагает определить цель урока
Цель: продолжить формирование умения решать неравенства с одной переменной путем перехода к равносильному неравенству
4. Усовершенствование знаний, умений
Вопросы
– Дайте определение решения неравенства с одной переменной.
– Что значит «решить неравенство»?
– Какие неравенства называются равносильными?
– Сформулируйте свойства равносильности неравенств, используемые при решении неравенства с одной переменной.
Учитель возвращает к неравенству, предлагает составить устно алгоритм решения и решить на доске (один ученик у доски, остальные в тетрадях). Ученик у доски и досрочно выполнившие в тетради ученики получают баллы (максимальное 3)
4(2 - 5х) – 3(4 + х) 18 – х
8 - 20х – 12 – 3x 18 – х
- 20х – 3x + x 18 – 8 +12
- 22х 22
х -1
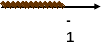
Ответ: х Î (- ¥; -1)
Разминка Игра в домино (на каждую парту выдаются карточки с домино, для удобства проверки учителем карточки цветные)

В парах обучающиеся составляют верную игру, учитель проверяет, выставляет баллы (максимальный 3 балла)
5. Физкультминутка, включающая специальную гимнастику для
глаз.
Цель: снятие зрительного утомления.
1 Вертикальные движения глаз вверх-вниз.
2 Горизонтальное вправо-влево.
3 Вращение глазами по часовой стрелке и против.
4 Закрыть глаза и представить по очереди цвета радуги как можно
отчётливее.
5 Глазами« нарисовать» 8 и знак бесконечности несколько раз, сначала в одном, а затем в другомнаправлении.
Учитель предлагает решить тринадцатое задание ОГЭ (самостоятельно)
| Решите неравенство: 6х-2(2х+9) 6x-4x-18x-18 2x 2x x 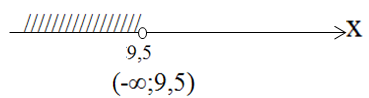
| Варианты (ответа) 1.[-8,5;+∞) 2.[9,5; ∞) 3.(-∞;9,5) 4.(-∞;-8,5] Ответ: 3 |
За первый правильный ответ обучающийся получает 3 балла
5.Исторические сведения о неравенствах
Понятия «больше» и «меньше» наряду с понятием равенства возникли в связи со счётом предметов и необходимостью сравнивать различные величины. Понятиями неравенства пользовались уже древние греки. Архимед, занимаясь вычислением длины окружности, установил, что «периметр всякого круга равен утроенному диаметру с избытком, который меньше седьмой части диаметра, но больше десяти семьдесят первых». Иначе говоря, Архимед указал границы числа π:
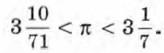
Ряд неравенств приводит в своём знаменитом трактате «Начала» Евклид. Он, например, доказывает, что среднее геометрическое двух положительных чисел не больше их среднего арифметического, т. е. что верно неравенство
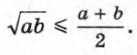
В «Математическом собрании» Паппа Александрийского (III в.) доказывается, что для положительных чисел а, b, с и d
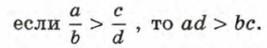
Однако все эти рассуждения проводили словесно, опираясь в большинстве случаев на геометрическую терминологию. Современные знаки неравенств появились лишь в XVII—XVIII вв. Знаки ввёл английский математик Т. Гарриот (1560—1621), знаки ≤ и ≥ — французский математик П. Буге (1698—1758).
6. Подведение итогов урока. Рефлексия
В качестве рефлексии учитель предлагает составить синквейн к уроку (на обратной стороне оценочных листов)
«Синквейн»
Это способ творческой рефлексии, который позволяет в художественной форме оценить изученное понятие, процесс или явление. В данном случае информация не только более активно воспринимается, но и систематизируется, и оценивается. Слово происходит от французского “5”. Это стихотворение из 5 строк, которое строится по правилам:
1 строка – тема или предмет (одно существительное);
2 строка – описание предмета (два прилагательных);
3 строка – описание действия (три глагола);
4 строка – фраза, выражающая отношение к предмету;
5 строка – синоним, обобщающий или расширяющий смысл темы или предмета (одно слово).
Обучающиеся по желанию могут зачитать свой синквейн классу.
Обучающиеся подсчитывают полученное количество баллов на оценочных листах, переводят в оценки. Сдают оценочные листы учителю для выставления оценок в журнал.
6. Постановка домашнего задания
Повторить правила решения неравенств
№ 842 (а,б), № 843 (б), № 845, № 847 (в, г),
Список использованной литературы:
1. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова «Алгебра. 8 класс». учебник для общеобразовательных учреждений, под ред. С.А. Теляковского. –– М.: Просвещение, 2014 г.
2. Алгебра 8 класс. Задания для обучения и развития учащихся. Учебное пособие / Лебединцева Е.А., Беленкова Е.Ю. – М.: Интеллект-Центр, 2013 г.
3. Брадис В.М., Минковский В.Л., Харчева А.К. Ошибки в математических рассуждениях. Москва: Государственное учебно-педагогическое издательство министерства просвещения РСФСР, 1959.
4. Открытый банк заданий ФИПИ (http://oge.fipi.ru/)
Оценочный лист
Учени _________________________________________
«5» - 15 баллов и выше
«4» - 11 - 14 баллов
«3» - 7-10 баллов
| № | Вид работы | Количество баллов |
| 1. | Графический диктант |
|
| 2. | Устный счет |
|
| 3. | Домино |
|
| 4. | Решение упражнений |
|
| 5. | Работа в группе |
|
«Синквейн»
Это способ творческой рефлексии, который позволяет в художественной форме оценить изученное понятие, процесс или явление. В данном случае информация не только более активно воспринимается, но и систематизируется, и оценивается. Слово происходит от французского "5”. Это стихотворение из 5 строк, которое строится по правилам:
1 строка – тема или предмет (одно существительное);
2 строка – описание предмета (два прилагательных);
3 строка – описание действия (три глагола);
4 строка – фраза, выражающая отношение к предмету;
5 строка – синоним, обобщающий или расширяющий смысл темы или предмета (одно слово).
Графический диктант








 , если же утверждение неверное, то так
, если же утверждение неверное, то так  .
. 
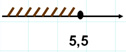 Ответ: [-∞;5,5]
Ответ: [-∞;5,5]