НЕСТАНДАРТНЫЕ ЗАДАЧИ КАК СРЕДСТВО РАЗВИТИЯ ДЕЦЕНТРАЦИИ МЛАДШЕГО ШКОЛЬНИКА
Децентрация - признание того, что мнение ребенка не является абсолютным, что его восприятие объекта, ситуации, отношений субъективно. В психологической литературе о децентрации говорится и как о результате преодоления эгоцентрической позиции (Ж. Пиаже, Л.Ф. Обухова и др.) и как о механизме (Т.И. Пашукова) преодоления этой позиции. Природа децентрации носит социальный и биологический характер, так, по мнению Ж. Пиаже, децентрация возможна, во-первых, при взаимодействии ребенка с другими людьми; во-вторых, при созревании интеллектуальных структур.
Согласно точки зрения психологов (Л.С. Выготского, Д.Б. Эльконина, П.Я. Гальперина, Ж.Пиаже и др.) можно ускорить процесс децентрации с помощью обучения. Большие возможности для развития децентрации дает математика, в которой значительное место отдается вопросам формирования у младших школьников умения решать задачи, в том числе и нестандартного вида.
В данной статье нам хотелось бы осветить некоторые положения относительно использования нестандартных задач в развитии децентрации младшего школьника.
Анализ педагогической и методической литературы показал, что вопросами работы с нестандартными задачами занимались Т.Е. Демидова, Ю.М. Колягин, Л.Л. Николау, Е.Е. Останина, Ж. Пойа, А.П. Тонких, Е.Н. Турецкий, Л.И. Фридман и др.
В методической литературе существует две точки зрения на определение понятия нестандартной задачи. Л.М. Фридман, Г.Г. Левитас и др.) под нестандартной задачей считают такую, для которой в курсе математики не имеется общих правил и положений, определяющих точную программу ее решения [3], тематика которой не является сама по себе объектом изучения [4]. А.П. Тонких и др. отмечают относительность нестандартной задачи, которая является нестандартной до тех пор, пока учащиеся не овладели способами ее решения [2]. При этом обе стороны согласны, что содержание задачи не сковывают ученика жесткими рамками одного решения, то есть существует возможность рассмотреть задачу с различных точек зрения, что будет способствовать процессу децентрации.
А.П. Тонких, Т.Е. Демидова выделяют следующие виды нестандартных задач: принцип Дирихле, инвариант, магические фигуры, лабиринты [2].
Принцип Дирихле. Пусть дано п классов и т предметов. Если т n, то при отнесении каждого из m предметов к одному из п классов хотя бы в один класс попадет не менее двух предметов.
Пример. В мешке лежат шарики двух разных цветов: черного и белого. Какое наименьшее число шариков нужно вынуть из мешка вслепую так, чтобы среди них оказались два шарика одного цвета?
Инвариант. Главная идея применения: берутся некие объекты, над которыми разрешено выполнять определенные операции, и задается вопрос: «Можно ли из одного объекта получить другой при помощи этих операций?». Чтобы ответить на него, строят некоторую величину, которая не меняется при указанных операциях. Если значения этой величины для двух указанных объектов не равны, то ответ на заданный вопрос отрицателен.
Пример. На доске написано 11 чисел - 6 нулей и 5 единиц. Предлагается 10 раз подряд выполнить такую операцию: зачеркнуть любые два числа и, если они были одинаковы, дописать к оставшимся числам один ноль, а если разные - единицу. Какое число останется на доске?
Главное в решении задач на инвариант - придумать сам инвариант. В этом примере инвариант — это четность суммы написанных чисел.
Магические фигуры. Магические фигуры делятся на плоские и пространственные, на магические квадраты, треугольники, прямоугольники, многоугольники, круги, кубы. Магические (волшебные) квадраты - квадратные таблицы натуральных чисел (с одинаковым количеством строк и столбцов), имеющие одну и ту же сумму чисел по всем строкам, столбцам и диагоналям. Существуют различные классификации магических квадратов: в зависимости от прогрессии, арифметические и геометрические; в зависимости от числа клеток вдоль противоположных его сторон - нечетные (3, 5, 7, 9 и т.д.), нечетно-четные (6, 10, 14, 18 и т.д.) и четно-четные (4, 8, 12, 16 и т.д.); в зависимости от расстановки чисел в квадрате - магические обычные, магические с особыми свойствами и сверхмагические (супермагические).
Лабиринты – сооружения разнообразной формы и устройства, со сложным и запутанным планом. Методами решения (т.е. маршрута, ведущего к цели) являются: метод проб и ошибок, метод зачеркивания тупиков, алгоритмом (правилом) одной руки.
Метод проб и ошибок. Выбирайте любой путь, а если он заводит в тупик, то возвращайтесь назад и начинайте все сначала.
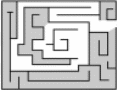 Метод зачеркивания тупиков. Необходимо последовательно зачеркивать тупики, т.е. маршруты, не имеющие ответвлений и заканчивающиеся перегородкой.
Метод зачеркивания тупиков. Необходимо последовательно зачеркивать тупики, т.е. маршруты, не имеющие ответвлений и заканчивающиеся перегородкой.
Рис. 1.
Незачеркнутая часть коридоров будет выходом или маршрутом от выхода к выходу или к центру (рис. 1).
Алгоритм (правило) одной руки. Идите по лабиринту, не отрывая правой (или левой) руки от стены лабиринта. Алгоритм позволяет найти решение лабиринта, стены которого хоть и имеют сложные повороты или изгибы, но составляют непрерывное продолжение наружной стены.
| 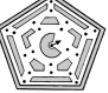 
Рис.2. | Пример. Комендант крепости, проверяя посты, выходит из центрального помещения и, обойдя посты, возвращается обратно. Каким должен быть его маршрут, |
чтобы побывать у каждого часового и дважды по одному и тому же пути не проходить? Рис.2.
Арифметические лабиринты представляют собой частный случай числовых лабиринтов. Они, как правило, имеют вид концентрических кругов с воротами, у которых стоят числа. Для того чтобы дойти до центра, нужно получить стоящее в центре число. Арифметические лабиринты могут требовать для своего решения или одного действия (обычно сложения), или нескольких.
В решении нестандартных задач Е.Ю. Лавлинскова выделяет три основных метода: аналитический, синтетический, аналитико-синтетический [1]. Аналитический метод представляет собой стройную логическую цепь заключений, органически связанных между собой. В основе метода лежит умение строить дедуктивные рассуждения (от общего к частному).
Пример Числовой треугольник. В кружках этого треугольника расставь девять цифр так, чтобы сумма их на каждой стороне составляла 20.
Сущность синтетическою метода поиска решения задачи состоит в установлении связей между данными условия задачи и получении новых данных, между которыми также устанавливаются связи до тех пор, пока не будет получено требуемое. В основе метода решения лежит умение строить индуктивные рассуждения. В начальной школе возможно использование двух видов индукций: полной (когда частные посылки исчерпывают все возможные случаи) и неполной.
Аналитико-cинтетический анализ задачи состоит в том, что мы предполагаем её уже решенной и находим различные следствия этого решения, а затем в зависимости от вида этих предположений, пытаемся найти путь отыскания решения поставленной задачи.
Пример. Беседуют трое друзей: Белокуров, Рыжов и Чернов. Брюнет сказал Белокурову: «Любопытно, что один из нас блондин, другой брюнет, третий - рыжий, но ни у кого цвет волос не соответствует фамилии». Какой цвет волос у каждого из друзей?
| 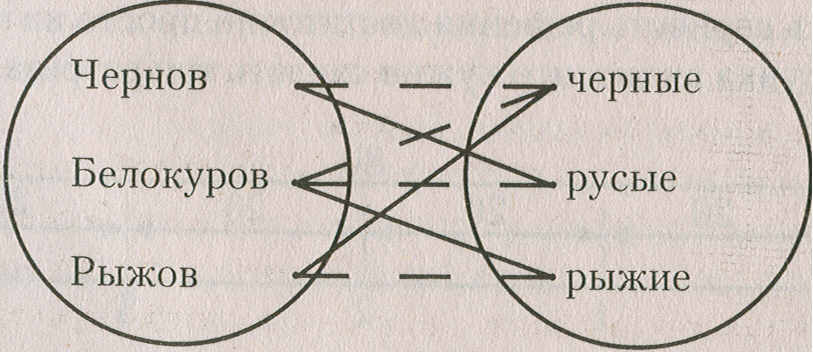 Рис. 3. | Для решения задачи можно воспользоваться таблицей, отмечая по горизонтали фамилии, а по вертикали - цвета волос беседующих или графиками: элементы множеств |
изображают точками плоскости, соответствие между множествами будем соединять сплошной линией, несоответствие - пунктирной линией (рис.3).
По мнению Л.М. Фридмана, процесс решения любой нестандартной задачи состоит в последовательном применении двух основных операций: сведение (преобразование, переформулирование) нестандартной задачи к другой, ей эквивалентной, но уже стандартной; разбиение нестандартной задачи на несколько вспомогательных стандартных подзадач [3].
По мнению Л.Л. Николау эффективным является прием моделирования, при котором учащиеся используют различные символы и образы [5]. Пример. На детской площадке 8 двух - трехколесных велосипедов. Всего у них 21 колесо. Сколько двух - и сколько трехколесных велосипедов на площадке?
Используя символы, обозначим велосипеды - ▲, а колеса велосипеда -2 кружками (рис. 4).
| ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | | °° | °° | °° | °° | °° | °° | °° | °° |
| | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | | °°° | °°° | °°° | °°° | °°° | °° | °° | °° |
|
| Рис.4. | Рис. 5. |
Мы использовали 16 колес, осталось 5 колес. Для того, чтобы найти число трехколесных велосипедов дорисуем по одному колесу к уже имеющимся 2 колесам, начиная с первого треугольника (рис. 5). Ответ: 5 трехколесных и 3 двухколесных велосипеда.
Говоря о формах работы над данными задачами особое внимание надо уделить групповой форме как наиболее эффективной, так как она позволяет организовать взаимодействие мнений сверстников - кооперацию. При кооперировании возникает потребность приспособиться к другому лицу. Столкновение собственной мысли с чужой вызывает сомнение и необходимость доказательства, таким образом происходит осознание существования других точек зрения, то есть децентрация.
Таким образом, ссылаясь на все вышесказанное можно утверждать, что нестандартные задачи можно использовать для децентрации детей.
Литература
Лавлинскова Е.Ю. Методика работы с задачами повышенной трудности в начальной школе. - Волгоград: «Панорама», 2006.-112 с.
Теория и практика решения текстовых задач. Учеб. пособие для вузов. /Под ред. Т.Е. Демидова, А.П. Тонких.- М.: Академия, 2002. - 285с.
Фридман Л. М., Турецкий Е.Н. Как научиться решать задачи. - М.: Просвещение, 1989. -192 с.
Левитас Г.Г.. Нестандартные задачи в курсе математики начальной школы. // «Начальная школа». – 2001. - №5. - С.61.
Николау Л.Л. 3адачи повышенной трудности.// «Начальная школа». – 1998. - № 7. - С. 55.






 Метод зачеркивания тупиков. Необходимо последовательно зачеркивать тупики, т.е. маршруты, не имеющие ответвлений и заканчивающиеся перегородкой.
Метод зачеркивания тупиков. Необходимо последовательно зачеркивать тупики, т.е. маршруты, не имеющие ответвлений и заканчивающиеся перегородкой.












