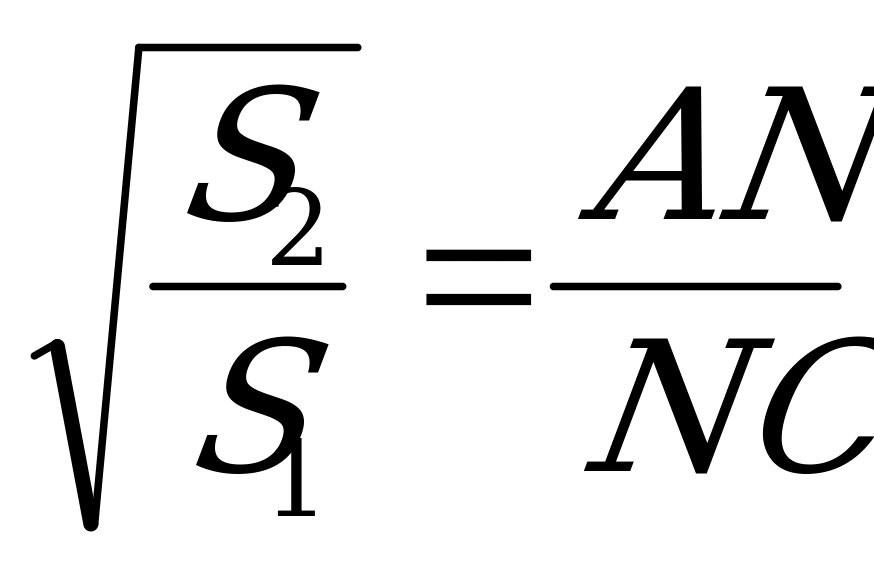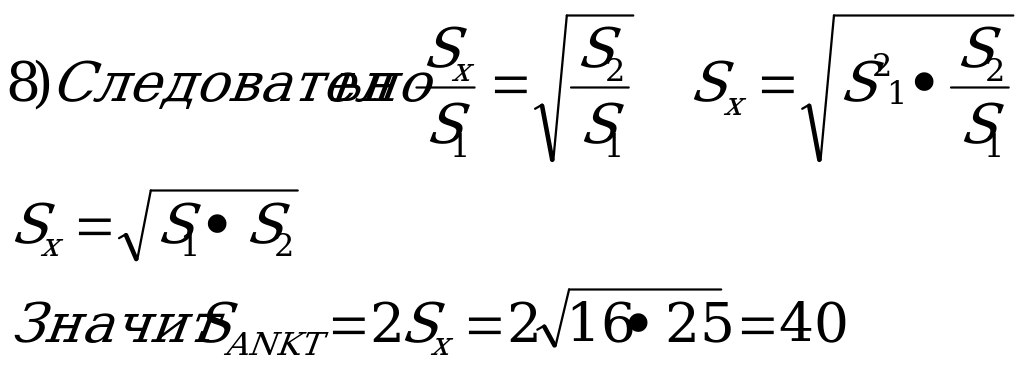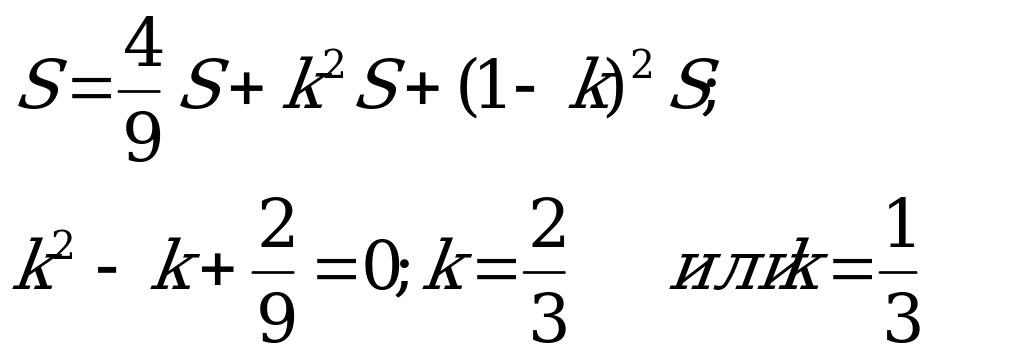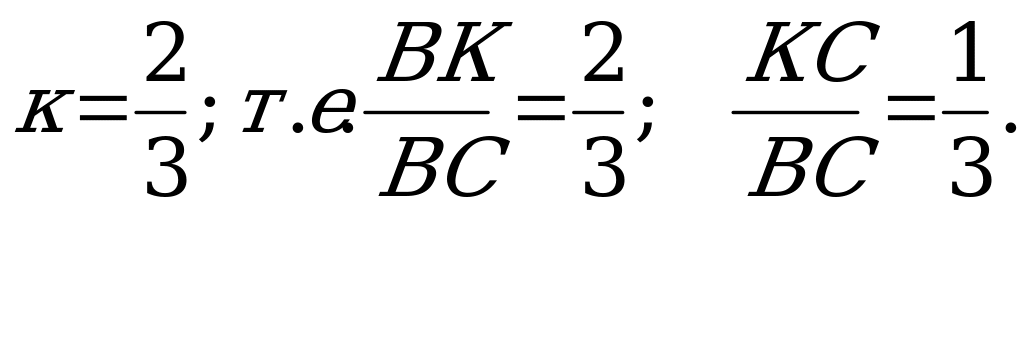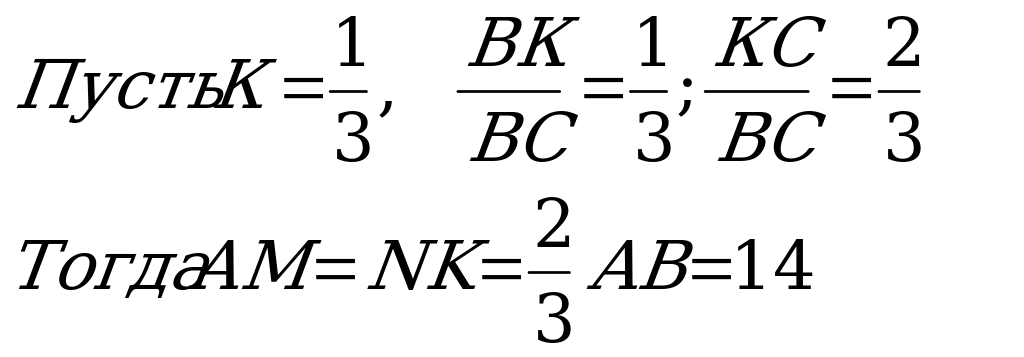24
Слет научных обществ обучающихся
образовательных организаций общего и дополнительного образования
города Нижневартовска в 2018-2019 учебном году
Секция 5. Прикладная математика.
Проектно-исследовательская работа
«Нетривиальные идеи и методы»
Автор проекта:
Русских Виктория Владимировна,
ученица 8Б класса
муниципальное бюджетное общеобразовательное учреждение
«Средняя школа №12».
Руководитель проекта:
Латыпова Зугура Минигалимовна,
учитель математики,
муниципальное бюджетное общеобразовательное учреждение
«Средняя школа №12».
Нижневартовск
2019
Проектно-исследовательская работа
«Нетривиальные идеи и методы»
Русских Виктория Владимировна, муниципальное бюджетное общеобразовательное учреждение «Средняя школа №12», ученица 8Б класса.
Аннотация
Цель работы: Изучить использование в планиметрических задачах метод дополнительных построений как специальный метод решения этих задач.
Задачи:
Исследовать и показать нетривиальные идеи решения задач, используя метод дополнительных построений различной конструкции.
Используя интерактивную программу GeoGebra и проводить исследования при перемещении объектов и изменении параметров.
Проанализировать и систематизировать полученную информацию.
Создать с помощью программы « Geogebra» электронное пособие и чертежи для показа через интерактивную доску.
Методы реализации проекта: анализ литературы; систематизация материала; метод дополнительного построения, метод подобия, метод площадей, преобразования и конструкция задач.
Гипотеза исследования: метод дополнительного построения могут успешно применяться при решении планиметрических задач.
Практическая ценность работы: решение задач из ОГЭ, задач олимпиадного характера, развитие творчества.
Планируемый результат реализации проекта: повышение интереса подростков к изучению предмета; приобретение навыков проектно-исследовательской деятельности; создание электронного пособия по геометрии для подготовки к ОГЭ.
Сфера применения результатов проекта: материал исследовательской работы может быть использован на уроках и элективных курсах по математике, в процессе самостоятельной учебной деятельности обучающихся при подготовке к сдаче ОГЭ, ЕГЭ.
Проектно-исследовательская работа
«Нетривиальные идеи и методы»
Русских Виктория Владимировна, муниципальное бюджетное общеобразовательное учреждение «Средняя школа №12», ученица 8Б класса
ПЛАН ИССЛЕДОВАНИЙ
Планиметрия охватывает большой класс задач. При решении задач проводят их классификацию по темам, выделяют ключевые задачи. Для поиска решения задачи при изучении геометрии, используют метод прямого решения, метод сравнения, метод подобия, метод дополнительных построений, метод площадей и др.
В проектной работе я исследовала и решила задачи, требующие нетривиальные идеи, метод дополнительных построений, метод площадей, метод подобия. Решая такую задачу, нужно в первую очередь проанализировать предложенную в задаче конфигурацию и увидеть те свойства, которые необходимы при решении.
Актуальность проекта заключается в знакомстве учащихся с методами решения геометрических задач, выделению в них общих подходов и методов, их теоретическое осмысление и обоснование, решение задач несколькими способами. Нетривиальные задачи требуют от решающего достаточно большого опыта, изобретательности, геометрической интуиции и использование в таких задачах дополнительных построений можно рассматривать, как специальный метод решения этих задач. Знание методов решения геометрических задач позволяет решать, казалось бы, сложные математические задачи просто, понятно и красиво.
Объект исследования: планиметрические задачи.
Предмет исследования: нетривиальные идеи решения планиметрических задач, основанных на методе дополнительного построения.
Методы исследования: анализ литературы; систематизация материала; метод сравнения, метод площадей, метод дополнительного построения, преобразования и конструкция задач. При работе над проектом я пользовалась материалом из книг, журналов, использовал Интернет - ресурсы.
Гипотеза исследования: метод дополнительного построения могут успешно применяться при решении планиметрических задач.
Цель исследования: Изучить использование в планиметрических задачах метод дополнительных построений как специальный метод решения этих задач.
Для достижения поставленной цели предусматриваю решение следующих задач:
Исследовать и показать, что нетривиальные идеи решения задач, используя метод дополнительных построений различной конструкции.
Используя интерактивную программу GeoGebra и проводить исследования при перемещении объектов и изменении параметров.
Проанализировать и систематизировать полученную информацию.
Создать с помощью программы « Geogebra» электронное пособие и чертежи для показа через интерактивную доску.
Новизна исследования для меня состоит в том, что я изучила компьютерную программу GeoGebra, и с помощью этой программы научилась решать более сложные планиметрические задачи с различными идеями.
Продукт исследования: создание электронного пособия по геометрии для подготовки к ОГЭ.
Практическая значимость работы решение задач из ОГЭ, задач олимпиадного характера, развитие творчества. На основе этой работы можно в дальнейшем провести урок для своих одноклассников. В действительности заинтересовать учащихся, привить любовь к математике.
Содержание
Введение 2 стр
Глава 1. Теоретический материал (приложение 1)
Глава II. Нетривиальные идеи и методы
2.Метод дополнительных построений .…………………………..……………….……3 стр.
2.1. Конструкция 1. О точке на стороне и двух параллельных………….................3 -5 стр.
2.2. Конструкция 2. Удвоение медианы……………………………………………….5 - 6 стр.
2.3. Конструкция 3. Трапеция и прямая параллельная диагонали или боковой
стороне………………………………………………………………………………….6 - 7 стр.
3.Метод подобия…………………………………………………………………………7 стр.
3.1. Конструкция 4. Свойство биссектрисы внутреннего и внешнего угла треугольника…… ……………………………………………………………………..7 -- 8 стр
3.2. Конструкция 5. Пересекающие отрезки в треугольнике…………………….. 8 - 10 стр
Заключение.............................................................................................................11 стр
Литература…………………………………………………………………………12 стр.
Приложения
1.Теоретический материал………………………………………………13- 14 стр.
2. Подбор задач ОГЭ 2018 – 2019 г……………………………………………………...15 стр
Проектно-исследовательская работа
«Нетривиальные идеи и методы»
Русских Виктория Владимировна, муниципальное бюджетное общеобразовательное учреждение «Средняя школа №12», ученица 8Б класса.
Научная статья
Введение
Планиметрия охватывает большой класс задач. В геометрической задаче главную роль играет чертеж, являющийся средством создания геометрического образа по словесному описанию. Существует целый класс таких задач, к которым традиционные методы (метод прямого решения, метод цепочек равных треугольников, метод геометрических преобразований и др.) либо вовсе не применимы, либо дают сложные и громоздкие решения. В геометрии существует целый класс задач, решение которых предполагает преобразование геометрического чертежа Во многих случаях решать такого рода задачи помогает введение в чертеж дополнительных линий – так называемое дополнительное построение. В одних случаях эти построения напрашиваются сами собой, в других они не так очевидны и требуют от решающего достаточно большого опыта,изобретательности, геометрической интуиции.
Так, чертеж данной в задаче фигуры можно достраивать до фигуры другого типа, можно с многоугольной фигурой связывать окружность, а можно целью дополнительного построения ставить выделение на чертеже равных, равновеликих или подобных фигур.
В проектной работе я исследовала и решила задачи, требующие нетривиальные идеи, метод дополнительных построений, метод подобия. Решая такую задачу, нужно в первую очередь проанализировать предложенную в задаче конфигурацию и увидеть те свойства, которые необходимы при решении. В результате удается построить несколько чертежей, удовлетворяющих условию задачи, выявлять различные ситуации которые соответствуют одному и тому же условию, но приводят к различным решениям.
Так как в небольшой работе достаточно сложно описать все методы решения задач данного класса, то цель моей работы – сформулировать некоторые приемы решения таких задач и продемонстрировать их на конкретных примерах.
Глава II. Нетривиальные идеи и методы
Суть метода дополнительных построений заключается в том, что чертеж к задаче, на котором трудно заметить связи между данными и искомыми величинами, дополняется новыми (вспомогательными) элементами, после чего эти связи становятся более ощутимыми или даже очевидными. Существуют задачи, в которых дополнительное построение определяет единственный способ решения; в них решение. В других задачах используется смешанный прием решения, когда дополнительное построение реализует лишь часть решения. В третьих задачах оно применяется как один из возможных методов наряду с другими. Часто решающий задачу интуитивно использует дополнительное построение, но, не выделяя его как метод, может не увидеть целесообразности его применения в других, более сложных или даже аналогичных задачах.
2. Метод дополнительных построений
2.1. О точке на стороне и двух параллельных
| Конструкция 1. 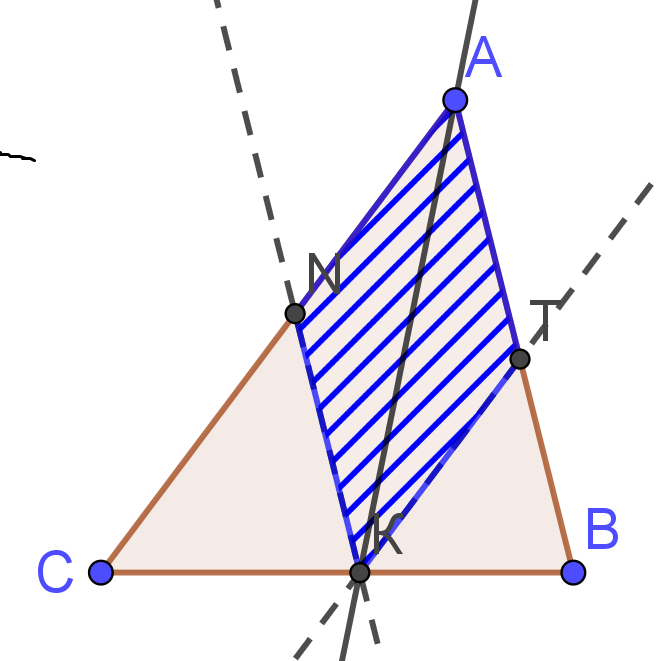 | В треугольнике ABC: точка K движется по стороне BC; из нее проведены KN || AB и KT || AC (рис. 1). В результате получены два треугольника BTK и CNK, подобные данному треугольнику ABC (по двум углам), а также параллелограмм ANKT. Данная конструкция заслуживает внимания, имеет ряд интересных и полезных закономерностей. |
| Задача 1. Площади треугольников CNK и BTK соответственно равны 16 и 25. Найдите площадь параллелограмма ANKT. |
| 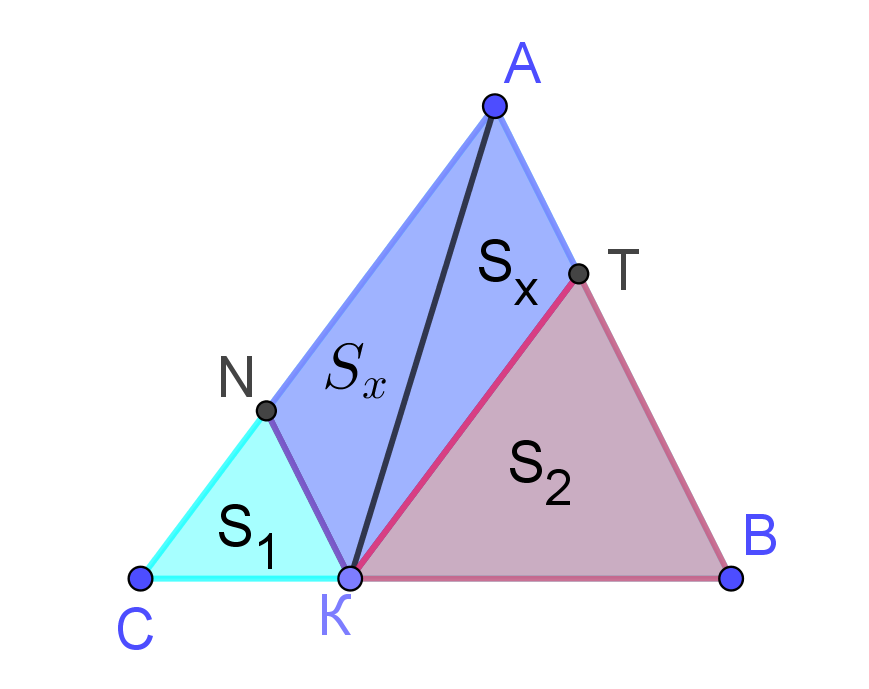 | 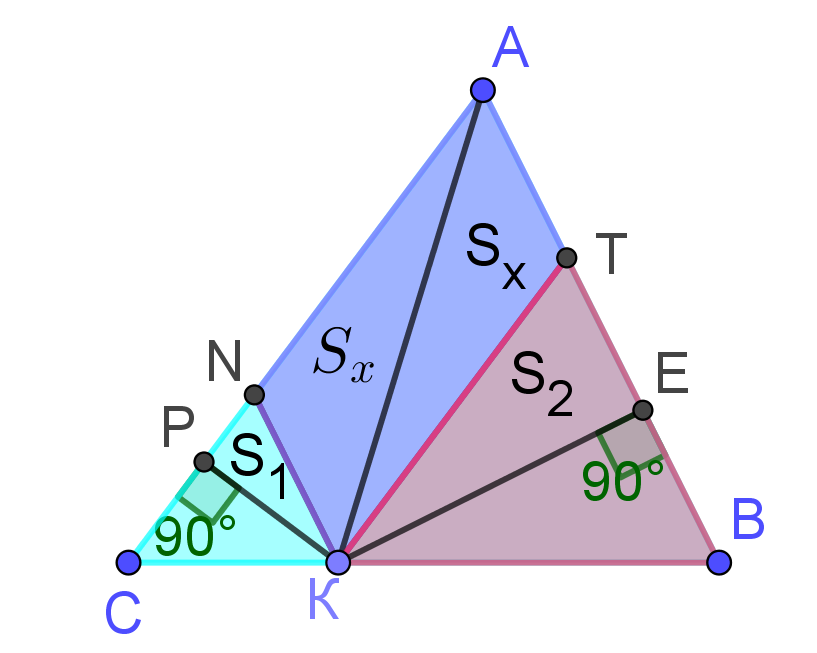 |
| Решение. 1)Проведем в параллелограмме ANKT диагональ AK и обозначим каждую из половинок образовавшихся площадей через Sх. 2. Проведем из точки К перпендикуляры к сторонам АС и АВ. 3.КЕ┴ АВ, является высотой треугольников КТВ и АКТ. 4. КР┴АС, является высотой треугольников CKN и AKN. 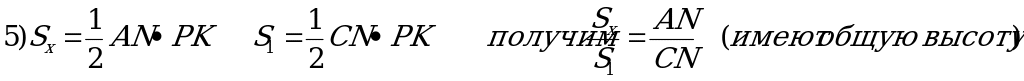 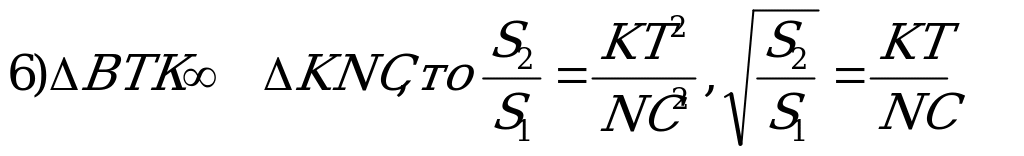 (как квадраты соответствующих линейных размеров) (как квадраты соответствующих линейных размеров) 7. Так как КТ = АN, то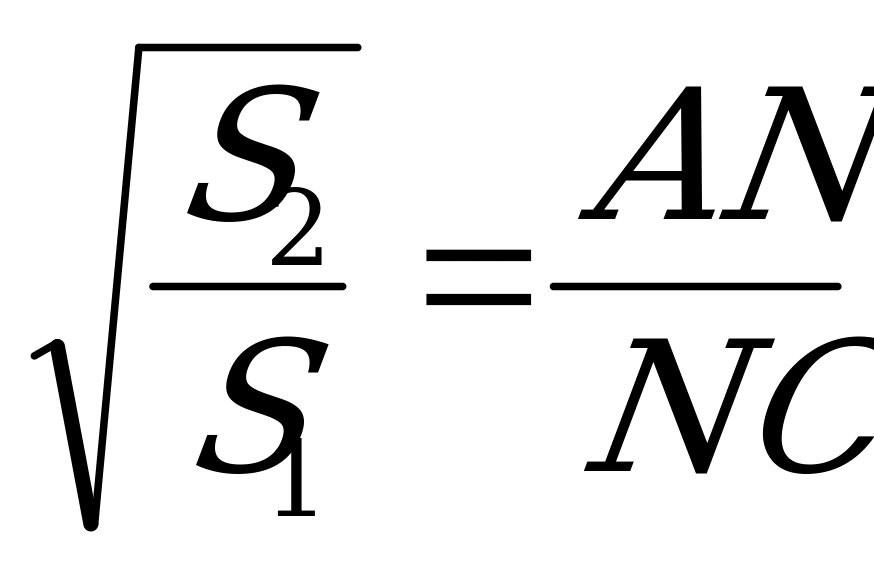 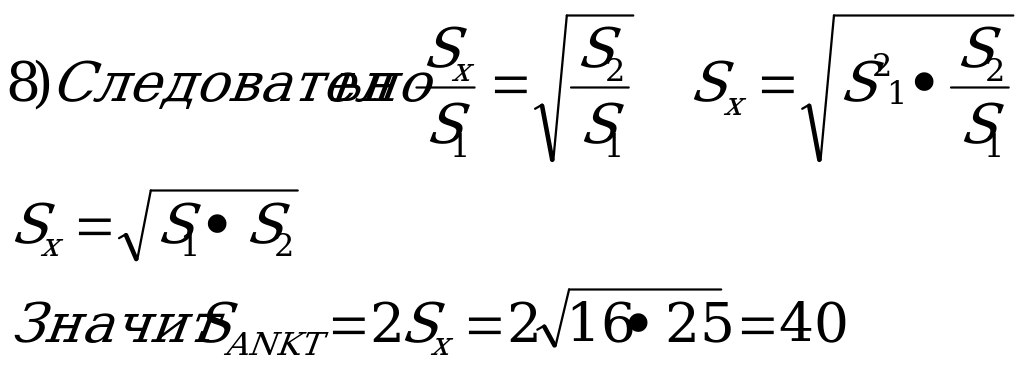 |
| Задача 2 .Точки М, К, и N лежат на сторонах соответственно АВ, ВС и АС треугольника АВС, причем АМNK – параллелограмм, площадь которого составляет 4/9 площади треугольника АВС. Найти диагональ МN параллелограмма, если известно, что АВ=21, АС =12 и угол равен 1200. Решение. Анализ условия задачи показывает, что существует два параллелограмма АМNK, удовлетворяющих условию задачи. Пусть площадь треугольника SАВС = S, тогда ВК/ВС = К. Тогда ∆МВК ∞∆АВС с коэффициентом подобия К. Треугольники ∆N KC ∞ ∆АВС с коэффициентом подобия (1 – к). Площадь SАВС = SАМКN +SMBK +SNKC, то 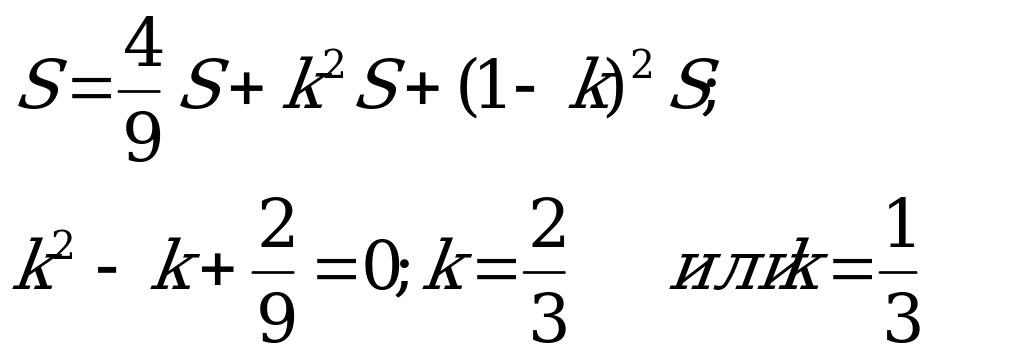 | 1 случай. 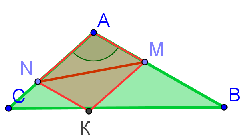 2 случай 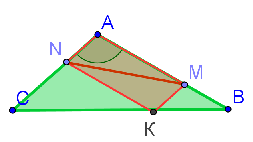
|
| | 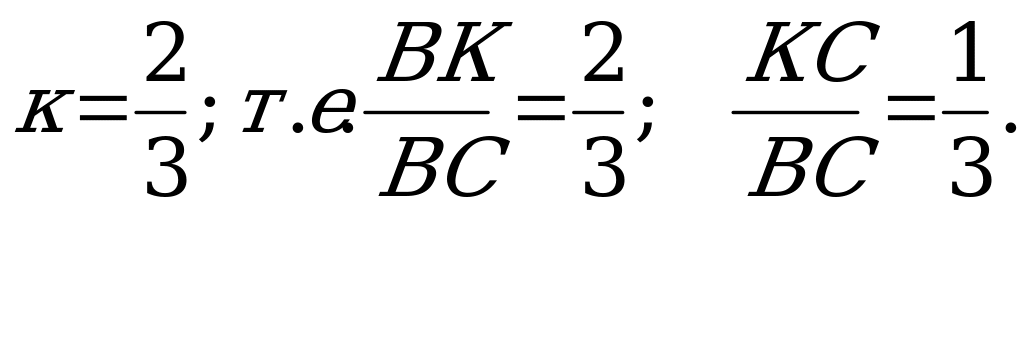 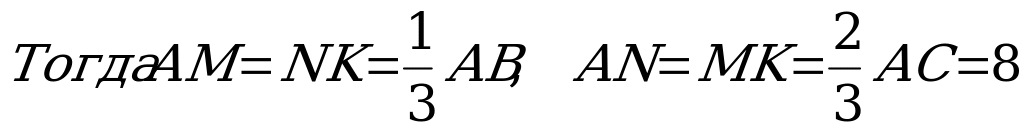 Из ∆NAM находим М N. 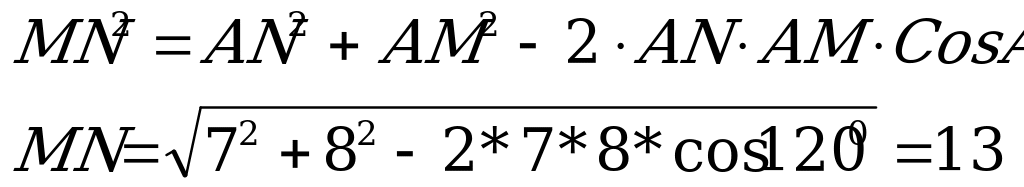
| 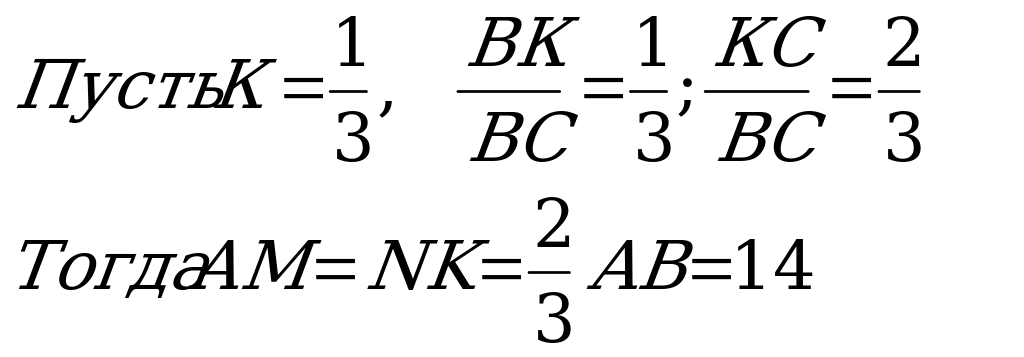 АN =MK =1/3 AC = 4.по теореме косинусов получим МN/ 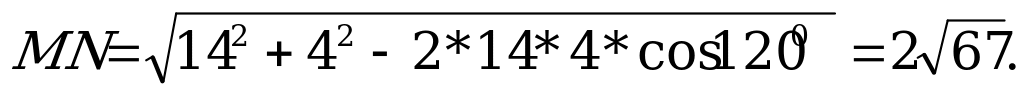 Ответ; 13 или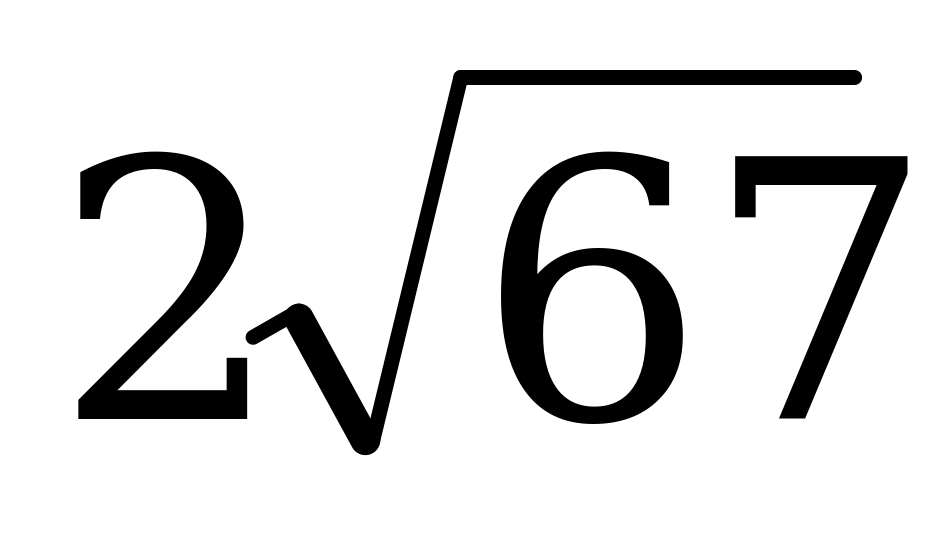 . . |
|
2.2. Удвоение медианы
| Конструкция 2. Если в треугольнике задана медиана, то треугольник достраивается до параллелограмма с центром в основании этой медианы. В зависимости от содержания задачи такое достраивание можно выполнять для одной, двух или даже трех медиан. При этом возможно использование не всего параллелограмма, а лишь его части (например, треугольника АСМ1) |
| 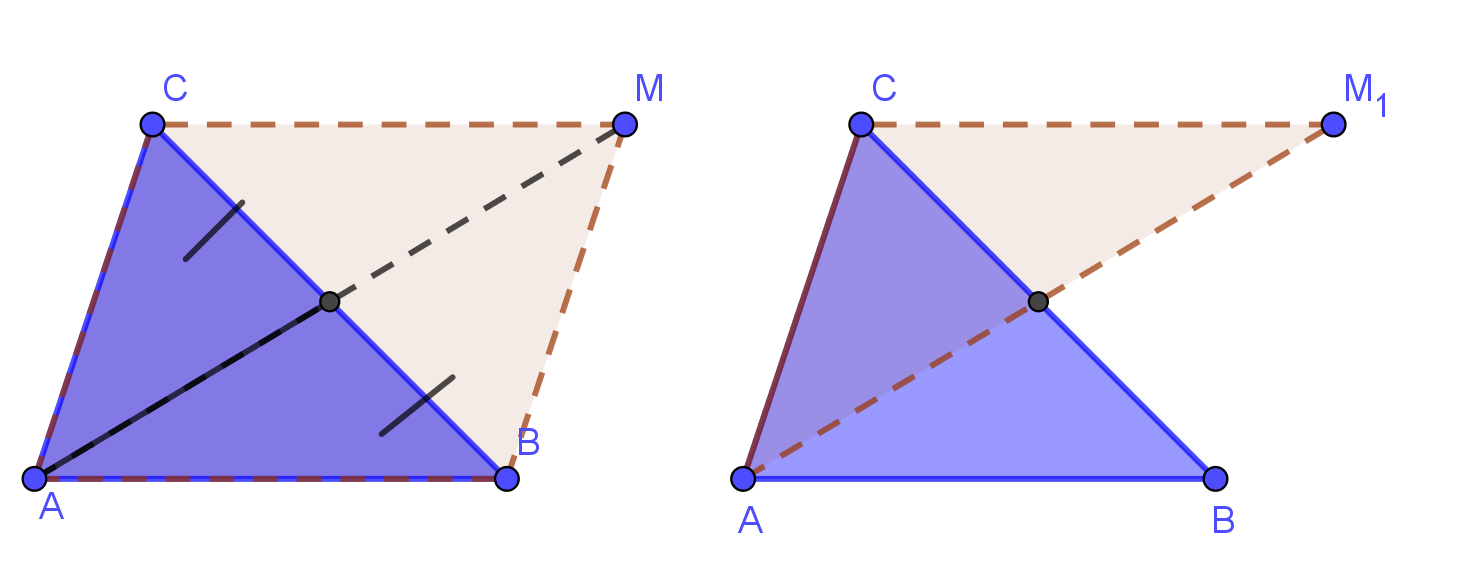 |
| Задача 1. Найдите площадь треугольника, если две его стороны равны 27 и 29, а медиана, проведённая к третьей, равна 26. |
| 
|
| Задача 2. Диагонали трапеции равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найдите площадь трапеции. 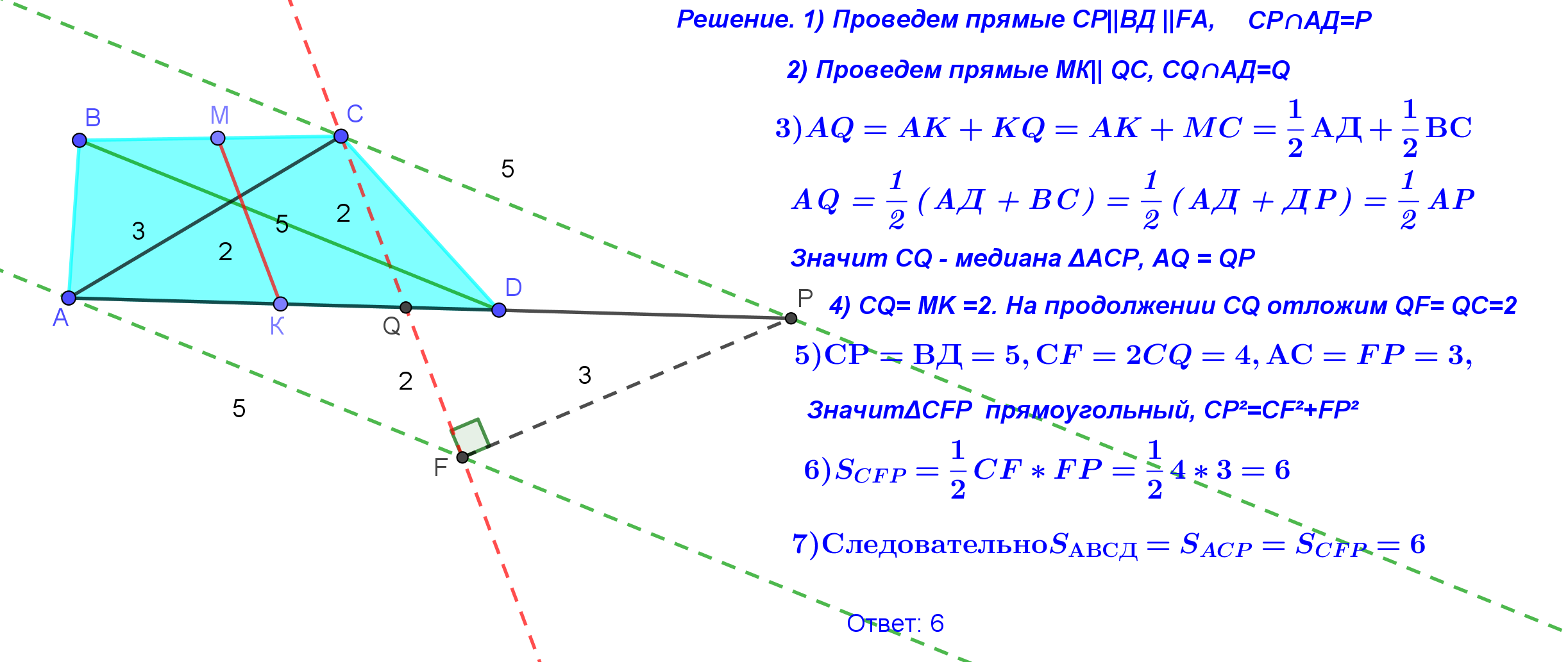 |
| 2.3. Трапеция, прямая параллельная диагонали или боковой стороне трапеции Конструкция 3. Если дана трапеция, то ее диагональ или боковая сторона переносятся на вектор, определяемый одним из оснований. |
| 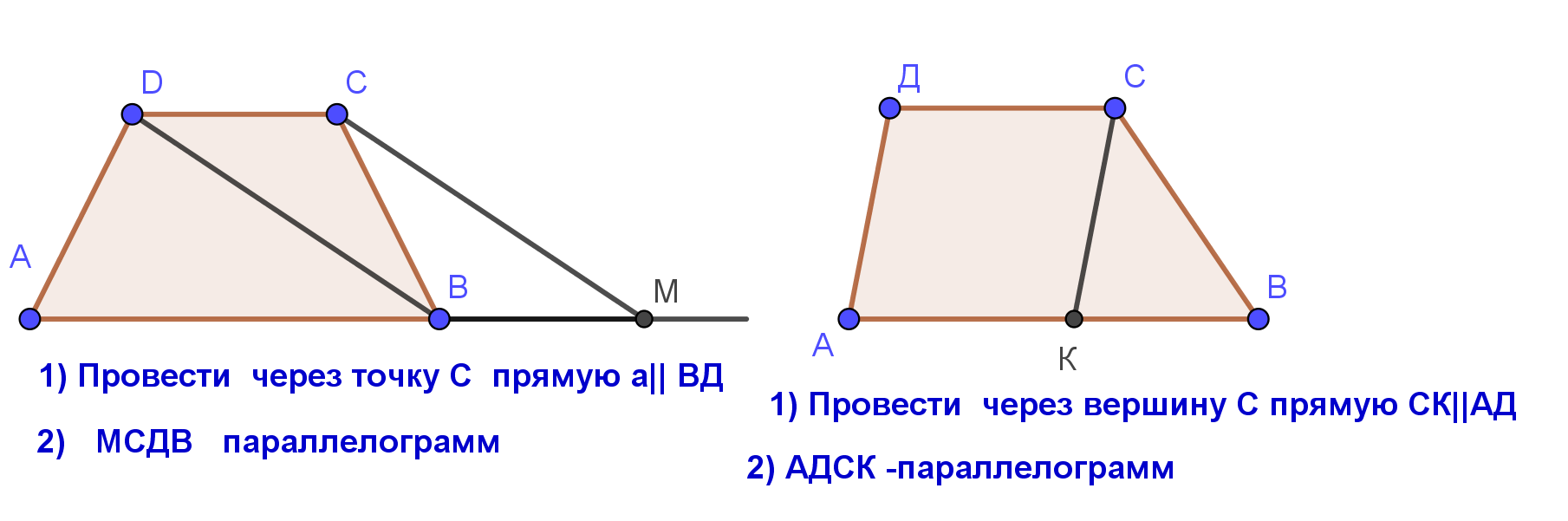 |
|
ОГЭ 2019. Пособие 50 вариантов. Под.ред. И.В.Ященко. Вариант 10. Задание №26. Найдите площадь трапеции, диагонали которой равны 15 и 13, а средняя линия равна 7. |
| 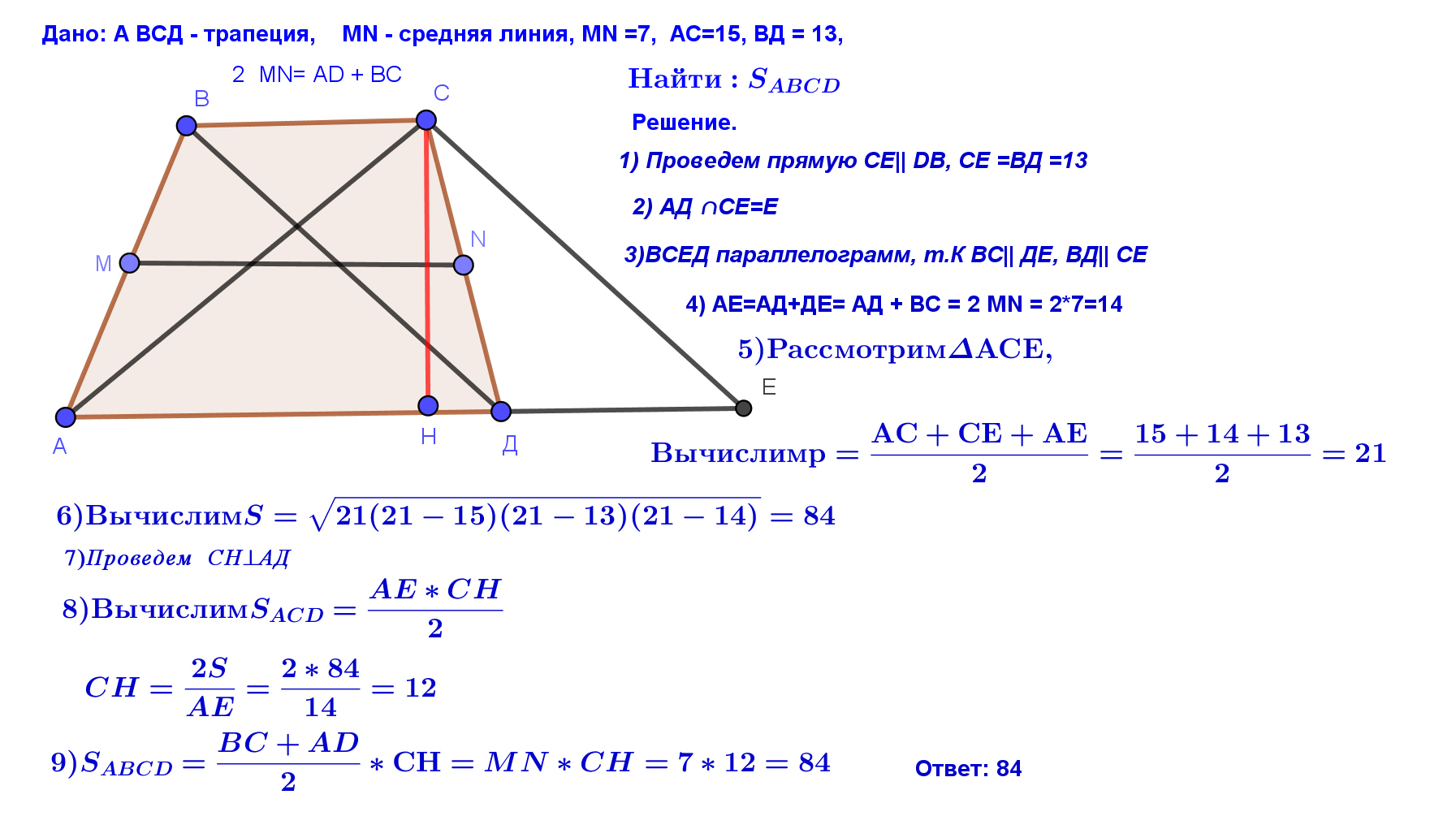 |
3. ПОДОБИЕ, ТЕОРЕМА ФАЛЕСА, ПЕРЕНОС ПРОПОРЦИЙ ВНУТРИ ТРЕУГОЛЬНИКА.
Задачи решаются либо с помощью теоремы о пропорциональных отрезках (обобщённой теоремы Фалеса), либо с помощью дополнительного построения, которое приводит к двум парам подобных треугольников. Самое главное необходимо « увидеть» предварительно проведя анализ-сравнение всех входящих в геометрическую конструкцию углов и отрезков. Информацию о подобии можно получить и из сравнения площадей фигур, результатом которого могут оказаться нужные для подобия пропорции. После того как подобие зафиксировано и обосновано следует перенос информации из одного треугольника в другой.
3.1. Свойство биссектрисы внутреннего и внешних углов треугольника.
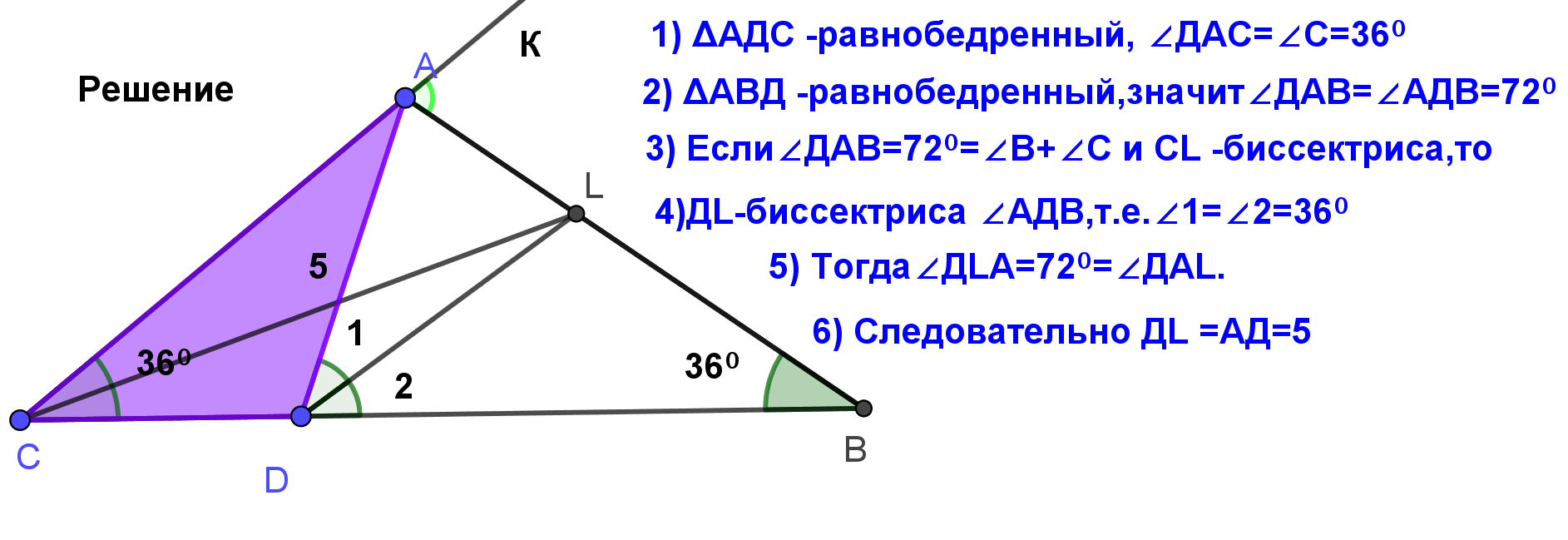
| Конструкция № 4. Провести прямую РС || АС.∆МАВ∞∆МСР, ∆ВРС – равнобедренный. 
|
| Задача 1. В треугольнике СДЕ известно, что СД=8 , ДЕ=6, СЕ=7. Через вершину Д проведены биссектрисы внутреннего и внешнего углов треугольника, пересекающие прямую СЕ в точках К и М. Найдите длину отрезка КМ. 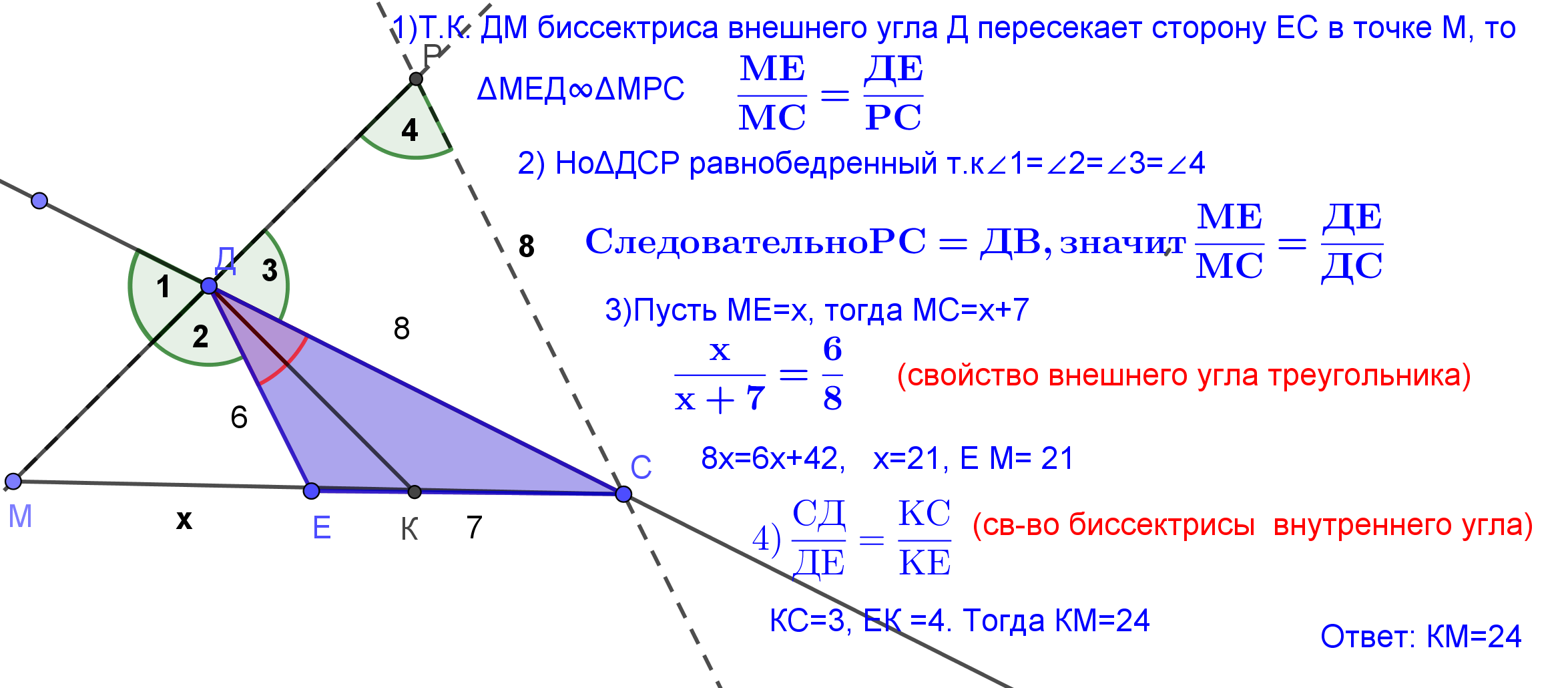 |
| Задача 2. В треугольнике АВС проведена биссектриса CL.На стороне ВС взята точка Д, такая, что 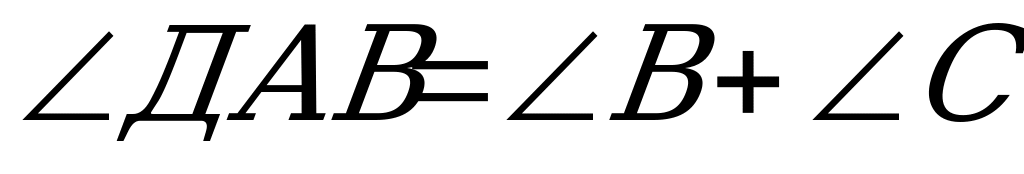 .Доказать, что ДL – биссектриса угла АДВ. .Доказать, что ДL – биссектриса угла АДВ. |
| 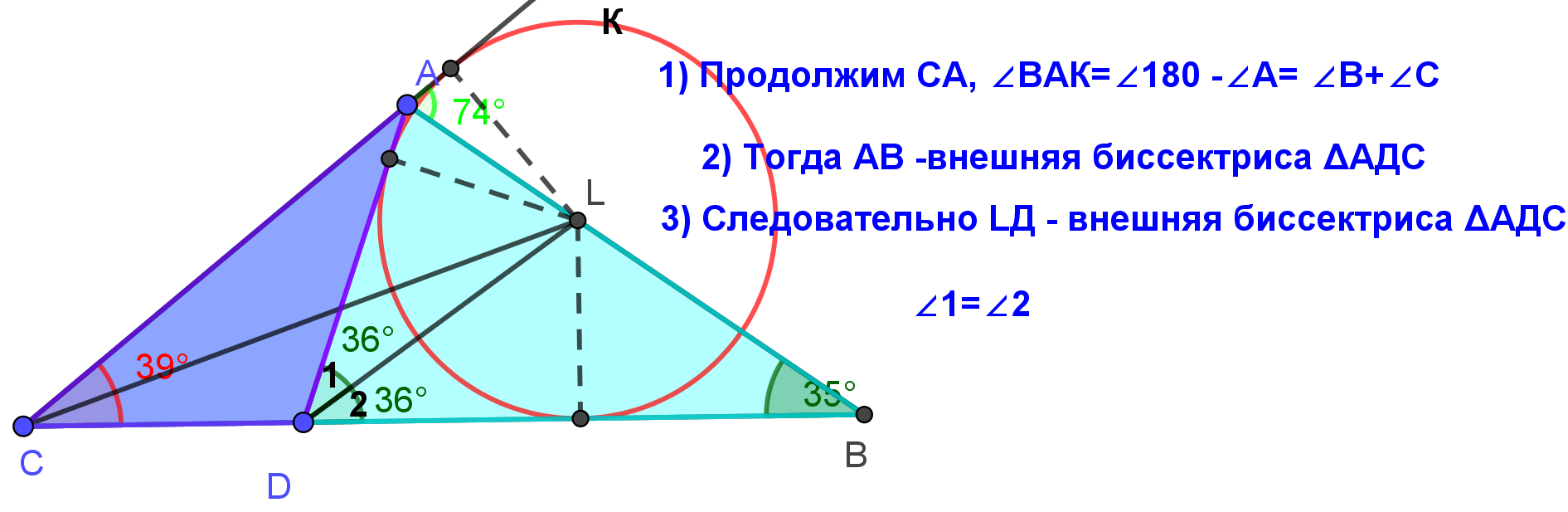 3.2. Отношение отрезков Конструкция 5. Задача 1. ( использование теоремы Фалеса) Дан треугольник ABC. На продолжении стороны AC за точку C взята точка N , причём AC = 2CN . Точка M находится на стороне BC , причём BM : MC = 1 : 3. В каком отношении прямая MN делит сторону AB? 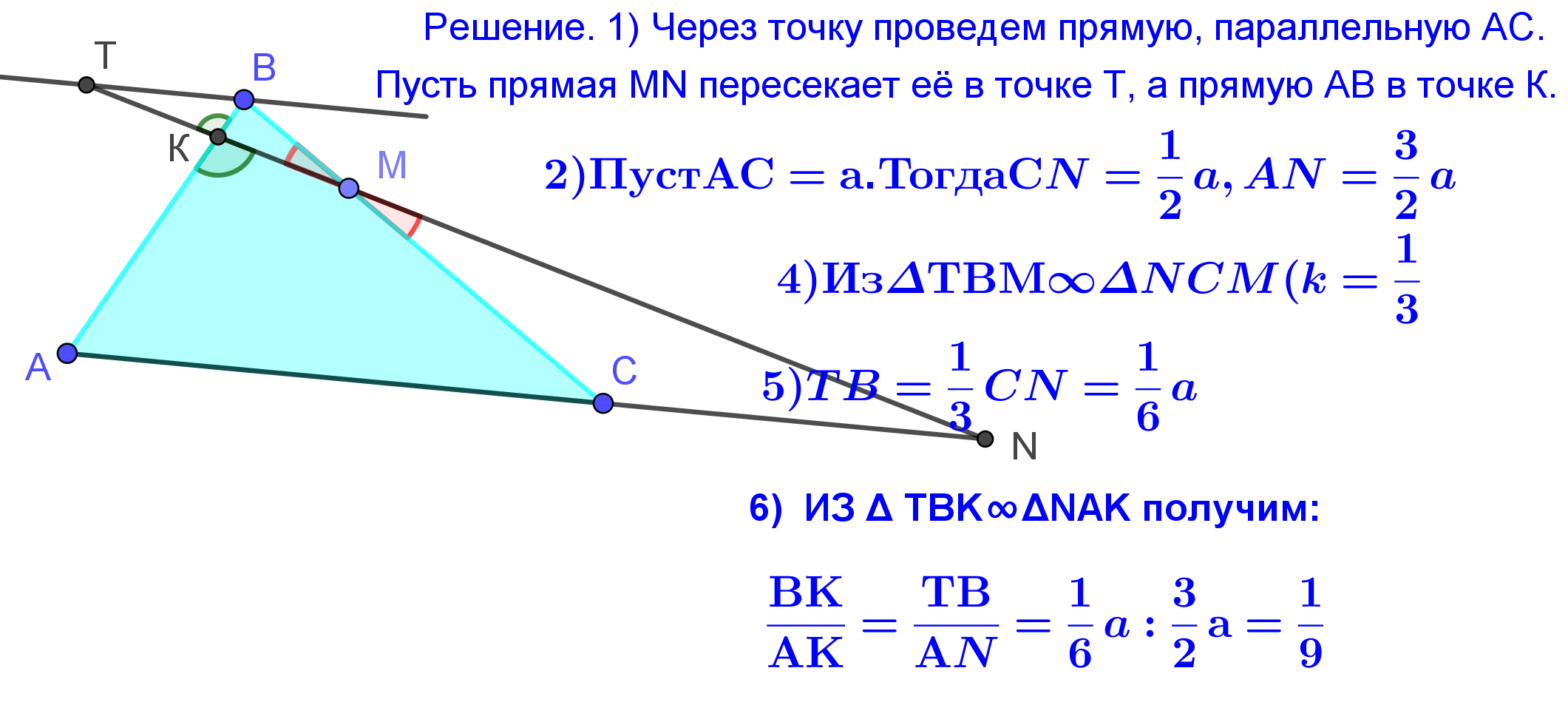 Задача 2. ОГЭ 2019. Пособие 50 вариантов. Под.ред. И.В.Ященко. Вариант 6 Задание № 24 Прямая, параллельная основаниям трапеции АВСД, пересекает ее боковые стороны АВ и СД в точках Е и F соответственно. Найдите длину отрезка EF, если АД =36, ВС = 18, CF: DF =7 :2  Задача 5. В треугольнике АВС: АС = 8, ВС = 5. Прямая, параллельная биссектрисе внешнего угла С, проходит через середину стороны АВ и точку Е на стороне АС. Найдите АЕ. 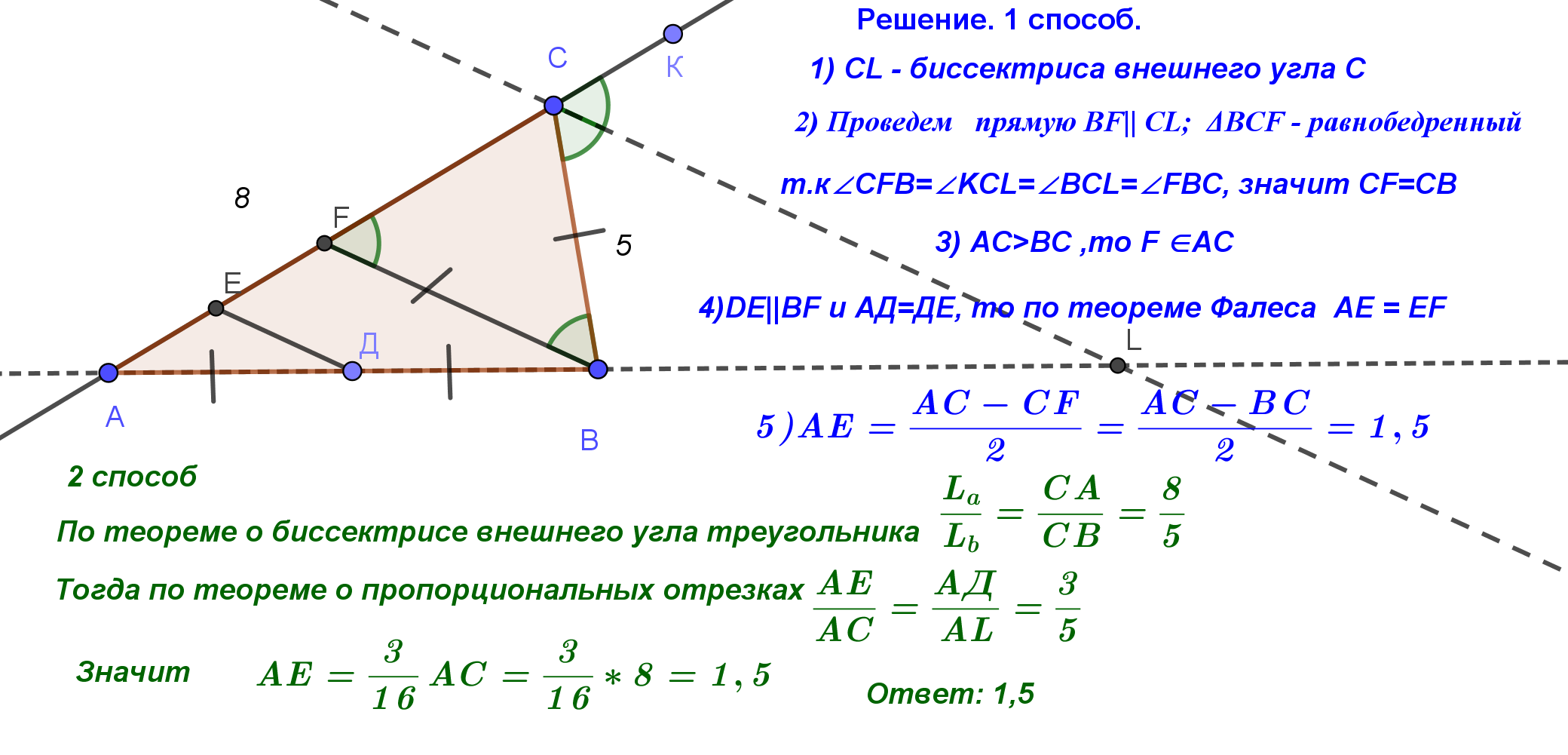
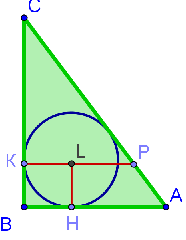
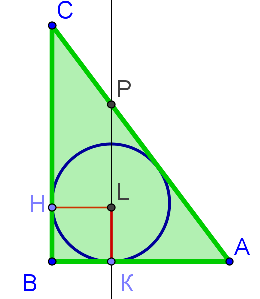
Задача 6. Дан прямоугольный треугольник АВС, с катетами АВ и ВС (АВ=5, ВС=12 ). Пусть точка I – центр окружности, вписанной в треугольник АВС. Прямая, проходящая через точку I, параллельна одной из сторон треугольника АВС и пересекает две другие стороны в точках К и Р. Найдите длину отрезка КР. Решение. При решении данной задач в условии рассмотреть 3 случая.
Заключение. Выполняя проектную работу, я повторила теоретический материал по планиметрии и научилась решать задачи, при решении которых нужно применить число геометрических фактов из школьного курса в измененной ситуации. Решая такую задачу в первую очередь необходимо проанализировать предложенную в задаче конфигурацию и увидеть те свойства, которые необходимы при решении. Большинство задач требует применения разнообразных теоретических знаний, доказательства утверждений, справедливых лишь при определенном расположении фигуры. Приобрести навыки в решении задач можно, лишь решив достаточно большое их количество, ознакомившись с различными методами, приёмами и подходами. В работе достаточно сложно описать все методы решения задач данного класса, но я показала в своей работе лишь некоторые приемы решения таких задач и продемонстрировала с помощью программы Geogebra их на конкретных примерах.
Литература 1.Готман Э.Г.Задачи по планиметрии и методы их решения: Пособие для учащихся.- М,; Просвещение: АО « Учеб. лит.», 1996. – 240с. 2.Гордин Р.К.ЕГЭ 2010. Математика. Задача С4/Под ред.А.Л.Семенова, И.В.Ященко- М,:МЦНМО, 2010,-148 с. 3. ЕГЭ 2010. Математика: Сборник тренировочных работ/Высоцкий И.Р., Захаров П.И.; Смирнов В.А.; Ященко С.А. – М: МЦНМО, 2010. 3.Зеленский А.С., Панфилов И.И., Геометрия в задачах. – М,:Научно – технический центр « Университетский»; УНИВЕР – ПРЕСС,2008. – 272 с,; ил.( серия « Математика: перезагрузка»). 4. http://alexlarin.net сайт по оказанию информационной поддержки студентам и абитуриентам при подготовке к ЕГЭ, поступлению в ВУЗы и изучению различных разделов высшей математики. 5. http://www.dovuz.mgppu.ru/ Учебный центр « Довузовское и дополнительное образование». 6. http://ege-study.ru/ Подготовка к ЕГЭ и олимпиадам.
Приложение 1 Глава 1. Теоретический материал 1. Треугольник. Выбор линейного элемента. Выбор средней линии треугольника. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному. 2.Формулы, правила и свойства | Нетривиальный треугольник 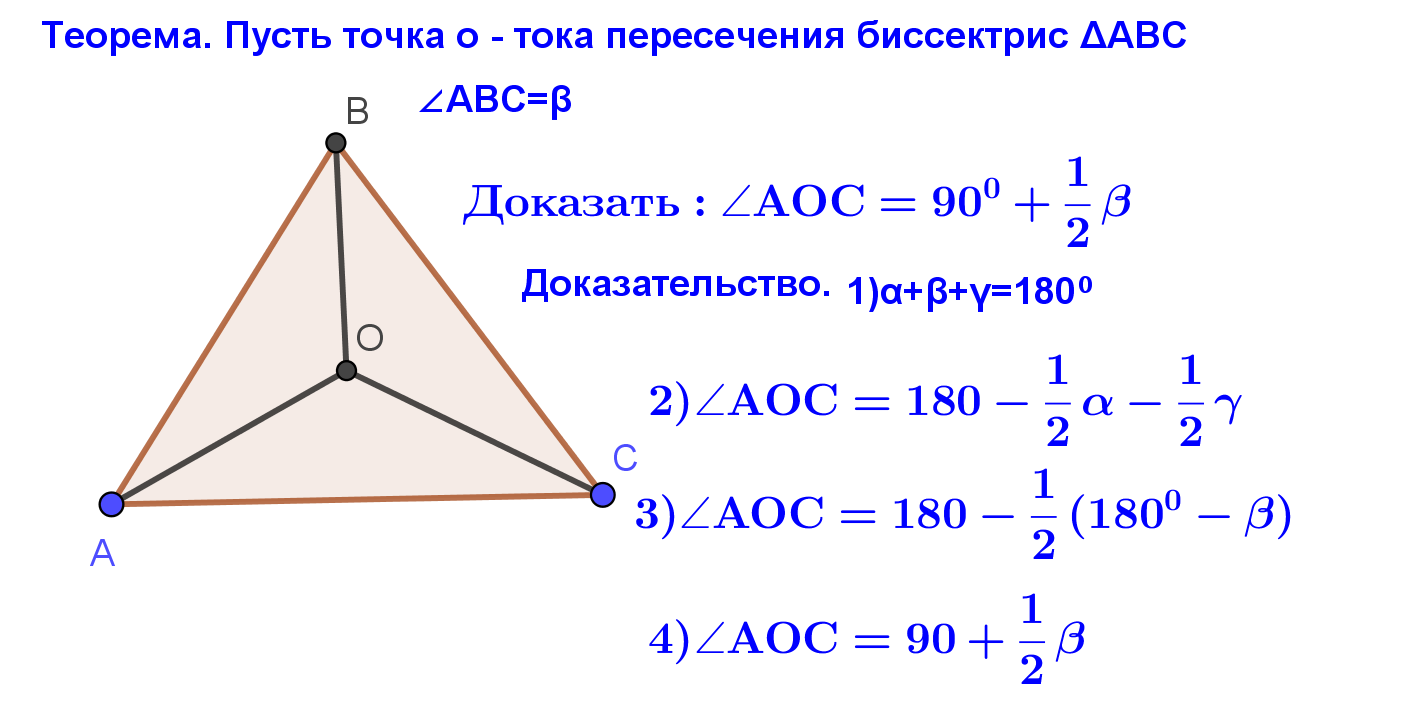 | | 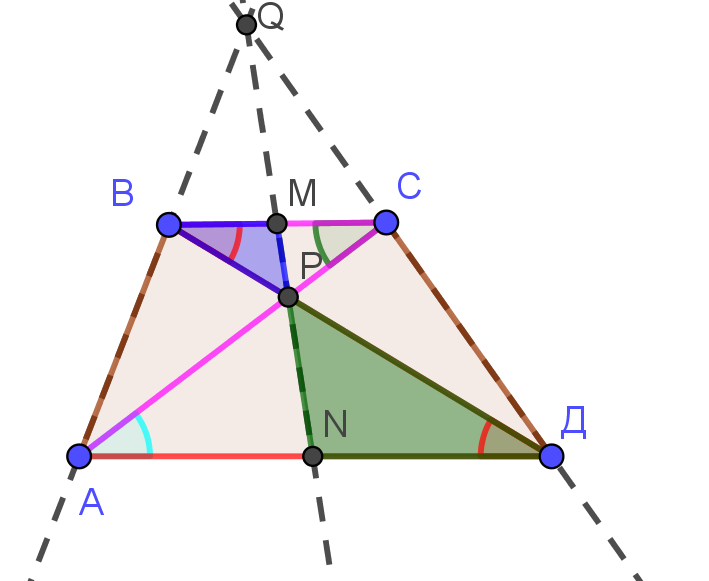 | Теорема:Точка пересечения диагоналей любой трапеции, точка пересечения продолжений боковых сторон и середины оснований ле-жат на одной прямой.
| | 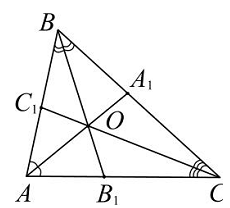 | Биссектриса любого внутреннего угла делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника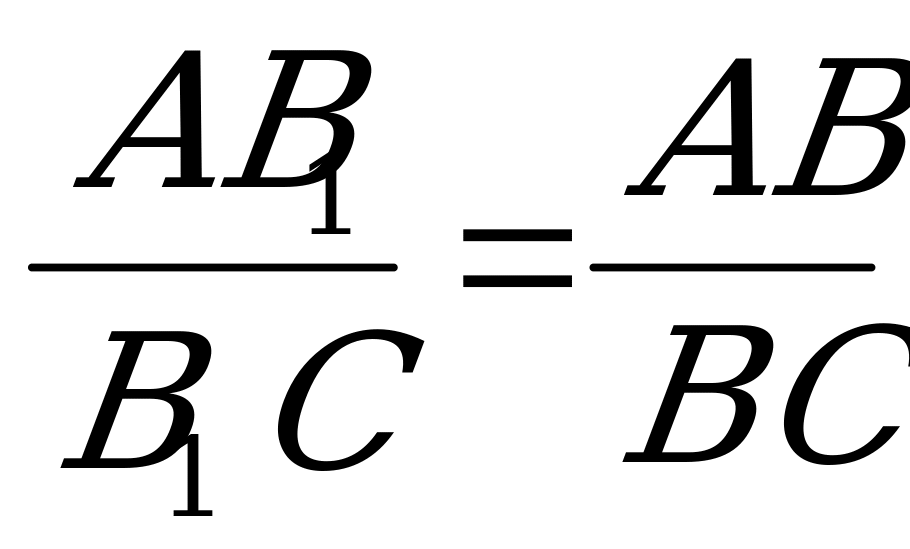 Биссектриса ВВ1 треугольника АВС делит площадь треугольника на части, пропорциональные прилежащим сторонам: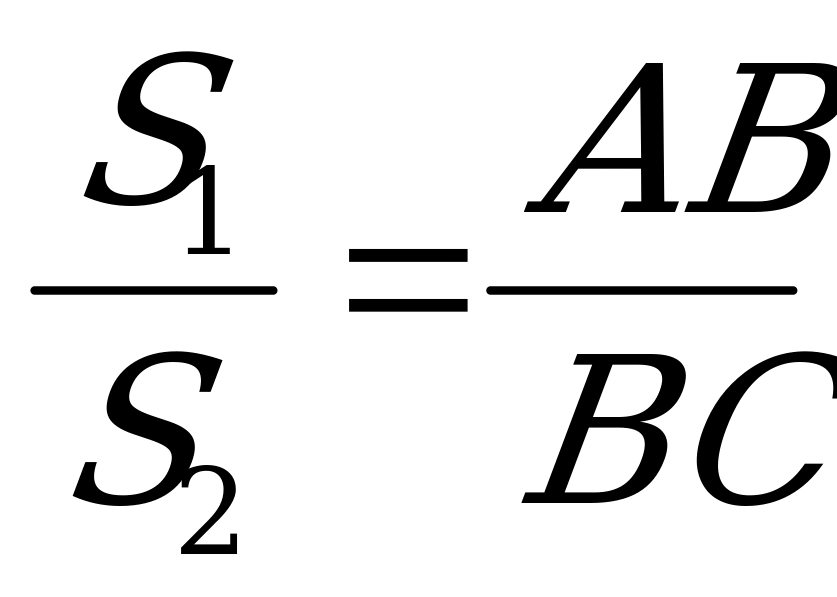 | |  | | 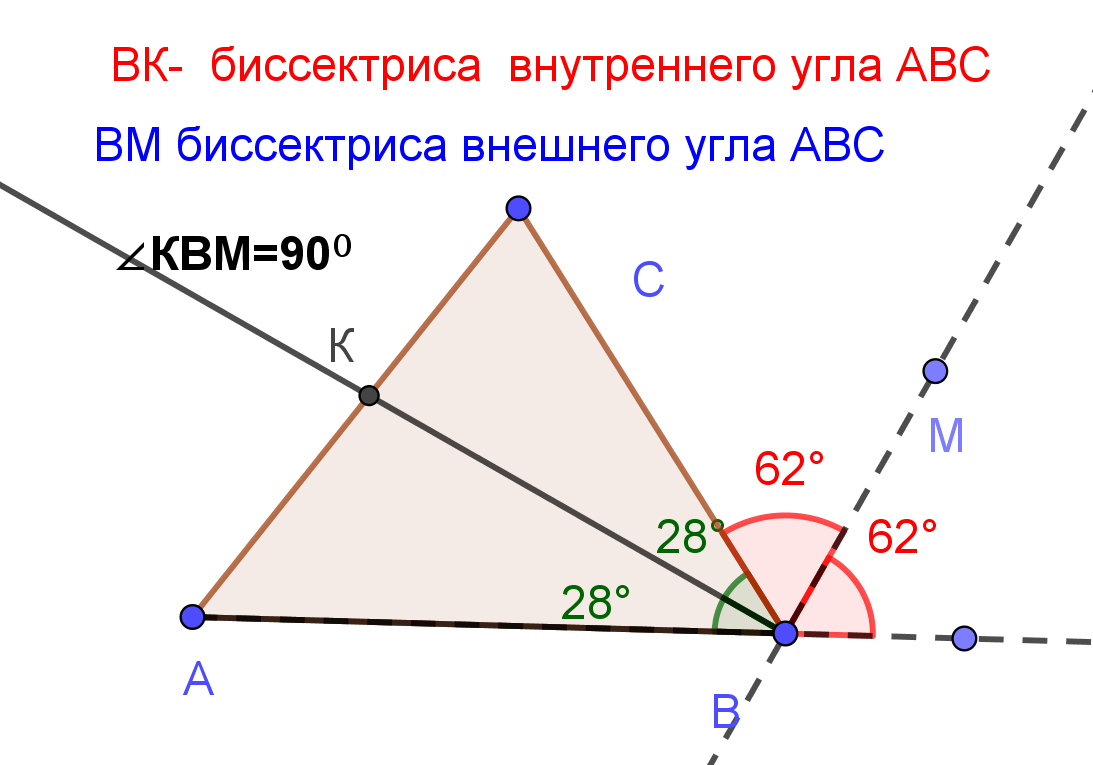 | Биссектрисы внутреннего и смежного с ним внешнего угла треугольника перпендикулярны. | | 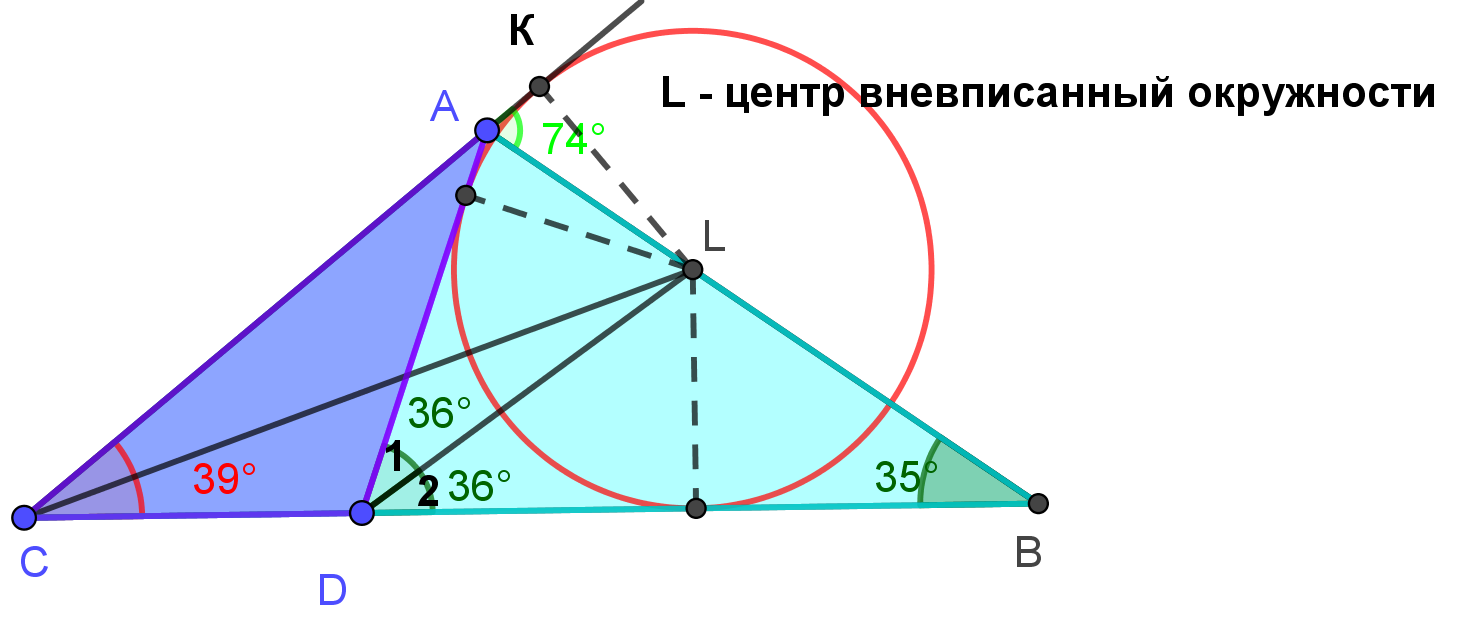 | Окружность, касающаяся стороны треугольника и продолжений двух других сторон называется вневписанной. Точка пересечения биссектрисы внутреннего угла треугольника и биссектрис двух внешних углов- центр вневписанной окружности. | | 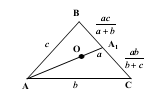 | Каждая биссектриса делится точкой пересечения биссектрист в отношении суммы прилежащих сторон к противолежащей, считая от вершины. АВ=с, ВС= а, АС=в |
|
|
|
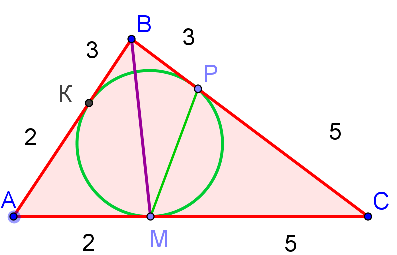
Задача. Дан треугольник ABC, где BA=5, BC=8. В треугольник вписана окружность, касающася стороны BC в точке Р. Известно, что ВР=3. Найдите площадь треугольника ВМР, где М-точка касания окружности со стороной треугольника АВС.
Решение.










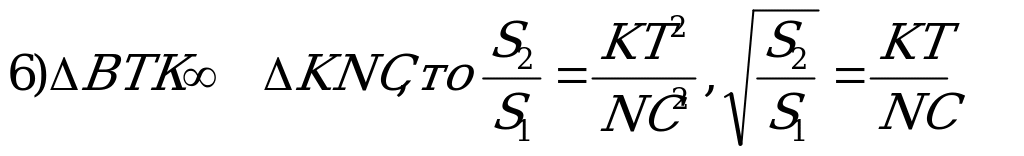 (как квадраты соответствующих линейных размеров)
(как квадраты соответствующих линейных размеров)