К. Останов,
к.п.н., доцент,
СамГУ,
г. Самарканд, Узбекистан
О ФОРМИРОВАНИИ ИССЛЕДОВАТЕЛЬСКИХ УМЕНИЙ У УЧАЩИХСЯ ПРИ ИЗУЧЕНИИ РАСПОЛОЖЕНИЯ КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ
Важное значение имеет в процессе исследовательских умений учащихся изучение и исследование корней квадратного уравнения в зависимости от коэффициентов уравнения[1].
Задача 1. Задача об определении количества корней квадратного уравнения или их существования на заданном полу бесконечном (луче) или выделение корней, принадлежащих лучу. Учащимся уже известно, что: для того, чтобы квадратный трехчлен  имел двух положительных корней необходимо и достаточно должны выполняться одновременно условия:
имел двух положительных корней необходимо и достаточно должны выполняться одновременно условия:
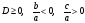
На практике этот признак используется в следующем виде:

Этот признак вытекает из теоремы Виета :
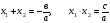
Теперь найдем необходимые и достаточные условия, того, что корни  трехчлена
трехчлена 
Больше заданного числа  (т.е. чтобы корни принадлежали интервалу
(т.е. чтобы корни принадлежали интервалу  .) Эта задача может быть решена приведением к предыдущей задаче. На самом деле, функция
.) Эта задача может быть решена приведением к предыдущей задаче. На самом деле, функция  также будет квадратным трехчленом; его корнями будет
также будет квадратным трехчленом; его корнями будет  , так как
, так как

это условие примет следующий вид:

Здесь  - дискриминант трехчлена
- дискриминант трехчлена  , так как от того, что трехчлены
, так как от того, что трехчлены  имеют одновременно корней или не имеют, неравенство
имеют одновременно корней или не имеют, неравенство  равносильно неравенству
равносильно неравенству  .
.
Значит, выше приведенное необходимое и достаточное условие будет иметь следующий вид

Доказательство. Необходимость. Пусть трехчлен  имеет корней
имеет корней  большей, чем числа
большей, чем числа .
.
Тогда его дискриминант неотрицательный (потому что имеет корней)  так как число
так как число  меньшем ,чем не меньшего корня , то
меньшем ,чем не меньшего корня , то

и по теореме Виета  . С этим необходимость теоремы полностью доказана (для
. С этим необходимость теоремы полностью доказана (для  ).
).
Достаточность. Пусть выполнены условия  . Тогда трехчлен имеет корней
. Тогда трехчлен имеет корней  и если эти корни будет различными, то из второго неравенства или число р больше большого корня, или число меньше меньшего корня , но в первом случае мы имели бы
и если эти корни будет различными, то из второго неравенства или число р больше большого корня, или число меньше меньшего корня , но в первом случае мы имели бы  , т.е.
, т.е.  .Это противоречит третьему неравенству. Значит, р меньше обоих корней, если корни совпадают, т.е. то
.Это противоречит третьему неравенству. Значит, р меньше обоих корней, если корни совпадают, т.е. то  , тогда неравенство 3 -
, тогда неравенство 3 -  , означает, что два корня больше числа р[2].
, означает, что два корня больше числа р[2].
Задача 2. Какое необходимое и достаточное условие можно найти для того, чтобы квадратный трехчлен имел двух корней меньше заданного числа (корни необязательно должны быть разными). Решение этой задачи выражается следующими условиями
 .
.
Рассмотренные выше две задачи дополняют следующая задача:
Задача 3. Как выразить необходимое и достаточное условие того, что трехчлен  имел корней один из которого больше заданного числа и а другой меньше его?
имел корней один из которого больше заданного числа и а другой меньше его?
Решение этой задачи состоит из условия  Доказательство этого признака вытекает из переформулировки доказательства выше приведенного признака. Это свойство трехчлена означает, что заданное число расположены между двумя корнями, а этот признак известен: значение трехчлена в точке р должна быть противоположна знаку главного коэффициента трехчлена[3].
Доказательство этого признака вытекает из переформулировки доказательства выше приведенного признака. Это свойство трехчлена означает, что заданное число расположены между двумя корнями, а этот признак известен: значение трехчлена в точке р должна быть противоположна знаку главного коэффициента трехчлена[3].
Таким образом, проведение исследований по нахождению необходимые и достаточных условия расположения корней трехчлен,  в интервалах
в интервалах  или
или или в интервалах
или в интервалах  ,
, мы вынуждены использовать свойства квадратичной функции Теперь рассмотрим расположения корней трехчлена в открытом конечном интервале[4].
мы вынуждены использовать свойства квадратичной функции Теперь рассмотрим расположения корней трехчлена в открытом конечном интервале[4].
Вследствие этого можно составить следующую таблицу расположения корней трехчлена
|
| 
| 
| 
| 
| 
|
|  | + | + | + | + | + |
|  | + | - |
| + |
|
|  | + | - |
| + |
|
|  | + | + | - | + | + |
|  | + | + |
| - |
|
|  | + | + | - | + | - |
Здесь + и – означает знаки выражений. Например, в первом случае корни не принадлежат интервалу (p,q) и расположены слева, т.е. они меньше чем заданного числа, то необходимо и достаточно выполнения условий
 .
.
Во втором случае, р расположен между двумя корнями, число q больше большого корня, должно выполняться условия

Литература и примечания:
[1] Потапов М. К., Олехник С. Н., Нестеренко Ю. В. Конкурсные задачи по математике: Справочное пособие. – Изд. 3-е, стер. – М.: ФИЗМАТЛИТ, 2003. – 416с.
[2] Сахабиева ГА., Сахабиев В. А. Учебное пособие по математике. – М.: ФИЗМАТЛИТ, 2005. - 160 с.
[3] Ткачук В. В. Математика – абитуриенту. – 14-е изд., исправленное и дополненное. М.: МЦНМО, 2007. - 976 с.
[4] Голубев В.И. Решение сложных и нестандартных задач по математике. – М: ИЛЕКСА, 2007. – 252 с: ил.






 имел двух положительных корней необходимо и достаточно должны выполняться одновременно условия:
имел двух положительных корней необходимо и достаточно должны выполняться одновременно условия: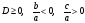

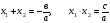
 трехчлена
трехчлена  (т.е. чтобы корни принадлежали интервалу
(т.е. чтобы корни принадлежали интервалу  .) Эта задача может быть решена приведением к предыдущей задаче. На самом деле, функция
.) Эта задача может быть решена приведением к предыдущей задаче. На самом деле, функция  также будет квадратным трехчленом; его корнями будет
также будет квадратным трехчленом; его корнями будет  , так как
, так как

 - дискриминант трехчлена
- дискриминант трехчлена  , так как от того, что трехчлены
, так как от того, что трехчлены  имеют одновременно корней или не имеют, неравенство
имеют одновременно корней или не имеют, неравенство  равносильно неравенству
равносильно неравенству  .
.
 имеет корней
имеет корней  так как число
так как число 
 . С этим необходимость теоремы полностью доказана (для
. С этим необходимость теоремы полностью доказана (для 









