Тест
Объём пирамиды
I варинт
1. Найдите объём правильного тетраэдра, если его ребро равно 2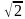 см.
см.
а) 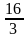 см3; б)
см3; б) 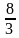 см3; в) 2 см3; г) 4 см3; д) 8 см3.
см3; в) 2 см3; г) 4 см3; д) 8 см3.
2. Найдите объём правильной четырёхугольной пирамиды, если все её рёбра равны 2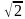 см.
см.
а) 2 см3; б) 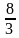 см3; в)
см3; в) 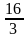 см3; г) 8 см3; д) 4 см3.
см3; г) 8 см3; д) 4 см3.
3. Выберите верное утверждение.
а) Объём пирамиды равен произведению одной трети площади основания на высоту;
б) объём правильного тетраэдра вычисляется по формуле V= 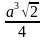 , где а – ребро тетраэдра;
, где а – ребро тетраэдра;
в ) объём усечённой пирамиды, высота которой равна h, а площади оснований равны S и М, вычисляется по формуле V =
) объём усечённой пирамиды, высота которой равна h, а площади оснований равны S и М, вычисляется по формуле V = 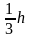 (S + M +
(S + M + 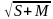 );
);
г) объём правильной треугольной пирамиды, ребро основания которой равно а и все боковые рёбра наклонены к плоскости основания под углом 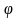 , вычисляется по формуле
, вычисляется по формуле
V = 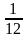 a3sin
a3sin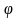 ;
;
д) объём правильной четырёхугольной пирамиды, ребро основания которой равно а и все боковые рёбра наклонены к плоскости основания под углом φ, вычисляется по формуле
V = 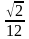 a3tg
a3tg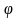 12.
12.
4. Найдите объём усечённой пирамиды, площади оснований которой равны 3 см2 и 12 см2, а высота - 2 см.
а) Определить нельзя; б) 7 см3; в) 42 см3; г) 14 см3; д) 56 см3.
5. Основанием пирамиды МАВС служит треугольник со сторонами АВ = 5 см, ВС = 12 см, АС = 13 см. Найдите объём пирамиды, МВ ⊥ АВС и МВ = 10 см.
а) 300 см3; б) 260 см3; в) 780 см3; г) определить нельзя; д) 100 см3.
6. Основанием пирамиды служит прямоугольный треугольник, катеты которого 3 и 4. Боковые грани пирамиды наклонены к плоскости основания под углом 45˚. Найдите объём пирамиды.
а) 1; б) 4; в) 6; г) 2; д) определить нельзя.
7. Объём правильной треугольной пирамиды равен 6. Найдите угол между высотой и боковым ребром пирамиды, если сторона основания равна 2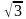 .
.
а) 30˚; б) 45˚; в) 60˚; г) 15˚; д) 75˚.
8.В правильной шестиугольной пирамиде боковое ребро равно 4 см, а сторона основания – 2 см. Найдите объём пирамиды.
а) 9 см3; б) 6 см3; в) 12 см3; г) 18 см3; д) определить нельзя.
9. В каком отношении параллельная основанию плоскость делит объём пирамиды, если она делит высоту в отношении 2:3?
а) 2:3; б) 8:117; в) 8:27; г) 27:98; д) 27:8.
10. Основанием пирамиды служит прямоугольный треугольник с гипотенузой с и острым углом . Все боковые рёбра наклонены к плоскости основания под углом β. Найдите объём пирамиды.
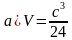 sin2*tgβ; б) ) V =
sin2*tgβ; б) ) V = 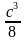 sin2*tgβ; в) V =
sin2*tgβ; в) V = 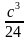 sin*tg2β; г) V =
sin*tg2β; г) V = 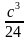 sin*tgβ; д) V =
sin*tgβ; д) V = 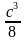 sin*tgβ*cos.
sin*tgβ*cos.
11. Диагональное сечение правильной четырехугольной пирамиды является равносторонним треугольником, площадь которого равна 6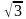
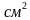 . Найдите объем пирамиды.
. Найдите объем пирамиды.
а) 9
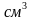 ; б) 18
; б) 18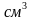 ; в) 12
; в) 12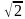
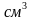 ; г) 15
; г) 15
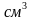 ; д) верного ответа нет.
; д) верного ответа нет.
12. В треугольной пирамиде КАВС АК ВК и ВК
ВК и ВК СК, а угол АКС равен 30 град. Найдите объем пирамиды, если АК = 8 см, ВК = 12 см, СК = 10 см.
СК, а угол АКС равен 30 град. Найдите объем пирамиды, если АК = 8 см, ВК = 12 см, СК = 10 см.
а) 64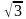
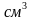 ; б)64
; б)64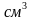 ; в) 60
; в) 60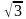
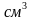 ; г) 80
; г) 80
II вариант
1. Объем правильного тетраэдра равен 9 см3. Найдите его ребро.
а) 4 см; б) 2√3 см; в) 3√2 см; г) 6 см; д) 3 см.
2. Найдите ребро правильной четырёхугольной пирамиды, если ее объем равен 18 см3, а все ребра имеют одинаковую длину. а) 2 см; б) 2√3 см; в) 3√2 см; г) 6 см; д) 3 см.
3. Выберите неверное утверждение.
а) Объём пирамиды равен произведению одной трети площади основания на высоту;
б) объём правильного тетраэдра вычисляется по формуле V = а3√2/12, где а – ребро тетраэдра;
в ) объём усечённой пирамиды, высота которой равна h , а площади оснований равны S и М, вычисляется по формуле V = 1/3h(S + M + √S + M );
) объём усечённой пирамиды, высота которой равна h , а площади оснований равны S и М, вычисляется по формуле V = 1/3h(S + M + √S + M );
г) объём правильной треугольной пирамиды, ребро основания которой равно а и все боковые рёбра наклонены к плоскости основания под углом φ, вычисляется по формуле V = 1/12a3tgφ;
д) объём правильной шестиугольной пирамиды, ребро основания которой равно а, и все боковые рёбра наклонены к плоскости основания под углом φ, вычисляется по формуле V = √3/12a3tgφ.
4. Найдите объём усечённой пирамиды, площади оснований которой равны 28 см2 и 7 см2, а высота -3 см.
а)49 см3; б) 56 см3; в) 98 см3; г) 14 см3; д) определить нельзя.
5. Основанием пирамиды SKLM служит треугольник со сторонами KL = 9 см, KM = 15 см, LM = 12 см. Найдите объём пирамиды, если SK ⊥ MKL и SK = 4 см.
а) 216 см3; б) 240 см3; в) 72 см3; г) определить нельзя; д) 120 см3.
6. Основанием пирамиды служит ромб с углом 300 и стороной, равной 2√3. Боковые грани пирамиды наклонены к плоскости основания под углом 60˚. Найдите объём пирамиды.
а) 1; б) 9; в) 6; г) 3; д) определить нельзя.
7. Объём правильной треугольной пирамиды равен 3. Найдите угол между высотой и апофемой пирамиды, если сторона основания равна 2√3.
а) 15˚; б) 30˚; в) 45˚; г) 60˚; д) 75˚.
8.В правильной шестиугольной пирамиде апофема и сторона основания равны 6 см. Найдите объём пирамиды.
а) 18√3 см3; б) 162√3 см3; в) 54√3 см3; г) 108√ см3; д) определить нельзя.
9. В каком отношении параллельная основанию плоскость делит объём пирамиды, если она делит высоту в отношении 3:4?
а) 27:316; б) 27:347; в) 3:4; г) 64:27; д) 27:64.
10. Основанием пирамиды служит прямоугольный треугольник с гипотенузой p и острым углом φ. Все боковые рёбра образуют с высотой угол . Найдите объём пирамиды.
а) V = 1/8p3sin2φ*ctg; б) V = 1/24p3sin2φ*ctg; в) V = 1/24p3sinφ*ctg2;
г) V = 1/24p3sinφ*ctg; д) V = 1/8p3sinφ*ctg*cosφ.
11. Диагональное сечение правильной треугольной пирамиды является прямоугольным треугольником, площадь которого равна 24 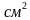 . Найдите объем пирамиды.
. Найдите объем пирамиды.
а) 40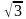
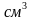 ; б) 32
; б) 32
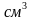 ; в) 48
; в) 48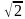
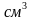 ; г) 54
; г) 54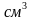 ; д) верного ответа нет.
; д) верного ответа нет.
12. В треугольной пирамиде MNKP MN MК и МК
MК и МК МP, а угол РМN равен 60 град. Найдите объем пирамиды, если МN = 2
МP, а угол РМN равен 60 град. Найдите объем пирамиды, если МN = 2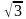 см, МК = 12 см и РМ = 4 см.
см, МК = 12 см и РМ = 4 см.
а) 28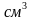 ; б) ) 18
; б) ) 18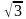
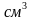 ; в) 24
; в) 24 20
20
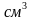 ; д) верного ответа нет.
; д) верного ответа нет.






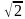 см.
см.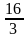 см3; б)
см3; б) 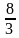 см3; в) 2 см3; г) 4 см3; д) 8 см3.
см3; в) 2 см3; г) 4 см3; д) 8 см3.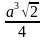 , где а – ребро тетраэдра;
, где а – ребро тетраэдра;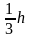 (S + M +
(S + M + 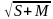 );
);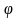 , вычисляется по формуле
, вычисляется по формуле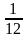 a3sin
a3sin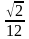 a3tg
a3tg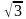 .
.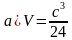 sin2*tgβ; б) ) V =
sin2*tgβ; б) ) V = 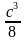 sin2*tgβ; в) V =
sin2*tgβ; в) V = 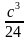 sin*tg2β; г) V =
sin*tg2β; г) V =  . Найдите объем пирамиды.
. Найдите объем пирамиды.
 ; б) 18
; б) 18









