Просмотр содержимого документа
«Обратные тригонометрические функции»
Тема: Арксинус, арккосинус и арктангенс.
Цель: - сформировать у учащихся понятия арксинуса, арккосинуса, арктангенса;
- научить учащихся вычислять арксинус, арккосинус, арктангенс.
Ход урока.
Орг. момент
Пост. цели
Объяснение нового материала
Опр. Арксинусом числа а называется такое число из отрезка 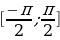 , что его синус равен а (об. arcsin)
, что его синус равен а (об. arcsin)
н./р. arcsin 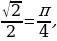 т.к. sin
т.к. sin 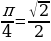 и
и 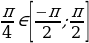
arcsin (-а)= - arcsin a
н./р. Arc sin 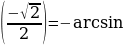 = -
= -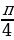
Опр. Арккосинусом числа а называется такое число из
отрезка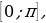 что его косинус равен а (об. arccos).
что его косинус равен а (об. arccos).
н./р. arccos 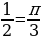
Arccos (-а) =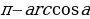
н./р. arccos 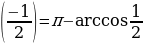 =
=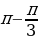 =
= 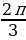
Опр. Aрктангенсом числа а называется такое число из
интервала 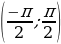 , что его тангенс равен а (об. arctg a)
, что его тангенс равен а (об. arctg a)
н./р. arctg 1 = 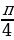
Arctg (-а) = - arctg а
н./р. arctg (-1) = 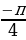
Опр. Aрккотангенсом числа а называется такое число из
интервала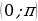 , что его котангенс равен а (об. arcctg a)
, что его котангенс равен а (об. arcctg a)
н./р. arcctg 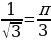
arcctg (-a ) = 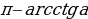
н./р. arcctg 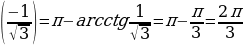
4. Решение задач №124, 126, 128, 130, 133, 134 (а, б)
№124 а) arcsin0 = 0 №126 а) arccos0 = 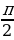
б) arcsin1=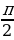 б) arccos 1 = 0
б) arccos 1 = 0
в) arcsin (-1)= 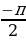 в) arccos (-1) =
в) arccos (-1) =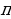
г) arcsin 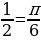 г) arccos
г) arccos 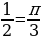
д) arcsin 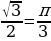 д) arccos
д) arccos 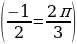
е) arcsin 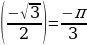 е) arccos
е) arccos 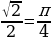
ж) arcsin 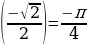 ж) arccos
ж) arccos 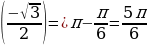
№128 а) arctg 0= 0 №130 а) arcctg0 =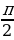
б) arctg (-1) = 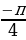 б) arcсtg 1=
б) arcсtg 1=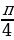
в) arctg 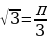 в) arcсtg (-1)=
в) arcсtg (-1)=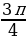
г) arctg 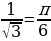 г) arcctg
г) arcctg 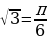
д) arctg 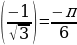 д) arcctg
д) arcctg 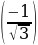 =
= 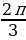
№133 а) arcsin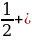 arccos
arccos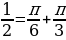 =
= 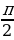
б) arcsin 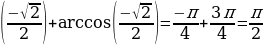
в) arcsin 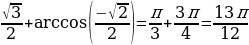
г) arcsin 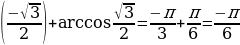
№134 а) arctg 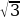 + arctg (-1) =
+ arctg (-1) = 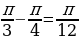
б) arctg 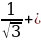 arctg 1 =
arctg 1 = 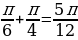
5. Итоги Д/з. §4, п. 10, №134(в, д)
№134 в) arctg (-1) + arcsin 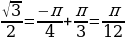
г) arctg 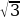 + arccos
+ arccos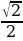 = -
= -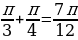
д) arcsin 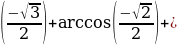 arctg
arctg 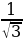 = =-
= =- 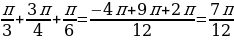







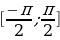 , что его синус равен а (об. arcsin)
, что его синус равен а (об. arcsin)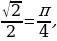 т.к. sin
т.к. sin 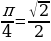 и
и 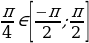
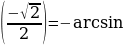 = -
= -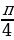
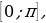 что его косинус равен а (об. arccos).
что его косинус равен а (об. arccos).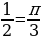
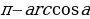
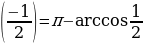 =
=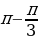 =
= 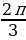
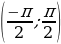 , что его тангенс равен а (об. arctg a)
, что его тангенс равен а (об. arctg a)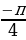
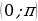 , что его котангенс равен а (об. arcctg a)
, что его котангенс равен а (об. arcctg a)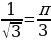
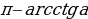
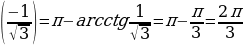
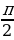
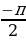 в) arccos (-1) =
в) arccos (-1) =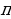
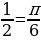 г) arccos
г) arccos 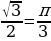 д) arccos
д) arccos 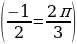
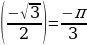 е) arccos
е) arccos 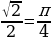
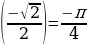 ж) arccos
ж) arccos 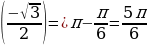
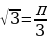 в) arcсtg (-1)=
в) arcсtg (-1)=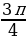
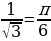 г) arcctg
г) arcctg 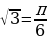
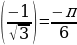 д) arcctg
д) arcctg 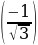 =
= 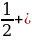 arccos
arccos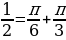 =
= 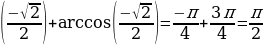
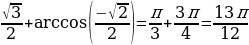
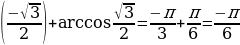
 + arctg (-1) =
+ arctg (-1) = 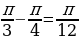
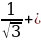 arctg 1 =
arctg 1 = 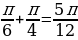
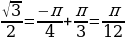
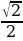 = -
= -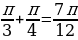
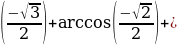 arctg
arctg 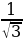 = =-
= =-