ОБУЧЕНИЕ РЕШЕНИЮ ПРАКТИКО-ОРИЕНТИРОВАННЫХ ЗАДАЧ ПРИ ПОДГОТОВКЕ К ОГЭ ПО МАТЕМАТИКЕ
ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА
БАКАЛАВРСКАЯ РАБОТА
студентки 5 курса 531 группы
Фроловой Юлии Александровны
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 3
1. ОБУЧЕНИЕ РЕШЕНИЮ ПРАКТИКО-ОРИЕНТИРОВАННЫХ ЗАДАЧ ПРИ ПОДГОТОВКЕ К ОГЭ ПО МАТЕМАТИКЕ: ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ 6
1.1 Определение практико-ориентированных задач, их специфика, классификация и структура 6
1.2 ПРАКТИКО-ОРИЕНТИРОВАННЫЕ ЗАДАЧИ В ОТКРЫТОМ БАНКЕ ОГЭ 2025 ПО МАТЕМАТИКЕ 12
ВВЕДЕНИЕ
Актуальность бакалаврской работы. В Федеральном государственном образовательном стандарте основного общего образования (далее ФГОС ООО) одним из основных требований к усвоению знаний учащихся является «способность обучающихся использовать на практике универсальные учебные действия» [13, с. 6], то есть, применять полученные знания в реальных жизненных ситуациях. В соответствии с Федеральной рабочей программой по учебному предмету «Математика» основного общего образования одной из приоритетных целей изучения математики является «формирование функциональной математической грамотности: умения распознавать проявления математических понятий, объектов и закономерностей в реальных жизненных ситуациях и при изучении других учебных предметов, проявления зависимостей и закономерностей, формулировать их на языке математики и создавать математические модели, применять освоенный математический аппарат для решения практико-ориентированных задач, интерпретировать и оценивать полученные результаты» [17, с. 5].
Для реализации этих требований в ОГЭ по математике включены практико-ориентированные задачи. В рамках ОГЭ под практико-ориентированными будем понимать задачи, материал для составления которых взят из окружающей действительности и ориентирован на формирование практических навыков учащихся. Практико-ориентированные задачи – это задачи из окружающей действительности, связанные с формированием практических навыков, необходимых в повседневной жизни, в том числе с использованием материалов краеведения, элементов производственных процессов. Практико-ориентированная задача – это вид сюжетных задач, требующий в своем решении реализации всех этапов метода математического моделирования. Все эти условия обусловили актуальность выбора темы бакалаврской работы.
В рамках данной бакалаврской работы будем считать понятия «задание» и «задача» синонимичными.
Рассматриваемые проблемы были объектами изучения авторов:
1 А.Д. Александров занимался изучением методологии математического образования, написал о сущности математики и её истории, указал на закономерности её развития. Его интересовало выражение специфичности и значимости математического знания для общества.
2 В.С. Абатурова внесла значительный вклад в расширение темы взаимосвязи практико-ориентированных задач и отдельных разделов школьного курса математики, Е.М. Ложкина занималась включением практико-ориентированных задач в отдельные разделы школьного курса математики, С.Ю. Полякова внесла значительный вклад в расширение темы применения практико-ориентированных задач в процессе обучения математике, Л.Э. Хаймина занималась проблемой развития темы включения практико-ориентированных задач в отдельные разделы школьного курса математики.
3 В.А. Далингер посвящала свои работы вопросам практико-ориентированного подхода при обучении математике; М.В. Егупова исследовала проблемы подготовки учителя к практико-ориентированному обучению математике в школе; В.П. Кизилова занималась исследованиями в области практико-ориентированного подхода при обучении математике; В.В. Пикан рассматривала прикладную направленность обучения математике как ориентацию содержания и методов обучения на применение математики в технике и смежных науках, в профессиональной деятельности, в сельском хозяйстве и в быту; Н.А. Терешина считала, что одна из функций таких задач – дать учащимся представление о возможностях использования математики для решения проблем, поставленных другими областями знаний; И.М. Шапиро выделила дидактические цели использования практико-ориентированных задач; Е.Н. Эрентраут провела исследование, в котором разработала технологию обучения решению практико-ориентированных задач для учащихся классов физико-математического профиля, занималась вопросами практико-ориентированного подхода при обучении математике.
Цель бакалаврской работы: теоретическое обоснование и практическая разработка методического обеспечения курса внеурочной деятельности по обучению решению практико-ориентированных задач при подготовке к ОГЭ по математике.
В соответствии с целью были поставлены следующие задачи:
1. Уточнить определение практико-ориентированных задач, их специфику,
классификацию и структуру.
2. Показать возможность использования практико-ориентированных задач на уроках и во внеурочной работе по математике в ходе реализации требований ФГОС ООО.
3. Систематизировать практико-ориентированные задачи, которые представлены в открытом банке ОГЭ по математике на сайте ФИПИ.
4. Составить рабочую программу курса внеурочной деятельности «Математика: от теории к жизни» для учащихся 9 класса.
5. Разработать методические рекомендации по организации обучения решению практико-ориентированных задач при подготовке к ОГЭ.
Методы бакалаврской работы: анализ психолого-педагогической, методико-математической литературы; обобщение опыта работы практикующих учителей; разработка и апробация методических материалов; педагогический эксперимент.
Структура бакалаврской работы: титульный лист, введение, два раздела («Обучение решению практико-ориентированных задач при подготовке к ОГЭ по математике: теоретические аспекты»; «Обучение решению практико-ориентированных задач при подготовке к ОГЭ по математике: практические аспекты»); список использованных источников.
1. ОБУЧЕНИЕ РЕШЕНИЮ ПРАКТИКО-ОРИЕНТИРОВАННЫХ ЗАДАЧ ПРИ ПОДГОТОВКЕ К ОГЭ ПО МАТЕМАТИКЕ: ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ 1.1 Определение практико-ориентированных задач, их специфика, классификация и структура
Термин «задача» в настоящее время применяется и в жизни, и в науке. В учебно-педагогической литературе встречаются самые разнообразные подходы к определению задачи, но общего определения понятия «задача» на сегодняшний день нет.
В словаре С. И. Ожегова определение задачи звучит следующим образом: «Задача – то, что требует исполнения, разрешения. Это упражнение, которое выполняется посредством умозаключения, вычисления» [12, с. 232].
Е. И. Титова [15, с. 761] считает, что наиболее простое определение задачи, было дано известным педагогом-математиком С. О. Шатуновским: «Задача есть изложение требования «найти» по «данным» вещам другие «искомые» вещи, находящиеся друг к другу и к данным вещам в указанных соотношениях». При этом предполагается, что понятия «вещь», «найти», «данные», «искомые» в каждом отдельном случае особо определяются.
Т. Ф. Ефремова под задачей предлагает рассматривать «цель, к которой стремятся, которую хотят достичь, обстоятельства, затруднения, которые надо преодолеть, поручение, задание (обычно трудно выполнимые, сложные), вопрос (обычно математического характера), требующий нахождения решения по известным данным с соблюдением определенных условий» [9, с. 384].
Для человека очень важна способность применять обобщённые знания и умения для разрешения конкретных ситуаций, возникающих в реальной жизни. По мнению педагога-психолога В. В. Давыдова и методистов - математиков Д. Пойа, Л. М. Фридмана, Г. И. Саранцева, Т. А. Ивановой, формировать способность разрешения проблем помогают специальные задачи. Практико-ориентированные задачи – это задачи из окружающей действительности, связанные с формированием практических навыков, необходимых в повседневной жизни, в том числе с использованием материалов краеведения, элементов производственных процессов. Практико-ориентированная задача – это вид сюжетных задач, требующий в своем решении реализации всех этапов метода математического моделирования.
В данной работе будем придерживаться определения задачи, данное Л. М. Фридманом. С точки зрения Л. М. Фридмана, «задача является проблемной ситуацией, которая выражается с помощью знаков естественного или научного языка» [19, с. 160]. Он считает, что если субъект при выполнении какой–либо деятельности на своём пути встречает трудности, то в результате возникает проблемная ситуация. Значит, проблемная ситуация – это не просто трудности, возникающие на пути субъекта, а его желание и стремление их устранить. Поэтому, субъект является элементом задачи, осознавший затруднение в своей деятельности.
Л. М. Фридман [20, с. 161] четко различает понятие задачи и проблемной ситуации по следующим признакам:
1. Проблемная ситуация всегда богаче содержанием, чем задача, ибо задач – это модель ситуации, отражающая лишь некоторые ее стороны.
2. Для каждой проблемной ситуации существует одна или несколько задач, которые могут отличаться друг от друга как совокупностью представленных в них свойств ситуации, так и языком, на котором задача выражена.
3. Проблемная ситуация существует реально, вне зависимости от какого-либо языка, а задача всегда связана с языком, на котором она изложена [20, с. 161].
Н. В. Соларёва даёт следующее определение: практико-ориентированная задача – это текстовое задание, носящее «не только дидактический характер, но и достоверность описываемой ситуации, и доступность ее разрешения средствами школьного курса» [14, с. 13].
Таким образом, практико-ориентированная задача – это задача из окружающей действительности, связанная с формированием практических навыков, необходимых в повседневной жизни.
Цель задач – формирование умений действовать в социально значимой ситуации. Практико-ориентированные задачи помогают учащимся работать с информацией, выделять и отбирать главное, выстраивать собственные пути решения и обосновывать их, работать в парах и в группах, развить свои точки зрения, чувства, убеждения и желания в поисковой творческой деятельности учащихся.
Виды практико-ориентированных заданий:
– аналитические – это определение и анализ цели, выбор и анализ условий и способов решения, средств достижения цели;
– организационно-подготовительные – это планирование и организация практико-ориентированной работы индивидуальной, групповой или коллективной по созданию объектов; анализ и исследование свойств объектов труда, формирование понятий и установление связей между ними;
– оценочно-коррекционные – это формирование действий оценки и коррекции процесса и результатов деятельности, поиск способов совершенствования, анализ деятельности.
Специфика практико-ориентированных задач заключается в следующем:
1.Значимость (познавательная, профессиональная, общекультурная, социальная) получаемого результата, что обеспечивает познавательную мотивацию учащегося.
2. Условие задачи сформулировано как сюжет, ситуация или проблема, для разрешения которой необходимо использовать знания из разных разделов основного предмета, из другого предмета или из жизни, на которые нет явного указания в тексте задачи.
3. Информация и данные в задаче могут быть представлены в различной форме (рисунок, таблица, схема, диаграмма, график и т. д.), что потребует распознавания объектов.
4. Указание (явное или неявное) области применения результата решения. Кроме этих обязательных особенностей, практико-ориентированные задачи могут иметь ещё и следующие:
– нестандартная структура (когда некоторые элементы не определены);
– наличие избыточных, недостающих и противоречивых данных в условии, делающих его объёмным;
– наличие нескольких способов решения, причём не все из них могут быть известны учащимся.
Структура практико-ориентированной задачи включает следующие элементы:
1. Стимул (фабула). Введение в проблему, текст, связанный с практической деятельностью или реальной жизнью, который погружает в контекст задания и мотивирует учащихся на его выполнение.
2. Задачная формулировка. Планирование (описание) деятельности ученика, необходимое для выполнения задания.
3. Источник информации. Объект, который содержит необходимый материал для успешного выполнения задания. Может быть представлен в виде сплошных (художественные и технические тексты, репортажи, комментарии, резюме и др.) и несплошных (рисунки, графики, таблицы данных, диаграммы, фотографии, афиши, карты, лента времени и др.) текстов.
4. Бланк для выполнения задания. Задает структуру предъявления учащимся результата своей деятельности по выполнению задания.
5. Инструмент оценивания (проверки). Это или модельный ответ, или оценочный бланк, ключ.
Практика показывает, что школьники с интересом решают и воспринимают задачи практического содержания. Учащиеся с увлечением наблюдают, как из практической задачи возникает теоретическая, и как чисто теоретической задаче можно придать практическую форму.
Отличительной особенностью практико-ориентированных заданий является возможность создания на их основе проблемной ситуации с привлечением фактов из реальной жизни. Обучение с использованием практико-ориентированных заданий положительно влияет на прочность знаний и качество обученности, так как у обучающегося возникают ассоциации с конкретными действиями и событиями. Необычная формулировка заданий, связь с жизнью, межпредметные связи вызывают интерес учащихся к освоению профессии, способствуют развитию любознательности, творческой активности.
По мнению Арнст Е. А. [4, с. 23], практико-ориентированные задания в обучении математике реализуют ряд функций:
– обучающая функция состоит в формировании знаний, умений и навыков, сохранении в памяти и воспроизведении фактов науки, понятий, правил, законов, теорий, усвоенные таким образом знания характеризуются полнотой, системностью, осознанностью;
– развивающая функция состоит в развитии обучаемого во всех направлениях: развитие речи, мышления, эмоционально-волевой и потребностно-мотивационной сфер личности;
– воспитательная функция состоит в формировании нравственных и эстетических представлений, системы взглядов на мир, способности следовать нормам поведения в обществе;
– побуждающая функция состоит в обеспечении активности личности, определяет собой субъективную значимость данной ситуации для учащегося;
– прогностическая функция состоит в предвидении последствий, дальнейших изменений решаемой ситуации, предупреждении возможных опасных тенденций, формулировании рекомендаций по их преодолению;
– интегративная функция состоит в системном, целостном обобщении внутридисциплинарных, и междисциплинарных знаний;
– контролирующая функция состоит в выявлении либо исходного, либо конечного состояния знаний и умений учащихся, изучении глубины и объема их усвоения.
Таким образом, использование практико-ориентированных заданий позволяет качественно осуществлять подготовку выпускников основного образования, обобщать внутридисциплинарные и междисциплинарные знания обучающихся, формировать умение решать практические задачи, связанные с реальными жизненными ситуациями в соответствии с требованиями ФГОС ООО.
Выделяют четыре уровня возрастающей сложности:
1. В тексте задачи есть прямая ссылка на математическую модель.
2. Прямой ссылки на модель нет, но предмет или отношение задачи явно сравнивается с соответствующим математическим объектом или отношением.
3. Предмет или отношение задачи сравнивается с математическим объектом или отношением, но неоднозначно и требует учёта реальной ситуации.
4. Предмет или отношение задачи не определено явно или его математический эквивалент неизвестен ученику.
Задачи первых двух уровней целесообразно использовать на уроках математики. Систематическое решение этих задач готовит учащихся к решению задач третьего и четвёртого уровней. Задачи третьего и четвёртого уровня лучше применять во внеурочное время, на факультативных занятиях.
Некоторые принципы составления практико-ориентированных задач:
– при формулировании условия взять за основу реальную практическую ситуацию, знакомую для учащихся;
– выбирать ситуации, которые позволят эффективно проверить не только знания и умения из различных тем и разделов школьного курса математики, но и других учебных предметов;
– предложенная ситуация должна привести учащихся к проблеме, для разрешения которой им необходимо применить математические знания, собственный жизненный опыт;
– текст задачи не должен содержать явного указания на область знаний и способ решения, необходимые для его успешного выполнения;
– для активизации мыслительной деятельности учащихся целесообразно включать в условие дополнительную информацию, являющуюся незначительной для решения поставленной проблемы;
– составляя задачу, полезно использовать разнообразные формы предоставления информации (таблицы, схемы, диаграммы, графики, рисунки);
– задача должна содержать ряд дополнительных вопросов, способствующих привлечению личного практического опыта, стимулированию исследовательской и творческой деятельности школьников.
1.2 ПРАКТИКО-ОРИЕНТИРОВАННЫЕ ЗАДАЧИ В ОТКРЫТОМ БАНКЕ ОГЭ 2025 ПО МАТЕМАТИКЕ
ОГЭ по математике начинается с пяти практико-ориентированных задач. Составители КИМ ОГЭ по математике утверждает, что эти задачи проверяют умение выполнять вычисления и преобразования, использовать приобретённые знания и умения в практической деятельности и повседневной жизни, строить и исследовать простейшие математические модели. Другими словами, эти задания проверяют, смогут ли ученики применить математику в реальной жизни.
В контрольно-измерительных материалах ОГЭ практико-ориентированные задачи включены в 1-5 задания. В открытом банке заданий сайта ФИПИ задания 1-5 разделены на 7 тем:
1) Участок
2) Квартира
3) План местности (деревня) - 2 вида
4) Листы
5) Тарифы связи
6) Печь для бани
7) Шины
Вариации ситуаций бытового содержания обширны, область исследования разнообразна, что повышает разностороннее применение математических знаний на ситуации бытового характера. Численные значения тех или иных элементов могут быть заданы в неявном виде, формул для вычисления неизвестных элементов не представлено, тем самым значительно повышает проблему разрешения данных задач. Для успешного решения таких задач необходимо выделить необходимые и достаточные условия из всего объема условий, схематически их интерпретировать, применить формулы вычисления неизвестных элементов, изученные в процессе всего обучения.
Рассмотрим конкретно практико-ориентированную задачи на тему «Шины» (рис. 1,2)

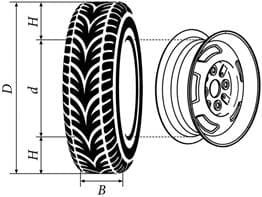
Рисунок 1 Рисунок 2
Автомобильное колесо представляет собой металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине. Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1). Первое число означает ширину шины В в миллиметрах. Следующее число означает высоту боковины шины H в процентах ширины.
В приведённом примере ширина шины равна 195 мм, а высота боковины равна 65 % от 195, то есть 126,75 мм.
Буква обозначает тип конструкции шины. Буква R означает, что шина радиальная, то есть нити каркаса в шине расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За буквой указан диаметр диска d в дюймах. На рисунке шина рассчитана на диск диаметром 15 дюймов. В одном дюйме 25,4 мм.
Таким образом, зная маркировку шины, можно найти общий диаметр колеса D.
Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 185/70 R14.
Задание 1.1
Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин
| Ширина шины(мм) | Диаметр диска(дюймы) |
| 13 | 14 | 15 |
| 165 | 165/70 | 165/65 | – |
| 175 | 175/65 | 175/65;175/60 | – |
| 185 | 185/65;185/60 | 185/60 | 185/55 |
| 195 | 165/60 | 195/55 | 195/55;195/50 |
Шины какой наименьшей ширины можно установить на автомобиль, если диаметр диска равен 15 дюймам? Ответ дайте в миллиметрах.
Ответ__________________________
Задание 1.2
Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин
| Ширина шины(мм) | Диаметр диска(дюймы) |
| 13 | 14 | 15 |
| 165 | 165/70 | 165/65 | – |
| 175 | 175/65 | 175/65;175/60 | – |
| 185 | 185/65;185/60 | 185/60 | 185/55 |
| 195 | 165/60 | 195/55 | 195/55;195/50 |
Шины какой наибольшей ширины можно устанавливать на автомобиль, если диаметр диска равен 13 дюймам? Ответ дайте в миллиметрах.
Ответ__________________________
Задание 2.1
На сколько миллиметров радиус колеса с шиной маркировки 205/45 R17 меньше, чем радиус колеса с шиной маркировки 215/55 R17?
Ответ__________________________
Задание 2.2
Сколько миллиметров составляет высота боковины шины, имеющей маркировку 245/60 R18?
Ответ__________________________
Задание 3
На сколько миллиметров увеличится диаметр колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 225/45 R17?
Ответ__________________________
Задание 4.
Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте
в миллиметрах.
Ответ__________________________
Задание 5.1
На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 215/55 R16? Результат округлите до десятых.
Ответ__________________________
Задание 5.2
Дмитрий планирует заменить зимнюю резину на летнюю на своём автомобиле. Для каждого из четырёх колёс последовательно выполняются четыре операции: снятие колеса, замена шины, балансировка колеса и установка колеса. Он выбирает между автосервисами А и Б. Затраты на дорогу и стоимость операций даны в таблице.
| Авто-сервис | Суммарные затраты на дорогу | Стоимость для одного колеса |
| Снятие колеса | Замена шины | Балансировка колеса | Установка колеса |
| А | 250 руб. | 52 руб. | 270 руб. | 190руб. | 52 руб. |
| Б | 430 руб. | 45 руб. | 250 руб. | 170 руб. | 45 руб. |
Сколько рублей заплатит Дмитрий за замену резины на своём автомобиле, если выберет самый дешёвый вариант?
Ответ__________________________
Таким образом, в открытом банке заданий ФИПИ по математике практико-ориентированные задачи по 7 темам при этом их численные значения могут быть заданы в неявном виде; формул для вычисления неизвестных элементов не представлено, что значительно повышает пробле



















