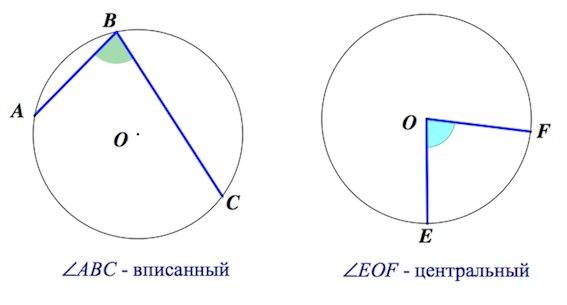
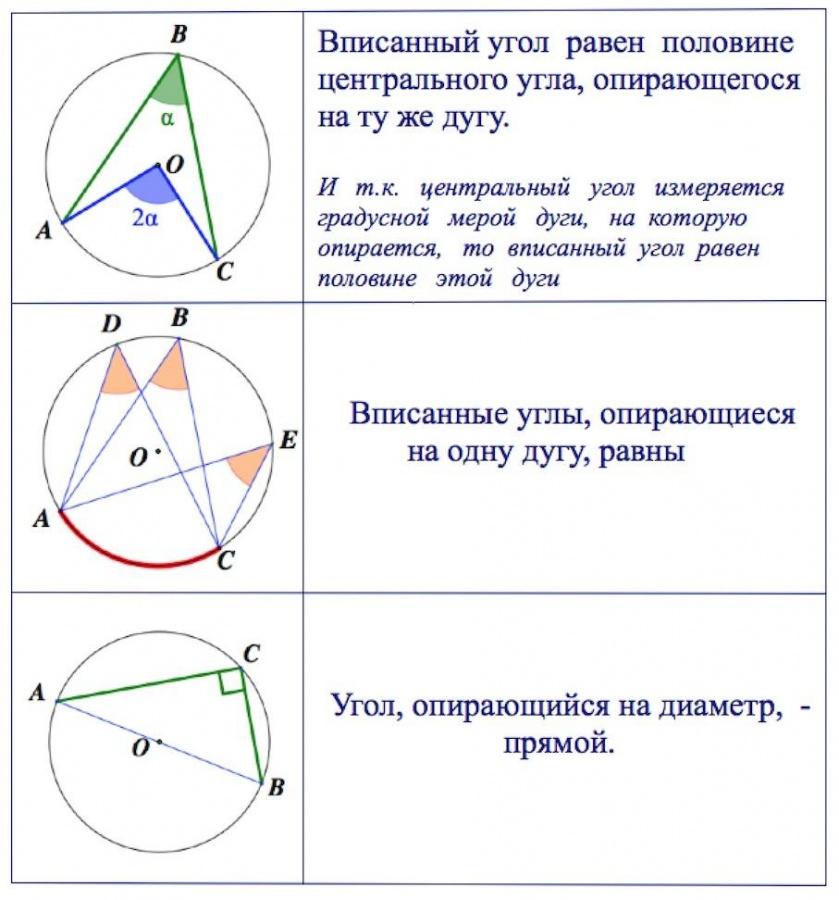
Просмотр содержимого документа
«вписанные и центральные углы А3»
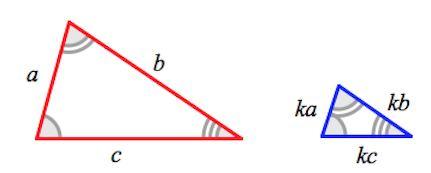
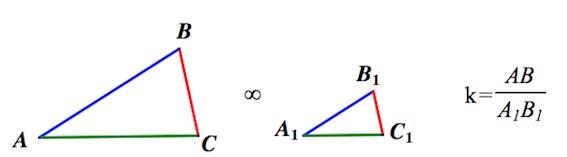
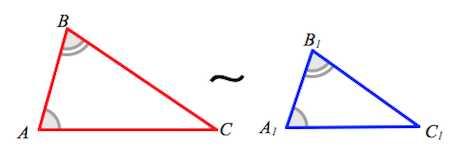
Просмотр содержимого документа
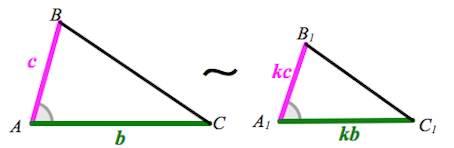
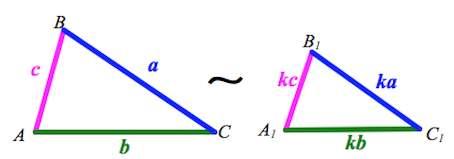
«подобные треугольники А3»
Просмотр содержимого документа
«хорды и окружности, медиана А3»
Хорда – отрезок, соединяющий две точки
окружности.
В частности, хорда, проходящая через центр окружности, называется диаметром.
Секущей к окружности называется прямая, которая пересекает окружность в двух различных точках.
Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.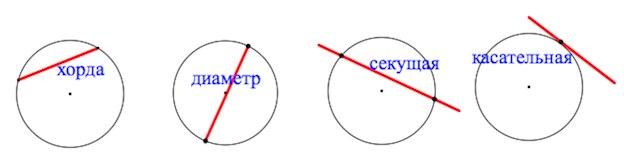
Свойства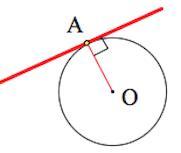
Радиус, проведенный в точку касания, перпендикулярен касательной
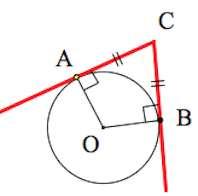
Отрезки касательных,
проведенных к окружности из одной точки, равны.
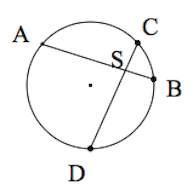
Отрезки пересекающихся
хорд связаны соотношением:
AS SB=DS
SB=DS SC
SC
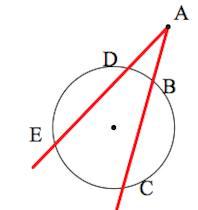
Произведения отрезков
секущих, проведенных из одной точки, равны: AB AC=AD
AC=AD AE
AE
Квадрат отрезка касательной равен произведению отрезков секущей, проведенной из той же точки: 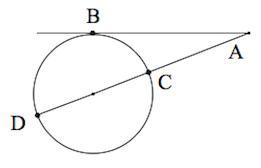
AB2=AC AD
AD
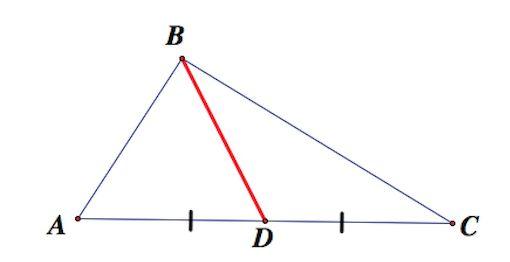
Медианой треугольника
называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны
Свойства
1. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.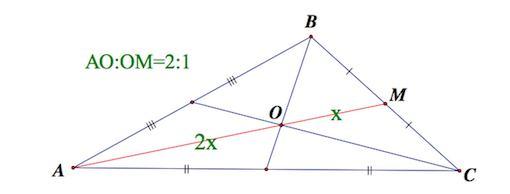
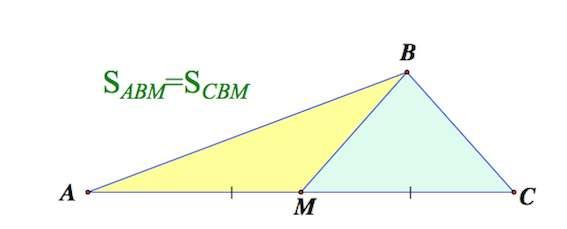
2. Медиана треугольника делит его на
два треугольника равной площади (равновеликих треугольника)
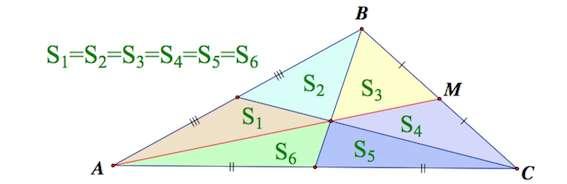
3. Медианы треугольника делят треугольник
на 6 равновеликих треугольников
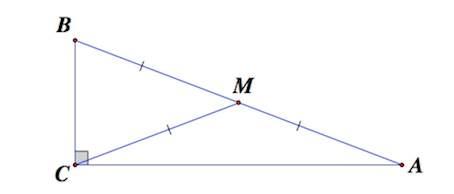
4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы
5. Длина медианы треугольника вычисляется по формуле:
ma=
где ma— медиана к стороне a![]() ; a,b,c — стороны треугольника
; a,b,c — стороны треугольника










 SB
SB

















