8.2. На доске нарисованы 23 знака — несколько плюсов и несколько минусов. Если среди них выбрать 10 любых знаков, то среди них точно окажется хотя бы один плюс. Если же среди них выбрать 15 любых знаков, то среди них точно окажется хотя бы один минус. Сколько всего плюсов выписано?
Ответ: 14. Решение. Поскольку среди любых 10 знаков есть плюс, то минусов на доске не больше 9 (иначе можно было бы выбрать 10 минусов). Поскольку среди любых 15 знаков есть минус, то плюсов на доске не больше 14 (иначе можно было бы выбрать 15 плюсов). Тогда всего знаков на доске не больше 9 + 14 = 23. Поскольку и по условию ровно 23, получаем, что минусов на доске ровно 9, а плюсов — ровно 14.
8.3. В роще живут 140 хамелеонов — синие и красные. Однажды несколько синих хамелеонов изменили свой окрас на красный. Тогда число синих хамелеонов уменьшилось в 5 раз, а число красных увеличилось в 3 раза. Сколько хамелеонов изменило свой окрас? Ответ: 80. Решение.
Пусть синих хамелеонов стало 𝑥. Тогда изначально синих хамелеонов было 5𝑥. Соответственно, красных хамелеонов изначально было 140 − 5𝑥. Тогда красных хамелеонов стало 3 ⋅ (140 − 5𝑥). Поскольку общее количество хамелеонов сохранилось, получаем уравнение 𝑥 + 3 ⋅ (140 − 5𝑥) = 140. Решая его, находим 𝑥 = 20. Тогда цвет изменили 5𝑥 − 𝑥 = 4𝑥 = 4⋅20 = 80 хамелеонов.
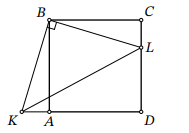
8.4. Дан квадрат 𝐴𝐵𝐶𝐷. Точка 𝐿 на стороне 𝐶𝐷 и точка 𝐾 на продолжении стороны 𝐷𝐴 за точку 𝐴 таковы, что ∠𝐾𝐵𝐿 = 90∘ . Найдите длину отрезка 𝐿𝐷, если 𝐾𝐷 = 19 и 𝐶𝐿 = 6.

8-5. В квадрате ABCD проведен такой отрезок CE, что углы, показанные на чертеже, равны 7α и 8α. Найдите значение угла α в градусах. Если необходимо, округлите ответ до 0,01 или запишите ответ в виде обыкновенной дроби.
8.6 Что получится, если в выражении (a + 1)(a + 3)(a + 4)(a + 5)(a + 6) раскрыть скобки и привести подобные члены?
a) a5 + 360.
b) a5 + 19a4 + 137a3 + 461a2 + 702a + 360.
c) a5 + 19a4 + 138a3 + 476a2 + 776a + 480.
d) a4 + 18a3 + 119a2 + 342a + 360.
e) a5 + 18a4 + 123a3 + 402a2 + 656a + 480
8.7. Про четырёхугольник 𝐴𝐵𝐶𝐷 известно, что ∠𝐵𝐴𝐶 = ∠𝐶𝐴𝐷 = 60∘ , 𝐴𝐵 + 𝐴𝐷 = 𝐴𝐶. Также известно, что ∠𝐴𝐶𝐷 = 230 . Сколько градусов составляет угол 𝐴𝐵𝐶?
Решение. Отметим на луче 𝐴𝐵 такую точку 𝐾, что 𝐴𝐾 = 𝐴𝐶. Тогда треугольник 𝐾𝐴𝐶 равносторонний; в частности, ∠𝐴𝐾𝐶 = 60∘ и 𝐾𝐶 = 𝐴𝐶. При этом 𝐵𝐾 = 𝐴𝐾 − 𝐴𝐵 = 𝐴𝐶 − 𝐴𝐵 = 𝐴𝐷. Это означает, что треугольники 𝐵𝐾𝐶 и 𝐷𝐴𝐶 равны по двум сторонам и углу 60∘ между ними (рис. 2). Осталось заметить, что угол 𝐴𝐵𝐶 — внешний для треугольника 𝐵𝐾𝐶 — равен внешнему углу при вершине 𝐷 треугольника 𝐷𝐴𝐶, который вычисляется как сумма двух внутренних: 60∘ + 23∘ = 83∘ .
8.2. На доске нарисованы 23 знака — несколько плюсов и несколько минусов. Если среди них выбрать 10 любых знаков, то среди них точно окажется хотя бы один плюс. Если же среди них выбрать 15 любых знаков, то среди них точно окажется хотя бы один минус. Сколько всего плюсов выписано?
8.3. В роще живут 140 хамелеонов — синие и красные. Однажды несколько синих хамелеонов изменили свой окрас на красный. Тогда число синих хамелеонов уменьшилось в 5 раз, а число красных увеличилось в 3 раза. Сколько хамелеонов изменило свой окрас?
8.4. Дан квадрат 𝐴𝐵𝐶𝐷. Точка 𝐿 на стороне 𝐶𝐷 и точка 𝐾 на продолжении стороны 𝐷𝐴 за точку 𝐴 таковы, что ∠𝐾𝐵𝐿 = 90∘ . Найдите длину отрезка 𝐿𝐷, если 𝐾𝐷 = 19 и 𝐶𝐿 = 6.


8-5. В квадрате ABCD проведен такой отрезок CE, что углы, показанные на чертеже, равны 7α и 8α. Найдите значение угла α в градусах. Если необходимо, округлите ответ до 0,01 или запишите ответ в виде обыкновенной дроби.
8.6 Что получится, если в выражении (a + 1)(a + 3)(a + 4)(a + 5)(a + 6) раскрыть скобки и привести подобные члены?
a) a5 + 360.
b) a5 + 19a4 + 137a3 + 461a2 + 702a + 360.
c) a5 + 19a4 + 138a3 + 476a2 + 776a + 480.
d) a4 + 18a3 + 119a2 + 342a + 360.
e) a5 + 18a4 + 123a3 + 402a2 + 656a + 480
8.7. Про четырёхугольник 𝐴𝐵𝐶𝐷 известно, что ∠𝐵𝐴𝐶 = ∠𝐶𝐴𝐷 = 60∘ , 𝐴𝐵 + 𝐴𝐷 = 𝐴𝐶. Также известно, что ∠𝐴𝐶𝐷 = 230 . Сколько градусов составляет угол 𝐴𝐵𝐶?
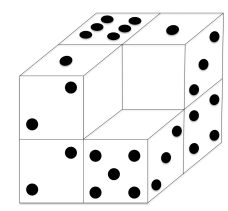
8.8 . Есть 7 абсолютно одинаковых кубиков, у каждого из которых на одной грани отмечена 1 точка, на другой — 2 точки, …, на шестой — 6 точек. Причём на любых двух противоположных гранях суммарно отмечено 7 точек. Из этих 7 кубиков сложили фигуру, изображённую на рисунке, так, что на каждой паре склеенных граней отмечено одинаковое количество точек. На всех гранях, кроме девяти, все точки стёрли, как показано на рисунке. Какое суммарное количество точек изначально было отмечено на поверхности фигуры?