Просмотр содержимого документа
«ОЛИМПИАДНЫЕ ЗАДАНИЯ И РЕШЕНИЯ ПО МАТЕМАТИКЕ.»
ОЛИМПИАДНЫЕ ЗАДАНИЯ
Решите арифметический ребус
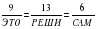 , в котором одинаковыми буквами обозначены одинаковые цифры, разными буквами – разные цифры.
, в котором одинаковыми буквами обозначены одинаковые цифры, разными буквами – разные цифры.
В кучке 2016 камешков. Двое играющих поочерёдно берут из кучки камешки, каждый не менее одного и не больше трёх. Выигрывает тот, кто берёт последний камешек. Кто выиграет при правильной игре: начинающий или его партнёр?
В школе все учащиеся сидят за партами по двое. У 60% мальчиков сосед по парте тоже мальчик. У 20% девочек сосед по парте тоже девочка. Сколько процентов учащихся в этой школе составляют девочки.
Найдите гипотенузу прямоугольного треугольника с острым углом 15°, если известно, что высота треугольника, опущенная на гипотенузу, равна 1.
В шести коробках лежат шарики: в первой – 1, во второй – 2, в третьей – 3, в четвертой – 4, в пятой – 5, в шестой – 6. За один ход разрешается в любые две коробки прибавить по одному шарику. Можно ли за несколько ходов уравнять количество шариков во всех коробках?
Какой цифрой заканчивается выражение 811 – 416 + 645 ?
РЕШЕНИЯ.
Ответ:  .
.
Решение. Число ЭТО кратно 9. Полагая ЭТО=9k, где kN, получаем: РЕШИ=13k, САМ=6k, ЭТО+РЕШИ+САМ=28k. Поскольку все буквы в ребусе различны, то использованы все 10 цифр, а, следовательно,
Э+Т+О+Р+Е+Ш+И+С+А+М=0+1+2+3+4+5+6+7+8+9=45,
т.е. сумма цифр в сумме ЭТО+РЕШИ+САМ кратна 9 и 28k кратно 9.
Из равенства ЭТО=9k находим k=ЭТО:9, откуда k
Из равенства РЕШИ=13k получаем k=РЕШИ:13, т.е. k76.
Таким образом, k81, 90, 99, 108. Перебором находим k=81.
Ответ. Выигрывает второй игрок.
Тактика основана на том, что число 2016 делится на 4. Если первый взял один камешек, то второй берёт 3. Если первый взял 2 камешка, то второй берёт 2. Если первый взял 3 камешка, то второй берёт 1. Настанет момент, когда первому камешек не достанется, а, значит, он проиграл.
Ответ. 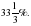
Мальчиков сидят с девочками 100% – 60% = 40% от числа мальчиков 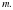 Девочек с мальчиками 100% – 20% = 80% от числа девочек
Девочек с мальчиками 100% – 20% = 80% от числа девочек 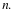 Числа
Числа 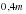 и
и 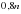 равны, отсюда
равны, отсюда 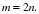 Мальчиков в 2 раза больше. Девочки составляют одну треть от общего числа учащихся.
Мальчиков в 2 раза больше. Девочки составляют одну треть от общего числа учащихся.
Ответ: 4.
Решение: Пусть в прямоугольном треугольнике АBC
угол АBC равен 15°,
высота CН =1(см. рис).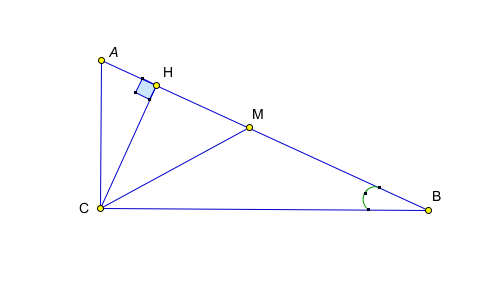
Проведем медиану CM .
Она разбивает треугольник
АBC на два равнобедренных треугольника АMC и BMC, причем АМ = CM = MB. Но тогда MCB =15°, AMC = 30°(внешний для треугольника BMC, а значит гипотенуза CM прямоугольного треугольника CHM равна 2. Окончательно получаем: АB = AM + MB = 4.
Ответ: нельзя.
Решение: Первоначально шариков в коробках 1 + 2 + 3 + 4 + 5 + 6 = 21, а после n ходов станет 21 + 2n. С другой стороны, общее число шариков в коробках, когда их станет поровну, станет равно 6m, где m – число шариков в одной коробе. Получим, что 21 + 2n = 6m. Но это равенство невозможно при натуральных n и m, т.к. его левая часть нечетна, а правая четна.
Ответ: 0.
Решение:
811 – 416 + 645 = 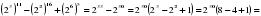
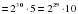 .
.







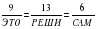 , в котором одинаковыми буквами обозначены одинаковые цифры, разными буквами – разные цифры.
, в котором одинаковыми буквами обозначены одинаковые цифры, разными буквами – разные цифры. .
.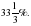
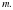 Девочек с мальчиками 100% – 20% = 80% от числа девочек
Девочек с мальчиками 100% – 20% = 80% от числа девочек 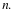 Числа
Числа 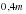 и
и 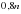 равны, отсюда
равны, отсюда 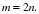 Мальчиков в 2 раза больше. Девочки составляют одну треть от общего числа учащихся.
Мальчиков в 2 раза больше. Девочки составляют одну треть от общего числа учащихся.
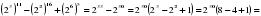
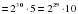 .
.









