Просмотр содержимого документа
«Опорный конспект по теме "Преобразование алгебраических выражений"»
Преобразование алгебраических выражений
Преобразование любого алгебраического выражения можно свести к сложению, вычитанию, умножению иди делению алгебраических дробей. Из правил действий с дробями следует, что сумму, разность, произведение и частное алгебраических дробей всегда можно представить в виде алгебраической дроби. Значит, и всякое алгебраическое выражение можно представить в виде алгебраической дроби.
Итак, формулы, которые нам понадобятся:
Действия с дробями:



Свойства степени:





Решим несколько примеров:
Пример 1
Найдите значение выражения:

Пример решается в два действия: сначала считается результат выражения в скобках, затем – умножение. Обозначим действия:

1. 
2. 
2) 
1. 
2. 
Пример 2
Найдите значение выражения: 
1) 
2) 
Пример 3
Найдите значение выражения:
1) 
2) 
Пример 4
Найдите сумму чисел:  и
и  .
.

Пример 5
Найдите значение выражения:
1) 
2) 
Пример 6
Представим выражение в виде алгебраической дроби:

Преобразование можно вести по-разному. Можно представить в виде алгебраических дробей отдельно числитель и знаменатель, а затем разделить первый результат на второй. А можно умножить числитель и знаменатель на ху, воспользовавшись основным свойством дроби. В этом случае преобразование окажется проще:
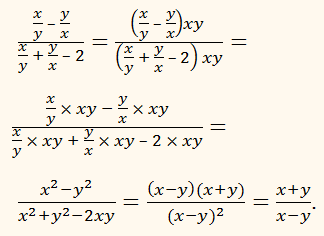
Если надо выполнить несколько действий над данными алгебраическими дробями или упростить, громоздкое выражение с алгебраическими дробями, можно выполнить преобразования двумя способами: по частям и цепочкой.
Пример 7
Упростить выражение:


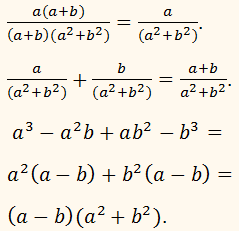

Решите самостоятельно
Найдите значение выражения  , если
, если  ,
,  .
.
Найдите значение выражения  , если
, если  .
.
Упростите выражение  .
.
Найдите значение выражения  , если
, если  ,
, 
Упростите выражение  .
.

Разность квадратов:

Квадрат суммы или разности:

Это основные формулы, которые нам понадобятся. Также вы должны уметь группировать многочлены и выносить общие множители за скобки.
Разберем основные примеры, встречающиеся в экзаменационных работах.
Пример 1.
Сократите дробь.

Решение:

Пример 2.
Разложите на множители.

Решение:

Пример 3
Упростите выражение.

Решение:

Пример 4.
Упростите выражение.

Решение:

Пример 5.
Какое из чисел больше:  или
или  ?
?
Решение:
Найдем квадраты чисел

Так как

то

получаем что

Примеры для самостоятельного решения.
1.

Решение:

2.
Решите уравнение.

Решение:

3.

Решение:

4.

Решение:

Домашнее задание
1.
Упростить.

Решение:

2.
Решить уравнение

Решение:

3.
Сократите дробь.

Решение:

4.
Сократите дробь

Решение:

5.

Решение:












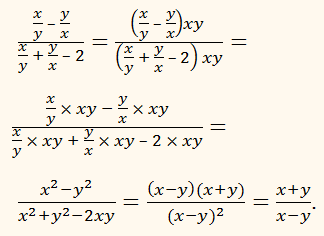


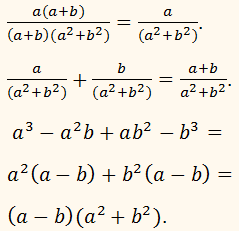

 , если
, если  ,
,  .
. , если
, если  .
. , если
, если  ,
, 
 .
.
 или
или  ?
?









