Определение подобных треугольников

Бермудские острова, владение Великобритании в северо-западной части Атлантического океана, близ берегов Северной Америки .

Пуэрто-Рико, содружество Пуэрто-Рико, владение США в Вест-Индии, на острове Пуэрто-Рико и близ лежащих островах

Флорида, полуостров на юго-востоке Северной Америки, часть штата Флорида (США).

Треугольник

В

∆ АВС – треугольник

А,В,С – вершины

АВ, ВС, АС – стороны

А

С

А

Равнобедренный треугольник

• Две стороны равны
• Углы при основании равны

• Биссектриса, проведённая к основанию, является медианой и высотой

Равносторонний треугольник

• Все стороны равны

• Углы все равны

Прямоугольный треугольник

• Один угол прямой

• Сумма двух острых углов равна 90 °

• Катет, лежащий против угла в 30 ° равен половине гипотенузы (а = с)

• с ² = а ² + в ²

• S = а · в

30 °

с

в

90 °

а

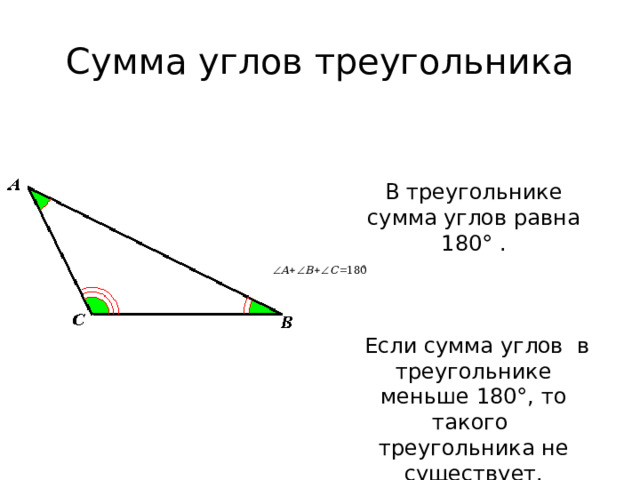
Сумма углов треугольника

В треугольнике сумма углов равна 180° .

Если сумма углов в треугольнике меньше 180° , то такого треугольника не существует.

Признаки равенства треугольников

• По двум сторонам и углу между ними

• По стороне и двум прилежащим к ней углам

• По трём сторонам

ВПР

Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола

дерева на 1,8 м?

ОГЭ

Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 5,5 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 4,8 м. Найдите длину троса. Ответ дайте в метрах.

Исследовать пары треугольников

1 этап исследования

2 этап исследования

Ответьте на вопросы:

• Что можно сказать про углы каждой пары треугольников?
• Что можно сказать про стороны каждой пары треугольников?

Заполните пропуски, используя ответы на предыдущие этапы исследования:

Если углы двух треугольников __________и стороны одного треугольника ___________ сходственным сторонам другого треугольника, то такие треугольники называются ПОДОБНЫМИ.

3 этап исследования

Найдите коэффициенты подобия каждой пары треугольников из 1 этапа исследования:

4 этап исследования

Сравните данные коэффициенты подобия треугольников с соответствующими им отношениями периметров и площадей

Сделайте вывод:

• Отношение периметров подобных треугольников равно ______________________.
• Отношение площадей подобных треугольников равно ________________________.

Вывод:

• Отношение периметров подобных треугольников равно коэффициенту подобия.

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Решение задач