Тема урока: Площадь криволинейной трапеции.
Урок приобретения новых знаний и умений.
Цели урока:
1. Обучающая цель: создать условия для формирования представления о площади
криволинейной трапеции и интеграле.
2. Развивающая цель: развивать логическое мышление школьников через
установление причинно-следственных связей.
3. Мотивационная цель: побудить интерес к изучению предмета.
План урока:
Содержание этапов урока Виды и формы работы
1. Организационный момент Приветствие
2. Мотивационное начало урока Постановка цели урока
3. Работа по повторению ранее
изученного материала
Выполнение заданий на повторение. Коллективная и
самостоятельная формы работы.
4. Изучение нового материала Приобретение новых знаний и их первичное осмысление. Работа с дополнительными источниками информации.
5. Решение заданий, домашнее задание
Письменная работа в рабочих тетрадях
6. Подведение итогов урока Выставление оценок, анализ работы учеников на уроке
7. Рефлексия
Ход урока:
1. Организационный момент
2. Мотивационное начало урока
Учитель: Здравствуйте, тема нашего сегодняшнего урока: Площадь криволинейной трапеции. Цель
нашего урока – узнать какая фигура называется криволинейной трапецией, как находится площадь
криволинейной трапеции, что такое интеграл, познакомиться с формулой Ньютона – Лейбница, научиться вычислять площадь криволинейной трапеции.
Авторы: Дорофеев Г.В., Муравин Г.К., Седова Е.А., Москва , «Дрофа», 2000.)
Является ли функция F(x)=x³-3x+1 первообразной функции f(x)=3(x²-1)?
Решение:
D(F)=R, D(f)=R.
F(x)- определена , непрерывна и дифференцируема на R.
Найдем производную:
F'(x)=(x³-3x+1)ꞌ=3x²-3=3(x²-1)=f(x)
Т.к.F'(x)=f(x),то F(x) – является первообразной функции f(x).
Самостоятельная работа:
Вариант – 1 Вариант – 2
1.Найдите одну из первообразных для данной функции на R:
a) f(x)=x³+5; a) f(x)= - x² - 8;
б) f(x)= -3,5; б) f(x)= 6,4;
в) f(x)= 2sinx + 3cosx в) f(x)=3sinx – 2cosx.
2.Для функции f(x) найдите первообразную, график которой проходит через точку:
а) f(x)=x²; М( -1;2); а) f(x)=x³; М( 1; -1);
б) f(x)= sinx ; А(π/2; -1); б) f(x)= cosx; А(π; 1);
в) f(x)= 2x – 2; А(2;1). в) f(x)= cosx; А( -1;1).
1. Пусть на отрезке [a;b] оси ОХ задана непрерывная функция f(x), не меняющая на нем знака.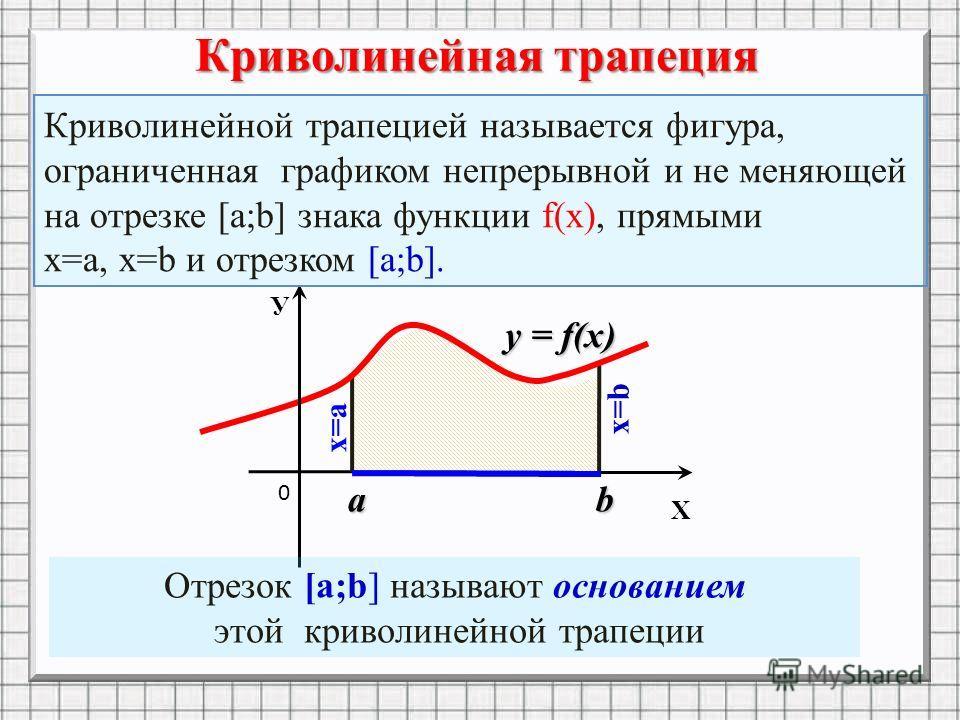
Определение: Фигуру, ограниченную графиком функции f(x), отрезком [a;b] и прямыми
х=a, х=b, называют криволинейной трапецией.
Рисунки, на которых изображены различные виды криволинейных трапеций, показываются на экране, либо на выдвижных досках.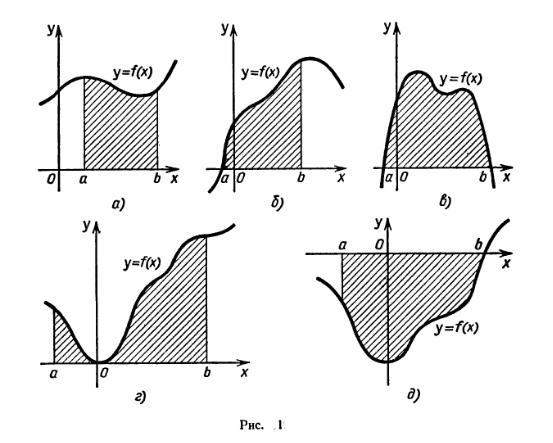
2. Для вычисления площадей криволинейных трапеций применяется следующая теорема:
Теорема: Если функция f(x) – непрерывная и неотрицательная на отрезке [a;b], a F – ее
первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна
приращению первообразной на отрезке [a;b], т.е.
S(x) = F(b) – F(a). (1)
Доказательство:Т.к. S – первообразная для f, то в силу основного свойства первообразных для
всех х из [a;b] имеем: S(x) = F(x) + C, где С – некоторая постоянная, а F – одна из
первообразных для функции f.
Для нахождения С подставим х = а:
F(a) + C = S(a) = 0,
Откуда С = - F(a). Следовательно,
S(x) = F(x) – F(a) (2)
Поскольку площадь криволинейной трапеции равна S(b), подставляя x=b в формулу (2),
получим S = S(b) = F(b) – F(a).
3. Пример. Вычислить площадь криволинейной трапеции, ограниченной графиком функции
f(x) = x² и прямыми: y = 0; x = 1; x = 2.
Решение: Для функции f(x) = x² одной из первообразных является F(x) = x³/3.Следовательно: S = F(2) – F(1) = 8/3 – 1/3 = 7/3(кв. ед.)
Ответ: 7/3(кв.ед.)
4. Разность F(b) – F(a) называется интегралом от функции f(x) на отрезке [a;b] и обозначают
так: ∫ f(x) dx
∫ f(x)dx = F(a) – F(b) - формула Ньютона – Лейбница.
Задача: Найти площадь криволинейной трапеции, ограниченной линиями:
1. y = (x – 1)², осью ОХ и прямой х = 2.
2. y =2/√x, осью ОХ и прямыми х = 1, х = 4.
3. y = x³, a = 2, b = 4, y = 0.
4. y = x² + 1, a = 1, b = 2.
5. y = sinx, a = π/3, b = π .
Алгебра и начала анализа для 10 -11класса, авторы: А.Н.Колмогоров и др., Москва,
«Просвещение», 2002, п.29, №353,354,355(а,б).
6.Подведение итогов урока. Выставление оценок.


















