МБОУ «Средняя общеобразовательная школа – интернат поселка Ефимовский»
Учитель математики: Ванжа Л.М.
Из опыта работы по методической теме: «Формирование интереса к учебной деятельности через применение игровых технологий на уроках математики»
Условия возникновения и становления опыта
Целью воспитательного процесса педагогический коллектив школы ставит создание необходимых условий для саморазвития, самореализации личности каждого ученика. Мой опыт работы в школе доказывает, что глубокие , прочные и , главное, осознанные знания могут получить все школьники, если у них развит стойкий познавательный интерес , создаются благоприятные и эффективные условия для развития познавательной активности детей, повышения их интеллектуального и творческого потенциала.
Задача, конечно, не слишком простая:
Играя учить и учиться, играя.
Но если с учёбой сложить развлеченье,
То праздником станет любое ученье!
Актуальность и перспективность опыта, практическая значимость
Жизнь в условиях быстро меняющегося мира ставит перед школой задачу: дать человеку не просто систему знаний и определённый запас информации, знания и информация сейчас быстро устаревают. Главное – школа должна воспитать личность, готовую к творческому поиску, самостоятельному добыванию и обновлению знаний, саморазвитию и самосовершенствованию, способную успешно адаптироваться в новых жизненных условиях.
На современных школьников обрушивается огромный поток информации. Не умея быстро сконцентрировать свое внимание, запомнить нужное и отсеять второстепенное, ребенок не может ориентироваться в безбрежном информационном море.
Использование разнообразных форм и методов ведения урока, применение на уроках элементов передовых педагогических технологий, большая индивидуальная урочная и внеурочная работа с учащимися позволяет учителю добиваться прочных знаний по математике.
В своей работе я стараюсь разумно сочетать и использовать сильные стороны традиционных и активных форм обучения. Активные формы обучения отнесены к классу образовательных технологий, обозначенных как «технологии модернизации традиционного обучения на основе активизации и интенсификации деятельности учащихся». Одной из форм являются игровые технологии.
Игровые технологии, я считаю, являются одной из уникальных форм обучения, которая позволяет сделать интересным и увлекательным не только работу учащихся на творческо – поисковом уровне, но и будничные шаги по изучению предмета математики.
Прочные знания, умения и навыки учащиеся приобретают в процессе активной познавательной деятельности, важнейшей предпосылкой которой является интерес. Как известно, стойкий познавательный интерес формируется при сочетании эмоционального и рационального обучения. Вот почему включение игры и игровых ситуаций делает процесс обучения интересным, способствует преодолению трудностей в усвоении материала.
Проблема умственного развития учащихся, падение интереса и внимания к учению, увеличение умственной нагрузки на уроках математики являются одними из важных в образовании.
Работать над этой темой также подтолкнули противоречия:
между сложившимися малоэффективными формами и методами проведения стандартных уроков и необходимостью использования форм и методов работы, способствующими повышению активной мыслительной деятельности учащихся на уроках;
между полученными теоретическими знаниями и неумением применять их на практике;
между сложностью материала и недостаточным количеством часов, отведённых для его закрепления;
между различным темпом усвоения учащимися трудных тем программы;
между стремлением личности к самоутверждению и обязательными требованиями учебных программ.
Ведущая педагогическая идея
Ведущей педагогической идеей опыта является учение без принуждения, основанная на достижении успеха, на переживании радости познания, на подлинном интересе, развитие личности ребёнка, его творческих способностей, интереса к учению, формирование желания и умения учиться.
Основной целью моей работы является формирование заинтересованности учащихся в получении новых, закреплении полученных ранее знаний, саморазвитии, чтобы каждый ученик чувствовал себя полноценным участником учебного процесса. В ходе работы выделены основные задачи:
• Провести теоретический анализ философской, психологической и педагогической литературы с целью выявления сущности игры.
Выявить педагогические и методические основы конструирования и использования игровых технологий;
Раскрыть особенности использования игр и игровых ситуаций на разных этапах изучения различного по характеру математического материала;
Помочь ученику увидеть основную проблему познавательного задания и наметить план поиска путей выхода из возникшего затруднения, побудить его к активной поисковой деятельности;
Указать направление и границы поиска наиболее рациональных путей выхода из проблемной ситуации.
исследовать отношение детей к различного вида играм на уроках математики;
определить место игр и игровых ситуаций в системе других видов деятельности на уроке.
Интерес – сложное понятие, которое можно рассмотреть с позиций разных групп авторов. В переводе с латинского языка слово «интерес» (interest) означает «имеет значение, важно». Филологи дают следующее определение: «Интерес – это особое внимание к чему-нибудь, желание вникнуть в суть, узнать, понять; занимательность, значительность». С точки зрения психологов: «Интерес – это активная познавательная направленность человека на тот или иной предмет, явление или деятельность, связанная с положительным эмоциональным отношением к ней». Значит, каковы бы ни были трактовки этого понятия, можно сказать, что значение интереса велико. Интерес побуждает к овладению знаниями, заставляют учеников активно работать, преодолевая трудности и препятствия.
Познавательный интерес – более узкое понятие, суть которого заключается в целенаправленном стремлении учащихся к овладению знаниями, в активном поиске новых способов углубления познания. По характеру проявления познавательного интереса в процессе изучения предмета выделяются уровни развития познавательного интереса: 1 – низкий уровень, 2 – средний и 3 – высокий уровень. Так, у учащихся с низким уровнем развития познавательного интереса активность на уроках ситуативная, часты отвлечения, предпочтение отдается задачам репродуктивного характера, со стереотипными действиями. Учащиеся со средним уровнем развития познавательного интереса предпочитают также поисковый характер деятельности, но не всегда склонны к выполнению творческих заданий, их самостоятельная деятельность носит эпизодический характер, зависит от внешних стимулов. Учащиеся с высоким уровнем развития интереса отличаются самостоятельностью, активным участием на уроке, предпочтением учебной деятельности более трудного характера. Таким образом, развитие познавательных процессов школьников основывается на создании интереса к предмету. Умелое применение учителем знаний по психологии, педагогике и по предмету в целом, дают гарантию результативности образовательного процесса. Д
 ля развития познавательного интереса на уроках математики используется игра. «Каков ребёнок в игре, таков во многом он будет в работе, когда вырастет. Поэтому воспитание будущего деятеля происходит прежде всего в игре. И вся история отдельного человека как деятеля и работника может быть представлена в развитии игры и в постепенном переходе её в работу…» Эта мысль принадлежит А.С. Макаренко, большому поборнику детской игры. Современная дидактика, обращаясь к игровым формам обучения на уроках и во внеурочное время, справедливо усматривает в них возможности эффективного взаимодействия педагога и учащихся. Современное образование характеризуется вариативностью и многообразием, как в содержании, так и в технологиях, используемых в учебно-воспитательном процессе. Поддерживать интерес, активизировать мыслительную деятельность детей можно с помощью игровых технологий.
ля развития познавательного интереса на уроках математики используется игра. «Каков ребёнок в игре, таков во многом он будет в работе, когда вырастет. Поэтому воспитание будущего деятеля происходит прежде всего в игре. И вся история отдельного человека как деятеля и работника может быть представлена в развитии игры и в постепенном переходе её в работу…» Эта мысль принадлежит А.С. Макаренко, большому поборнику детской игры. Современная дидактика, обращаясь к игровым формам обучения на уроках и во внеурочное время, справедливо усматривает в них возможности эффективного взаимодействия педагога и учащихся. Современное образование характеризуется вариативностью и многообразием, как в содержании, так и в технологиях, используемых в учебно-воспитательном процессе. Поддерживать интерес, активизировать мыслительную деятельность детей можно с помощью игровых технологий.
Новизна опыта:
в комбинации элементов известных методик,
в рационализации, усовершенствовании отдельных сторон педагогического труда,
Технология опыта
Игра – творчество и труд одновременно. Игра и работа неразделимы: работа и учение не теряют элементов игры и могут приобретать характер игры. Игры открывают практически неограниченные возможности для проявления активности обучающихся, создают уникальные условия для личностного проявления. Игру можно использовать на различных этапах урока и во внеурочной деятельности обучающихся.
Создаются благоприятные и эффективные условия для развития познавательной активности детей, повышения их интеллектуального и творческого потенциала, расширения математического кругозора, в приобретении учащимися знаний в процессе активной мыслительной деятельности в условиях проблемной ситуации.
Интерес – один из инструментов, побуждающих учащихся к более глубокому познанию предмета, развивающий их способности.
Увеличение умственной нагрузки на уроках математики заставляет задуматься над тем, как поддержать у учащихся интерес к изучаемому материалу, их активность, внимательность на протяжении всего урока. В связи с этим ведутся поиски новых эффективных методов обучения и таких методических приемов, которые активизировали бы мысль школьников, стимулировали бы их к самостоятельному приобретению знаний, развивали бы качества внимания.
Возникновение интереса к математике у значительного числа учащихся зависит в большей степени от методики ее преподавания, от того, насколько умело будет построена учебная работа. Надо позаботиться о том, чтобы на уроках каждый ученик работал активно и увлеченно, и использовать это как отправную точку для возникновения и развития любознательности, глубокого познавательного интереса. Это особенно важно в подростковом возрасте, когда еще формируются, а иногда и только определяются постоянные интересы и склонности к тому или иному предмету. Именно в этот период нужно стремиться раскрыть притягательные стороны математики. Чтобы не быть голословной, я поделюсь некоторыми идеями и находками, которые я применяю на практике, используя свой педагогический опыт. Большое внимание уделяю началу урока: считаю, что интересное начало урока позволяет с первых минут создать необходимые условия для успешной работы учащихся.
Перечислю некоторые способы организации начала урока:
Цель: создать с первых минут урока необходимые условия для успешной совместной деятельности учителя и учащихся по достижению намеченной цели.
а) устный счёт с включением задач, которые решаются с опорой на их жизненный опыт, на их смекалку;
б) решение игровых и занимательных задач,
в) даются задания и ответы к ним, среди которых есть как верные, так и неверные. Предлагается проверить их.
г) традиционным способом записано на доске решение задачи. Предлагается найти более короткое решение.
д) перед учащимися ставится математическая проблема, которая ещё не обсуждалась в классе. Ученики намечают план поиска её решения.
е) учащиеся считают устно и выдают ответы с помощью сигнальных карточек или перфокарт.
Результативность:
Нетрадиционное начало урока позволяет учащимся с первых минут урока включиться в работу по развитию мыслительной деятельности, а это даёт успех всему уроку
Устная работа – один из важнейших этапов урока.
Во время устной работы выясняется, хорошо ли усвоен теоретический материал; соответствующий подбор вопросов позволяет подготовить к восприятию нового; это одна из удобных форм организации повторения.
Во время устной работы можно задействовать всех учащихся класса, что позволяет значительно оживить урок, сделать его более динамичным и эмоциональным; в зависимости от формы организации устной работы возможно проследить, как хорошо учащиеся владеют определёнными навыками, насколько грамотно они строят предложения. Регулярно использую устную работу в 5-7 классах на каждом уроке. Начинаю с более лёгких заданий, постепенно их усложняя. Это делается с одной стороны для того, чтобы учащиеся постепенно втянулись в быстрый ритм устной работы, а с другой – чтобы не подавить уверенность в своих силах у слабых учеников.
Виды устного счёта, например, « Математический футбол», « Молчанка», « Лесенка», « Цепочка»…
Выполнение этих заданий включает в работу и развивает все виды памяти – слуховую, зрительную, моторную, разговорную.
Устный счёт в развитии логического мышления и математической речи преследует следующие цели и задачи:
воспитание культуры вычислительных навыков;
развитие познавательной активности, логически совершенной речи;
способности ясно, убедительно, чётко аргументировать свой ответ и рассуждения;
повторение ранее изученного;
подготовка к изучению новой темы.
Игровые ситуации в процессе изучения и закрепления нового материала.
Цель: развитие познавательного интереса, создание положительной мотивации к учению.
Возможность и целесообразность использования игровых ситуаций на уроках математики в процессе изучения и закрепления нового материала различны в зависимости от дидактических целей урока. В большинстве случаев они применяются в качестве вспомогательного средства для возбуждения познавательного интереса и создания проблемных ситуаций.
Для создания игровых ситуаций на уроках математики используются исторические экскурсы, жизненные факты, занимательные задачи, научно-популярные рассказы, отрывки из литературных произведений, в математическом содержании которых содержатся противоречия научных фактов с привычными жизненными представлениями учащихся, противоречия между необходимостью выполнить определённое задание и невозможностью осуществить его.
Рассмотрим примеры использования игровых ситуаций
Геометрия 7 класс. «Теорема о сумме углов треугольника»
Учащимся предлагается построить треугольник по трём сторонам:
1 ряд: АВ = 7, АС = 2, ВС = 3.
2 ряд: АВ = 4, ВС = 3, АС = 7.
3 ряд: АВ = 3, ВС = 2, АС = 8.
Выполняя задания, ребята убеждаются в невозможности такого построения. Как следствие этого, актуализируются знания об условии существования треугольника.
Дальше предлагается построить треугольник по заданным углам:
1 ряд: А = 37, В = 28, С = 90.
2 ряд: А = 72, В = 50, С = 110.
3 ряд: А = 23, В = 50, С = 38.
В данном задании не выполняется условие о сумме внутренних углов треугольника. Создаётся проблемная ситуация. Учитель усиливает проблемность вопросами: зависит ли сумма внутренних углов треугольника от его размеров, положения на плоскости, формы? Предлагается начертить два треугольника, измерить с помощью транспортира внутренние углы и найти их сумму. После размышлений учащиеся выдвигают гипотезу: треугольник можно построить, если сумма внутренних углов его равна 180. Доказывается соответствующая теорема.
При закреплении изученного материала целесообразно создавать игровые ситуации с помощью задач – рисунков. На первом этапе закрепления материала подбираются простые рисунки, в которых отчётливо выступает закономерность, о которой идёт речь на данном уроке. Если же на закрепление отводится весь урок, то здесь нужно соблюдать последовательность перехода от простого к сложному. При работе с рисунками учитель легко определяет степень усвоения учащимися материала, выявляет пробелы в знаниях.
Так, например, при закреплении темы « Сумма углов треугольника» каждому ряду предлагаются соответственно задачи – рисунки. Задание состоит в том, чтобы найти величину угла. Набирает большее количество очков тот ряд, где наибольшее число учащихся правильно ответили на вопрос задачи. Рисунки поочерёдно предлагаются каждому ряду. Ответы подаются к столу учителя капитанами с указаниями фамилии ученика .
Подведение учащихся к необходимости вывода общей формулы, создания математической модели реальных явлений и процессов на основе интуитивных рассуждений.
Тема: « Геометрическая прогрессия».
В виде игровой ситуации учащимся предлагается задача, которая содержит жизненные факты, но при решении, которой возникает необходимость в выводе новой формулы. Так, перед выводом формулы суммы членов геометрической прогрессии школьникам предлагается, например, такая жизненная ситуация.
Однажды незнакомец постучал в окно к богатому купцу и предложил такую сделку: « Я буду ежедневно в течение 30 дней приносить тебе по 100 000 рублей. А ты мне в первый день за 100 000 рублей дашь 1 копейку, во второй день за 100 000 рублей – 2 копейки и так каждый день будешь увеличивать предыдущее число денег в два раза. Если тебе выгодна сделка, то с завтрашнего дня начнём ». Купец обрадовался такой удаче. Он подсчитал, что за 30 дней получит от незнакомца 3 000 000 рублей. На следующий день пошли к нотариусу и узаконили сделку.
Создаётся проблемная ситуация. Кто в этой сделке проиграл: купец или незнакомец? Учащиеся составляют последовательность чисел: 1; 2; 4; 8; 16; 32; 64; 128; 256; … . Убеждаются, что эти числа составляют геометрическую прогрессию со знаменателем равным 2, первым членом равным 1 и количеством членов равным 30. Большинство школьников стремятся составить всю последовательность , чтобы потом найти её сумму. Но видят, что это громоздкая работа, которая требует времени. Напрашивается вопрос: «Возможно ли вывести формулу суммы первых членов геометрической прогрессии в общем виде?» Под руководством учителя учащиеся выводят формулу и убеждаются, что купец проиграл.
Игровые ситуации , основанные на имитации процессов реальной жизни.
Тема « Исследование свойств функции»
Отправимся в путь на автомобиле по шоссе из города А в город В. Будем внимательно приглядываться к рельефу дороги. Ровный участок дороги естественно ассоциируется с термином « константа». Дорога идёт под уклон – это монотонное убывание. Кончился спуск и водитель включает газ, отмечая тем самым точку минимума. Дорожный знак указывает подъём, а у математика наготове свой термин – монотонное возрастание. Перевалили через гребень холма – пройдена точка максимума. И снова началось монотонное убывание, т.е. спуск. На холмах дорога выпукла, а в ложбинах вогнута. Не отмеченные дорожными знаками стыки таких участков дороги математик отметит про себя как точки перегиба. Математические понятия, о которых шла речь в этом описании, естественным образом делятся на две группы. Одни описывают поведение функции в окрестностях некоторых характерных точек (максимум, минимум, перегиб),другие – в некоторых промежутках (выпуклость, вогнутость, возрастание, убывание ).чтобы в общих чертах воспроизвести профиль дороги, достаточно описать поведение функции сначала в окрестностях характерных точек, а затем в промежутках между этими точками. Игровая ситуация состоит в том, что «водитель» из каждой команды должен проехать «дорогу» и объяснить все её участки языком водителя и математика.
Использование ситуаций, приведённых в пословицах.
Чтобы проиллюстрировать характерные свойства функции, часто обращаемся к пословицам. Ведь пословицы – это отражение устойчивых закономерностей, выверенных многовековым опытом народа. Аналогия с пословицами позволяет учащимся лучше понять и запомнить определённые свойства функции и служит своего рода опорным сигналом для запоминания свойств функции.
1. « Чем дальше в лес, тем больше дров» , гласит пословица. Изобразим графиком, как нарастает количество дров по мере продвижения вглубь леса. Горизонтальная ось графика – это лесная дорога. По вертикали будем откладывать количество дров на данном километре. График представляет собой количество дров как функцию пути. Согласно пословице , эта функция неизменно возрастает
2. Пословица « Выше меры конь не скачет» . Если изобразить траекторию скачущего коня графически, то высота скачков в полном соответствии с пословицей будет ограничена сверху некоторой мерой. Это свойство присуще функциям синус и косинус. Здесь тоже есть своя мера, за пределы которой не вздымаются волны синусоиды и косинусоиды. Графики этих функций находятся в полосе между прямыми у = - 1 и у = 1.
Важнейшим средством активизации самостоятельной творческой деятельности учащихся, развития их умственных способностей является решение задач. В учебной литературе задачи, как правило, формулируются предельно кратко, чётко, определённо. В такой математической, корректной, лаконичной редакции не всегда улавливается практическая направленность задачи, отсутствуют моменты, возбуждающие любознательность, интерес учащихся. Фабула большинства школьных задач формальна и не вводит школьников в условия жизненных ситуаций. Где нужно принимать решения, выполнять определённые действия. Поэтому условия некоторых задач иногда полезно переформулировать так, чтобы получить проблемные задачи. Следует в них включать также и элементы, вызывающие у учащихся чувство удивления, сомнения, доставляющие эстетическое удовлетворение. Иначе говоря, учителю так следует изменить условие задачи, чтобы появилась возможность обратить на задачу внимание всех учащихся класса, вызвать интерес к ней и продолжить беседу о задаче после её решения.
Пример : внучка с собачкой увидела своего дедушку на расстоянии 300 метров от себя и побежала ему навстречу. Дедушка в тот же момент также увидел свою внучку и направился к ней. Собачка всё время бегала между дедушкой и внучкой до тех пор. Пока они не встретились. Какой путь пробежала собачка, если её скорость 30 км/ч, скорость дедушки 3 км/ч. А внучки 6 км/ч?
Исключение из текста задачи её вопроса значительно повышает её проблемность: учащиеся вынуждены самостоятельно выдвигать гипотезы, проводить исследования.
Большое значение при изучении математики имеет интерес, являющийся следствием увлекательности самой математики, её идей, логического построения, практических применений. Поэтому так важны занимательные упражнения, требующие смекалки:
- Две противоположные стороны квадрата увеличили, а две другие уменьшили на 5 см каждую. Как изменится площадь квадрата?
- С помощью цифр 2 и 3 , не употребляя знаков действий, записать, возможно большее число.
К занимательным задачам можно отнести старинные исторические задачи.
Проблемные ситуации на уроке
Цель: воспитание внимательности, мыслительных способностей, развитие навыков самостоятельной работы, активизация познавательной деятельности учащихся.
В процессе обучения создаю на уроках проблемные ситуации. Например:
задание на исправление преднамеренно сделанных ошибок в решении;
решение софизмов;
задания на исправление частично стёртых записей.
Например: Найдите ошибки в следующих рассуждениях :
Например, 5 класс:
Возьмём верное равенство 35+10-45=42+12-54. Вынесем в каждой части общий множитель за скобки. 5(7+2-9)=6(7+2-9). Разделим обе части на общий множитель. Получаем 5=6.
Задание: Объясните в чём ошибка.
« Четырежды четыре – двадцать пять»
16 : 16 = 25 : 25
Это очевидное равенство. После вынесения за скобки общего множителя из каждой части этого равенства будем иметь: 16 ( 1:1) = 25 (1:1). Зная, что
1:1 =1, получаем : 4×4 = 25.
Многократные тренировки заставляют учеников быть внимательными; следить за речью учителя, решением на доске, своими записями в тетради.
Результативность: формируется внимательность и заинтересованность; развивается мыслительная деятельность учащихся.
Творческая работа учащихся
Цель: развитие творческих способностей учащихся, интереса к предмету, активизация мыслительной и познавательной деятельности учащихся.
В своей работе широко практикую задания творческого характера: составление математических сказок, ребусов, составление графиков по условию пословиц, задач. Например, при изучении темы: «Координатная плоскость» детям предлагается изобразить точки по заданным координатам, последовательно соединить их. В итоге получается график - рисунок предмета или животного. Ребята выполняют и дополнительные задания к рисунку, например, повернуть рисунок в другую сторону или поднять рисунок на несколько делений и симметрично отобразить относительно оси ОХ или ОУ и.т.д. Заинтересовавшись, дети придумывают рисунки самостоятельно и дополняют их записью координат.
Для привлечения внимания ребят, стимулирования их работы, развития интереса к предмету применяю всевозможные формы кодирования заданий и ответов: шифрование пословиц, загадок, поговорок.
С интересом разгадывают дети математические ребусы, головоломки, с удовольствием придумывают их сами.
Результативность:
развивается их пространственное мышление;
осуществляется связь математики с окружающим миром.
Имитационные и деловые игры уроках математики.
Как известно, играют не только дети, играют и взрослые. Существуют так называемые деловые игры, в процессе которых на основе игрового замысла моделируется реальная обстановка, в которой выполняются конкретные действия, выбирается оптимальный вариант решения задачи и имитируется его реализация в практической жизни.
Деловая игра – это модель процесса принятия решений в реальной ситуации с чётко выраженной структурой. Деловая игра позволяет создавать производственные ситуации, в ходе которых играющему необходимо найти правильную линию поведения, оптимальное решение проблемы, соответственно реальным обстоятельствам производства, имитированным в игре.
В ходе игры каждому участнику необходимо максимально мобилизовать все свои знания, опыт, воображение. Особенно ценно то, что здесь дело не сводится лишь к механическому использованию программного материала. В процессе игры вырабатывается умение мыслить системно, продуктивно, пробуждается стремление к поиску новых идей, а это уже шаг к творчеству. Учащиеся в условиях игры охотно перевоплощаются в тех или иных специалистов и выступают в адекватной роли в моделируемой обстановке.
Межпредметные связи на уроках математики
Цель: повышение эффективности работы учащихся на уроке, расширение кругозора, использование знаний других учебных дисциплин на уроках математики.
Повышению эффективности работы учащихся на уроках способствуют задачи, содержание которых связано с интересной информацией об окружающем мире или с материалом, изученным по другим предметам. Стимулируют работу учащихся различные формы ответов. Рядом с заданием записываю ответ, закодированный буквой. После решения задания, выбирается правильный ответ, а буква - код записывается в тетрадь. Если задание выполнено правильно, то у учащихся получается слово. Обычно это слово содержит интересную информацию для школьников.
Результативность: особенность таких заданий в использовании нематематической информации, разнообразии форм подачи условий задачи, развитие математической речи, формирование интереса через применение знаний других учебных дисциплин.
Логические тесты на уроках математики.
Задачи:
усвоение новых математических понятий, терминов;
формирование практических навыков, умений наблюдать, сравнивать, обобщать, делать выводы.
Решить логический тест – значит, определить способ решения первых заданий и, применив метод аналогии, использовать его для решения остальных заданий, для нахождения ответа на поставленные вопросы. Каждый предлагаемый тест содержит некоторый «секрет» - основная задача решающего.
Тесты позволяют организовывать на уроках математики интересные деятельностные ситуации, способствующие лучшему усвоению программного материала и, в целом, развитию логического мышления учащихся.
1 задание: 3х – 7 = 2 53 28 – 5х = 3
17 – 4х = 1 ? 6х + 2 = 8
2 задание: 2х – 2 = 18 9 7х – 1 = 6
9 – х = 2 6 23 – 6х = 17
13 + 2х = 35 ? 28 – 3х = 7
Для осуществления связи математики с языковым развитием учащихся применяю комбинированные тесты.
Комбинированные тесты – это задания, содержащие как вербальную версию, так и символико-графическую. Данные тесты требуют от детей не только наблюдательности, но и умения устанавливать необычные связи между объектами, а также осуществлять связь математики с языковым развитием учащихся.
При решении данных упражнений можно провести разного вида беседы: обучающие, контролирующие, обобщающие…
Алгоритм решения комбинированных тестов:
Прочитай задание.
Внимательно изучи первую часть задания.
Найди логический признак, по которому выполнено решение первой (второй) части.
Примени аналогию при исследовании второй (третьей) части задания.
Вставь пропущенное слово (число).
Обоснуй ответ.
Пример комбинированного теста:
12 – ( 3 + 4 ) 2 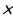 4 – 5 Д В
4 – 5 Д В
3 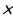 5 – 28 : 4 ( 16 + 5 ) – 10 ?
5 – 28 : 4 ( 16 + 5 ) – 10 ?
Ответ Ж Й 8 11
Такие задания посильны даже слабым учащимся, тем самым вовлекаю в учебный процесс каждого ученика. При практическом применении комбинированных тестов возрастает организованность и сосредоточенность, познавательная активность и устремлённость учащихся на получение необходимого результата.
Символико – графический тест:
Предназначается для формирования умений и навыков применения теоретического материала при решении задач , для повторения и закрепления материала.
Представляет собсй эффективный способ взаимосвязи алгебраического материала с изображением математических фигур, способствует формированию у учащихся правильных геометрических представлений.
Решение теста можно сопроводить эвристической беседой.
Примеры символико- графических тестов.
1 задание.
Вставьте пропущенное число:
2,1
Х 8 ?
Ответ: 9 : обобщили знания по темам « Решение неравенств» и « Целые числа»
2 задание:
1/2 5/6 1/3
1/7 ? 1/8
Ответ: 15/56: систематизировали знания по теме» Сложение дробей с разными знаменателями»
Анаграммы.
Анаграммой называется слово, в котором поменяли местами все или несколько букв, в сравнении с исходным словом.
Задание: Решите анаграммы и исключите лишнее слово:
ЧАДАЗА ; МЕНПЕРНАЕЯ ; ВАРУНИЕНЕ ; ЦИЯКУНФ.
МАПРЯЯ ; ЧУЛ ; РЕЗЕТОК ; РИПЕТРЕМ,
Применяя словесные логические задания, учащиеся с успехом усваивают математическую терминологию.
В своей работе использую следующие средства обучения: карточки задания, карточки – схемы, карточки – логические задачи, иллюстрированные карточки,
Различные формы контроля знаний учащихся
Самоконтроль ( заполняют листы самоконтроля, карточки с управленческими функциями)
Взаимоконтроль ( проверка работы друг у друга)
Контроль учителя:
Разноуровневые тесты,
Карточки
Контрольные работы
Графические и математические диктанты
Тематические зачёты и уроки зачёты
Задания и упражнения на готовых чертежах
Результативность:
- формируется устойчивое внимание,
- отрабатываются навыки само- и взаимоконтроля, обеспечивается коррекция знаний,
- отслеживаются ЗУН по каждой теме курса.
Тематический зачёт : цель – систематизировать знания учащихся, развивать память, логическое мышление, математическую речь и повышать ответственность за результаты своего учебного труда.
Математические и диктанты: цель – проверить знания учащихся по изученному на прошлом уроке или по серии уроков, осуществление возможности с помощью шаблонов быстро проверить учителю или самим учащимся знания при графическом диктанте и выработать умения быстро понимать учителя во время диктовки.
Разноуровневые тесты: цель – проверить прочность усвоения изученного материала, научить учащихся из нескольких ответов выбирать правильный, готовить учащихся к сдаче ЕГЭ по предмету.
Задания и упражнения на готовых чертежах : цель – лучше развить пространственное воображение учащихся, увеличить объём рассматриваемого материала на уроке, повысить его эффективность.
Урок – зачёт – с помощью сильных учащихся и учителя помочь остальным учащимся лучше усвоить теоретический и практический материал по данной теме, посильный для каждого ученика.
Развитие интереса к предмету средствами внеклассной работы
Цель : углубить знания учащихся по предмету, показать важность изучения предмета, воспитать интерес учащихся к математике и развить их математические способности.
Формы внеклассной работы
Математические олимпиады
Математические недели
Математические часы
Математические ролевые игры:
« Счастливый случай »;
« Звёздный час » ;
КВН
Факультативы и элективные курсы.
Источники получения передового педагогического опыта:
- курсы повышения квалификации,
- периодические издания по предмету,
- участие в заседаниях МО учителей математики
- посещение районных семинаров учителей математики,
-интернет-ресурсы
Результативность
В результате проводимых занятий в рамках опыта сформировалась положительная мотивация изучения предмета у большинства учащихся, серия проведённых занятий благоприятно сказалась на уровне развития познавательного интереса, смягчила трудности в привыкании к новым условиям обучения у школьников 5 класса ( более 50% учащихся высказали повышенный интерес к математике, в результате анкетирования, более 80% испытывали психологический комфорт при изучении этого предмета ).
Наблюдается рост мотивации к изучению математики почти во всех классах. Это объясняется тем, что в педагогической практике используются современные образовательные технологии, создаются условия для самореализации школьников.
Одной из задач опыта было выявление отношения детей к играм. В результате этого было проведено анкетирование учащихся. В анкетировании приняло участие 32 ученика из 5 – 9 классов по произвольному выбору. В таблице приведены ответы , которые выбрали ученики.
| Какие уроки ты больше всего любишь? | Если ты был бы учителем, чего бы было больше у тебя на уроке? | Как часто в вашем классе на уроках бывают игры? | Как ты относишься к игре на уроке? | Как ты думаешь, какая польза от игры на уроке? |
| Люблю все уроки - 12 | Работы с учебником – 6 | Очень часто – 12 | Очень хочется участвовать - 32 | Очень большая –12 |
| С использованием таблиц, схем, картин - 8 | Таблиц, схем, рисунков - 2 | Часто - 16 |
| Большая – 12 |
| С использованием различных игр –10 | Различных игр - 18 | Не очень часто -4 |
| Не очень большая - 4 |
| Главное, чтобы на уроке было интересно - 2 | Самостоятельных работ - 6 |
|
| Небольшая - 4 |
Из всего этого можно сделать вывод: учащимся нравятся разнообразные уроки, дети положительно относятся к использованию игры на уроках. Если бы учащиеся были учителями, то более 50 % использовали бы на своих уроках игры. И практически основная масса детей считают, что игра на уроках приносит большую пользу, и они с удовольствием принимали бы в ней участие. Таким образом, необходимо в каждый урок включать игровые моменты, но не в качестве разрядки обстановки, а с целью активизации знаний детей, их умственной деятельности, развития творческих способностей. Использование дидактических игр даёт наибольший эффект в классах, где преобладают ученики с неустойчивым вниманием, пониженным интересом к предмету, для которых математика является скучной и сухой наукой. Создание игровых ситуаций на уроках математики повышает интерес к математике, вносит разнообразие и эмоциональную окраску в учебную работу, снимает утомление, развивает внимание, сообразительность, чувство соревнования, взаимопомощь.







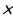 4 – 5 Д В
4 – 5 Д В









