Стереометрия - формулы, определение и вычисление с примерами решения
Содержание:
Что такое стереометрия
Аксиомы стереометрии
Следствия из аксиом стереометрии
Сечения
Стереометрия:
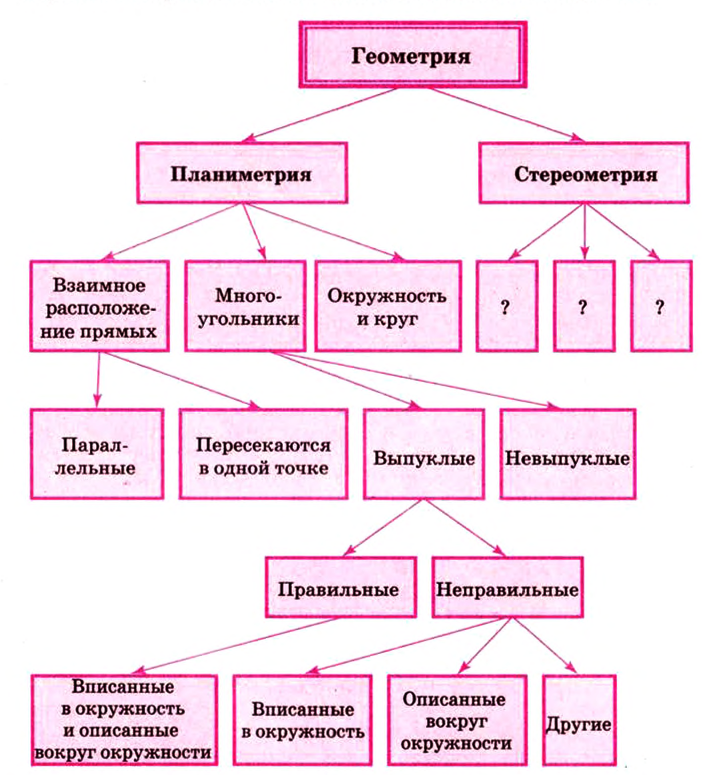
Напомним, что геометрия - это наука о свойствах геометрических фигур, которая состоит из двух частей: планиметрии и стереометрии. Планиметрию - раздел геометрии, изучающий свойства фигур на плоскости, вы изучили. В модуле 1 систематизированы и обобщены факты и свойства таких фигур.
Что такое стереометрия
Стереометрия - это раздел геометрии о свойствах фигур в пространстве -изучают в старших классах.
Схематически это выглядит так:
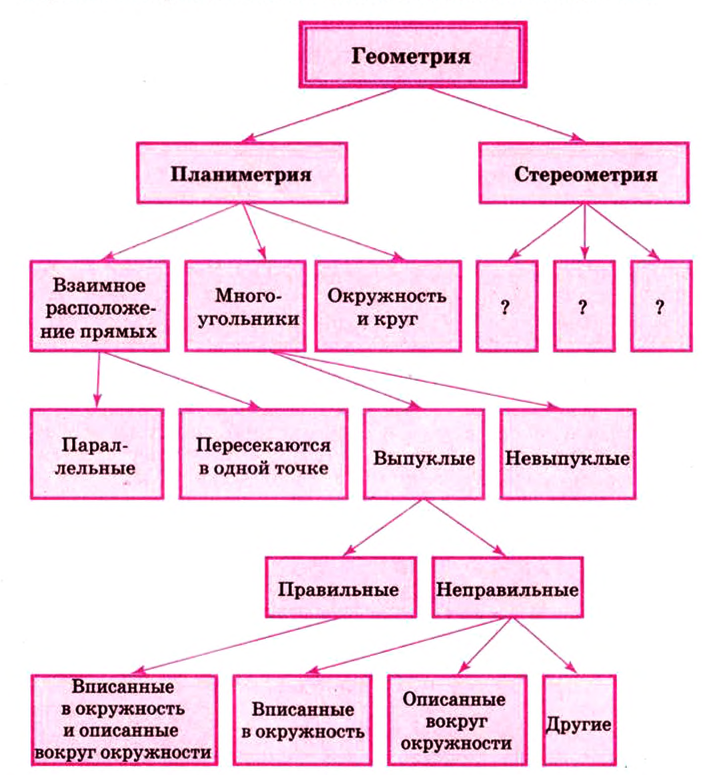
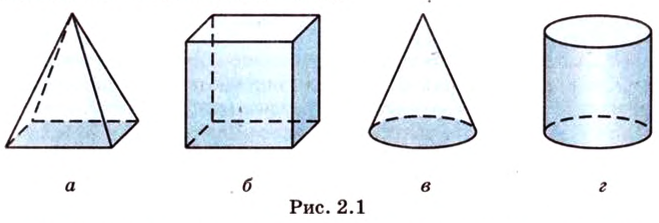
Фигуры, которые изучаются в стереометрии, называются геометрическими или пространственными. На рисунке 2.1 изображены некоторые пространственные фигуры: пирамида, параллелепипед, конус, цилиндр.
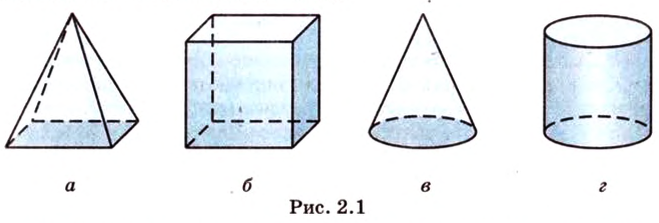
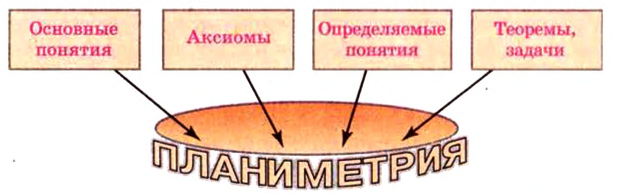
Напомним структуру логического построения планиметрии:
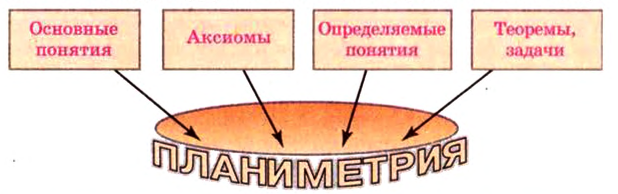
Поскольку стереометрия также является составляющей геометрии, то строится она по тому же принципу. Некоторые понятия принимаются как основные (простейшие, неопределяемые). Для них формулируются основные свойства - аксиомы, а далее рассматриваются другие, определяемые, понятия и их свойства.
Все фигуры, которые рассматривались на плоскости, можно рассматривать и в пространстве. Поэтому основные фигуры (понятия) планиметрии - точка и прямая - автоматически становятся основными фигурами стереометрии. Описываются они так же. В пространстве рассматривается еще одна основная фигура - плоскость. Ее можно представить как идеально гладкую поверхность доски или поверхность листа бумаги, которые продолжены во все стороны до бесконечности. Плоскость также понимают как множество точек.
На базе основных понятий определяются другие основные определяемые понятия: расстояние между точками, отрезок, луч, треугольник и т.д.
Прямая - подмножество точек плоскости, отрезок - подмножество точек прямой. Некоторые подмножества точек плоскости являются плоским треугольником, четырехугольником и т.д., а некоторые - неплоскими фигурами. Пространство состоит из бесконечного множества точек.
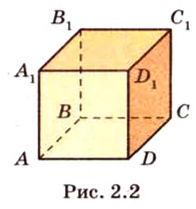
Итак, основными фигурами (понятиями) в стереометрии являются точка, прямая и плоскость. Эти понятия называют неопределяемыми. Каждая пространственная геометрическая фигура состоит из множества точек. Рассмотрим куб на рисунке 2.2.
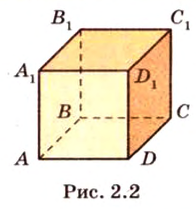
У него 8 вершин (точки), 12 ребер (части прямых) и 6 граней (части плоскостей). Гранями куба являются квадраты - фигуры планиметрии.
В стереометрии рассматривают более одной плоскости. Пространство состоит из бесконечного количества плоскостей, прямых и точек. Поэтому все аксиомы планиметрии имеют место и в стереометрии. Однако при этом некоторые из них приобретают другой смысл. Так, аксиома I, в планиметрии утверждает, что существуют точки вне данной прямой на плоскости, в которой лежит прямая. Именно в таком понимании эта аксиома применялась в процессе построения геометрии на плоскости. Теперь эта аксиома утверждает вообще существование точек, не лежащих на данной прямой, в пространстве. Из нее непосредственно не вытекает, что существуют точки вне данной прямой на плоскости, в которой лежит прямая. Это требует уже специального доказательства.
Аксиомы стереометрии
Формулирование некоторых аксиом планиметрии как аксиом стереометрии требует уточнения. Это касается, например, аксиом 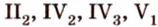 .
.
Приведем эти уточнения.
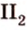 . Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости.
. Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости.
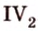 . От любой полупрямой на содержащей ее плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
. От любой полупрямой на содержащей ее плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
 . Каков бы ни был треугольник, существует треугольник, который равен ему в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.
. Каков бы ни был треугольник, существует треугольник, который равен ему в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.
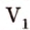 ,. На плоскости через данную точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.
,. На плоскости через данную точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.
Понятно, что с увеличением количества основных фигур появляются новые аксиомы об их свойствах:
Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, непринадлежащие ей (рис. 2.3, а).
Если две различные прямые имеют общую точку, то че рез них можно провести плоскость, и притом только одну (рис. 2.3, б).
Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (рис. 2.3, в).
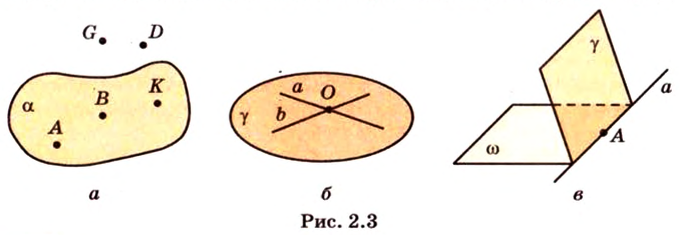
Аксиома 1 указывает на то, что любая плоскость все пространство не исчерпывает. Существуют точки пространства, которые ей не принадлежат.
Аксиома 2 утверждает, что две прямые, пересекающиеся в пространстве, всегда определяют одну плоскость. Из аксиомы 3 следует, что если две различные плоскости имеют общую точку, то они имеют множество общих точек, образующих прямую, которая содержит эту точку.
Эти три аксиомы дополняют пять групп аксиом планиметрии и вместе с ними образуют аксиоматику стереометрии. Аксиому 1 стереометрии отнесем к группе аксиом принадлежности (обозначим I3), а аксиомы 2 и 3 - к группе аксиом взаимного расположения (соответственно обозначим II3, II4).
Плоскости обозначаются строчными буквами греческого алфавита - 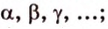 точки - большими буквами латинского алфавита -
точки - большими буквами латинского алфавита - 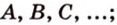 прямые - малыми буквами латинского алфавита -
прямые - малыми буквами латинского алфавита - 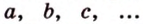 или двумя прописными буквами латинского алфавита -
или двумя прописными буквами латинского алфавита - 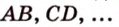 .
.
Для кратких записей утверждений используют символы -  принадлежит,
принадлежит, 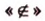 - не принадлежит,
- не принадлежит,  - подмножество и т.д. Краткие записи взаимного расположения точек, прямых и плоскостей:
- подмножество и т.д. Краткие записи взаимного расположения точек, прямых и плоскостей:
Точка 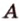 принадлежит прямой
принадлежит прямой 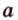 (точка
(точка 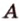 лежит на прямой
лежит на прямой 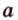 , прямая
, прямая 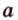 проходит через точку
проходит через точку 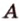 ). Обозначение:
). Обозначение: 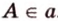 .
.
Точка 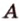 не принадлежит прямой
не принадлежит прямой 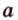 (точка
(точка 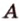 не лежит на прямой
не лежит на прямой 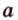 , прямая
, прямая 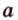 не проходит через точку
не проходит через точку 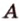 ). Обозначение:
). Обозначение: 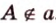 .
.
Точка 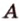 принадлежит плоскости
принадлежит плоскости 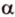 (точка
(точка 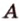 лежит на плоскости
лежит на плоскости 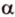 , плоскость
, плоскость 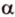 проходит через точку
проходит через точку 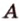 ). Обозначение:
). Обозначение: 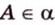 .
.
Прямая 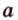 принадлежит плоскости
принадлежит плоскости 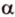 (прямая
(прямая 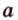 лежит на плоскости
лежит на плоскости 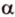 , плоскость
, плоскость 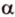 проходит через прямую
проходит через прямую 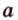 ). Обозначение:
). Обозначение:  .
.
Итак, используя рисунок 2.3, аксиомы можно записать:
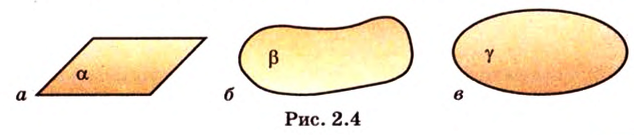
Плоскости изображают по-разному. На рисунке 2.4 показаны некоторые примеры различных изображений плоскостей.
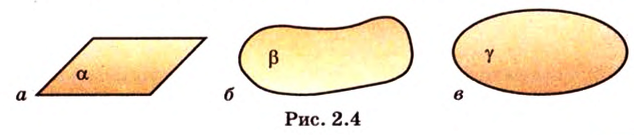
Далее в стереометрии мы будем использовать все определяемые понятия планиметрии, дополнять их новыми, собственно стереометрическими, формулировать и доказывать свойства пространственных фигур.
Как видим, логическое построение планиметрии и стереометрии одинаково, отличаются они лишь некоторым содержанием основных понятий, аксиом, определений, теорем.
Пример №1 Точки 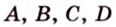 не лежат на одной плоскости. Докажите, что прямые
не лежат на одной плоскости. Докажите, что прямые 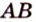 и
и 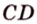 не пересекаются.
не пересекаются.
Доказательство:
Докажем методом от противного. Допустим, что прямые 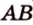 и
и 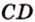 пересекаются (рис. 2.5).
пересекаются (рис. 2.5).

Тогда, по аксиоме II3, через них можно провести плоскость, которой принадлежат эти прямые. Это означает, что точки 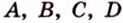 также принадлежат этой плоскости, что противоречит условию. Предположение неверно. Прямые
также принадлежат этой плоскости, что противоречит условию. Предположение неверно. Прямые 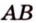 и
и  не пересекаются, что и требовалось доказать.
не пересекаются, что и требовалось доказать.
Заметим, что школьный курс геометрии посвящен евклидовой геометрии. Несмотря на то что с течением времени геометрия Евклида была существенно дополнена и откорректирована, ее по-прежнему называют именем древнего ученого. Такое уважение вызвано широтой практического применения евклидовой геометрии. Она используется в технических науках, картографии, геодезии, астрономии и др.
Следствия из аксиом стереометрии Проанализировав все сказанное ранее, можно утверждать, что логическое построение геометрии имеет следующий вид:
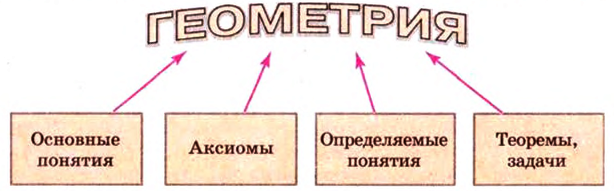
Важное место в геометрии занимают аксиомы. Они выражают наиболее существенные свойства основных геометрических фигур. Все остальные свойства геометрических фигур устанавливаются рассуждениями, опирающимися на аксиомы или ранее доказанные утверждения, которые опираются на аксиомы. Такие рассуждения называют доказательствами. Утверждение, истинность которого доказана и которое используют для доказательства других утверждений, называют теоремой. Простейшими из них являются утверждения для основных фигур стереометрии. Они называются следствиями из аксиом стереометрии. Рассмотрим теоремы, которые являются следствиями из аксиом стереометрии.
Теорема 1
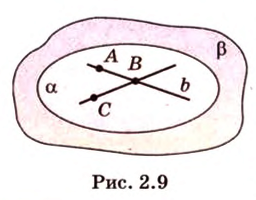
Через прямую и точку, не принадлежащую ей, можно провести плоскость, и притом только одну.
Доказательство:
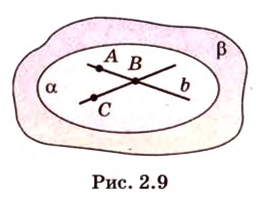
Пусть 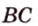 - данная прямая и
- данная прямая и 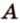 - точка, не принадлежащая ей (рис. 2.9). Через точки
- точка, не принадлежащая ей (рис. 2.9). Через точки 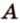 и
и 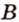 проведем прямую
проведем прямую 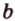 . Прямые
. Прямые 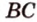 и
и 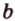 различны и пересекаются в точке
различны и пересекаются в точке 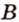 . По аксиоме II3 через них можно провести плоскость
. По аксиоме II3 через них можно провести плоскость 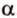 . Докажем, что она единственная, методом от противного.
. Докажем, что она единственная, методом от противного.
Допустим, что существует другая плоскость 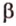 , которая содержит прямую
, которая содержит прямую 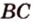 и точку
и точку 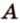 . Тогда, согласно аксиоме II4, плоскости
. Тогда, согласно аксиоме II4, плоскости 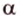 и
и 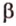 пересекаются по общей прямой, которой принадлежат точки
пересекаются по общей прямой, которой принадлежат точки 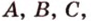 что противоречит условию. Предположение неверно. Плоскость
что противоречит условию. Предположение неверно. Плоскость 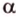 - единственная. Теорема доказана.
- единственная. Теорема доказана.
Теорема 2
Если две точки прямой принадлежат плоскости, то и вея прямая принадлежит этой плоскости.
Доказательство:
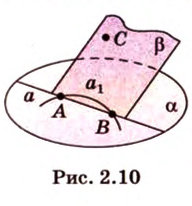
Пусть заданы прямая 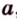 , плоскость
, плоскость 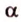 и точки А и В прямой
и точки А и В прямой 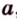 , принадлежащие
, принадлежащие 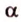 (рис. 2.10). Выберем точку С, которая не принадлежит прямой
(рис. 2.10). Выберем точку С, которая не принадлежит прямой 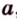 . Через точку С и прямую
. Через точку С и прямую 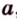 проведем плоскость
проведем плоскость 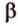 . Если
. Если 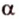 и
и 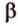 совпадут, то прямая
совпадут, то прямая 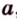 принадлежит плоскости
принадлежит плоскости 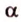 . Если же плоскости
. Если же плоскости 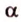 и
и 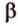 различны и имеют две общие точки
различны и имеют две общие точки 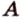 и
и 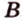 , то они пересекаются по прямой
, то они пересекаются по прямой 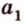 , содержащей эти точки. Поэтому через две точки
, содержащей эти точки. Поэтому через две точки 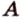 и
и 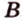 проходят две прямые
проходят две прямые 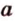 и
и 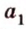 , что противоречит аксиоме принадлежности I2. Поэтому
, что противоречит аксиоме принадлежности I2. Поэтому 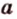 и
и 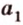 - совпадают. Однако поскольку
- совпадают. Однако поскольку 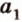 , принадлежит плоскости
, принадлежит плоскости 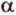 , то и прямая
, то и прямая 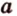 также принадлежит
также принадлежит 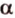 .
.
Теорема доказана.
Теорема 3
Через три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.
Доказательство:

Пусть 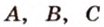 - заданные точки (рис. 2.11). Проведем через точки
- заданные точки (рис. 2.11). Проведем через точки 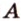 и
и 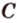 прямую
прямую 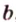 , а через точки
, а через точки 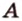 и
и 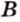 - прямую
- прямую 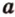 . Прямые
. Прямые 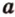 и
и 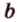 различны и имеют общую точку
различны и имеют общую точку 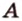 . Через них можно провести плоскость
. Через них можно провести плоскость 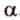 . Докажем, что она единственная, методом от противного. Допустим, что существует другая плоскость
. Докажем, что она единственная, методом от противного. Допустим, что существует другая плоскость 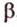 , содержащая точки
, содержащая точки 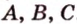 . Тогда, по теореме 2, прямые
. Тогда, по теореме 2, прямые 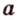 и
и 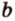 принадлежат плоскости
принадлежат плоскости 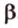 . Поэтому плоскости
. Поэтому плоскости 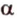 и
и 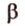 имеют две общие прямые
имеют две общие прямые 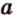 и
и 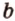 , которые пересекаются, что противоречит аксиоме II3. Итак, плоскость
, которые пересекаются, что противоречит аксиоме II3. Итак, плоскость 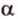 - единственная. Теорема доказана.
- единственная. Теорема доказана.
Отметим, если плоскость определена тремя точками, которые не лежат на одной прямой, например 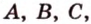 то в таком случае пользуются обозначением: (
то в таком случае пользуются обозначением: (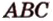 ). Читается: «плоскость, заданная точками
). Читается: «плоскость, заданная точками 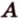 ,
, 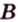 и
и 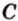 », или сокращенно «плоскость
», или сокращенно «плоскость 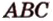 ».
».
Если грань многогранника - четырехугольник, например 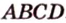 , то выбирают запись плоскости произвольной тройкой его вершин. Например, (
, то выбирают запись плоскости произвольной тройкой его вершин. Например, (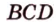 ), (
), (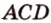 ) или (
) или (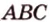 ). Однако иногда в записи плоскости оставляют все четыре вершины, например (
). Однако иногда в записи плоскости оставляют все четыре вершины, например (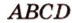 ).
).
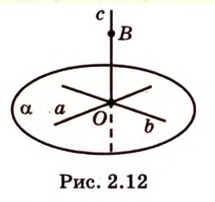
Пример №2 Можно ли через точку пересечения двух данных прямых провести третью прямую, которая бы не лежала с ними в одной плоскости?
Решение:
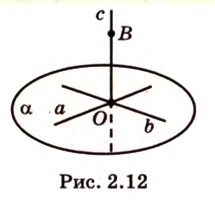
Через прямые 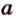 и
и 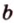 (рис. 2.12), которые имеют общую точку
(рис. 2.12), которые имеют общую точку  , можно провести плоскость
, можно провести плоскость 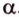 . Возьмем точку
. Возьмем точку 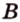 , которая не принадлежит
, которая не принадлежит 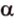 . Через точки
. Через точки  и
и 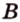 проведем прямую
проведем прямую 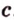 . Прямая
. Прямая 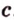 не лежит на плоскости
не лежит на плоскости 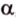 , так как если бы прямая
, так как если бы прямая 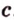 принадлежала плоскости
принадлежала плоскости 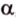 , то и точка
, то и точка 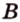 принадлежала бы плоскости
принадлежала бы плоскости 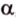 . Поэтому через точку пересечения прямых
. Поэтому через точку пересечения прямых 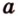 и
и 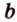 можно провести третью прямую, которая не лежит с ними в одной плоскости. Ответ. Можно.
можно провести третью прямую, которая не лежит с ними в одной плоскости. Ответ. Можно.
Почему именно так?
Очевидно, что точки плоскости задают прямые, которые будут принадлежать этой самой плоскости. Если же взять точку пересечения двух прямых на плоскости и точку вне плоскости, то через любые две точки пространства можно провести прямую. Эта прямая будет иметь только одну общую точку с плоскостью, а значит, будет ее пересекать.
Пример №3 Докажите, что все прямые, пересекающие две данные параллельные прямые, лежат в одной плоскости.
Доказательство:
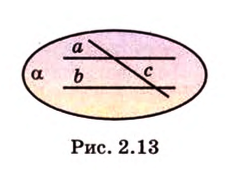
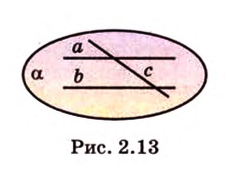
Поскольку прямые 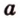 и
и 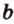 параллельны, то по определению эти прямые лежат в одной плоскости
параллельны, то по определению эти прямые лежат в одной плоскости 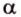 (рис. 2.13). Произвольная прямая
(рис. 2.13). Произвольная прямая 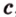 , пересекающая
, пересекающая 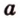 и
и 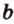 , имеет с плоскостью
, имеет с плоскостью 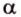 две общие точки - точки пересечения. Согласно теореме 2, эта прямая принадлежит плоскости
две общие точки - точки пересечения. Согласно теореме 2, эта прямая принадлежит плоскости 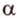 . Следовательно, все прямые, пересекающие две параллельные прямые, лежат в одной плоскости, что и требовалось доказать.
. Следовательно, все прямые, пересекающие две параллельные прямые, лежат в одной плоскости, что и требовалось доказать.
Пример №4 Докажите, что если прямые 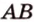 и
и 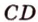 не лежат в одной плоскости, то прямые
не лежат в одной плоскости, то прямые 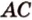 и
и 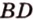 также не лежат в одной плоскости.
также не лежат в одной плоскости.
Доказательство:
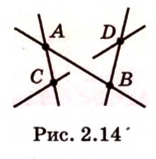
Докажем методом от противного. Допустим, что прямые 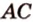 и
и 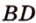 лежат в одной плоскости (рис. 2.14). Тогда точки
лежат в одной плоскости (рис. 2.14). Тогда точки 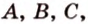
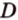 принадлежат этой плоскости, а следовательно, прямые
принадлежат этой плоскости, а следовательно, прямые 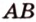 и
и 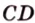 принадлежат этой плоскости, что противоречит условию. Предположение неверно, поэтому прямые
принадлежат этой плоскости, что противоречит условию. Предположение неверно, поэтому прямые 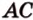 и
и 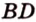 не принадлежат одной плоскости, что и требовалось доказать.
не принадлежат одной плоскости, что и требовалось доказать.
Почему именно так?
При доказательстве принадлежности или непринадлежности часто используют метод доказательства от противного. В этом случае он сразу выводит на противоречия, а значит - доказывает требование задачи.
Пример №5 Сколько всего существует различных плоскостей, проходящих через прямую и точку в пространстве?
Решение:
Если в пространстве даны прямая и точка, лежащая на ней, то ими определяется множество плоскостей, поскольку через прямую проходит множество различных плоскостей.
Если же точка не лежит на прямой, то по следствию из аксиом стереометрии такую плоскость можно построить только одну.
Ответ. Бесконечно много или одна.
Почему именно так?
Взяв вне этой прямой произвольную точку, мы всякий раз будем иметь другую плоскость, не совпадающую с ранее построенной. Таких плоскостей множество.
Через данную точку вне прямой можно провести либо прямую, которая пересекает данную прямую, либо прямую, параллельную данной. Оба случая задают одну плоскость.
Сечения Анализируя окружающий мир и систематизируя его предметы по форме, мы убеждаемся, что много из них «усечены» или «склеены». Разъединив их, получим поверхность, которую называют их сечением.
С сечениями мы сталкиваемся в разнообразных ситуациях: в быту, в столярничестве, токарстве и т.д. Решением задач на сечения геометрических фигур или других тел занимаются в черчении и конструкторской практике. Сечения выполняют для пространственных геометрических фигур.
Мы будем рассматривать сечения трех пространственных фигур: пирамиды, куба и прямоугольного параллелепипеда (их относят к многогранникам; с понятием многогранника вы ознакомитесь позднее). Для введения понятия сечения геометрической фигуры напомним понятие об отрезке, пересекающем или не пересекающем прямую: если в заданной плоскости концы отрезка лежат в различных полуплоскостях относительно заданной прямой, то отрезок пересекает прямую, если же в одной, - то нет. Аналогией такой ситуации в пространстве является плоскость и отрезок, т.е. их взаимное расположение.
Каждая плоскость разбивает пространство на два полупространства, а концы отрезка могут лежать в различных полупространствах (рис. 2.20, а) относительно некоторой плоскости, на плоскости (рис. 2.20, б) или в одном полупространстве (рис. 2.20, в).
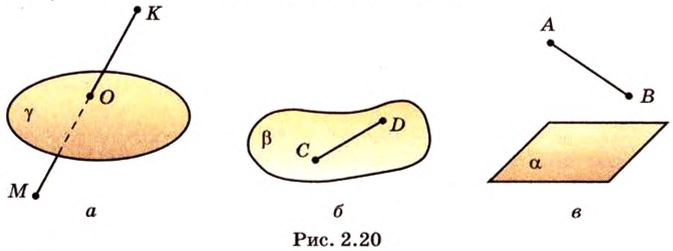
Если ни одна из двух точек не принадлежит плоскости, а отрезок, соединяющий их, имеет с этой плоскостью общую точку, то говорят, что данные точки лежат по разные стороны относительно плоскости, или отрезок пересекает плоскость. Если же как минимум две точки пространственной геометрической фигуры лежат по разные стороны плоскости, то говорят, что плоскость эту фигуру пересекает, такую плоскость называют секущей.
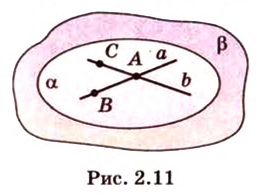
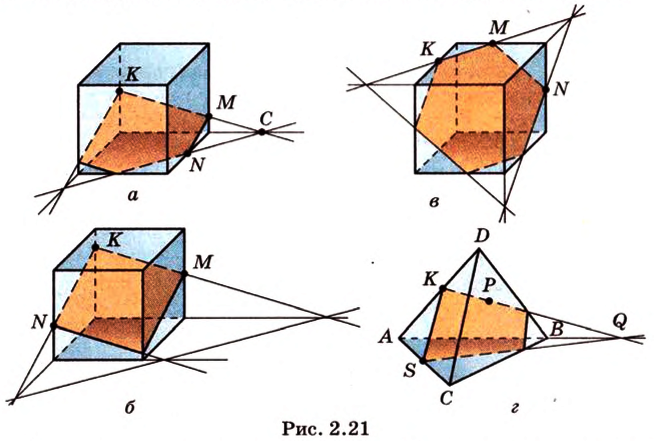
Фигура, которая состоит из всех общих точек геометрической фигуры и секущей плоскости, называется сечением геометрической фигуры. На рисунке 2.21 сечения изображены цветом.
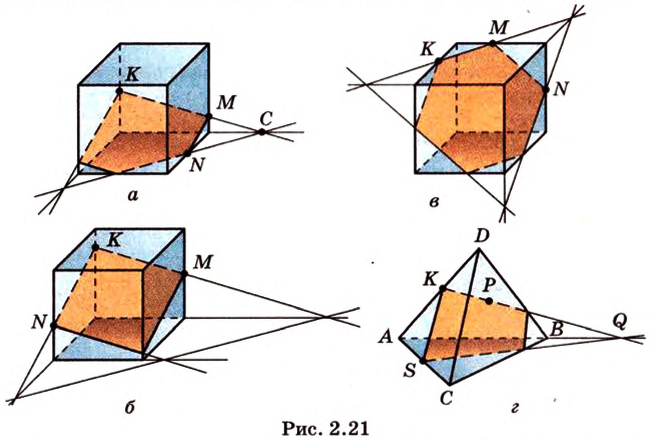
Сечение задают условием задачи. В зависимости от этих условий и выполняют построение сечения. Учитывая изученное, мы будем решать задачи, в которых сечение задается тремя точками или прямой и точкой вне ее. Почти во всем курсе стереометрии нам придется работать с разными сечениями.
Существуют различные методы построения сечений. Наиболее распространенный в практике изучения курса геометрии средней школы - метод следов. Рассмотрим его.
Если плоскость грани многогранника и плоскость сечения имеют две общие точки, то они пересекаются по прямой, проходящей через эти точки. Эту прямую называют линией пересечения данных плоскостей.
Плоскость сечения многогранника имеет общие прямые с плоскостями граней многогранника. Прямую, по которой плоскость сечения пересекает плоскость любой грани многогранника, называют следом плоскости сечения. Следов столько, сколько плоскостей граней пересекает плоскость сечения.
При построении сечения следует помнить:
через две точки, принадлежащие плоскости, проходит только одна прямая, и эта прямая также принадлежит этой плоскости;
чтобы построить линию пересечения двух плоскостей, необходимо найти две точки, которые принадлежат обеим плоскостям, и через них провести линию пересечения;
при построении сечений многогранников секущей плоскостью нужно найти отрезки, по которым секущая плоскость пересекается с гранями многогранника.
Рассмотрим примеры построения сечения многогранника секущей плоскостью.
Пример №6 Постройте сечение куба плоскостью, проходящей через середины ребер с общей вершиной.
Построение
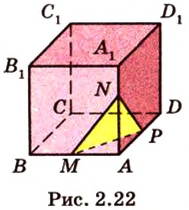
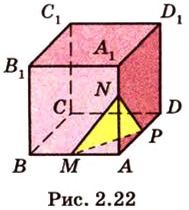
Пусть 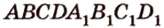 - заданный куб (рис. 2.22). Выберем одну из вершин, например
- заданный куб (рис. 2.22). Выберем одну из вершин, например 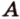 , являющуюся общей для трех ребер
, являющуюся общей для трех ребер 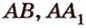 и
и 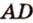 . Обозначим на этих ребрах точки
. Обозначим на этих ребрах точки 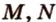 и
и 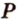 соответственно, являющиеся их серединами. Точки
соответственно, являющиеся их серединами. Точки 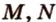 и
и 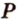 не лежат на одной прямой, а поэтому определяют секущую плоскость (
не лежат на одной прямой, а поэтому определяют секущую плоскость (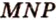 ). Точки
). Точки 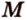 и
и 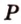 - общие точки плоскости сечения и грани
- общие точки плоскости сечения и грани 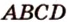 , поэтому
, поэтому 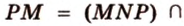
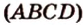 ,
, 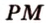 - сторона сечения.
- сторона сечения.
Аналогично 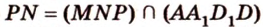 и
и 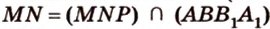 , поэтому
, поэтому 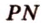 и
и  - две другие стороны сечения. Таким образом,
- две другие стороны сечения. Таким образом, 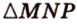 - искомое сечение.
- искомое сечение.
Пример №7 Постройте сечение пирамиды 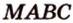 плоскостью, которая проходит через ребро
плоскостью, которая проходит через ребро 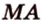 и середину ребра
и середину ребра 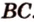 .
.
Построение
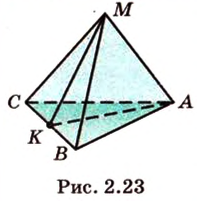
Плоскость сечения задается прямой 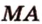 и серединой ребра
и серединой ребра 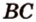 (обозначим ее точкой
(обозначим ее точкой 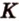 ) (рис. 2.23). (МАК) - плоскость сечения. Найдем прямые пересечения
) (рис. 2.23). (МАК) - плоскость сечения. Найдем прямые пересечения
этой плоскости с плоскостями (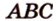 ) и (
) и (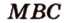 ). Ими будут соответствующие прямые
). Ими будут соответствующие прямые 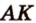 и
и  , а
, а 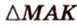 , образованный пересечением прямых
, образованный пересечением прямых 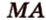 ,
,  и
и 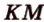 , - искомое сечение.
, - искомое сечение.
Пример №8 Постройте сечение пирамиды  плоскостью, проходящей через три точки, которые лежат соответственно на ребрах
плоскостью, проходящей через три точки, которые лежат соответственно на ребрах 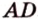 ,
, 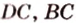 .
.
Построение
Рассмотрим случай, когда ни одна из прямых, проходящих через эти точки, не будет параллельна сторонам граней.
Пусть 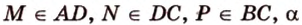 - секущая плоскость, проходящая через заданные точки
- секущая плоскость, проходящая через заданные точки 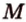 ,
, 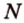 и
и 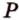 . Построим сечение, выполняя последовательно шаги:
. Построим сечение, выполняя последовательно шаги:
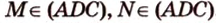 , тогда
, тогда 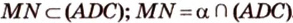 .
.
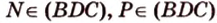 , тогда
, тогда 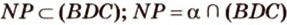 .
.
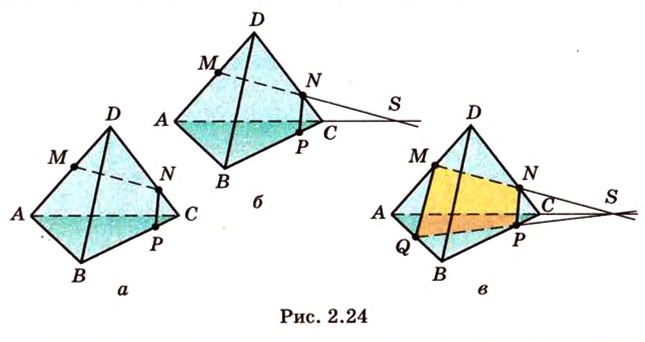
Мы нашли две стороны фигуры сечения: отрезки 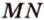 и
и 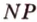 (рис. 2.24, а). Точка
(рис. 2.24, а). Точка 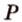 - общая точка двух плоскостей (
- общая точка двух плоскостей (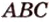 ) и (
) и (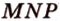 ). Такие плоскости (по аксиоме II4) пересекаются по прямой, проходящей через точку
). Такие плоскости (по аксиоме II4) пересекаются по прямой, проходящей через точку 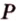 . Для построения такой прямой нужна вторая точка.
. Для построения такой прямой нужна вторая точка.
3. Плоскости (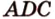 ) и (
) и (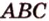 ) пересекаются по прямой
) пересекаются по прямой 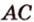 .
. 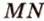 по условию не параллельна
по условию не параллельна 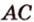 и
и 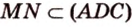 , поэтому
, поэтому 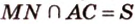 (рис. 2.24, б).
(рис. 2.24, б).
4. Прямая 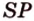 - линия пересечения плоскостей (
- линия пересечения плоскостей (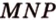 ) и (
) и (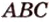 ). Пересечение этой прямой с ребром
). Пересечение этой прямой с ребром 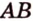 дает точку
дает точку 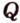 , которая является вершиной сечения. Таким образом, четырехугольник
, которая является вершиной сечения. Таким образом, четырехугольник  - искомое сечение (рис. 2.24, в).
- искомое сечение (рис. 2.24, в).
Пример №9 Постройте сечение прямоугольного параллелепипеда 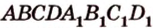 плоскостью, проходящей через середины
плоскостью, проходящей через середины 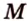 и
и 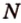 ребер
ребер 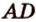 и
и 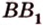 и точку
и точку 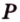 пересечения диагоналей грани (рис. 2.25, а).
пересечения диагоналей грани (рис. 2.25, а).
Построение
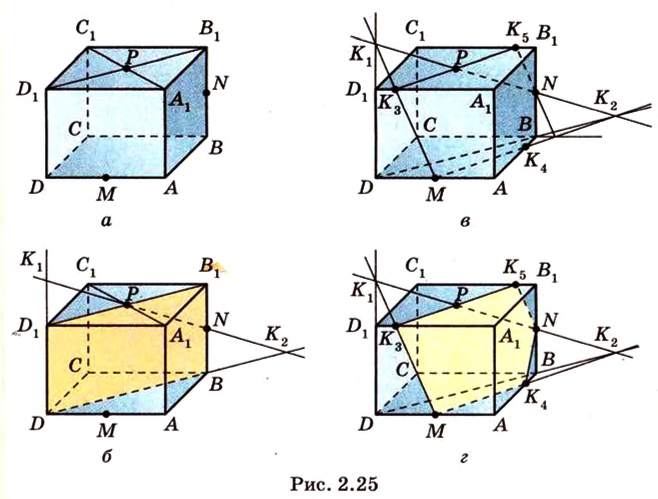
Обозначим секущую плоскость 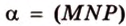 . Выполним последовательно шаги, выполняя поиск фигуры, образованной плоскостью сечения.
. Выполним последовательно шаги, выполняя поиск фигуры, образованной плоскостью сечения.
Найдем точку пересечения прямой 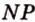 с плоскостью (
с плоскостью (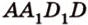 ). Эта прямая лежит в плоскости (
). Эта прямая лежит в плоскости (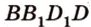 ), пересекающейся с плоскостью (
), пересекающейся с плоскостью (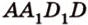 ) по прямой
) по прямой 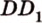 . Точка
. Точка 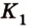 - точка пересечения прямых
- точка пересечения прямых 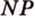 и
и 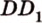 . Точка
. Точка 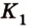 - искомая (рис. 2.25, б).
- искомая (рис. 2.25, б).
Аналогично находим точку 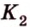 как точку пересечения прямой
как точку пересечения прямой 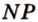 с плоскостью (
с плоскостью (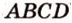 ). Точка
). Точка 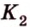 - искомая.
- искомая.
Плоскость а пересекает плоскость (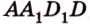 ) по прямой
) по прямой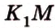 , а плоскость (
, а плоскость (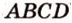 ) - по прямой
) - по прямой 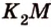 . Прямые
. Прямые 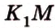 и
и 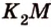 пересекают ребра прямоугольного параллелепипеда
пересекают ребра прямоугольного параллелепипеда 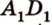 и
и 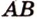 в точках
в точках 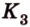 и
и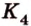 соответственно (рис. 2.25, в).
соответственно (рис. 2.25, в).
Прямая 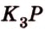 пересекает ребро прямоугольного параллелепипеда
пересекает ребро прямоугольного параллелепипеда 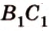 в некоторой точке
в некоторой точке 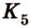 - последней вершине сечения (рис. 2.25, в).
- последней вершине сечения (рис. 2.25, в).
Таким образом, пятиугольник 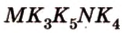 - искомое сечение (рис. 2.25, г).
- искомое сечение (рис. 2.25, г).
Приведем краткие описания построения сечения куба плоскостью, проходящей через три точки.
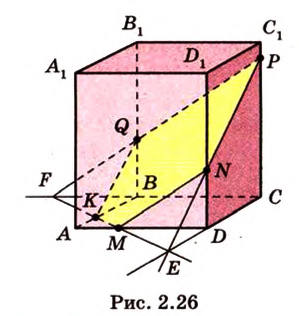
Пример №10 Постройте сечение куба плоскостью, проходящей через точки 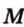 ,
, 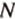 ,
, 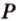 , которые принадлежат соответственно ребрам
, которые принадлежат соответственно ребрам 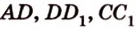 .
.
Построение
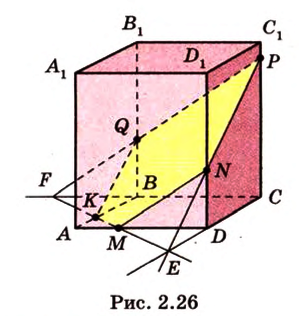
Секущая плоскость 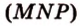 ) (рис. 2.26).
) (рис. 2.26).
Точки 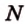 и
и 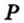 лежат в
лежат в 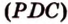 . Проведем прямую
. Проведем прямую 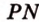 ,
, 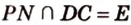 .
.
Точки 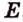 ,
, 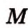 лежат в
лежат в 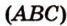 . Проведем прямую
. Проведем прямую  ,
, 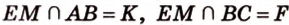 .
.
Точки 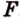 ,
, 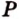 лежат в
лежат в 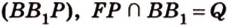 .
.
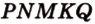 - искомое сечение.
- искомое сечение.
Пример №11 Постройте сечение куба плоскостью, проходящей через точки К, М, Т, которые принадлежат соответственно ребрам 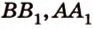 ,
, 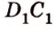 .
.
Построение
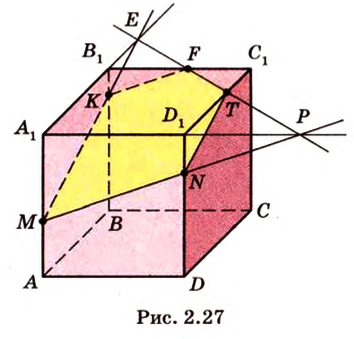
Секущая плоскость 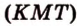 (рис. 2.27).
(рис. 2.27).
Точки 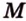 и
и 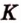 лежат в
лежат в 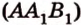 ,
, 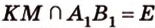 .
.
Точки 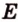 ,
, 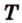 лежат в
лежат в 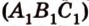 ,
, 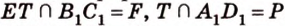 .
.
Точки 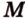 ,
, 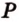 лежат в
лежат в 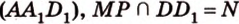 .
.
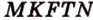 - искомое сечение.
- искомое сечение.
Пример №12 Постройте сечение куба плоскостью, проходящей через точки 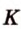 ,
, 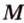 ,
, 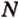 , которые принадлежат соответственно ребрам
, которые принадлежат соответственно ребрам  ,
,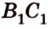 ,
, 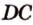 .
.
Построение
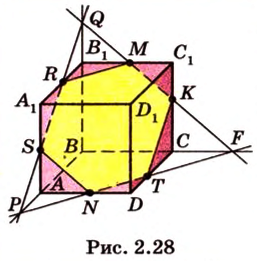
Секущая плоскость 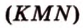 (рис. 2.28).
(рис. 2.28).
Точки 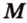 ,
, 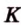 лежат в
лежат в  ,
, 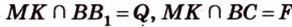 .
.
Точки 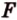 и
и 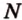 лежат в
лежат в 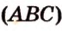 ,
, 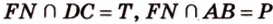 .
.
Точки 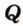 и
и 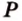 лежат в
лежат в 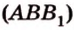 ,
, 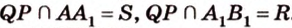 .
.
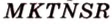 - искомое сечение.
- искомое сечение.






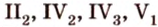 .
.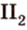 . Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости.
. Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости.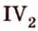 . От любой полупрямой на содержащей ее плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
. От любой полупрямой на содержащей ее плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.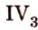 . Каков бы ни был треугольник, существует треугольник, который равен ему в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.
. Каков бы ни был треугольник, существует треугольник, который равен ему в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.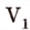 ,. На плоскости через данную точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.
,. На плоскости через данную точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.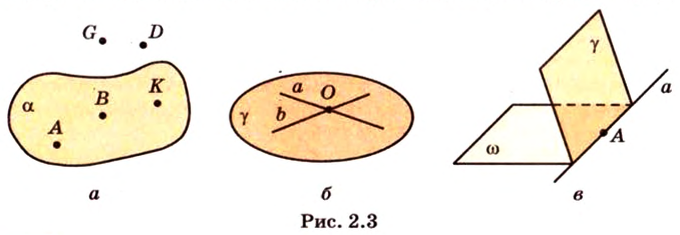
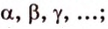 точки - большими буквами латинского алфавита -
точки - большими буквами латинского алфавита - 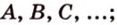 прямые - малыми буквами латинского алфавита -
прямые - малыми буквами латинского алфавита - 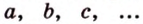 или двумя прописными буквами латинского алфавита -
или двумя прописными буквами латинского алфавита - 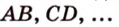 .
. принадлежит,
принадлежит, 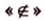 - не принадлежит,
- не принадлежит,  - подмножество и т.д. Краткие записи взаимного расположения точек, прямых и плоскостей:
- подмножество и т.д. Краткие записи взаимного расположения точек, прямых и плоскостей: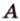 принадлежит прямой
принадлежит прямой 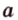 (точка
(точка 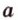 , прямая
, прямая 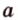 проходит через точку
проходит через точку 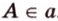 .
.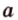 (точка
(точка 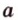 , прямая
, прямая 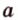 не проходит через точку
не проходит через точку 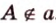 .
.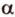 (точка
(точка 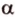 , плоскость
, плоскость 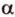 проходит через точку
проходит через точку 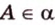 .
.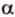 (прямая
(прямая 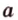 лежит на плоскости
лежит на плоскости 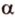 , плоскость
, плоскость 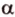 проходит через прямую
проходит через прямую 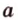 ). Обозначение:
). Обозначение:  .
.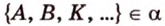 и точки
и точки 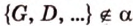 .
.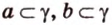 и
и 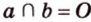 , то
, то 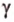 - единственная.
- единственная.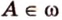 и и
и и  , то
, то 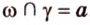 , причем
, причем 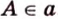 .
.
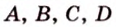 не лежат на одной плоскости. Докажите, что прямые
не лежат на одной плоскости. Докажите, что прямые 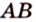 и
и 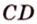 не пересекаются.
не пересекаются.
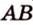 и
и 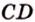 пересекаются (рис. 2.5).
пересекаются (рис. 2.5).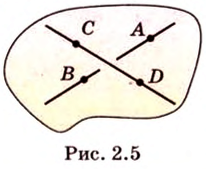
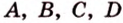 также принадлежат этой плоскости, что противоречит условию. Предположение неверно. Прямые
также принадлежат этой плоскости, что противоречит условию. Предположение неверно. Прямые 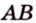 и
и 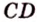 не пересекаются, что и требовалось доказать.
Заметим, что школьный курс геометрии посвящен евклидовой геометрии. Несмотря на то что с течением времени геометрия Евклида была существенно дополнена и откорректирована, ее по-прежнему называют именем древнего ученого. Такое уважение вызвано широтой практического применения евклидовой геометрии. Она используется в технических науках, картографии, геодезии, астрономии и др.
не пересекаются, что и требовалось доказать.
Заметим, что школьный курс геометрии посвящен евклидовой геометрии. Несмотря на то что с течением времени геометрия Евклида была существенно дополнена и откорректирована, ее по-прежнему называют именем древнего ученого. Такое уважение вызвано широтой практического применения евклидовой геометрии. Она используется в технических науках, картографии, геодезии, астрономии и др.
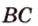 - данная прямая и
- данная прямая и 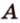 - точка, не принадлежащая ей (рис. 2.9). Через точки
- точка, не принадлежащая ей (рис. 2.9). Через точки 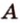 и
и 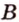 проведем прямую
проведем прямую 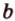 . Прямые
. Прямые 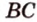 и
и 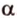 . Докажем, что она единственная, методом от противного.
. Докажем, что она единственная, методом от противного.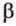 , которая содержит прямую
, которая содержит прямую 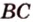 и точку
и точку 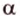 и
и 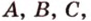 что противоречит условию. Предположение неверно. Плоскость
что противоречит условию. Предположение неверно. Плоскость 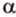 - единственная. Теорема доказана.
- единственная. Теорема доказана.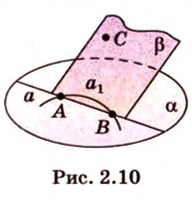
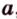 , плоскость
, плоскость 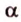 и точки А и В прямой
и точки А и В прямой 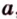 , принадлежащие
, принадлежащие 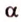 (рис. 2.10). Выберем точку С, которая не принадлежит прямой
(рис. 2.10). Выберем точку С, которая не принадлежит прямой 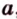 . Через точку С и прямую
. Через точку С и прямую 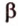 . Если
. Если 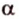 и
и 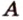 и
и 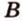 , то они пересекаются по прямой
, то они пересекаются по прямой 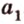 , содержащей эти точки. Поэтому через две точки
, содержащей эти точки. Поэтому через две точки 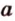 и
и 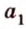 , что противоречит аксиоме принадлежности I2. Поэтому
, что противоречит аксиоме принадлежности I2. Поэтому 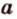 и
и 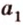 - совпадают. Однако поскольку
- совпадают. Однако поскольку 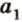 , принадлежит плоскости
, принадлежит плоскости 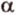 , то и прямая
, то и прямая 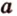 также принадлежит
также принадлежит 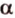 .
.
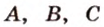 - заданные точки (рис. 2.11). Проведем через точки
- заданные точки (рис. 2.11). Проведем через точки 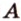 и
и 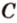 прямую
прямую 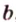 , а через точки
, а через точки 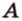 и
и 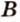 - прямую
- прямую 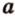 . Прямые
. Прямые 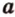 и
и 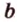 различны и имеют общую точку
различны и имеют общую точку 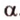 . Докажем, что она единственная, методом от противного. Допустим, что существует другая плоскость
. Докажем, что она единственная, методом от противного. Допустим, что существует другая плоскость 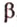 , содержащая точки
, содержащая точки 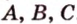 . Тогда, по теореме 2, прямые
. Тогда, по теореме 2, прямые 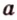 и
и 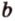 принадлежат плоскости
принадлежат плоскости 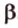 . Поэтому плоскости
. Поэтому плоскости 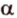 и
и 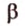 имеют две общие прямые
имеют две общие прямые 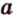 и
и 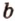 , которые пересекаются, что противоречит аксиоме II3. Итак, плоскость
, которые пересекаются, что противоречит аксиоме II3. Итак, плоскость 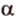 - единственная. Теорема доказана.
- единственная. Теорема доказана.
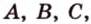 то в таком случае пользуются обозначением: (
то в таком случае пользуются обозначением: (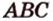 ). Читается: «плоскость, заданная точками
). Читается: «плоскость, заданная точками 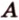 ,
, 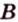 и
и 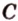 », или сокращенно «плоскость
», или сокращенно «плоскость 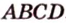 , то выбирают запись плоскости произвольной тройкой его вершин. Например, (
, то выбирают запись плоскости произвольной тройкой его вершин. Например, (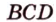 ), (
), (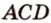 ) или (
) или (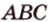 ). Однако иногда в записи плоскости оставляют все четыре вершины, например (
). Однако иногда в записи плоскости оставляют все четыре вершины, например (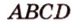 ).
).
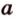 и
и 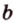 (рис. 2.12), которые имеют общую точку
(рис. 2.12), которые имеют общую точку 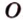 , можно провести плоскость
, можно провести плоскость 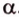 . Возьмем точку
. Возьмем точку 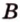 , которая не принадлежит
, которая не принадлежит 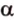 . Через точки
. Через точки 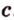 . Прямая
. Прямая 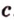 не лежит на плоскости
не лежит на плоскости 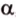 , так как если бы прямая
, так как если бы прямая 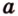 и
и 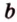 можно провести третью прямую, которая не лежит с ними в одной плоскости. Ответ. Можно.
можно провести третью прямую, которая не лежит с ними в одной плоскости. Ответ. Можно.
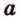 и
и 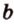 параллельны, то по определению эти прямые лежат в одной плоскости
параллельны, то по определению эти прямые лежат в одной плоскости 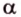 (рис. 2.13). Произвольная прямая
(рис. 2.13). Произвольная прямая 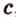 , пересекающая
, пересекающая 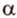 . Следовательно, все прямые, пересекающие две параллельные прямые, лежат в одной плоскости, что и требовалось доказать.
. Следовательно, все прямые, пересекающие две параллельные прямые, лежат в одной плоскости, что и требовалось доказать.
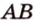 и
и 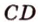 не лежат в одной плоскости, то прямые
не лежат в одной плоскости, то прямые 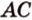 и
и 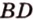 также не лежат в одной плоскости.
также не лежат в одной плоскости.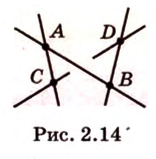
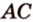 и
и 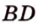 лежат в одной плоскости (рис. 2.14). Тогда точки
лежат в одной плоскости (рис. 2.14). Тогда точки 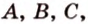
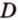 принадлежат этой плоскости, а следовательно, прямые
принадлежат этой плоскости, а следовательно, прямые 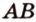 и
и 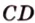 принадлежат этой плоскости, что противоречит условию. Предположение неверно, поэтому прямые
принадлежат этой плоскости, что противоречит условию. Предположение неверно, поэтому прямые 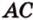 и
и 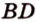 не принадлежат одной плоскости, что и требовалось доказать.
не принадлежат одной плоскости, что и требовалось доказать.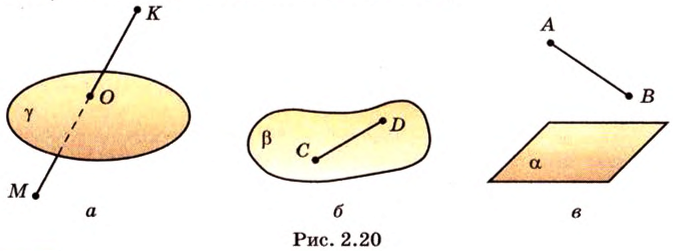
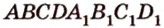 - заданный куб (рис. 2.22). Выберем одну из вершин, например
- заданный куб (рис. 2.22). Выберем одну из вершин, например 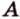 , являющуюся общей для трех ребер
, являющуюся общей для трех ребер 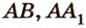 и
и 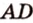 . Обозначим на этих ребрах точки
. Обозначим на этих ребрах точки 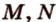 и
и 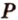 соответственно, являющиеся их серединами. Точки
соответственно, являющиеся их серединами. Точки 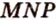 ). Точки
). Точки 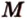 и
и 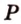 - общие точки плоскости сечения и грани
- общие точки плоскости сечения и грани 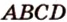 , поэтому
, поэтому 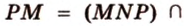
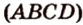 ,
, 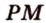 - сторона сечения.
Аналогично
- сторона сечения.
Аналогично 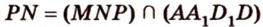 и
и 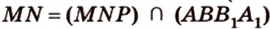 , поэтому
, поэтому 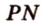 и
и 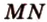 - две другие стороны сечения. Таким образом,
- две другие стороны сечения. Таким образом, 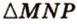 - искомое сечение.
- искомое сечение.
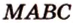 плоскостью, которая проходит через ребро
плоскостью, которая проходит через ребро 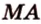 и середину ребра
и середину ребра 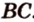 .
.
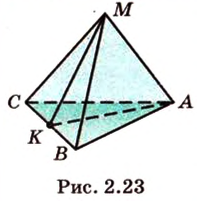
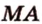 и серединой ребра
и серединой ребра 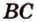 (обозначим ее точкой
(обозначим ее точкой 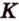 ) (рис. 2.23). (МАК) - плоскость сечения. Найдем прямые пересечения
этой плоскости с плоскостями (
) (рис. 2.23). (МАК) - плоскость сечения. Найдем прямые пересечения
этой плоскости с плоскостями (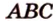 ) и (
) и (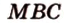 ). Ими будут соответствующие прямые
). Ими будут соответствующие прямые 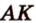 и
и 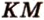 , а
, а 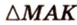 , образованный пересечением прямых
, образованный пересечением прямых 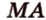 ,
,  и
и 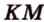 , - искомое сечение.
, - искомое сечение. плоскостью, проходящей через три точки, которые лежат соответственно на ребрах
плоскостью, проходящей через три точки, которые лежат соответственно на ребрах 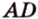 ,
, 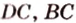 .
.
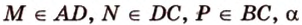 - секущая плоскость, проходящая через заданные точки
- секущая плоскость, проходящая через заданные точки 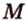 ,
, 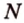 и
и 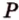 . Построим сечение, выполняя последовательно шаги:
. Построим сечение, выполняя последовательно шаги: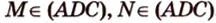 , тогда
, тогда 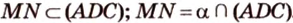 .
.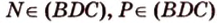 , тогда
, тогда 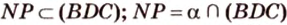 .
.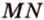 и
и 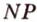 (рис. 2.24, а). Точка
(рис. 2.24, а). Точка 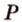 - общая точка двух плоскостей (
- общая точка двух плоскостей (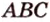 ) и (
) и (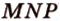 ). Такие плоскости (по аксиоме II4) пересекаются по прямой, проходящей через точку
). Такие плоскости (по аксиоме II4) пересекаются по прямой, проходящей через точку 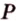 . Для построения такой прямой нужна вторая точка.
. Для построения такой прямой нужна вторая точка.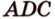 ) и (
) и (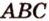 ) пересекаются по прямой
) пересекаются по прямой 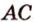 .
. 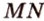 по условию не параллельна
по условию не параллельна 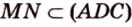 , поэтому
, поэтому 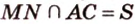 (рис. 2.24, б).
4. Прямая
(рис. 2.24, б).
4. Прямая 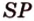 - линия пересечения плоскостей (
- линия пересечения плоскостей (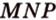 ) и (
) и (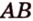 дает точку
дает точку 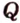 , которая является вершиной сечения. Таким образом, четырехугольник
, которая является вершиной сечения. Таким образом, четырехугольник 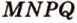 - искомое сечение (рис. 2.24, в).
- искомое сечение (рис. 2.24, в).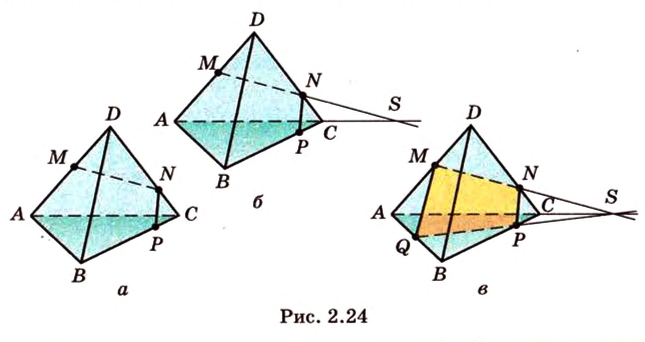
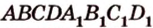 плоскостью, проходящей через середины
плоскостью, проходящей через середины 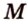 и
и 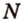 ребер
ребер 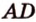 и
и 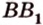 и точку
и точку 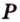 пересечения диагоналей грани (рис. 2.25, а).
пересечения диагоналей грани (рис. 2.25, а).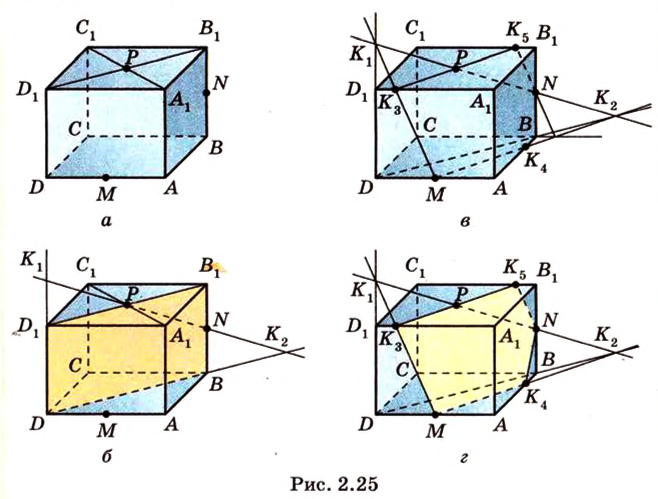
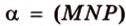 . Выполним последовательно шаги, выполняя поиск фигуры, образованной плоскостью сечения.
. Выполним последовательно шаги, выполняя поиск фигуры, образованной плоскостью сечения.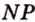 с плоскостью (
с плоскостью (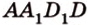 ). Эта прямая лежит в плоскости (
). Эта прямая лежит в плоскости (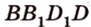 ), пересекающейся с плоскостью (
), пересекающейся с плоскостью (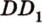 . Точка
. Точка 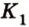 - точка пересечения прямых
- точка пересечения прямых 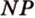 и
и 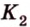 как точку пересечения прямой
как точку пересечения прямой 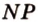 с плоскостью (
с плоскостью (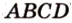 ). Точка
). Точка 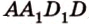 ) по прямой
) по прямой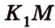 , а плоскость (
, а плоскость (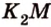 . Прямые
. Прямые 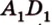 и
и 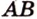 в точках
в точках 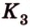 и
и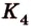 соответственно (рис. 2.25, в).
соответственно (рис. 2.25, в).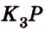 пересекает ребро прямоугольного параллелепипеда
пересекает ребро прямоугольного параллелепипеда 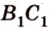 в некоторой точке
в некоторой точке 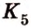 - последней вершине сечения (рис. 2.25, в).
- последней вершине сечения (рис. 2.25, в).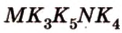 - искомое сечение (рис. 2.25, г).
Приведем краткие описания построения сечения куба плоскостью, проходящей через три точки.
- искомое сечение (рис. 2.25, г).
Приведем краткие описания построения сечения куба плоскостью, проходящей через три точки.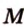 ,
, 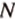 ,
, 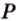 , которые принадлежат соответственно ребрам
, которые принадлежат соответственно ребрам 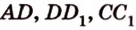 .
.
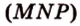 ) (рис. 2.26).
) (рис. 2.26).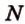 и
и 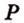 лежат в
лежат в 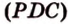 . Проведем прямую
. Проведем прямую 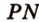 ,
, 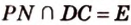 .
.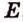 ,
, 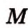 лежат в
лежат в 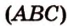 . Проведем прямую
. Проведем прямую 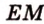 ,
, 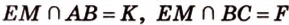 .
.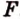 ,
, 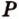 лежат в
лежат в 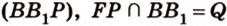 .
. - искомое сечение.
- искомое сечение.
 ,
,  .
.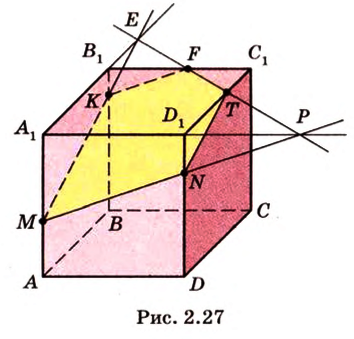
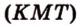 (рис. 2.27).
(рис. 2.27).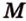 и
и 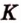 лежат в
лежат в 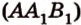 ,
, 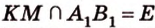 .
.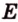 ,
, 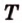 лежат в
лежат в 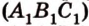 ,
, 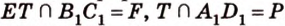 .
.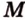 ,
, 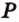 лежат в
лежат в 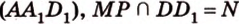 .
.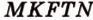 - искомое сечение.
- искомое сечение.
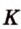 ,
, 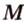 ,
, 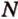 , которые принадлежат соответственно ребрам
, которые принадлежат соответственно ребрам 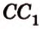 ,
,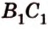 ,
, 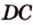 .
.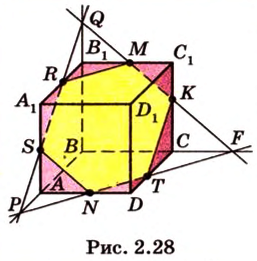
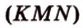 (рис. 2.28).
(рис. 2.28).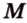 ,
, 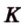 лежат в
лежат в 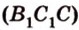 ,
, 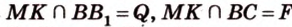 .
.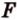 и
и 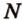 лежат в
лежат в 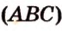 ,
, 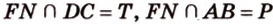 .
.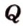 и
и 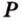 лежат в
лежат в 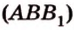 ,
, 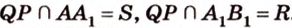 .
. - искомое сечение.
- искомое сечение.

































