Презентация к уроку: "Стереометрия"

Стереометрия. Основные понятия стереометрии. Аксиомы стереометрии.

Содержание

• Что такое стереометрия?
• Возникновение и развитие стереометрии
• Основные фигуры в пространстве
• Обозначение точек и примеры их моделей
• Обозначение прямых
• Примеры моделей прямых
• Обозначение плоскостей и примеры их моделей
• Что еще изучает стереометрия?
• Окружающие нас предметы и геометрические тела
• Изображение геометрических тел на чертежах
• Практическое (прикладное) значение стереометрии
• Аксиомы стереометрии
• Следствия из аксиом стереометрии
• Закрепление
• Используемая литература

Что такое стереометрия?

Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве.

к содержанию

Возникновение и развитие стереометрии.

• Развитие стереометрии началось значительно позднее планиметрии.
• Стереометрия развивалась из наблюдений и решений вопросов, которые возникали в процессе практической деятельности человека.

к содержанию

• Уже первобытный человек, занявшись земледелием, делал попытки оценивать, хотя бы в грубых чертах, размер собранного им урожая по массам хлеба, сложенного в кучи, копны или скирды.
• Строитель даже самых древних примитивных построек должен был как-то учитывать материал, которым он располагал, и и уметь подсчитать, сколько материала потребуется для возведения той или иной постройки.

к содержанию

• Каменотесное дело у древних египтян и халдеев требовало знакомства с метрическими свойствами хотя бы простейших геометрических тел.
• Потребность земледелия, мореплавания, ориентировки во времени толкали людей к астрономическим наблюдениям, а последние – к изучению свойств сферы и её частей, а следовательно и законов взаимного расположения плоскостей и линий в пространстве.

к содержанию

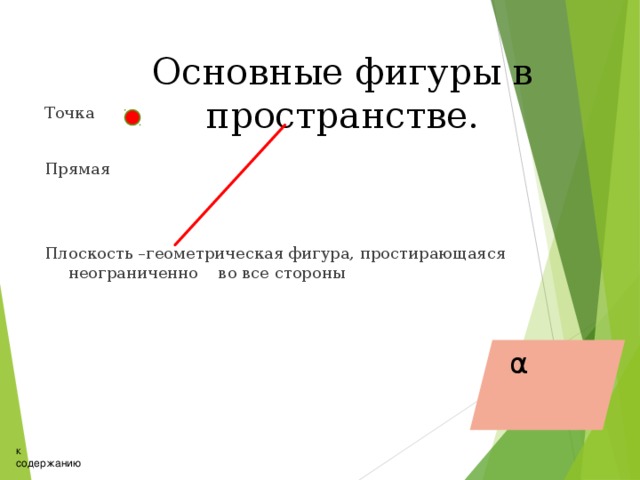
Основные фигуры в пространстве.

Точка

Прямая

Плоскость –геометрическая фигура, простирающаяся неограниченно во все стороны

α

к содержанию

Обозначение точек и примеры их моделей.

Точки обозначаются прописными латинскими буквами А, В, С, …

Примерами моделей точек являются:

атомы и молекулы

планеты в масштабах вселенной

А

С

В

к содержанию

Обозначение прямых.

• Прямые обозначаются :
• строчными латинскими буквами a, b, c, d, e, k, …
• двумя заглавными латинскими буквами AB, CD …

а

A

B

к содержанию

Примеры моделей прямых.

Примерами моделей прямых могут служить:

инверсионные следы самолетов

рельсы

к содержанию

Обозначение плоскостей и примеры их моделей.

Плоскости обозначаются греческими буквами α, β, γ,…

Примерами моделей плоскостей могут служить:

поверхность воды

поверхность стола

α

β

к содержанию

Что еще изучает стереометрия?

На ряду с точкой, прямой и плоскостью стереометрия изучает геометрические тела и их поверхности.

к содержанию

Окружающие нас предметы и геометрические тела.

Окружающие нас предметы дают представления о геометрических телах.

А изучая свойства геометрических фигур – воображаемых объектов, мы получаем сведения о геометрических свойствах реальных предметов и можем использовать эти свойства в практической деятельности.

кристаллы- многогранники

жестяная банка - цилиндр

мяч - шар

упаковка для конфет - конус

к содержанию

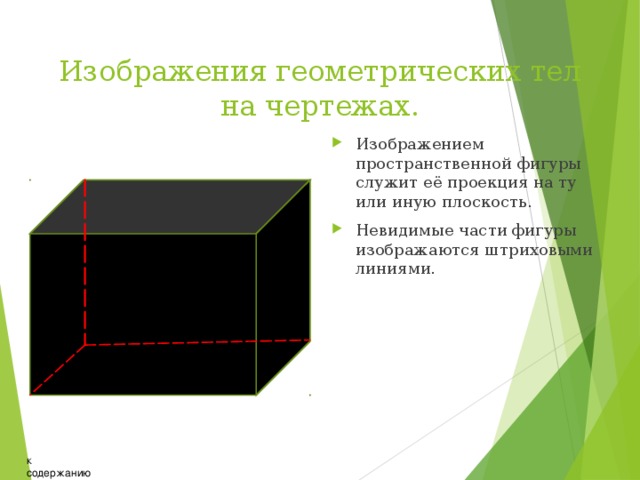
Изображения геометрических тел на чертежах.

• Изображением пространственной фигуры служит её проекция на ту или иную плоскость.
• Невидимые части фигуры изображаются штриховыми линиями.

к содержанию

Практическое (прикладное) значение стереометрии.

• Геометрические тела являются вымышленными объектами
• Изучая свойства геометрических фигур, мы получаем представления о геометрических свойствах реальных предметов (их форме, взаимном расположении и т.д.)
• Стереометрия широко используется в строительном деле, архитектуре, машиностроении и других областях науки и техники

к содержанию

Аксиомы стереометрии.

• Аксиома – это утверждение о свойствах геометрических фигур, принимается в качестве исходных положений, на основе которых доказываются далее теоремы и вообще строится вся геометрия.

к содержанию

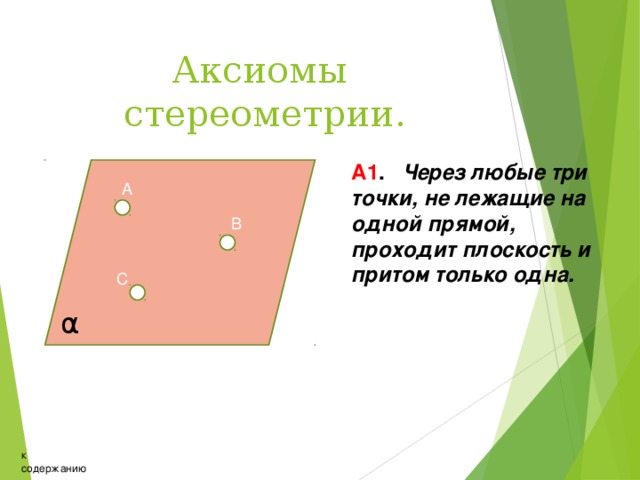
Аксиомы стереометрии.

А1 . Через любые три точки, не лежащие на одной прямой, проходит плоскость и притом только одна.

А

В

С

α

к содержанию

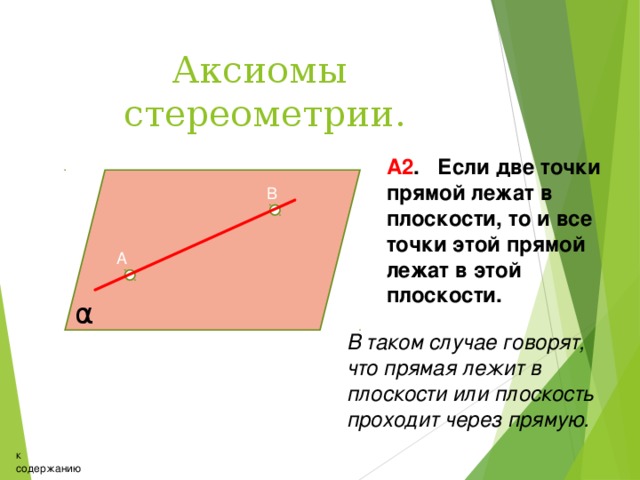
Аксиомы стереометрии.

А2 . Если две точки прямой лежат в плоскости, то и все точки этой прямой лежат в этой плоскости.

В

А

α

В таком случае говорят, что прямая лежит в плоскости или плоскость проходит через прямую.

к содержанию

Аксиомы стереометрии.

β

А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Говорят, что плоскости пересекаются по прямой

α

А

а

к содержанию

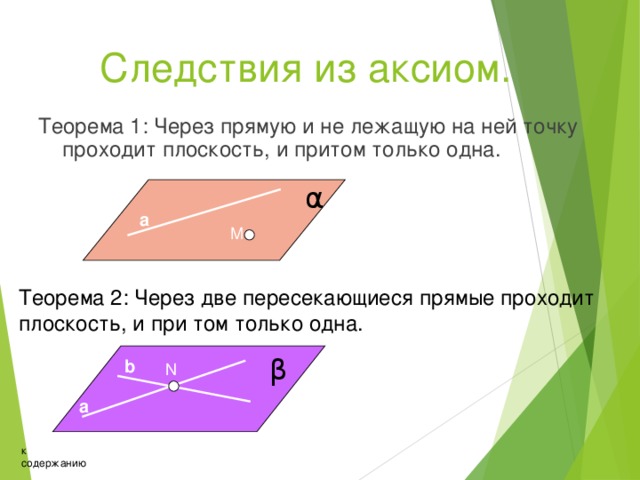
Следствия из аксиом.

Теорема 1: Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

α

а

М

Теорема 2: Через две пересекающиеся прямые проходит плоскость, и при том только одна.

β

b

N

а

к содержанию

Закрепление.

1.Назовите плоскости, в которых лежат прямые:

а) PE;

б) DB;

в) AB;

г) EC.

D

P

A

C

E

B

к содержанию

Закрепление.

2. Назовите точку пересечения прямой СE с плоскостью ADB.

3. Назовите прямые, по которым пересекаются плоскости:

а) ABC и DCB;

б) ABD и CDA;

D

P

C

A

E

B

к содержанию

Используемая литература

• Геометрия. 10-11 классы: учеб. Для общеобразоват. учреждений: базовый и профил. уровни/Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 21-е изд. – М.: Просвещение, 2012.- 255 с.: ил.
• Геометрия: методическое пособие для высших педагогических заведений и преподавателей средней школы: ч. 2 Стереометрия/ под ред. Проф. И.К. Андронова.

к содержанию