Числовые ряды
Числовой ряд – это выражение вида 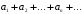 Числа
Числа 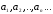 называются членами ряда. Они образуют бесконечную последовательность.
называются членами ряда. Они образуют бесконечную последовательность.
Общий член ряда – это член 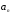 с произвольным номером. Сокращенно ряд обозначают следующим образом:
с произвольным номером. Сокращенно ряд обозначают следующим образом: 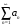 .
.
Частичные суммы ряда – это суммы конечного числа членов ряда.
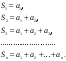
Пример: Дан ряд  . Найти
. Найти  .
.
Решение: 1)  .
.
2) 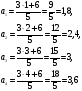
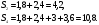
Ответ: 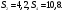
ЗАДАНИЕ! Дан числовой ряд 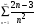 . Найти
. Найти  .
.
Сходящийся ряд – это ряд, у которого последовательность его частичных сумм имеет конечный предел при 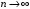 :
: 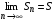 .
.
Сумма ряда – это число S, к которому сходится эта последовательность частичных сумм: 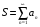 . Ряд называется расходящимся, если такой предел
. Ряд называется расходящимся, если такой предел  не существует или бесконечен.
не существует или бесконечен.
Пример 1. Исследовать на сходимость ряд  .
.
Решение: 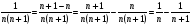 .
.
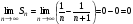 . Этот предел существует, и ряд сходится.
. Этот предел существует, и ряд сходится.
Признаки сходимости ряда
Необходимый признак сходимости: Если ряд 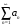 сходится, то общий член ряда
сходится, то общий член ряда 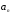 стремится к нулю при неограниченном возрастании n (при
стремится к нулю при неограниченном возрастании n (при 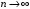 ).
). 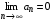 .
.
Следствие: Если общий член 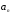 ряда,
ряда, 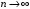 не стремится к нулю, то такой ряд расходится. Если
не стремится к нулю, то такой ряд расходится. Если  , то ряд
, то ряд 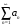 расходится.
расходится.
Признак Даламбера: Пусть дан ряд 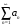 с положительными членами. Если для этого ряда существует конечный предел
с положительными членами. Если для этого ряда существует конечный предел  , то при p ряд сходится, а при p 1 ряд расходится. (При p = 1 вопрос о сходимости ряда остается нерешенным в этом случае требуется исследовать ряд с помощью других методов).
, то при p ряд сходится, а при p 1 ряд расходится. (При p = 1 вопрос о сходимости ряда остается нерешенным в этом случае требуется исследовать ряд с помощью других методов).
Признак Коши: Пусть дан ряд 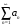 с положительными членами. Если для этого ряда существует предел
с положительными членами. Если для этого ряда существует предел  , то при q ряд сходится, а при q 1 ряд расходится. (При q = 1 вопрос о сходимости ряда остается нерешенным в этом случае требуется исследовать ряд с помощью других методов).
, то при q ряд сходится, а при q 1 ряд расходится. (При q = 1 вопрос о сходимости ряда остается нерешенным в этом случае требуется исследовать ряд с помощью других методов).
Пример 2. Исследовать ряд по необходимому признаку  .
.
Решение: Находим


 .
.
Следовательно, ряд расходится.
Пример 3. Исследовать ряд по признаку Даламбера  .
.
Решение:  ,
,  . Найдем
. Найдем  .
.
Найдем
Следовательно, ряд расходится.
Пример 4. Исследовать ряд по признаку Коши  .
.
Решение:
Следовательно, ряд сходится.
ЗАДАНИЕ!
Исследовать ряд на сходимость по необходимому признаку  .
.
Исследовать ряд на сходимость по признаку Даламбера  .
.
Исследовать рад на сходимость по признаку Коши  .
.
Знакопеременные ряды – это ряды, содержащие как положительные, так и отрицательные члены.
Пусть дан знакопеременный ряд 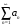 . С каждым таким рядом связан ряд с неотрицательными членами, составленный из модулей членов данного ряда, т.е. ряд
. С каждым таким рядом связан ряд с неотрицательными членами, составленный из модулей членов данного ряда, т.е. ряд


Теорема. Если сходится ряд  , то сходится и ряд
, то сходится и ряд 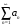 .
.
Абсолютная сходимость: знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов.
Знакочередующийся ряд – это ряд, в котором положительные и отрицательные члены следуют друг за другом поочередно.
Например, это ряд вида:  , где
, где 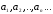 - положительные числа.
- положительные числа.
Для знакочередующихся рядов имеет место следующий достаточный признак сходимости.
Признак Лейбница. Ряд  сходится, если его члены монотонно убывают по абсолютной величине
сходится, если его члены монотонно убывают по абсолютной величине  и общий член ряда стремится к нулю при
и общий член ряда стремится к нулю при 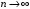 :
: 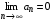 .
.
Функциональные ряды
Функциональный ряд – это выражение вида  , где
, где  ,
,  , …,
, …,  , … - члены ряда – некоторая последовательность функций от х.
, … - члены ряда – некоторая последовательность функций от х.
Если в данном функциональном ряде положить  , где
, где  - некоторое число, то получим числовой ряд.
- некоторое число, то получим числовой ряд.
 При одних значениях х ряд может сходиться, а при других – расходиться.
При одних значениях х ряд может сходиться, а при других – расходиться.
Функциональный ряд называется сходящимся в точке  , если при
, если при  он обращается в сходящийся числовой ряд.
он обращается в сходящийся числовой ряд.
Если же при  получается расходящийся числовой ряд, то ряд называется расходящимся в точке
получается расходящийся числовой ряд, то ряд называется расходящимся в точке  .
.
Область сходимости функционального ряда – это совокупность всех значений  , при которых ряд сходится.
, при которых ряд сходится.
Степенной ряд – это функциональный ряд вида:
где  - переменная,
- переменная,  - некоторое число. Числа
- некоторое число. Числа  называются коэффициентами ряда.
называются коэффициентами ряда.
Если  , то ряд примет вид:
, то ряд примет вид:

Область сходимости степенного ряда – это совокупность вех значений  , при которых ряд сходится.
, при которых ряд сходится.
Радиусом сходимости степенного ряда называется число R, вычисляемое по формуле  .
.
Интервал сходимости ряда – это интервал  . Если
. Если  , то интервал сходимости
, то интервал сходимости  . Если ряд сходится на всей числовой прямой, то пишут
. Если ряд сходится на всей числовой прямой, то пишут  . Если расходится только при
. Если расходится только при  , то пишут
, то пишут  .
.
Пример 5. Дан ряд  Чему равен радиус сходимости?
Чему равен радиус сходимости?
Решение: Здесь  ,
,  . Тогда
. Тогда 
 .
.
Если функция  определена в некоторой точке
определена в некоторой точке  и имеет производные всех порядков в этой точке, то степенной ряд вида:
и имеет производные всех порядков в этой точке, то степенной ряд вида:
называется рядом Тейлора для функции  в точке
в точке  .
.
Если  , то получается ряд
, то получается ряд  , который называется рядом Маклорена.
, который называется рядом Маклорена.
Алгоритм представления элементарной функции в виде суммы ряда Тейлора (Маклорена)
Вычислить последовательные производные данной функции в точке  .
.
Составить ряд Тейлора (Маклорена) для функции, используя формулу
Определить промежуток сходимости полученного ряда.
В этом промежутке ряд Тейлора (Маклорена) сходимости к порождающей его функции  , если только все значения
, если только все значения  получаются непосредственной подстановкой значения
получаются непосредственной подстановкой значения  в выражения для функции
в выражения для функции  и ее производных
и ее производных 
Применяя этот алгоритм, найдем разложение функции  :
:
 При
При  получаем
получаем
Составим ряд Маклорена:

Найдем интервал сходимости ряда  .
.
Вывод: ряд абсолютно сходится по всей числовой прямой.
Покажем, что ряд  имеет своей суммой
имеет своей суммой  . Согласно необходимому условию сходимости ряда для любого х справедливо равенство:
. Согласно необходимому условию сходимости ряда для любого х справедливо равенство:
 и
и  .
.
Следовательно, функция  является суммой ряда
является суммой ряда 
Таким образом, при любом х имеет место:
.
2







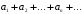 Числа
Числа 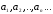 называются членами ряда. Они образуют бесконечную последовательность.
называются членами ряда. Они образуют бесконечную последовательность. 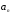 с произвольным номером. Сокращенно ряд обозначают следующим образом:
с произвольным номером. Сокращенно ряд обозначают следующим образом: 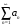 .
.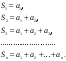
 . Найти
. Найти  .
. .
.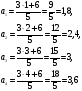
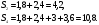
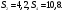
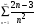 . Найти
. Найти  .
.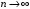 :
: 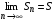 .
.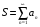 . Ряд называется расходящимся, если такой предел
. Ряд называется расходящимся, если такой предел  не существует или бесконечен.
не существует или бесконечен. .
.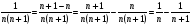 .
.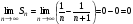 . Этот предел существует, и ряд сходится.
. Этот предел существует, и ряд сходится.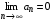 .
.









